Abstract
Traffic sign classification (TSC) based on deep neural networks (DNNs) plays a crucial role in the perception subsystem of autonomous driving systems (ADSs). However, studies reveal that the TSC system can make dangerous and potentially fatal errors under adversarial attacks. Existing defense strategies, such as adversarial training (AT), have demonstrated effectiveness but struggle to generalize across diverse attack scenarios. Recent advancements in self-supervised learning (SSL), particularly adversarial contrastive learning (ACL) methods, have demonstrated strong potential in enhancing robustness and generalization compared to AT. However, conventional ACL methods lack mechanisms to ensure effective defense transferability across different learning stages. To address this, we propose a robust pre-training–fine-tuning algorithm for meta-adversarial defense (RPF-MAD), designed to enhance the sustainability of adversarial robustness throughout the learning pipeline. Dual-track meta-adversarial pre-training (Dual-MAP) integrates meta-learning with ACL methods, which improves the generalization ability of the upstream model to different adversarial conditions. Meanwhile, adaptive variance anchoring robust fine-tuning (AVA-RFT) utilizes adaptive prototype variance regularization to stabilize feature representations and reinforce the generalizable defense capabilities of the downstream model. Leveraging the meta-adversarial defense benchmark (MAD) dataset, RPF-MAD ensures comprehensive robustness against multiple attack types. Extensive experiments across eight ACL methods and three robust fine-tuning (RFT) techniques demonstrate that RPF-MAD significantly improves both standard accuracy () by 1.53% and robust accuracy () by 2.64%, effectively enhances the lifelong adversarial resilience of TSC models, achieves a 13.77% improvement in the equilibrium defense success rate (), and reduces the attack success rate () by 9.74%, outperforming state-of-the-art (SOTA) defense methods.
1. Introduction
With the growing maturity of autonomous driving technology, ensuring the robustness of ADS has become a key research focus [1,2]. As a core multimodal interface, the TSC module performs hierarchical visual–semantic parsing via DNNs to interpret regulatory instructions and guide real-time driving policies [1,2,3,4]. Enhanced by adaptive feature disentanglement mechanisms [5], TSC balances robustness and decision granularity. However, numerous studies have demonstrated that subtle adversarial examples (AEs) [6] can mislead TSC models, posing potentially fatal risks [7,8,9]. This challenge has motivated researchers to prioritize the development of robust and effective defense mechanisms for TSC systems.
Pavlitska et al. [10] offered a comprehensive overview of attacks on TSC systems, while highlighting a significant research gap in adversarial defense strategies. Our analysis of recent defense approaches reveals that most of them focus on input transformation [11,12,13,14,15,16,17] and detection-based methods [18,19,20]. For digital defenses, Wu et al. [13] utilized 5G capabilities and mobile edge computing with singular value decomposition to mitigate perturbations from traditional attacks such as CW [21], DeepFool [22], and I-FGSM [23]. Inspired by attention mechanisms, Li et al. [14] employed a CNN to extract affine coordinates and filter pixels to counter various attacks. Salek et al. [15] explored the use of GANs for AE denoising, though it suffers from poor transferability. Suri et al. [16] proposed a bit-plane isolation system, utilizing a voting mechanism across models for defense, though it demands significant resources. Huang et al. [20] used a deep image prior combined with U-Net for image reconstruction, employing a multi-stage decision-making mechanism to defend against physical AEs targeting traffic signs. Collectively, these studies indicate that current defense strategies are predominantly inclined to image reconstruction, neglecting the model’s inherent robustness. In contrast, AT [24] has emerged as a widely used strategy for directly enhancing model robustness. Well-designed AT schemes have demonstrated considerable success in balancing robustness and accuracy [25,26,27,28]. Therefore, a comprehensive TSC system should achieve intrinsic robustness and strong generalization through AT, while maintaining minimal resource consumption.
Inspired by the cost-effective success of parameter-efficient fine-tuning [29] in large-scale models such as GPT-3 [30,31]. The robust pre-training–fine-tuning paradigm [32] has garnered increasing attention, which consists of two stages, namely, robust pre-training (RPT) and RFT. Within this context, recent innovations in AT-based RPT techniques, such as ACL methods [33,34,35,36], have made notable contributions to robust representation learning [37,38]. Correspondingly, the following three representative RFT strategies have emerged: standard linear fine-tuning (SLF), adversarial linear fine-tuning (ALF), and adversarial full fine-tuning (AFF). These techniques have been successfully leveraged in TSC systems, yielding outstanding performance in both standard and adversarial settings [39].
Nevertheless, challenges remain, particularly with the rise of upstream attacks [40,41], where AEs generated during pre-training compromise the robustness of downstream models. To provide a more holistic evaluation of defense capabilities in TSC systems, we categorize traditional attacks such as the fast gradient sign method (FGSM) [6] and projected gradient descent (PGD) [24] as downstream attacks. Additionally, our previous work, MAD [42], introduced a benchmark dataset specifically designed to assess robustness against unknown attacks, further broadening the adversarial threat landscape considered in this study.
Motivation. Through a review of the existing defense methods against these diverse and complex attacks, we identify the following drawbacks in current research: (1) SSL-based defense benchmarks tailored to upstream attacks, such as genetic evolution-nurtured adversarial fine-tuning (Gen-AF) [39], suffer drastic performance drops when deployed on downstream tasks or unseen attack scenarios. (2) ACL methods remain vulnerable to unknown attacks, revealing limitations in robustness-oriented encoder pre-training, as shown in Figure 1. (3) Current robust pre-training–fine-tuning paradigm fails to address comprehensive security-performance trade-offs in TSC systems.
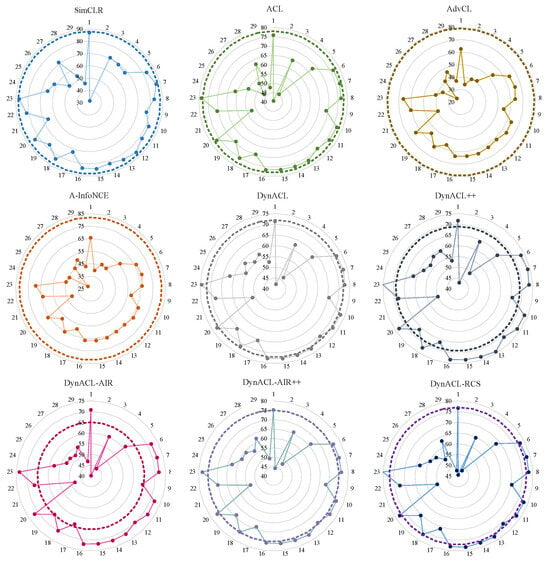
Figure 1.
(%) of SimCLR and eight robust ACL methods under different offline adversarial attacks. The dashed line represents , which indicates the intrinsic classification capability of the upstream models.
To address these limitations, we propose RPF-MAD, a robust pre-training–fine-tuning method aimed at providing comprehensive defense for TSC systems, with a focus on mitigating fundamental digital attacks. Following the widely adopted and efficient two-stage paradigm in Robust-SSL [43], we introduce targeted innovations in both the upstream and downstream stages. In the RPT phase, we proposed a Dual-MAP algorithm, which optimizes ACL strategies to reinforce SSL-based defenses. In the RFT stage, we proposed AVA-RFT, designed as an implicit manifold alignment mechanism to preserve feature space integrity and enhance the inheritance of meta-generalized defense knowledge from the upstream model. Furthermore, by integrating meta-adversarial learning during pre-training and enforcing structure-preserving fine-tuning, RPF-MAD is inherently designed to improve adaptability and resilience against future novel adversarial attacks, thereby ensuring the sustainable robustness of TSC systems even in the presence of emerging threats. The detailed framework for RPF-MAD is depicted in Figure 2. Experimental results demonstrate that the RPF-MAD optimized TSC model achieves comprehensive outstanding performance across upstream, downstream, and unknown attacks, with an average improvement of 1.53% in , 2.64% in , and 13.77% in equilibrium defense success rate (), significantly outperforming existing methods. In summary, the specific contributions of this study are as follows:
- We propose RPF-MAD as a comprehensive SSL-based defense algorithm for TSC systems, which is capable of defending against upstream, downstream, and unknown attacks.
- We introduce the Dual-MAP algorithm, which empowers upstream models to maintain inherent robustness while ensuring generalized defense capabilities.
- We propose the AVA-RFT algorithm, which preserves the structural integrity of the feature space, ensuring effective transfer of meta-learned robustness to downstream models. Extensive experiments validate the sustainability of the proposed defense mechanism and its adaptability across different attacks.
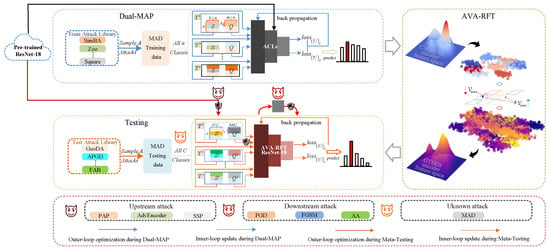
Figure 2.
Overview of RPF-MAD and classification of adversarial attacks in the pre-training–fine-tuning paradigm.
The remainder of this article is structured as follows: Section 2 reviews related work on adversarial attacks and defense strategies in TSC systems. Section 3 introduces the theoretical foundation. Section 4 details the design of RPF-MAD and key components, while Section 5 presents experimental evaluations and ablation studies. Section 6 discusses broader implications, and Section 7 concludes the study with future research directions.
2. Related Work
The following section begins by reviewing the implementation of adversarial attacks in TSC systems, highlighting their risks and providing a defense-oriented analysis. Next, we present a more detailed examination of AT-based approaches, contrasting them with earlier defense strategies to demonstrate their effectiveness and versatility. Finally, both attack and defense techniques for TSC systems are then explored through the lenses of supervised and self-supervised learning, highlighting the limitations of existing methods.
2.1. Adversarial Attacks in TSC Systems
Attacks on the supervised model. In terms of digital attacks, Papernot et al. [44] improved the white-box FGSM [6] to attack Own-CNN, while Li et al. [45] achieved black-box adversarial attacks on CNN-ST [46] by enhancing the square attack [47] and SimBA [48]. For physical attacks, Eykholt et al. [49] proposed the foundational RP2 attack, inspiring numerous subsequent methods, while Liu et al. [50] utilized GANs to create physical adversarial patches effectively. Overall, digital attacks in TSC systems primarily leverage traditional classification methods, aligning with the core principles of AEs. In contrast, physical attacks focus on crafting adversarial-sensitive patches, often exhibiting visible defects but with practical research significance.
Attacks on the self-supervised model. The rise of SSL and the widespread adoption of the pre-training–fine-tuning paradigm provided by cloud servers have shifted adversarial attacks from task-specific targets to widely used upstream pre-trained models, introducing new challenges to system robustness. A significant advancement in this area is the development of downstream-agnostic adversarial examples (DAEs) [40], designed to achieve cross-fine-tuning transferability and compromise downstream tasks. Among the SOTA methods, pre-trained adversarial perturbations (PAPs) [41] and AdvEncoder [40] have emerged as prominent techniques, demonstrating high in downstream classification tasks, particularly on the TSC systems. These sophisticated attacks underscore the urgency of broadening research into defense strategies to fortify upstream models and ensure secure downstream deployments.
2.2. Adversarial Defenses in TSC Systems
Defenses on the supervised model. Defense strategies based on AT for TSC systems have received significantly less attention than adversarial attack research. Aung et al. [51] first explored digital defenses on the GTSRB dataset using FGSM and Jacobian-based saliency map attack (JSMA) [52], showing that combining AT with defensive distillation improves robustness. However, their study lacked focus on the same network and advanced attack validation. Notably, their work indirectly supports our approach, highlighting the effectiveness of offline AEs from MAD in AT. Metzen et al. [53] proposed meta-adversarial training (MAT), integrating AT with meta-learning to dynamically generate adversarial patches, and improving robustness against universal patch attacks. However, MAT requires substantial resources, relies on online patch generation, and does not address generic digital attacks. Our goal is to establish a comprehensive robustness model for TSC systems against digital attacks, laying the groundwork for defenses against physical attacks.
Defenses on the self-supervised model. Renowned for enhancing the robustness of SSL, ACL [33] has evolved into numerous variants, including RoCL [36], AdvCL [34], DynACL [54], and ACL-RCS [55]. Despite these advancements, the impact of upstream attacks and the robustness of SSL-based TSC systems remain underexplored. Frameworks such as Gen-AF have been proposed to defend SSL models against upstream attacks. As shown in Table 1, Gen-AF achieves promising performance under upstream attack scenarios. However, models fine-tuned under such frameworks still exhibit significant vulnerabilities to sophisticated downstream attacks, such as AutoAttack (AA) [56], and to unknown threats. To address these gaps, we propose a holistic defense algorithm, RPF-MAD, which not only achieves comparable performance to Gen-AF under upstream attacks but also substantially improves robustness against downstream and unknown attacks while effectively preserving task-specific performance.

Table 1.
Performance comparison between SimCLR (Vanilla), Gen-AF (Baseline), and RPF-MAD (Our) under upstream, downstream, and unknown attacks.
3. Materials and Methods
This section provides the theoretical background and essential methodologies for robust model learning in both supervised and self-supervised modes. We first introduce the formulation of supervised RFT, followed by a detailed explanation of ACL-based RPT and corresponding RFT strategies.
3.1. Supervised Robust Fine-Tuning
Recent advancements in supervised transfer learning have increasingly concentrated on RFT, with notable methods such as TWINS [59] and AutoLoRa [60] paving the way. Additionally, Hua et al. [61] provided a comprehensive survey of various parameter-efficient fine-tuning strategies. The core principle remains consistent: fine-tuning robust pre-trained models with AT for downstream tasks [32]. The context of RFT is shown in (1):
where represents the loss function of supervised learning (SL), typically chosen as cross-entropy loss. and represent the frozen and tunable parameters, respectively. is the training pair sampled from the downstream dataset , and denotes an adversarial perturbation constrained by its r-norm with a bound of . Normally, adversarial perturbations are generated using the PGD-10 with , step size , and .
3.2. Self-Supervised Robust Pre-training–Fine-tuning
Contrastive learning (CL) is a self-supervised paradigm that learns generalizable feature representations by maximizing positive sample similarity and minimizing negative sample similarity, reducing reliance on labeled data. ACL methods incorporate AEs into CL methods, enhance the robustness of pre-trained models, and facilitate the transferability of adversarial resilience to downstream tasks. Analogous to the role of AT in SL, the fundamental formulation of ACL methods is as follows:
Here, denotes the dataset from which samples x are drawn, while represents the positive sample set. AEs are incorporated into , where represents a view of used to generate AEs. Variations among ACL methods primarily lie in the choice of contrastive loss (), while other AE-related settings align with vanilla AT.
The pre-training–fine-tuning paradigm in Robust-SL involves loading AT-trained checkpoints derived from large-scale datasets [32], with innovations predominantly concentrated in RFT techniques. In contrast, Robust-SSL emphasizes enhancing downstream robustness through refined RPT, ensuring seamless adversarial resilience transfer while integrating diverse RFT strategies.
SLF trains a linear classifier () atop a frozen pre-trained feature extractor () using clean examples. By freezing the encoder, SLF preserves the pre-trained representations and adheres to SSL principles by restricting gradient updates to the classifier. The objective is to minimize the supervised loss with respect to the true labels y, as shown below:
ALF extends SLF by training on AEs leveraging principles of AT while keeping remains frozen. The optimization objective is defined as follows:
AFF generalizes ALF by jointly updating both and on AEs. This approach enhances robustness and generalization, making it one of the most effective fine-tuning strategies. The training objective is expressed as follows:
Standard full fine-tuning (SFF), which updates both the classifier and the feature extractor on clean examples, is excluded due to its inferior performance in robust settings [62].
The use of robust weight initialization derived from SSL models significantly accelerates convergence and enhances model performance [63]. Moreover, robustness evaluation is typically conducted on the complete model under adversarial attacks such as PGD or AA, ensuring a comprehensive assessment of model resilience.
4. Robust Pre-training–Fine-tuning Algorithm for Meta-Adversarial Defense
MAD augments AT by introducing broadly adaptable defensive capabilities while maintaining classification accuracy. However, its potential applicability and effectiveness within the domain of Robust-SSL are underexplored. To address this, we propose the RPF-MAD, as depicted in Figure 2. The approach consists of two stages, as follows: (1) Dual-MAP, which enhances the robustness and defense generalization of the upstream model, and (2) Meta-RFT, which facilitates the effective transfer of upstream robustness to the downstream model, thereby ensuring comprehensive defense against various adversarial attacks.
4.1. Dual-Track Meta-Adversarial Pre-Training Algorithm (Dual-MAP)
Given an upstream MAD dataset and an ACL pre-trained encoder , we construct meta-task from a batch of AE pairs . During training, each comprises the following:
- Support set (S): AEs with k-shot samples from attack types across n classes.
- Query set (Q): AEs generated using distinct attack types.
The validation/testing phase adopts an “-way, K-shot” protocol with non-overlapping sets and following equivalent sizing rules. Distinct from the vanilla Meta-AT, Dual-MAP introduces a dual-track optimization strategy. We apply differentiated learning rates to the and , explicitly formulated as follows:
where governs the learning rate decay for the encoder to prevent catastrophic forgetting of generic features. Consequently, the upstream model is optimized to satisfy the following:
where denotes the distribution of tasks, and during the training process, term s denotes the number of episodes, multiple norms () of perturbations are learned. Furthermore, the upstream meta-adversarial pre-training loss is the objective function that incorporates task-specific cross-entropy loss with a smoothness-inducing adversarial regularizer (SAR) as below.
is a tuning parameter, and SAR is applied during the meta-update phase to effectively control the complexity of the model. These implementations are based on the TRADES framework [64]. We define the and as follows:
Specifically, where is chosen as the symmetrized KL-divergence. We seek to determine the optimal parameter set of the parameterized function at the point of minimal loss, such that the fine-tuned model under the ath attack generalizes effectively to a new task under the bth attack. The meta-update process is then expressed as follows:
The detailed pre-training phase of Dual-MAP is outlined in Algorithm 1.
| Algorithm 1 Dual-MAP (pre-training phase). |
|
4.2. Adaptive Variance Anchoring Robust Fine-Tuning Algorithm (AVA-RFT)
Traditional fine-tuning distorts the latent space geometry of pre-trained models, compromising adversarial robustness and weakening the rapid adaptation capability of Dual-MAP against unknown attacks. To mitigate this, we propose the AVA-RFT algorithm, which serves as an implicit manifold alignment mechanism. It preserves intra-class compactness and enhances inter-class separability, ensuring consistency between downstream optimization and latent space evolution. AVA-RFT introduces an adaptive variance anchoring (AVA) term into the traditional fine-tuning loss function. The overall fine-tuning loss is defined as follows (using AFF as an example):
AFF follows the TRADES paradigm. The pre-trained encoder maps input data to a high-dimensional implicit differentiable manifold . The geometric properties of this manifold encode meta-knowledge. The geometric structure of encodes meta-knowledge, which AVA leverages to enforce structure-preserving fine-tuning. This process comprises three key components, mathematically formulated as follows:
Intra-class compactness and local manifold linearization. Minimizing intra-class variance forces features of the same class to contract toward their class centroid on manifold . This ensures feature compactness in the local tangent space:
Using the Euclidean distance approximation (L2-norm), this assumption implies that the manifold is locally flat, aligning with the low-curvature property of pre-trained models. Here, represents the size of the current mini-batch, denotes the subset of belonging to class c, denote the feature representations, and denotes the class centroid.
Inter-class separability and global topology preservation. Maximizing inter-class variance increases the geodesic distance between different class centroids, preventing feature collapse and maintaining global manifold distinguishability:
Here, C is the number of classes, and , represent different class centroids. This is equivalent to maximizing the deviation of all centroids from the global mean under Euclidean assumptions.
AVA achieves adaptability by computing variance within each mini-batch, ensuring independence from batch size while dynamically adjusting feature distributions to align with local manifold structures. This mechanism prevents bias accumulation in global statistics and enhances feature separation. To validate the effectiveness of AVA, we analyze the dynamic behavior of and . From a qualitative perspective, the reduction of encourages intra-class samples to cluster within the tangent space, while the increase of enhances inter-class separability, thereby optimizing feature distribution on the manifold. This attraction-repulsion mechanism, jointly optimized with the task loss, ensures both compactness and discriminability of feature representations. Furthermore, we quantitatively track the variance changes throughout training, as illustrated in Figure 3. It is evident that exhibits a relatively decreasing trend, while gradually increases. Despite some fluctuations, their overall trends align with theoretical expectations. These results demonstrate that AVA effectively regulates feature distribution as a structural constraint, thereby enhancing model robustness and generalization. Overall, the AVA-RFT procedure is outlined in Algorithm 2, taking AFF as an example. To further address unknown attacks, we provide the pseudo-code for the complete model evaluation process at the testing stage in Algorithm 3.
| Algorithm 2 AVA-RFT (Fine-tuning phase). |
|
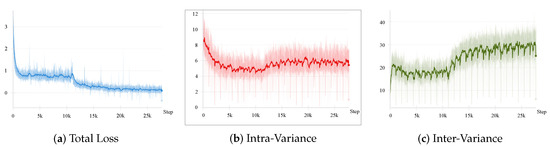
Figure 3.
The variation curves of total loss, intra-class variance, and inter-class variance during the training process.
| Algorithm 3 RPF-MAD (testing phase). |
|
5. Experiments
In this section, we conduct a structured set of experiments to verify the effectiveness of RPF-MAD across the upstream task and the downstream TSC system. We evaluate its two main modules, Dual-MAP and AVA-RFT, through comparisons with SOTA ACL methods, aiming to assess robustness, transferability, and generalization under diverse adversarial conditions. Ablation studies are further conducted to examine their individual contributions to the overall defense performance.
5.1. Experimental Setup
We first present the experimental environment and basic configurations used to evaluate the proposed RPF-MAD. To ensure fair comparisons, all models were trained under identical random seeds, learning rate schedules, and evaluation protocols. Additionally, all reported results are averaged over three independent runs to mitigate performance variance due to randomness.
5.1.1. Basic Settings
All experiments were conducted on a high-performance computing (HPC) server equipped with an Intel Xeon Gold 6132 CPU and four NVIDIA Tesla P100 GPUs (12 GB VRAM each). The software environment was implemented using PyTorch (v1.13.1) with torchvision for data preprocessing and augmentation. GPU acceleration was enabled through CUDA 11.6, with mixed-precision training (FP16) applied to optimize computational efficiency.
5.1.2. Datasets and Models
To rigorously evaluate the proposed method, we conducted experiments on (1) CIFAR-10 [65], a canonical image classification dataset comprising 50,000 training images and 10,000 test images spanning 10 classes, and (2) MAD-C [42], a benchmark dataset comprising offline AEs generated using 29 attacks on the CIFAR-10 validation set, specifically designed for meta-adversarial defense in upstream evaluations. For downstream application analysis, we utilized (3) the GTSRB dataset [66], which is a large-scale traffic sign classification dataset containing 39,209 training images and 12,630 test images across 43 traffic sign classes.
To ensure a fair comparison, we selected eight ACL methods from the Robust-SSL framework, all developed under the SimCLR paradigm to align with modern contrastive learning protocols. The baseline models are described as follows:
- ACL [33]. A pioneering framework that integrates AEs into contrastive learning by perturbing positive pairs to improve robustness.
- AdvCL [34]. Introduces adversarial augmentation to both anchors and positives in contrastive learning, enhancing robustness against perturbations.
- A-InfoNCE [67]. Adapts the InfoNCE loss by incorporating adversarial perturbations, improving feature discrimination under adversarial conditions.
- DynACL [54]. Applies dynamic loss scaling to balance clean and adversarial views during training.
- DynACL++ [54]. Builds upon DynACL by adding distribution-level adversarial perturbations for stronger generalization across attack types.
- DynACL-AIR [68]. Enhances DynACL by introducing adversarial instance reweighting to emphasize harder examples.
- DynACL-AIR++ [68]. Refines DynACL-AIR with adaptive instance-level perturbation scheduling to further improve sample-wise robustness.
- DynACL-RCS [55]. Introduces regularized contrastive sampling to improve robustness to unknown and distributional shifts.
For architectural uniformity, all models adopt a ResNet-18 backbone pretrained as the feature encoder, followed by a single fully connected layer for classification.
5.1.3. Adversarial Attack Protocols
- Upstream attacks. To systematically evaluate the transferability of AEs generated during the pre-training phase and their impact on downstream models, we select four cutting-edge adversarial attacks: AdvEncoder [40], PAP [41], SSP [57], and UAPGD [58];
- Downstream attacks. For robustness assessment on fine-tuned models, we implement two standard adversarial attacks: PGD-20 [24] (20 iterations, , in norm) and AA (evaluated on 1000 test samples with the “standard” protocol) [56];
- Unknown attacks. To assess generalization against novel threats, we curate six test attacks used in MAD-C [42]: 2, 10, 11, 27, 28, and 29. The remaining attacks are listed in Table A1.
5.1.4. Evaluation Metrics
To systematically evaluate the effectiveness of the proposed RPF-MAD, we employ the following key metrics:
- . Measures the classification accuracy on clean examples, serving as a baseline indicator of general classification performance;
- . Evaluates the classification accuracy under different attacks, quantifying the model’s resilience against adversarial perturbations;
- . Provides a standardized benchmark by AutoAttack for assessing robustness across different attack scenarios, facilitating direct comparisons among defense strategies. To ensure better comparability with results reported in prior works, we also provide evaluations on the full test set, denoted as (full).
- . Quantify the proportion of AEs that successfully manipulate the model’s predictions, serving as a key evaluation metric for upstream attack effectiveness. To ensure fair comparison, we standardize its definition as follows:
- . Captures the trade-off between adversarial robustness and clean sample classification following rapid adaptation. A higher reflects strong few-shot learning capabilities with minimal degradation in clean accuracy.
Furthermore, to enhance clarity in our evaluations, we introduce distinct notations to differentiate between various scenarios. Specifically, metrics for upstream models are denoted with the subscript “u”, while those for downstream models are labeled as “d”. Additionally, pre- and post-few-shot learning evaluations are distinguished using the superscript “*”. Notably, we set , and in the absence of few-shot learning, the penalty term vanishes (), reducing to a conventional defense success rate, thereby ensuring its broad applicability across diverse defense frameworks.
5.1.5. Implementation Details
To rigorously assess the effectiveness of RPF-MAD, we provide a detailed breakdown of the experimental hyperparameter configurations across different stages. The specific settings for Dual-MAP training and testing of RPF-MAD are summarized in Table 2. Additionally, the core innovation of AVA-RFT lies in its loss function design. To ensure a controlled experimental setup, the primary hyperparameter configurations remain consistent with those used in various ACL methods across different RFT strategies. A comprehensive summary of these settings is presented in Table 3.

Table 2.
Hyperparameter configuration for Dual-MAP.

Table 3.
Hyperparameter configuration for fine-tuning various ACL methods on the downstream GTSRB.
5.2. Comprehensive Evaluation of Dual-MAP on Upstream Models
The robustness of upstream models plays a crucial role in determining the performance of downstream models. To investigate this relationship, we first evaluate the robustness of both vanilla RPT and Dual-MAP models, as presented in Table 4. The results indicate that while Dual-MAP generally enhances standard classification ability, it also leads to a slight degradation in robustness. The highest metric values are in bold. Among these, is a key indicator of the meta-learning capability of upstream models. Notably, negative values, marked in red, indicate that unknown attacks fail against DynACL++ and Meta_AdvCL. In these cases, the exceeds the for vanilla RPT and Dual-MAP models, leading to negative scores. Additionally, an extreme outlier is observed, with a value of 1327.80. This anomaly arises due to model overfitting to AEs during meta-learning, resulting in a significantly higher than , while remains largely unchanged.

Table 4.
Robust evaluation (%) of vanilla RPT and Dual-MAP (Our) models on CIFAR10.
To further analyze the meta-learning defense capability of the models against unknown attacks, we conduct cross-attack generalization analysis through Figure A1. The figure reveals that during meta-testing under unknown attacks, the increase in and approaches 100%, but this improvement comes at the expense of robustness, reflected in a decrease in . Additionally, since each type of attack in meta-testing is repeated five times, we present box plots for values in Figure A1. These box plots demonstrate that Dual-MAP models exhibit greater stability during meta-testing, suggesting that meta-learning enables models to generalize better under previously unseen adversarial conditions.
In addition to the quantitative analysis, we also conduct a qualitative evaluation, as illustrated in Figure A3. The figure demonstrates that models trained with Dual-MAP exhibit notable differences in feature representations compared to their vanilla counterparts. Specifically, clusters in the meta-trained models appear more compact and well-separated, indicating enhanced feature discriminability. This suggests that Dual-MAP effectively refines the feature space, potentially improving the model’s ability to generalize under adversarial conditions.
Overall, these results demonstrate that Dual-MAP enhances meta-learning defense capabilities, offering improved generalization under unknown attacks while maintaining stability during meta-testing. These findings align with our previous work, Meta-AT, which confirmed that meta-training enhances robustness against unknown attacks. Therefore, we establish that this method is also applicable within the SSL framework, further broadening its potential applications.
5.3. Comprehensive Evaluation of RPF-MAD on TSC System
In the previous evaluation of upstream models, both quantitative and qualitative analyses revealed that Dual-MAP enhances intra-class compactness and inter-class separation. This insight motivated the development of AVA-RFT to transfer the meta-defense knowledge from upstream to downstream models. To validate the effectiveness of RPF-MAD, we conduct a comprehensive evaluation of the best-performing model, A-InfoNCE, assessing its robustness against various adversarial threats in TSC systems.
We begin by evaluating model robustness, which is a central concern in the design of TSC systems. Table 5 presents the performance of different models under varying levels of defense, where A-InfoNCE is fine-tuned under the AFF strategy. The results show that SimCLR, when fine-tuned to downstream tasks, exhibits the weakest robustness and meta-defense capacity, displaying negligible resistance to adversarial attacks. Gen-AF, as the defense baseline for comparison, improves by 12.08% compared to the original model. However, its improvements in overall robustness and meta-defense capabilities remain limited. Notably, even the vanilla A-InfoNCE surpasses Gen-AF in robustness metrics. When equipped with RPF-MAD, the model exhibits substantial performance gains across all evaluation indicators. These results confirm that RPF-MAD effectively strengthens adversarial robustness while maintaining task-specific performance in TSC systems.

Table 5.
Evaluation (%) of vanilla and RPF-MAD (Our) models under downstream attacks.
Table 6 evaluates the impact of RPF-MAD on A-InfoNCE under four SOTA upstream attacks. For clarity, we highlight the highest and lowest values in bold. Notably, we observe a negative outlier case where exceeds , according to Equation (16), indicating a failed attack. A comprehensive analysis of the table reveals several key insights. First, SimCLR, lacking any dedicated defense, is highly susceptible to upstream perturbations, with attacks such as PAP achieving a 100% , and all four attacks yielding less than 16% . This demonstrates its complete vulnerability to upstream attacks. Second, while Gen-AF demonstrates strong resistance across upstream attacks and achieves an average of 89.20% and of 1.57%, outperforming vanilla A-InfoNCE in all cases. However, its limited robustness under downstream attacks constrains its practical deployment in real-world TSC systems. In contrast, when enhanced with RPF-MAD, A-InfoNCE achieves comparable or even superior robustness, with an average of 88.98% and reduced to 1.31%. Specifically, RPF-MAD achieves the lowest in three out of four attack settings, including a substantial reduction under UAPGD from 1.40% to 0.23%. Moreover, in the PAP attack, RPF-MAD even results in a negative , which signifies complete defense success. These results confirm that RPF-MAD not only offers robust protection against upstream adversarial threats but also enhances the transferability and consistency of robustness across stages. This highlights its potential as a comprehensive defense solution for TSC systems, ensuring greater resilience from pre-training through downstream deployment.

Table 6.
Evaluation (%) of vanilla and RPF-MAD (Our) models under upstream attacks.
To evaluate the meta-defense capabilities inherited from upstream models, we analyze in Table 5. The results demonstrate that RPF-MAD significantly enhances the transferability of adversarial robustness, where improves from 8.79% to 30.78%, indicating a more effective retention of meta-adversarial knowledge throughout the fine-tuning process. Figure A2 provides a visual comparison of meta-defense effectiveness under unknown attacks. Across all attacks, exhibits a slight decline during meta-testing, but RPF-MAD consistently outperforms vanilla RFT across all evaluation metrics. Surprisingly, the fact that exceeds its baseline value further suggests that RPF-MAD not only enhances meta-defense transfer but also substantially improves downstream model robustness. This suggests that the integration of adversarial meta-learning within RPF-MAD effectively balances robustness and generalization, ensuring consistent adversarial protection across both pre-training and downstream deployment stages.
Figure 4 provides a qualitative summary of model predictions across both upstream and downstream datasets under various adversarial attack settings. Overall, qualitative and quantitative analyses of both upstream and downstream models confirm that RPF-MAD offers comprehensive defense against upstream, downstream, and unknown attacks, outperforming traditional approaches. In particular, the results under unknown attack scenarios demonstrate that RPF-MAD not only improves robustness but also increases the difficulty for adversaries to discover effective attack strategies. Specifically, compared to baseline methods, RPF-MAD significantly reduces the ASR and achieves substantial improvements in the EDSR. Since EDSR represents a comprehensive measure of the defense success rate against adversarial perturbations, its consistent increase directly indicates that the attack surface has been effectively constrained and that adversaries face greater difficulty in crafting successful attacks. Furthermore, the successful validation on the GTSRB dataset demonstrates the potential of RPF-MAD as a novel and effective robust pre-training–fine-tuning paradigm for meta-adversarial defense in TSC systems within autonomous driving. This highlights its potential for real-world deployment, ensuring enhanced model resilience against adversarial threats in safety-critical applications.
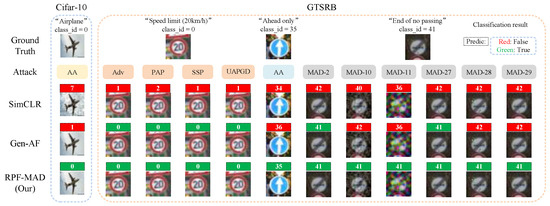
Figure 4.
Visual comparison of classification results on both upstream (CIFAR-10) and downstream (GTSRB) datasets under various adversarial attacks.
5.4. Ablation Study
In this section, we conduct ablation experiments to systematically validate the selection of A-InfoNCE as the primary robust model for TSC systems. Additionally, we evaluate the two major innovations proposed in this study: Dual-track LR optimization and the AVA term. These components are designed to enhance the robustness and generalization capabilities of our proposed RPF-MAD framework by improving both upstream meta-learning effectiveness and downstream fine-tuning stability.
5.4.1. Selection of Primary Models for TSC System
To identify the most suitable model for robust TSC systems, we conduct a comprehensive evaluation of various upstream SSL models under different RFT strategies. As shown in Table 7, we place particular emphasis on their ability to withstand adversarial perturbations while maintaining high classification accuracy. Among these strategies, AFF consistently delivers the strongest defense performance across all models, significantly outperforming both SLF and ALF. While models such as ACL and DynACL-AIR demonstrate competitive robustness, A-InfoNCE emerges as the most balanced candidate in terms of both robustness and generalization. It is worth noting that this ablation study is conducted on the GTSRB dataset, which aligns with our primary focus on TSC systems. The optimal backbone configuration may vary for other downstream tasks, depending on the dataset characteristics and task-specific requirements.

Table 7.
Robust evaluation (%) of vanilla and PRF-MAD (Our) models on GTSRB.
Building on this observation, we further assess all models under the AFF configuration using the standardized AA protocol. As shown in Table 8, RPF-MAD consistently improves downstream robustness across all evaluated models, with notable gains across all metrics. Although remains relatively similar among models, A-InfoNCE achieves the highest (78.20%), underscoring its superior adversarial resilience.

Table 8.
Evaluation (%) of vanilla and PRF-MAD (Our) models under downstream attacks.
We further assess the meta-defense capability of A-InfoNCE through its score, which increases substantially from 8.79% to 30.78%, ranking among the top three improvements across all models (Table 8). Complementary results in Figure A2 show that most models benefit from enhanced meta-defense when integrated with RPF-MAD. Taking both adversarial robustness () and standard classification accuracy () into account, A-InfoNCE demonstrates the most consistent and stable performance, maintaining lower variance and greater resilience across diverse unknown attack scenarios. These results suggest that A-InfoNCE effectively retains transferable meta-defense knowledge while preserving structural feature integrity under perturbations.
Upstream adversarial attack defense is also a central focus of our study. Table 9 presents a comprehensive evaluation of vanilla and RPF-MAD models under four representative upstream attack types. Overall, the integration of RPF-MAD yields consistent improvements across all models, as evidenced by increased downstream robustness () and reduced . Among them, A-InfoNCE exhibits the most balanced and robust performance. It achieves the highest average across attacks and the lowest average , including the best result under UAPGD, where drops to 0.23%. Moreover, under the more challenging PAP attack, A-InfoNCE achieves a negative of −0.86%, indicating complete defense success in certain instances. These findings further underscore its superior resistance to upstream adversarial transfer and its capacity to retain transferable meta-defense knowledge.

Table 9.
Evaluation (%) of vanilla and PRF-MAD (Our) models under upstream attacks.
Qualitative analyses further support these findings. As shown in the t-SNE visualization in Figure A4, A-InfoNCE, alongside other RPF-MAD models, exhibits clearer inter-class boundaries and reduced feature overlap compared to vanilla variants, indicating enhanced feature separability and adversarial robustness.
In summary, both quantitative and qualitative evidence establish A-InfoNCE as the most reliable and well-rounded choice for robust TSC systems. Its exceptional generalization, adversarial resilience, and structural representation capabilities justify its adoption as the primary robust model within the RPF-MAD framework.
5.4.2. Dual-Track Learning Rate Optimization
In this experiment, we conducted a Pareto front-based visualization (Figure 5) to analyze the impact of different LR configurations on model performance, specifically focusing on the LR of the encoder and the fully connected layer (FC) in ACL. The dataset comprises multiple results, with the objective of identifying an optimal LR combination that maximizes while maximizing .
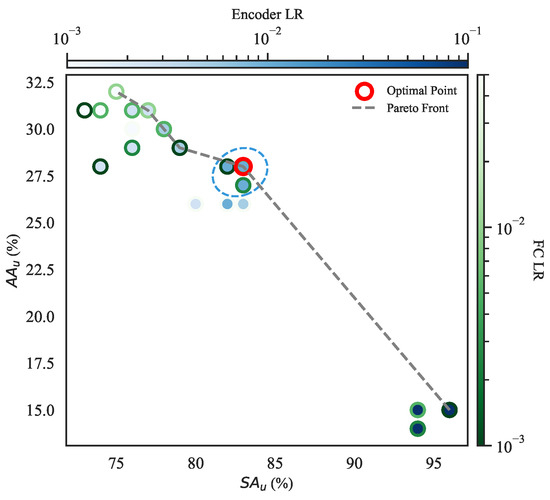
Figure 5.
Pareto front analysis of dual-track learning rate optimization.
To systematically assess the effect of different LRs, each experimental configuration is represented using a dual-layer color encoding. The inner solid color (blue) represents Encoder LR, with darker shades signifying higher values and lighter shades indicating lower values. Similarly, the outer circular border (green) reflects FC LR, where deeper shades correspond to smaller values and lighter shades denote larger ones. This dual-layer representation effectively distinguishes the respective influences of the encoder and FC LRs on model performance. A Pareto front (depicted as a gray dashed line) is constructed to identify optimal LR trade-offs. Among all tested configurations, is selected as the optimal setting, with Encoder LR = 0.01 and FC LR = 0.005. This point is explicitly highlighted with a bold red circular marker, while a surrounding elliptical blue dashed boundary encloses other near-optimal configurations. These results validate the dual-track optimization strategy, demonstrating its efficacy in refining model performance through targeted learning rate selection.
5.4.3. Adaptive Variance Anchoring Term
Table 10 and Table 11 present an ablation study evaluating the impact of the AVA term on the robustness of various downstream models under both vanilla and meta-pre-trained settings. The results indicate that incorporating AVA consistently enhances model robustness across different architectures. Specifically, in the vanilla setting (Table 10), the inclusion of AVA improves robust accuracy and adversarial accuracy in all models. For instance, in the ACL model, increases from 59.83% to 64.52%, and rises from 45.26% to 49.33%. Similarly, DynACL-RCS exhibits an improvement in from 58.61% to 64.14% and in from 43.67% to 48.55%.

Table 10.
Impact (%) of AVA-RFT on ACL methods (vanilla).

Table 11.
Impact (%) of AVA-RFT on ACL methods (RPF-MAD).
In the meta-pre-trained setting (Table 11), the benefits of AVA are also evident, particularly in models such as AdvCL and A-InfoNCE. The AdvCL model achieves an increase in from 58.27% to 65.46% and in from 44.20% to 49.26%. Likewise, A-InfoNCE with AVA attains the highest improvement in the meta-setting, rising from 45.28% to 50.17%. While some models exhibit minor reductions in with AVA, these decreases are marginal and offset by significant gains in robust and adversarial accuracy.
For the horizontal comparison in vanilla and RPF-MAD, we observe that without AVA, meta-pre-trained models do not consistently outperform traditional fine-tuning methods. This may be attributed to the increased feature dispersion introduced during meta-pre-training, which can lead to suboptimal adaptation. However, with the anchoring constraint of AVA, the robustness of meta-pre-trained models improves significantly during fine-tuning, surpassing traditional methods while preserving the benefits of meta-knowledge. This highlights AVA’s role in mitigating the instability of pre-trained features, ensuring more structured adaptation to downstream tasks.
The consistent improvements across various architectures confirm that AVA serves as a crucial mechanism in stabilizing the meta-adaptation process, reinforcing the model’s resilience while maintaining strong generalization capabilities. These findings validate RPF-MAD as a promising solution for adversarial robustness in the pre-training–fine-tuning paradigm.
6. Discussion
While our study presents a comprehensive framework for meta-adversarial defense through RPF-MAD, several aspects warrant further investigation to enhance its robustness and generalization. Specifically, the current study has the following limitations:
- Limited evaluation under diverse attack scenarios: Although Dual-MAP and AVA-RFT improve robustness against standard adversarial perturbations, the performance of RPF-MAD under a broader spectrum of adaptive and physical adversarial attacks remains to be thoroughly evaluated.
- Idealized training assumptions: Our training setup assumes that adversarial perturbations are generated under known constraints, whereas real-world attackers may employ complex strategies such as adversarial patches and backdoor attacks [69]. Extending RPF-MAD to handle dynamically evolving threats is a critical direction for future work.
- Fixed optimization scheme in AVA-RFT: Although adaptive variance anchoring helps maintain feature space stability, its effectiveness across different network architectures and datasets requires further validation. Dynamic adjustment mechanisms, such as reinforcement learning-based tuning, could enhance the flexibility of the optimization process.
- Practical deployment challenges: Adversarial robustness must be validated not only on benchmark datasets but also under real-world conditions, where noise, sensor errors, and environmental variations are prevalent. Evaluating RPF-MAD on large-scale real-world datasets and analyzing its impact on computational efficiency and latency is crucial for practical adoption.
Despite these challenges, RPF-MAD provides a scalable and generalizable framework for adversarial robustness. By integrating pre-training–fine-tuning strategies with meta-learning principles, it enhances a model’s ability to withstand adversarial manipulations across multiple tasks. Moreover, while RPF-MAD incorporates an optional few-shot adaptation phase during testing to further improve robustness against novel attacks, this procedure is not mandatory for deployment. In practical applications, the model can perform standard inference directly without additional adaptation, ensuring minimal computational overhead and compatibility with resource-constrained platforms such as NVIDIA Jetson Nano [70] and Google Coral [71]. Future advancements in meta-adversarial learning, robust SSL, and dynamic adversarial adaptation will further strengthen the foundation laid by this work, contributing to next-generation adversarial defense paradigms.
7. Conclusions
In this paper, we propose RPF-MAD, a novel meta-adversarial defense algorithm designed to enhance the sustainability and safety of TSC systems. RPF-MAD integrates Dual-MAP for upstream robustness enhancement and AVA-RFT for structured fine-tuning. By leveraging meta-learning principles, our approach constructs a scalable and generalizable adversarial defense strategy that effectively addresses the limitations of traditional AT and conventional pre-training–fine-tuning paradigms. Specifically, Dual-MAP optimizes ACL-based self-supervised learning methods to enhance the upstream model’s capacity to generalize across diverse adversarial attacks. Meanwhile, AVA-RFT preserves latent feature structure during fine-tuning, ensuring that the downstream model inherits upstream robustness while maintaining strong generalization.
To systematically evaluate RPF-MAD, we conducted extensive experiments on eight SOTA ACL methods and three RFT techniques using the CIFAR-10 and GTSRB datasets, demonstrating its superiority across multiple attack scenarios. Our results show that RPF-MAD significantly improves , , , and , outperforming existing SOTA defense methods. In particular, our method enables rapid adaptation to novel attacks while ensuring long-term robustness, a critical requirement for autonomous perception systems.
While RPF-MAD offers significant advantages, it also presents certain challenges. Future work will focus on further enhancing the framework, including integrating backdoor defenses to mitigate potential vulnerabilities. Additionally, beyond image classification, we plan to extend RPF-MAD to object detection, multimodal learning, and large-scale adversarial adaptation in safety-critical environments.
Author Contributions
Conceptualization, X.P. and D.Z.; methodology, X.P.; software, X.P.; validation, X.P., D.Z. and G.S.; formal analysis, X.P.; investigation, X.P.; resources, X.P.; data curation, X.P.; writing—original draft preparation, X.P.; writing—review and editing, X.P., J.Z. and J.S.; visualization, X.P.; supervision, D.Z.; project administration, D.Z.; funding acquisition, G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This study was kindly supported by the Joint Funds of the National Natural Science Foundation of China through grant no. U23A20346 and the National Natural Science Foundation of China through grant no. 62403162.
Data Availability Statement
Data are contained within the article. The code used in this research is publicly available at https://github.com/PXX1110/RPF-MAD (accessed on 12 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AA | AutoAttack |
| ACL | Adversarial Contrastive Learning |
| AE | Adversarial Example |
| AFF | Adversarial Full Fine-Tuning |
| ALF | Adversarial Linear Fine-Tuning |
| ASR | Attack Success Rate |
| AVA-RFT | Adaptive Variance Anchoring Robust Fine-Tuning |
| ADS | Autonomous Driving Systems |
| DSR | Defense Success Rate |
| Dual-MAP | Dual-Track Meta-Adversarial Pre-training |
| EDSR | Equilibrium Defense Success Rate |
| Gen-AF | Genetic Evolution-Nurtured Adversarial Fine-Tuning |
| GTSRB | German Traffic Sign Recognition Benchmark |
| MAD | Meta-Adversarial Defense |
| MAD-C | Meta-Adversarial Defense Benchmark Dataset |
| PAP | Pre-trained Adversarial Perturbation |
| PFP | Pre-training–Fine-tuning Paradigm |
| RA | Robust Accuracy |
| RFT | Robust Fine-Tuning |
| RPF-MAD | Robust Pre-training–Fine-tuning Meta-Adversarial Defense |
| SA | Standard Accuracy |
| SFF | Standard Full Fine-Tuning |
| SLF | Standard Linear Fine-Tuning |
| SOTA | State-of-the-Art |
| SSL | Self-Supervised Learning |
| SSP | Self-Supervised Perturbation |
| TSC | Traffic Sign Classification |
| UAPGD | Universal Adversarial Perturbation via Gradient Descent |
Appendix A

Table A1.
Introduction to various adversarial attacks in MAD.
Table A1.
Introduction to various adversarial attacks in MAD.
| ID | Name | Measurement | Type | Introduction |
|---|---|---|---|---|
| 0 | JSMA [52] | W | Generates perturbations by modifying salient input features. | |
| 1 | Deep Fool [22] | W | Computes minimal perturbations to reach the decision boundaries. | |
| 2 | Universal Perturbation [72] | W | Finds universal perturbations applicable to multiple samples. | |
| 3 | NewtonFool [73] | / | W | Generates AEs using gradient-based optimization. |
| 4 | Boundary Attack [74] | B | Reduces perturbation size while maintaining misclassification. | |
| 5 | ElasticNet [75] | W | Formulates adversarial attacks as an elastic net optimization problem. | |
| 6 | Zoo-Attack [76] | B | Uses zero-order gradient estimation to craft adversarial samples. | |
| 7 | Spatial Transformation [77] | B | Applies spatial transformations such as translation and rotation. | |
| 8 | Hop-Skip-Jump [78] | / | B | Estimates gradient directions using decision-boundary queries. |
| 9 | Sim-BA [48] | B | Iteratively perturbs samples using a predefined basis. | |
| 10 | Shadow Attack [79] | W | Keeps AEs far from the decision boundary while remaining imperceptible. | |
| 11 | GeoDA [80] | B | Query-based iterative attack leveraging geometric information. | |
| 12 | Wasserstein [81] | W | Generates adversarial perturbations based on the Wasserstein distance. | |
| 13 | FGSM [6] | W | Fast gradient sign method for single-step adversarial generation. | |
| 14 | BIM [82] | W | Iterative extension of FGSM for stronger attacks. | |
| 15 | CW [21] | W | Optimizes perturbations to minimize classification confidence. | |
| 16 | MIFGSM [83] | W | Enhances FGSM via momentum-based updates. | |
| 17 | TIFGSM [84] | W | Improves transferability by optimizing input transformations. | |
| 18 | PGD [24] | W | Iterative gradient-based attack with projection constraints. | |
| 19 | PGD- [24] | W | PGD variant using norm constraints. | |
| 20 | TPGD [64] | W | Gradient-based attack using KL-Divergence loss. | |
| 21 | RFGSM [85] | W | FGSM variant incorporating random initialization. | |
| 22 | APGD [86] | / | W | Adaptive step-size gradient attack using cross-entropy loss. |
| 23 | APGD2 [86] | / | W | Adaptive step-size gradient attack using DLR loss. |
| 24 | FFGSM [87] | W | Random-initialized fast gradient sign method. | |
| 25 | Square [47] | / | B | Random-search attack updating local pixel regions. |
| 26 | TIFGSM2 [84] | W | Improved TIFGSM with varied resize rates. | |
| 27 | EOTPGD [88] | W | PGD variant considering input transformations. | |
| 28 | One-Pixel [89] | B | Generates adversarial samples by modifying a single pixel. | |
| 29 | FAB [90] | // | W | Optimizes minimal perturbations with adaptive boundary search. |
indicates the unconventional perturbation measurement. W: White-box attack. B: Black-box attack.
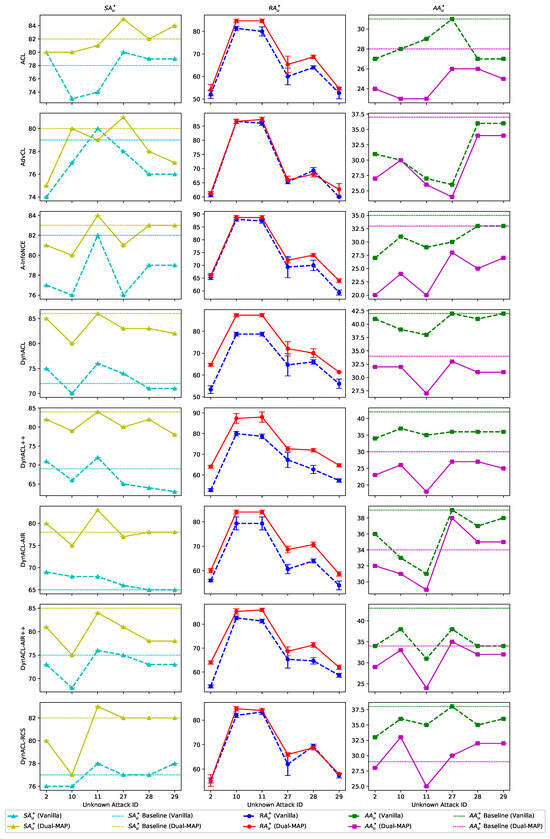
Figure A1.
Comparison (%) of vanilla RPT and Dual-MAP models under unknown attacks.
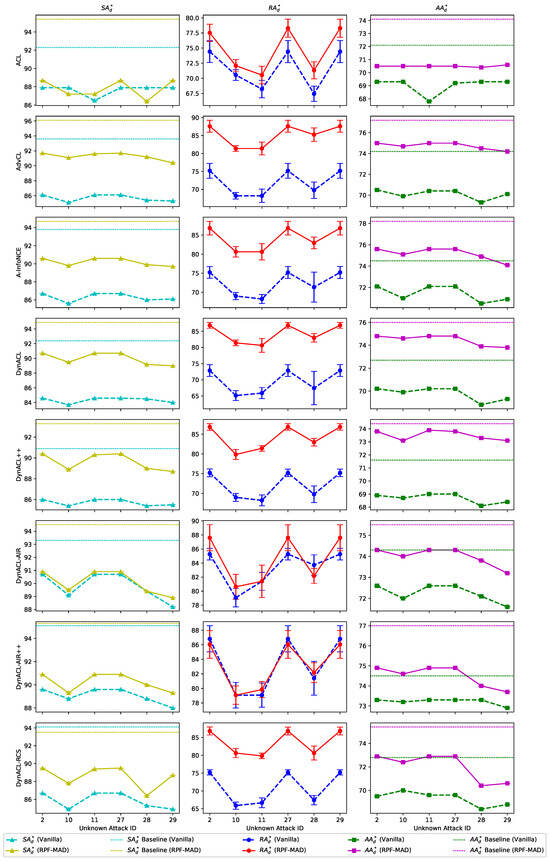
Figure A2.
Comparison (%) of vanilla and RPF-MAD models under unknown attacks.

Figure A3.
t-SNE visualization of feature representations in vanilla RPT and Dual-MAP models on CIFAR-10 (Different colors represent the 10 classes).
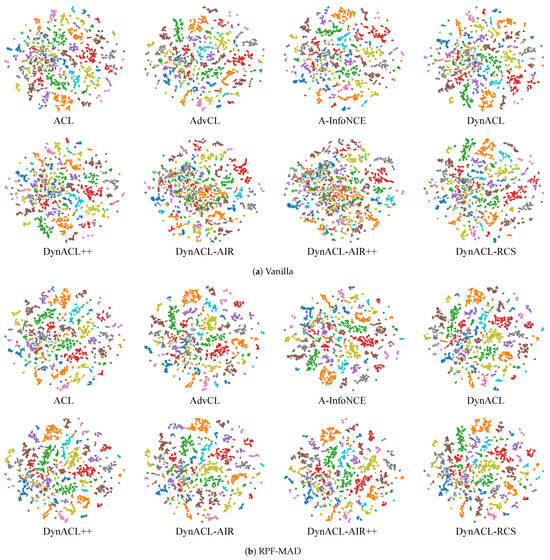
Figure A4.
t-SNE visualization of feature representations in vanilla and RPF-MAD models on GTSRB (Different colors represent the 43 classes).
References
- Li, J.; Liu, X.; Wei, S.; Chen, Z.; Li, B.; Guo, Q.; Yang, X.; Pu, Y.; Wang, J. Towards Benchmarking and Assessing the Safety and Robustness of Autonomous Driving on Safety-critical Scenarios. arXiv 2025, arXiv:2503.23708. [Google Scholar]
- Karle, P.; Furtner, L.; Lienkamp, M. Self-Evaluation of Trajectory Predictors for Autonomous Driving. Electronics 2024, 13, 946. [Google Scholar] [CrossRef]
- Ibrahum, A.D.M.; Hussain, M.; Hong, J.E. Deep learning adversarial attacks and defenses in autonomous vehicles: A systematic literature review from a safety perspective. Artif. Intell. Rev. 2025, 58, 28. [Google Scholar] [CrossRef]
- Kim, T.; Park, S.; Lee, K. Traffic Sign Recognition Based on Bayesian Angular Margin Loss for an Autonomous Vehicle. Electronics 2023, 12, 3073. [Google Scholar] [CrossRef]
- Chung, J.; Park, S.; Pae, D.; Choi, H.; Lim, M. Feature-selection-based attentional-deconvolution detector for German traffic sign detection benchmark. Electronics 2023, 12, 725. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar]
- Enan, A.; Chowdhury, M. GAN-Based Single-Stage Defense for Traffic Sign Classification Under Adversarial Patch Attack. arXiv 2025, arXiv:2503.12567. [Google Scholar]
- Jiang, W.; Wang, L.; Zhang, T.; Chen, Y.; Dong, J.; Bao, W.; Zhang, Z.; Fu, Q. Robuste2e: Exploring the robustness of end-to-end autonomous driving. Electronics 2024, 13, 3299. [Google Scholar] [CrossRef]
- Jiang, W.; Zhang, T.; Liu, S.; Ji, W.; Zhang, Z.; Xiao, G. Exploring the physical-world adversarial robustness of vehicle detection. Electronics 2023, 12, 3921. [Google Scholar] [CrossRef]
- Pavlitska, S.; Lambing, N.; Zöllner, J.M. Adversarial attacks on traffic sign recognition: A survey. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Canary Islands, Spain, 19–21 July 2023; pp. 1–6. [Google Scholar]
- Tao, G.; Ma, S.; Liu, Y.; Zhang, X. Attacks meet interpretability: Attribute-steered detection of adversarial samples. Adv. Neural Inf. Process. Syst. 2018, 31, 1–12. [Google Scholar]
- Li, S.; Zhu, S.; Paul, S.; Roy-Chowdhury, A.; Song, C.; Krishnamurthy, S.; Swami, A.; Chan, K.S. Connecting the dots: Detecting adversarial perturbations using context inconsistency. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXIII 16. Springer: Cham, Switzerland, 2020; pp. 396–413. [Google Scholar]
- Wu, F.; Xiao, L.; Yang, W.; Zhu, J. Defense against adversarial attacks in traffic sign images identification based on 5G. EURASIP J. Wirel. Commun. Netw. 2020, 2020, 173. [Google Scholar] [CrossRef]
- Li, H.; Zhang, B.; Zhang, Y.; Dang, X.; Han, Y.; Wei, L.; Mao, Y.; Weng, J. A defense method based on attention mechanism against traffic sign adversarial samples. Inf. Fusion 2021, 76, 55–65. [Google Scholar] [CrossRef]
- Salek, M.S.; Mamun, A.A.; Chowdhury, M. AR-GAN: Generative Adversarial Network-Based Defense Method Against Adversarial Attacks on the Traffic Sign Classification System of Autonomous Vehicles. arXiv 2023, arXiv:2401.14232. [Google Scholar]
- Suri, A.; Vaidya, B.; Mouftah, H.T. Assessment of Adversarial Attacks on Traffic Sign Detection for Connected and Autonomous Vehicles. In Proceedings of the 2023 IEEE 28th International Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Edinburgh, UK, 6–8 November 2023; pp. 240–245. [Google Scholar]
- Garg, S.; Chattopadhyay, N.; Chattopadhyay, A. Robust Perception for Autonomous Vehicles using Dimensionality Reduction. In Proceedings of the 2022 IEEE International Conference on Trust, Security and Privacy in Computing and Communications (TrustCom), Wuhan, China, 9–11 December 2022; pp. 1516–1521. [Google Scholar]
- Guo, C.; Rana, M.; Cisse, M.; Van Der Maaten, L. Countering adversarial images using input transformations. arXiv 2017, arXiv:1711.00117. [Google Scholar]
- Raff, E.; Sylvester, J.; Forsyth, S.; McLean, M. Barrage of random transforms for adversarially robust defense. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 6528–6537. [Google Scholar]
- Huang, S.; Tan, Q.; Zhang, Z.; Fan, Q.; Zhang, Y.; Li, X. Trusted Perception Method for Traffic Signs That Are Physically Attacked. Transp. Res. Rec. 2024, 2678, 670–683. [Google Scholar] [CrossRef]
- Carlini, N.; Wagner, D. Towards evaluating the robustness of neural networks. In Proceedings of the 2017 IEEE Symposium on Security and Privacy (SP), San Jose, CA, USA, 22–26 May 2017; pp. 39–57. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2574–2582. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Hu, X.; Zhu, J. Discovering adversarial examples with momentum. arXiv 2017, arXiv:1710.06081. [Google Scholar]
- Mądry, A.; Makelov, A.; Schmidt, L.; Tsipras, D.; Vladu, A. Towards deep learning models resistant to adversarial attacks. Stat 2017, 1050, 9. [Google Scholar]
- Pang, T.; Yang, X.; Dong, Y.; Su, H.; Zhu, J. Bag of tricks for adversarial training. arXiv 2020, arXiv:2010.00467. [Google Scholar]
- Peng, S.; Xu, W.; Cornelius, C.; Hull, M.; Li, K.; Duggal, R.; Phute, M.; Martin, J.; Chau, D.H. Robust principles: Architectural design principles for adversarially robust cnns. arXiv 2023, arXiv:2308.16258. [Google Scholar]
- Tang, S.; Gong, R.; Wang, Y.; Liu, A.; Wang, J.; Chen, X.; Yu, F.; Liu, X.; Song, D.; Yuille, A.; et al. Robustart: Benchmarking robustness on architecture design and training techniques. arXiv 2021, arXiv:2109.05211. [Google Scholar]
- Liu, C.; Dong, Y.; Xiang, W.; Yang, X.; Su, H.; Zhu, J.; Chen, Y.; He, Y.; Xue, H.; Zheng, S. A comprehensive study on robustness of image classification models: Benchmarking and rethinking. Int. J. Comput. Vis. 2025, 133, 567–589. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. Lora: Low-rank adaptation of large language models. arXiv 2021, arXiv:2106.09685. [Google Scholar]
- Brown, T.B. Language models are few-shot learners. arXiv 2020, arXiv:2005.14165. [Google Scholar]
- Jeddi, A.; Shafiee, M.J.; Wong, A. A simple fine-tuning is all you need: Towards robust deep learning via adversarial fine-tuning. arXiv 2020, arXiv:2012.13628. [Google Scholar]
- Salman, H.; Ilyas, A.; Engstrom, L.; Kapoor, A.; Madry, A. Do adversarially robust imagenet models transfer better? Adv. Neural Inf. Process. Syst. 2020, 33, 3533–3545. [Google Scholar]
- Jiang, Z.; Chen, T.; Chen, T.; Wang, Z. Robust pre-training by adversarial contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 16199–16210. [Google Scholar]
- Fan, L.; Liu, S.; Chen, P.Y.; Zhang, G.; Gan, C. When does contrastive learning preserve adversarial robustness from pretraining to finetuning? Adv. Neural Inf. Process. Syst. 2021, 34, 21480–21492. [Google Scholar]
- Gowal, S.; Huang, P.S.; van den Oord, A.; Mann, T.; Kohli, P. Self-supervised adversarial robustness for the low-label, high-data regime. In Proceedings of the International Conference on Learning Representations, Vienna, Austria, 3–7 May 2021. [Google Scholar]
- Kim, M.; Tack, J.; Hwang, S.J. Adversarial self-supervised contrastive learning. Adv. Neural Inf. Process. Syst. 2020, 33, 2983–2994. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A simple framework for contrastive learning of visual representations. In Proceedings of the International Conference on Machine Learning, Online, 13–18 July 2020; pp. 1597–1607. [Google Scholar]
- Chen, X.; Fan, H.; Girshick, R.; He, K. Improved baselines with momentum contrastive learning. arXiv 2020, arXiv:2003.04297. [Google Scholar]
- Zhou, Z.; Li, M.; Liu, W.; Hu, S.; Zhang, Y.; Wan, W.; Xue, L.; Zhang, L.Y.; Yao, D.; Jin, H. Securely fine-tuning pre-trained encoders against adversarial examples. In Proceedings of the 2024 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2024; pp. 3015–3033. [Google Scholar]
- Zhou, Z.; Hu, S.; Zhao, R.; Wang, Q.; Zhang, L.Y.; Hou, J.; Jin, H. Downstream-agnostic adversarial examples. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 4345–4355. [Google Scholar]
- Ban, Y.; Dong, Y. Pre-trained adversarial perturbations. Adv. Neural Inf. Process. Syst. 2022, 35, 1196–1209. [Google Scholar]
- Peng, X.; Zhou, D.; Sun, G.; Shi, J.; Wu, L. MAD: Meta Adversarial Defense Benchmark. arXiv 2023, arXiv:2309.09776. [Google Scholar]
- RobustSSL Benchmark. Robust Self-Supervised Learning Benchmark. 2024. Available online: https://robustssl.github.io/ (accessed on 25 July 2024).
- Papernot, N.; McDaniel, P.; Goodfellow, I.; Jha, S.; Celik, Z.B.; Swami, A. Practical black-box attacks against machine learning. In Proceedings of the 2017 ACM on Asia Conference on Computer and Communications Security, Abu Dhabi, United Arab Emirates, 2–6 April 2017; pp. 506–519. [Google Scholar]
- Li, Y.; Xu, X.; Xiao, J.; Li, S.; Shen, H.T. Adaptive square attack: Fooling autonomous cars with adversarial traffic signs. IEEE Internet Things J. 2020, 8, 6337–6347. [Google Scholar] [CrossRef]
- Wan, C.; Zhang, Q. A Novel Dual-Component Radar-Signal Modulation Recognition Method Based on CNN-ST. Appl. Sci. 2024, 14, 5499. [Google Scholar] [CrossRef]
- Andriushchenko, M.; Croce, F.; Flammarion, N.; Hein, M. Square attack: A query-efficient black-box adversarial attack via random search. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; Proceedings, Part XXIII. Springer: Cham, Switzerland, 2020; pp. 484–501. [Google Scholar]
- Guo, C.; Gardner, J.; You, Y.; Wilson, A.G.; Weinberger, K. Simple black-box adversarial attacks. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 2484–2493. [Google Scholar]
- Eykholt, K.; Evtimov, I.; Fernandes, E.; Li, B.; Rahmati, A.; Xiao, C.; Prakash, A.; Kohno, T.; Song, D. Robust physical-world attacks on deep learning visual classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 1625–1634. [Google Scholar]
- Liu, A.; Liu, X.; Fan, J.; Ma, Y.; Zhang, A.; Xie, H.; Tao, D. Perceptual-sensitive gan for generating adversarial patches. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 1028–1035. [Google Scholar]
- Aung, A.M.; Fadila, Y.; Gondokaryono, R.; Gonzalez, L. Building robust deep neural networks for road sign detection. arXiv 2017, arXiv:1712.09327. [Google Scholar]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrucken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar]
- Metzen, J.H.; Finnie, N.; Hutmacher, R. Meta adversarial training against universal patches. arXiv 2021, arXiv:2101.11453. [Google Scholar]
- Luo, R.; Wang, Y.; Wang, Y. Rethinking the effect of data augmentation in adversarial contrastive learning. arXiv 2023, arXiv:2303.01289. [Google Scholar]
- Xu, X.; Zhang, J.; Liu, F.; Sugiyama, M.; Kankanhalli, M.S. Efficient adversarial contrastive learning via robustness-aware coreset selection. Adv. Neural Inf. Process. Syst. 2024, 36, 75798–75825. [Google Scholar]
- Liu, Y.; Cheng, Y.; Gao, L.; Liu, X.; Zhang, Q.; Song, J. Practical evaluation of adversarial robustness via adaptive auto attack. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 15105–15114. [Google Scholar]
- Naseer, M.; Khan, S.; Hayat, M.; Khan, F.S.; Porikli, F. A self-supervised approach for adversarial robustness. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 262–271. [Google Scholar]
- Deng, Y.; Karam, L.J. Universal adversarial attack via enhanced projected gradient descent. In Proceedings of the 2020 IEEE International Conference on Image Processing (ICIP), Virtual, 25–28 October 2020; pp. 1241–1245. [Google Scholar]
- Liu, Z.; Xu, Y.; Ji, X.; Chan, A.B. Twins: A fine-tuning framework for improved transferability of adversarial robustness and generalization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 16436–16446. [Google Scholar]
- Xu, X.; Zhang, J.; Kankanhalli, M. Autolora: A parameter-free automated robust fine-tuning framework. arXiv 2023, arXiv:2310.01818. [Google Scholar]
- Hua, A.; Gu, J.; Xue, Z.; Carlini, N.; Wong, E.; Qin, Y. Initialization matters for adversarial transfer learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 24831–24840. [Google Scholar]
- Zhang, C.; Zhang, K.; Zhang, C.; Niu, A.; Feng, J.; Yoo, C.D.; Kweon, I.S. Decoupled adversarial contrastive learning for self-supervised adversarial robustness. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 725–742. [Google Scholar]
- Pan, H.; Guo, Y.; Deng, Q.; Yang, H.; Chen, J.; Chen, Y. Improving fine-tuning of self-supervised models with contrastive initialization. Neural Netw. 2023, 159, 198–207. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, Y.; Jiao, J.; Xing, E.; El Ghaoui, L.; Jordan, M. Theoretically principled trade-off between robustness and accuracy. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 7472–7482. [Google Scholar]
- Krizhevsky, A.; Hinton, G. Learning Multiple Layers of Features from Tiny Images; University of Tront: Trento, Italy, 2009. [Google Scholar]
- Arcos-García, Á.; Alvarez-Garcia, J.A.; Soria-Morillo, L.M. Deep neural network for traffic sign recognition systems: An analysis of spatial transformers and stochastic optimisation methods. Neural Netw. 2018, 99, 158–165. [Google Scholar] [CrossRef]
- Yu, Q.; Lou, J.; Zhan, X.; Li, Q.; Zuo, W.; Liu, Y.; Liu, J. Adversarial Contrastive Learning via Asymmetric InfoNCE. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Cham, Switzerland, 2022; pp. 53–69. [Google Scholar]
- Xu, X.; Zhang, J.; Liu, F.; Sugiyama, M.; Kankanhalli, M. Enhancing Adversarial Contrastive Learning via Adversarial Invariant Regularization. In Proceedings of the Thirty-Seventh Conference on Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023. [Google Scholar]
- Li, Y.; Lyu, L.; Bai, S.; Li, B. Backdoor Learning: A Survey. arXiv 2020, arXiv:2007.08745. [Google Scholar] [CrossRef] [PubMed]
- Corporation, N. Jetson Nano Developer Kit. 2024. Available online: https://developer.nvidia.com/embedded/jetson-nano/ (accessed on 23 April 2025).
- LLC, Google Coral USB Accelerator. 2024. Available online: https://iot.asus.com/gpu-edge-ai-accelerators/google-tpu/ (accessed on 23 April 2025).
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1765–1773. [Google Scholar]
- Jang, U.; Wu, X.; Jha, S. Objective metrics and gradient descent algorithms for adversarial examples in machine learning. In Proceedings of the 33rd Annual Computer Security Applications Conference, Orlando, FL, USA, 4–8 December 2017; pp. 262–277. [Google Scholar]
- Brendel, W.; Rauber, J.; Bethge, M. Decision-based adversarial attacks: Reliable attacks against black-box machine learning models. arXiv 2017, arXiv:1712.04248. [Google Scholar]
- Chen, P.Y.; Sharma, Y.; Zhang, H.; Yi, J.; Hsieh, C.J. Ead: Elastic-net attacks to deep neural networks via adversarial examples. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 30 October–3 November 2017; pp. 15–26. [Google Scholar]
- Engstrom, L.; Tran, B.; Tsipras, D.; Schmidt, L.; Madry, A. Exploring the landscape of spatial robustness. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 1802–1811. [Google Scholar]
- Chen, J.; Jordan, M.I.; Wainwright, M.J. Hopskipjumpattack: A query-efficient decision-based attack. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–21 May 2020; pp. 1277–1294. [Google Scholar]
- Ghiasi, A.; Shafahi, A.; Goldstein, T. Breaking certified defenses: Semantic adversarial examples with spoofed robustness certificates. arXiv 2020, arXiv:2003.08937. [Google Scholar]
- Rahmati, A.; Moosavi-Dezfooli, S.M.; Frossard, P.; Dai, H. Geoda: A geometric framework for black-box adversarial attacks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 8446–8455. [Google Scholar]
- Wong, E.; Schmidt, F.; Kolter, Z. Wasserstein adversarial examples via projected sinkhorn iterations. In Proceedings of the International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; pp. 6808–6817. [Google Scholar]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: Boca Raton, FL, USA, 2018; pp. 99–112. [Google Scholar]
- Dong, Y.; Liao, F.; Pang, T.; Su, H.; Zhu, J.; Hu, X.; Li, J. Boosting adversarial attacks with momentum. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 9185–9193. [Google Scholar]
- Dong, Y.; Pang, T.; Su, H.; Zhu, J. Evading defenses to transferable adversarial examples by translation-invariant attacks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 4312–4321. [Google Scholar]
- Tramèr, F.; Kurakin, A.; Papernot, N.; Goodfellow, I.; Boneh, D.; McDaniel, P. Ensemble adversarial training: Attacks and defenses. arXiv 2017, arXiv:1705.07204. [Google Scholar]
- Croce, F.; Hein, M. Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks. In Proceedings of the International Conference on Machine Learning, Virtual, 12–18 July 2020; pp. 2206–2216. [Google Scholar]
- Wong, E.; Rice, L.; Kolter, J.Z. Fast is better than free: Revisiting adversarial training. arXiv 2020, arXiv:2001.03994. [Google Scholar]
- Liu, X.; Li, Y.; Wu, C.; Hsieh, C.J. Adv-bnn: Improved adversarial defense through robust bayesian neural network. arXiv 2018, arXiv:1810.01279. [Google Scholar]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Croce, F.; Hein, M. Minimally distorted adversarial examples with a fast adaptive boundary attack. In Proceedings of the International Conference on Machine Learning, Virtual, 12–18 July 2020; pp. 2196–2205. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).