Heterogeneous Multi-Sensor Fusion for AC Motor Fault Diagnosis via Graph Neural Networks
Abstract
1. Introduction
- (1)
- Multi-Task Enhanced (MTE) Autoencoder for Feature Extraction: This module is designed to learn discriminative feature representations, particularly within heterogeneous sensor data. By combining the representation learning capability of autoencoders with two auxiliary tasks—an anomaly detection task to enhance feature discriminability for fault diagnosis and a sensor-type classification task to embed sensor-specific information—the module improves feature robustness. The encoder architecture is able to extract multi-scale features using a CNN and self-attention mechanism, optimizing its effectiveness in processing vibration and current signals from AC motor systems.
- (2)
- Physics-Informed Adjacency Matrix Construction: By incorporating data-driven correlation learning and the physical constraints from sensor configurations, an adjacency matrix builder is established for the connections between nodes. This hybrid approach improves both the generalization capability and noise robustness of the resulting graph representations.
- (3)
- GIN-Based Diagnostic Framework: We have developed an end-to-end fault diagnosis system that uses a GIN for node information aggregation and stacking readouts for effective graph-level feature learning. This framework achieves a state-of-the-art performance on new heterogeneous multi-sensor datasets, demonstrating its strong generalizability.
2. Preliminaries
2.1. Problem Definition
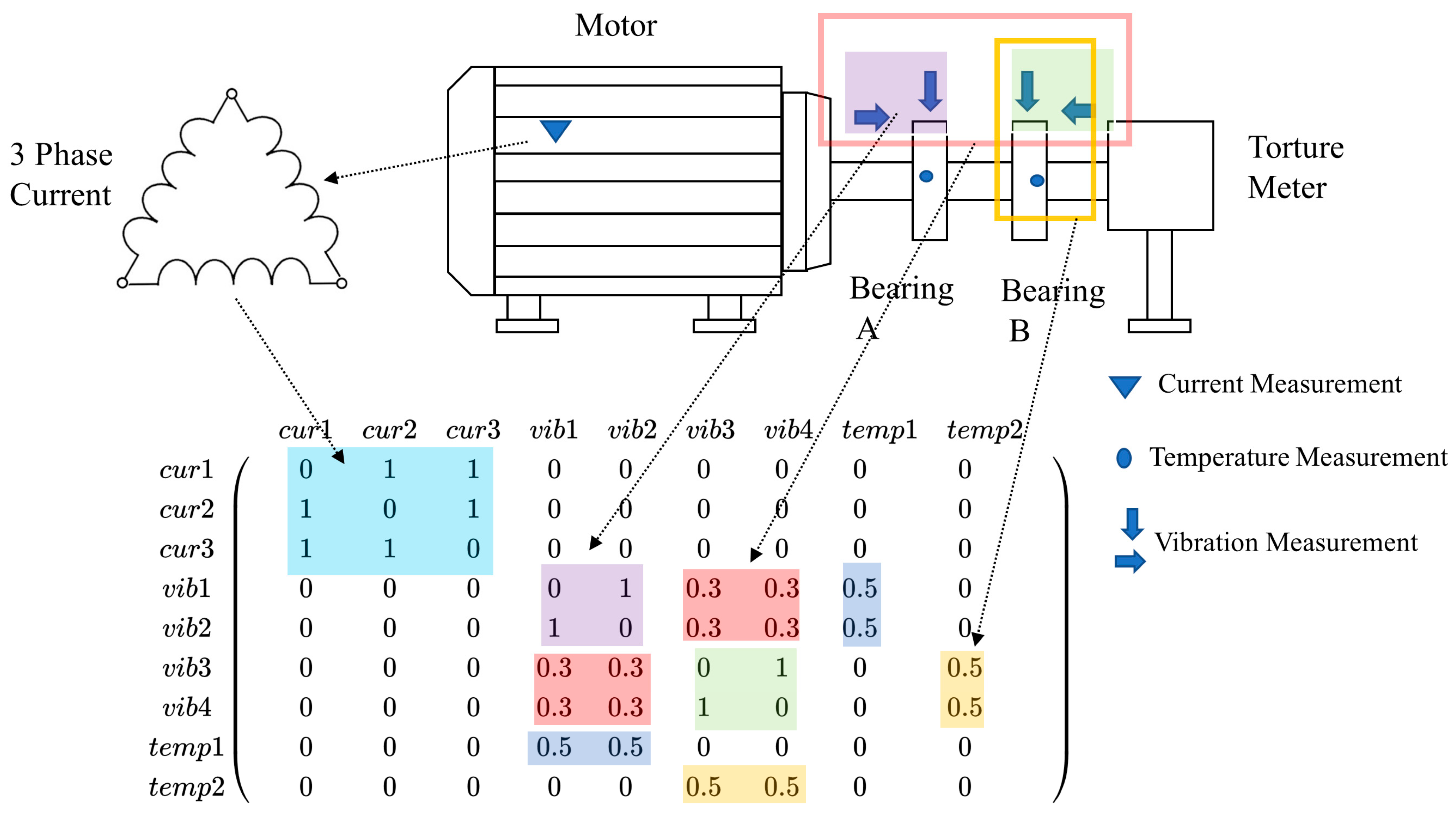
2.2. Multi-Sensor Signals for Fault Diagnosis
2.3. Background to the GNN
3. Proposed Method
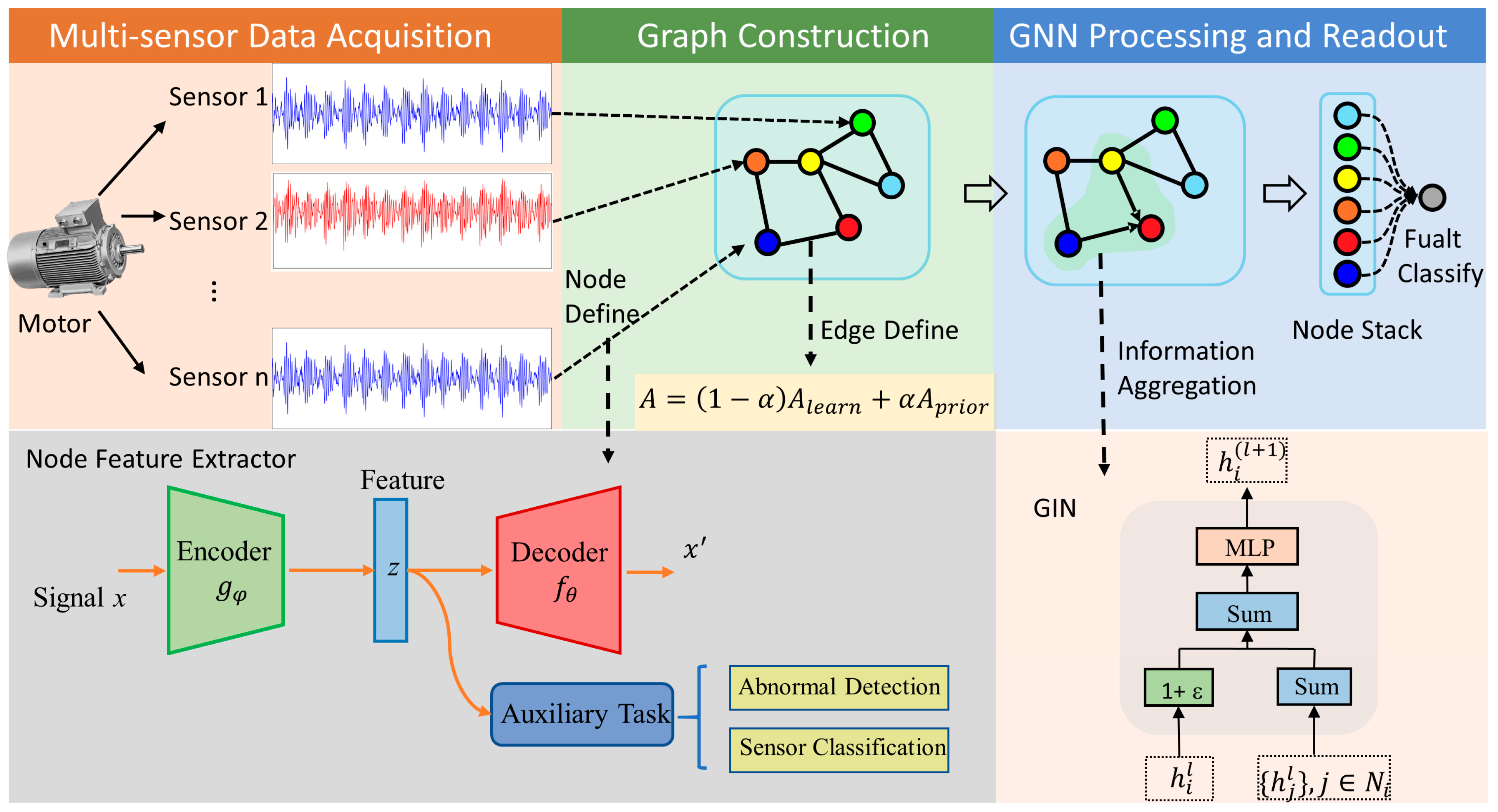
3.1. Overview of Model Architecture
- (1)
- Multi-sensor Data Acquisition
- (2)
- Graph Construction
- (3)
- GNN Processing and Graph Readout
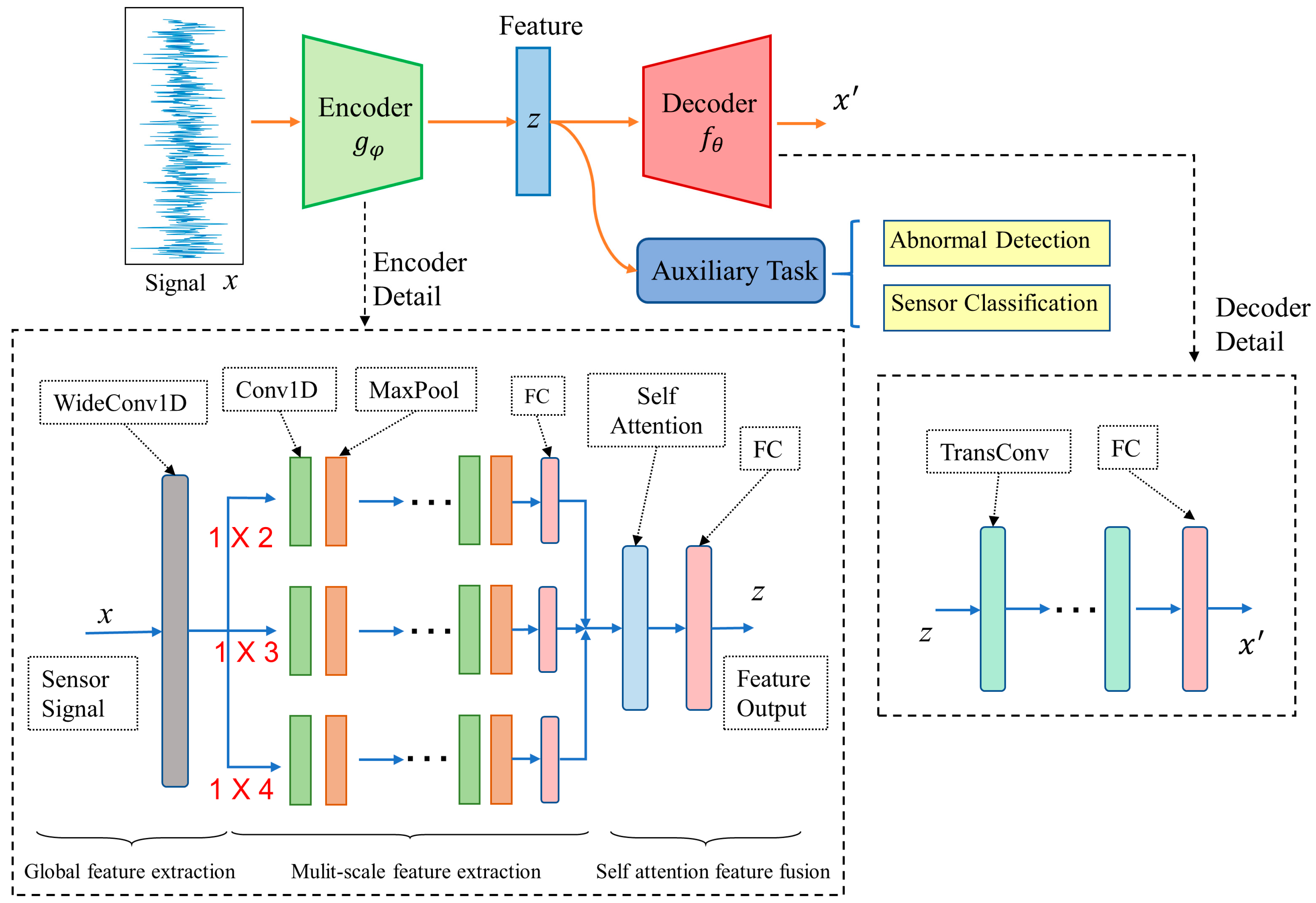
3.2. Multi-Task Enhanced Autoencoder for Feature Extraction
3.2.1. General Framework for Node Extractor
3.2.2. Multi-Scale CNN Encoder
3.2.3. Transposed CNN-Based Decoder
3.3. Adjacent Matrix Builder with Physical Constraint
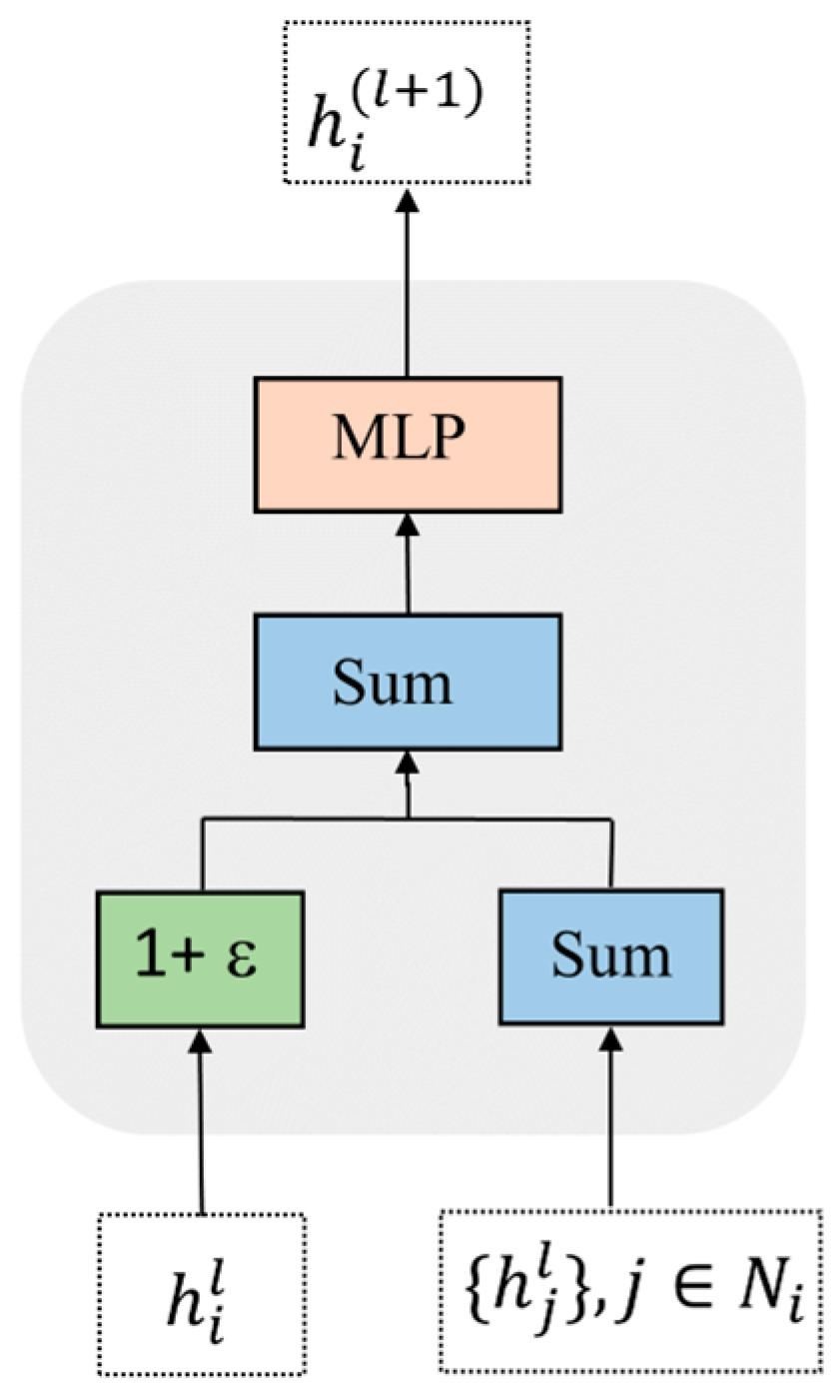
3.4. GIN Processing and Readout
4. Experiments
4.1. Dataset Description
4.2. Data Preprocessing and Model Training
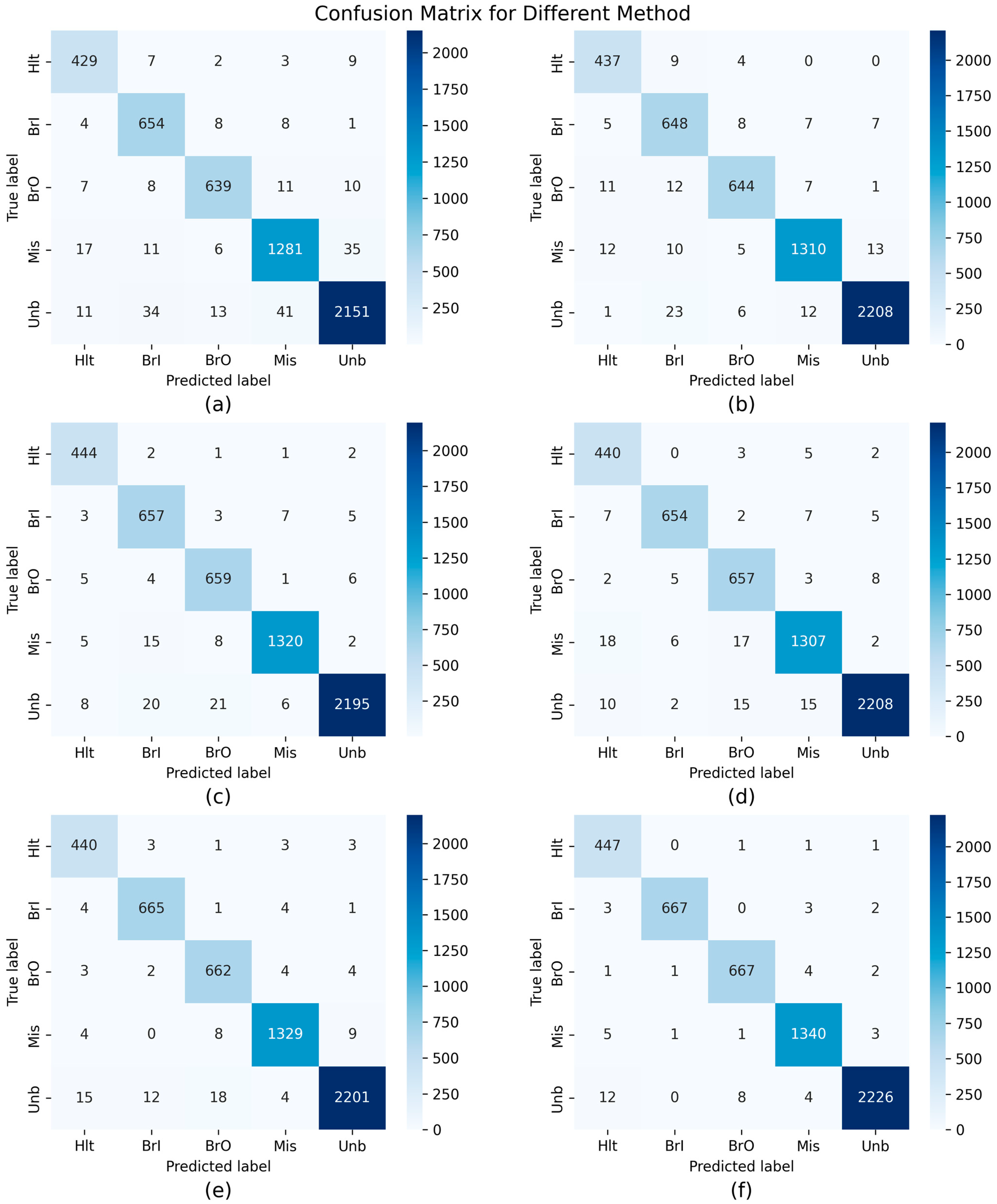
4.3. Comparative Experiment
4.4. Analysis of MTE Node Feature Extractor
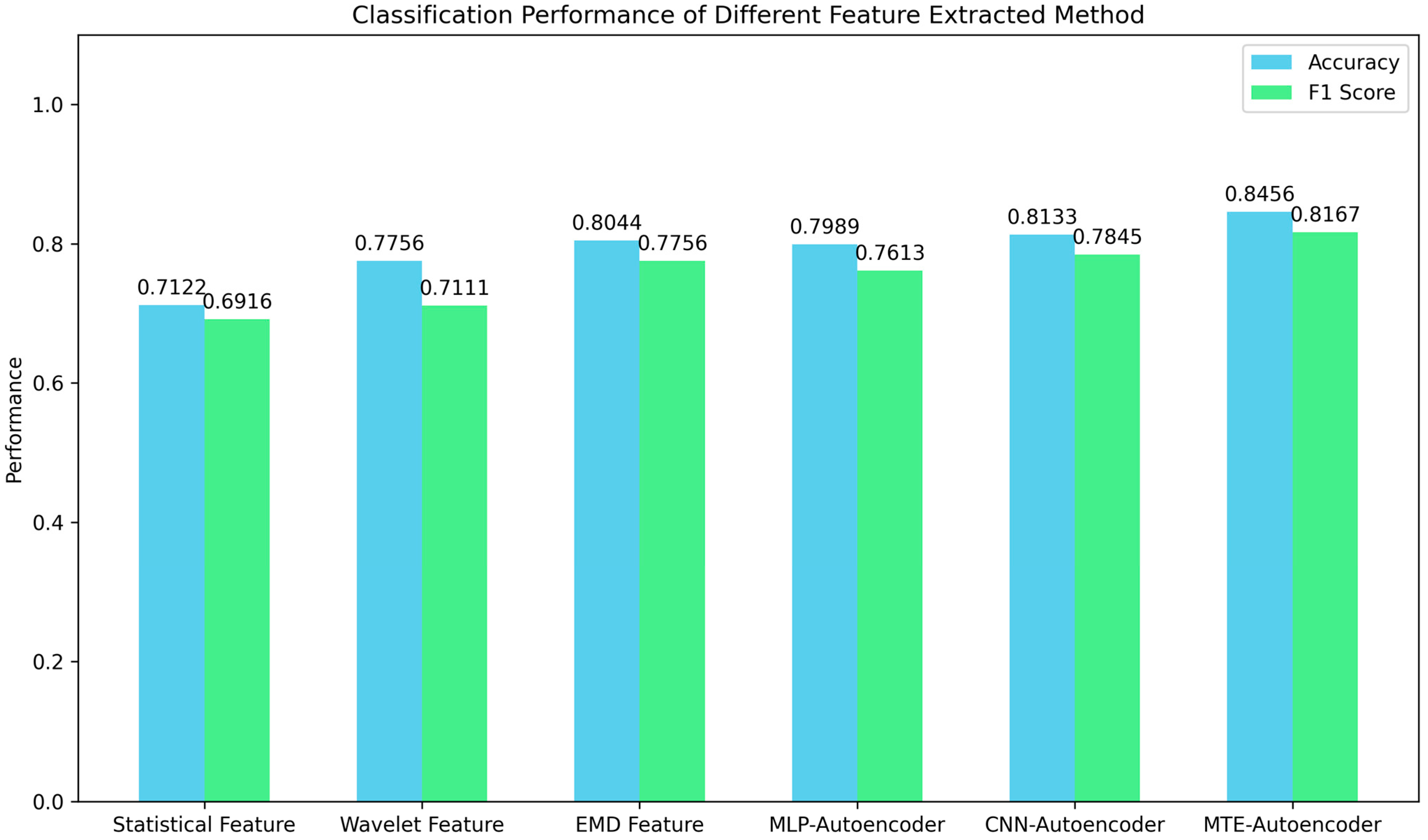
4.4.1. Comparative Study of Different Feature Extraction Methods
4.4.2. Comparative Study of Different Task Combinations
4.5. Noise Resistance
4.6. Hyperparameter Sensitivity Analysis
4.6.1. Weighting Factor of Physical Prior Constraints
4.6.2. Number of Retained Edges
5. Conclusions
- (1)
- Dynamic Correlation Modeling: developing adaptive feature representations and GNN architectures to capture the spatiotemporal correlations seen under varying operational conditions.
- (2)
- Enhanced Physical Information Integration: exploring methods that could be used to incorporate additional physical knowledge (e.g., motor specifications, fault physics) into the model through techniques like physics-guided data augmentation or physics-embedded network structures.
- (3)
- Model Interpretability: developing explainable AI techniques that could provide diagnostic insights, support root-cause analyses, and enable predictive maintenance strategies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bahgat, B.H.; Elhay, E.A.; Elkholy, M.M. Advanced fault detection technique of three phase induction motor: Comprehensive review. Discov. Discov. Electron. 2024, 1, 9. [Google Scholar] [CrossRef]
- Niu, G.; Dong, X.; Chen, Y. Motor Fault Diagnostics Based on Current Signatures: A Review. IEEE Trans. Instrum. Meas. 2023, 72, 1–19. [Google Scholar] [CrossRef]
- Hu, W.; Xin, G.; Wu, J.; An, G.; Li, Y.; Feng, K.; Antoni, J. Vibration-based bearing fault diagnosis of high-speed trains: A literature review. High-Speed Railw. 2023, 1, 219–223. [Google Scholar] [CrossRef]
- Kibrete, F.; Engida Woldemichael, D.; Shimels Gebremedhen, H. Multi-Sensor data fusion in intelligent fault diagnosis of rotating machines: A comprehensive review. Measurement 2024, 232, 114658. [Google Scholar] [CrossRef]
- Jing, L.; Wang, T.; Zhao, M.; Wang, P. An Adaptive Multi-Sensor Data Fusion Method Based on Deep Convolutional Neural Networks for Fault Diagnosis of Planetary Gearbox. Sensors 2017, 17, 414. [Google Scholar] [CrossRef]
- Janssens, O.; Loccufier, M.; Van Hoecke, S. Thermal Imaging and Vibration-Based Multisensor Fault Detection for Rotating Machinery. IEEE Trans. Ind. Inform. 2019, 15, 434–444. [Google Scholar] [CrossRef]
- Shao, S.; Yan, R.; Lu, Y.; Wang, P.; Gao, R.X. DCNN-Based Multi-Signal Induction Motor Fault Diagnosis. IEEE Trans. Instrum. Meas. 2020, 69, 2658–2669. [Google Scholar] [CrossRef]
- Mousavi, S.; Bayram, D.; Seker, S. Current Data Fusion through Kalman Filtering for Fault Detection and Sensor Validation of an Electric Motor. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics, ACEMP 2019 and 2019 International Conference on Optimization of Electrical and Electronic Equipment, OPTIM 2019, Istanbul, Turkey, 27–29 August 2019; pp. 155–160. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Sarda, K.; Acernese, A.; Russo, L.; Manfredi, L.; Glielmo, L.; Del Vecchio, C. A fuzzy logic-based approach for fault diagnosis and condition monitoring of industry 4.0 manufacturing processes. Eng. Appl. Artif. Intell. 2022, 115, 105317. [Google Scholar] [CrossRef]
- Hamda, N.E.I.; Hadjali, A.; Lagha, M. Multisensor Data Fusion in IoT Environments in Dempster-Shafer Theory Setting: An Improved Evidence Distance-Based Approach. Sensors 2023, 23, 5141. [Google Scholar] [CrossRef]
- Teng, S.; Chen, G.; Liu, Z.; Cheng, L.; Sun, X. Multi-Sensor and Decision-Level Fusion-Based Structural Damage Detection Using a One-Dimensional Convolutional Neural Network. Sensors 2021, 21, 3950. [Google Scholar] [CrossRef]
- Parai, M.; Srimani, S.; Ghosh, K.; Rahaman, H. Multi-source data fusion technique for parametric fault diagnosis in analog circuits. Integration 2022, 84, 92–101. [Google Scholar] [CrossRef]
- Song, Q.; Zhao, S.; Wang, M. On the Accuracy of Fault Diagnosis for Rolling Element Bearings Using Improved DFA and Multi-Sensor Data Fusion Method. Sensors 2020, 20, 6465. [Google Scholar] [CrossRef] [PubMed]
- Pan, L.; Zhu, D.; She, S.; Song, A.; Shi, X.; Duan, S. Gear fault diagnosis method based on wavelet-packet independent component analysis and support vector machine with kernel function fusion. Adv. Mech. Eng. 2018, 10, 1687814018811036. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, W.; Kang, S.; Tian, X.; Kang, X.; Sun, F. Enhanced Feature Extraction Network Based on Acoustic Signal Feature Learning for Bearing Fault Diagnosis. Sensors 2023, 23, 8703. [Google Scholar] [CrossRef] [PubMed]
- Grover, C.; Turk, N. A novel fault diagnostic system for rolling element bearings using deep transfer learning on bispectrum contour maps. Eng. Sci. Technol. Int. J. 2022, 31, 101049. [Google Scholar] [CrossRef]
- Gong, W.; Chen, H.; Zhang, Z.; Zhang, M.; Wang, R.; Guan, C.; Wang, Q. A Novel Deep Learning Method for Intelligent Fault Diagnosis of Rotating Machinery Based on Improved CNN-SVM and Multichannel Data Fusion. Sensors 2019, 19, 1693. [Google Scholar] [CrossRef]
- Qian, L.; Li, B.; Chen, L. CNN-Based Feature Fusion Motor Fault Diagnosis. Electronics 2022, 11, 2746. [Google Scholar] [CrossRef]
- Wang, H.; Sun, W.; He, L.; Zhou, J. Rolling Bearing Fault Diagnosis Using Multi-Sensor Data Fusion Based on 1D-CNN Model. Entropy 2022, 24, 573. [Google Scholar] [CrossRef]
- Wang, D.; Li, Y.; Jia, L.; Song, Y.; Liu, Y. Novel Three-Stage Feature Fusion Method of Multimodal Data for Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Hao, S.; Ge, F.-X.; Li, Y.; Jiang, J. Multisensor bearing fault diagnosis based on one-dimensional convolutional long short-term memory networks. Measurement 2020, 159, 107802. [Google Scholar] [CrossRef]
- Xie, T.; Huang, X.; Choi, S.K. Multi-sensor data fusion for rotating machinery fault diagnosis using residual convolutional neural network. In Proceedings of the ASME Design Engineering Technical Conference 2, Virtual, Online, 17–19 August 2021. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X.; Zhang, X.; Yan, R. A Deep Coupled Network for Health State Assessment of Cutting Tools Based on Fusion of Multisensory Signals. IEEE Trans. Ind. Inform. 2019, 15, 6415–6424. [Google Scholar] [CrossRef]
- Ma, M.; Sun, C.; Chen, X. Deep Coupling Autoencoder for Fault Diagnosis With Multimodal Sensory Data. IEEE Trans. Ind. Inform. 2018, 14, 1137–1145. [Google Scholar] [CrossRef]
- He, Y.; Tang, H.; Ren, Y.; Kumar, A. A deep multi-signal fusion adversarial model based transfer learning and residual network for axial piston pump fault diagnosis. Measurement 2022, 192, 110889. [Google Scholar] [CrossRef]
- Long, Z.; Guo, J.; Ma, X.; Wu, G.; Rao, Z.; Zhang, X.; Xu, Z. Motor fault diagnosis based on multisensor-driven visual information fusion. ISA Trans. 2024, 155, 524–535. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Z.; Li, X.; Shao, H.; Han, T.; Xie, M. Attention-aware temporal–spatial graph neural network with multi-sensor information fusion for fault diagnosis. Knowl.-Based Syst. 2023, 278, 110891. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, J.C.; Ni, Q.; Feng, K.; Beer, M.; Chen, H. A graph-guided collaborative convolutional neural network for fault diagnosis of electromechanical systems. Mech. Syst. Signal Process. 2023, 200, 110609. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Li, M.; Dai, X.; Wang, R.; Shi, L. A Gearbox Fault Diagnosis Method Based on Graph Neural Networks and Markov Transform Fields. IEEE Sens. J. 2024, 24, 25186–25196. [Google Scholar] [CrossRef]
- Duan, H.; Chen, G.; Yu, Y.; Du, C.; Bao, Z.; Ma, D. DyGAT-FTNet: A Dynamic Graph Attention Network for Multi-Sensor Fault Diagnosis and Time-Frequency Data Fusion. Sensors 2025, 25, 810. [Google Scholar] [CrossRef]
- Wang, C.; Wang, Y.; Wang, Y.; Li, X.; Chen, Z. Richly connected spatial–temporal graph neural network for rotating machinery fault diagnosis with multi-sensor information fusion. Mech. Syst. Signal Process. 2025, 225, 112230. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Vibration response of spalled rolling element bearings: Observations, simulations and signal processing techniques to track the spall size. Mech. Syst. Signal Process. 2011, 25, 846–870. [Google Scholar] [CrossRef]
- Khemani, B.; Patil, S.; Kotecha, K.; Tanwar, S. A review of graph neural networks: Concepts, architectures, techniques, challenges, datasets, applications, and future directions. J. Big Data 2024, 11, 18. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. End-to-end heterogeneous graph neural networks for traffic assignment. Transp. Res. Part C Emerg. Technol. 2024, 165, 104695. [Google Scholar] [CrossRef]
- Yan, R.; Shang, Z.; Xu, H.; Wen, J.; Zhao, Z.; Chen, X.; Gao, R.X. Wavelet transform for rotary machine fault diagnosis:10 years revisited. Mech. Syst. Signal Process. 2023, 200, 110545. [Google Scholar] [CrossRef]
- Yang, Y.; YuDejie; Cheng, J. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J. Sound Vib. 2006, 294, 269–277. [Google Scholar] [CrossRef]
- Chen, X.; Zhang, B.; Gao, D. Bearing fault diagnosis base on multi-scale CNN and LSTM model. J. Intell. Manuf. 2020, 32, 971–987. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Z.; Li, X.; Deng, X.; Jiang, W. Comprehensive dynamic structure graph neural network for aero-engine remaining useful life prediction. IEEE Trans. Instrum. Meas. 2023, 72, 3533816. [Google Scholar] [CrossRef]
- Chen, X.; Zeng, M. Convolution-Graph Attention Network With Sensor Embeddings for Remaining Useful Life Prediction of Turbofan Engines. IEEE Sens. J. 2023, 23, 15786–15794. [Google Scholar] [CrossRef]
- Xu, K.; Hu, W.; Leskovec, J.; Jegelka, S. How powerful are graph neural networks? arXiv 2018, arXiv:1810.00826. [Google Scholar]
- Jung, W.; Kim, S.-H.; Yun, S.-H.; Bae, J.; Park, Y.-H. Vibration, acoustic, temperature, and motor current dataset of rotating machine under varying operating conditions for fault diagnosis. Data Brief 2023, 48, 109049. [Google Scholar] [CrossRef]
- Sehri, M.; Dumond, P. University of Ottawa constant and variable speed electric motor vibration and acoustic fault signature dataset. Data Brief 2024, 53, 110144. [Google Scholar] [CrossRef]

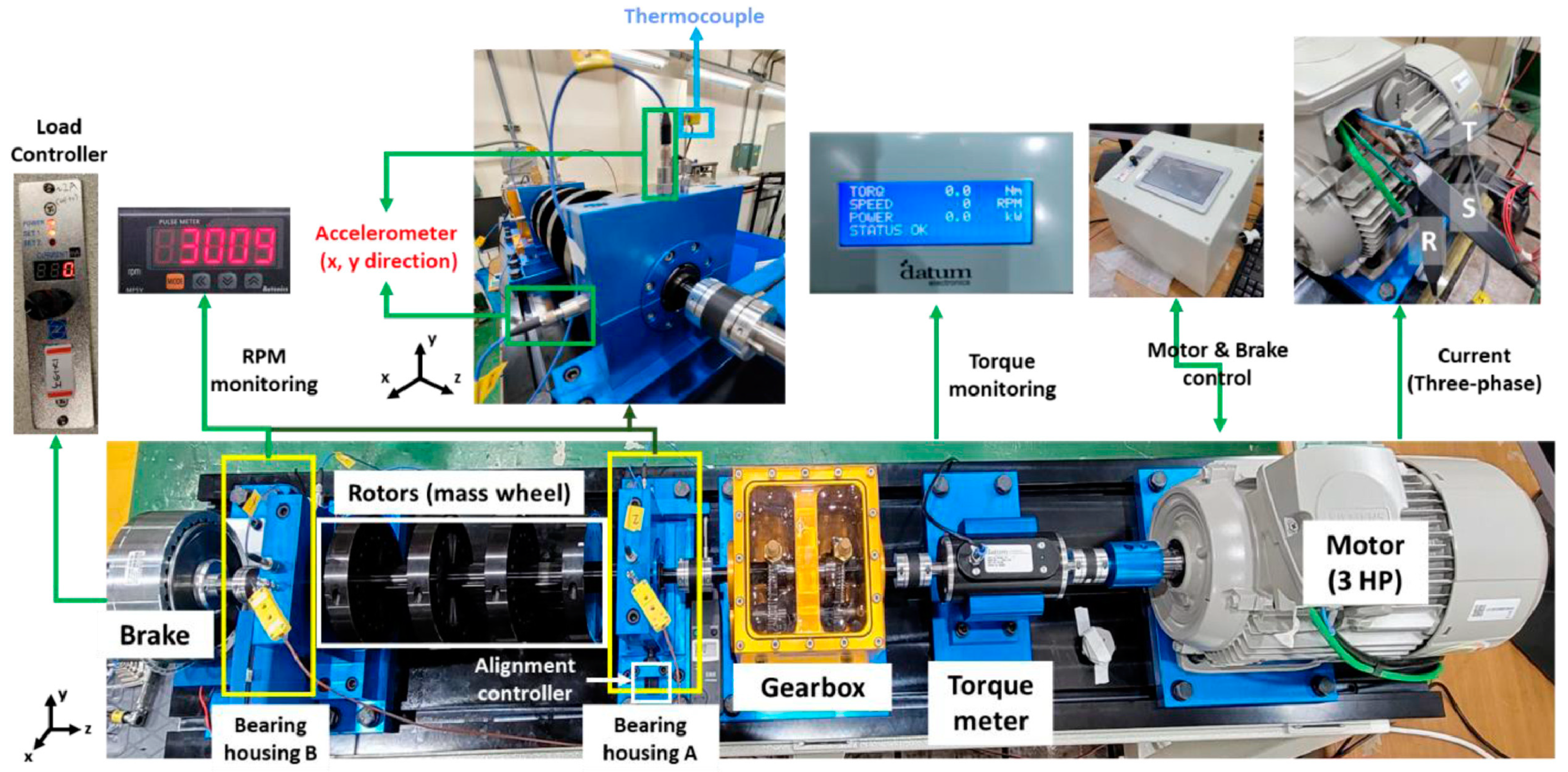


| Dataset | Sensor | Data Type | Model | Quantity | Location | Load Condition | Sample Rate (kHz) |
|---|---|---|---|---|---|---|---|
| VATMCD | Accelerometers | Vibration | PCB35234 | 4 | Bearing A&B (x,y) | 0, 2, 4 (Nm) | 25.6 |
| Thermocouples | Temperature | PCB378B02 | 2 | Bearing A&B | 0, 2, 4 (Nm) | 25.6 | |
| Microphones | Acoustic | K-type | 1 | Near bearing A | 0 (Nm) | 51.2 | |
| Current Sensors | Current | Hioki CT6700 | 3 | Motor | 0, 2, 4 (Nm) | 25.6 | |
| UOEMD | Accelerometers | Vibration | PCB623C01 | 3 | Motor drive, Bearing L&R | Loaded, Unloaded | 42 |
| Thermocouples | Temperature | PCB603C01 | 1 | Motor drive | Loaded, Unloaded | 42 | |
| Microphones | Acoustic | PCB 130F20 | 1 | Near bearing L | Loaded, Unloaded | 42 |
| Module | Hyperparameter | Value |
|---|---|---|
| Node Feature Extractor | Number of CNN layers in each encoder branch | 3 |
| Self-attention input dimension | 64 | |
| Number of self-attention heads | 3 | |
| Encoder output dimension | 32 | |
| Number of transposed convolution layers | 4 | |
| Number of MLP layers for auxiliary task | 3 | |
| Batch size | 32 | |
| Training epochs | 100 | |
| Learning rate | 0.001 | |
| Adjacent Matrix Builder | Weighting factor of physical prior constraints | 0.4/0.4 * |
| Number of retained edges | 20/7 * | |
| GIN | Number of hidden layers | 4 |
| Batch size | 32 | |
| Training epochs | 100 | |
| Learning rate | 0.001 |
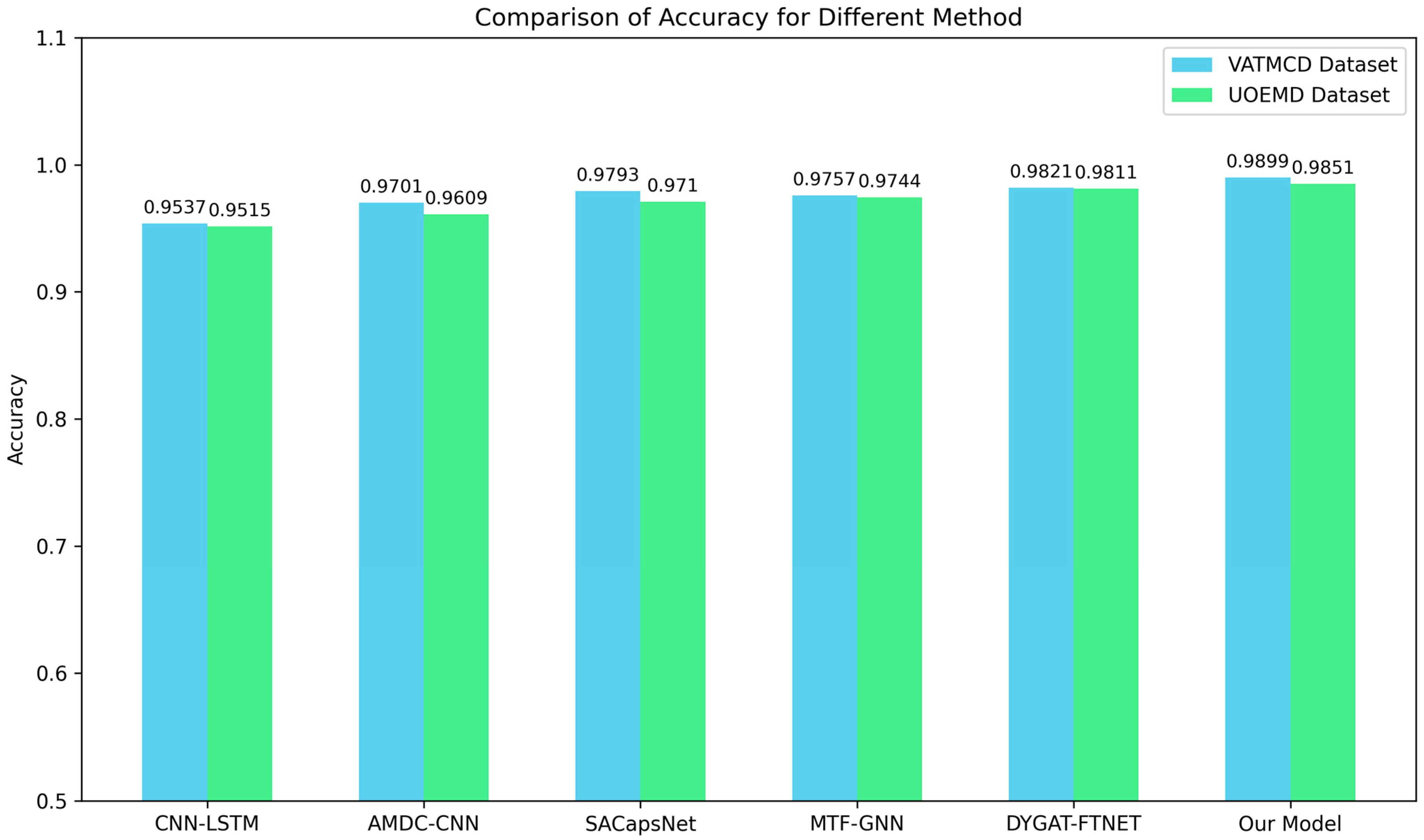
| Method | VATMCD | UOEMD | ||
|---|---|---|---|---|
| Accuracy | F1 Score | Accuracy | F1 Score | |
| CNN-LSTM | 0.9537 | 0.9434 | 0.9515 | 0.9514 |
| AMDC-CNN | 0.9701 | 0.9623 | 0.9609 | 0.9609 |
| SACapsNet | 0.9793 | 0.9751 | 0.9710 | 0.9708 |
| MTF-GNN | 0.9757 | 0.9697 | 0.9744 | 0.9743 |
| DYGAT-FTNET | 0.9821 | 0.9772 | 0.9811 | 0.9809 |
| Our Model | 0.9899 | 0.9878 | 0.9851 | 0.9850 |
| Method | Description |
|---|---|
| Statistical Feature-Based Model | A total of 16 time-domain and frequency-domain statistical features including the mean amplitude, root mean square, square mean root, peak value, peak-to-peak value, variance, standard deviation, waveform factor, kurtosis coefficient, skewness coefficient, frequency center, mean frequency, frequency variance, mean standard frequency, frequency ratio, and standard deviation frequency. |
| Wavelet Feature-Based Model | Signal decomposition using db4 wavelet with three decomposition levels (yielding eight sub-bands). Four features (mean, root mean square, energy ratio, and kurtosis) were extracted from each sub-band, resulting in 24-dimensional feature vectors. |
| EMD Feature-Based Model | Empirical mode decomposition produced eight intrinsic mode functions (IMFs), with four features (mean, root mean square, energy ratio, and kurtosis), per IMF, yielding 24-dimensional feature vectors. |
| MLP Autoencoder | Four-layer MLP encoder and decoder architecture with 32-dimensional representation of latent space. |
| CNN Autoencoder | Four-layer CNN encoder and transposed CNN decoder architecture with 32-dimensional representation of latent space. |
| Multi-task Enhanced Autoencoder | Architecture as described in Section 3.2, with 32-dimensional representation of latent space. |
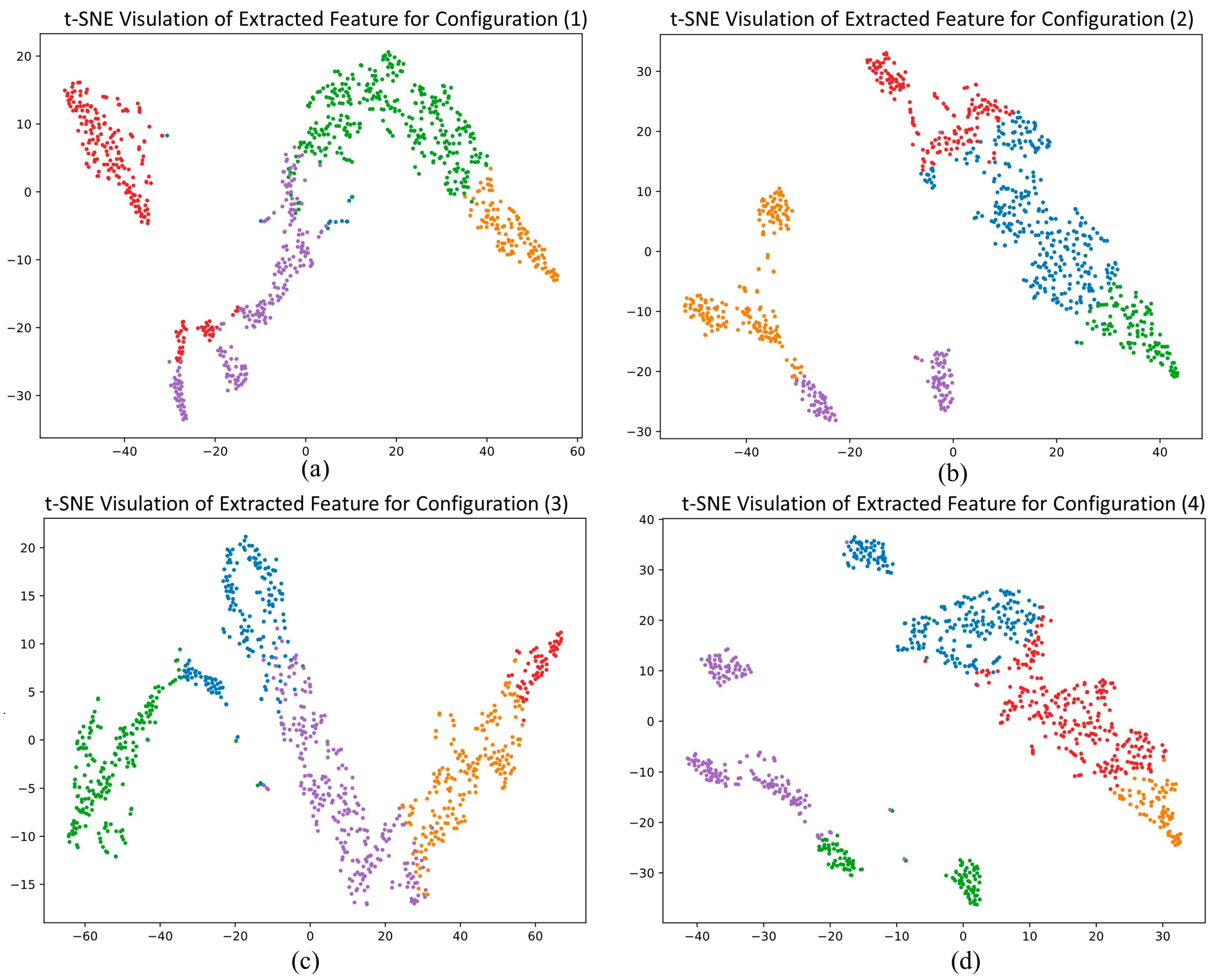
| Configurations | SI | CHI | DBI |
|---|---|---|---|
| (1) Reconstruction alone | 0.3914 | 1030.62 | 0.8891 |
| (2) Reconstruction with abnormal detection | 0.4736 | 1202.06 | 0.8695 |
| (3) Reconstruction with sensor-typeclassification | 0.4063 | 1153.18 | 0.8809 |
| (4) Reconstruction with both abnormal detection and sensor-type classification | 0.5195 | 1610.89 | 0.8519 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Y.; Li, W.; Lian, G.; Li, J. Heterogeneous Multi-Sensor Fusion for AC Motor Fault Diagnosis via Graph Neural Networks. Electronics 2025, 14, 2005. https://doi.org/10.3390/electronics14102005
Liao Y, Li W, Lian G, Li J. Heterogeneous Multi-Sensor Fusion for AC Motor Fault Diagnosis via Graph Neural Networks. Electronics. 2025; 14(10):2005. https://doi.org/10.3390/electronics14102005
Chicago/Turabian StyleLiao, Yuandong, Wenyong Li, Guan Lian, and Junzhuo Li. 2025. "Heterogeneous Multi-Sensor Fusion for AC Motor Fault Diagnosis via Graph Neural Networks" Electronics 14, no. 10: 2005. https://doi.org/10.3390/electronics14102005
APA StyleLiao, Y., Li, W., Lian, G., & Li, J. (2025). Heterogeneous Multi-Sensor Fusion for AC Motor Fault Diagnosis via Graph Neural Networks. Electronics, 14(10), 2005. https://doi.org/10.3390/electronics14102005






