Efficiency-Enhanced Hybrid Dickson Converter with Quasi-Complete Soft Charging for Direct Large-Ratio Step-Down Applications
Abstract
1. Introduction
- (1)
- The proposed N-order hybrid Dickson converter extends the switch duty cycle by a factor of (2N-1), demonstrating a significant improvement over the N-fold and N/2-fold duty cycle expansions in DIH and HD converters.
- (2)
- An intrinsic charge-ratio-based capacitance optimization method is proposed to achieve quasi-complete soft charging of the flying capacitors, thereby minimizing the spike currents during capacitor network reconfiguration, optimizing the efficiency, and enhancing the capacitor utilization.
- (3)
- To address the unequal inductor currents, a duty-cycle-matching-based current equalization method is proposed. By adjusting the PWM duty cycle ratio, the average currents are equalized, ensuring a balanced loss distribution between inductors.
- (4)
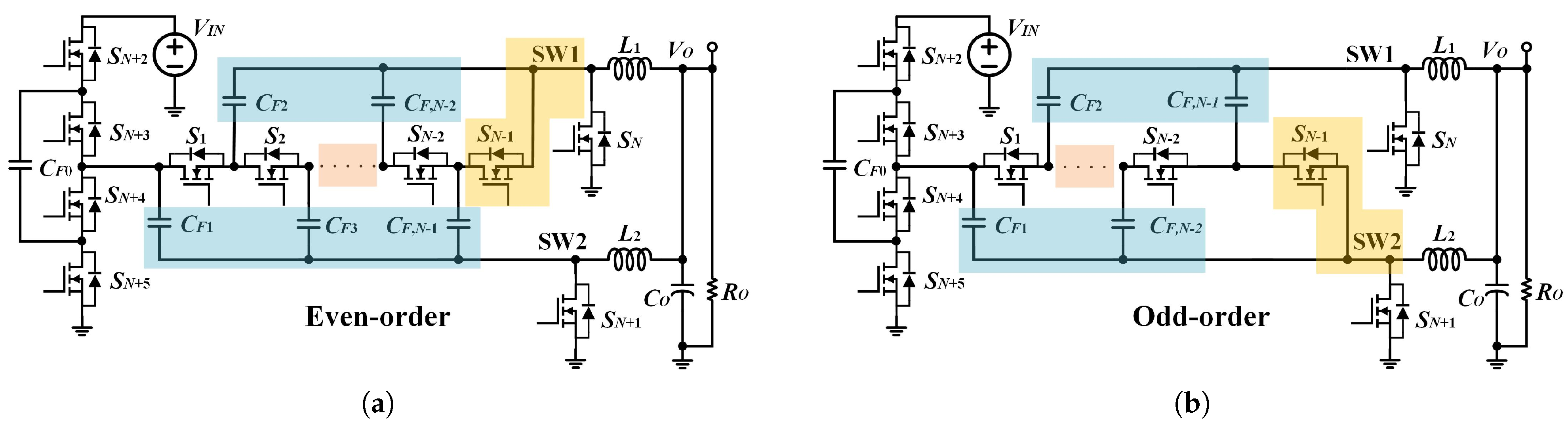
2. The Proposed Converter
2.1. Principle of Operation
2.2. Steady-State Characteristics
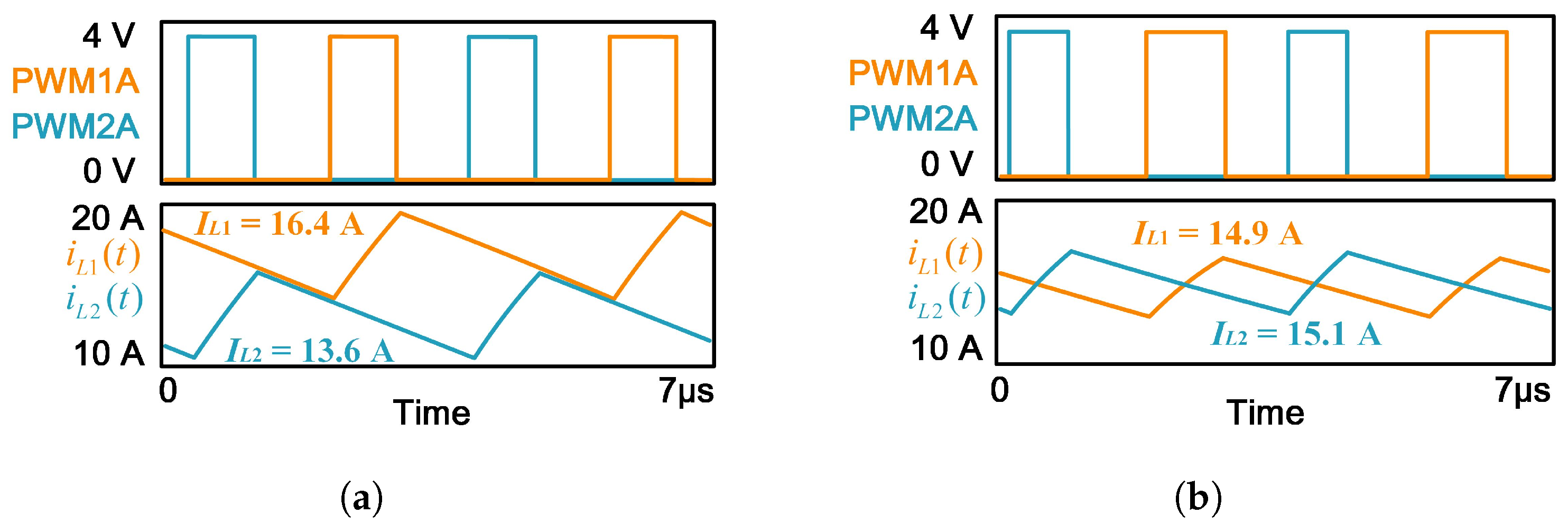
3. Equalization of the Inductor Current
3.1. A Duty-Cycle-Matching-Based Current Equalization Method
3.2. An Analysis of the Inductor Loss
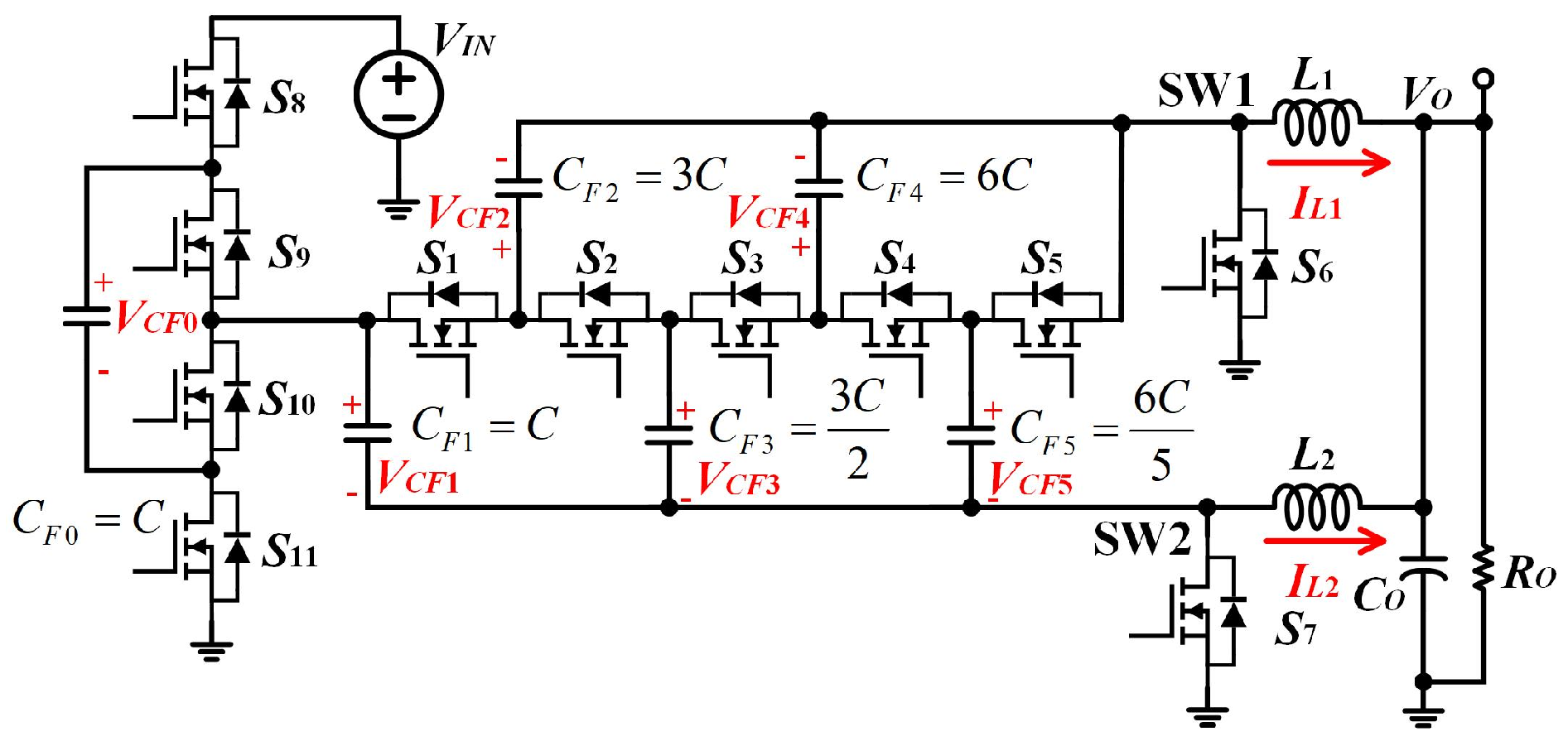
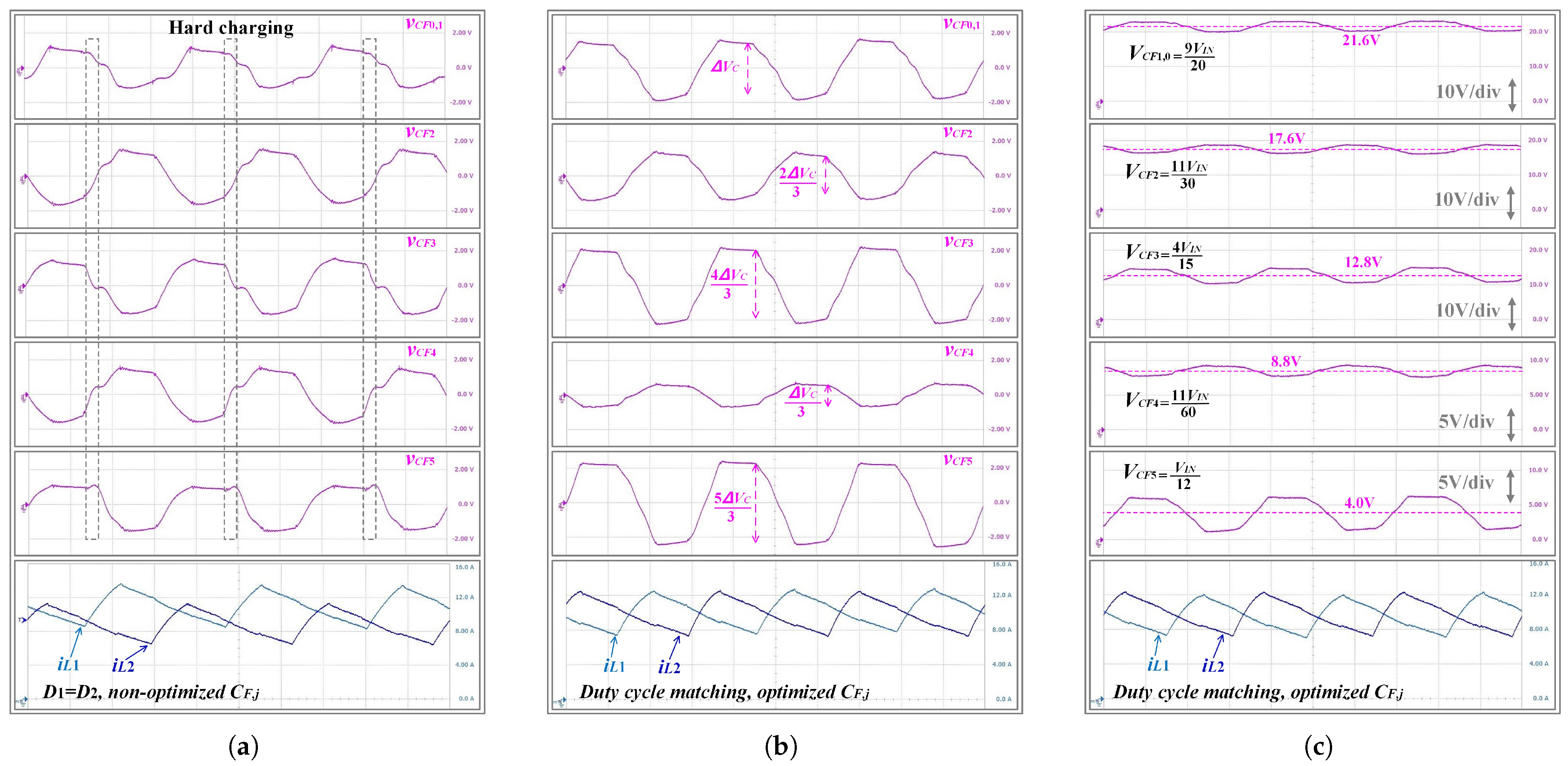
4. Quasi-Complete Soft Charging of Flying Capacitors
4.1. Intrinsic Charge-Ratio-Based Capacitance Optimization
4.2. Capacitance Optimization for N-Order QCSC-TLAHD Converters
4.3. Considerations
5. The Prototype and Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency. Electricity 2024—Analysis and Forecast to 2026. Available online: https://iea.blob.core.windows.net/assets/6b2fd954-2017-408e-bf08-952fdd62118a/Electricity2024-Analysisandforecastto2026.pdf (accessed on 10 March 2025).
- Li, X.; Jiang, S. Google 48 V Power Architecture. Available online: https://ieeetv.ieee.org/ieeetv-specials/keytalk-xin-li-and-shuai-jiang-google-48v-power-architecture-apec-2017 (accessed on 10 March 2025).
- Folmer, S.; Kosakowski, M.; Stala, R. 48-V Input DC-DC High Step-Down Converter in GaN-Based Design. IEEE Access 2022, 10, 115958–115973. [Google Scholar] [CrossRef]
- Rahman, S.; Ayaz, M.A.; Khan, I.A. Review of Non-Isolated DC/DC Converters for Application in Data Center Power Delivery. In Proceedings of the 4th International Conference on Smart Grid and Renewable Energy (SGRE), Doha, Qatar, 8–10 January 2024; pp. 1–6. [Google Scholar]
- Khan, I.; Rahman, S.; Ayaz, M.A.; Amir, M.; Shehada, H. Review of Isolated DC-DC Converters for Application in Data Center Power Delivery. IEEE Trans. Ind. Appl. 2024, 60, 5436–5446. [Google Scholar] [CrossRef]
- Ge, T.; Ye, Z.; Pilawa-Podgurski, R.C.N. A 48-to-12 V Cascaded Multi-Resonant Switched Capacitor Converter with 4700 W/in3 Power Density and 98.9% Efficiency. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 1959–1965. [Google Scholar]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. 48-V Voltage Regulator Module with PCB Winding Matrix Transformer for Future Data Centers. IEEE Trans. Ind. Electron. 2017, 64, 9302–9310. [Google Scholar] [CrossRef]
- Ye, Z.; Lei, Y.; Pilawa-Podgurski, R.C.N. The Cascaded Resonant Converter: A Hybrid Switched-Capacitor Topology with High Power Density and Efficiency. IEEE Trans. Power Electron. 2020, 35, 4946–4958. [Google Scholar] [CrossRef]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. Single-Stage High-Efficiency 48/1 V Sigma Converter with Integrated Magnetics. IEEE Trans. Ind. Electron. 2020, 67, 192–202. [Google Scholar] [CrossRef]
- Ahmed, M.H.; Fei, C.; Lee, F.C.; Li, Q. High-efficiency high-power-density 48/1V sigma converter voltage regulator module. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 2207–2212. [Google Scholar]
- Ahmed, M.H.; Fei, C.; Li, V.; Lee, F.C.; Li, Q. Startup and control of high efficiency 48/1V sigma converter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 2010–2016. [Google Scholar]
- Zou, J.; Brooks, N.C.; Coday, S.; Ellis, N.M.; Pilawa-Podgurski, R.C.N. On the Size and Weight of Passive Components: Scaling Trends for High-Density Power Converter Designs. In Proceedings of the IEEE 23rd Workshop on Control and Modeling for Power Electronics (COMPEL), Tel Aviv, Israel, 20–23 June 2022; pp. 1–7. [Google Scholar]
- Pilawa-Podgurski, R.C.; Giuliano, N.D.M.; Perreault, D.J. Merged two-stage power converter architecture with soft charging switched-capacitor energy transfer. In Proceedings of the IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 4008–4015. [Google Scholar]
- Ye, Z.; Sanders, S.R.; Pilawa-Podgurski, R.C.N. Modeling and Comparison of Passive Component Volume of Hybrid Resonant Switched-Capacitor Converters. IEEE Trans. Power Electron. 2022, 37, 10903–10919. [Google Scholar] [CrossRef]
- Rentmeister, J.S.; Stauth, J.T. A 48V:2V flying capacitor multilevel converter using current-limit control for flying capacitor balance. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 26–30 March 2017; pp. 367–372. [Google Scholar]
- Liu, X.; Mok, P.K.T.; Jiang, J.; Ki, W.-H. Analysis and Design Considerations of Integrated 3-Level Buck Converters. IEEE Trans. Circuits Syst. I, Reg. Papers. 2016, 63, 671–682. [Google Scholar] [CrossRef]
- Das, R.; Le, H.-P. Analysis of Capacitor Voltage Imbalance in Hybrid Converters and Inherently Balanced Operation Using Symmetric Architecture. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 1205–1209. [Google Scholar] [CrossRef]
- Tanzawa, T. On-Chip High-Voltage Generator: Design Methodology for Charge Pumps; Springer: New York, NY, USA, 2016; Available online: https://link.springer.com/book/10.1007/978-3-319-21975-2 (accessed on 25 March 2025).
- Ballo, A.; Grasso, A.D.; Palumbo, G. High-Performance Integrated Charge Pumps: Design and Novel Solutions; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Cao, H.; Yang, X.; Xue, C.; He, L.; Tan, Z.; Zha, M. A 12-Level Series-Capacitor 48-1V DC–DC Converter with On-Chip Switch and GaN Hybrid Power Conversion. IEEE J. Solid-State Circuits. 2021, 56, 3628–3638. [Google Scholar] [CrossRef]
- Lei, Y.; May, R.; Pilawa-Podgurski, R. Split-Phase Control: Achieving Complete Soft-Charging Operation of a Dickson Switched-Capacitor Converter. IEEE Trans. Power Electron. 2016, 31, 770–782. [Google Scholar] [CrossRef]
- Ashourloo, M. Fault Detection in a Hybrid Dickson DC–DC Converter for 48-V Automotive Applications. IEEE Trans. Power Electron. 2021, 36, 4254–4268. [Google Scholar] [CrossRef]
- Das, R.; Seo, G.-S.; Le, H.-P. A 120V-to-1.8V 91.5%-Efficient 36-W Dual-Inductor Hybrid Converter with Natural Soft-charging Operations for Direct Extreme Conversion Ratios. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Portland, OR, USA, 23–27 September 2018; pp. 1266–1271. [Google Scholar]
- Seo, G.-S.; Das, R.; Le, H.-P. Dual Inductor Hybrid Converter for Point-of-Load Voltage Regulator Modules. IEEE Trans. Ind. Appl. 2020, 56, 367–377. [Google Scholar] [CrossRef]
- Das, R.; Seo, G.-S.; Le, H.-P. Analysis of Dual-Inductor Hybrid Converters for Extreme Conversion Ratios. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 5249–5260. [Google Scholar] [CrossRef]
- Ellis, N.M.; Pilawa-Podgurski, R.C.N. Modified Split-Phase Switching with Improved Fly Capacitor Utilization in a 48V-to-POL Dual Inductor Hybrid-Dickson Converter. In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 1735–1740. [Google Scholar]
- Ellis, N.M.; Pilawa-Podgurski, R.C.N. A Symmetric Dual-Inductor Hybrid Dickson Converter for Direct 48V-to-PoL Conversion. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), Houston, TX, USA, 20–24 March 2022; pp. 1267–1271. [Google Scholar]
- Ellis, N.M.; Sambo, H.; Robert Pilawa-Podgurski, C.N. Closed-Loop Split-Phase Control Applied to the Symmetric Dual Inductor Hybrid (SDIH) Converter. In Proceedings of the IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; pp. 1–6. [Google Scholar]
- Ellis, N.M.; Abramson, R.A.; Mahony, R.; Pilawa-Podgurski, R.C.N. The Symmetric Dual Inductor Hybrid Converter for Direct 48V-to-PoL Conversion. IEEE Trans. Power Electron. 2024, 39, 7278–7289. [Google Scholar] [CrossRef]
- Baba. Benefits of a Multiphase Buck Converter. Texas Instruments. Available online: https://www.ti.com/lit/an/slyt449/slyt449.pdf (accessed on 12 March 2025).
- Reatti, A.; Kazimierczuk, M.K. Comparison of various methods for calculating the AC resistance of inductors. IEEE Trans. Magn. 2002, 38, 1512–1518. [Google Scholar] [CrossRef]
- Vishay Dale. IHLP Inductor Core Loss Calculator Tool. Available online: https://www.vishay.com/en/inductors/calculator/calculator/ (accessed on 10 March 2025).
- Henriksen, M.M.; Otten, J.; Gehl, A.; Wicht, B. The ΔV-Method: An Intuitive Method for Analyzing Soft-Charging Capabilities of Hybrid Switched-Capacitor DC-DC Converters. In Proceedings of the IEEE 24th Workshop on Control and Modeling for Power Electronics (COMPEL), Ann Arbor, MI, USA, 25–28 June 2023; pp. 1–6. [Google Scholar]
- Seeman, M.D.; Sanders, S.R. Analysis and Optimization of Switched-Capacitor DC–DC Converters. IEEE Trans. Power Electron. 2008, 23, 841–851. [Google Scholar] [CrossRef]
- Jauregui, D.; Wang, B.; Chen, R. Power Loss Calculation with Common Source Inductance Consideration for Synchronous Buck Converters. Application Report (SLPA009A), Texas Instruments. 2011. Available online: https://www.ti.com/lit/an/slpa009a/slpa009a.pdf (accessed on 10 March 2025).
- Chen, C.; Liu, J.; Lee, H. Dual-Path Hybrid Dickson Converter for High-Ratio Conversions in Point-of-Load Applications. IEEE Trans. Ind. Appl. 2023, 59, 6914–6925. [Google Scholar] [CrossRef]






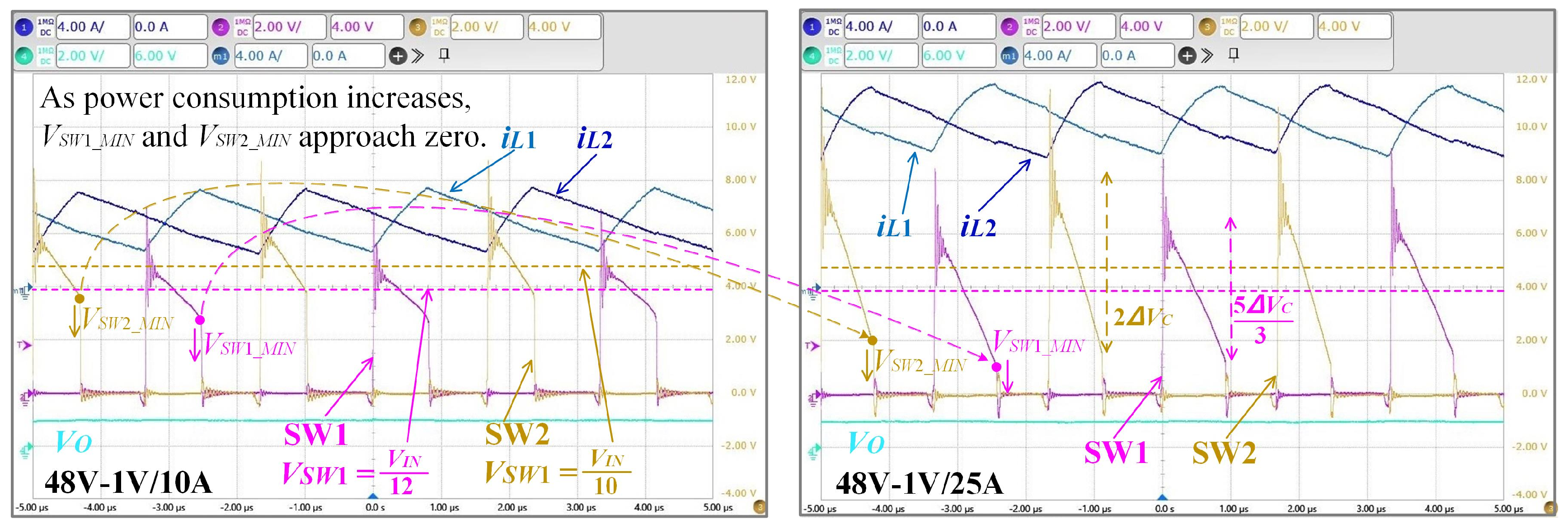
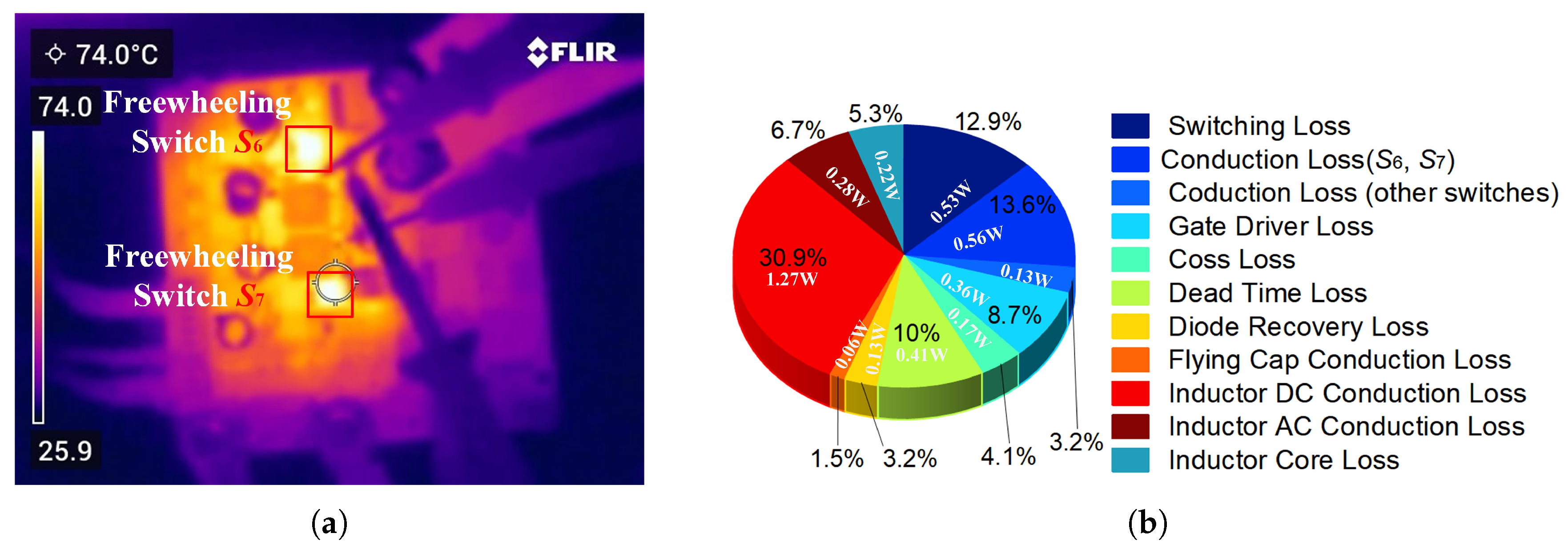

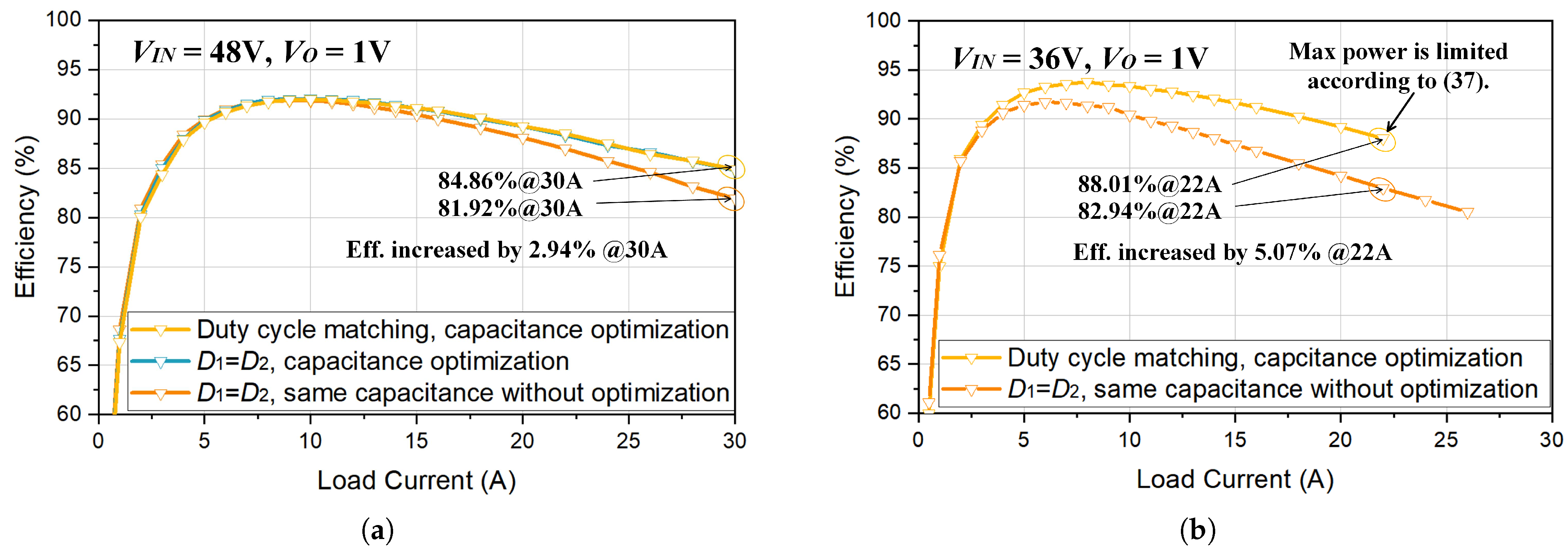
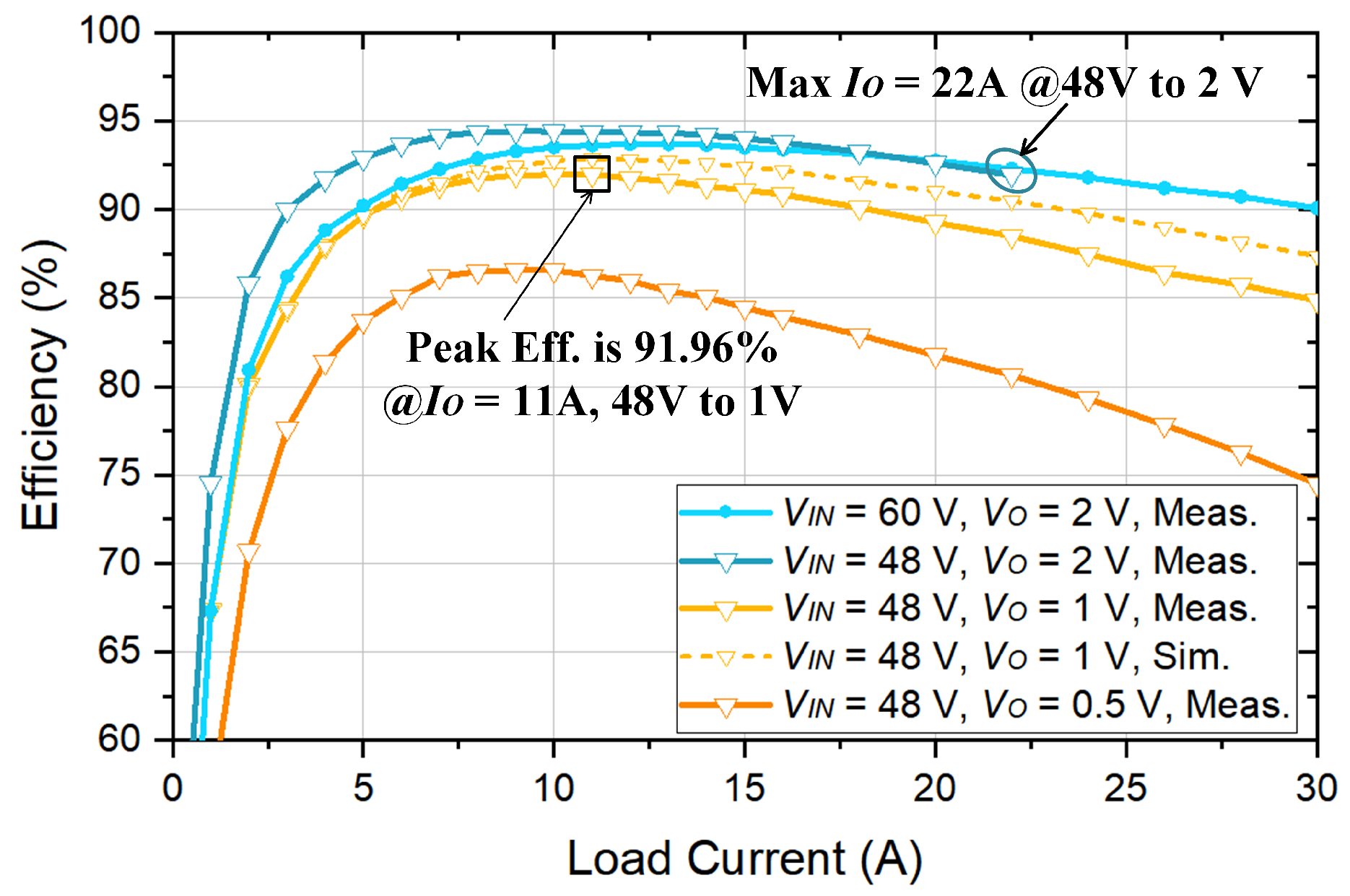
| Parameter | D1 = D2 | Duty Cycle Matching | |||
|---|---|---|---|---|---|
| Even-Order | Odd-Order | Even-Order | Odd-Order | ||
| D1 = D2 | D1,2 Matching | |||
|---|---|---|---|---|
| Inductor | ||||
| Pcore (W) | 0.109 | 0.109 | 0.117 | 0.102 |
| PDC (W) | 0.757 | 0.527 | 0.636 | 0.636 |
| PAC (W) | 0.137 | 0.137 | 0.145 | 0.130 |
| Ptotal (W) | 1.003 | 0.773 | 0.898 | 0.868 |
| Temp. rise (℃) | 22.7 | 17.5 | 20.3 | 19.7 |
| Phase | Parameter | D1 = D2 | Duty Cycle Matching | ||||
|---|---|---|---|---|---|---|---|
| Initial | Final | Initial | Final | ||||
| Component | Design Selection |
|---|---|
| – | 3 × 0.22 µF, 3 × 0.22 µF, 4 × 0.47 µF/0.1 µF, 2 × 0.47 µF, 8 × 0.47 µF/2 × 0.1 µF, 0.47 µF/0.22 µF/0.1 µF, Murata, C0G |
| 6 × 47 µF, 6.3 V, Murata, X7R | |
| 6 × 10 µF, 100 V, TDK, X7R | |
| – | BSC026NE2LS5, Infineon |
| , | BSC009NE2LS5I, Infineon |
| BSC066N06NS, Infineon | |
| – | BSC059N04LS6, Infineon |
| , | IHLP3232DZERR47M01, VISHAY |
| Microcontroller | TMS320F28335PGFA, TI |
| High-side driver | 8 × LTC4440-5, ADI |
| Low-side driver | 3 × UCC27517DBVR, TI |
| TPE 2020 [22] | TPE 2023 [29] | JESTPE 2021 [25] | TIA 2023 [36] | ECCE 2021 [26] | This Work | |
|---|---|---|---|---|---|---|
| Topology | HD | SDIH | DIH | DPHD | DIH | QCSC-TLAHD |
| M () | (Even) (Odd) | |||||
| VIN/VO | 48 V/3.3V | 48 V/1–3 V | 48 V/1–2 V | 36–65 V/1–2 V | 48 V/1–3 V | 48 V/0.5–2 V |
| Max. IO | 10.9 A | 116 A | 20 A | 32 A | 70 A | 30 A |
| Type/Num. of Switches | MOS/32 | MOS/14 | GaN/9 | MOS/10 | MOS/8 | MOS/11 |
| fSW | 250 kHz | 750 kHz | 150 kHz | 250 kHz | 750 kHz | 300 kHz |
| Capacitor | 12 | 10 | 6 | 6 | 5 | 6 |
| Inductor | 4 × 3.3 µH | 2 × 150 nH | 2 × 2.2 µH | 260 nH | 2 × 1 µH | 2 × 470 nH |
| Component Volume (a) | N/A | 0.073 in3 | N/A | 0.135 in3 | 0.168 in3 | 0.0635 in3 |
| Power Density (a) | N/A | 1588 W/in3 | N/A | 481 W/in3 | 892 W/in3 | 944.88 W/in3 |
| Peak Efficiency | N/A | 83.5% @48/1 V | 92.4% @48/1 V | 90.6% @48/1 V, 13 A | 87.5% @48/1 V | 91.96% @48V/1 V, 11 A |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Zhang, C.; Liou, J.J.; Wang, Y. Efficiency-Enhanced Hybrid Dickson Converter with Quasi-Complete Soft Charging for Direct Large-Ratio Step-Down Applications. Electronics 2025, 14, 2001. https://doi.org/10.3390/electronics14102001
Chen R, Zhang C, Liou JJ, Wang Y. Efficiency-Enhanced Hybrid Dickson Converter with Quasi-Complete Soft Charging for Direct Large-Ratio Step-Down Applications. Electronics. 2025; 14(10):2001. https://doi.org/10.3390/electronics14102001
Chicago/Turabian StyleChen, Ruike, Changming Zhang, Juin Jei Liou, and Yao Wang. 2025. "Efficiency-Enhanced Hybrid Dickson Converter with Quasi-Complete Soft Charging for Direct Large-Ratio Step-Down Applications" Electronics 14, no. 10: 2001. https://doi.org/10.3390/electronics14102001
APA StyleChen, R., Zhang, C., Liou, J. J., & Wang, Y. (2025). Efficiency-Enhanced Hybrid Dickson Converter with Quasi-Complete Soft Charging for Direct Large-Ratio Step-Down Applications. Electronics, 14(10), 2001. https://doi.org/10.3390/electronics14102001






