A Generative Model-Based Method for Inverse Design of Microstrip Filters
Abstract
1. Introduction
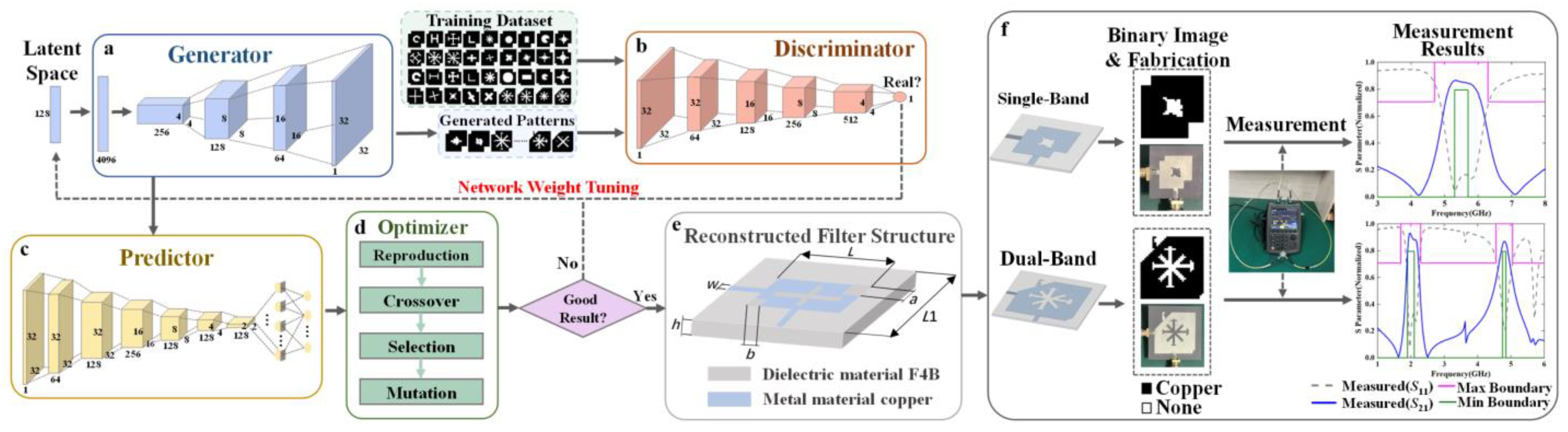
2. Materials and Methods
2.1. Structures of Filters and Training Datasets
2.2. Inverse Design Process
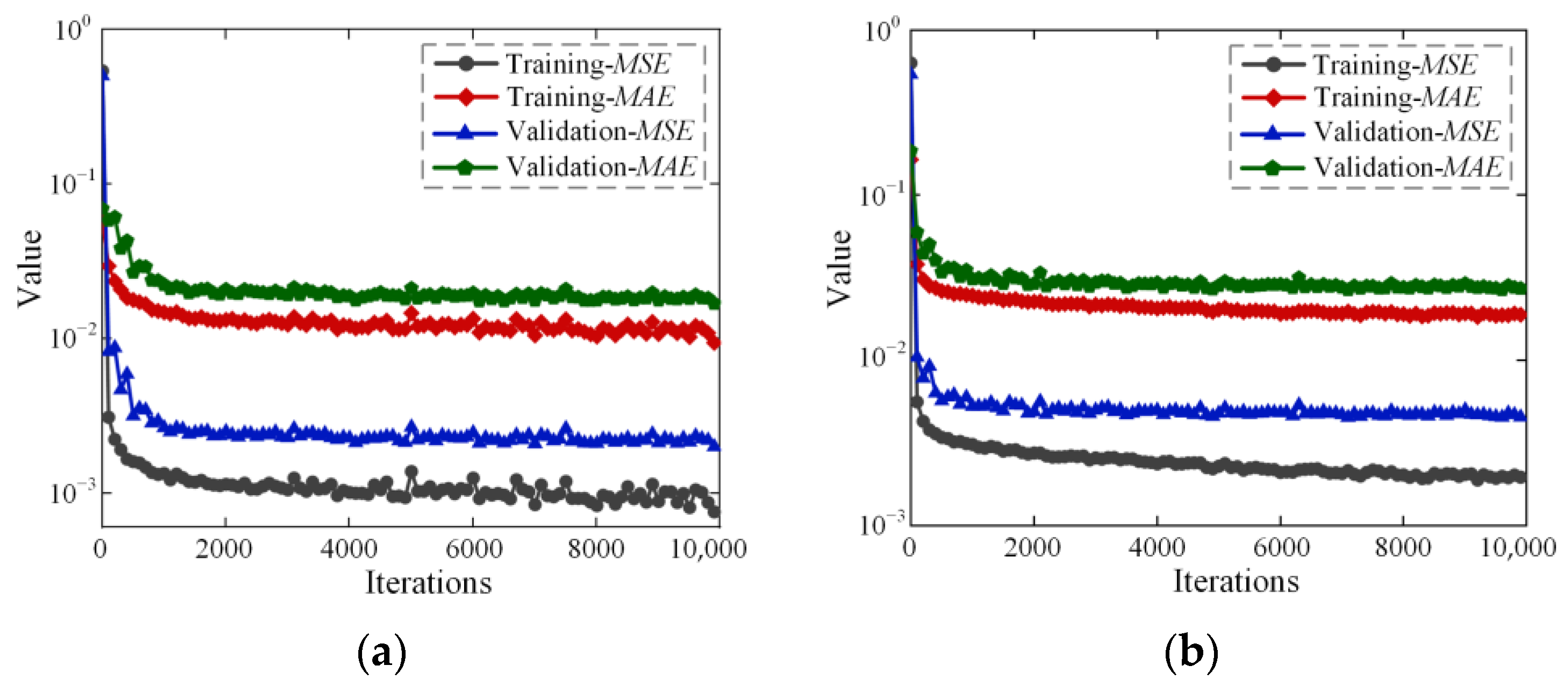
2.3. Neural Network Architecture
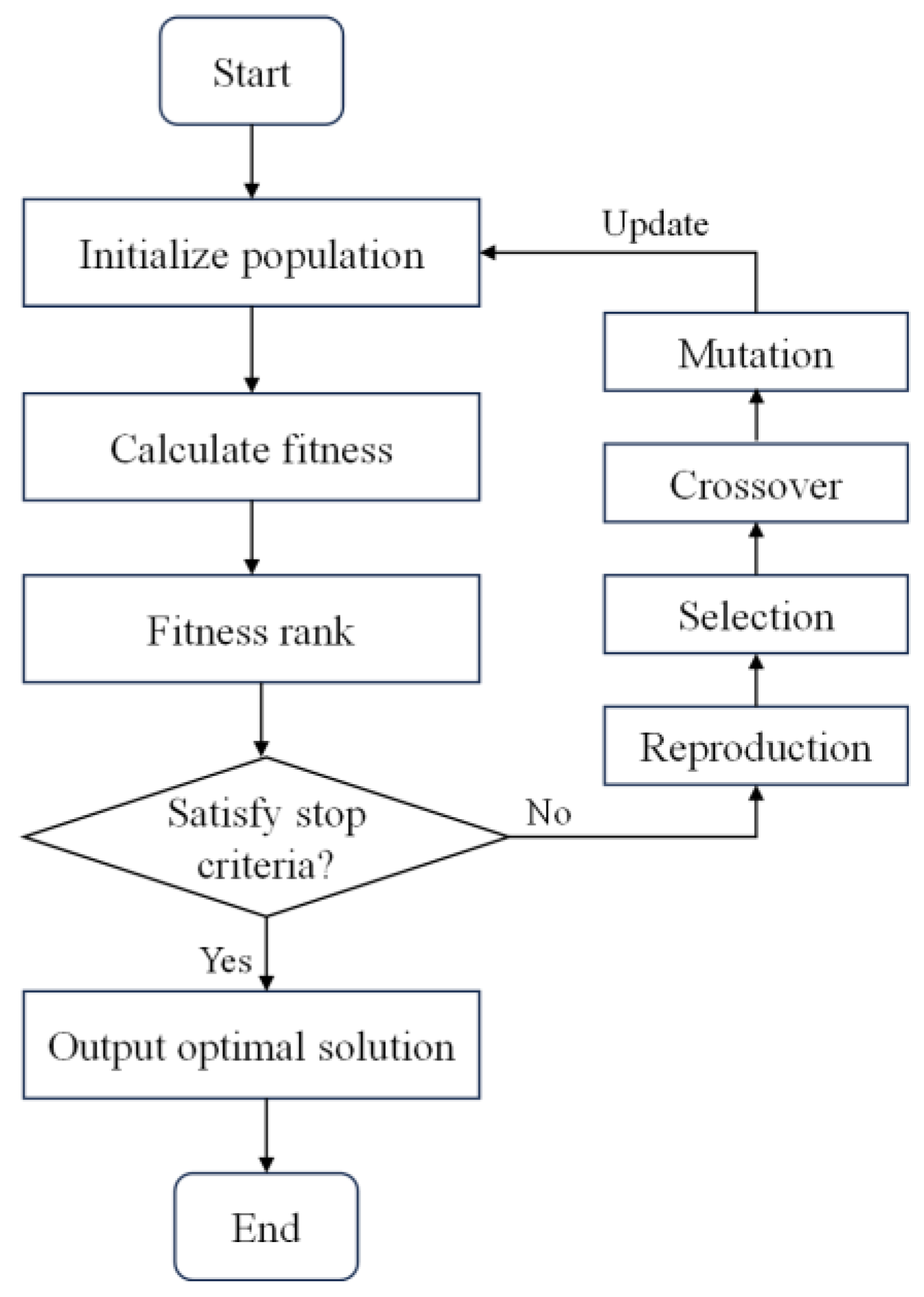
2.4. Genetic Algorithm Optimizer
3. Results and Analysis
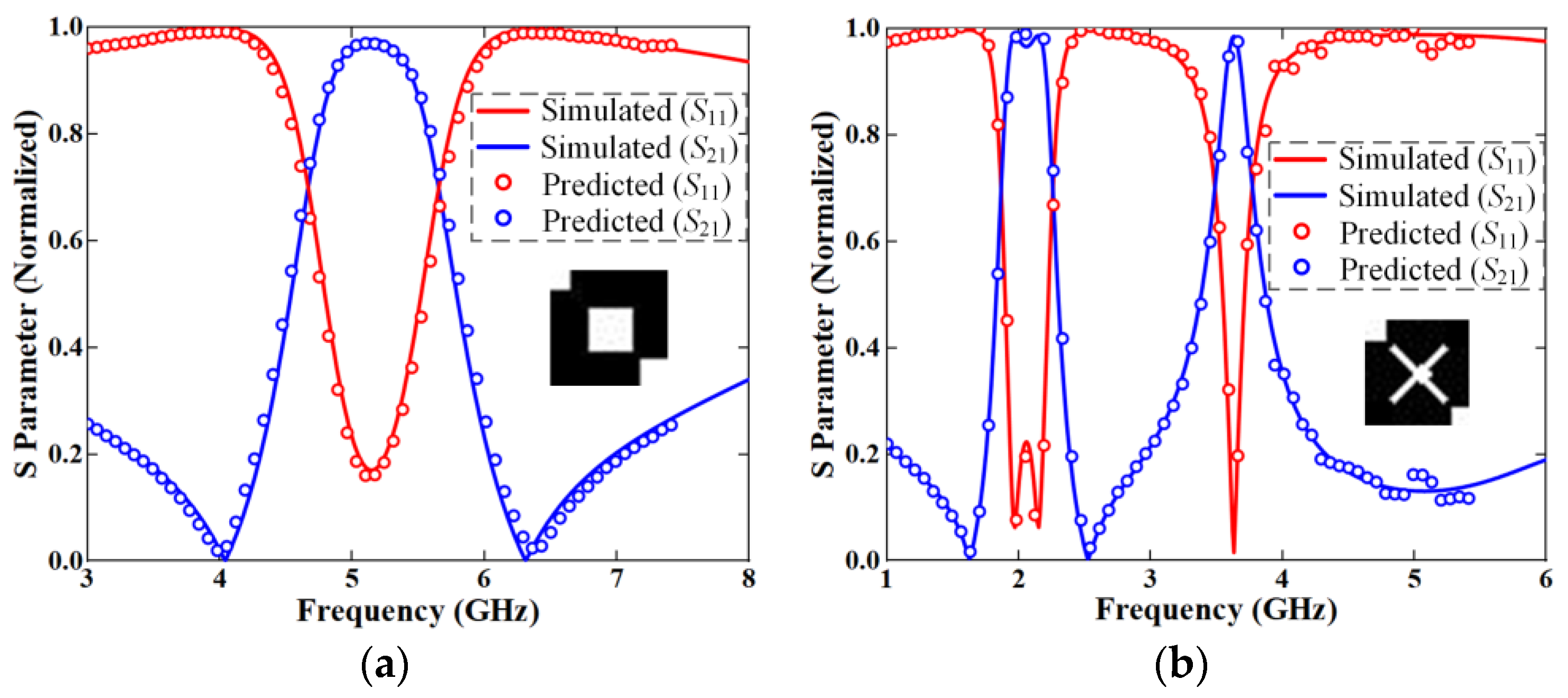
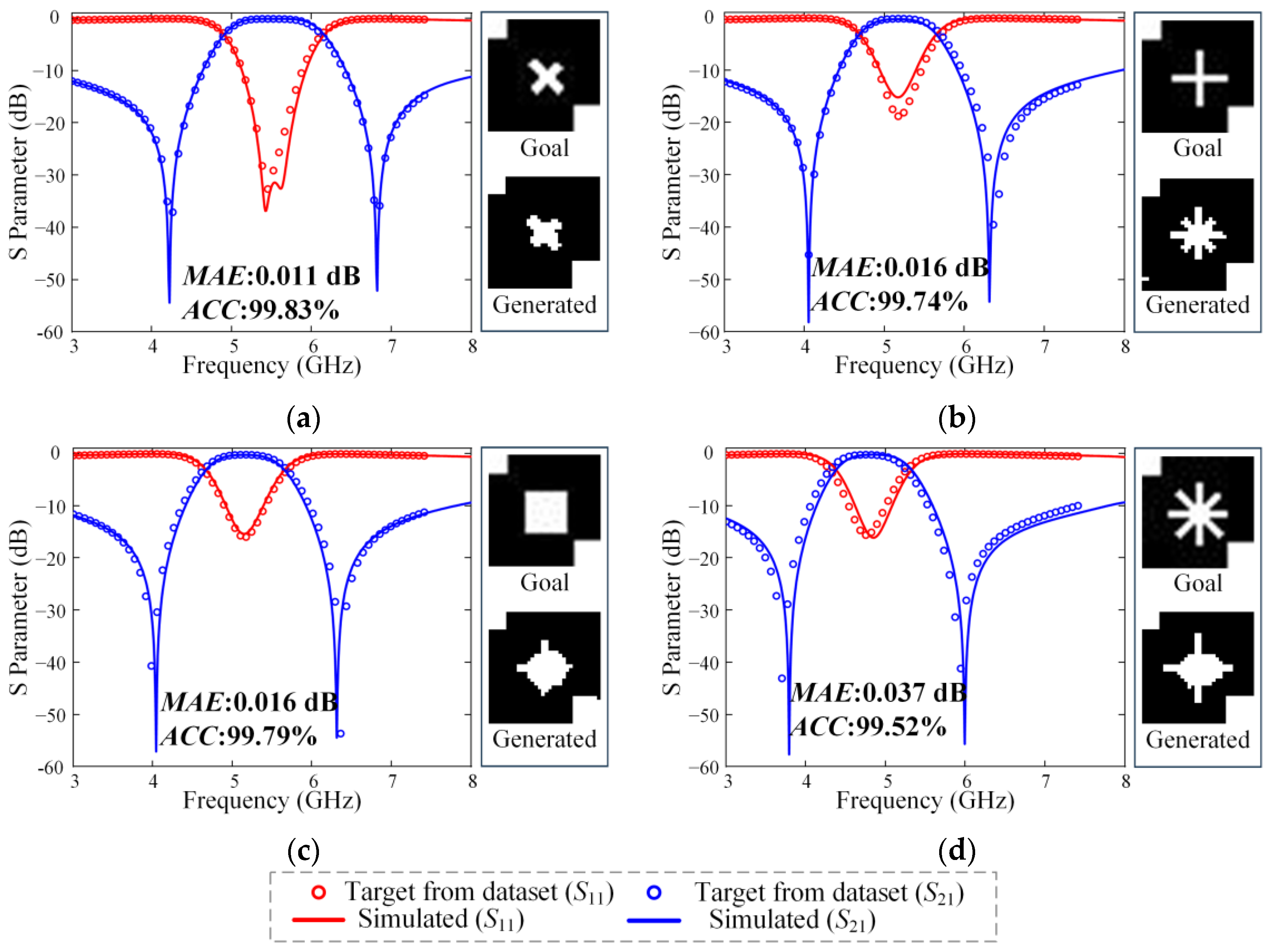
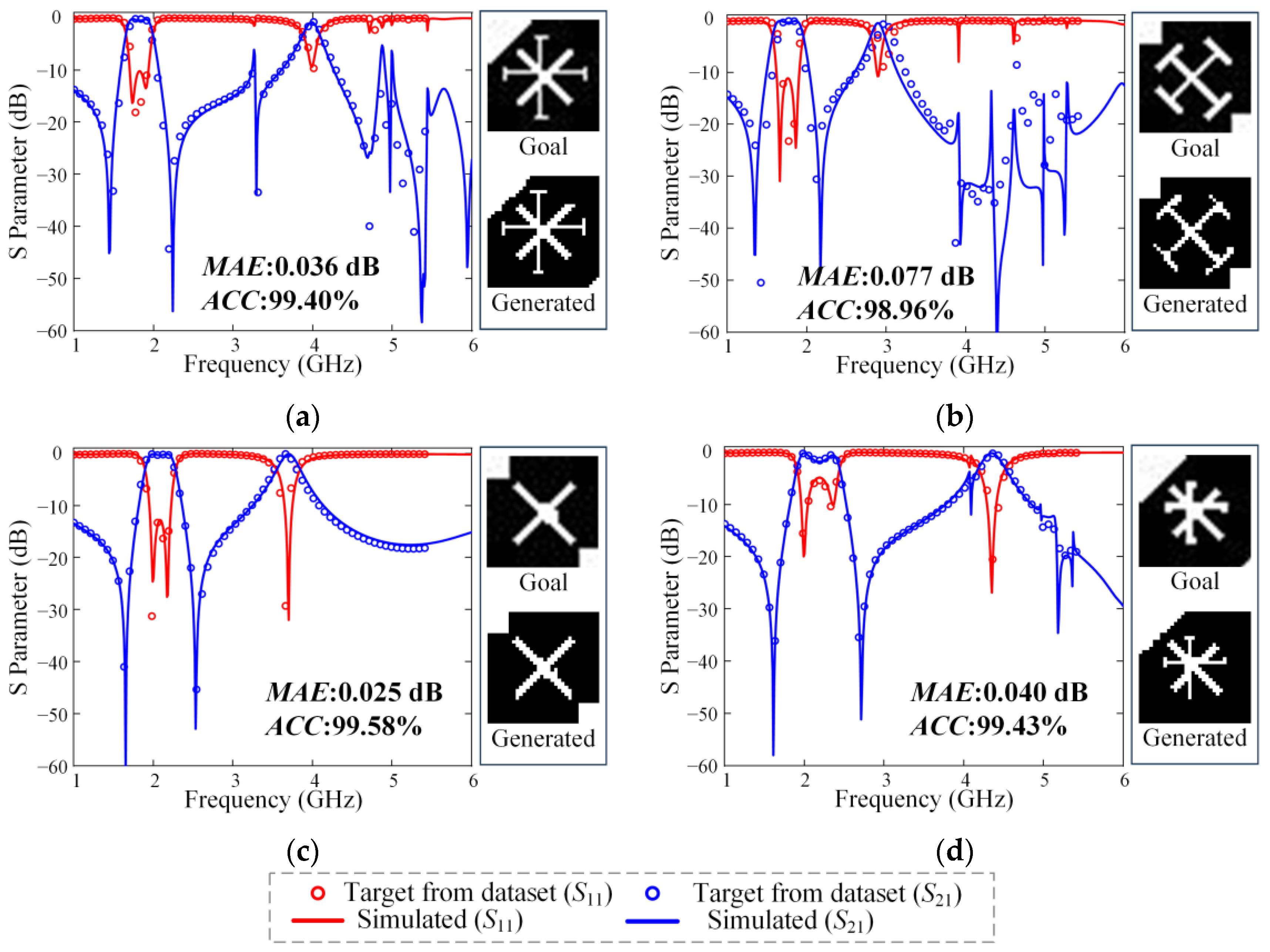
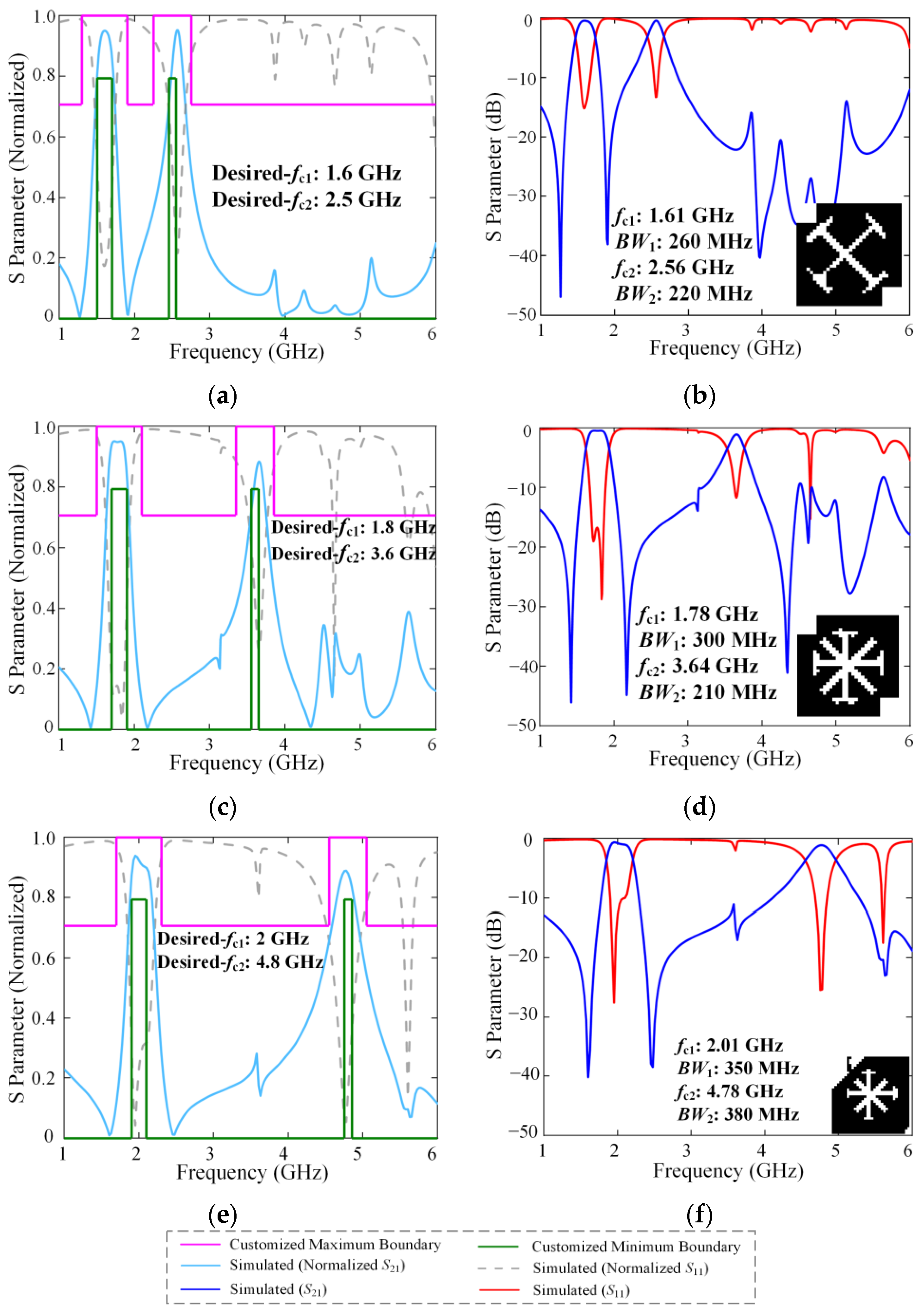
3.1. Inverse Design Test Under the Target Curve of Dataset
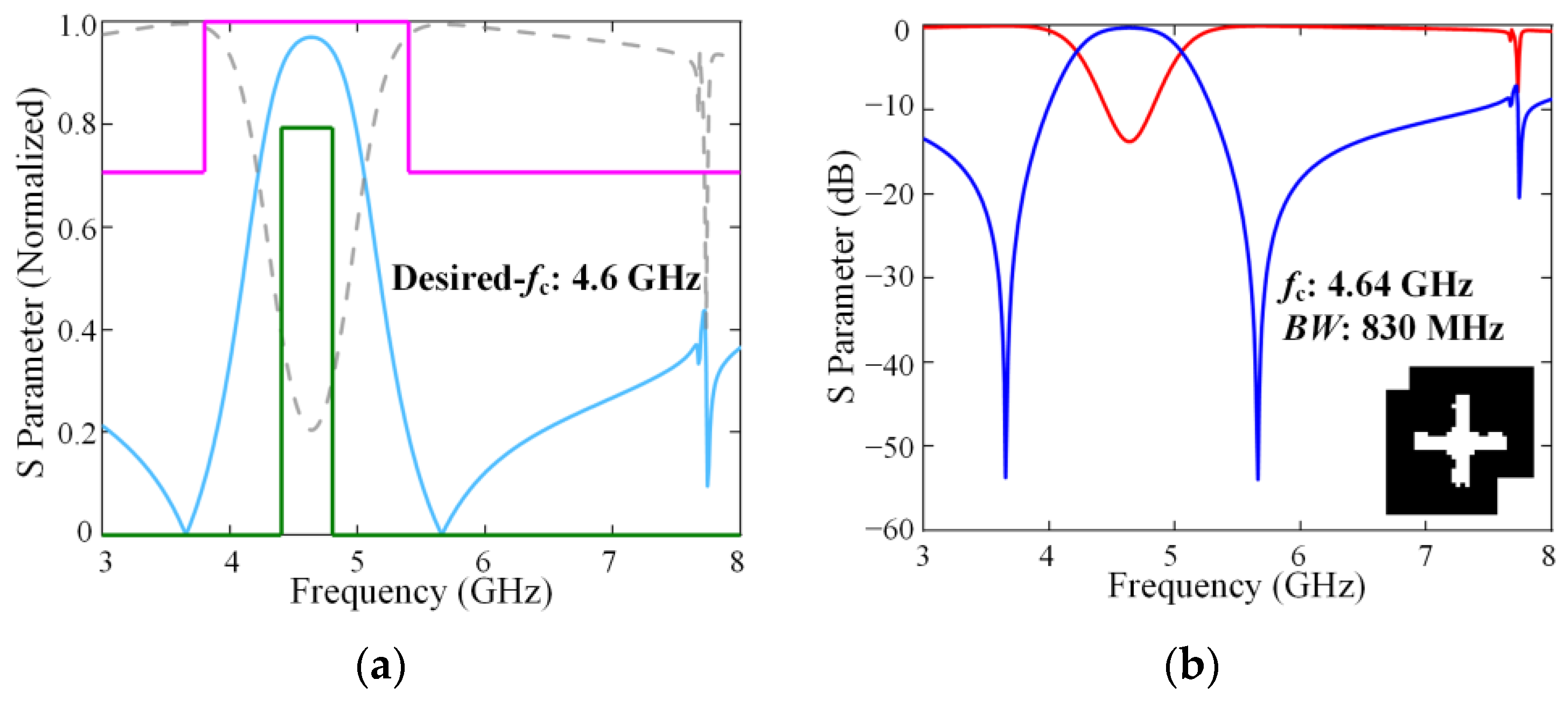
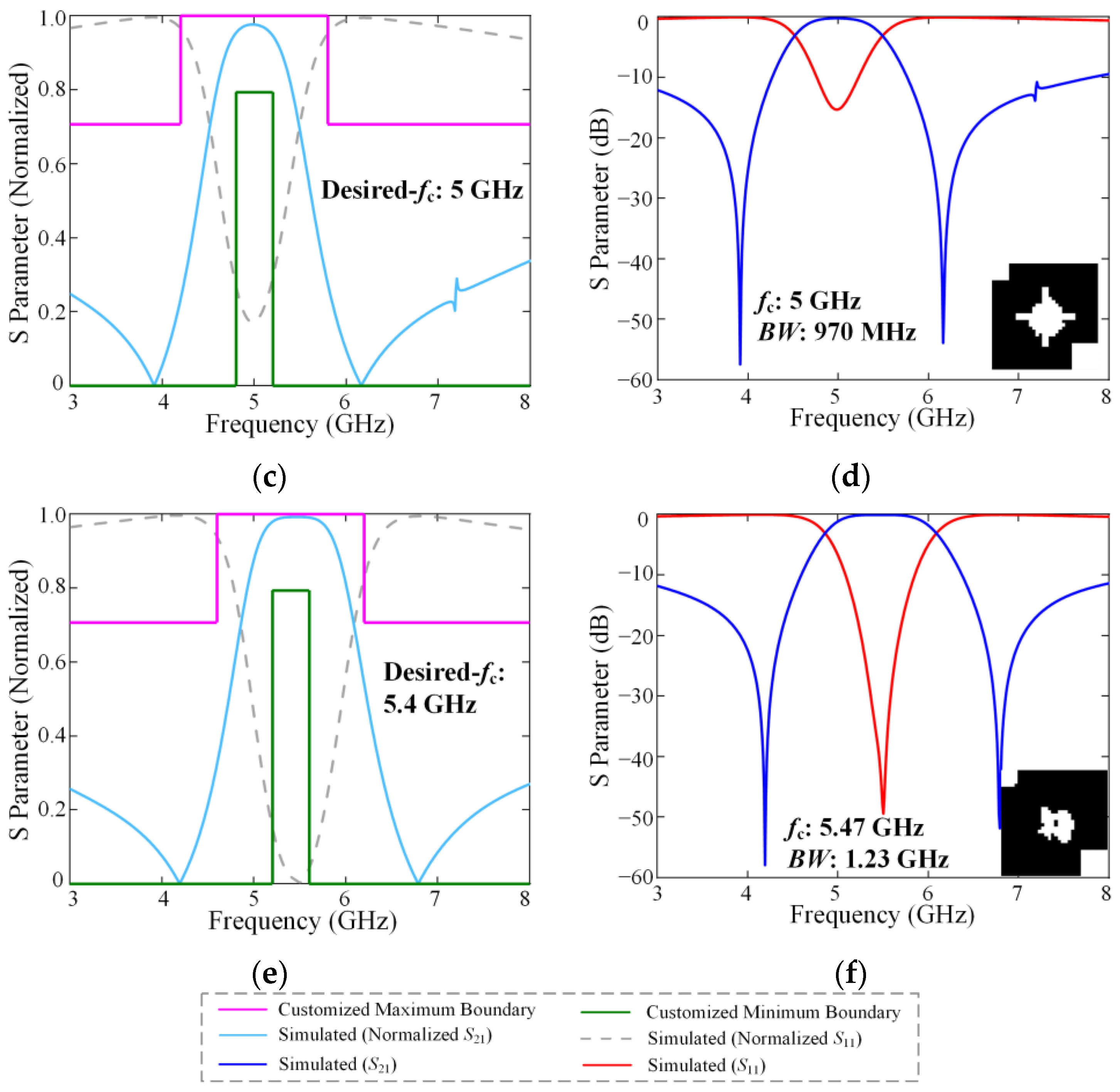
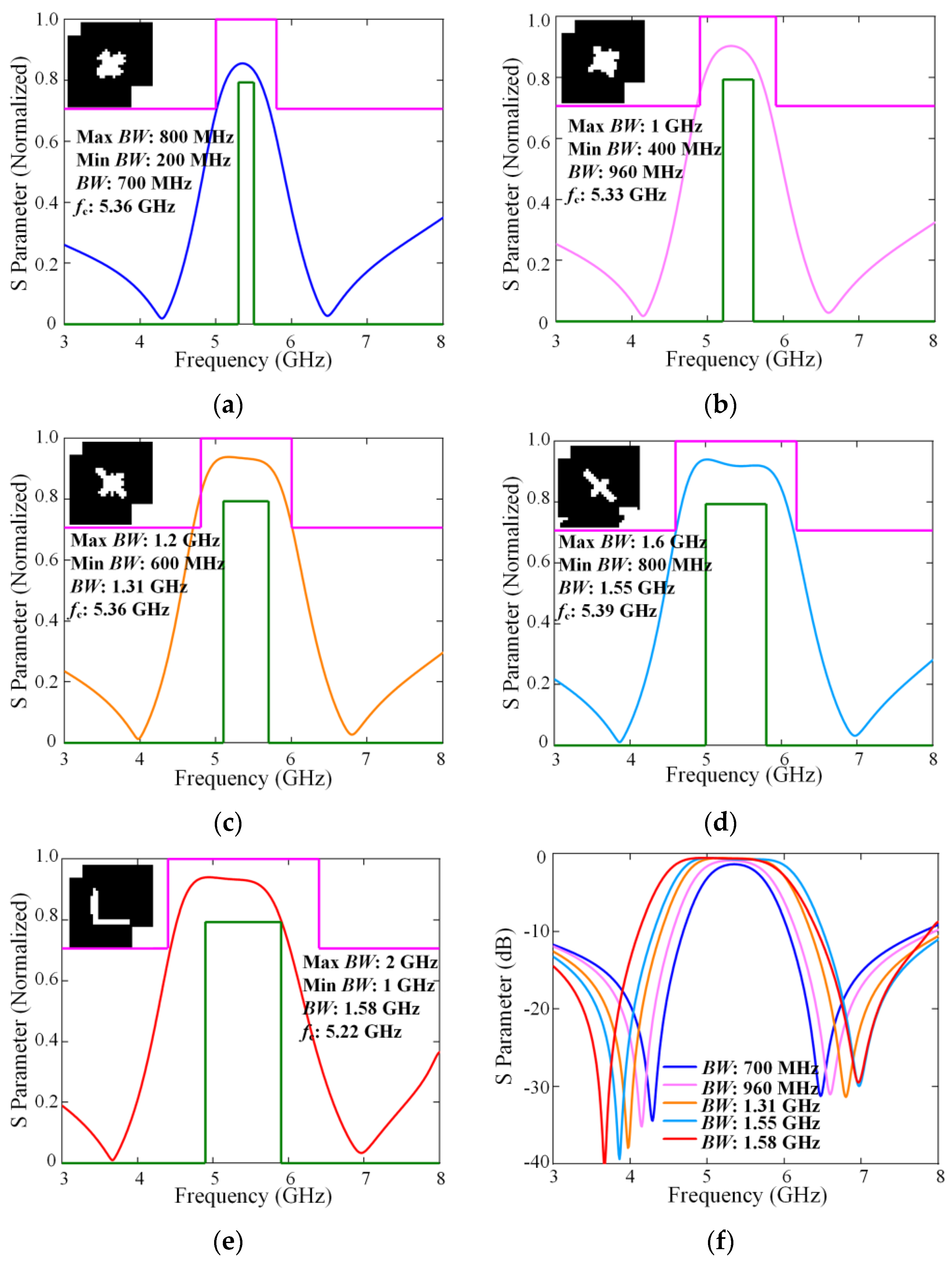
3.2. Inverse Design Test Under the Self-Defined Target Curve
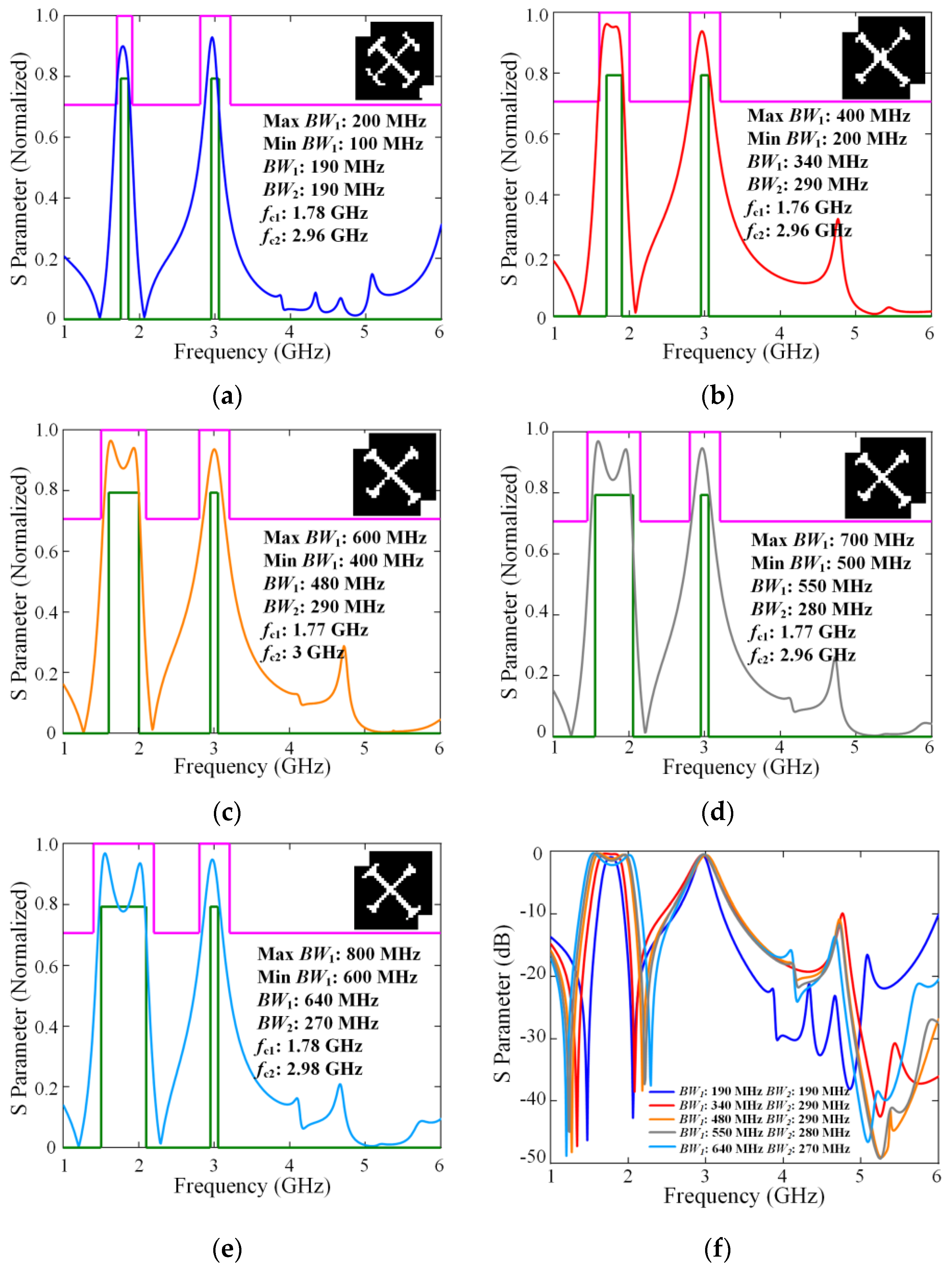
3.3. Inverse Design Test Under the Bandwidth-Transformations Target Response
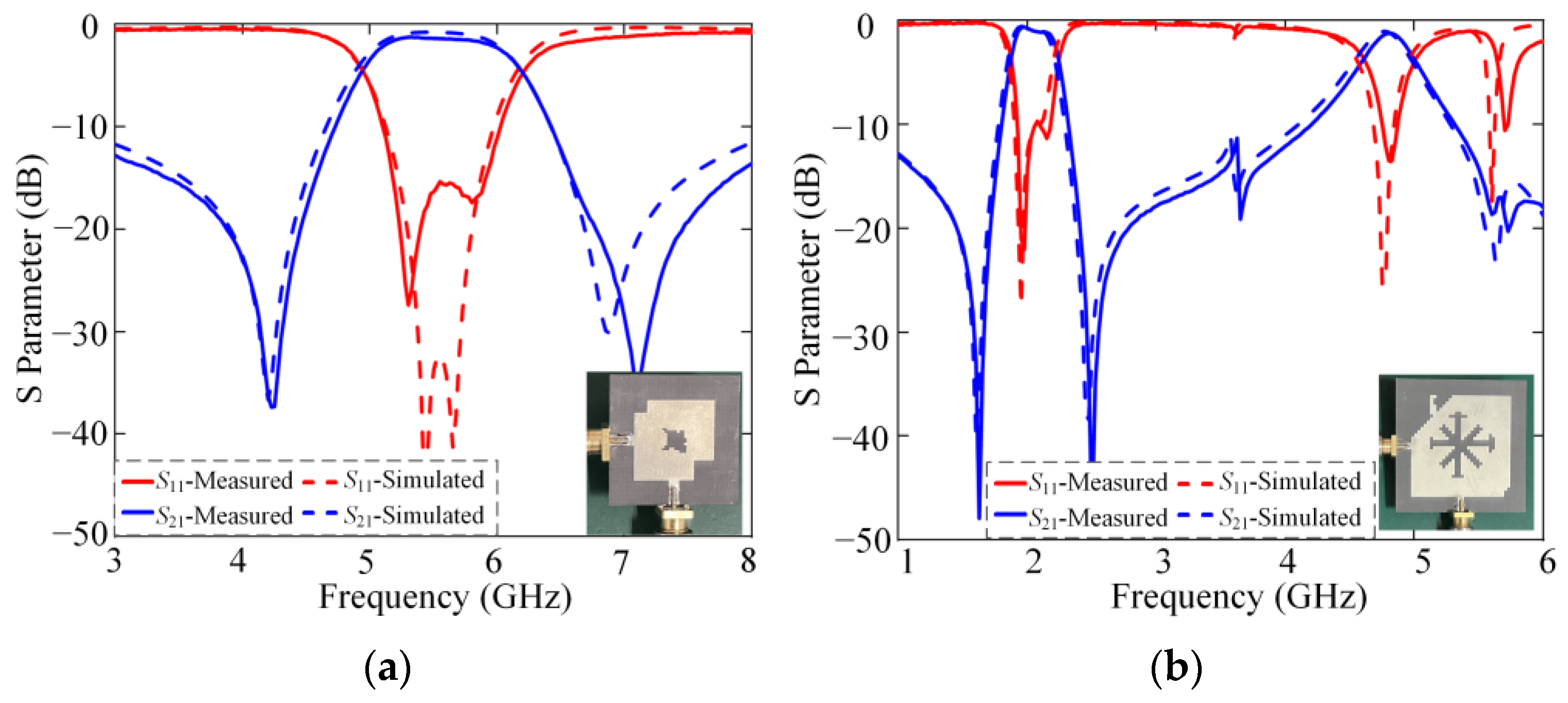
4. Fabrication and Measurement
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, F.; Zhang, C.; Na, W.; Zhang, J.; Zhang, W.; Zhang, Q.J. Adaptive feature zero assisted surrogate-based EM optimization for microwave filter design. IEEE Microw. Wireless Compon. Lett. 2019, 29, 2–4. [Google Scholar] [CrossRef]
- Feng, F.; Na, W.; Jin, J.; Zhang, J.; Zhang, W.; Zhang, Q.J. Artificial neural networks for microwave computer-aided design: The state of the art. IEEE Trans. Microw. Theory Tech. 2022, 70, 4597–4619. [Google Scholar] [CrossRef]
- Zhang, H.; Kang, W.; Wu, W. Dual-band substrate integrated waveguide bandpass filter utilising complementary split-ring resonators. Electron. Lett. 2018, 54, 85–87. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Zhang, A. Generative Model for Dual-Band Filters Based on Modified Complementary Split-Ring Resonators. Electronics 2024, 13, 2321. [Google Scholar] [CrossRef]
- Xu, S.; He, C.; Yan, B.; Wang, M. A Multi-Stage Acoustic Echo Cancellation Model Based on Adaptive Filters and Deep Neural Networks. Electronics 2023, 12, 3258. [Google Scholar] [CrossRef]
- Daylak, F.; Ozoguz, S. Automated Neural Network-Based Optimization for Enhancing Dynamic Range in Active Filter Design. Electronics 2025, 14, 786. [Google Scholar] [CrossRef]
- Jiang, J.; Chen, M.; Fan, J.A. Deep neural networks for the evaluation and design of photonic devices. Nat. Rev. Mater. 2021, 6, 679–700. [Google Scholar] [CrossRef]
- So, S.; Badloe, T.; Noh, J.; Bravo-Abad, J.; Rho, J. Deep learning enabled inverse design in nanophotonics. Nanophotonics 2020, 9, 1041–1057. [Google Scholar] [CrossRef]
- Tahersima, M.H.; Kojima, K.; Koike-Akino, T.; Jha, D.; Wang, B.; Lin, C.; Parsons, K. Deep neural network inverse design of integrated photonic power splitters. Sci. Rep. 2019, 9, 1368. [Google Scholar] [CrossRef]
- Zhou, Z.; Guo, Y. Adjusting Optical Polarization with Machine Learning for Enhancing Practical Security of Continuous-Variable Quantum Key Distribution. Electronics 2024, 13, 1410. [Google Scholar] [CrossRef]
- Khatib, O.; Ren, S.; Malof, J.; Padilla, W.J. Deep learning the electromagnetic properties of metamaterials—A comprehensive review. Adv. Funct. Mater. 2021, 31, 2101748. [Google Scholar] [CrossRef]
- Ajmi, H.A.; Bait-Suwailam, M.M.; Khriji, L.; Al-Lawati, H. Prediction Enhancement of Metasurface Absorber Design Using Adaptive Cascaded Deep Learning (ACDL) Model. Electronics 2024, 13, 822. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, C.; Wan, X.; Zhang, L.; Liu, S.; Yang, Y.; Cui, T.J. Machine-learning designs of anisotropic digital coding metasurfaces. Adv. Theory Simul. 2019, 2, 1800132. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Ma, J.; Cui, T.J.; del Hougne, P.; Li, L. Semantic–Electromagnetic Inversion With Pretrained Multimodal Generative Model. Adv. Sci. 2024, 11, 2406793. [Google Scholar] [CrossRef]
- Ma, W.; Cheng, F.; Xu, Y.; Wen, Q.; Liu, Y. Probabilistic representation and inverse design of metamaterials based on a deep generative model with semi-supervised learning strategy. Adv. Mater. 2019, 31, 1901111. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Rodrigues, S.P.; Lee, K.T.; Cai, W. Generative model for the inverse design of metasurfaces. Nano Lett. 2018, 18, 6570–6576. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.P.; Li, Y.B.; Li, H.; Dong, S.; Liu, C.; Jin, S.; Cui, T.J. Deep learning designs of anisotropic metasurfaces in ultrawideband based on generative adversarial networks. Adv. Intell. Syst. 2020, 2, 2000068. [Google Scholar] [CrossRef]
- Naseri, P.; Hum, S.V. A generative machine learning-based approach for inverse design of multilayer metasurfaces. IEEE Trans. Antennas Propag. 2021, 69, 5725–5739. [Google Scholar] [CrossRef]
- Wei, Z.; Zhou, Z.; Wang, P.; Ren, J.; Yin, Y.; Pedersen, G.F. Equivalent circuit theory-assisted deep learning for accelerated generative design of metasurfaces. IEEE Trans. Antennas Propag. 2022, 70, 5120–5129. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Lee, K.T.; Kim, A.S.; Raju, L.; Cai, W. Compounding meta-atoms into metamolecules with hybrid artificial intelligence techniques. Adv. Mater. 2020, 32, e1904790. [Google Scholar] [CrossRef]
- Zhu, D.; Liu, Z.; Raju, L.; Kim, A.S.; Cai, W. Building multifunctional metasystems via algorithmic construction. ACS Nano 2021, 15, 2318–2326. [Google Scholar] [CrossRef] [PubMed]
- Naseri, P.; Goussetis, G.; Fonseca, N.J.G.; Hum, S.V. Inverse Design of a Dual-Band Reflective Polarizing Surface Using Generative Machine Learning. In Proceedings of the 2022 16th European Conference on Antennas and Propagation (EuCAP), Madrid, Spain, 27 March–1 April 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Zhao, P.; Wu, K. Homotopy optimization of microwave and millimeter-wave filters based on neural network model. IEEE Trans. Microwave Theory Tech. 2020, 68, 1390–1400. [Google Scholar] [CrossRef]
- Pan, G.; Wu, Y.; Yu, M.; Li, H. Inverse modeling for filters using a regularized deep neural network approach. IEEE Microw. Wireless Compon. Lett. 2020, 30, 457–460. [Google Scholar] [CrossRef]
- Ohira, M.; Takano, K.; Ma, Z. A novel deep-Q-network-based fine-tuning approach for planar bandpass filter design. IEEE Microw. Wireless Compon. Lett. 2021, 31, 638–641. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, Q.; Liu, Q.; Tang, W.; Yang, J. Design of a new dual-band balanced-to-balanced filtering power divider based on the circular microstrip patch resonator. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3542–3546. [Google Scholar] [CrossRef]
- Yang, Y.; Yao, C.; Yang, J.; Yin, K. A network security situation element extraction method based on conditional generative adversarial network and trans-former. IEEE Access 2020, 10, 107416–107430. [Google Scholar] [CrossRef]
- Kabir, H.; Wang, Y.; Yu, M.; Zhang, Q.J. Neural network inverse modeling and applications to microwave filter design. IEEE Trans. Microw. Theory Tech. 2008, 56, 867–879. [Google Scholar] [CrossRef]
- Jin, J.; Feng, F.; Na, W.; Yan, S.; Liu, W.; Zhu, L.; Zhang, Q.J. Recent advances in neural network-based inverse modeling techniques for microwave applications. Int. J. Numer. Model. El. 2020, 33, e2732. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, J.; Na, W.; Zhang, Q.J.; Yu, M. Multivalued neural network inverse modeling and applications to microwave filters. IEEE Trans. Microw. Theory Tech. 2018, 66, 3781–3797. [Google Scholar] [CrossRef]
- Lee, M.C.; Yu, C.H.; Yao, C.K.; Li, Y.L.; Peng, P.C. A neural-network-based inverse design of the microwave photonic filter using multiwavelength laser. Opt. Commun. 2022, 523, 128729. [Google Scholar] [CrossRef]
- Wu, Y.; Pan, G.; Lu, D.; Yu, M. Artificial neural network for dimensionality reduction and its application to microwave filters inverse modeling. IEEE Trans. Microw. Theory Tech. 2022, 70, 4683–4693. [Google Scholar] [CrossRef]
- Jin, J.; Zhang, C.; Feng, F.; Na, W.; Ma, J.; Zhang, Q.J. Deep neural network technique for high-dimensional microwave modeling and applications to parameter extraction of microwave filters. IEEE Trans. Microw. Theory Tech. 2019, 67, 4140–4155. [Google Scholar] [CrossRef]
- Du, H.; Yang, Q.; Dai, X.; Liao, X.; Zhang, A. A parameter extraction method for LC circuit of DB-BPF based on fully connected network. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 3558–3562. [Google Scholar] [CrossRef]
- Du, H.; Yang, Q.; Dai, X.; Guo, C.; Liao, X.; Zhang, A. A structure parameter estimation method for microstrip BPF based on multilayer FCN. IEEE Microw. Wireless Compon. Lett. 2020, 30, 581–584. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, J.; Jiang, S. Inverse design of tunable lowpass microstrip filters based on generative adversarial network and transfer learning. IEEE Trans. Circuits Syst. II Express Briefs 2024, 71, 2594–2598. [Google Scholar] [CrossRef]
| Refs. | Technology | ACC (%) | MAE (dB) | MSE (dB) | Time Cost (min) |
|---|---|---|---|---|---|
| [10] | CDCGAN | 99.19 | 0.056 | 0.5189 | 12.5 |
| This work | CPPN-GAN with GA | 99.58 | 0.039 | 0.2574 | 3.6 |
| Refs. | Techniques | PB Type | Order | IL | RL | 3 dB FBW |
|---|---|---|---|---|---|---|
| [5] | FCN | Single | 5 | 0.5 | 15 | 40 |
| [6] | Comprehensive NN | Single | 6 | 2 | 20 | 0.5 |
| [8] | Multivalued NN | Dual | 8 | -/- | 10/9 | 2.6/2.4 |
| [9] | CSRR | Dual | 1 | 1.5/1.9 | 14/12 | 3.42/3.39 |
| [10] | CDCGAN | Dual | 1 | 2.35/1 | 23.3/25.7 | 7.3/12 |
| Figure 11a | CPPN-GAN with GA | Single | 1 | 1.23 | 15.3 | 23.4 |
| Figure 11b | Dual | 1 | 0.61/1.19 | 10.1/13.5 | 17.4/7.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Nie, C.; Ren, Z.; Li, Y. A Generative Model-Based Method for Inverse Design of Microstrip Filters. Electronics 2025, 14, 1989. https://doi.org/10.3390/electronics14101989
Wang H, Nie C, Ren Z, Li Y. A Generative Model-Based Method for Inverse Design of Microstrip Filters. Electronics. 2025; 14(10):1989. https://doi.org/10.3390/electronics14101989
Chicago/Turabian StyleWang, Haipeng, Chenchen Nie, Zhongfang Ren, and Yunbo Li. 2025. "A Generative Model-Based Method for Inverse Design of Microstrip Filters" Electronics 14, no. 10: 1989. https://doi.org/10.3390/electronics14101989
APA StyleWang, H., Nie, C., Ren, Z., & Li, Y. (2025). A Generative Model-Based Method for Inverse Design of Microstrip Filters. Electronics, 14(10), 1989. https://doi.org/10.3390/electronics14101989






