Abstract
Semantic communication has garnered increasing attention due to its ability to shift the focus from pixel-level transmission to the transfer of fundamental semantic information representing the core content of images. This paper proposes a novel reinforcement learning-based layered semantic coding (RL-SC) method aimed at optimizing image communication systems under bandwidth constraints. By leveraging deep reinforcement learning (DRL), the proposed method efficiently allocates semantic bits to maximize semantic fidelity while minimizing bitrates. By incorporating semantic segmentation and image reconstruction networks, the framework utilizes both semantic maps and residual information to enhance the image coding process. Experiments demonstrate that the proposed method outperforms traditional image compression techniques and layered image encoding methods without reinforcement learning in preserving semantic content and achieving high-quality image reconstruction. In particular, the proposed method excels in low-bitrate scenarios, effectively maintaining both semantic accuracy and perceptual quality.
1. Introduction
Since Claude Shannon introduced information theory, he and Warren Weaver have continued to develop and refine its underlying principles, ultimately defining three levels of communication: the bit level, the semantic level, and the effective level [1]. Traditional communication paradigms focus on accurate bit transmission while often overlooking the semantic correlations within the transmitted information. As communication technologies advance rapidly and data exchange grows exponentially, conventional systems struggle to meet the requirements of high efficiency and low latency. Moreover, by relying solely on raw data transmission, these systems fail to capture the underlying semantic significance of the conveyed information. In contrast, semantic communication transmits only task-relevant semantic content rather than complete raw data. By adopting a semantic-aware framework, semantic communication systems can significantly reduce data volume while maintaining superior performance in subsequent tasks, including image reconstruction and semantic segmentation.
In bit-level image communication, traditional methods such as JPEG [2] and J2K [3] achieve compression through frequency domain transformation and quantization. More advanced approaches, such as BPG [4] and JPEG XL, further enhance compression efficiency by incorporating advanced entropy coding and perceptual metrics. However, severely compressed images inherently distort human perception and often suffer from degradations, including blocking artifacts, ringing, blurring, and checkerboard artifacts [5,6], which can negatively impact semantic tasks, including segmentation, classification, and detection [7,8]. Consequently, blindly minimizing pixel-level distortion may result in excessive bit overhead.
Recently, image compression methods based on deep learning have been extensively studied and applied. Refs. [9,10,11,12] utilize neural networks, including autoencoders and generative adversarial networks (GANs), to model high-dimensional image distributions, allowing for more efficient and adaptive compression. Toderici et al. [13] pioneered an end-to-end optimized image compression method employing recurrent neural networks (RNN) for image reconstruction. Balle et al. [14] introduced an image compression framework leveraging the variational autoencoder (VAE) architecture. Rippel et al. [15] pioneered the use of adversarial loss functions within an end-to-end framework to enhance the visual quality of compressed images.
The rapid development of artificial intelligence has led to the emergence of semantic communication as a new research frontier in information and communication, which has garnered widespread interest. The core concept of semantic communication is to transmit information based on its semantic content rather than relying solely on bitstreams, aiming to improve communication efficiency and reduce redundant information transmission. Recent studies have investigated the applications of semantic communication in various domains, including natural language processing, image transmission, and multimodal tasks, demonstrating its significant advantages in low-bandwidth and high-latency scenarios.
Firstly, many studies have attempted to integrate deep learning models with semantic communication, leveraging the automatic learning of high-level semantic representations to optimize information transmission. As introduced in [16,17], text-based semantic communication systems enable intelligent exchanges between humans and machines, as well as machine-to-machine interactions. The concept of lossless semantic data compression is explored in [18], proposing that substantial compression can be achieved at the semantic level.
Early attempts at semantic image communication [19,20,21] have developed joint source channel coding (JSCC) methods and achieved promising performance under challenging conditions such as low signal-to-noise ratio (SNR) and constrained bandwidth. For instance, Ref. [19] directly mapped image pixel values to complex-valued channel input symbols and learned noise-robust encoded representations, outperforming traditional separate digital communication methods across all SNRs. Subsequently, Kurka et al. [20] introduced a multi-description JSCC scheme designed for bandwidth-adaptive image transmission. Attention-based JSCC image transmission [21] effectively enabled robust operation across varying SNRs during transmission. Employing semantic labels, DSSLIC [22] proposed a framework for deep-layered image compression. However, this method primarily focuses on traditional pixel-level fidelity, which limits its capability to effectively reconstruct semantic information.
In the design of efficient communication systems, resource allocation optimization is critical, and reinforcement learning (RL) has played a significant role in this area. In particular, deep Q networks (DQN) [23] have emerged as powerful tools for addressing sequential decision-making problems, as they can approximate complex value functions using deep neural networks. DQN is especially well suited for tasks that require adaptive optimization, such as semantic bit allocation in communication systems, where it dynamically adjusts parameters under changing constraints to maximize system performance.
Task-driven semantic encoding, which adopts a conventional hybrid coding framework, incorporates semantic fidelity metrics into the optimization process and leverages RL to achieve semantic bit allocation. In [24], researchers utilized deep Q-learning to optimize the selection of quantization parameters for various coding units, yielding compelling results for decoded images in tasks such as classification, detection, and segmentation. Ref. [25] introduces RL-ASC, a deep learning-driven image semantic encoding approach that employs RL for adaptive semantic bit allocation and integrates GANs for semantic decoding. This technique effectively reconstructs visually compelling and semantically consistent images, even at low bitrates.
Despite significant progress in semantic communication and image compression, existing hierarchical image encoding methods, such as deep semantic segmentation-based learned image compression (DSSLIC) [22], still face notable limitations. DSSLIC relies on a predefined layered semantic structure to guide bit allocation, yet it lacks adaptive decision-making during the encoding process. The bit-allocation strategy is often manually designed or heuristic-based, making it less flexible when dealing with images of varying semantic importance. As a result, it may over-allocate bits to less critical regions while failing to preserve essential semantic details, leading to suboptimal performance in both rate-distortion efficiency and downstream semantic analysis tasks.
To overcome these challenges, this paper proposes a reinforcement learning-based layered semantic coding (RL-SC) method, which dynamically adjusts quantization levels based on the semantic significance of different image regions. The core idea is to model the bit-allocation process as a Markov Decision Process (MDP), where an agent learns an optimal policy to maintain semantic integrity while improving bitrate effectiveness. Specifically, we employ a DQN to guide the adaptive selection of quantization levels, ensuring that critical semantic components receive higher priority while redundant information is compressed more aggressively. Unlike DSSLIC, which follows a fixed layered structure, the proposed method optimizes bit allocation through an adaptive decision-making process, enabling more flexible adjustments to varying the image content.
The proposed method’s effectiveness is validated by experimental findings, highlighting its capability to optimize semantic image compression by adaptively allocating bits based on semantic importance. The approach effectively balances compression efficiency and semantic fidelity, making it a promising solution for future semantic communication systems.
The remainder of the paper is structured as follows. Section 2 presents the architecture of the proposed RL-SC method. Section 3 describes the proposed RL-based semantic quantization along with its training algorithm. Section 4 introduces the Adaptive Residual Compression method. Section 5 presents the details of the experiment and the performance of the proposed method. Section 6 summarizes the main contributions of this paper and discusses potential future research directions.
2. Reinforcement Learning-Based Layered Image Semantic Coding
The proposed RL-SC is illustrated in Figure 1. At the sender, the semantic map and residual information of the image are first extracted using the semantic segmentation network and the image generation network. These are then input into the RL-based semantic quantizer and the Adaptive Residual Compression module, with the former performing adaptive semantic quantization and the latter generating the final residual. At the receiver, the extracted semantic map is used to generate a synthesized image via a generative adversarial network. This image is subsequently combined with the decoded residual to obtain the final target image. The goal of the system is to maximize semantic fidelity under low-bitrate conditions. Details of the semantic encoder and semantic decoder are provided below.
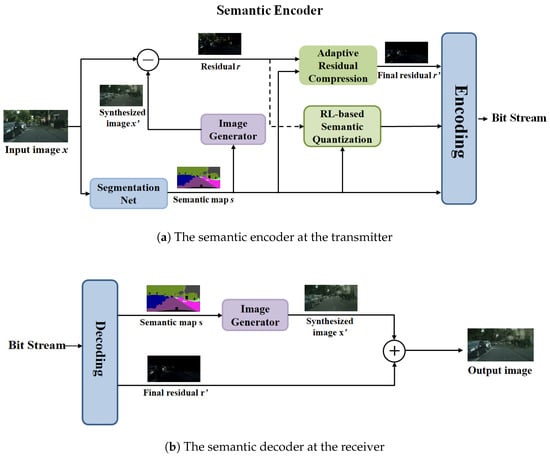
Figure 1.
Proposed reinforcement learning-based layered image semantic coding method. The encoder extracts a semantic map and computes residuals using an image generator. The RL-based semantic quantization adaptively allocates quantization levels for different semantic concepts. The decoder uses an image generator to produce a coarse image and adds the residual to reconstruct the final image, ensuring semantic fidelity and efficient compression.
2.1. Semantic Encoder
At the transmitter, the semantic map of the image is initially extracted using a semantic segmentation network. This network processes the input image and assigns a semantic label to each pixel. Next, we obtain the residual information using an image generator. This network reconstructs the image based on the extracted semantic map, and the residual information is calculated as the discrepancy between the original and the generated image.
Denote the input image as , where H and W represent the image’s height and width, respectively, and “3” indicates the number of channels. The input image is processed by the semantic segmentation network to generate the semantic map . The value at the coordinate () in is denoted as , and represents the class label. Next, we utilize an image generator, such as a GAN or other image generation networks, to produce a coarse reconstruction of the image and then compute the residual by subtracting from the input image .
Existing algorithms directly compress and transmit residuals, but this approach fails to fully consider the semantic importance of different regions, leading to inefficient bit allocation. To address this issue, we introduce the RL-based semantic quantizer and residual processing model. The RL-based semantic quantizer leverages reinforcement learning to adaptively adjust the quantization strategy, ensuring that key semantic regions receive finer encoding while less critical information is compressed more efficiently. Meanwhile, the Adaptive Residual Compression module optimizes the encoding of residual information based on semantic relevance, reducing redundancy and enhancing both semantic fidelity and visual quality under low-bitrate conditions. This design enables more efficient bit allocation at the same bitrate, ensuring the effectiveness and robustness of the semantic communication system.
The importance of different semantic concepts varies in downstream analysis tasks. Therefore, our goal is to achieve precise encoding without losing semantic information. Taking the Cityscapes dataset as an example, semantic segmentation and object detection tasks mainly focus on vehicles, pedestrians, and traffic signs, whereas background elements such as the sky and buildings have less impact on the key semantic content of the image. Although traditional compression methods, such as JPEG and BPG, perform well with respect to pixel-based metrics like Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index (SSIM), they often lead to significant distortion of semantic information in the reconstructed image.
To focus on semantic concepts and achieve precise encoding, we propose a semantic encoding method based on deep reinforcement learning. We model the encoding process as an MDP, where the semantic concepts are encoded in the order of labels , with N denoting the total number of semantic classes, by selecting the optimal quantization levels. This approach ensures an aggressive bitrate and an optimal encoding scheme. The RL agent adaptively allocates quantization levels by balancing semantic performance and encoding cost. This process will be explained in detail in Section 3.
To further compress the residual information, we utilize a residual processing model, which mainly consists of two modules: Semantic-based Patch Selection and Selective Zeroing. This method effectively preserves the residual information of the low-proportion categories, thereby improving the semantic performance of the output image while maintaining an aggressive compression ratio. This process will be explained in detail in Section 4.
After determining the optimal quantization levels through an RL-based semantic quantizer, the final step is to encode the quantized semantic concepts into a compressed bit stream. Specifically, the semantic map is losslessly compressed using Huffman coding, ensuring efficient storage and transmission of semantic information. Meanwhile, we adopt the JPEG XL compression framework to encode each semantic concept separately based on its assigned quantization level. This approach ensures that semantically important regions are preserved with high precision, while less critical areas undergo more aggressive compression, effectively balancing bitrate and semantic fidelity.
2.2. Generative Semantic Decoder
At the receiver, the received bitstream is first decoded to reconstruct the semantic map and the quantized semantic concepts . Specifically, the semantic map is losslessly decoded using Huffman coding, ensuring that the transmitted semantic segmentation information is accurately recovered. Meanwhile, the residual is decoded using the JPEG XL framework, which efficiently restores the compressed residual information while maintaining a balance between compression efficiency and reconstruction quality.
Once the semantic map and quantized semantic concepts are reconstructed, an image synthesis network is used to generate the reconstructed image . Unlike traditional decoding methods, which primarily focus on pixel-wise reconstruction, semantic communication emphasizes the preservation of meaningful content. To achieve this, the image synthesis network leverages the semantic map to guide the generation of a visually and semantically coherent image.
A variety of generative models can be used for this purpose, including GAN-based architectures, which have demonstrated strong capabilities in generating high-resolution images with complex structures. Specifically, GANs aim to capture the underlying distribution of real-world images, making them well suited for semantic-guided image reconstruction. For instance, LGGAN [26] is one possible approach that integrates both local class-specific and global image-level features to enhance scene generation. However, our framework is not limited to a specific generative model, providing flexibility in selecting different architectures based on performance requirements and computational constraints.
In this paper, we employ a pre-trained image generation network, where the semantic map serves as input, conditioning the synthesis of the reconstructed image . The decoded quantized semantic concepts are then added to the output of the image generator to produce the final reconstructed image.
3. Reinforcement Learning-Based Semantic Quantization
This section presents our proposed RL-based semantic quantization model, designed to optimize semantic encoding and residual compression for image communication systems. The model adaptively allocates bitrates to different categories based on their importance in the image, using RL to optimize the encoding process by balancing compression efficiency and semantic fidelity. The architecture and training procedure of the model are detailed in the following sections.
3.1. Architecture of the RL-Based Semantic Quantization Model
Traditional image communication methods primarily evaluate images at the pixel level, requiring the reconstructed image to be identical to the original at the pixel level after transmission. However, semantic communication shifts the focus from pixel-wise accuracy to semantic fidelity and coding efficiency, allowing for certain pixel-level deviations as long as the core semantic information is preserved.
A common approach to encoding semantic information involves heuristic methods, such as threshold-based schemes, which allocate higher bitrates to critical semantic components. However, these methods rely heavily on manual design and lack adaptability, making them less efficient for complex image communication tasks. To overcome these limitations, we propose an RL-based semantic quantization model that adaptively allocates bitrates based on the importance of semantic concepts. Specifically, we employ DQN to optimize the semantic quantization process. The architecture of the proposed RL-based semantic quantization model is illustrated in Figure 2.
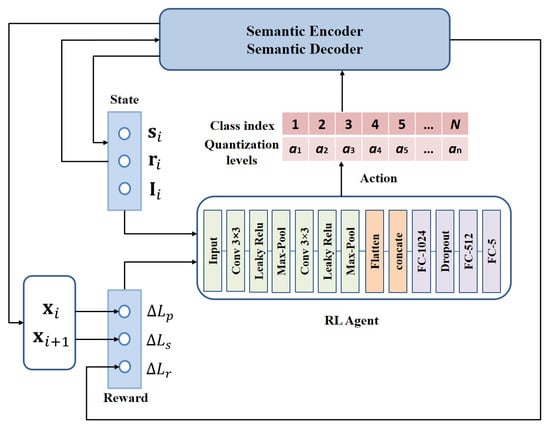
Figure 2.
The architecture of the proposed RL-based semantic quantization model. The agent selects quantization levels for each semantic category based on the observed state, which includes the semantic mask, residual, and category information. After quantization and reconstruction, the reward is calculated according to the reduction in semantic loss, guiding the agent to balance semantic fidelity and bitrate efficiency.
We define as the category semantic mask, where , and its entries are represented as follows:
The residual is element-wise multiplied with the category semantic mask to obtain the category residual :
where ⊙ denotes element-wise multiplication.
To obtain an optimal encoding scheme, the encoding process is modeled as an MDP. In this process, the agent observes the current state and selects an appropriate quantization level for compressing and encoding the category residual , executing the process sequentially according to the label index from to . This process includes five key elements: state, action, reward, state transition probability, and policy. The agent’s behavior is defined as a policy. Since the state transitions are deterministic, the state transition probability is always 1. The details are as follows:
(1) State: To decide on the next action, the agent must collect and analyze all relevant information from the current environment. At step i, the state is defined as , which consists of the category semantic mask, category residual, and category information. Here, is a one-hot vector representing the category information, where the i-th element is set to 1.
(2) Action: The action space A is defined as a set of quantization levels, , where m refers to the total number of levels. In traditional image coding methods such as JPEG/JPEG XL, the quantization level directly determines the number of coding bits and coding quality. Higher quantization levels correspond to higher bitrates and better reconstruction quality. At each state , the agent selects an action from the action space A, determining the quantization level for the corresponding category residual. This decision is made based on the agent’s observations, enabling adaptive encoding tailored to different semantic concepts. Once is determined, is compressed using methods such as JPEG XL.
(3) Reward: The cumulative reward, as a measure of action evaluation, acts as the optimization objective in MDP. By observing the rewards, the agent is directed to learn the optimal behavior. In the semantic communication system, our goal is to retain as much semantic information as possible while maintaining a low bitrate. At the i-th step, the semantic loss of the reconstructed image can be expressed as:
where denotes the bits per pixel (BPP) of the encoded class mask for the i-th category, which is the ratio of the encoded bitstream length to the total number of pixels in the image. represents the semantic loss, which measures the difference between the reconstructed image’s labels and the ground truth labels, while indicates the perceptual loss that reflects the perceptual quality of the reconstructed image. These losses will be formally defined in the next subsection. and are hyper parameters. The agent can learn different encoding strategies by adjusting them, thereby optimizing various semantic encoding models.
In the MDP process, our reward is defined as the reduction in semantic loss from to , which can be expressed as:
The agent’s goal is to maximize the cumulative reward G throughout the episode, where represents the discount factor, and the discounted cumulated reward can be expressed as:
(4) Agent: We design an agent capable of observing the environmental state and executing a sequence of actions for semantic encoding. To accomplish this, we adopt the DQN algorithm, which enables the agent to learn an optimal quantization policy through trial and error. In this paper, the agent predicts the optimal action through the Q-network. The architecture of the Q-network is illustrated in Figure 2. Initially, from the state is processed through two consecutive convolutional layers, each followed by a max-pooling operation. The output of the convolutional layers is subsequently flattened into a one-dimensional vector and concatenated with . The resulting vector is passed through three fully connected layers, ultimately producing an vector. All convolutional layers are activated using Leaky Rectified Linear Units (Leaky ReLU), while the output layer utilizes a SoftMax function to compute the selection probabilities for each action. To reduce overfitting, a dropout layer is added to the network.
By inputting the , the Q-network outputs the discounted cumulative reward for each action a as . The optimal action can then be obtained using the following formula:
3.2. Semantic Perceptual Loss
Traditional image communication systems commonly use PSNR and SSIM to evaluate image reconstruction quality. However, semantic communication typically focuses on transmitting the underlying semantic information and features of the image. In the previous section, we introduced the semantic loss function in (3), which balances the trade-off among bitrate , semantic fidelity , and perceptual quality .
The semantic loss is calculated using the Mean Intersection over Union (MIoU), which quantifies the discrepancy between the reconstructed image’s labels and the ground truth labels. Formally, the semantic loss is expressed as:
MIoU is a commonly employed metric in semantic segmentation, measuring the average classification accuracy across all semantic categories. It is computed as:
where N represents the total number of semantic categories, and denotes the Intersection over Union (IoU) for class i. The IoU for each class i is given by:
where the metrics , , and quantify the model’s performance for class i. Specifically, denotes the number of pixels correctly classified as belonging to class i, while denotes the pixels mistakenly assigned to that class. Conversely, corresponds to the pixels that should have been classified as class i but were misidentified.
Minimizing naturally maximizes MIoU, ensuring that the reconstructed image retains its semantic fidelity. The MIoU computes the Intersection over Union (IoU) for each class and derives an overall score by averaging these values across all classes. This metric thoroughly evaluates how accurately each pixel is classified, taking into account correct classifications as well as misclassifications. Consequently, MIoU provides a comprehensive assessment of the model’s semantic reconstruction performance across N classes. In this work, we use a pre-trained [27] to obtain semantic segmentation predictions for calculating MIoU.
Although MIoU effectively quantifies the reconstruction quality at the semantic level and performs well in semantic communication, it primarily focuses on the recovery of each semantic class and lacks a comprehensive capture of the high-level structural information and perceptual effects of the image. To address this limitation, we introduce perceptual loss . Pre-trained VGG [28] networks can be used to extract high-dimensional features of the image, and these features are then used to evaluate the perceptual similarity of the image. The Euclidean distance between the feature maps of the original and the reconstructed images at these layers is calculated as the perceptual loss. Specifically, the perceptual loss is computed using the following formula:
here, and represent the feature maps of the original image and the reconstructed image . In this way, perceptual loss can effectively capture the semantic information and high-level structural details of the image, thereby improving image reconstruction quality and making the reconstructed image visually closer to the perceptual effect of the real image.
3.3. Training Algorithm
During training, we adopt the DQN [23] training framework and approximate the Q-value function using a deep neural network. We initialize the Q-network and the target Q-network and use an experience replay buffer to store the agent’s interaction experiences with the environment.
In the initialization step of each training round, we input the semantic map into the image generator to obtain the initial reconstructed image . By feeding into the agent, we can adaptively obtain the corresponding quantization parameters. We denote as the reconstructed image from the previous step. The semantic decoder processes the received bitstream to obtain the category residual , which is then added to to obtain the current reconstructed image . The image is fed into both the semantic segmentation network and the VGG network to obtain the semantic loss for the current state. Based on (4), the reward is obtained, indicating whether the selected action is beneficial. The reward is determined by the reduction in perceptual loss, semantic loss, and bitrate after executing the action.
At each training step, the agent follows the -greedy policy to select an action, execute it, and then store the transition in the replay buffer. Then, a batch of experiences is randomly sampled to calculate the target Q-values. The network parameters are updated by minimizing the error between the Q-network output and the target values. Meanwhile, the target Q-network parameters are periodically synchronized to ensure training stability. This iterative process approximates the optimal policy, enabling efficient decision-making. The training process of the RL-based semantic quantization model is outlined in Algorithm 1.
| Algorithm 1 Training Process |
| Input: Semantic map , residual , dataset X, action space A, training epoch , discount |
| factor , update interval C, total number of semantic classes N |
Output: Q-network parameter
|
4. Residual Processing Module
To further enhance the compression efficiency of residual information while preserving the semantic representation of the image, we adopt a residual processing method proposed in our previous work [29]. This method leverages semantic information to perform differentiated processing based on the pixel proportions of different categories, with an emphasis on preserving the residuals of categories that have a greater impact on semantic recognition but occupy a smaller proportion in the image. As a consequence, it enhances the semantic fidelity of the reconstructed image while maintaining a reasonable compression ratio. As presented in Figure 3, the module consists of two parts: Semantic-based Patch Selection and Selective Zeroing.
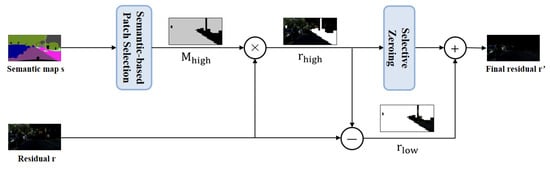
Figure 3.
Internal details diagram of the residual processing module.
Semantic-based Patch Selection: Different semantic categories in an image exhibit significant spatial imbalance. For example, in the Cityscapes dataset, the number of pixels belonging to the road category is significantly larger than that of the streetlight category. Consequently, for high-proportion categories such as road, slight deviations in pixel values may not significantly impact the recognition performance of the semantic segmentation network. However, for low-proportion categories such as streetlight, deviations in pixel values can severely affect semantic recognition. Therefore, residual processing should prioritize the retention of residuals for categories that have a greater impact on semantic performance while suppressing residuals for high-proportion categories to enhance compression efficiency.
First, we calculate the proportion of each semantic category in the image and classify categories with proportions below a predefined threshold as low-proportion categories. Then, through the patch selection process, a binary matrix with the same size as the original image is generated, which is divided into patches. Patches containing low-proportion categories are assigned a value of 0, while the remaining patches are set to 1, effectively distinguishing between high-proportion and low-proportion regions.
Selective Zeroing: To further enhance residual compression efficiency, we introduce the selective zeroing strategy. This approach refines the residual representation by eliminating insignificant values, thereby reducing redundancy while preserving critical information. The fundamental principle is to set residuals with absolute values below a predefined threshold to zero, increasing the proportion of zero values in the overall residual map. The residual is element-wise multiplied by the binary mask to obtain , which contains only the residuals of high-proportion categories. Then, elements in with an absolute value smaller than a predefined threshold are set to zero, effectively removing insignificant residual information. This strategy ensures a high compression ratio, even under lossy compression with high-quality factors, while mitigating the adverse effects of lossy encoding and decoding on low-proportion categories.
By combining these two methods, we are able to balance compression efficiency and semantic reconstruction performance, ensuring that the semantic information in the image is maximized during the reconstruction process.
5. Experiments
This section provides a detailed description of the dataset, training settings, and the performance of the proposed image semantic coding method. It also discusses the effect of varying compression rates on the semantic transmission of images.
5.1. Experimental Settings
Datasets: The experiments in this paper were conducted on the Cityscapes dataset, a widely used benchmark for urban street scene image semantic segmentation tasks. The dataset contains up to 5000 high-quality pixel-level annotated images, containing 2975 training images, 500 validation images, and 1525 test images. It includes 30 categories, primarily covering various objects and scenes in urban environments such as buildings, roads, pedestrians, and vehicles, making it ideal for assessing the performance of semantic segmentation and image reconstruction models. We downsampled the images and semantic labels to a size of 256 × 512 and conducted testing on the validation set.
Training Settings: In the simulations, the DQN training parameters are randomly initialized. The learning rate is set , and the discount factor is . The -greedy strategy is employed for action selection, where is initialized to 0.9. The experience replay buffer has a capacity of 10,000, with a mini-batch size of 1. The target network parameters are updated every 50 steps. Training is conducted over episodes. The action space is defined as . The total number of semantic classes is set to . The model is implemented using the PyTorch framework (version 1.10.1).
Baselines: We compare the proposed method with standard image compression techniques such as JPEG, J2K, JPEG XL, and BPG, as well as with the deep learning-based image codec DSSLIC [22] and MLIC [30].
Evaluation Metrics: To comprehensively assess the model’s performance, MIoU was used as an objective metric, where a higher MIoU value, up to 1, indicates less semantic information loss. To ensure fair comparisons across different codecs, including traditional methods, learning-based models, and the proposed RL-SC method, a pre-trained semantic segmentation model was uniformly applied to the reconstructed images to generate predicted segmentation maps. These were then compared with ground truth labels to compute MIoU, enabling a consistent evaluation of semantic fidelity. In addition, kernel inception distance (KID) [31] and Fréchet inception distance (FID) [32], which align closely with human perception, were employed to measure the similarity between the reconstructed and input images in the deep feature space. Specifically, KID and FID measure the distributional differences between reconstructed images and real samples through the Inception network. These metrics are commonly used in the context of GANs to measure the quality and diversity of generated samples.
5.2. Results and Analysis
In Figure 4, we compared various image compression methods at different BPP using MIoU as the primary evaluation metric. The results confirm that the proposed method outperforms all alternatives across the entire bitrate range.
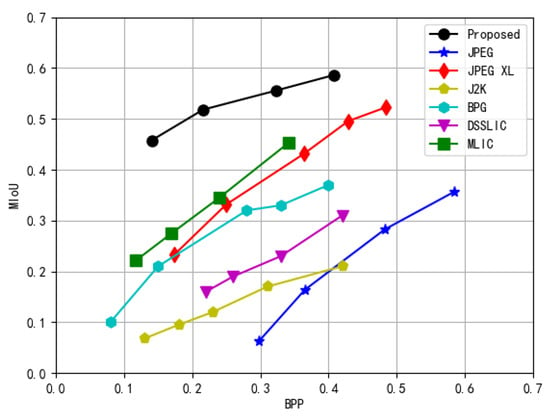
Figure 4.
The MIoU of various image codecs for semantic segmentation tasks. Higher MIoU values reflect superior performance.
Specifically, at an extremely low bitrate (0.14 BPP), the proposed RL-SC achieves an MIoU of approximately 0.46, which is significantly higher than that of other methods. This demonstrates that the proposed RL-SC can more effectively preserve semantic information under extremely low-bitrate conditions. Meanwhile, at a high bitrate (0.4 BPP), the proposed RL-SC achieves an MIoU close to 0.6, significantly outperforming DSSLIC (0.3) and BPG (0.38), exhibiting stronger semantic awareness compared to traditional compression methods.
These results indicate that the proposed RL-SC effectively reduces the loss of semantic information at low bitrates and further enhances semantic reconstruction performance at high bitrates. This can be attributed to the introduction of RL-based semantic quantization, which allocates encoding resources to different semantic categories, achieving an effective balance between semantic preservation and compression efficiency.
In Figure 5 and Figure 6, we compared the perceptual quality of various image compression methods at different BPP using KID and FID as evaluation metrics. Lower KID and FID values indicate smaller distribution discrepancies between the reconstructed and original images, reflecting higher perceptual quality.
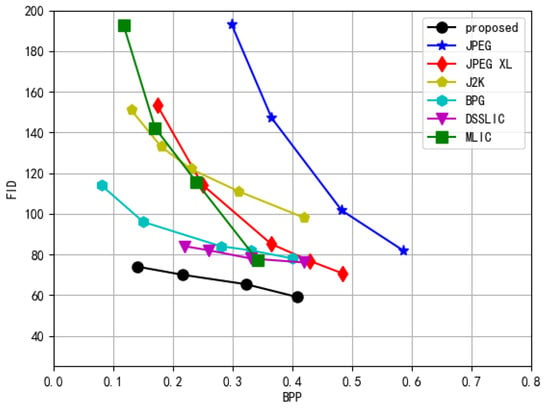
Figure 5.
Evaluation of image codec perceptual performance using the FID metric, with lower values representing superior quality.
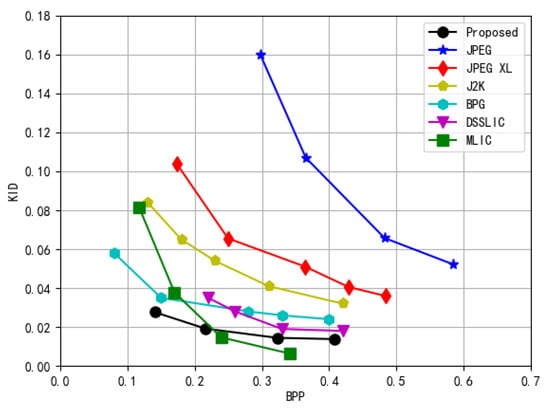
Figure 6.
Evaluation of image codec perceptual performance using the KID metric, with lower values representing superior quality.
The experimental results demonstrate that the proposed RL-SC outperforms other image compression methods across all bitrate ranges. Specifically, at a low bitrate (0.14 BPP), the proposed RL-SC achieved a KID of approximately 0.03 and an FID of around 70, whereas BPG reported a KID of approximately 0.04 and an FID close to 100. Traditional methods, such as J2K, exhibited a KID exceeding 0.08 and an FID surpassing 150. These findings indicate that, under extremely low-bitrate conditions, the proposed RL-SC is significantly more effective in preserving the perceptual quality of images. Furthermore, at a higher bitrate (0.4 BPP), the proposed RL-SC achieved a KID of approximately 0.01 and an FID of around 60, indicating strong perceptual performance. Although MLIC slightly outperforms RL-SC in terms of KID when BPP exceeds 0.25, RL-SC consistently demonstrates competitive results and superior perceptual fidelity compared to traditional codecs and other learning-based methods across the entire bitrate range.
This performance improvement can be attributed to the introduction of perceptual loss during the encoding process, enabling the model to effectively capture semantic information and high-level structural details of the image. Consequently, the quality of reconstructed images is significantly enhanced, with perceptual effects closely resembling those of the original images. Furthermore, the proposed RL-SC integrates a GAN architecture and employs adversarial loss, which contributes to the naturalness and realism of reconstructed images, clearly validating the effectiveness of the designed RL-based coding strategy.
To evaluate the rate-distortion performance of the proposed RL-SC framework, we report the PSNR and SSIM across various bitrates, as shown in Figure 7. While these metrics are standard in traditional image coding systems, they primarily emphasize pixel-wise fidelity and structural similarity. As expected, baseline methods achieve higher PSNR and SSIM values, since they are directly optimized for these distortion metrics. In contrast, RL-SC is designed to preserve semantic content under bandwidth constraints and is inherently tolerant to pixel-level distortions. Unlike conventional methods that enforce local consistency, our approach focuses on maintaining global semantic integrity, which inevitably leads to a moderate degradation in pixel-level metrics. Nonetheless, this trade-off is aligned with the objective of semantic communication, where the preservation of meaningful content is prioritized over precise pixel reconstruction.
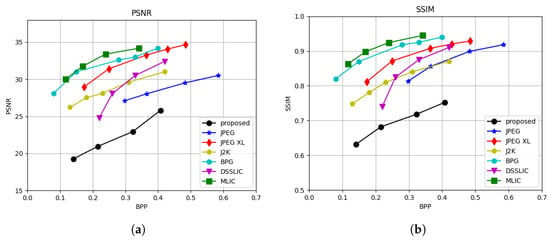
Figure 7.
Rate-distortion performance of different methods. (a) PSNR. (b) SSIM.
This study further evaluates the memory overhead and scalability of the model during the inference stage. The experiments were conducted on an NVIDIA RTX 1080 GPU and an Intel Core i9-7900X CPU (NVIDIA Corporation, Santa Clara, CA, USA; Intel Corporation, Santa Clara, CA, USA). The proposed encoding framework has a peak memory consumption of approximately 2.5 GB when compressing a single image. These results demonstrate that the proposed framework achieves a reasonable trade-off between performance and computational cost, making it suitable for offline image compression tasks under moderate hardware constraints.
The results above validate that the proposed RL-SC not only preserves semantic consistency but also significantly enhances perceptual quality, especially at low bitrates, demonstrating superior performance and practical value.
5.3. Ablation Study
To evaluate the effectiveness of individual components in the proposed semantic compression framework, we conducted two ablation experiments: one to assess the contribution of the RL-based quantization and the other to evaluate the impact of the residual processing module.
To examine the effectiveness of the reinforcement learning (RL)-based quantizer, a comparative experiment was conducted by replacing it with a fixed quantization strategy. In the fixed setting, a constant quantization level was applied uniformly across all residual components, without considering semantic importance. As illustrated in Figure 8, the proposed RL-based quantizer consistently achieves higher mean Intersection over Union (MIoU) values across different bit-per-pixel (BPP) settings compared to the fixed approach. This improvement is particularly noticeable under lower BPP conditions, where efficient bit allocation becomes crucial. The adaptive quantization policy learned via RL focuses bits on semantically significant regions, leading to a more accurate reconstruction in terms of semantic fidelity. These findings underscore the contribution of the RL module to the overall performance of the framework.
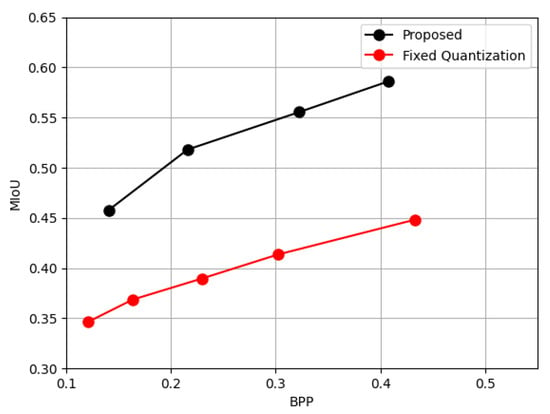
Figure 8.
Comparison between the proposed RL-based quantization and fixed-level quantization.
The second ablation experiment aimed to evaluate the influence of the residual processing module on semantic reconstruction performance. This study compares the proposed method, which integrates the residual processing module, with an ablated variant that excludes it entirely. By removing residual processing, the system no longer benefits from selective zeroing or semantic-guided filtering of less significant information. The experimental results, presented in Figure 9, show a noticeable decline in performance when the residual processing module is excluded. This finding confirms that the residual processing module is instrumental in balancing compression efficiency with semantic fidelity. By discarding uninformative residuals while retaining significant details, the module helps maintain higher accuracy in downstream semantic tasks, thereby reinforcing its value within the overall framework.
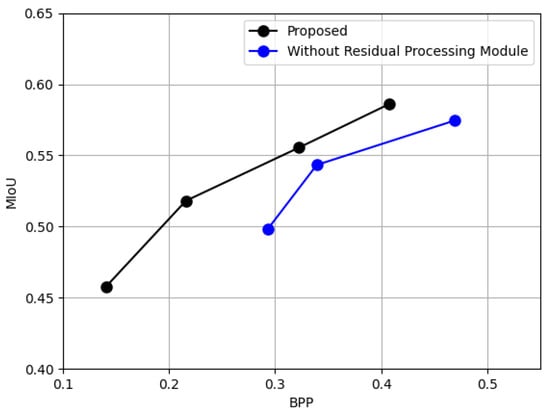
Figure 9.
Comparison between the proposed framework and a variant without the residual processing module.
6. Conclusions
In this paper, we propose an RL-based layered image semantic coding method for semantic communication. By integrating semantic communication, advanced image compression, and reinforcement learning, RL-SC adaptively allocates semantic bits using a DQN-based strategy, effectively minimizing semantic distortion under bandwidth constraints. Perceptual and semantic loss further enhance reconstruction quality, ensuring the preservation of both low-level details and high-level semantic content. Extensive experiments on the Cityscapes dataset validate the superiority of RL-SC. Evaluated using MIoU, FID, and KID, it outperforms traditional compression methods and learning-based codecs such as DSSLIC and MLIC. The results demonstrate that reinforcement learning enables more efficient semantic encoding by dynamically optimizing bit allocation, preserving essential semantic information while maintaining efficiency under limited bandwidth.
Author Contributions
Conceptualization, J.Y.; methodology, J.Y.; software, J.Y.; validation, J.Y., Y.M. and Y.W.; formal analysis, J.Y. and Y.M.; investigation, Y.W.; resources, D.H.; data curation, Y.W.; writing—original draft preparation, J.Y.; writing—review and editing, D.H. and Y.M.; visualization, Y.M.; supervision, D.H.; project administration, D.H.; funding acquisition, D.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by NSFC under Grant 62271155 and NSFC ‘Ye Qisun’ Science Fund under Grant U2441252.
Data Availability Statement
The original code presented in this study is openly available in the GitHub repository: https://github.com/AusteRee/Image-Semantic-Coding.git (accessed on 11 May 2025).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Wallace, G. The JPEG still picture compression standard. IEEE Trans. Consum. Electron. 1992, 38, xviii–xxxiv. [Google Scholar] [CrossRef]
- Christopoulos, C.; Skodras, A.; Ebrahimi, T. The JPEG2000 still image coding system: An overview. IEEE Trans. Consum. Electron. 2000, 46, 1103–1127. [Google Scholar] [CrossRef]
- Albalawi, U.; Mohanty, S.P.; Kougianos, E. A Hardware Architecture for Better Portable Graphics (BPG) Compression Encoder. In Proceedings of the 2015 IEEE International Symposium on Nanoelectronic and Information Systems, Indore, India, 21–23 December 2015; pp. 291–296. [Google Scholar] [CrossRef]
- Agustsson, E.; Tschannen, M.; Mentzer, F.; Timofte, R.; Gool, L.V. Generative Adversarial Networks for Extreme Learned Image Compression. arXiv 2019, arXiv:1804.02958. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. arXiv 2016, arXiv:1603.08155. [Google Scholar]
- Grm, K.; Štruc, V.; Artiges, A.; Caron, M.; Ekenel, H.K. Strengths and weaknesses of deep learning models for face recognition against image degradations. IET Biom. 2017, 7, 81–89. [Google Scholar] [CrossRef]
- Dodge, S.; Karam, L. Understanding how image quality affects deep neural networks. In Proceedings of the 2016 Eighth International Conference on Quality of Multimedia Experience (QoMEX), Lisbon, Portugal, 6–8 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Toderici, G.; Vincent, D.; Johnston, N.; Hwang, S.J.; Minnen, D.; Shor, J.; Covell, M. Full Resolution Image Compression with Recurrent Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5435–5443. [Google Scholar] [CrossRef]
- Johnston, N.; Vincent, D.; Minnen, D.; Covell, M.; Singh, S.; Chinen, T.; Jin Hwang, S.; Shor, J.; Toderici, G. Improved Lossy Image Compression with Priming and Spatially Adaptive Bit Rates for Recurrent Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4385–4393. [Google Scholar] [CrossRef]
- Minnen, D.C.; Ballé, J.; Toderici, G. Joint Autoregressive and Hierarchical Priors for Learned Image Compression. In Proceedings of the Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018. [Google Scholar]
- Mentzer, F.; Agustsson, E.; Tschannen, M.; Timofte, R.; Gool, L.V. Conditional Probability Models for Deep Image Compression. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4394–4402. [Google Scholar] [CrossRef]
- Toderici, G.; O’Malley, S.M.; Hwang, S.J.; Vincent, D.; Minnen, D.; Baluja, S.; Covell, M.; Sukthankar, R. Variable Rate Image Compression with Recurrent Neural Networks. arXiv 2016, arXiv:1511.06085. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. Density Modeling of Images using a Generalized Normalization Transformation. arXiv 2016, arXiv:1511.06281. [Google Scholar]
- Rippel, O.; Bourdev, L. Real-Time Adaptive Image Compression. arXiv 2017, arXiv:s1705.05823. [Google Scholar]
- Yan, L.; Qin, Z.; Zhang, R.; Li, Y.; Li, G.Y. Resource Allocation for Text Semantic Communications. IEEE Wirel. Commun. Lett. 2022, 11, 1394–1398. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, S.; Zhang, Y.; Cao, K.; Zhou, L.; Seet, B.C.; Zhao, H.; Wei, J. Extended context-based semantic communication system for text transmission. Digit. Commun. Netw. 2024, 10, 568–576. [Google Scholar] [CrossRef]
- Pumma, S.; Vishnu, A. Semantic-Aware Lossless Data Compression for Deep Learning Recommendation Model (DLRM). In Proceedings of the 2021 IEEE/ACM Workshop on Machine Learning in High Performance Computing Environments (MLHPC), St. Louis, MO, USA, 15 November 2021; pp. 1–8. [Google Scholar] [CrossRef]
- Bourtsoulatze, E.; Kurka, D.B.; Gündüz, D. Deep Joint Source-channel Coding for Wireless Image Transmission. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 4774–4778. [Google Scholar] [CrossRef]
- Kurka, D.B.; Gündüz, D. Bandwidth-Agile Image Transmission With Deep Joint Source-Channel Coding. IEEE Trans. Wirel. Commun. 2021, 20, 8081–8095. [Google Scholar] [CrossRef]
- Xu, J.; Ai, B.; Chen, W.; Yang, A.; Sun, P.; Rodrigues, M. Wireless Image Transmission Using Deep Source Channel Coding with Attention Modules. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 2315–2328. [Google Scholar] [CrossRef]
- Akbari, M.; Liang, J.; Han, J. DSSLIC: Deep Semantic Segmentation-based Layered Image Compression. In Proceedings of the ICASSP 2019–2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 2042–2046. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Li, X.; Shi, J.; Chen, Z. Task-Driven Semantic Coding via Reinforcement Learning. IEEE Trans. Image Process. 2021, 30, 6307–6320. [Google Scholar] [CrossRef] [PubMed]
- Huang, D.; Gao, F.; Tao, X.; Du, Q.; Lu, J. Toward Semantic Communications: Deep Learning-Based Image Semantic Coding. IEEE J. Sel. Areas Commun. 2023, 41, 55–71. [Google Scholar] [CrossRef]
- Tang, H.; Xu, D.; Yan, Y.; Torr, P.H.; Sebe, N. Local Class-Specific and Global Image-Level Generative Adversarial Networks for Semantic-Guided Scene Generation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 7867–7876. [Google Scholar] [CrossRef]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. arXiv 2017, arXiv:1612.01105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar]
- Wang, Y.; Yan, J.; Miao, Y.; Li, Z.; Hu, D. A New Residual-Based Image Semantic Transmission System. In Proceedings of the 2024 6th International Conference on Communications, Information System and Computer Engineering (CISCE), Guangzhou, China, 10–12 May 2024; pp. 674–677. [Google Scholar] [CrossRef]
- Jiang, W.; Yang, J.; Zhai, Y.; Ning, P.; Gao, F.; Wang, R. MLIC: Multi-Reference Entropy Model for Learned Image Compression. In Proceedings of the 31st ACM International Conference on Multimedia, ACM, 2023, MM’23, Ottawa, ON, Canada, 29 October–3 November 2023; pp. 7618–7627. [Google Scholar] [CrossRef]
- Bińkowski, M.; Sutherland, D.J.; Arbel, M.; Gretton, A. Demystifying MMD GANs. arXiv 2021, arXiv:1801.01401. [Google Scholar]
- Heusel, M.; Ramsauer, H.; Unterthiner, T.; Nessler, B.; Hochreiter, S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. arXiv 2018, arXiv:1706.08500. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).