Obstacle Avoidance Path Planning for UAV Applied to Photovoltaic Stations Based on Improved Dynamic Window Method
Abstract
1. Introduction
1.1. Global Path Planning
1.2. Local Path Planning
1.3. Cooperative Obstacle Avoidance for Multi-UAV Systems
- (1)
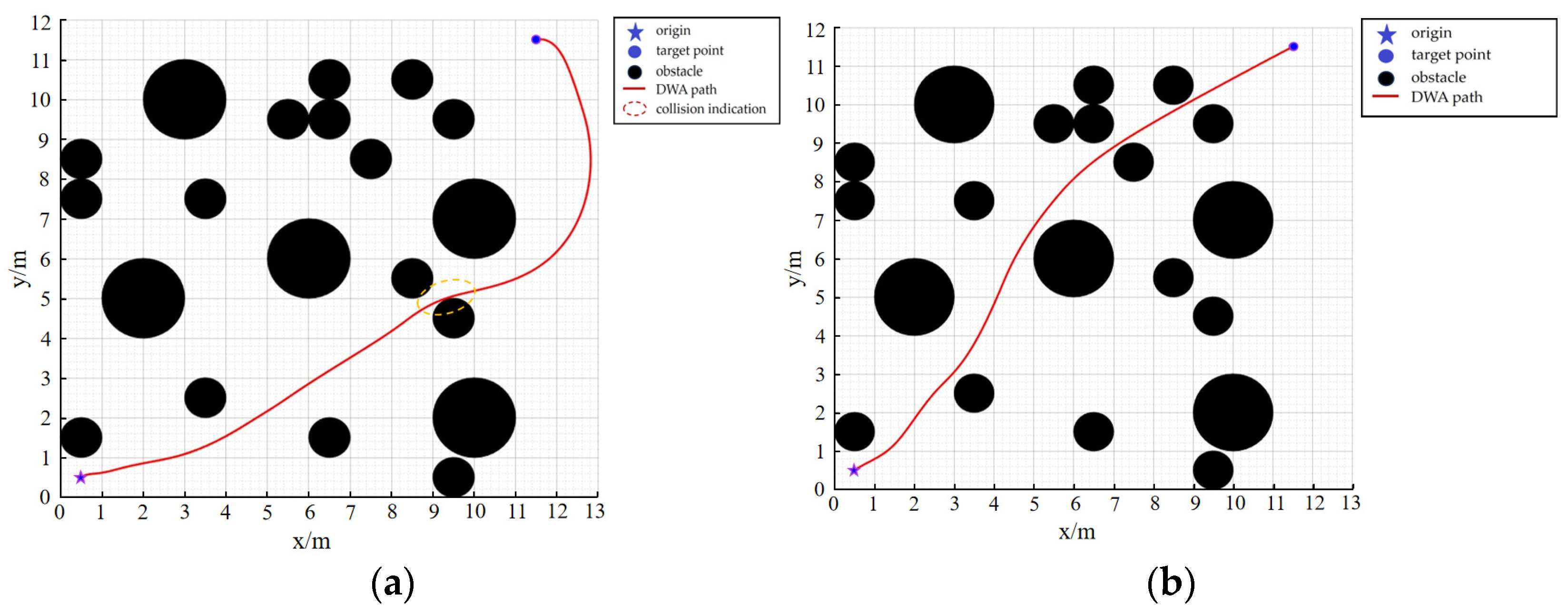
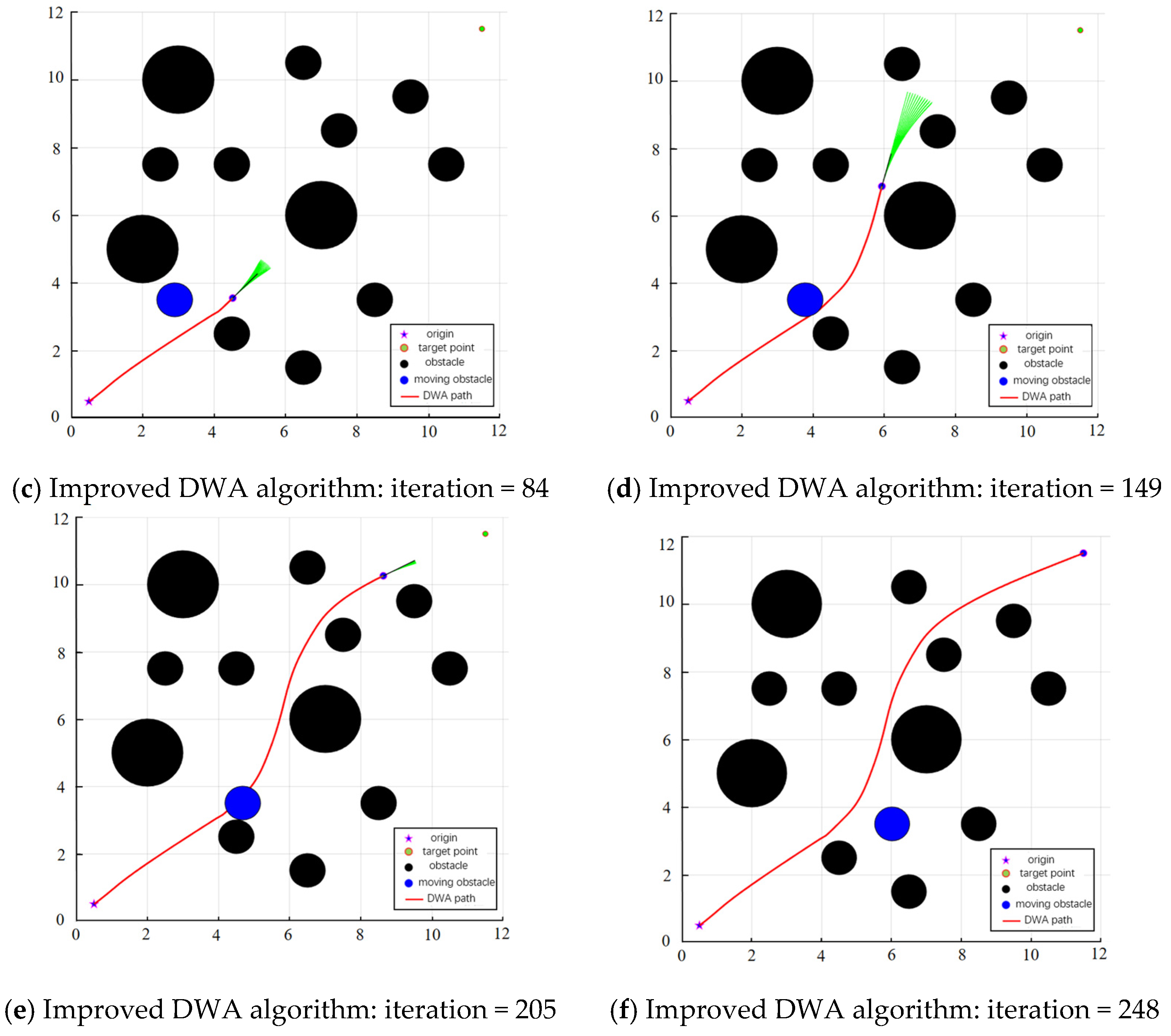
- An improved DWA algorithm is proposed, which optimizes the path planning process by considering the physical dimensions of the UAV for obstacle inflation, introducing adaptive weight adjustment mechanisms, and incorporating a global distance evaluation sub-function. These enhancements improve the algorithm’s adaptability, real-time performance, and obstacle avoidance capability across various environments, resulting in shorter, smoother paths that are closer to the global optimum.
- (2)
- A novel hybrid path planning algorithm is developed by combining the improved A* algorithm with the modified DWA algorithm specifically for the photovoltaic station environment. The global planner leverages the improved A* algorithm to generate an initial optimal path, while the local planner dynamically adjusts the trajectory in response to real-time environmental information using the modified DWA algorithm, thereby ensuring safe and efficient UAV flight in complex environments.
- (3)
- Extensive simulation experiments under various scenarios have been conducted to comprehensively validate the effectiveness, applicability, and robustness of both the improved DWA algorithm and the hybrid path planning algorithm. Results show that the improved DWA algorithm outperforms traditional methods in key metrics such as path length and runtime, while the hybrid algorithm demonstrates reliable path planning and obstacle avoidance capabilities in complex environments with column-like obstacles.
2. Materials and Methods
2.1. Improved A* Algorithm
2.2. Improved DWA Algorithm
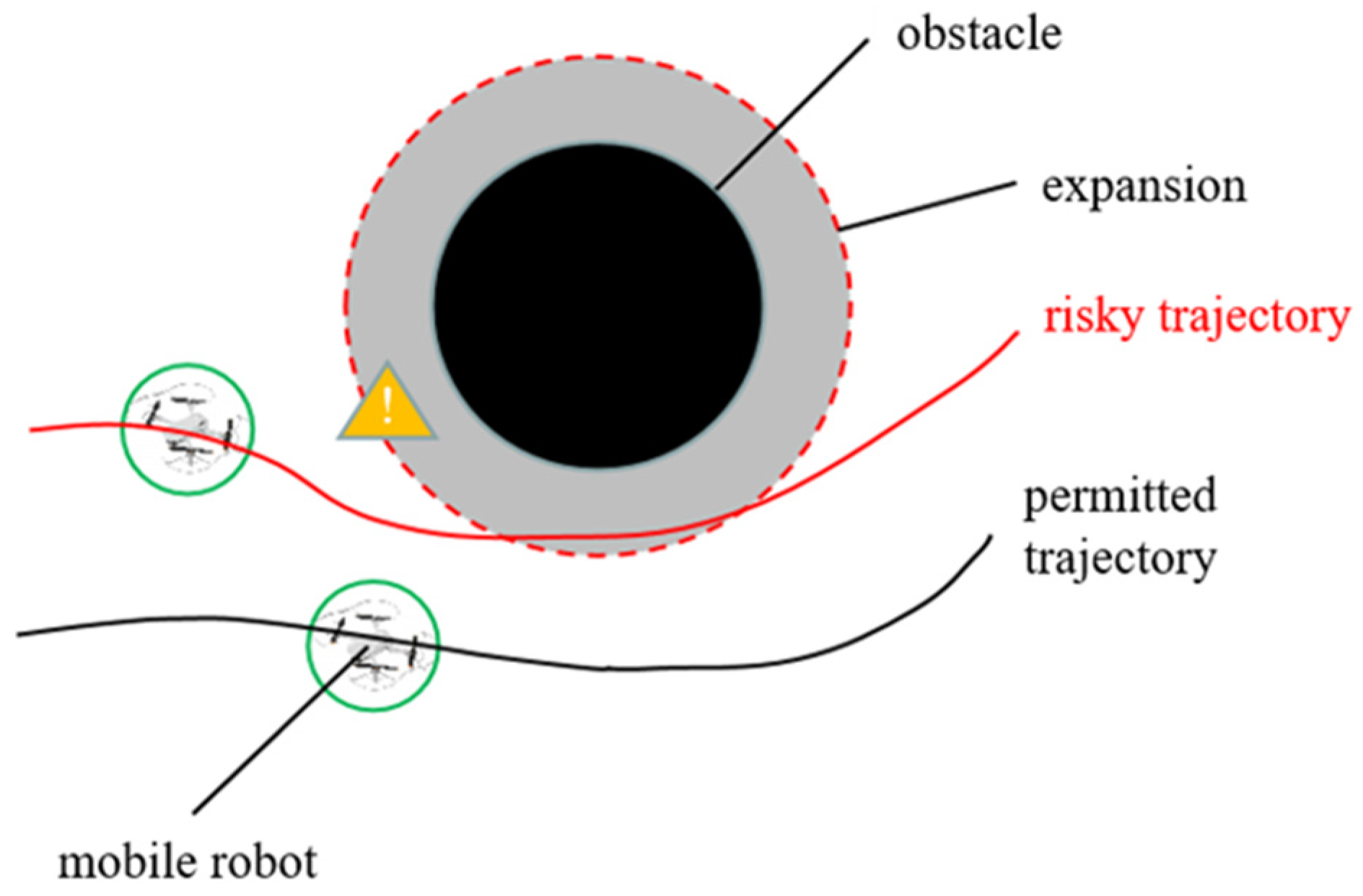
2.2.1. Obstacle Expansion Treatment
2.2.2. Adaptive Dynamic Adjustment of Weight Factors
2.2.3. Global Distance Evaluation Subfunction
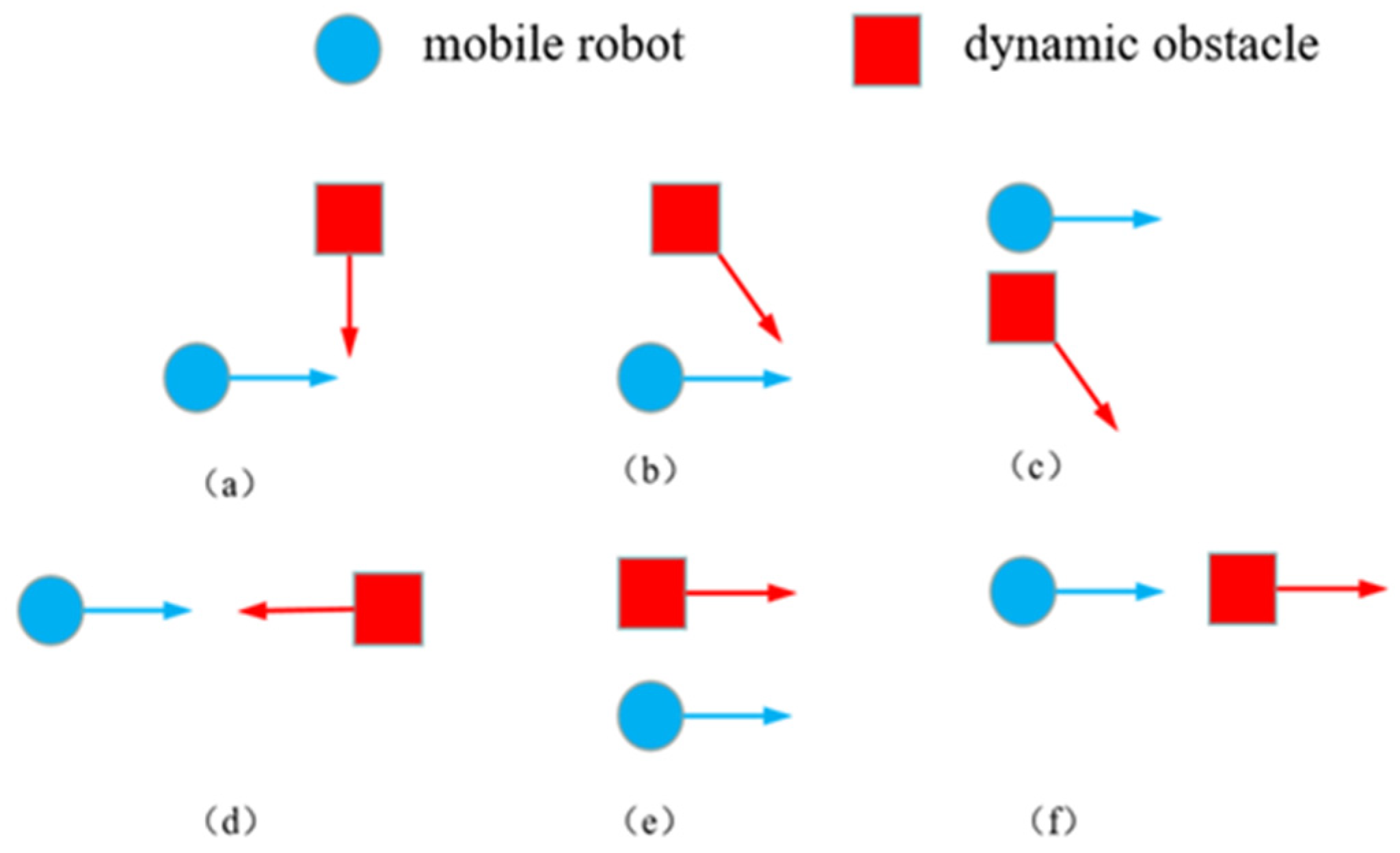
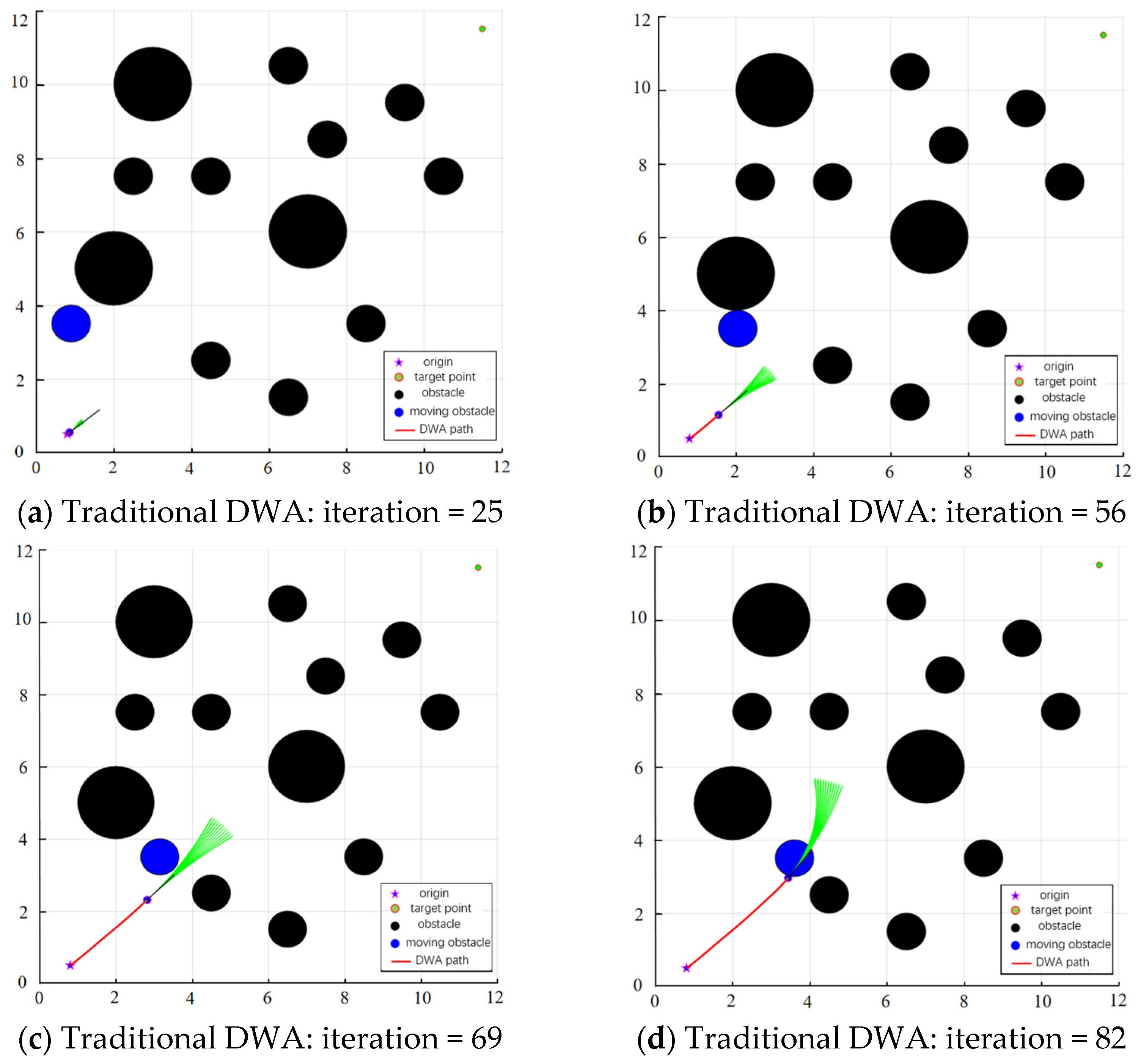
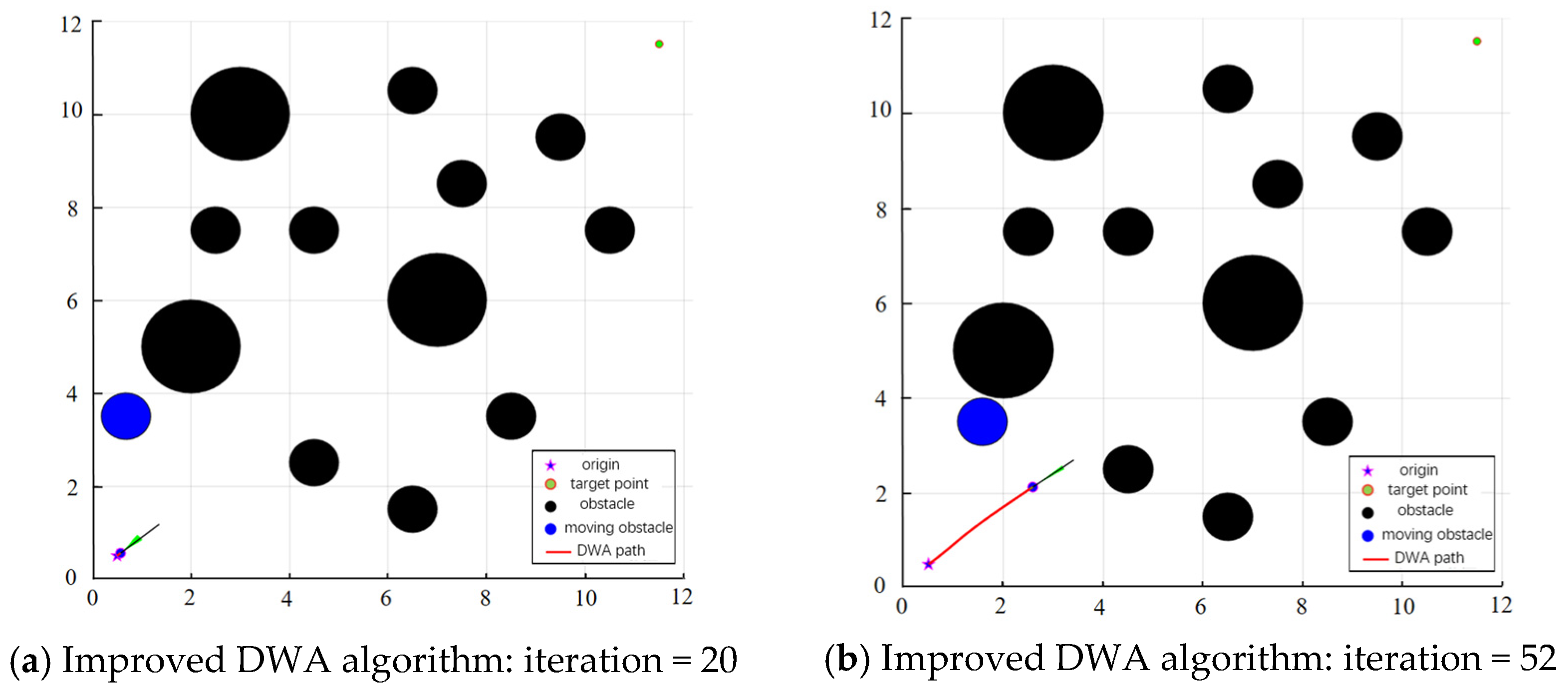
2.2.4. Dynamic Obstacle Prediction and Avoidance Strategy
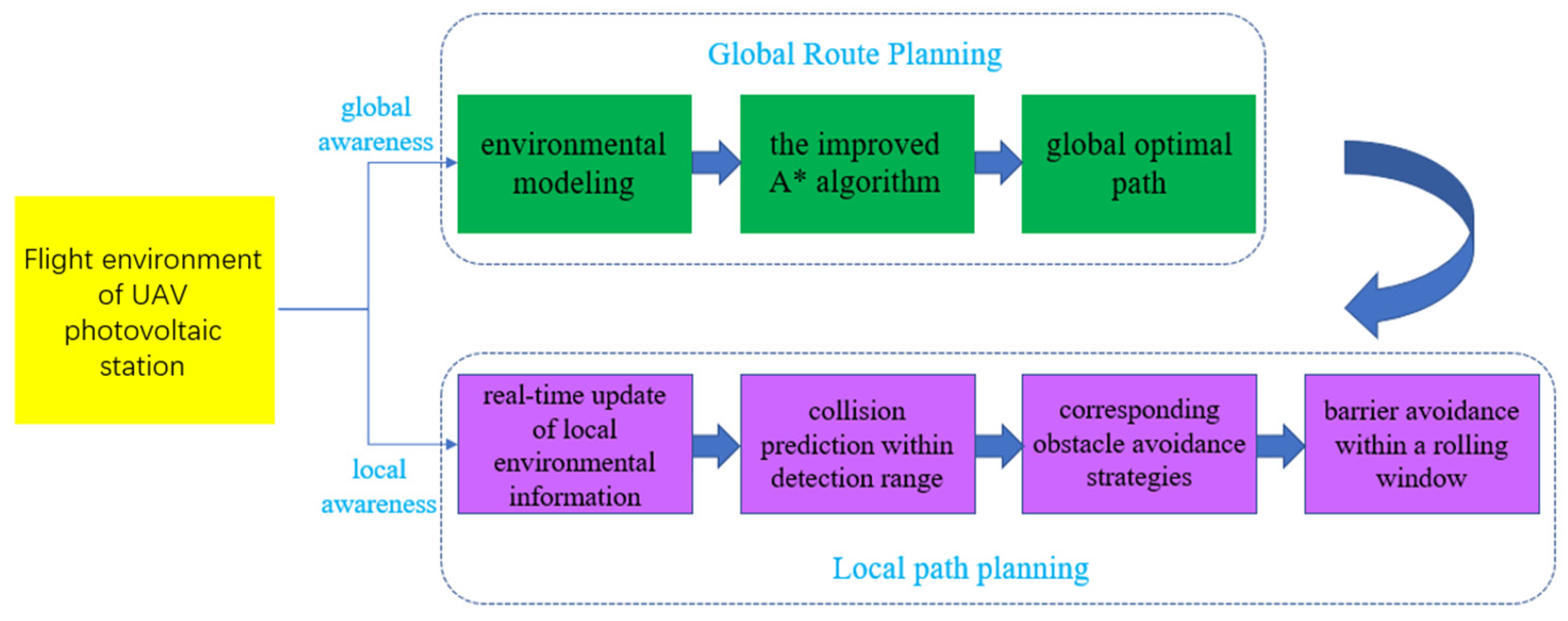
2.3. Hybrid Path Planning of UAV Photovoltaic Station Based on Improved A* Algorithm and Improved Dynamic Window Method
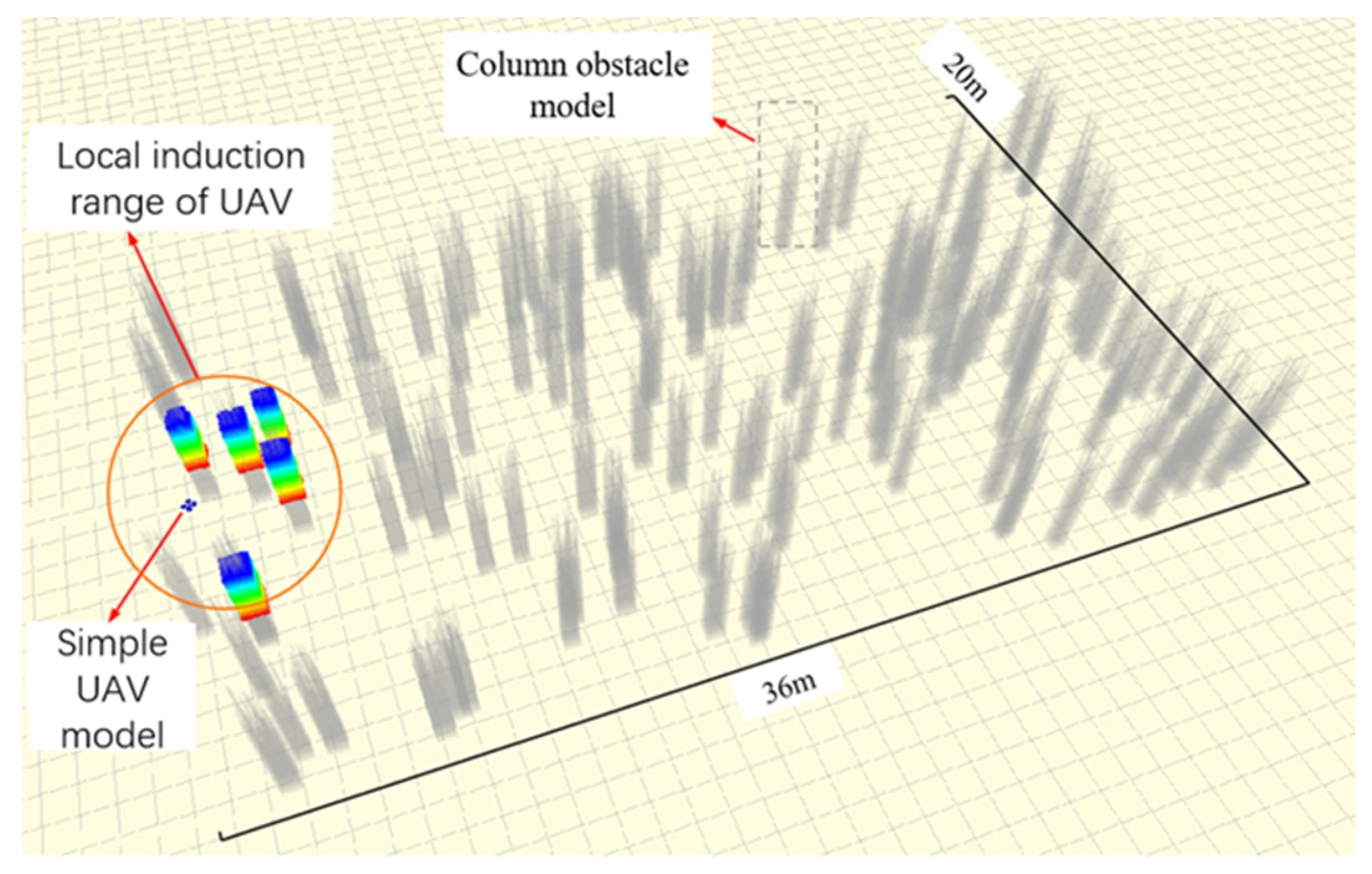
2.4. Simulation Verification of Hybrid Path Planning Method Based on Transmission Tower-Photovoltaic Scene Map
2.5. Simulation Verification of Hybrid Path Planning Method Based on Plantation Map
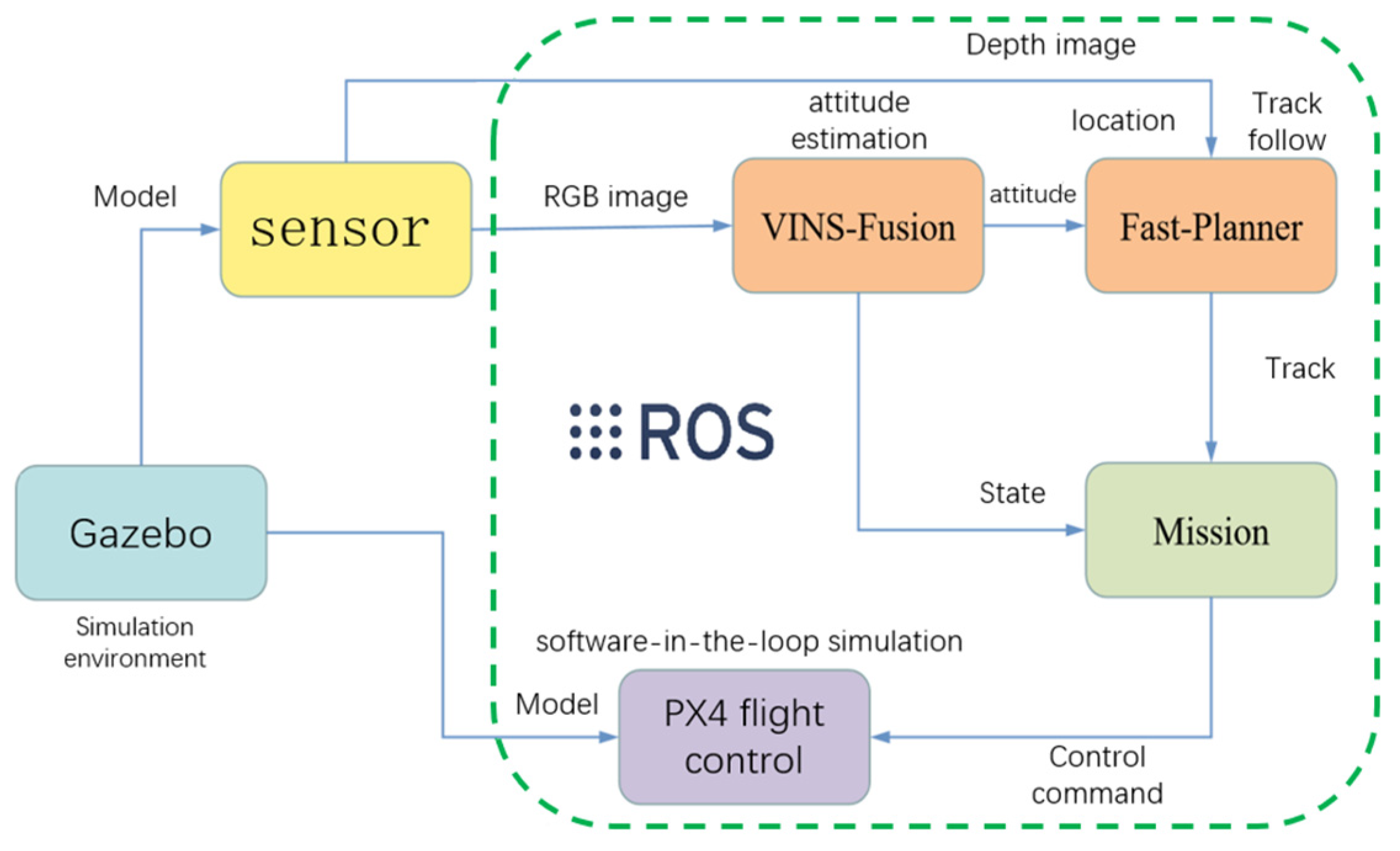
2.6. Path Planning Simulation of UAV in Photovoltaic Station Based on ROS Platform
3. Results and Discussion
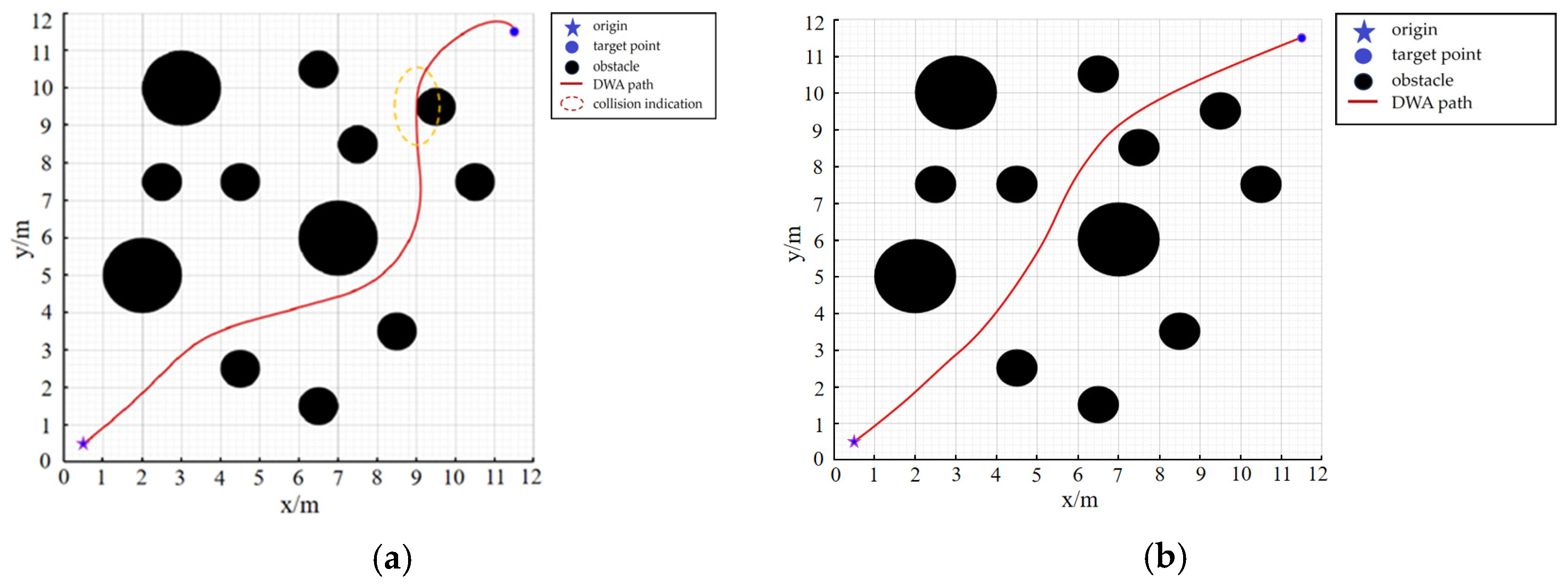
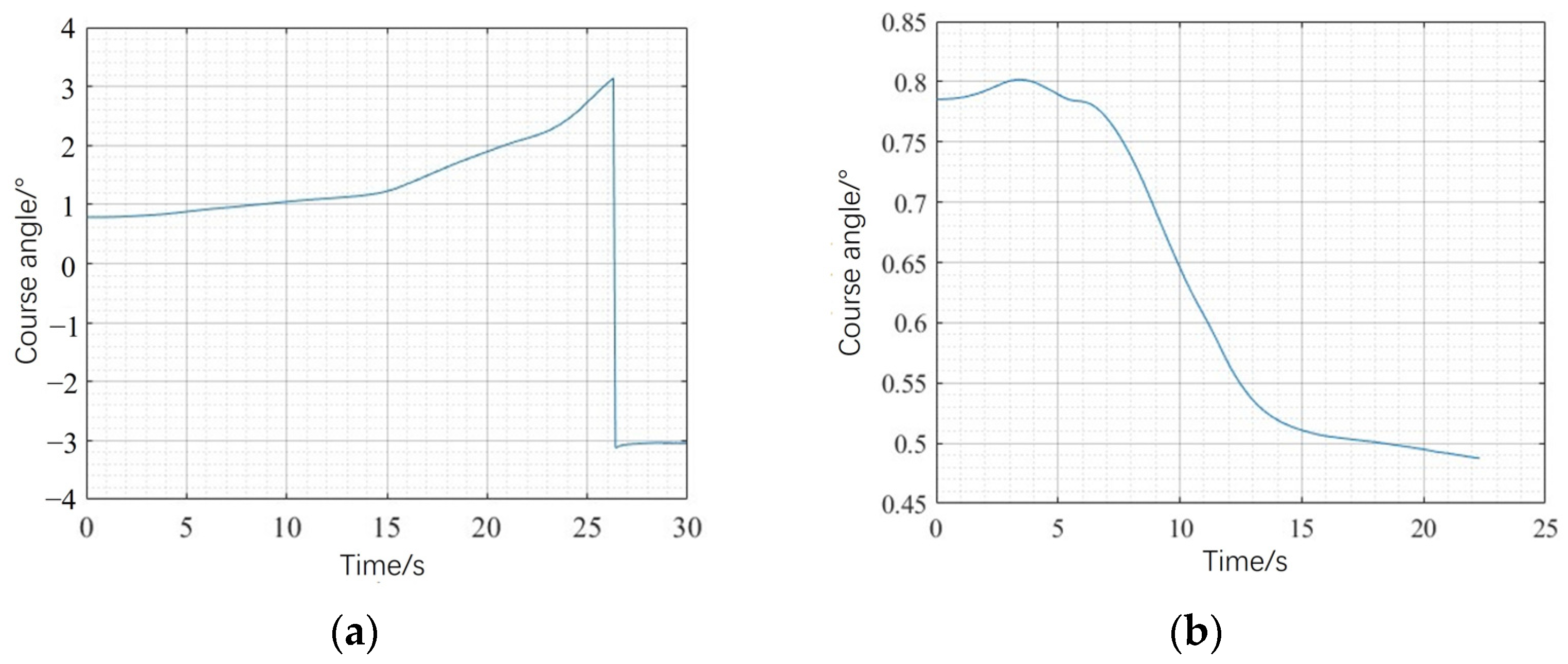
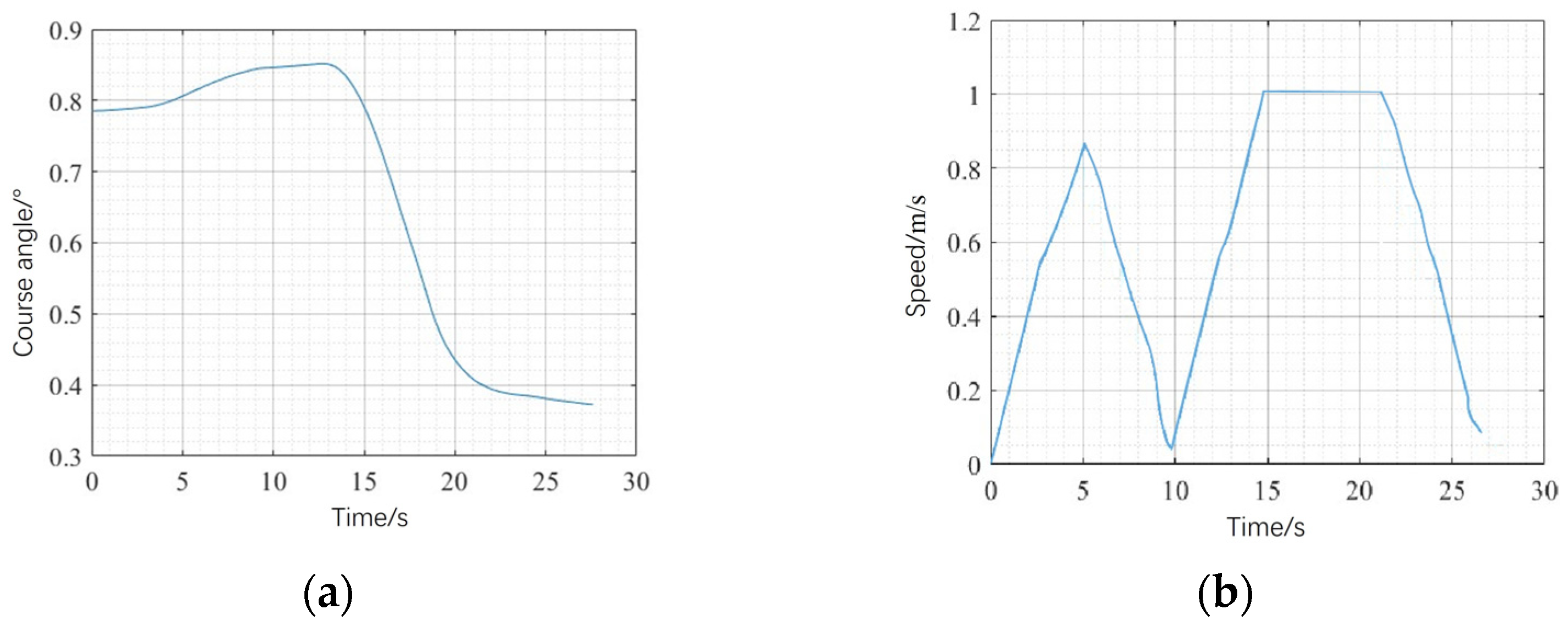
3.1. Simulation Experiment of Improved Dynamic Window Method
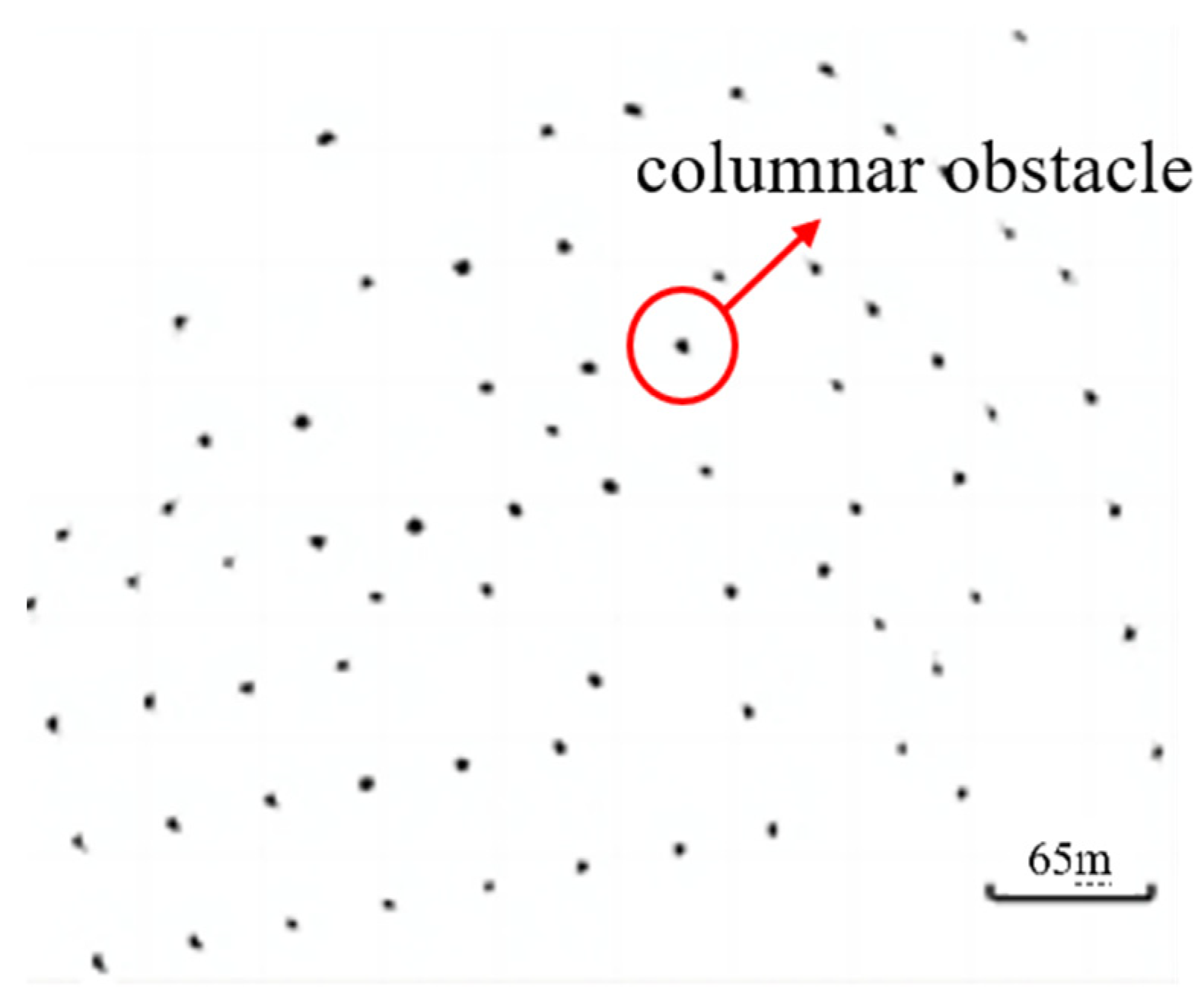
3.2. Simulation Verification of Hybrid Path Planning Method Based on Column Obstacle Map
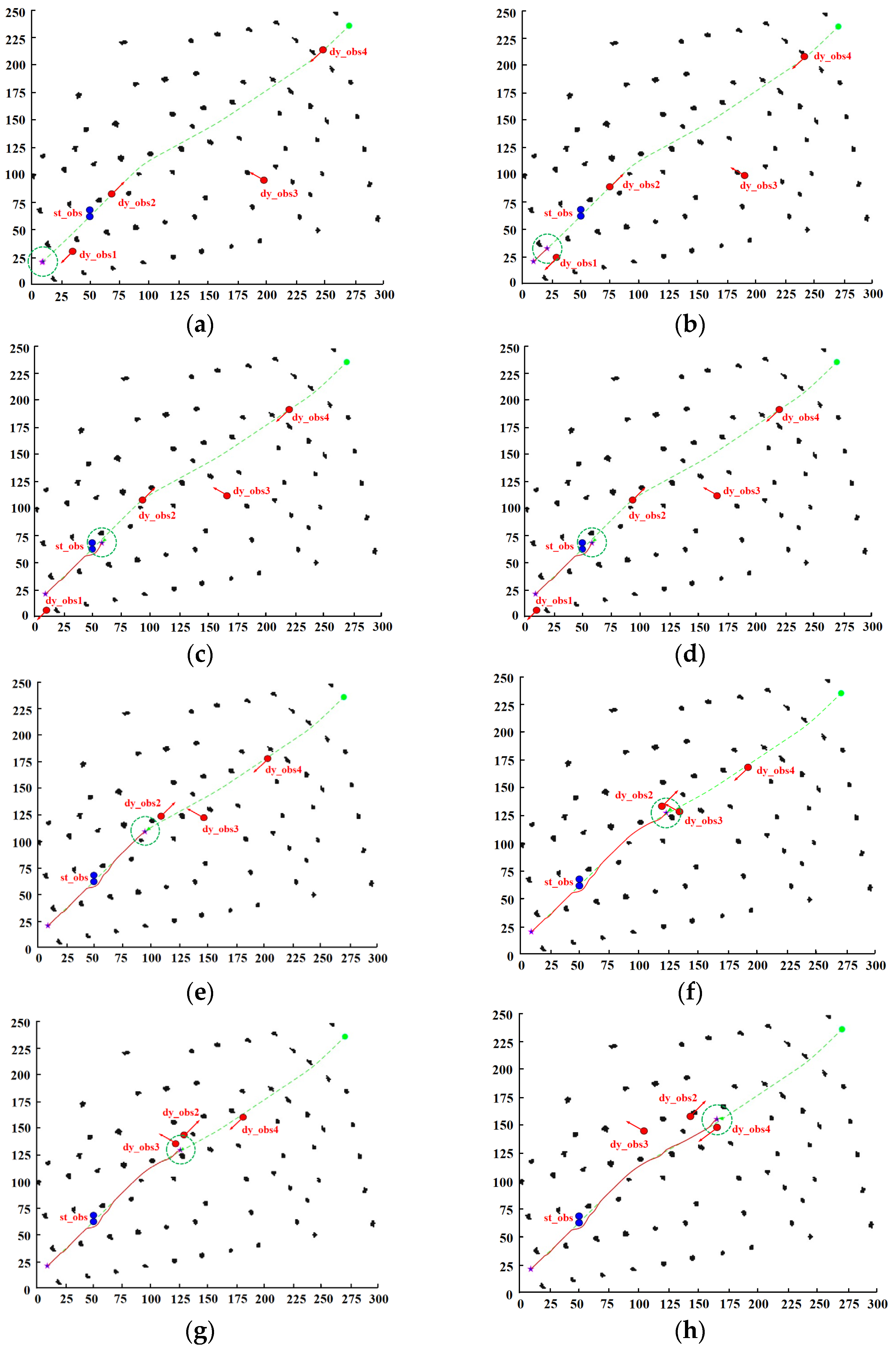
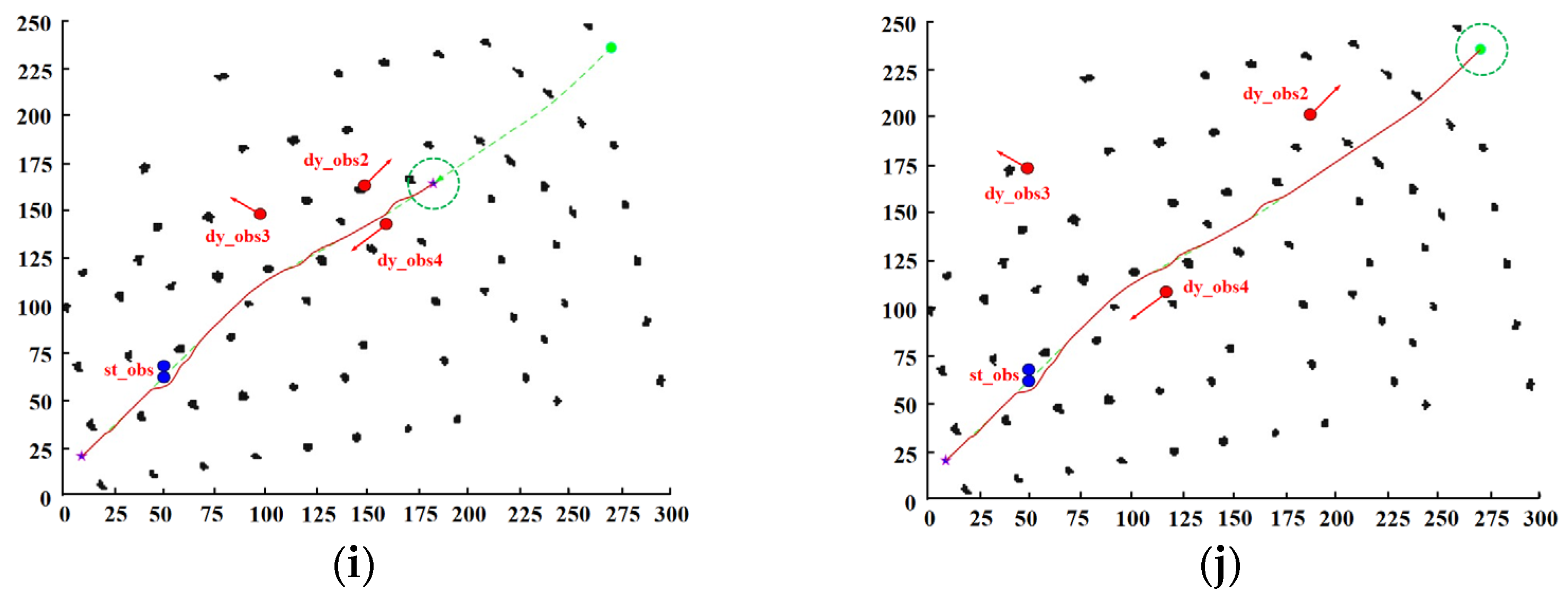
Simulation Experiment of Hybrid Path Planning in Transmission Tower-Detection Station-Photovoltaic Scenario
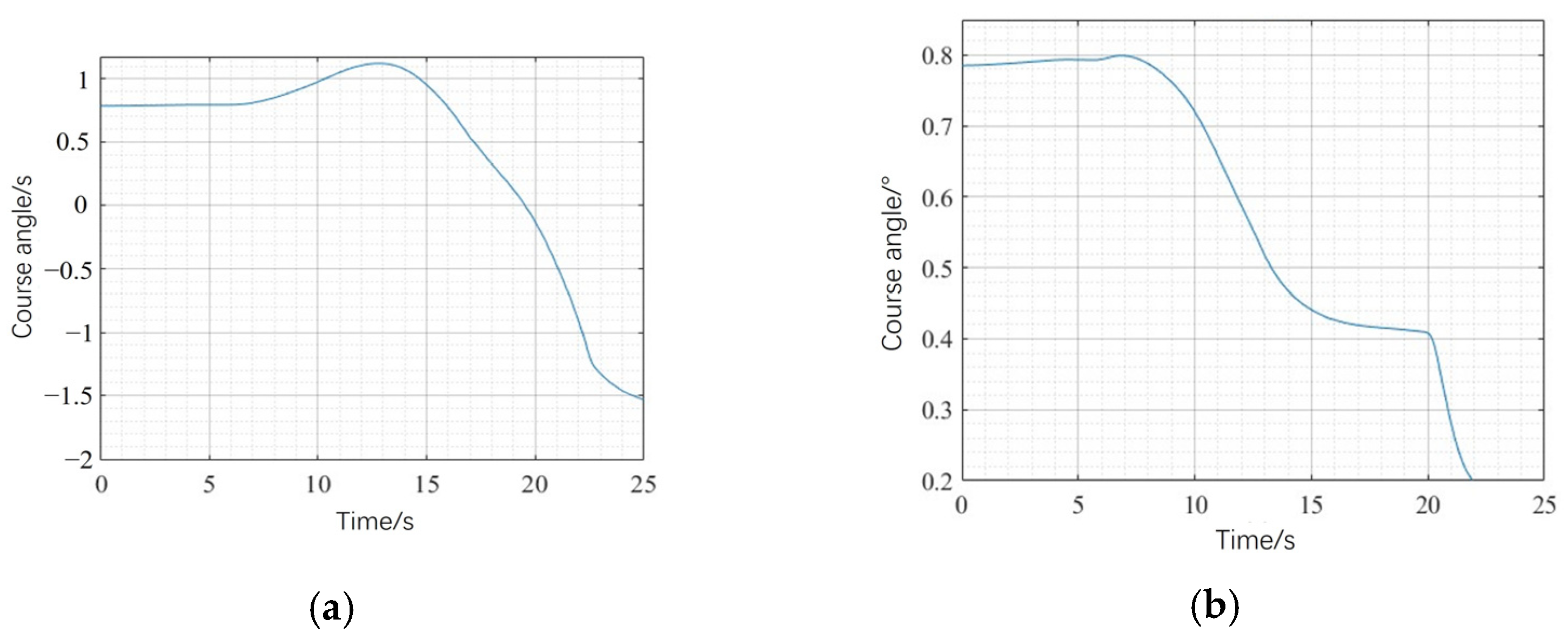
3.3. Simulation of UAV Path Planning in Pillar Obstacle Scene Based on ROS Platform
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, L.; Chen, C.; Xin, W. Review of Intelligent Path Planning for UAV Inspection of Solar Power Stations. Metrol. Meas. Tech. 2024, 50, 9396+100. [Google Scholar]
- Tang, Z. Design of a Scheduling System for Cleaning Robots for Photovoltaic Modules Based on UAV. Ph.D. Thesis, China Jiliang University, Hangzhou, China, 2021. [Google Scholar]
- Li, C.; Han, X. Application and development trend of multi-rotor UAV in agricultural plant protection. Shangdong Agric. Mech. 2024, 50–51. [Google Scholar] [CrossRef]
- Lan, Y.; Wang, L.; Zhang, Y. Application and prospect on obstacle avoidance technology for agricultural UAV. Trans. Chin. Soc. Agric. Eng. 2018, 34, 104–113. [Google Scholar]
- Huang, S. Research on Global Path Planning and Local Obstacle Avoidance of Multi-UAV. Master’s Thesis, Jilin University, Changchun, China, 2024. [Google Scholar]
- Liu, Q.; Shu, L.; Liu, G.; Li, A. A survey of low altitude UAV path planning algorithms. Adv. Aeronaut. Sci. Eng. 2023, 14, 24–34. [Google Scholar]
- Xiong, J.; Duan, X. Path planning for UAV based on improved dynamic step RRT algorithm. J. Phys. Conf. Ser. 2021, 1983, 012034. [Google Scholar] [CrossRef]
- Tang, F.; Li, K.; Xu, F.; Han, L.; Zhang, H.; Yang, Z. Optimal ant colony algorithm for UAV airborne LiDAR route planning in densely vegetated areas. J. Appl. Remote Sens. 2023, 17, 046506. [Google Scholar] [CrossRef]
- Li, Y.; Dong, X.; Ding, Q.; Xiong, Y.; Liao, H.; Wang, T. Improved A-STAR Algorithm for Power Line Inspection UAV Path Planning. Energies 2024, 17, 5364. [Google Scholar] [CrossRef]
- Liu, L.; Lin, J.; Yao, J.; He, D.; Zheng, J.; Huang, J.; Shi, P. Path Planning for Smart Car Based on Dijkstra Algorithm and Dynamic Window Approach. Wirel. Commun. Mob. Comput. 2021, 2021, 8881684. [Google Scholar] [CrossRef]
- Ju, C.; Luo, Q.; Yan, X. Path planning using an improved A* algorithm. In Proceedings of the 2020 11th International Conference on Prognostics and System Health Management, Jinan, China, 23–25 October 2020. [Google Scholar]
- Gao, J.; Zhang, Z. Obstacle Avoidance Path Planning of UAV in 3D Space Based on Improved A* Algorithm. Comput. Meas. Control 2023, 31, 203–209+223. [Google Scholar]
- Zhou, J.; Yang, L.; Zhang, C. Indoor robot path planning based on improved A* algorithm. Mod. Electron. Tech. 2022, 45, 181–186. [Google Scholar]
- He, Y.; Cao, L.; Xu, L. Mobile robot path planning based on improved A* algorithm. China South. Agric. Mach. 2024, 55, 31–34. [Google Scholar]
- Shi, Y.; Chen, H.; Zhang, L.; Sun, P.; Pei, P.; Li, D. Research on path planning of AGV transport robot based on improved A* algorithm. Manuf. Technol. Mach. Tool 2022, 19–22. [Google Scholar] [CrossRef]
- Yan, S.; Shi, X.; Zhang, Z. Three-dimensional Path Planning of Urban Logistics UAVs. Sci. Technol. Eng. 2024, 24, 12781–12788. [Google Scholar]
- Tang, Y.; Zheng, E.; Qiu, X. 3D UAV Trajectory Planning Based on Optimized Bidirectional A and Artificial Potential Field Method. J. Air Force Eng. Univ. 2024, 25, 69–75. [Google Scholar]
- Hu, M.; Li, X.; Ren, Z.; Zeng, S. UAV 3D Path Planning Based on A* Algorithm with Improved Heuristic Function. Acta Armamentarii 2024, 45, 302–307. [Google Scholar]
- Li, J.; Kang, F.; Chen, C.; Tong, S.; Jia, Y.; Zhang, C.; Wang, Y. The Improved A* Algorithm for Quadrotor UAVs under Forest Obstacle Avoidance Path Planning. Appl. Sci. 2023, 13, 4290. [Google Scholar] [CrossRef]
- Lin, J.; Xi, W.; Zhou, J. Path planning of mobile robots based on improved PRM and APF. Foreign Electron. Meas. Technol. 2022, 41, 1–6. [Google Scholar]
- Jia, Q.; Zhao, X.; Meng, Z. Path Planning Algorithm in Dynamic Environment Based on Improved Dynamic Window Approach. Sci. Technol. Eng. 2024, 24, 6313–6319. [Google Scholar]
- Luan, T.; Wang, H.; You, B.; Sun, M. TEB unmanned vehicle navigation method for position and attitude auxiliary points in narrow space. Chin. J. Sci. Instrum. 2023, 44, 121–128. [Google Scholar]
- Yan, L.; Fan, X. AGV local path planning based on adaptive dynamic window approach. J. Nanjing Univ. Inf. Sci. Technol. 2024. [Google Scholar] [CrossRef]
- Jiang, H.; Wu, T.; Ren, J.; Li, M.; Xiong, A.; Jia, J. Research on Local Path Planning of Mobile Robot Based on Improved Dwa Algorithm. Mach. Des. Res. 2024, 40, 229–234. [Google Scholar]
- Han, Z.; Li, L.; He, Z.; Zong, L.; Dai, Y. USV collision avoidance method combining DWA and DDPG algorithm. Electron. Meas. Technol. 2024, 47, 80–87. [Google Scholar]
- Xiong, D.; Ning, Y.; Wang, J.; Zeng, L. Local Path Planning of Mobile Robot Based on Improved DWA. Ind. Control Comput. 2024, 37, 102–104. [Google Scholar]
- Li, X.; Fang, J. Research on UAV Path Planning by A* Algorithm and DWA Method in the Urban Environment. Unmanned Syst. Technol. 2023, 6, 61–70. [Google Scholar]
- Li, J.; Xiong, X.; Yang, K.; Yan, Y.; Liang, T.; Liu, J. Research on indoor UAV path planning based on fusion algorithm. Foreign Electron. Meas. Technol. 2024, 43, 173–181. [Google Scholar]
- Jiang, H.; Zhang, Z. Research on Fusion Optimization Strategy Based on A* and Dynamic Window Approach Algorithms. Mach. Electron. 2024, 42, 15–21. [Google Scholar]
- Ma, Z.; Zhu, X.; Ma, L. Research on robot path planning based on improved A* and DWA. Mod. Electron. Tech. 2024, 47, 177–186. [Google Scholar]
- Zhao, H.; Fu, H.; Yang, F.; Qu, C.; Zhou, Y. Data-driven offline reinforcement learning approach for quadrotor’s motion and path planning. Chin. J. Aeronaut. 2024, 37, 386–397. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Liu, Y.; Wu, J.; Lun, Y. 6-DOF UAV Path planning and tracking control for obstacle avoidance: A deep learning-based integrated approach. Aerosp. Sci. Technol. 2024, 151, 109320. [Google Scholar] [CrossRef]
- Varma, K.S.; Kumari, S.L. Robotic vision based obstacle avoidance for navigation of unmanned aerial vehicle using fuzzy rule based optimal deep learning model. Evol. Intell. 2023, 17, 2193–2212. [Google Scholar] [CrossRef]
- Ni, F.; Jin, B.; Gao, X.; Li, Q. Cooperative Obstacle Avoidance Planning via A*-BDWA Fusion for Unmanned Aerial Vehicles. IAENG Int. J. Comput. Sci. 2024, 51, 1793–1803. [Google Scholar]
- Zhao, Z.; Wan, Y.; Chen, Y. Deep Reinforcement Learning-Driven Collaborative Rounding-Up for Multiple Unmanned Aerial Vehicles in Obstacle Environments. Drones 2024, 8, 464. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, M.; Zhang, S.; Gong, H. Multi-UAV Cooperative Obstacle Avoidance of 3D Vector Field Histogram Plus and Dynamic Window Approach. Drones 2023, 7, 504. [Google Scholar] [CrossRef]
- Shen, K.; You, Z.; Liu, Y.; Huang, T. Mobile robot planning based on improved A* algorithm. Appl. Res. Comput. 2023, 40, 75–79. [Google Scholar]
- Tarokh, M. Hybrid intelligent path planning for articulated rovers in rough Terrain. Fuzzy Sets Syst. 2008, 159, 2927–2937. [Google Scholar] [CrossRef]

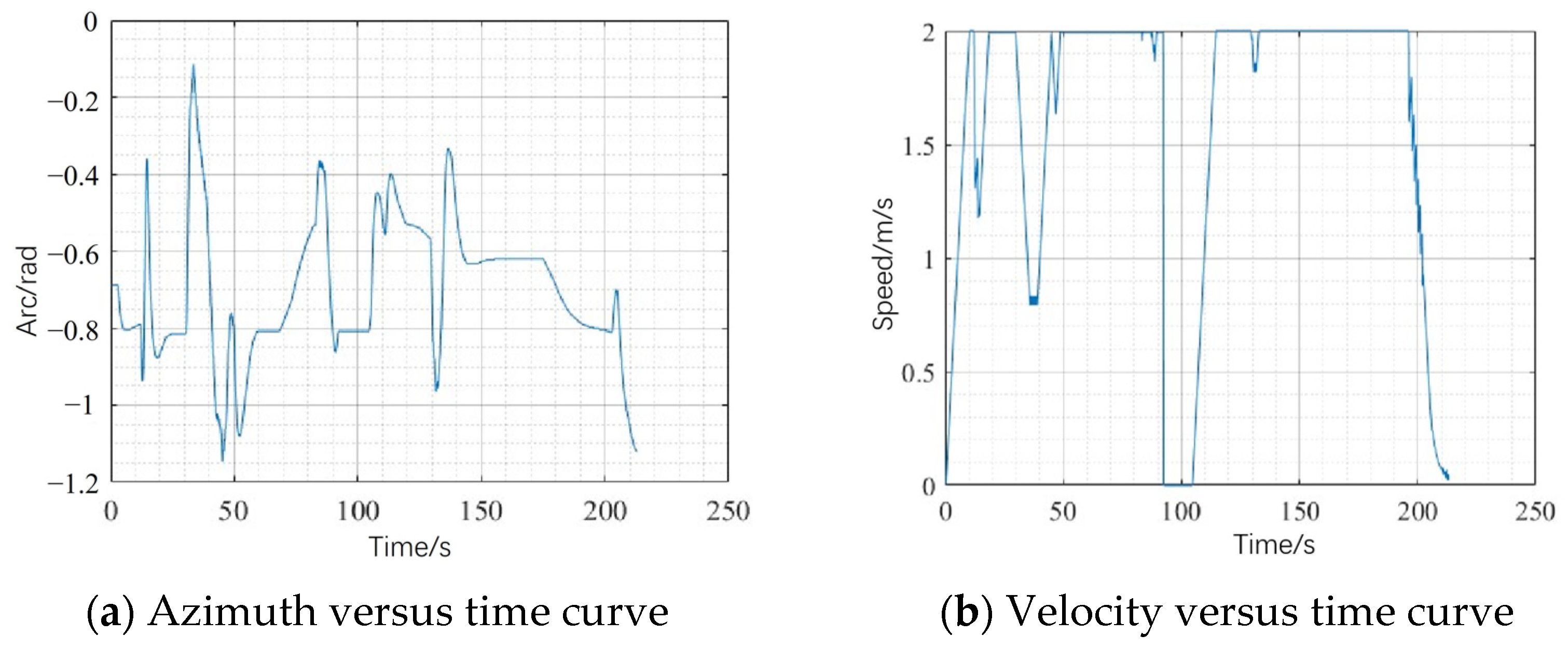
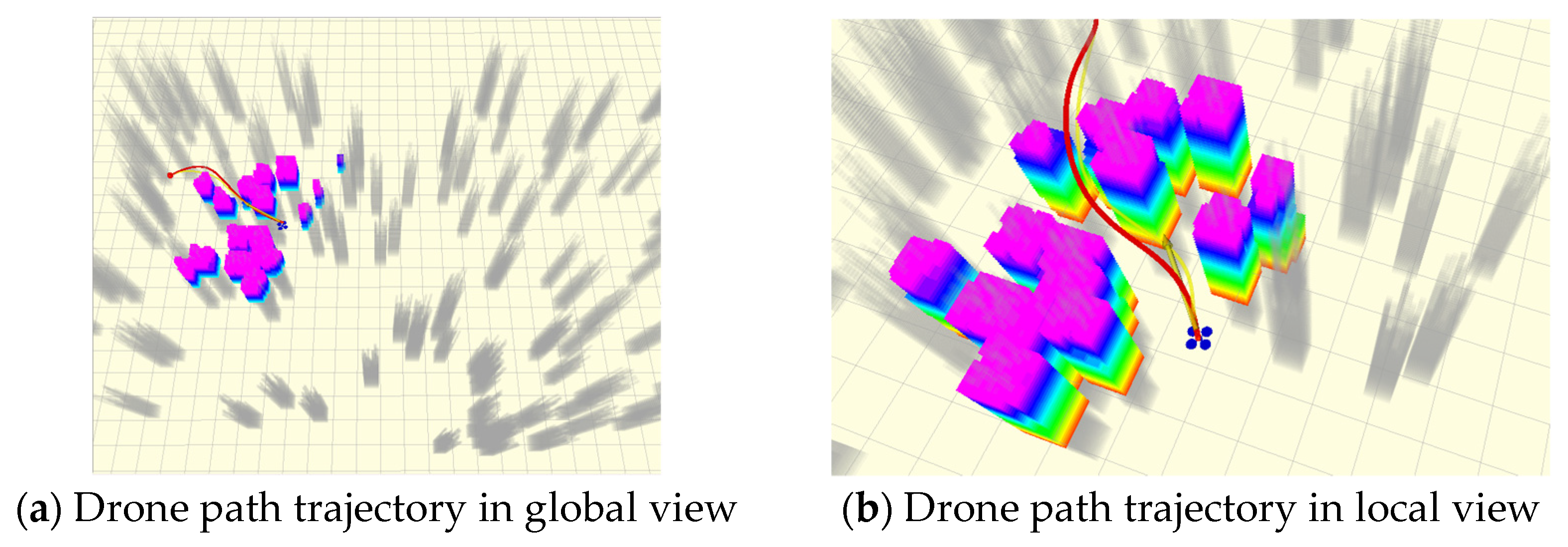
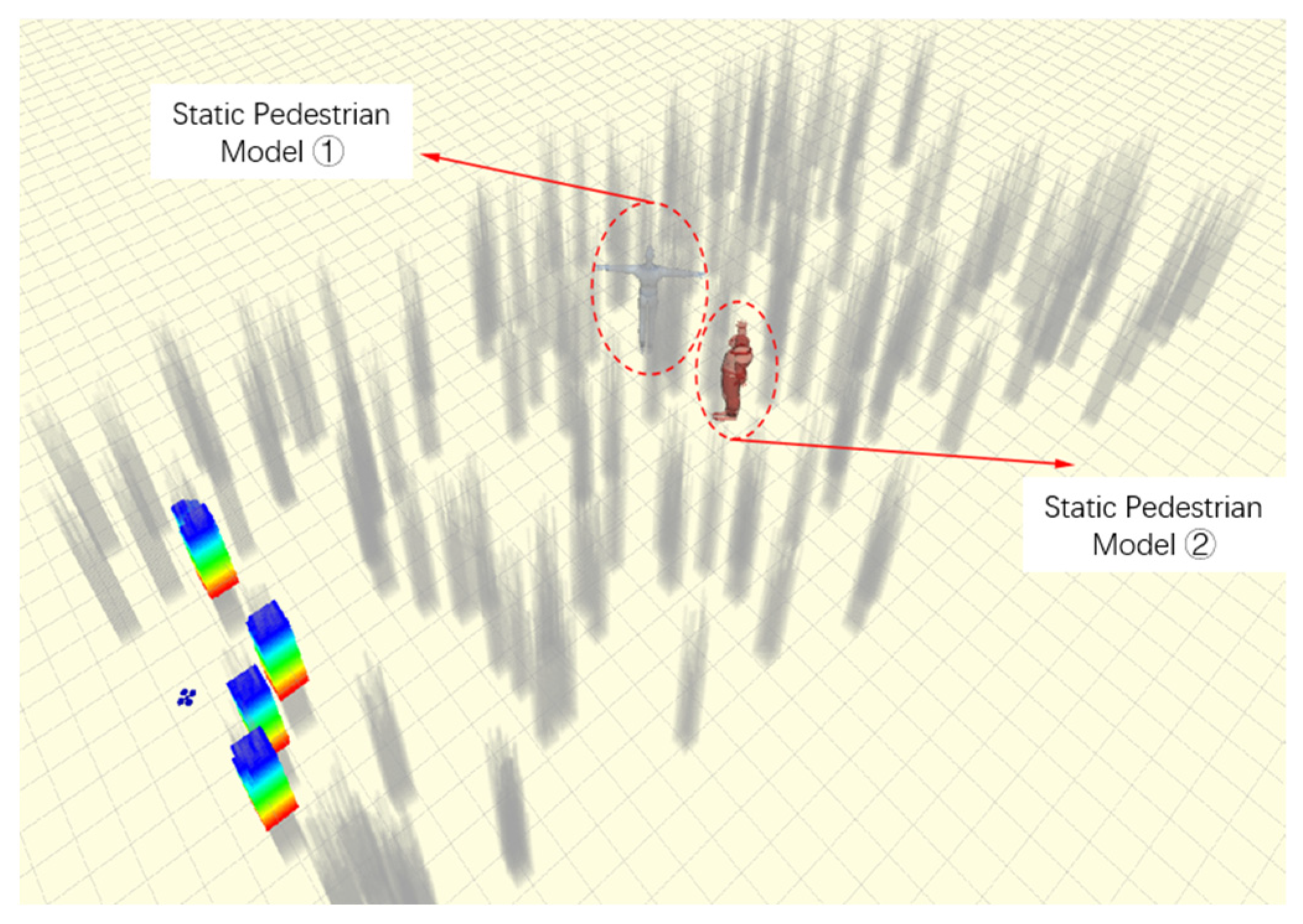
| Methodology | Path Length/m | Running Time/s | Minimum Safe Distance/m | Number of Iterations |
|---|---|---|---|---|
| Traditional DWA | 20.32 | 33.54 | 0.054 | 295 |
| Improved DWA | 16.05 | 22.11 | 0.273 | 220 |
| Methodology | Path Length/m | Running Time/s | Minimum Safe Distance/m | Number of Iterations |
|---|---|---|---|---|
| Traditional DWA | 21.03 | 31.51 | 0.030 | 288 |
| Improved DWA | 16.00 | 21.04 | 0.196 | 223 |
| Obstacles and Types | Crash Prediction | Whether or Not a Collision Occurs | Adoption of Avoidance Strategies |
|---|---|---|---|
| st_obs | Lie on the globally optimal path. | Yes | Decelerate and invoke the improved DWA algorithm for local planning. |
| dy_obs1 | The movement trajectory does not intersect with the drone trajectory and travels in opposite directions. | No | Null. |
| dy_obs2 | The trajectory partially overlaps with the drone trajectory and moves in the same direction. | Yes | Decelerate, stop, and wait. |
| dy_obs3 | The movement trajectory intersects with the drone trajectory and moves in a different direction. | Yes | Decelerate, stop, and wait. |
| dy_obs4 | The movement trajectory partially coincides with the drone trajectory and moves in the opposite direction. | Yes | Decelerate and invoke the improved DWA algorithm for local path replanning. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Li, S. Obstacle Avoidance Path Planning for UAV Applied to Photovoltaic Stations Based on Improved Dynamic Window Method. Electronics 2025, 14, 1963. https://doi.org/10.3390/electronics14101963
Gao Y, Li S. Obstacle Avoidance Path Planning for UAV Applied to Photovoltaic Stations Based on Improved Dynamic Window Method. Electronics. 2025; 14(10):1963. https://doi.org/10.3390/electronics14101963
Chicago/Turabian StyleGao, Yuan, and Sujian Li. 2025. "Obstacle Avoidance Path Planning for UAV Applied to Photovoltaic Stations Based on Improved Dynamic Window Method" Electronics 14, no. 10: 1963. https://doi.org/10.3390/electronics14101963
APA StyleGao, Y., & Li, S. (2025). Obstacle Avoidance Path Planning for UAV Applied to Photovoltaic Stations Based on Improved Dynamic Window Method. Electronics, 14(10), 1963. https://doi.org/10.3390/electronics14101963





