Electro-Thermal Model-Based Design of a Smart Latch in Automotive Systems for Performance and Reliability Evaluations
Abstract
1. Introduction
1.1. The Aim of This Work
1.2. Organization of This Paper
- Section 1: Objectives of the model-based design;
- Section 2: Electro-thermal modeling of the smart latch system;
- Section 3: Operation and verification of the Power Release and Cinch model specifications and parametric and disturbance robustness analyses of these models;
- Section 4: Development and examination of the fault scenarios for both models;
- Section 5: Validation using processor-in-the-loop simulations;
- Section 6: Discussion of implementation constraints vs. the real-world behavior;
- Section 7: Conclusions, analysis, and further developments.
2. System Overview and Electro-Thermal Modeling
2.1. The Parameters and Specifications of the System
2.2. Evaluations and Considerations for the Electro-Mechanic Parameters
2.3. The Thermal Parameters
3. Single-Loop Motor Control
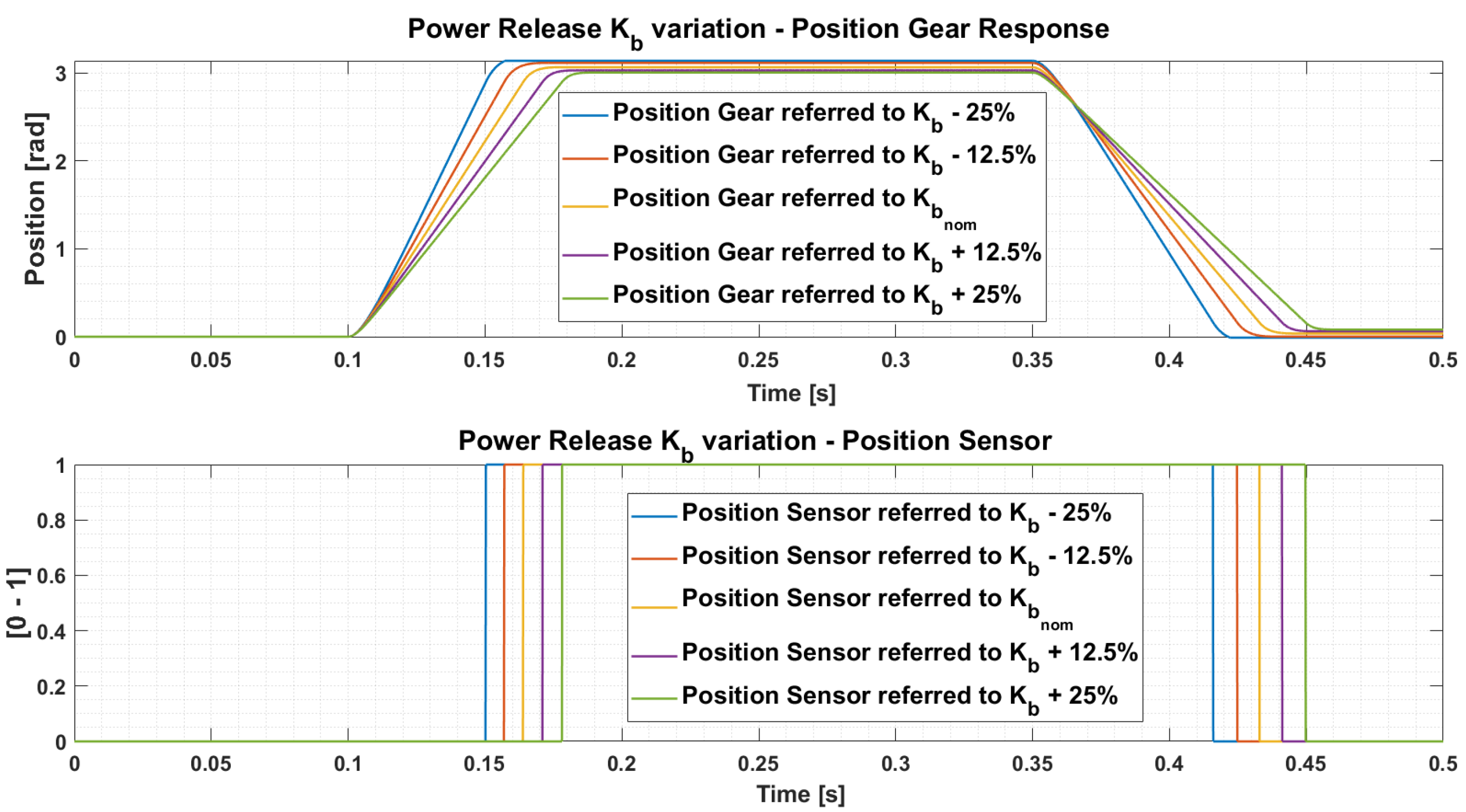
3.1. Analysis of the Robustness to Parametric Uncertainties
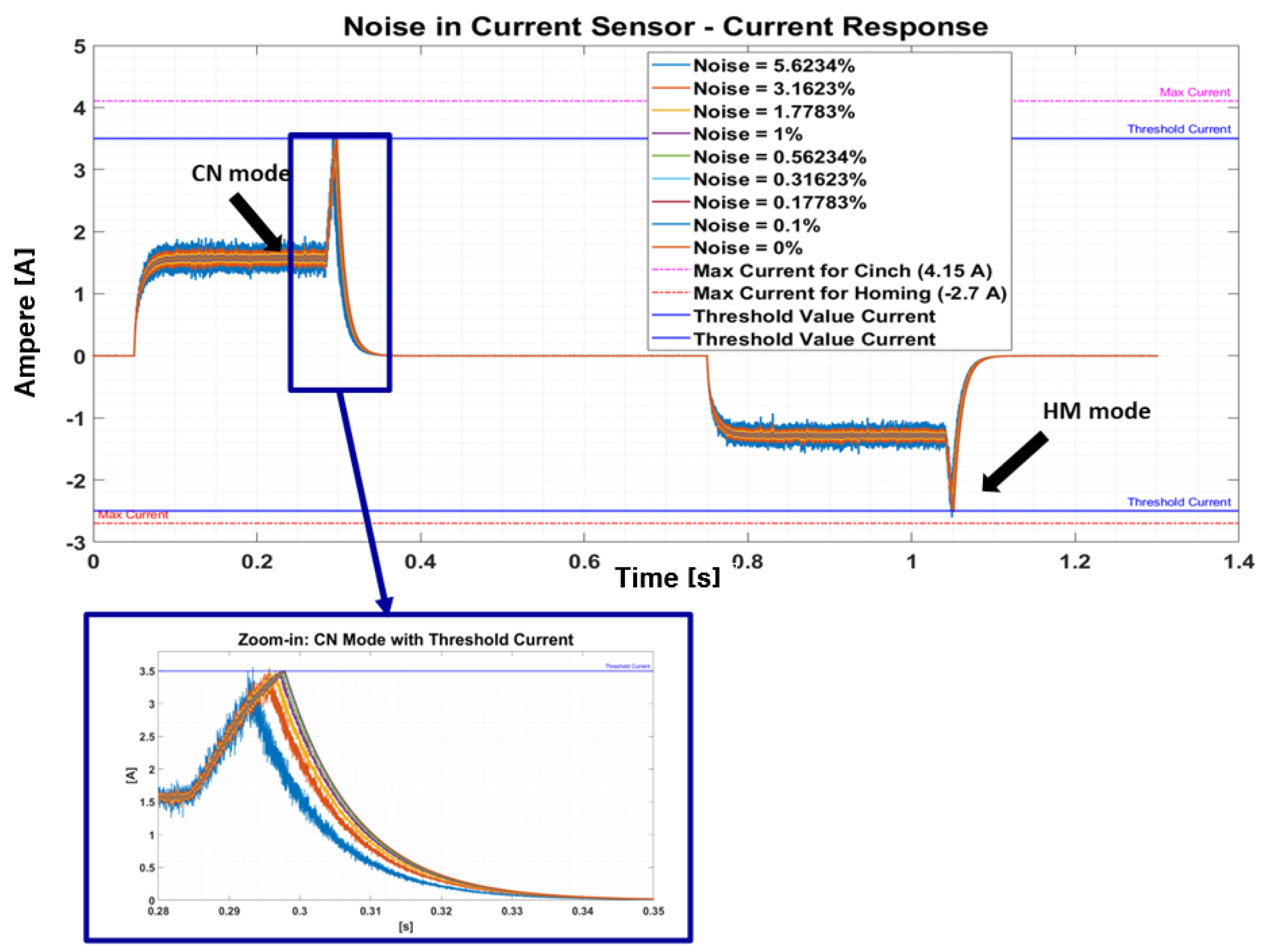
3.2. The Robustness to Noise Disturbances and Delay Effects
4. Fault Analysis
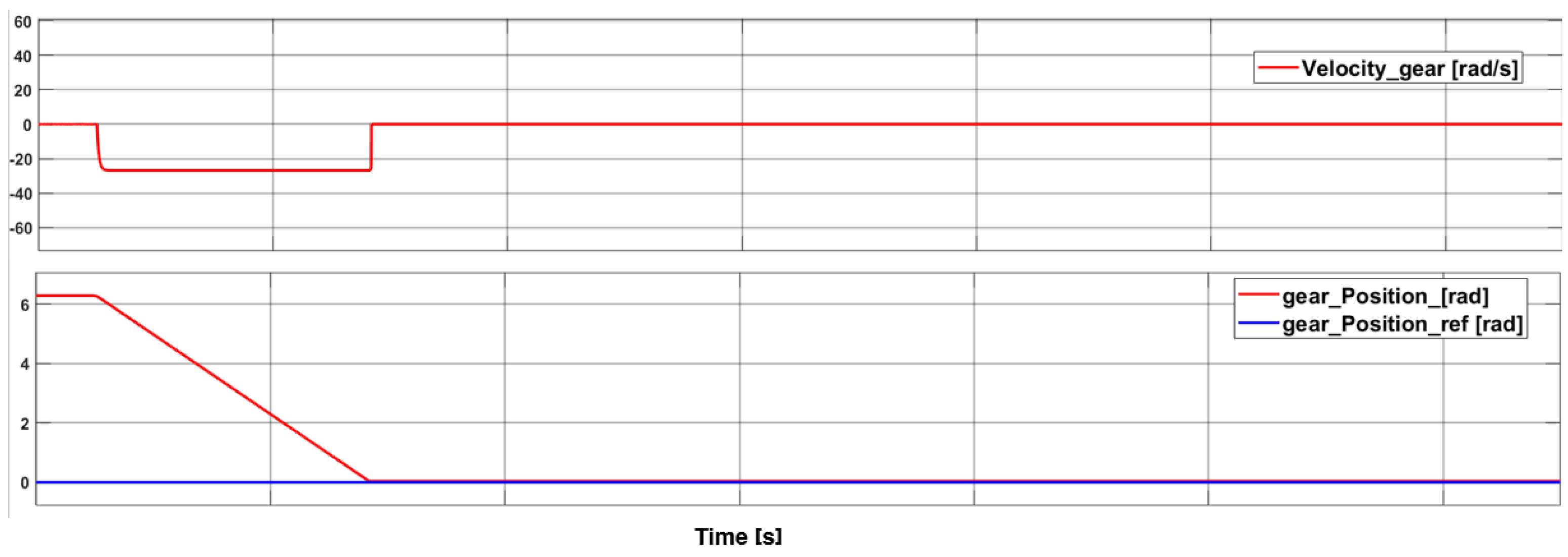
4.1. A Simulation Analysis of Faults in the Hall Effect Sensor and Computation Errors in the Current Feedback
4.2. Analysis of Thermal Effects Under Fault Conditions
5. PIL Simulations for One-Loop Control Systems
6. Hardware Constraints in the Real World
7. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hein-Pensel, F.; Winkler, H.; Brückner, A.; Wölke, M.; Jabs, I.; Mayan, I.J.; Kirschenbaum, A.; Friedrich, J.; Zinke-Wehlmann, C. Maturity assessment for Industry 5.0: A review of existing maturity models. J. Manuf. Syst. 2023, 66, 200–210. [Google Scholar] [CrossRef]
- Yang, J.; Liu, Y.; Morgan, P.L. Human-machine interaction towards Industry 5.0: Human-centric smart manufacturing. Digit. Eng. 2024, 2, 100013. [Google Scholar] [CrossRef]
- Yildiz, E.; Møller, C. Building a virtual factory: An integrated design approach to building smart factories. J. Glob. Oper. Strateg. Sourc. 2021, 14, 608–635. [Google Scholar] [CrossRef]
- Yildiz, E.; Møller, C.; Bilberg, A.; Rask, J.K. Virtual prototyping: Evaluating the digital twin based virtual factory for new product introduction. Complex Syst. Inform. Model. Q. 2021, 29, 1–16. [Google Scholar] [CrossRef]
- Salierno, G.; Leonardi, L.; Cabri, G. The future of factories: Different trends. Appl. Sci. 2021, 11, 9980. [Google Scholar] [CrossRef]
- Mourtzis, D.; Ong, S.; Wang, X.V.; Panopoulos, N.; Stark, R.; Wang, L. Modelling, Design and Simulation as-a-Service Based on Extended Reality (XR) in Industry 4.0. In CIRP Novel Topics in Production Engineering: Volume 1; Springer: Berlin/Heidelberg, Germany, 2024; pp. 99–143. [Google Scholar]
- Schumacher, A.; Nemeth, T.; Sihn, W. Roadmapping towards industrial digitalization based on an Industry 4.0 maturity model for manufacturing enterprises. Procedia CIRP 2019, 79, 409–414. [Google Scholar] [CrossRef]
- Kiefer, D.; Grimm, F.; Straub, T.; Bitsch, G.; Van Dinther, C.; Höllig, J. Speeding up CNC tool manufacturing: Implementing explainable AI for setup time reduction and production agility. Procedia CIRP 2024, 130, 982–987. [Google Scholar] [CrossRef]
- Špirková, S.; Straka, M.; Saniuk, A. VR Simulation and Implementation of Robotics: A Tool for Streamlining and Optimization. Appl. Sci. 2024, 14, 4434. [Google Scholar] [CrossRef]
- Akundi, A.; Lopez, V. A review on application of model based systems engineering to manufacturing and production engineering systems. Procedia Comput. Sci. 2021, 185, 101–108. [Google Scholar] [CrossRef]
- Bodendorf, F.; Franke, J. A machine learning approach to estimate product costs in the early product design phase: A use case from the automotive industry. Procedia CIRP 2021, 100, 643–648. [Google Scholar] [CrossRef]
- Dalla Vedova, M.D.; Germanà, A.; Berri, P.C.; Maggiore, P. Model-based fault detection and identification for prognostics of electromechanical actuators using genetic algorithms. Aerospace 2019, 6, 94. [Google Scholar] [CrossRef]
- Kukreja, A.; Chopra, P. Model-Based Fault Detection for Series Elastic Actuators. In Proceedings of the 2024 7th International Conference on Mechatronics, Robotics and Automation (ICMRA), Wuhan, China, 20–22 September 2024; pp. 178–182. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, Z.; Wei, L.; Wang, X.; Li, L. Braking Sensor and Actuator Fault Diagnosis with Combined Model-Based and Data-Driven Pressure Estimation Methods. IEEE Trans. Ind. Electron. 2023, 70, 11639–11648. [Google Scholar] [CrossRef]
- Trabucco, B.; Geng, X.; Kumar, A.; Levine, S. Design-Bench: Benchmarks for Data-Driven Offline Model-Based Optimization. In Proceedings of the 39th International Conference on Machine Learning, Baltimore, MD, USA, 17–23 July 2022; Chaudhuri, K., Jegelka, S., Song, L., Szepesvari, C., Niu, G., Sabato, S., Eds.; Proceedings of Machine Learning Research (PMLR): New York, NY, USA, 2022; Volume 162, pp. 21658–21676. [Google Scholar]
- Liu, X.; Wang, J.; Ouimet, J.A.; Phillip, W.A.; Dowling, A.W. Membrane characterization with model-based design of experiments. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2022; Volume 49, pp. 859–864. [Google Scholar]
- Li, W.J.; Li, D.S.; Zhang, J.W. Model-Based Design and Experimental Validation of Control System for a Three-Level Inverter. Electronics 2022, 11, 1979. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, C.; Tan, T.; Chen, L.; Xu, Y. Experimental verification of characteristic parameter analysis method for pipeline leak before break. In Proceedings of the Journal of Physics: Conference Series, Guangzhou, China, 22–23 May 2024; IOP Publishing: Bristol, UK, 2024; Volume 2842, p. 012001. [Google Scholar]
- Mazza, B.; Patanè, S.; Cordiano, F.; Giliberto, M.; Barletta, G.; Franco, G. Electrical overstress effect characterization on Power MOS Trenchfet and correlation with time dependent dielectric breakdown. Microelectron. Reliab. 2021, 125, 114351. [Google Scholar] [CrossRef]
- Dini, P.; Paolini, D.; Saponara, S.; Minossi, M. Leaveraging Digital Twin & Artificial Intelligence in Consumption Forecasting System for Sustainable Luxury Yacht. IEEE Access 2024, 12, 160700–160714. [Google Scholar]
- Xu, Y.; Zhang, Y.; Zeng, M.; Huang, X.; Wang, Z. An electrothermal coupling model for estimating the internal temperature of lithium-ion battery based on microthermal resistance method. Electrochem. Commun. 2024, 166, 107776. [Google Scholar] [CrossRef]
- Zajac, P. Compact Thermal Modelling Tool for Fast Design Space Exploration of 3D ICs with Integrated Microchannels. Energies 2020, 13, 2217. [Google Scholar] [CrossRef]
- He, J.; Hosen, M.S.; Youssef, R.; Kalogiannis, T.; Van Mierlo, J.; Berecibar, M. A lumped electro-thermal model for a battery module with a novel hybrid cooling system. Appl. Therm. Eng. 2023, 221, 119874. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Processor-in-the-Loop Validation of a Gradient Descent-Based Model Predictive Control for Assisted Driving and Obstacles Avoidance Applications. IEEE Access 2022, 10, 67958–67975. [Google Scholar] [CrossRef]
- Gao, S.; Song, Y.; Chen, Y.; Yu, Z.; Zhang, R. Fast Simulation Model of Voltage Source Converters with Arbitrary Topology Using Switch-State Prediction. IEEE Trans. Power Electron. 2022, 37, 12167–12181. [Google Scholar] [CrossRef]
- Gurumurthy, S.K.; Mirz, M.; Amevor, B.S.; Ponci, F.; Monti, A. Hybrid Dynamic Phasor Modeling Approaches for Accurate Closed-Loop Simulation of Power Converters. IEEE Access 2022, 10, 101643–101655. [Google Scholar] [CrossRef]
- Yohanandhan, R.V.; Elavarasan, R.M.; Manoharan, P.; Mihet-Popa, L. Cyber-Physical Power System (CPPS): A Review on Modeling, Simulation, and Analysis with Cyber Security Applications. IEEE Access 2020, 8, 151019–151064. [Google Scholar] [CrossRef]
- Saponara, S.; Saletti, R.; Fanucci, L.; Roncella, R.; Marlia, M.; Taviani, C. Supercap-based energy back-up system for automotive electronic control units. In Applications in Electronics Pervading Industry, Environment and Society; Springer: Cham, Switzerland, 2014; pp. 1–11. [Google Scholar]
- Mina, J.; Flores, Z.; López, E.; Pérez, A.; Calleja, J.H. Processor-in-the-loop and hardware-in-the-loop simulation of electric systems based in FPGA. In Proceedings of the 2016 13th International Conference on Power Electronics (CIEP), Guanajuato, Mexico, 20–23 June 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 172–177. [Google Scholar]
- Krishna Srinivasan, M.; Daya John Lionel, F.; Subramaniam, U.; Blaabjerg, F.; Madurai Elavarasan, R.; Shafiullah, G.; Khan, I.; Padmanaban, S. Real-time Processor-in-Loop investigation of a modified non-linear state observer using sliding modes for speed sensorless induction motor drive in electric vehicles. Energies 2020, 13, 4212. [Google Scholar] [CrossRef]
- Tramacere, E.; Luciani, S.; Feraco, S.; Bonfitto, A.; Amati, N. Processor-in-the-loop architecture design and experimental validation for an autonomous racing vehicle. Appl. Sci. 2021, 11, 7225. [Google Scholar] [CrossRef]
- Liu-Henke, X.; Jacobitz, S.; Scherler, S.; Göllner, M.; Yarom, O.A.; Zhang, J. A Holistic Methodology for Model-based Design of Mechatronic Systems in Digitized and Connected System Environments. In Proceedings of the ICSOFT, Virtual Event, 6–8 July 2021; pp. 215–223. [Google Scholar]
- Wang, H.; Li, H.; Wen, X.; Luo, G. Unified modeling for digital twin of a knowledge-based system design. Robot. Comput. Integr. Manuf. 2021, 68, 102074. [Google Scholar] [CrossRef]
- Wang, Y.; Steinbach, T.; Klein, J.; Anderl, R. Integration of model based system engineering into the digital twin concept. Procedia CIRP 2021, 100, 19–24. [Google Scholar] [CrossRef]
- Friederich, J.; Francis, D.P.; Lazarova-Molnar, S.; Mohamed, N. A framework for data-driven digital twins of smart manufacturing systems. Comput. Ind. 2022, 136, 103586. [Google Scholar] [CrossRef]
- Schnürer, D.; Hammelmüller, F.; Holl, H.J.; Kunze, W. Offline digital twin synchronization using measurement data and machine learning methods. Mater. Today Proc. 2022, 62, 2416–2420. [Google Scholar] [CrossRef]
- Nayak, P.S.R.; Kamalapathi, K.; Laxman, N.; Tyagi, V.K. Design and Simulation Of BUCK-BOOST Type Dual Input DC-DC Converter for Battery Charging Application in Electric Vehicle. In Proceedings of the 2021 International Conference on Sustainable Energy and Future Electric Transportation (SEFET), Hyderabad, India, 21–23 January 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Nayanasiri, D.; Li, Y. Step-down DC–DC converters: An overview and outlook. Electronics 2022, 11, 1693. [Google Scholar] [CrossRef]
- Salem, Q.; Liu, L.; Xie, J. Dual Operation Mode of a Transformerless H-Bridge Inverter in Low-Voltage Microgrid. IEEE Trans. Ind. Appl. 2019, 55, 5289–5299. [Google Scholar] [CrossRef]
- Kocabicak, Z.; Demir, U. Design and optimization of an electromechanical actuator for the latch of a foldable vehicle seat. Mater. Test. 2020, 62, 749–755. [Google Scholar] [CrossRef]
- Saponara, S.; Bove, A.; Baronti, F.; Roncella, R.; Saletti, R.; Dente, D.; Leonardi, E.; Marlia, M.; Taviani, C. Thermal, electric and durability characterization of supercaps for energy back-up of automotive ECU. In Proceedings of the 2013 IEEE International Symposium on Industrial Electronics, Melbourne, Australia, 19–21 June 2013; pp. 1–6. [Google Scholar] [CrossRef]
- McAdams, D.A.; Wood, K.L. A quantitative similarity metric for design-by-analogy. J. Mech. Des. 2002, 124, 173–182. [Google Scholar] [CrossRef]
- Ding, X.; Bhattacharya, M.; Mi, C. Simplified thermal model of PM motors in hybrid vehicle applications taking into account eddy current loss in magnets. J. Asian Electr. Veh. 2010, 8, 1337–1343. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, S.; Yu, J.; Liu, C. Thermal Analysis of Dual-Axis-Direction Hybrid Excitation Generator for Electric Vehicles. Energies 2022, 15, 3011. [Google Scholar] [CrossRef]
- Dimolikas, K.; Kefalas, T.D.; Karaisas, P.; Papazacharopoulos, Z.K.; Kladas, A. Lumped-parameter network thermal analysis of permanent magnet synchronous motor. In Materials Science Forum; Trans Tech Publications: Baech, Switzerland, 2014; Volume 792, pp. 233–238. [Google Scholar]
- Manana, M.; Arroyo, A.; Ortiz, A.; Renedo, C.; Perez, S.; Delgado, F. Field winding fault diagnosis in DC motors during manufacturing using thermal monitoring. Appl. Therm. Eng. 2011, 31, 978–983. [Google Scholar] [CrossRef]
- neXperia. BUK7K52-60E—Dual N-Channel 60 V, 45 mΩ Standard Level MOSFET. 2015. Available online: https://www.nexperia.com/products/mosfets/automotive-mosfets/BUK7K52-60E.html (accessed on 2 July 2024).
- Dini, P.; Saponara, S.; Chakraborty, S.; Hosseinabadi, F.; Hegazy, O. Experimental Characterization and Electro-Thermal Modeling of Double Side Cooled SiC MOSFETs for Accurate and Rapid Power Converter Simulations. IEEE Access 2023, 11, 79120–79143. [Google Scholar] [CrossRef]
- Dini, P.; Ariaudo, G.; Botto, G.; Greca, F.L.; Saponara, S. Real-time electro-thermal modelling and predictive control design of resonant power converter in full electric vehicle applications. IET Power Electron. 2023, 16, 2045–2064. [Google Scholar] [CrossRef]
- Dini, P.; Basso, G.; Saponara, S.; Romano, C. Real-time monitoring and ageing detection algorithm design with application on SiC-based automotive power drive system. IET Power Electron. 2024, 17, 690–710. [Google Scholar] [CrossRef]
- Colmenares, D.; Kania, R.; Liu, M.; Sitti, M. Characterization and Thermal Management of a DC Motor-Driven Resonant Actuator for Miniature Mobile Robots with Oscillating Limbs. arXiv 2020, arXiv:2002.00798. [Google Scholar]
- Shoujun, S.; Weiguo, L.; Peitsch, D.; Schaefer, U. Detailed design of a high speed switched reluctance starter/generator for more/all electric aircraft. Chin. J. Aeronaut. 2010, 23, 216–226. [Google Scholar] [CrossRef]
- Leng, J.; Sha, W.; Wang, B.; Zheng, P.; Zhuang, C.; Liu, Q.; Wuest, T.; Mourtzis, D.; Wang, L. Industry 5.0: Prospect and retrospect. J. Manuf. Syst. 2022, 65, 279–295. [Google Scholar] [CrossRef]
- Matt, D.T.; Pedrini, G.; Bonfanti, A.; Orzes, G. Industrial digitalization. A systematic literature review and research agenda. Eur. Manag. J. 2023, 41, 47–78. [Google Scholar] [CrossRef]
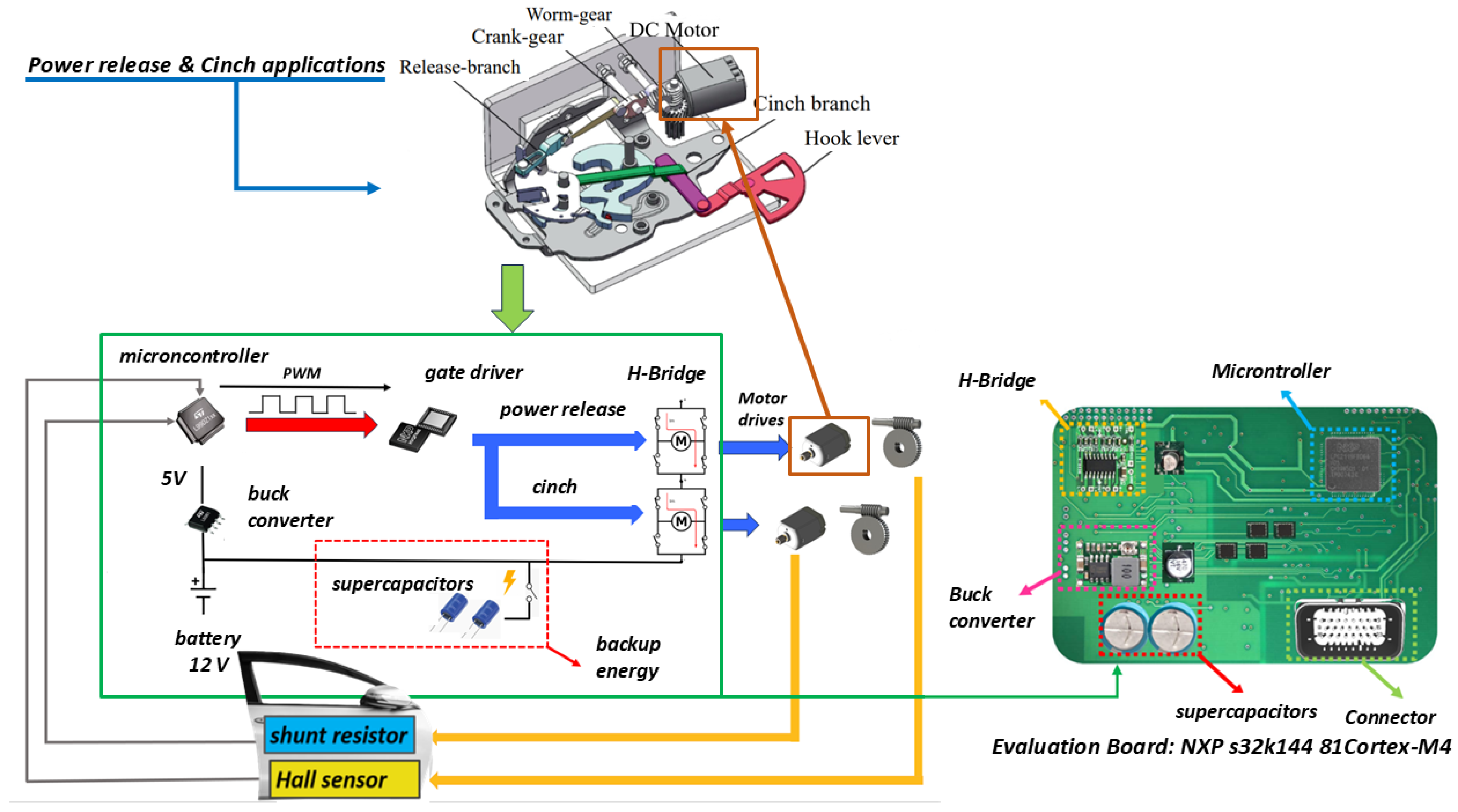









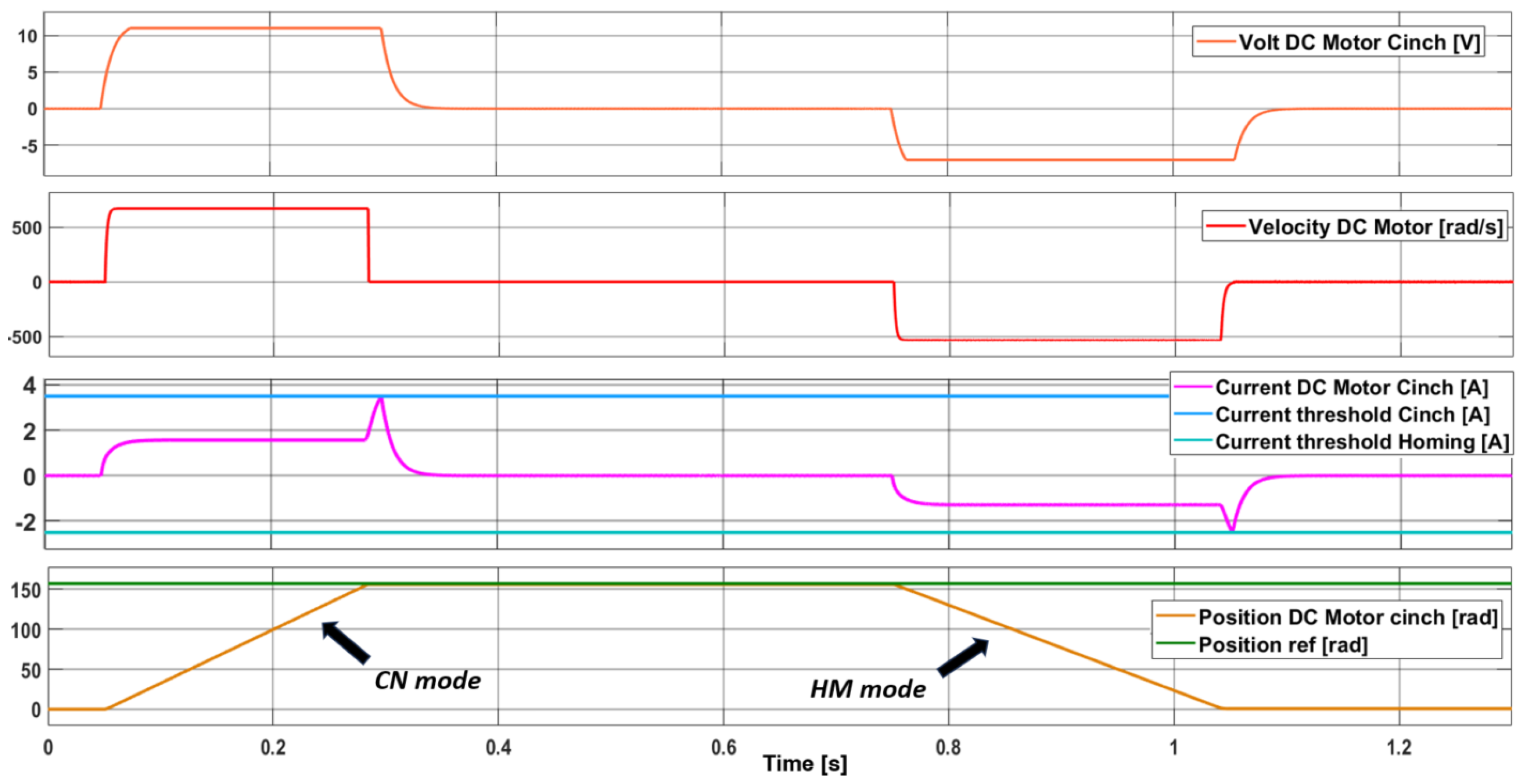
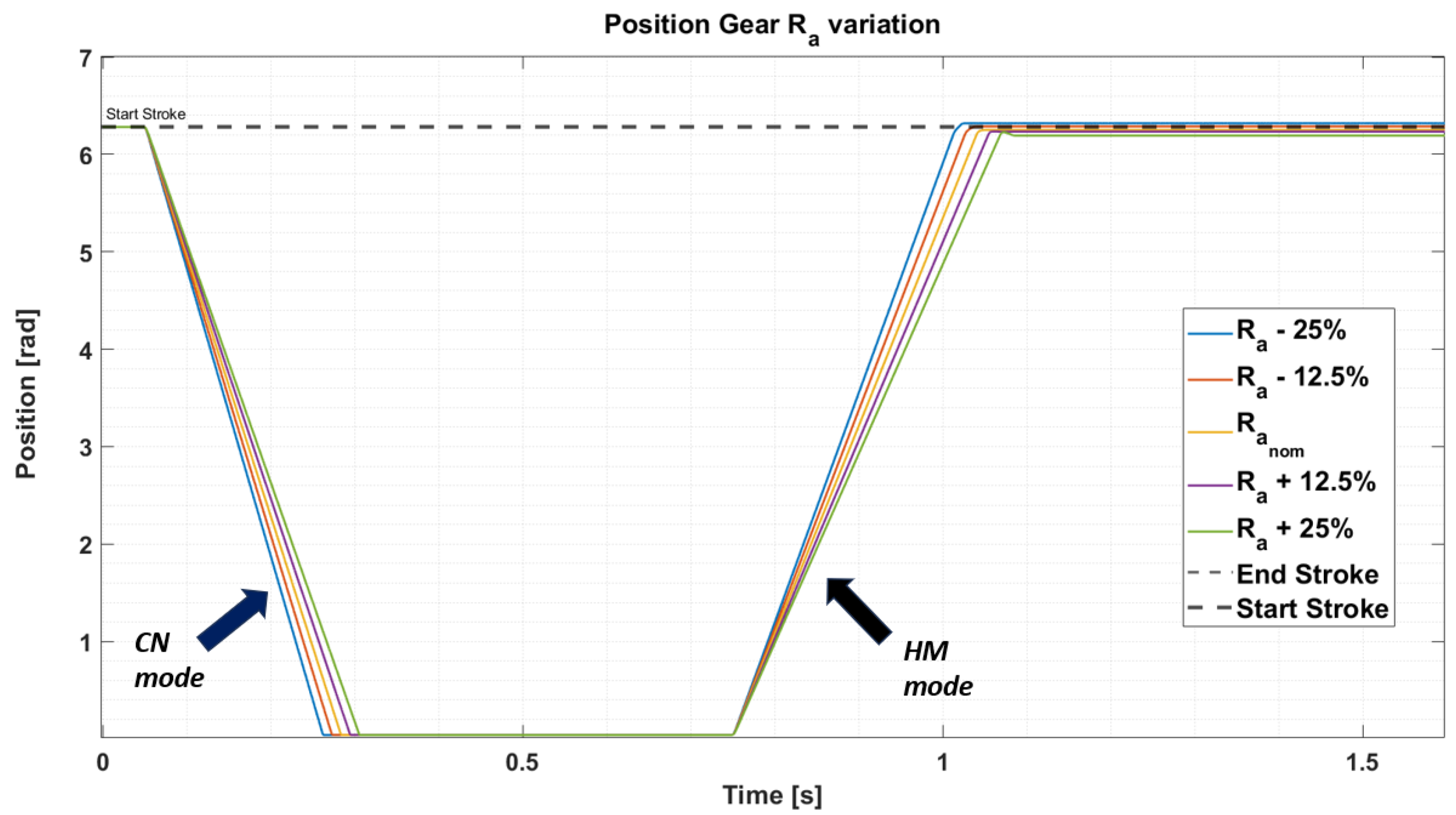



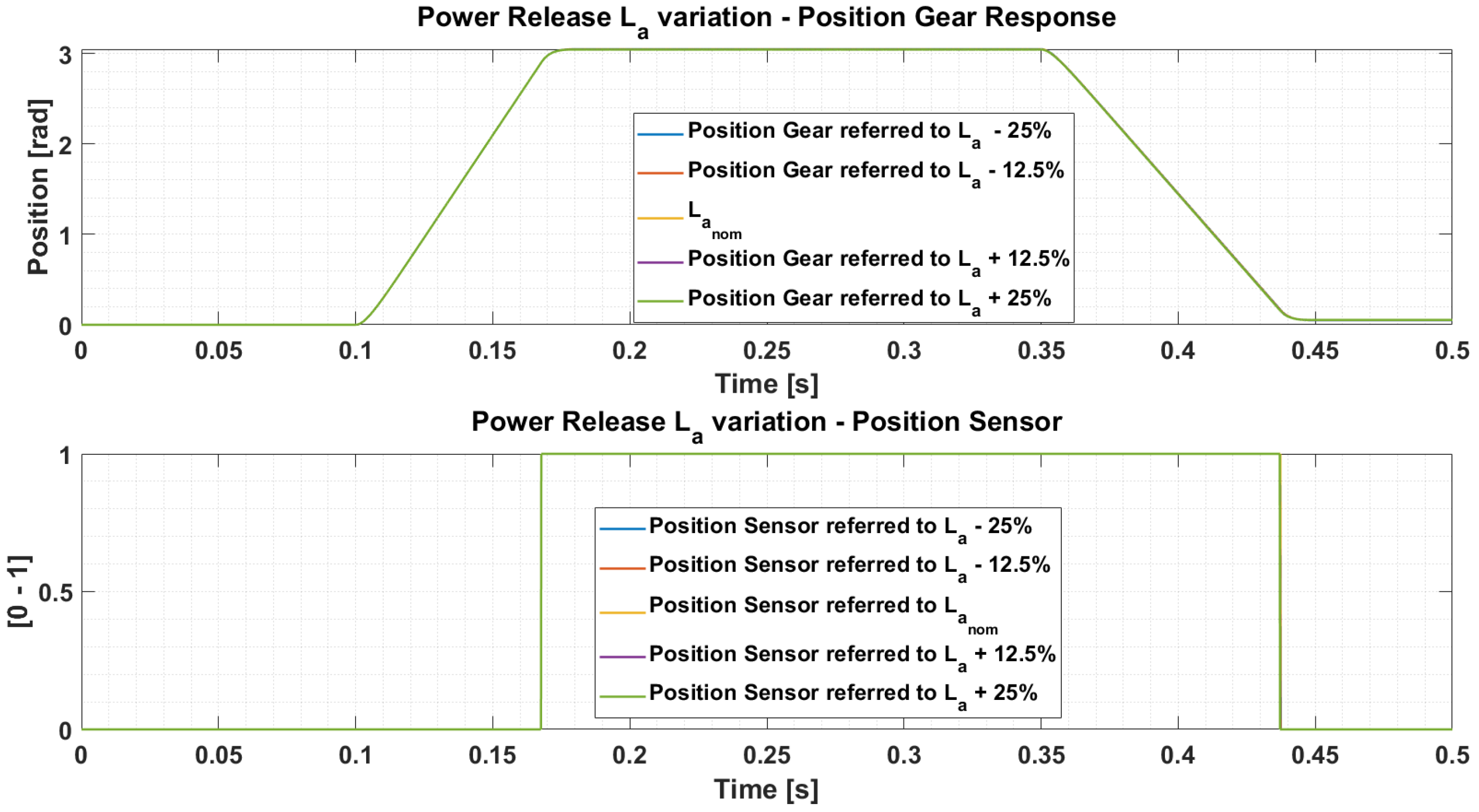











| Mode of Operation | Nominal Voltage | Timeout |
|---|---|---|
| PR door close | 7 V | s |
| PR door reset (RS) | 12 V | s |
| CN door open | 11 V | 3 s |
| CN door homing (HM) | 8 V | 4 s |
| Symbols | Thermal Parameters | PR | CN | Unit |
|---|---|---|---|---|
| armature resistance | 2.611 | 2.701 | ||
| back EMF constant | 8.25 | 11.349 | mVs/rad | |
| constant torque | 8.25 | 11.349 | m-Nm/A |
| Symbols | Thermal Parameters | PR | CN | Unit |
|---|---|---|---|---|
| Armature resistance | 2.611 | 2.701 | ||
| Armature inductance | H | |||
| J | Rotor inertia | kgm2 | ||
| Back EMF constant | 8.25 | 11.349 | mVs/rad | |
| Torque constant | 8.25 | 11.349 | mNm/A | |
| f | Viscous friction coefficient | Nms/rad | ||
| Breakaway torque | 0.195 | 0.118 | mNm | |
| Coulomb friction torque | 0.195 | 0.1165 | mNm | |
| Breakaway speed | 1 | 1 | rad/s |
| Symbols | Thermal Parameters | PR | CN | Unit |
|---|---|---|---|---|
| shaft–winding resistance | 6.25 | 6.64 | W/K | |
| convection thermal resistance in the air gap | 14.43 | 15.35 | W/K | |
| rotor–magnet resistance | 25.27 | 26.55 | W/K | |
| housing–air resistance, x-direction | 4.15 | 4.41 | W/K | |
| housing–air resistance, y-direction | 4.15 | 4.41 | W/K | |
| shaft–winding capacitance | 3.5 | 3.72 | J/K | |
| air gap capacitance | 0.01 | 0.011 | J/K | |
| rotor–magnet capacitance | 7.51 | 7.97 | J/K | |
| housing–air capacitance, x-direction | 4.52 | 4.78 | J/K | |
| housing–air capacitance, y-direction | 4.52 | 4.78 | J/K | |
| thermal coefficient for winding resistance |
| Symbol | Thermal Parameter | Value |
|---|---|---|
| Junction-to-Case Thermal Resistance | W/K | |
| Case-to-Sink Thermal Resistance | W/K | |
| Junction Thermal Capacitance | J/K | |
| Case Thermal Capacitance | J/K |
| Symbol | Description | Min | Typ | Max | Unit |
|---|---|---|---|---|---|
| Drain–source on-state resistance | – | 35 | 45 | m | |
| Gate threshold voltage | 2.4 | 3.0 | 4.0 | V | |
| Total gate charge | – | 4.9 | – | nC | |
| Turn-on delay time | – | 4.3 | – | ns | |
| Turn-off delay time | – | 8.4 | – | ns | |
| Rise time | – | 5.1 | – | ns | |
| Fall time | – | 5.4 | – | ns |
| Mode Operation | Execution Time | Timeout |
|---|---|---|
| Power Release—RS (Reset) Mode | 0.075 s | 0.15 s |
| Power Release—PR Mode | 0.1 s | 0.25 s |
| Cinch—CN Mode | 0.3 s | 3 s |
| Cinch—HM Mode | 0.35 s | 4.5 s |
| Parameters | Min | Nominal | Max |
|---|---|---|---|
| 2.023 | 2.701 | 3.376 | |
| H | H | H | |
| 8.512 mVs/rad | 11.349 mVs/rad | 14.186 mVs/rad | |
| 8.512 mNm/A | 11.349 mNm/A | 14.186 mNm/A |
| Mode Operation | PIL Execution Time | Timeout |
|---|---|---|
| Power Release—RS Mode | 0.08 s | 0.15 s |
| Power Release—PR Mode | 0.1 s | 0.2 s |
| Cinch—CN Mode | 0.32 s | 3 s |
| Cinch—HM Mode | 0.37 s | 4 s |
| Metric | Parameter | PR | CN | Unit |
|---|---|---|---|---|
| Flash | Program memory usage | 50 | 45 | KB |
| RAM | Data memory usage | 7.5 | 6 | KB |
| Execution time per step | 55 | 50 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nardi, D.; Dini, P.; Saponara, S. Electro-Thermal Model-Based Design of a Smart Latch in Automotive Systems for Performance and Reliability Evaluations. Electronics 2025, 14, 1962. https://doi.org/10.3390/electronics14101962
Nardi D, Dini P, Saponara S. Electro-Thermal Model-Based Design of a Smart Latch in Automotive Systems for Performance and Reliability Evaluations. Electronics. 2025; 14(10):1962. https://doi.org/10.3390/electronics14101962
Chicago/Turabian StyleNardi, Damiano, Pierpaolo Dini, and Sergio Saponara. 2025. "Electro-Thermal Model-Based Design of a Smart Latch in Automotive Systems for Performance and Reliability Evaluations" Electronics 14, no. 10: 1962. https://doi.org/10.3390/electronics14101962
APA StyleNardi, D., Dini, P., & Saponara, S. (2025). Electro-Thermal Model-Based Design of a Smart Latch in Automotive Systems for Performance and Reliability Evaluations. Electronics, 14(10), 1962. https://doi.org/10.3390/electronics14101962








