Coupled Sub-Feedback Hyperchaotic Dynamical System and Its Application in Image Encryption
Abstract
:1. Introduction
- (1)
- We have developed a novel method for chaos enhancement control. The W/Wavy function and Quartic function serve as the foundation for chaotic functions in coupled self-feedback systems. A novel chaotic system is developed utilizing logistic mapping as the perturbation factor. We evaluate and contrast the Lyapunov index, sample entropy, and permutation entropy with the established two-dimensional hyperchaos. The system presented in this work exhibits superior chaotic features, indicating the efficacy of the architecture.
- (2)
- A new three-dimensional roulette coordinate scrambling algorithm has been created. It adds the cross-plane bit level to the traditional plane-based roulette scrambling algorithm, which makes it easier to break the correlation between unit pixels and makes image encryption work better.
- (3)
- A double-layer diffusion algorithm is introduced. By combining the three-dimensional roulette coordinate scrambling method with the double-layer cross-channel method, the encryption algorithm works better while still being safe. We evaluate the encryption algorithm against the current one to determine its viability.
2. Related Work
2.1. Primal Function 1
2.2. Primal Function 2
2.3. Constructed Hyperchaotic Map
3. Chaos Performance Analysis
3.1. Analysis of Bifurcation Diagram
3.2. Analysis of Phase Diagrams
3.3. Analysis of Sensitivity
3.4. Analysis of
3.5. SE Analysis
3.6. PE Analysis
3.7. Spider Diagram Analysis
3.8. NIST Randomness Test
4. Encryption and Decryption Algorithms
4.1. Key Generation
| Algorithm 1. Key generation process |
| ; ,
|
| Algorithm 2. Chaotic sequence generation |
;
|
4.2. Lightweight Diffusion Algorithm
| Algorithm 3. Lightweight Diffusion Algorithm |
is generated by 2D-WQT, I is the Initial image.
|
4.3. Roulette Coordinate Scrambling
| Algorithm 4. Roulette coordinate scrambling algorithm |
| Input: Image I of size M × M and secret keys Sec_key, Sec_key2, Sec_key3 Output: Scrambled image I 1. Start; 2. Define traversal_order as an empty list; 3. For each row j from 1 to M: 4. If j is odd: 5. Append all positions (j, k) for k = 1 to M to traversal_order; 6. Else: 7. Append all positions (j, k) for k = M down to 1 to traversal_order; 8. End For 9. For i = 1 to 3: 10. For each position (j, k) in traversal_order: 11. temp = I(j, k, i); 12. index = (i − 1) × M × M + M × (j − 1) + k; 13. I(j, k, i) = I(Sec_key(index), Sec_key2(index), Sec_key3(index)); 14. I(Sec_key(index), Sec_key2(index), Sec_key3(index)) = temp; 15. End For 16. End For 17. End; 18. Stop; |
4.4. Overall Image Encryption Algorithm
4.5. Decryption Algorithm
5. Experimental Results
5.1. Algorithm Feasibility Verification
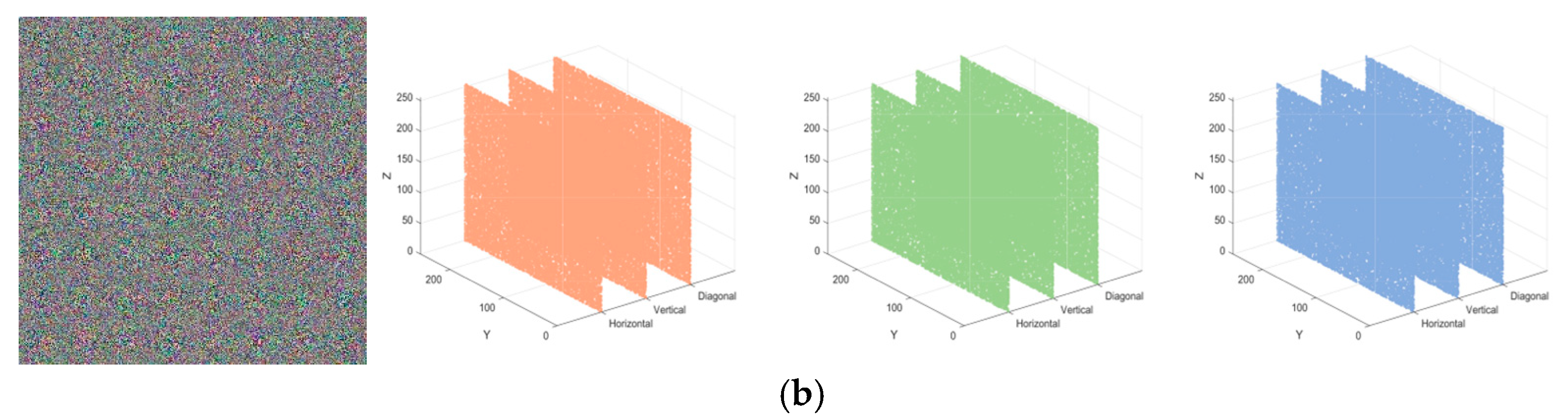
5.2. Histogram Analysis
5.3. Key Space Analysis
5.4. Correlation Analysis
5.5. Information Entropy Analysis
5.6. Differential Attack Analysis
5.7. Anti-Attack Test
5.7.1. Numerous Noise Attacks
5.7.2. Clipping and Channel Missing
5.8. Chosen Plaintext Attack
5.9. Analysis of Encryption Time
6. Conclusions and Outlooks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, S.; Chen, G.; Cheung, A.; Bhargava, B.; Lo, K.T. On the design of perceptual MPEG-video encryption algorithms. IEEE Trans. Circuits Syst. Video Technol. 2007, 17, 214–223. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, S.; Kaur, M. Computational image encryption techniques: A comprehensive review. Math. Probl. Eng. 2021, 2021, 5012496. [Google Scholar] [CrossRef]
- Kaur, M.; Singh, S.; Kaur, M.; Singh, A.; Singh, D. A systematic review of metaheuristic-based image encryption techniques. Arch. Comput. Methods Eng. 2021, 29, 2563–2577. [Google Scholar] [CrossRef]
- Liang, Q.; Zhu, C. A new one-dimensional chaotic map for image encryption scheme based on random DNA coding. Opt. Laser Technol. 2023, 160, 109033. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication theory of secrecy systems. Bell Syst. Tech. J. 1949, 28, 656–715. [Google Scholar] [CrossRef]
- Aihara, K.; Takabe, T.; Toyoda, M. Chaotic neural networks. Phys. Lett. A 1990, 144, 333–340. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. Single neuronal dynamical system in self-feedbacked Hopfield networks and its application in image encryption. Entropy 2021, 23, 456. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, L.; Chen, C.L.P. Image encryption using a new parametric switching chaotic system. Signal Process. 2013, 93, 3039–3052. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, H. An image encryption algorithm based on a compound-coupled chaotic system. Digit. Signal Process. 2024, 146, 104367. [Google Scholar] [CrossRef]
- Li, C.; Gao, Y.; Lei, T.; Li, R.Y.M.; Xu, Y. Two independent offset controllers in a three-dimensional chaotic system. Int. J. Bifurc. Chaos 2024, 34, 2450008. [Google Scholar] [CrossRef]
- Pankaj, S.; Dua, M. Chaos based medical image encryption techniques: A comprehensive review and analysis. Inf. Secur. J. A Glob. Perspect. 2024, 33, 332–358. [Google Scholar] [CrossRef]
- Cao, C.; Sun, K.; Liu, W. A novel bit-level image encryption algorithm based on 2D-LICM hyperchaotic map. Signal Process. 2018, 143, 122–133. [Google Scholar] [CrossRef]
- Toktas, F.; Erkan, U.; Yetgin, Z. Cross-channel color image encryption through 2D hyperchaotic hybrid map of optimization test functions. Expert Syst. Appl. 2024, 249, 123583. [Google Scholar] [CrossRef]
- Teng, L.; Wang, X.; Yang, F.; Xian, Y. Color image encryption based on cross 2D hyperchaotic map using combined cycle shift scrambling and selecting diffusion. Nonlinear Dyn. 2021, 105, 1859–1876. [Google Scholar] [CrossRef]
- Sun, J. 2D-SCMCI hyperchaotic map for image encryption algorithm. IEEE Access 2021, 9, 59313–59327. [Google Scholar] [CrossRef]
- Hua, Z.; Zhu, Z.; Chen, Y.; Li, Y. Color image encryption using orthogonal Latin squares and a new 2D chaotic system. Nonlinear Dyn. 2021, 104, 4505–4522. [Google Scholar] [CrossRef]
- Qiu, H.; Xu, X.; Jiang, Z.; Sun, K.; Xiao, C. A color image encryption algorithm based on hyperchaotic map and Rubik’s Cube scrambling. Nonlinear Dyn. 2022, 110, 2869–2887. [Google Scholar] [CrossRef]
- Wang, Q.; Zhang, X.; Zhao, X. Color image encryption algorithm based on novel 2D hyper-chaotic system and DNA crossover and mutation. Nonlinear Dyn. 2023, 111, 22679–22705. [Google Scholar] [CrossRef]
- Wang, X.; Chen, X.; Zhao, M. A new two-dimensional sine-coupled-logistic map and its application in image encryption. Multimed. Tools Appl. 2023, 82, 35719–35755. [Google Scholar] [CrossRef]
- Wang, X.; Liu, P. A new full chaos coupled mapping lattice and its application in privacy image encryption. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 69, 1291–1301. [Google Scholar] [CrossRef]
- Gao, Q.; Zhang, X. Multiple-image encryption algorithm based on a new composite chaotic system and 3D coordinate matrix. Chaos Solitons Fractals 2024, 189, 115587. [Google Scholar] [CrossRef]
- Cao, P.; Teng, L. A chaotic image encryption algorithm based on sliding window and pseudo-random stack shuffling. Nonlinear Dyn. 2024, 112, 13539–13569. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, M. Color image encryption algorithm using DNA encoding and fuzzy single neurons. IEEE Access 2022, 10, 127770–127782. [Google Scholar] [CrossRef]
- Alawida, M. A novel DNA tree-based chaotic image encryption algorithm. J. Inf. Secur. Appl. 2024, 83, 103791. [Google Scholar] [CrossRef]
- Liu, X.D.; Chen, Q.H.; Zhao, R.S.; Liu, G.Z.; Guan, S.; Wu, L.L.; Fan, X.K. Quantum image encryption algorithm based on four-dimensional chaos. Front. Phys. 2024, 12, 1230294. [Google Scholar] [CrossRef]
- He, J.; Zhu, H.; Zhou, X. Quantum image encryption algorithm via optimized quantum circuit and parity bit-plane permutation. J. Inf. Secur. Appl. 2024, 81, 103698. [Google Scholar] [CrossRef]
- Zhang, Z.; Tang, J.; Zhang, F.; Huang, T.; Lu, M. Medical image encryption based on Josephus scrambling and dynamic cross-diffusion for patient privacy security. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 9250–9263. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, R.; Liu, J. Partial-privacy image encryption algorithm based on time-varying delayed exponentially controlled chaotic system. Nonlinear Dyn. 2024, 112, 10633–10659. [Google Scholar] [CrossRef]
- Courrieu, P. The Hyperbell algorithm for global optimization: A random walk using Cauchy densities. J. Glob. Optim. 1997, 10, 37–55. [Google Scholar] [CrossRef]
- Storn, R. Differrential evolution: A simple and efficient adaptive scheme for global optimization over continuous spaces. Tech. Rep. Int. Comput. Sci. Inst. 1995, 11. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; You, Z.; Zhang, T. A Novel Color Image Encryption Algorithm Based on Hybrid Two-Dimensional Hyperchaos and Genetic Recombination. Mathematics 2024, 12, 3457. [Google Scholar] [CrossRef]
- Zhou, R.G.; Sun, Y.J.; Fan, P. Quantum image Gray-code and bit-plane scrambling. Quantum Inf. Process. 2015, 14, 1717–1734. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, J.; Liu, H.; Zhang, F. Dynamic analysis of a one-parameter chaotic system in complex field. IEEE Access 2020, 8, 28774–28781. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Cryptographic Requirements for Chaotic Secure Communications. arXiv 2003, arXiv:nlin/0311039. [Google Scholar]
- Li, Z.; Peng, C.; Tan, W.; Li, L. A novel chaos-based color image encryption scheme using bit-level permutation. Symmetry 2020, 12, 1497. [Google Scholar] [CrossRef]
- Mfungo, D.E.; Fu, X. Fractal-based hybrid cryptosystem: Enhancing image encryption with RSA, homomorphic encryption, and chaotic maps. Entropy 2023, 25, 1478. [Google Scholar] [CrossRef]
- Wang, S.; Sun, B.; Wang, Y.; Du, B. Image encryption algorithm using multi-base diffusion and a new four-dimensional chaotic system. Multimed. Tools Appl. 2024, 83, 10039–10060. [Google Scholar] [CrossRef]
- Khalil, N.; Sarhan, A.; Alshewimy, M.A. An efficient color/grayscale image encryption scheme based on hybrid chaotic maps. Opt. Laser Technol. 2021, 143, 107326. [Google Scholar] [CrossRef]
- Li, X.; Sun, B.; Bi, X.; Yan, H.; Wang, L. A novel color image encryption algorithm based on cross-plane scrambling and diffusion. Mob. Netw. Appl. 2024, 29, 583–594. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S. An optical image encryption method using Hopfield neural network. Entropy 2022, 24, 521. [Google Scholar] [CrossRef] [PubMed]
- Gao, S.; Zhang, Z.; Iu, H.H.C.; Ding, S.; Mou, J.; Erkan, U.; Toktas, A.; Li, Q.; Wang, C.; Cao, Y. A Parallel Color Image Encryption Algorithm Based on a 2D Logistic-Rulkov Neuron Map. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Gao, M.; Tian, Y.; Wang, C.; Lu, H.H.C. A color image encryption algorithm based on hash table, hilbert curve and hyper-chaotic synchronization. Mathematics 2023, 11, 567. [Google Scholar] [CrossRef]
- Xu, Y.Q.; Zhen, X.X.; Tang, M. Dynamical System in Chaotic Neurons with Time Delay Self-Feedback and Its Application in Color Image Encryption. Complexity 2022, 1, 2832104. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, Y.; Gu, Z. A novel color image encryption method based on sequence cross transformation and chaotic sequences. Eng. Lett. 2020, 28, 1088–1092. [Google Scholar]






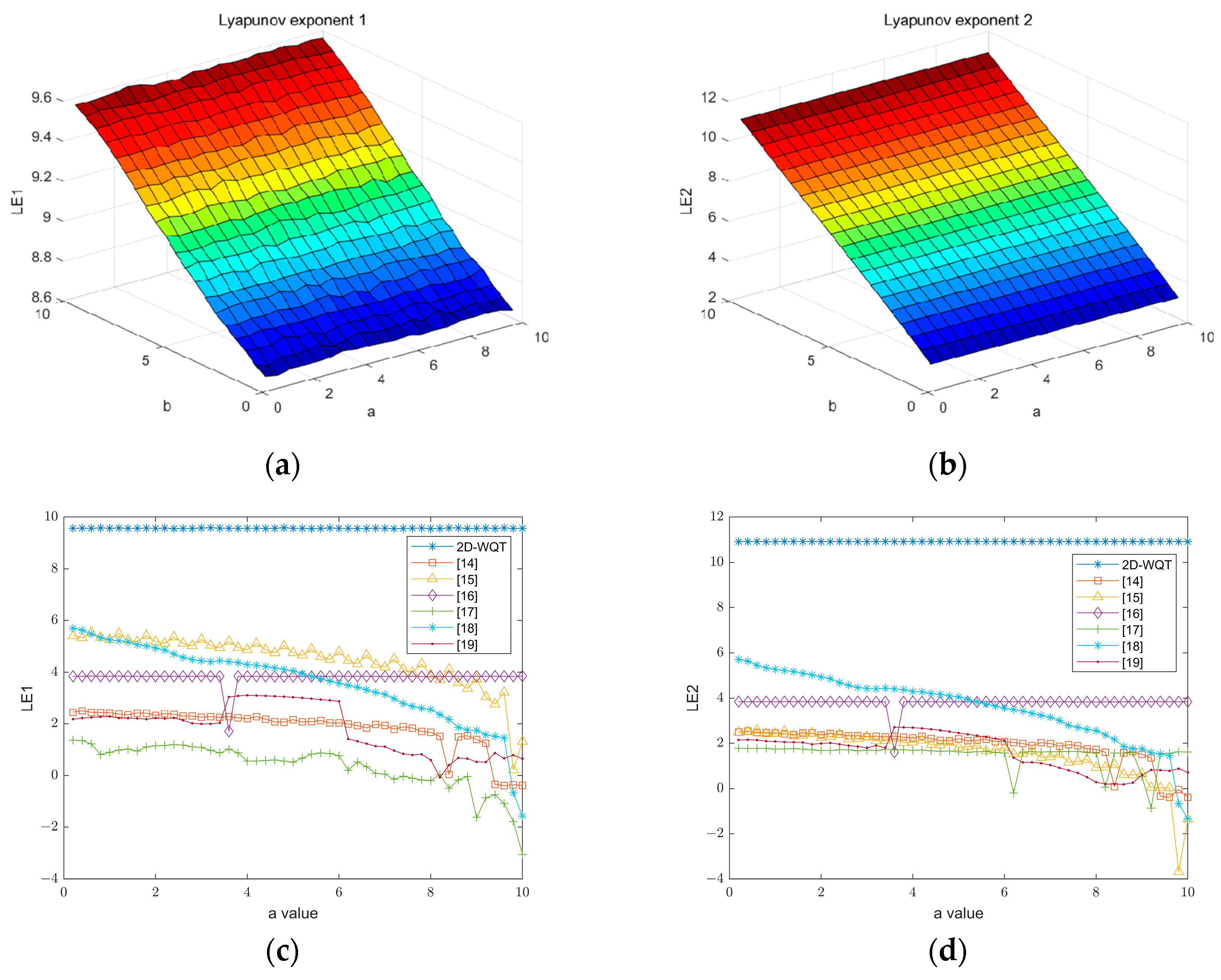














| Title | SE | PE | ||
|---|---|---|---|---|
| WQT | 9.5658 | 10.9239 | 2.3332 | 0.99903 |
| [14] | 1.9 | 1.8481 | 1.3982 | 0.96811 |
| [15] | 4.4839 | 1.549 | 1.807 | 0.99383 |
| [16] | 3.8005 | 3.7984 | 0.90858 | 0.99865 |
| [17] | 1.844 | 1.6131 | 1.3408 | 0.97261 |
| [18] | 0.37197 | 1.5189 | 0.49676 | 0.85285 |
| [19] | 3.5989 | 3.6037 | 1.592 | 0.98177 |
| Subset | X | Y | ||
|---|---|---|---|---|
| p-Value | Proportion | p-Value | Proportion | |
| Frequency | 0.191687 | 99/100 | 0.779188 | 99/100 |
| Block Frequency | 0.048716 | 100/100 | 0.275709 | 100/100 |
| Cumulative Sums | 0.334538 | 99/100 | 0.719747 | 99/100 |
| Runs | 0.108791 | 99/100 | 0.004981 | 99/100 |
| Longest Run | 0.236810 | 99/100 | 0.759756 | 100/100 |
| Rank | 0.419021 | 99/100 | 0.798139 | 100/100 |
| FFT | 0.911413 | 100/100 | 0.202268 | 100/100 |
| Non-Overlapping | 0.779188 | 100/100 | 0.102526 | 98/100 |
| Overlapping | 0.798139 | 100/100 | 0.779188 | 100/100 |
| Universal | 0.025193 | 99/100 | 0.834308 | 99/100 |
| Approximate Entropy | 0.334538 | 98/100 | 0.115387 | 100/100 |
| Random Excursions | 0.304126 | 99/100 | 0.911413 | 98/100 |
| Random Excursions Variant | 0.229900 | 70/70 | 0.517442 | 61/61 |
| Serial | 0.450564 | 70/70 | 0.452799 | 61/61 |
| Linear Complexity | 0.030806 | 98/100 | 0.759756 | 98/100 |
| Images | Size | Channel | —— | Horizontal | Vertical | Diagonal |
|---|---|---|---|---|---|---|
| House | 3 | R | Original | 0.95483 | 0.95736 | 0.92146 |
| This paper | −0.00304 | 0.00322 | −0.006822 | |||
| G | Original | 0.93696 | 0.94352 | 0.88982 | ||
| This paper | −0.00171 | −0.0024019 | −0.014512 | |||
| B | Original | 0.97119 | 0.96683 | 0.94281 | ||
| This paper | −0.00553 | −0.004458 | −0.00672 | |||
| Lena | 3 | R | Original | 0.9758 | 0.9872 | 0.9648 |
| This paper | −0.0015 | 0.0035 | −0.00016 | |||
| [17] | −0.0367 | −0.0059 | 0.0182 | |||
| [36] | −0.0022 | 0.0057 | 0.00007 | |||
| G | Original | 0.9760 | 0.9879 | 0.9638 | ||
| This paper | 0.0010 | 0.00290 | 0.00757 | |||
| [17] | 0.0030 | 0.0587 | −0.0123 | |||
| [36] | 0.0009 | −0.0041 | 0.0038 | |||
| B | Original | 0.95358 | 0.97332 | 0.93065 | ||
| This paper | −0.00067 | −0.00312 | −0.00152 | |||
| [17] | −0.0037 | −0.0227 | −0.0134 | |||
| [36] | 0.0013 | 0.0017 | 0.0104 |
| Images | Ciphertext | Plaintext | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| 4.1.05 | 6.4311 | 6.5389 | 6.5389 | 7.9973 | 7.9974 | 7.9974 |
| 4.1.06 | 7.2104 | 7.4136 | 7.4136 | 7.9972 | 7.9974 | 7.9974 |
| house | 7.4156 | 7.2295 | 7.2295 | 7.9993 | 7.9993 | 7.9993 |
| 4.2.07 | 7.3388 | 7.4963 | 7.0583 | 7.9994 | 7.9993 | 7.9994 |
| 2.2.01 | 7.7575 | 7.3387 | 6.9561 | 7.9998 | 7.9998 | 7.9998 |
| Image | File | R | G | B |
|---|---|---|---|---|
| Lena-512 | This paper | 7.9994 | 7.9994 | 7.9994 |
| [38] | 7.9992 | 7.9993 | 7.9993 | |
| [39] | 7.9992 | 7.9994 | 7.9993 | |
| [40] | 7.9975 | 7.9973 | 7.9973 | |
| Airplane-512 | This paper | 7.9994 | 7.9994 | 7.9994 |
| Baboon-256 | This paper | 7.9982 | 7.9980 | 7.9980 |
| Lena-256 | This paper | 7.9976 | 7.9978 | 7.9976 |
| [40] | 7.9968 | 7.9970 | 7.9969 | |
| [39] | 7.9969 | 7.9971 | 7.9968 |
| Images | NPCR (%) | UACI (%) | ||||
|---|---|---|---|---|---|---|
| R | G | B | R | G | B | |
| 4.1.05 | 99.5895% | 99.6541% | 99.5850% | 29.2090% | 31.2231% | 32.3875% |
| 4.1.06 | 99.7653% | 99.6353% | 99.6854% | 32.1960% | 34.1940% | 32.6740% |
| house | 99.5892% | 99.5911% | 99.6220% | 30.1640% | 31.2790% | 31.2910% |
| 4.2.07 | 99.5983% | 99.5975% | 99.6239% | 30.1340% | 33.9340% | 33.8485% |
| 2.2.01 | 99.6153% | 99.6067% | 99.6213% | 32.2513% | 32.1166% | 29.9989% |
| Attack | R Channel | G Channel | B Channel |
|---|---|---|---|
| Gauss Noise-0.05% | 40.0711 | 15.9197 | 27.7382 |
| Gauss Noise-0.5% | 21.5603 | 12.2238 | 19.0879 |
| Gauss Noise-1% | 17.7555 | 11.2555 | 16.2279 |
| Salt and pepper Noise | 21.7271 | 18.5129 | 21.3983 |
| Block Attack | 15.4182 | 13.4958 | 17.3099 |
| 6.25% Shearing | 21.5308 | 17.6211 | 20.2593 |
| 12.5% Shearing | 17.9937 | 14.6785 | 17.3420 |
| 25% Shearing | 15.2589 | 12.0405 | 14.2498 |
| 50% Shearing | 11.9813 | 10.0532 | 11.1216 |
| Algorithms | -- | 512 × 512 | 1024 × 1024 |
|---|---|---|---|
| This article | Encryption | 0.0621 | 0.2581 |
| [43] | Encryption | 0.5726 | 2.0181 |
| [44] | Encryption | 1.3676 | 3.0399 |
| [45] | Encryption | 2.2234 | 9.0013 |
| This article | Decryption | 0.1025 | 0.4271 |
| [45] [44] | Decryption Decryption | 2.3218 2.3772 | 9.1095 4.4680 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
You, Z.; Liu, J.; Zhang, T.; Xu, Y. Coupled Sub-Feedback Hyperchaotic Dynamical System and Its Application in Image Encryption. Electronics 2025, 14, 1914. https://doi.org/10.3390/electronics14101914
You Z, Liu J, Zhang T, Xu Y. Coupled Sub-Feedback Hyperchaotic Dynamical System and Its Application in Image Encryption. Electronics. 2025; 14(10):1914. https://doi.org/10.3390/electronics14101914
Chicago/Turabian StyleYou, Zelong, Jiaoyang Liu, Tianqi Zhang, and Yaoqun Xu. 2025. "Coupled Sub-Feedback Hyperchaotic Dynamical System and Its Application in Image Encryption" Electronics 14, no. 10: 1914. https://doi.org/10.3390/electronics14101914
APA StyleYou, Z., Liu, J., Zhang, T., & Xu, Y. (2025). Coupled Sub-Feedback Hyperchaotic Dynamical System and Its Application in Image Encryption. Electronics, 14(10), 1914. https://doi.org/10.3390/electronics14101914






