Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion
Abstract
1. Introduction
- (1)
- To increase the search space of the algorithm, a refractive backward learning method is employed, and an adaptive curve is included to control the size of the dung beetle population.
- (2)
- To enhance and balance local exploitation and global exploration, the algorithm’s convergence is accelerated in the ball-rolling dung beetle phase by using a triangular wandering approach and in the breeding dung beetle phase by using a fused subtractive averaging optimizer.
- (3)
- Late in the iteration, the globally optimal solution is variationally disturbed by an adaptive Gaussian–Cauchy hybrid variational perturbation factor, which improves algorithm efficiency and the impact of finding the ideal solution.
2. Dung Beetle Optimization Algorithm (DBO)
2.1. Rolling Dung Beetle
2.2. Breeding Dung Beetles
2.3. Foraging Dung Beetles
2.4. Stealing Dung Beetles
3. Improving the Dung Beetle Optimization Algorithm
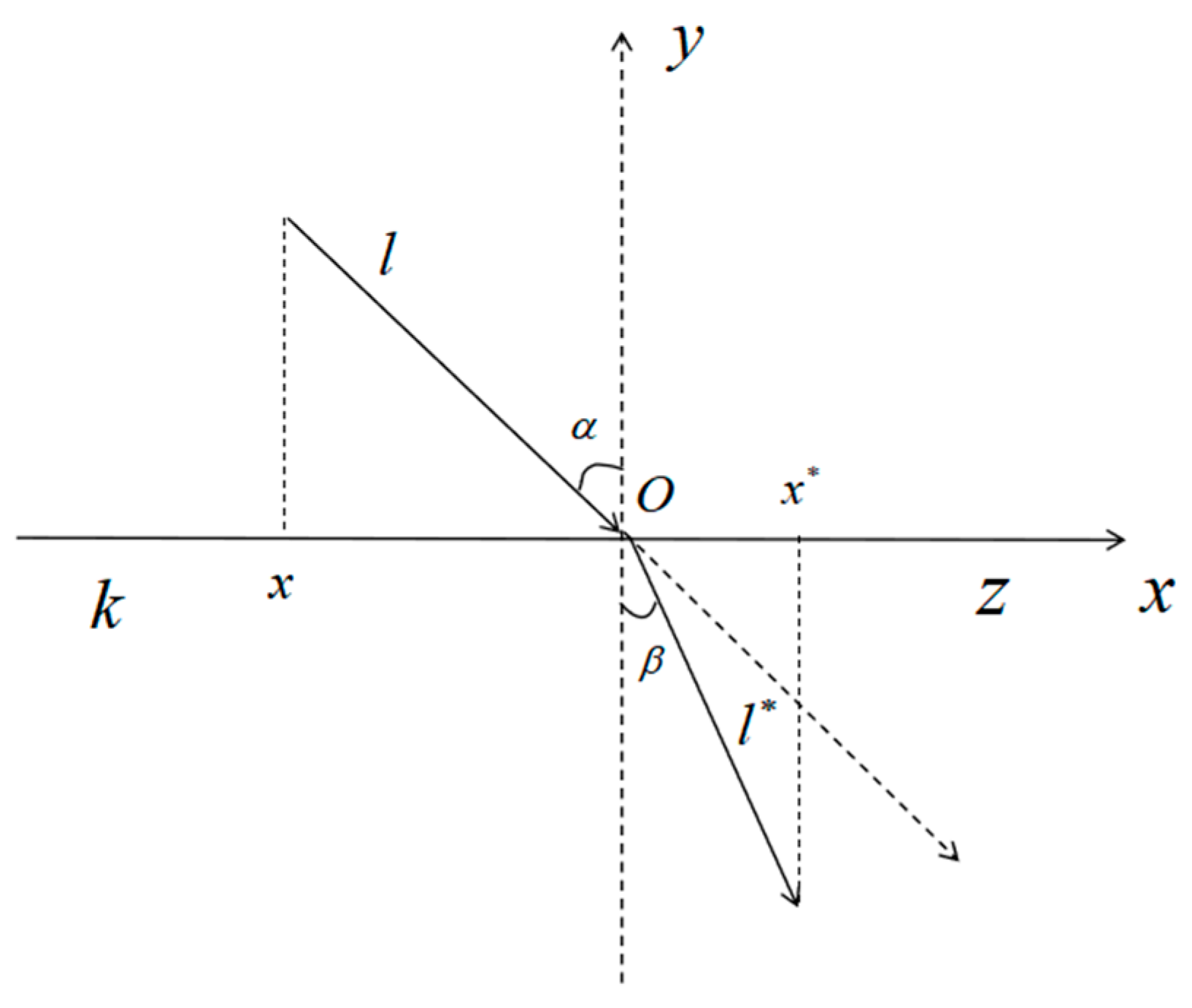
3.1. Refractive Reverse Learning Strategies
3.2. Multi-Strategy Integration Improvement
3.2.1. Adaptive Population Change
3.2.2. Fusion Subtractive Averaging Optimizer
3.2.3. Triangle Wandering Strategy
3.3. Adaptive Gauss–Cauchy Mixed-Variance Perturbation Factor
3.4. MSFDBO Complexity Analysis
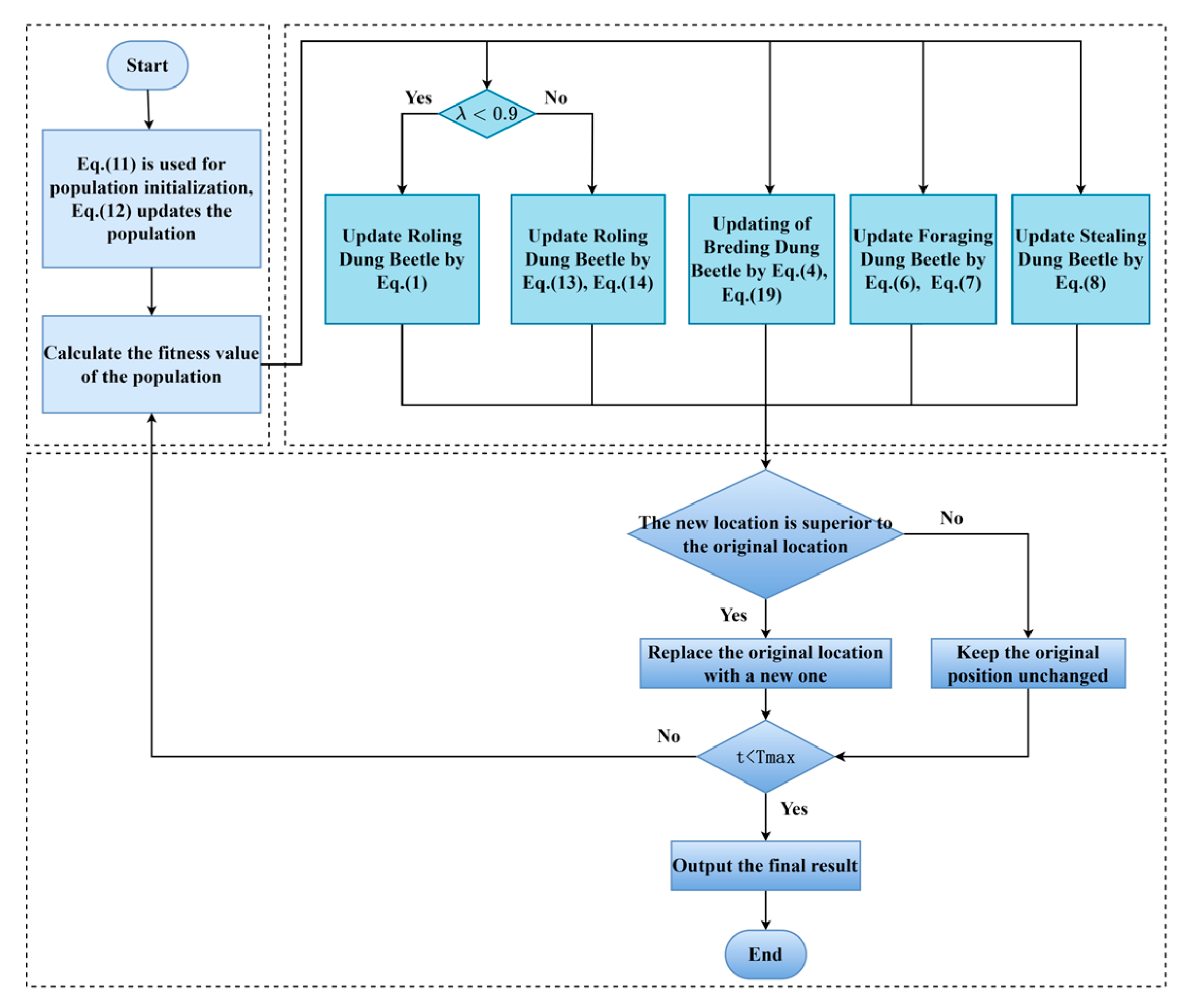
3.5. MSFDBO Algorithm Flowchart
4. Experimental Results and Discussion
4.1. CEC2017 Benchmark Function Results and Analysis
4.1.1. Analysis of CEC2017 Statistical Results
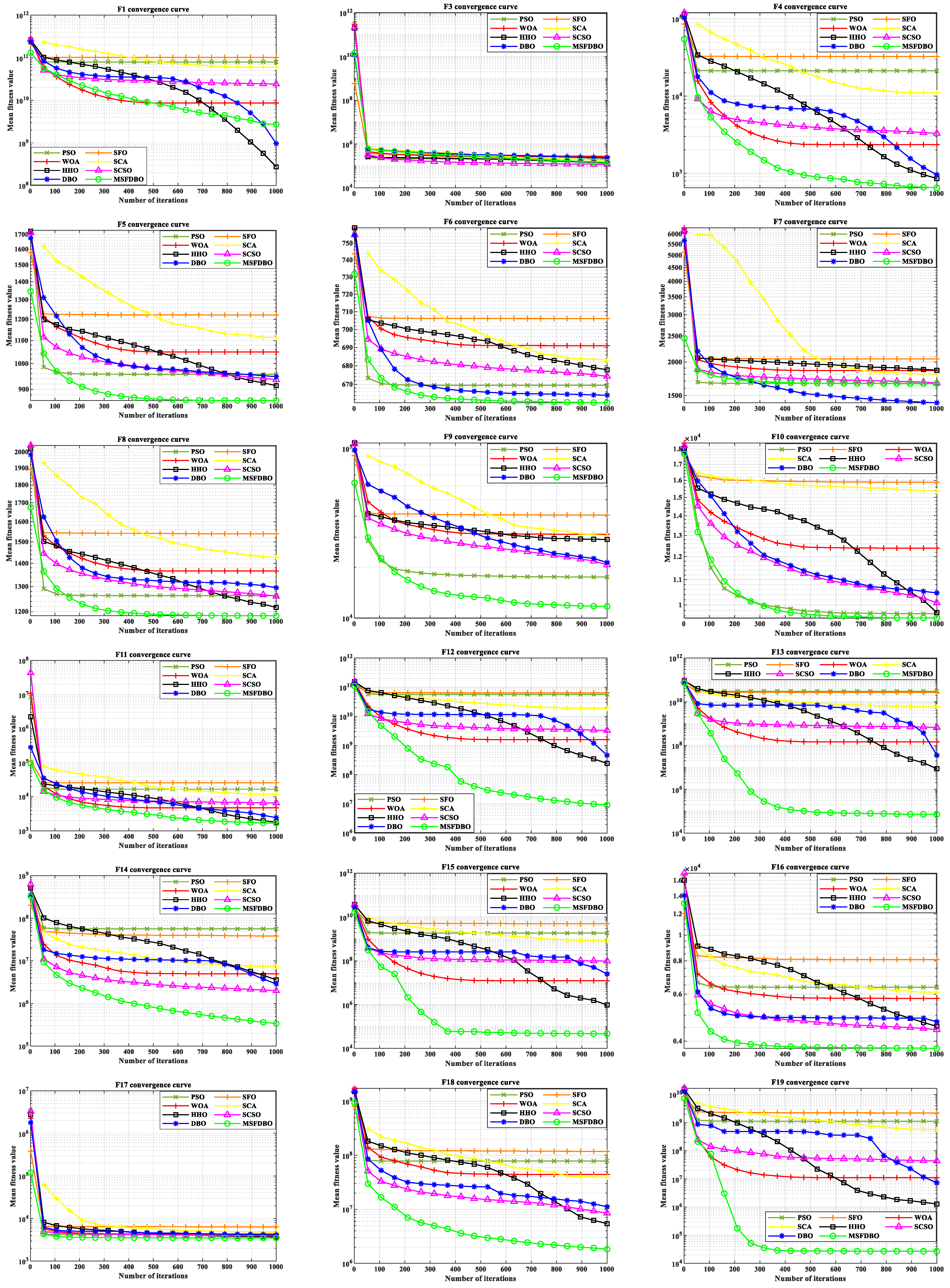
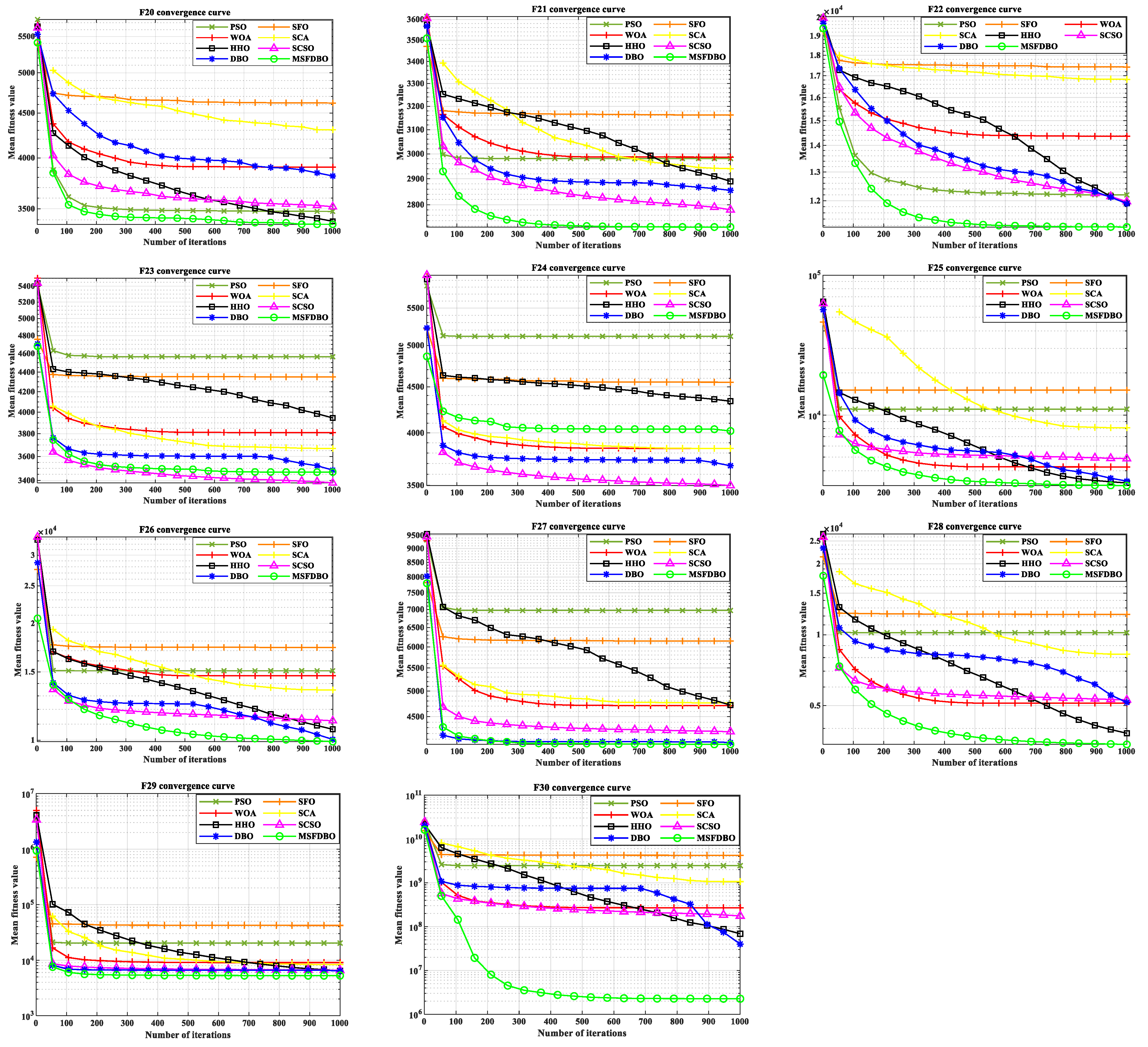
4.1.2. Comparative Analysis of CEC2017 Convergence Curves
4.2. Wilcoxon Rank Sum Test
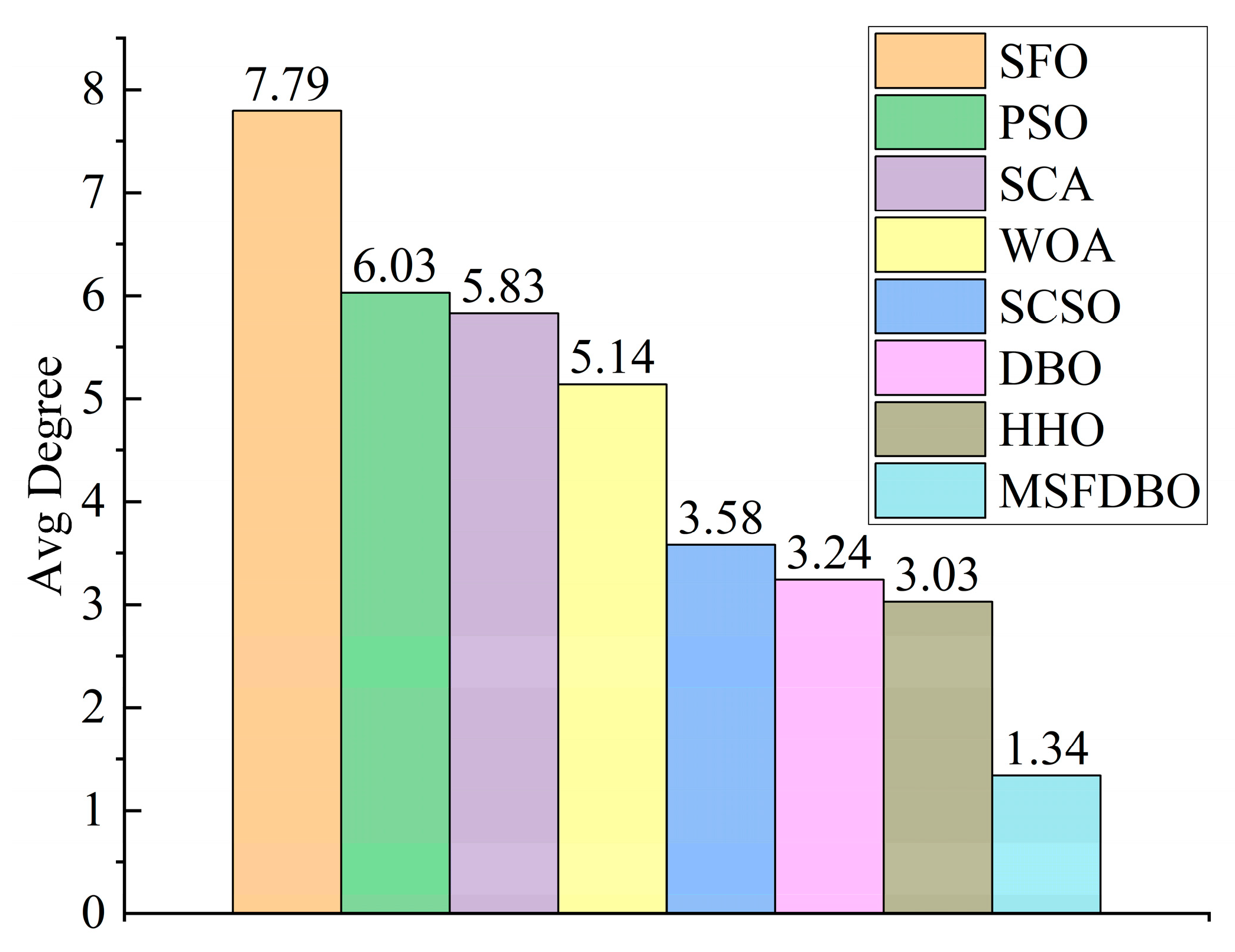
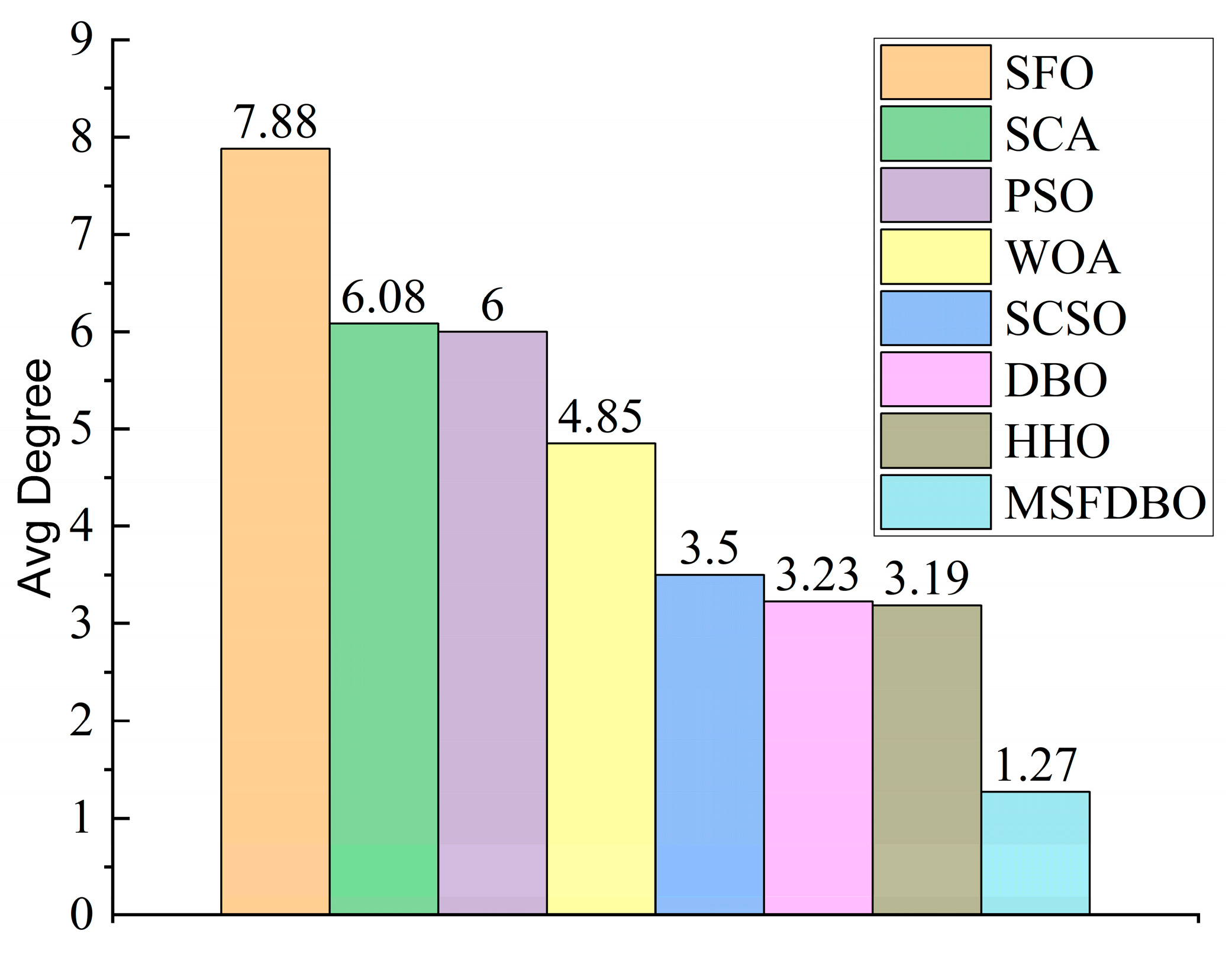
4.3. Friedman Test
5. Engineering Application Design Issues
5.1. Welded Beam Design Issues
5.2. Reducer Design Issues
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, A.; Jiang, J. Solving path planning problem based on logistic beetle algorithm search–pigeon-inspired optimisation algorithm. Electron. Lett. 2020, 56, 1105–1108. [Google Scholar] [CrossRef]
- Huang, Q.; Ding, H.; Razmjooy, N. Oral cancer detection using convolutional neural network optimized by combined seagull optimization algorithm. Biomed. Signal Process. Control. 2024, 87, 105546. [Google Scholar] [CrossRef]
- Luo, X.; Du, B.; Gui, P.; Zhang, D.; Hu, W. A Hunger Games Search algorithm with opposition-based learning for solving multimodal medical image registration. Neurocomputing 2023, 540, 126204. [Google Scholar] [CrossRef]
- Shen, Y.; Zhang, C.; Gharehchopogh, F.S.; Mirjalili, S. An improved whale optimization algorithm based on multi-population evolution for global optimization and engineering design problems. Expert Syst. Appl. 2023, 215, 119269. [Google Scholar] [CrossRef]
- Zhang, N.; Cai, Y.X.; Wang, Y.Y.; Tian, Y.T.; Wang, X.L.; Badami, B. Skin cancer diagnosis based on optimized convolutional neural network. Artif. Intell. Med. 2020, 102, 101756. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN'95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Jain, M.; Singh, V.; Rani, A. A novel nature-inspired algorithm for optimization: Squirrel search algorithm. Swarm Evol. Comput. 2019, 44, 148–175. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. Ournal Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl.-Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Chopra, N.; Ansari, M.M. Golden jackal optimization: A novel nature-inspired optimizer for engineering applications. Expert Syst. Appl. 2022, 198, 116924. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Zhu, F.; Li, G.; Tang, H.; Li, Y.; Lv, X.; Wang, X. Dung beetle optimization algorithm based on quantum computing and multi-strategy fusion for solving engineering problems. Expert Syst. Appl. 2024, 236, 121219. [Google Scholar] [CrossRef]
- Duan, Y.; Yu, X. A collaboration-based hybrid GWO-SCA optimizer for engineering optimization problems. Expert Syst. Appl. 2023, 213, 119017. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Saha, A.K.; Nama, S.; Masdari, M. An improved moth flame optimization algorithm based on modified dynamic opposite learning strategy. Artif. Intell. Rev. 2023, 56, 2811–2869. [Google Scholar] [CrossRef]
- Yan, S.; Yang, P.; Zhu, D.; Zheng, W.; Wu, F. Improved sparrow search algorithm based on iterative local search. Comput. Intell. Neurosci. 2021, 2021, 6860503. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, K.; Yao, Q.; Wang, L. A dual-optimization wind speed forecasting model based on deep learning and improved dung beetle optimization algorithm. Energy 2024, 286, 129604. [Google Scholar] [CrossRef]
- Wang, S.; Cao, L.; Chen, Y.; Chen, C.; Yue, Y.; Zhu, W. Gorilla optimization algorithm combining sine cosine and cauchy variations and its engineering applications. Sci. Rep. 2024, 14, 7578. [Google Scholar] [CrossRef] [PubMed]
- Ewees, A.A.; Mostafa, R.R.; Ghoniem, R.M.; Gaheen, M.A. Improved seagull optimization algorithm using Lévy flight and mutation operator for feature selection. Neural Comput. Appl. 2022, 34, 7437–7472. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, J.; Hu, Z.; Khan, N.A.; Sulaiman, M. Analysis of third-order nonlinear multi-singular Emden–Fowler equation by using the LeNN-WOA-NM algorithm. IEEE Access 2021, 9, 72111–72138. [Google Scholar] [CrossRef]
- Zhang, R.; Zhu, Y. Predicting the mechanical properties of heat-treated woods using optimization-algorithm-based BPNN. Forests 2023, 14, 935. [Google Scholar] [CrossRef]
- Guohua, W.; Rammohan, M.; Suganthan, P. Problem Definitions and Evaluation Criteria for the CEC 2017 Competition and Special Session on Constrained Single Objective Real-Parameter Optimization; Nanyang Technological University: Singapore, 2016. [Google Scholar]
- Shadravan, S.; Naji, H.R.; Bardsiri, V.K. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A sine cosine algorithm for solving optimization problems. Knowl.-Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Lang, C. Remora optimization algorithm. Expert Syst. Appl. 2021, 185, 115665. [Google Scholar] [CrossRef]
- Fan, Q.; Chen, Z.; Zhang, W.; Fang, X. ESSAWOA: Enhanced whale optimization algorithm integrated with salp swarm algorithm for global optimization. Eng. Comput. 2022, 38 (Suppl. S1), 797–814. [Google Scholar] [CrossRef]
- Zhao, Y.; Huang, C.; Zhang, M.; Lv, C. COLMA: A chaos-based mayfly algorithm with opposition-based learning and Levy flight for numerical optimization and engineering design. Ournal Supercomput. 2023, 79, 19699–19745. [Google Scholar] [CrossRef]


| Algorithm | Parameters |
|---|---|
| PSO | ω = 1, c1 = 1.1, c2 = 1.1 |
| SCA | a = 2 |
| WOA | a = 2 × (1 − t/Tmax), k = 1 |
| HHO | B = 1.5, E0 = [−1, 1] |
| SFO | A = 4, e = 0.001, SFP = 0.3 |
| SCSO | rG = 2~0, =−2rG~rG |
| DBO | RDB = 6, EDB = 6, FDB = 7, SDB = 11 |
| MSFDBO | R = 1 − t/Tmax |
| Test Function | PSO | SFO | WOA | SCA | HHO | SCSO | DBO | MSFDBO |
|---|---|---|---|---|---|---|---|---|
| CEC2017 50D | 6.0345 | 7.7931 | 5.1379 | 5.8276 | 3.0345 | 3.5862 | 3.2414 | 1.3448 |
| CEC2017 100D | 6.0690 | 7.7586 | 4.8966 | 6.0345 | 3.0345 | 3.5172 | 3.3448 | 1.3448 |
| Arithmetic | Cost Optimization | ||||
|---|---|---|---|---|---|
| PSO | 0.1525 | 6.0671 | 9.7399 | 0.2025 | 2.0597 |
| SFO | 0.1710 | 4.8328 | 8.2402 | 0.2545 | 2.0189 |
| WOA | 0.1580 | 6.4434 | 9.5400 | 0.2034 | 2.0850 |
| SCA | 0.2010 | 3.5951 | 9.5716 | 0.2107 | 1.8645 |
| HHO | 0.1682 | 4.8085 | 8.9901 | 0.2169 | 1.9105 |
| SCSO | 0.2009 | 3.3397 | 9.0395 | 0.2057 | 1.7003 |
| DBO | 0.2035 | 3.0899 | 9.5183 | 0.2036 | 1.7331 |
| MSFDBO | 0.2057 | 3.2444 | 9.0337 | 0.2059 | 1.6948 |
| Algorithms | Optimum Weight | |||||||
|---|---|---|---|---|---|---|---|---|
| PSO | 3.6000 | 0.7000 | 17.0000 | 8.3000 | 8.3000 | 3.4122 | 5.3642 | 3121.9650 |
| SFO | 3.5114 | 0.7000 | 18.2404 | 7.5813 | 7.7169 | 3.5598 | 5.2878 | 3281.4934 |
| WOA | 3.5355 | 0.7000 | 17.0000 | 7.8000 | 7.8464 | 3.6251 | 5.3290 | 3126.6302 |
| SCA | 3.6000 | 0.7000 | 17.0000 | 7.3000 | 8.1063 | 3.4789 | 5.3751 | 3134.3656 |
| HHO | 3.5000 | 0.7000 | 17.0000 | 7.6652 | 7.9002 | 3.5581 | 5.3308 | 3086.9231 |
| SCSO | 3.5015 | 0.7000 | 17.0001 | 7.6361 | 7.8095 | 3.3526 | 5.2888 | 3002.0753 |
| DBO | 3.6000 | 0.7000 | 17.0000 | 7.3000 | 8.3000 | 3.3502 | 5.2869 | 3046.7137 |
| MSFDBO | 3.5000 | 0.7000 | 17.0000 | 7.3000 | 7.7153 | 3.3502 | 5.2867 | 2994.4711 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R.; Zhou, T.; Yu, B.; Li, Z.; Ma, L.; Zhang, Y. Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion. Electronics 2025, 14, 197. https://doi.org/10.3390/electronics14010197
Fang R, Zhou T, Yu B, Li Z, Ma L, Zhang Y. Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion. Electronics. 2025; 14(1):197. https://doi.org/10.3390/electronics14010197
Chicago/Turabian StyleFang, Rencheng, Tao Zhou, Baohua Yu, Zhigang Li, Long Ma, and Yongcai Zhang. 2025. "Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion" Electronics 14, no. 1: 197. https://doi.org/10.3390/electronics14010197
APA StyleFang, R., Zhou, T., Yu, B., Li, Z., Ma, L., & Zhang, Y. (2025). Dung Beetle Optimization Algorithm Based on Improved Multi-Strategy Fusion. Electronics, 14(1), 197. https://doi.org/10.3390/electronics14010197




