1. Introduction
Convolutional neural networks (CNNs) have been successfully applied in a wide range of cognitive tasks such as image recognition and classification, natural language processing, object detection, voice recognition, and autonomous driving [
1,
2]. This is mainly due to CNN’s remarkable accuracy and performance. However, CNNs require significant computations and memory resources. Recent improvements in CNN accuracy have been achieved by over-parameterized models, which present a significant challenge when being deployed in resource-constrained applications [
1,
3].
The hardware implementation of CNNs has been studied and optimized in recent years. One motivation to implement CNN in hardware is to achieve the desired performance (i.e., in terms of high-accuracy and real-time response) with the least power and energy consumption. In fact, it is currently trendy to see CNN designs being implemented in digital devices, embedded systems, and edge devices; which are resource constrained [
4,
5]. However, with such CNN implementations on resource-constrained devices (RCDs) and as the number of neurons grows, the area, energy, and delay grow quadratically, and memory traffic increases significantly. Thus, realizing large CNNs in hardware is a significant challenge [
6].
RCDs, which are typically found in embedded systems and edge devices, have limited resources that include small memory (RAM and ROM) to execute the applications and store data/parameters, low data processing power, limited battery capacity, and small physical area [
7]. Consequently, designing CNNs for RCDs is challenging and requires a delicate balance between resources and model accuracy, and even unaffordable for larger CNN models [
4,
8,
9].
While it is important to streamline the CNN design, CNN layers have different design challenges and present a unique hurdle to the optimum method(s) that reduces CNNs complexity. On one hand, the convolutional layers are computation-centric as they contain a high volume of computations; and on the other hand, the fully connected (FC) layers are memory-centric and require large memory bandwidth. An efficient optimization method should focus on simplifying the computations and the memory system [
5].
Several optimization methods have been proposed to reduce the design complexity and simplify the implementation of CNNs. One such method is quantization, which involves replacing real-valued numbers with low-bit (i.e., low-precision) fixed-point integers. By reducing the bit width of parameters (i.e., weights and biases) and the outputs from each layer (activations), quantization unlocks speed gains, lower power consumption, and smaller memory footprints.
Numerous research has reported quantized CNNs using 32-, 16- and 8-bits [
5,
6,
10,
11,
12,
13,
14,
15]. Additionally, other research work proposed aggressive quantization techniques that constrain the parameters to as low as two bits (e.g., ternary networks) or even one bit (e.g., binarized networks). Aggressive quantization, however, potentially degrades CNN accuracy [
16]. To compensate for the accuracy drop, the number of neurons is increased, which, unfortunately, could offset quantization benefits [
17].
Another proposed method (to reduce CNN design complexity) involves approximating low-rank filters in pre-trained networks. For example, Zhang et al. [
18] proposed an approach that enables an asymmetric reconstruction, which reduces the rapidly accumulated error when multiple layers are approximated. Other methods restrict filters with low-rank constraints during the training phase. For example, the low-rank tensor decomposition proposed in [
19] removes the redundancy in the weights of a pre-trained neural network (NN) and reduces the number of parameters significantly.
Another proposed optimization method involves employing smaller and more efficient CNN architectures. One idea involves replacing
convolutional filters with
size to reduce the model complexity, as demonstrated in GoogLeNet [
20] and SqueezeNet [
21]. A second idea involves utilizing residual connections to relieve the gradient vanishing problem during deep network training, such as the design in ResNet [
22]. A third idea involves generalizing the group convolution and the depthwise separable convolution, such as the design in ShuffleNet [
23]. In fact, the utilized depthwise separable convolutions, as in Xception [
24] and MobileNet [
25], have been proved to be effective.
Other methods to reduce CNN complexity involve pruning and structural sparsity. Pruning reduces model size by removing redundant weights [
26]. It is typically achieved by setting some weights, neurons, or connections in the NN model to zero or near-zero values [
27]. Han et al. [
28] discussed pruning to reduce the memory requirement of CNNs with no loss of accuracy. Additionally, the research works in [
29,
30] employ structural sparsity for more energy-efficient compression. Further, singular value decomposition (SVD) is used, as in [
5], to reduce memory footprint.
Several technologies are used to realize CNN implementation, including CPUs, GPUs, FPGAs, or ASIC. However, FPGAs are believed to present attractive implementations compared to other technologies for several reasons [
1,
2,
31]:
FPGAs are more energy efficient compared with GPUs and CPUs.
FPGAs have parallel computing resources with high performance.
Reconfigurability in FPGAs provides significant flexibility to explore CNNs’ design options and alternatives.
FPGAs provide high security [
31].
While deep neural networks (DNNs) continue to be a major research focus, there is a growing enthusiasm for smaller and lightweight NNs. Future FPGA-based NN acceleration will be embedded, lightweight, and portable [
1]. Additionally, the lightweight CNN quantization method extends further to optimize DNNs. By strategically applying it to specific layers, we can minimize quantization errors and efficiently implement the DNN using fewer FPGAs, leading to significant power and energy savings. Hence, it is important to focus FPGA-based research on lightweight CNNs, which are targeted for embedded designs and applications such as AI-of-Things (AIoT) [
1] and are also beneficial for DNNs.
The main objective of this research is to develop an FPGA-based quantization method to reduce CNN hardware design, and to estimate-and-model the enhancements in area, power, and energy. This will enable implementing CNNs in RCDs (e.g., FPGA devices). Additionally, the derived models will facilitate the quick and easy evaluation of DNN design choices. Our research successfully addressed the above-stated objective by delivering the following key contributions.
Designed and validated an algorithm to quantize the full CNN model. The novelty of the algorithm is that it combines quantization-aware training (QAT) and post-training quantization techniques (PQT), and it provides full model quantization (weights and activations) without increasing the number of neurons.
Explored, designed, and verified multiple hardware designs of the quantized CNN; each design with different quantization bits to fit the FPGA capacity and resources.
Performed compilation and synthesis of the hardware designs in the FPGA device, which is Altera Stratix IV.
Analyzed and modeled the resources, timing, throughput, power, and energy results.
Estimated the performance metrics for a sample DNN design using the derived models.
The rest of the paper is organized as follows.
Section 2 summarizes the latest research work in CNN quantization.
Section 3 presents the research methodology and design flow.
Section 4 explains the proposed algorithm in detail.
Section 5 discusses the FPGA implementation of the quantized CNN model.
Section 6 summarizes the area, timing, throughput, power, and energy results of FPGA implementations.
Section 7 discusses modeling metrics and applying them to DNN.
Section 8 discusses concluding remarks and future research opportunities.
2. Related Work
In general, examining research work in CNN quantization, researchers have exercised two design options when quantizing a CNN model:
Quantization of parameters only versus quantization of the entire model (i.e., parameters and activations) [
26];
QAT versus PTQ. Generally speaking, with the same bit precision, QAT achieves higher accuracy [
32].
It is noteworthy to mention that the approach of “quantization of parameters only” somewhat strikes a balance between “no quantization”, which has expensive computations and high memory bandwidth, and “quantization of the entire model” that unleashes the full potential of quantization, but tends to be harder and requires careful implementation due to potential higher accuracy loss.
Additionally, we should mention that QAT involves a cyclical process of quantization and retraining to optimize a pre-trained CNN for quantized representations. The key steps, which are repeated until convergence, are as follows: quantizing the weights, forward pass using floating point activations, and lastly, back-propagation pass using floating point gradient. Because of the weight quantization, it is necessary to approximate the gradients using (for example) straight-through estimator (STE) [
33].
From the implementation point of view, the reader should notice that high accuracy QAT requires a long training time; however, it is justifiable for the models that will be deployed for long periods of time. On the other hand, PTQ quantizes a pre-trained NN without any extra training, which is helpful when training data are not sufficient or unavailable, and quickly provides quantized NN. In both QAT and PTQ, sometimes quantization can be fine-tuned with a small set of calibration data [
32].
Several quantization-based frameworks and tools were developed to automate and optimize NN implementation on FPGAs and ASICs [
34]. Examples include the Xilinx FINN [
35] and hls4ml [
36] frameworks. On one hand, the FINN framework leverages Brevitas [
37] for quantization-aware training. A research example, which explored the trade-off between accuracy and resource usage on FPGAs using such a framework is Ducasse et al. [
34]. This research implemented quantized NNs (with less than 8 bits) in FPGAs while maintaining 88% accuracy. On the other hand, hls4ml is an open-source framework that combines software and hardware design to translate NNs to FPGAs and ASICs. Its workflow integrates network optimization techniques, allowing for low-power implementations. While such frameworks are valuable for exploring efficient hardware solutions, it is important to consider their limitations such as customization and troubleshooting.
Researchers also use algorithm hardware co-design technique to automatically develop efficient NNs and hardware, which considers both software and hardware together during the design and quantization process. For example, Fan et al. [
38] proposed a three-phase co-design framework, which decouples training from the design space exploration and adopts the Gaussian process to predict accuracy and power consumption. In comparison with the manually-designed ResNet101, InceptionV2, and MobileNetV2, the authors’ proposed framework can achieve up to 5% higher accuracy with up to
speed up on the ImageNet dataset. Additionally, Wang et al. [
39] proposed a hardware/software co-design methodology targeting CPU+FPGA-based heterogeneous platforms. The authors’ proposed methodology includes optimization (i.e., hardware-aware NN pruning, clustering and quantization), and an end-to-end design space exploration flow. Experimental results show that the authors’ work can achieve a peak throughput of 2.13 TOPS. Moreover, Haris et al. [
40] proposed SECDA, a hardware/software co-design methodology, which combines the system’s simulation with FPGA execution. SECDA achieved an average performance speedup across models of up to
with a
reduction in energy consumption over CPU-only inference. Overall, we believe that a major challenge in algorithm-hardware co-design is the high cost of training NNs and the lengthy process of implementing hardware. This makes it impractical to explore the vast range of potential NN architectures and hardware designs [
27,
38].
The rest of this section discusses research in “parameter quantization only” or simply to be called “parameter quantization”, and “entire model quantization”.
2.1. Parameter Quantization
Compared with quantization of the entire NN model, parameter quantization is relatively easier in implementation and demonstrates high accuracy results [
9,
41,
42]. For example, Holt et al. [
43] performed training with fixed point 16-bit weights and 8-bit inputs. While parameter quantization reduces model size with minimal accuracy loss (i.e., by a few percent drop) for 32-bit and 16-bit precision, some researchers explore even lower bit widths, accepting a larger accuracy drop for further efficiency gains. For example, the binarized NN (BNN) approach constrains the weights to one bit, which can represent two possible values (e.g.,
or 1). This approach simplifies the hardware by replacing multiply-accumulate units with accumulate units [
44]. There are Ternary networks [
9], which increase weight bit width to 2 bits representing three values (e.g.,
). The additional bit improves accuracy compared with BNN [
9].
There is also a three-bit quantization of parameters examined as well. For example, Park et al. [
45] developed an FPGA-based fixed-point NN using only on-chip memory, by quantizing weights to 3 bits (for input and hidden layers) and 8 bits (for output layer). The authors utilized QAT, where the training is performed in three steps: floating-point training, optimal uniform quantization, and retraining with fixed-point weights. The FPGA implementation is tested for the Modified National Institute of Standards and Technology (MNIST) handwritten digit recognition benchmark and a phoneme recognition task on Texas Instruments/Massachusetts Institute of Technology (TIMIT) corpus. The implemented FPGA shows a throughput that is about one-quarter of a GPU system, but consumes 2˜4% of the energy consumption of the GPU system, resulting in over 10 times the power efficiency. One issue of the design is that the base design (with floating point prior to quantization) has an error rate up to 27.81%, which is significant and potentially affects the quantized design results.
Zhou et al. [
42] proposed an incremental network quantization (INQ) method to quantize model weights to either zero value or power of two values. The method consists of three operations: weight partition, group-wise quantization, and re-training. Weights in each layer are divided into two groups. The first group is from a low-precision base and quantized by a variable-length encoding method. The second group is retrained to compensate for the accuracy loss from the quantization. The operations are repeated until all the weights are converted into low-precision ones.
Abdelouahab et al. [
17] presented a method to optimize DSP utilization in FPGAs for CNN implementations while maintaining high accuracy. The method is based on exploring design space by varying the neuron count in each layer and the precision of weights and biases. The study concluded that classification accuracy increases with the number of neurons and with numerical precision.
2.2. Quantize the Entire Model: Weights and Activations
Despite the complexities of full model quantization, numerous works implemented, examined, and implemented this method. For example, the 16-bit quantization Q6.10 (6-bit integer and 10-bit fraction) is used as in [
6,
46], and quantization Q8.8 (8-bit integer and 8-bit fraction) is used as in [
47]. Additionally, as in [
48], 32-bit quantization is used during training while 16-bit is used in the inference phase.
Courbariaux et al. [
49] trained a set of CNNs on three benchmark datasets, with three formats: floating point, fixed point, and dynamic fixed point. The research concluded that the minimum bit-width for the activations is 10-bit and 12-bit for parameters. Below these bit-widths, the error rate rises significantly.
Vanhoucke et al. [
50] performed the training using a single precision floating point, while evaluation was performed with 8-bit weights and activations. When compared with floating-point, the 8-bit arithmetic provided an over two times speedup without having a loss of accuracy when being applied on speech recognition design.
Qiu et al. [
5] presented an FPGA design for large-scale CNN. The proposed method combines SVD and quantization. The authors’ implementation of the method consists of two phases: weight quantization and data quantization. The method reduces fraction bits in weights and activations while minimizing accuracy loss. Compared with 16-bit quantization, 8/4-bit quantizations halve the storage space for intermediate data and reduce three-fourths of the memory footprint. However, when 8/4-bit quantizations are used, a 0.4% accuracy loss is introduced by data quantization for the VGG16 model. One issue of this work is that the accuracy of the base design (i.e., VGG16 with floating point) is 68.1%. As such, the reported accuracy loss might not reflect the loss in the quantization accuracy.
Chen et al. [
6] presented a detailed study in hardware accelerators for small and large NNs. For small NNs, all neurons and synapses are realized in hardware. Small designs and short interconnects result in high-speed and low-energy implementation. The study shows that, as the number of neurons grow, the area, energy, and delay grow quadratically, which makes realizing large NNs in hardware very challenging. Another issue for large-scale NNs is the high memory traffic. Hence, the hardware implementation for large-scale NNs realizes a fraction of neurons and synapses. For hardware implementation, the research suggested the following techniques: tiling, pipelining, buffers, and DMAs. It also replaced the floating-point computations with 16 fixed-point computations (6 bits for the integer part, 10 bits for the fractional part), which reduces the power and area and slightly increases the error rate by 0.26%. The CNN was trained and tested on the standard MNIST machine-learning benchmark [
51], and the CNN implementation leverages a 65 nm process technology.
2.3. Discussion
In light of the above research, we believe it is important to highlight the following points.
Parameter quantization reduces CNN complexity efficiently, but misses out on potential reductions from activation quantization. Full model quantization targets both computation and memory but requires careful accuracy consideration.
Another issue is the accuracy of the base design (i.e., with floating point and prior to quantization). In some research works, the accuracy of the base design should have been better, which indicates issues with model training [
5,
45].
Some of the quantization methods add additional neuron operations to mitigate the accuracy drop, which in turn increases model complexity [
17].
Large NN implementation techniques (e.g., tiling and pipelining) are different from small NNs [
6].
Surprisingly, most research on quantized designs fail to model key performance metrics like power and energy.
Our focus in this research is to present a comprehensive approach to the quantization method. It includes:
Proposing a full-model quantization algorithm without requiring extra neurons;
Modeling the impact of quantization on resources (e.g., energy, power, and area);
It should scale up to DNNs.
To the best of our knowledge, our literature review found no prior work that encompassed such a comprehensive approach.
3. Research Methodology
In this section, we discuss our research methodology, which has a similar flow to those used in other similar research works, including [
52,
53,
54].
Figure 1 outlines the flow steps, which mainly consist of algorithm development and simulations, hardware design, and performance evaluation. The following subsections provide a detailed explanation of each step in
Figure 1.
3.1. Research Objectives
Clear research objectives should be set early in the project because they direct the activities and tasks of the research. One objective of this research is to develop a method to reduce the CNN hardware design. Quantization was chosen because it is effective and powerful. Another objective is to devise an algorithm that can be applied to CNNs. We are aware of numerous research works reporting the quantization of a wide range of bits; however, it is important to present an algorithm that could be applied to any CNN. Another objective is to understand the impact of quantization on resources, timing, throughput, power, and energy, which is achieved through modeling those metrics. Such understanding would enable implementing CNNs on RCDs (e.g., FPGA devices), as well as on DNNs.
Finally, determining the optimal bit-width for a specific CNN while maintaining accuracy is a common objective, and extensive research has been conducted on this aim. Instead, we challenge this approach by offering a more versatile method (i.e., a quantization algorithm and modeling of performance metrics) that can be seamlessly applied to any NN and DNN. This empowers broader applicability and adaptability.
3.2. Selection of CNN
The selection of a CNN architecture is a necessary step for conducting experiments and validating the design and implementation of an algorithm. Numerous CNNs have been proposed in the literature, with varying levels of complexity ranging from small models to deep architectures [
55]. In this work, the following criteria are considered desirable for the selection of the CNN model:
The model must fit in the FPGA device used in this research (i.e., Altera® Stratix® IV), and hence should be a small (i.e., lightweight) model;
The model should be known to the research community.
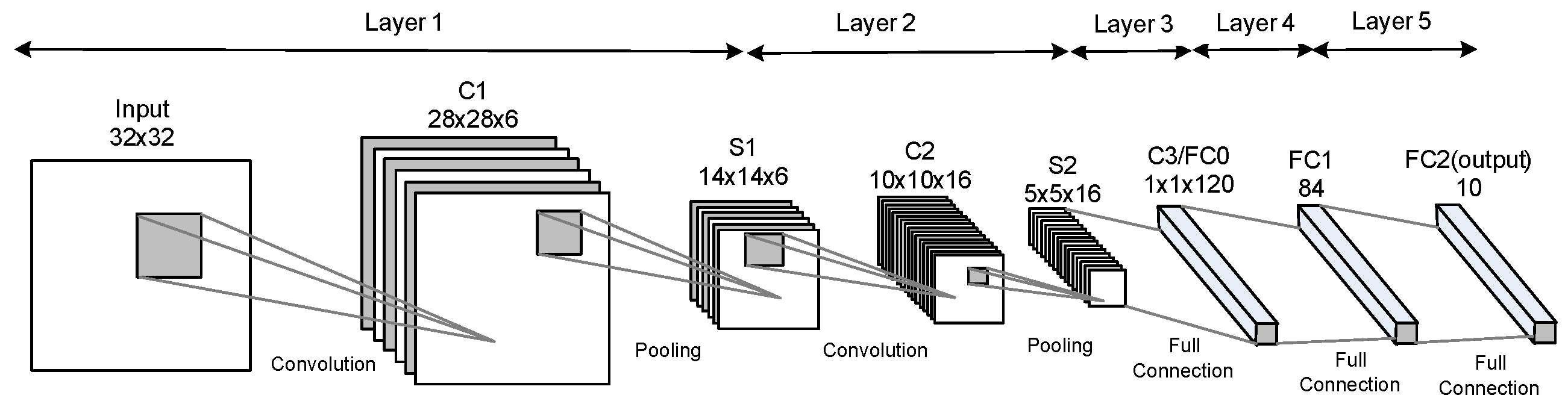
We decided to select the 5-layers LeNet captured in
Figure 2, which is designed for MNIST handwritten digits recognition [
51] since it is simple, lightweight, and considered a representative CNN [
1]. Also, LeNet CNN is well known and studied by numerous researchers in many studies such as the ones in [
56,
57,
58].
LeNet consists of convolutional, pooling (i.e., subsampling), and fully connected layers. It accepts
digit image and produces ten outputs to classify the input digit.
Table 1 describes the layers shown in
Figure 2. The third column in
Table 1 displays the feature map size, which is the size of the layer output. The feature map size is expressed as: width (
W) × length (
L) × depth (
D) for a convolutional layer output and as depth (
D) for an FC layer. The last column lists the number of parameters (weights and biases) required for the layer computations. The total number of parameters for the CNN model is 61,470 parameters. There are minor variations of LeNet in the literature (e.g., in terms of the activation functions). This research utilizes activation functions in the following way:
The rectified linear unit (ReLU) activation function in C1 and C2;
The sigmoid activation function in C3 and FC1;
Softmax in the output layer.
For the third layer (i.e., C3), the size of its input feature map is
, and its filter size is
(i.e.,
). In this case, the convolutional layer converges to an FC layer. This explains why this layer appears in both the convolutional and the FC entry (i.e., C3/FC0) in the 7th row in
Table 1. While LeNet is referred to as 5 layers, some researchers consider Pooling (and even non-linear functions) as a separate layer. If Pooling is counted as a separate layer, then LeNet is considered 7 layers [
2].
Table 1 follows the latter convention.
3.3. Algorithm Development and Simulations
This step encompasses the entire process from scratch, including design, debugging, and simulation of the proposed algorithm. Notably, we opted for a completely custom-designed CNN architecture (rather than utilizing pre-built libraries). This approach grants us maximum control over the network’s structure, enabling a more thorough debugging process. There are several programs written in Python to facilitate this step which are as follows.
The primary program implements the LeNet model and is capable of quantizing weights and/or activations of any layer with the desired bit width. This program is trained and tested with grayscale images of size
for the 10 digits (i.e., 0,1,…,9). The training and testing data are chosen from the MNIST dataset [
59]. The training parameters and hyper-parameters are listed in
Table 2. One important constraint for our algorithm, which is discussed in
Section 4, is to maintain the original architecture of the LeNet, which means it is not possible to add layers or neurons to the quantized CNN.
Another program was written to generate the files containing quantized weights to be used in the hardware design. The weights must be expressed in binary or hexadecimal format.
To debug and verify the hardware design, one more program was written to compare the model layer outputs with the hardware results and to determine the mismatching layer.
3.4. Hardware Design
In this research, the quantized CNN is implemented in hardware using a hardware description language (HDL), which is Verilog
TM. Our HDL design includes the CNN HDL implementation and the testbench to validate the results. The simulations are performed using the ModelSim simulator [
60]. The HDL design incorporates the quantized parameters computed by our algorithm, which is verified at the end based on the testbench simulations.
During the initial design phase, findings from HDL design feasibility studies and simulation trials are used to refine specific algorithm parameters (detailed in
Section 4).
Figure 1 illustrates this feedback loop with the dotted arrow from the HDL simulation back to the algorithm development. This iterative process provides valuable insights from hardware design to improve the algorithm development.
Once the design is verified, the HDL is ready to be processed by the FPGA software tools. In this research, the FPGA that we used is the Altera Stratix IV [
61], and we used the Quartus Prime
TM software tool to process the HDL.
Table 3 provides the versions of the FPGA device, tools, and simulator. Technical details regarding the software tool are available in [
62]. Then, the HDL design goes through a flow similar to the flows discussed in published research, such as [
63,
64]. Finally, the compiled design is being analyzed and examined using the following performance metrics, which are thoroughly discussed next: resource utilization, timing, throughput, power, and energy.
3.4.1. Resource Utilization Performance Metric
The resource utilization analysis lists the resources allocated for the design. The resources can be: Look-Up Table (LUT) and DSP blocks. An LUT is the smallest logical construct, which can be configured as a combinational logic or a register. Some versions of Altera FPGAs use Adaptive LUT (ALUT), which is an advanced version of the LUT and have the same number of inputs or outputs. From the documentation, there is no distinction in size between LUTs and ALUTs [
62].
The DSP block implements an
n-bit multiplier:
. Optionally, input
A or input
B data are saved in an
n-bit register; and the output
P result is saved in a
-bit register. To better compare different designs, we have chosen to approximate the resource utilization in terms of the LUTs. Consequently, an
n-bit multiplier is approximated by LUTs as was demonstrated in [
65] and based on Equation (
1):
where
represents an
n-bit multiplier size expressed in number of LUTs.
An
n-bit register size is approximated by Equation (
2):
where
represents an
n-bit register size expressed in number of LUTs.
3.4.2. Timing and Throughput Performance Metrics
The timing analysis computes the design frequency by calculating the longest timing paths. Several trials for the timing runs identified 25 ns as the clock period (i.e., our timing constraint) that ensures reliable operation on the targeted FPGA while avoiding excessive resource consumption during synthesis. Additionally, the timing results are used to compute the implementation throughput as discussed in
Section 6.2.
3.4.3. Power and Energy Performance Metrics
The power analysis, using the Power Analyzer
TM tool [
62], computes the power dissipation of our implementation. The power is computed based on the resources, routing information, and node activity. The node activity is extracted from the waveform files (i.e., value-change dump files), which are produced by the ModelSim during simulating the design. Power Analyzer
TM reports core dynamic power (in mW), which includes four components: DSP block, combinational, register, and clock. Finally, the energy consumed during the processing of an image is the product of the power consumption and the processing time per image.
3.5. Performance Evaluation
During this step, we analyze the results to gain insights into CNN performance and draw key conclusions. This involves parsing and summarizing reports generated by FPGA tools for each performance metric, extracting crucial data points and trends. These summaries not only reveal data behavior but also serve as a foundation for building mathematical models of CNN performance on the target FPGA.
It is important to note that meaningful comparisons with prior work or baselines require implementing the same NN model on the same FPGA device. Comparisons across different models or devices can be misleading due to inherent variations. Therefore, in this research, where feasible quantized designs are limited by FPGA capacity and desired accuracy, we focus on comparing the performance of our implemented CNN designs against each other.
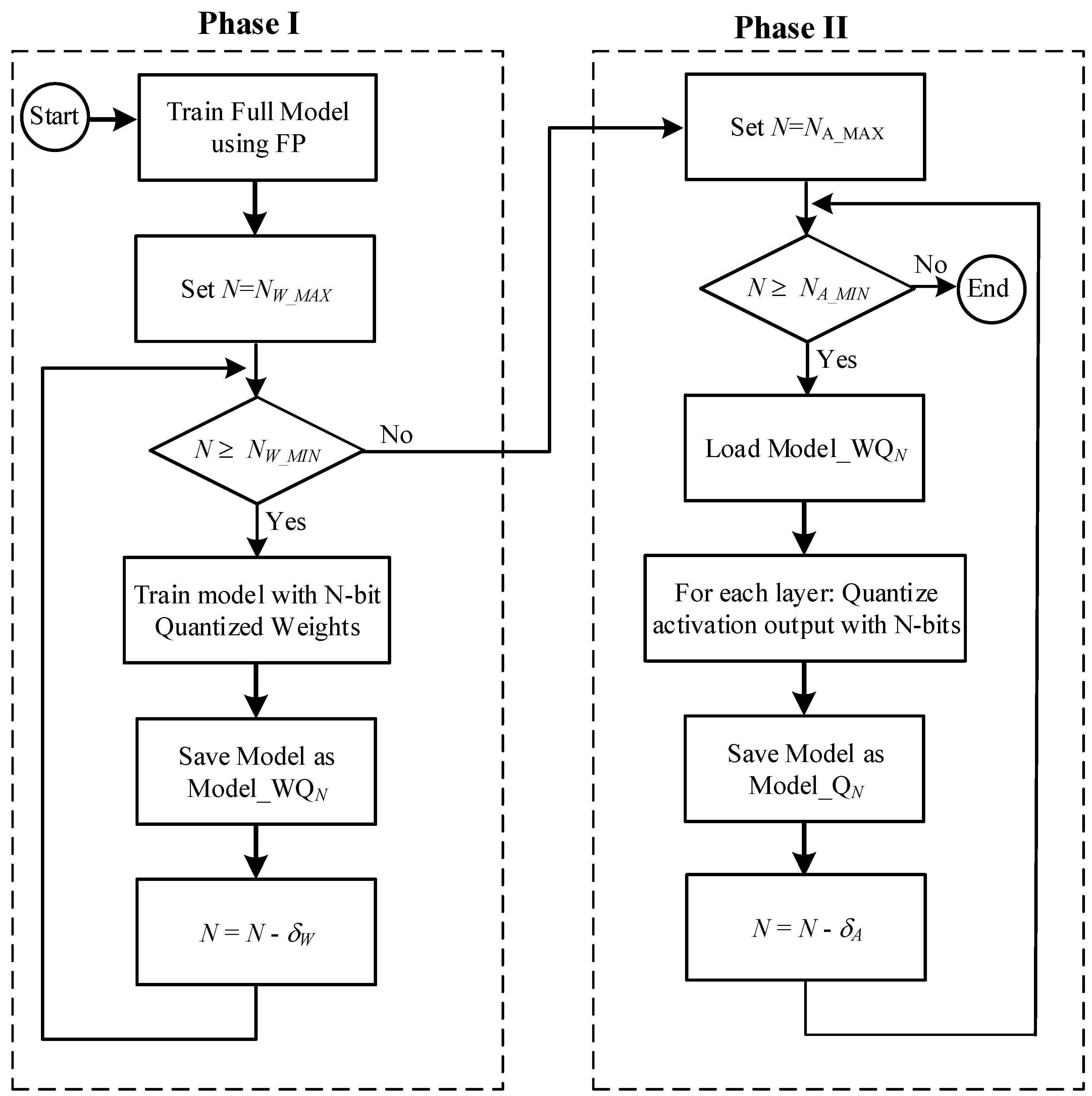
4. The Proposed Algorithm
Figure 3 illustrates the main steps of the proposed algorithm. This algorithm achieves full model quantization without introducing additional neurons. It leverages a hybrid approach, combining quantization training and post-training quantization. The process consists of two phases:
Phase-I: Quantization training, which quantizes weights through dedicated training procedures.
Phase-II: Post-training quantization, which further refines the model by optimally quantizing activations. No retraining is performed after the quantization because our experiments showed that it offered few advantages and could even have drawbacks.
Table 4 explains the algorithm parameters used in the algorithm discussion. Several parameters have recommended values or defined limits, which were established through extensive trial runs and feasibility simulations.
An
N-bit fixed point has
I integer bits and
F fraction bits, where
. For example, the fixed-point signed number
has
,
, and
. The
N-bit signed value of
Z is expressed by Equation (
3):
So, the signed value of Z is equal to
. The maximum and minimum values that can be represented by an
N-bit number are expressed in Equations (
4) and (
5):
For example, an 8-bit representation with , has a and a .
The algorithm phases, shown in
Figure 3, are discussed in the following subsections.
4.1. Phase-I: Quantizing Weights
This phase utilizes a progressive and iterative quantization scheme for modeling the weights. This approach aims to achieve a balance between accuracy preservation and efficient storage/computation by quantizing the weights in a step-by-step manner. Initially, weights are quantized to . In each iteration, the model is trained with the quantized weights. At the end of the iteration, N is decremented by to start a new iteration.
We now present a breakdown of the steps within this phase (as illustrated in
Figure 3):
Model is initially trained with a single precision floating point.
Set N = .
Quantize weights (and biases) to N-bit values, where .
Train the model:
Save quantized weights (and biases) as Model_WQN.
Decrement N by .
Check if iterations are completed:
4.2. Phase-II Quantizing Activations
Building upon Phase-I’s quantized weights, Phase-II refines the model by quantizing activations for specific bit-widths (
N). However, not all quantized models from Phase-I are utilized, resulting in a subset of
N values explored in Phase-II. For activation quantization, we employ an optimized technique called “funnel bit assignment”. The output bits’ selection in this approach works similarly to that of a funnel shifter design [
66]. This optimization leverages a set of the input images, known as “regression images”, to guide the quantization process, ensuring optimal bit allocation.
The following are the steps of Phase-II (as illustrated in
Figure 3):
Set .
Load Model_WQN, which is generated by Phase-I.
For the weights that have small integer part (i.e., integer part < ), assign more bits to the fractional part to achieve better accuracy.
Run regression images through the model.
For each layeri, , perform funnel bit assignment:
- (a)
Compute the maximum and minimum values of activation outputs.
- (b)
Determine the number of bits I required to store the integer part. This is done by computing the number of bits to store the maximum and minimum values of activations: , .
.
.
Set I to the larger value of and .
- (c)
Perform bit assignment:
If : assign I bits to the integer part and F bits to the fraction part, where .
If : assign all N bits to upper bits of the integer part and no bits are assigned to the fraction part. Effectively, and .
- (d)
Run regression images and record accuracy. When computing activation output:
If an activation is above the , then saturate the output to .
If an activation is below the , then saturate the output to .
- (e)
Decrement I by one, repeat steps (c)–(e) to find out the optimum assignment.
Save model as Model_QN.
Decrement N by A.
Check if iterations are completed:
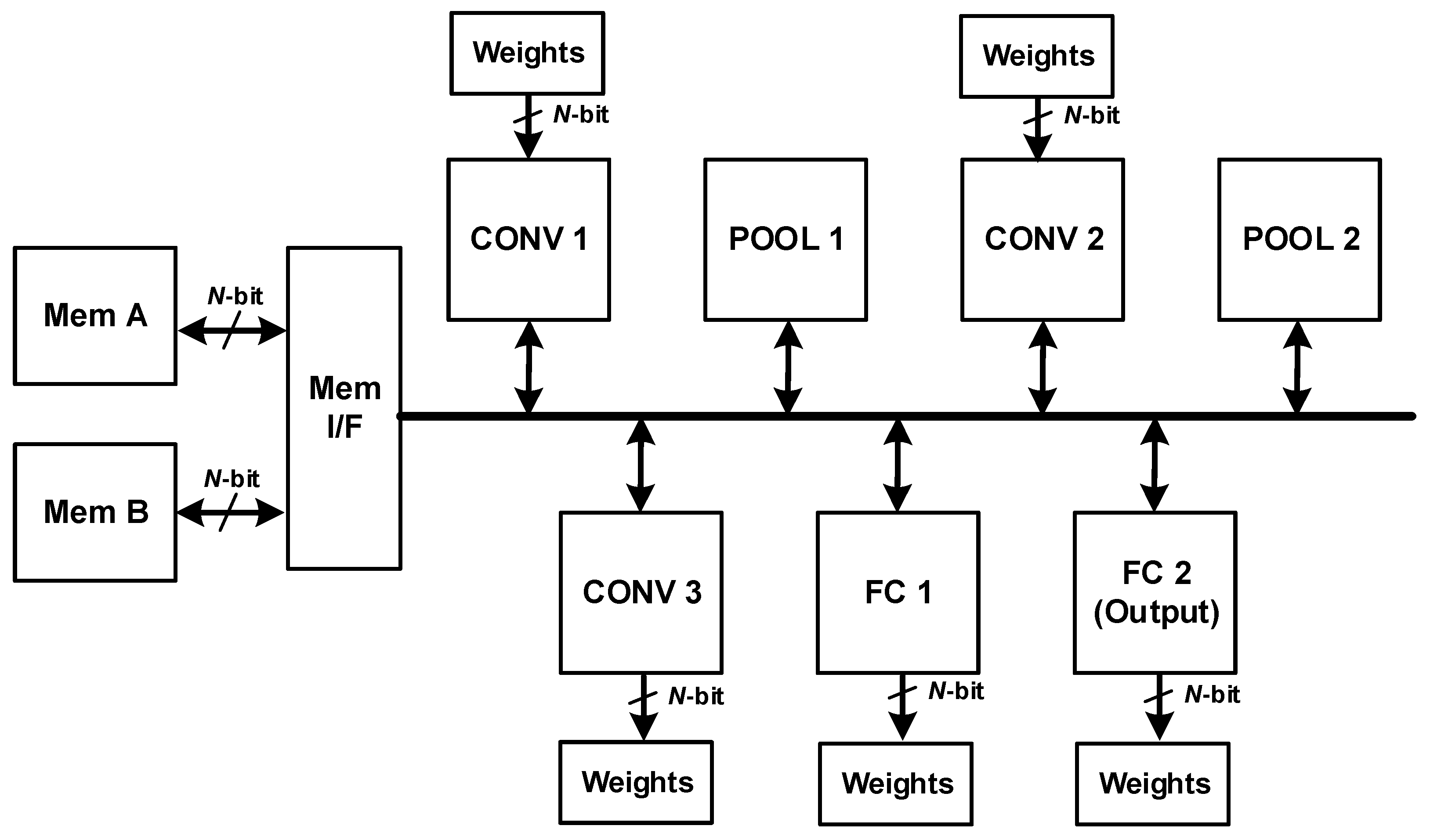
5. Hardware Design
In this section, we discuss the hardware implementation of the LeNet model, which is shown in
Figure 4. The implementation is scalable and can be fine-tuned to any other CNN’s. The hardware design consists of the following main units:
The following subsections present a detailed description of the hardware design and its configurability.
5.1. Design Configurability
Early in the design process, we faced an important issue: how to efficiently design multiple similar units like CONV 1, CONV 2, and CONV 3. Two options were examined: independent units versus configurable units. The option of independent units requires designing each CONV layer as a separate hardware unit. This approach requires individual design and verification efforts for each unit, leading to potentially higher development time. On the other hand, the configurable unit designs a single, configurable unit capable of executing the functionality of all three CONV layers. This option requires careful design for configuration and flexibility but allows for significant design reuse, which reduces development time and effort. We ultimately chose the second option, the configurable unit, to leverage the benefits of design reuse.
Furthermore, to accommodate diverse N-bit implementations, the design incorporates configurability within datapath units, memories, and buses. This allows for hardware customization based on specific bit-width requirements.
5.2. Layer Units
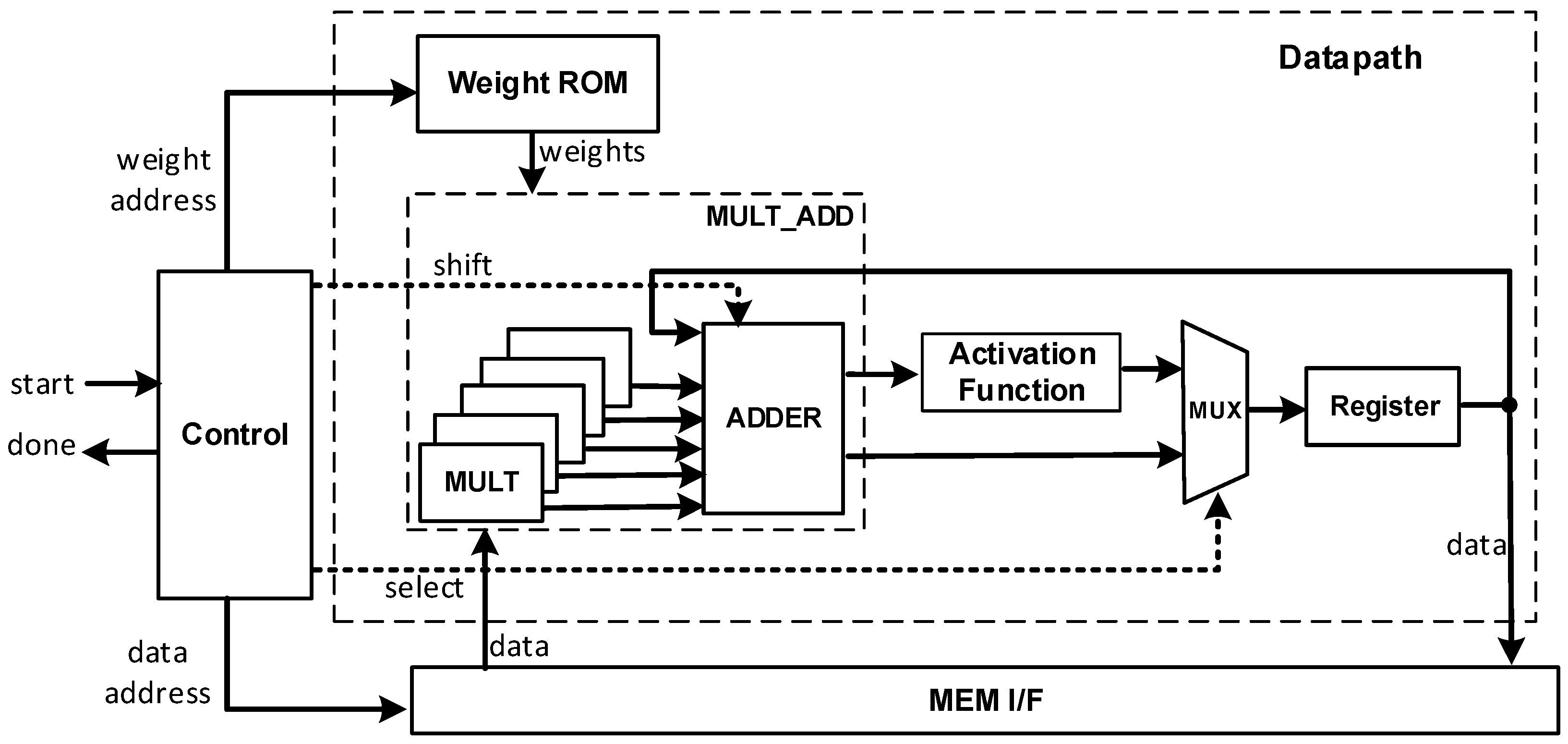
The design of CONV units (i.e., CONV 1, CONV 2, and CONV 3), which is illustrated in
Figure 5 and consists of a control unit and datapath unit. The control unit consists of the finite-state machine (FSM) to manage the activities. It handles the handshakes with other units, generates the control signals for the datapath blocks, and computes addresses for ROM and MEM I/F. The datapath unit consists of a Multiply-Add block, activation block, weight ROM, multiplexer, and register.
The Multiply-Add block computes one column of the 5 × 5 convolution operation, and hence, 5 cycles are required to complete the convolution. The activation function block performs the non-linear activation operation. The multiplexer and register send the registered partial results back to the Multiply-Add block or send the final result to the MEM/IF. The ROM and Mem I/F supply the Multiply-Add block with data and weights/biases.
The initial design exploration examined the ROM implementation options, which are the memory versus constant tables as synthesized by the FPGA tool. Ultimately, it was decided to use the tables due to energy concerns in the RCD (i.e., FPGA) that we considered in this research. The relatively small size of the ROMs and memory energy consumption played key roles in favoring the constant tables. In general, implementing small-sized ROMs using LUT is more energy-efficient compared with RAMs [
67].
The adder block is carefully designed to select the appropriate N-bits out of the addition operation result. This is to support the shifting operation required by the algorithm in Phase-II. The selection is controlled by the shift signal generated by the control unit. For example, if shift = 0, then the selected N-bits are the most significant N-bit of the addition result. If shift = 1, then the selected N-bits are those to the right of the most significant bit of the addition result. Furthermore, to avoid overflow, adder output is saturated to or values in the following cases:
If the addition result > , then the output is set to .
If the addition result < , then the output is set to .
“POOL” and “FC” units have similar overall structure with differences in the implementation details.
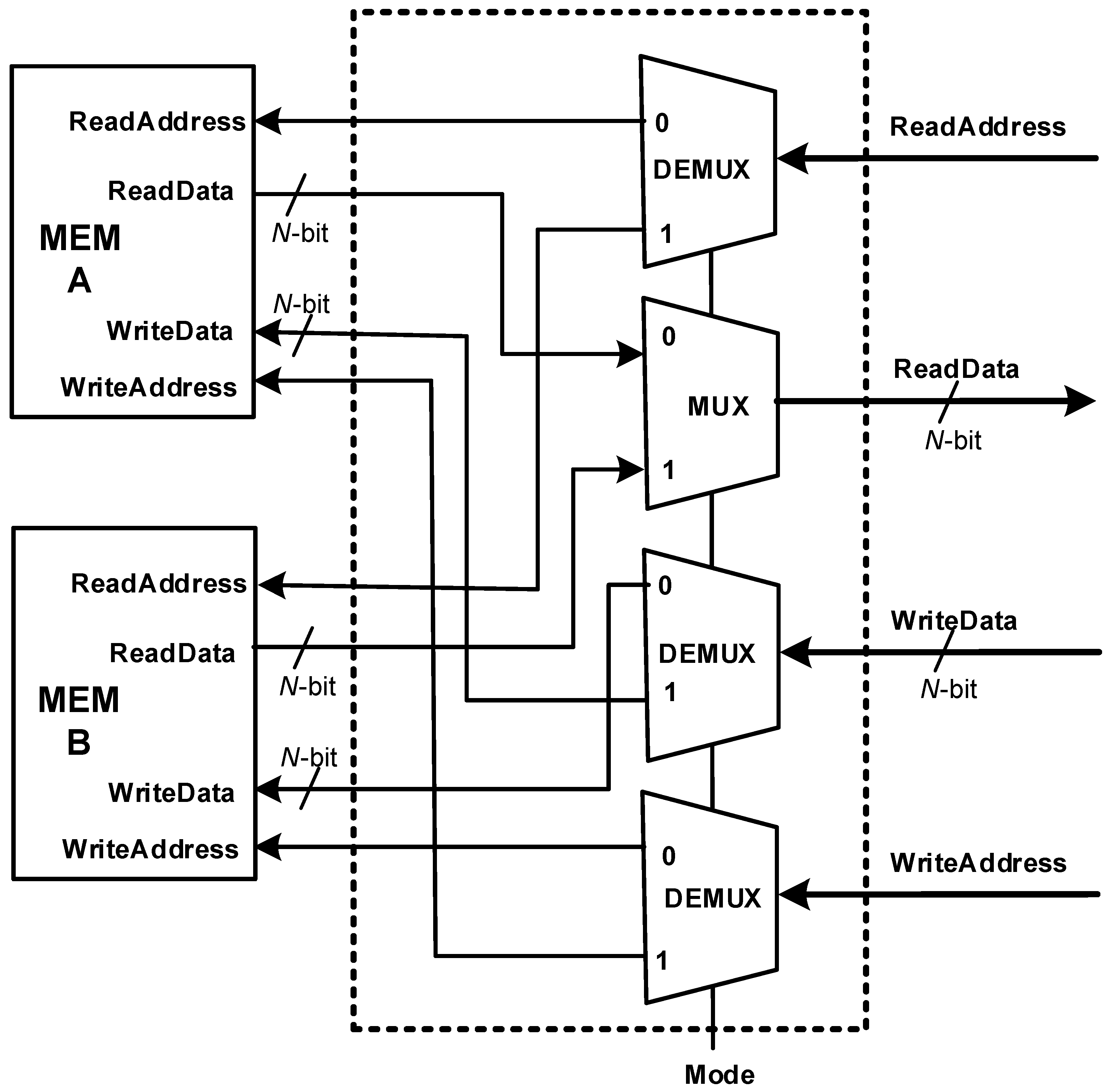
5.3. Memory Units
Figure 6 illustrates the block diagram of the memory interface and data memory. To optimize the design performance, the system leverages two distinct memories (MEM-A and MEM-B) and operates in two dedicated modes, maximizing efficiency and resource utilization. When mode = 0, the design reads from MEM-A and writes to MEM-B; when mode = 1, the design reads from MEM-B and writes to MEM-A. This organization allows the design to perform read/write operations without any interruption or delays. At the start of processing an image, the image is loaded in MEM-A. CONV 1 layer executes with mode = 0; it reads from MEM-A and writes to MEM-B. Then, POOL 1 executes with mode = 1; it reads from MEM-B and writes to MEM-A. This continues for the rest of the layers.
5.4. Execution Flow
The execution of the hardware operations in CNN hardware starts by asserting the “start” signal of CONV 1 unit. When CONV 1 completes its operations, it asserts the “done” signal, which triggers the “start” signal of POOL 1. This continues with the rest of the units, until FC 2 asserts “done”, which is the end of the CNN hardware operations.
Inside each unit, when the “start” signal arrives, it informs the unit to begin processing the data. In each clock, the addresses of data and weights are dispatched to the MEM I/Fs and the ROMs. When data and weight arrive, the Multiply-Add block performs multiplication operations and adds the results.
If the convolution operation is complete, the result is processed by the activation function and saved in the register. The next cycle, data, and its address are dispatched to the MEM I/F. If the convolution operation is in progress, the partial result is saved in the register. In the next cycle, the partial result is sent as input to the addder.
6. Implementation Results
As discussed in
Section 3, the HDL design is processed by the FPGA tools to compile, synthesize, and fit the design on the FPGA. The CNN model was quantized for
32-, 24-, 20-, 16-, 12-, and 8-bit. All quantized models have 1-top accuracy > 98.5%. During the fitting phase, the design with
32-, 24-, and 20-bit did not fit in the FPGA device due to insufficient resources (this can be inferred from the presented results in the last column of
Table 5 as shall be discussed in the following subsection). This truly presented us with a real challenge: to fit the CNN model in an RCD, which is the FPGA in this case. However, we succeeded in fitting the FPGA with
16-, 12-, and 8-bit. The rest of the section provides a summary of the performance metrics.
6.1. Resource Utilization
Table 5 summarizes the resource utilization, as discussed below:
The second and third columns list the LUTs and register utilization.
The fourth column to the seventh columns list the 9-bit, 12-bit, 18-bit, and 36-bit multipliers used in the design.
The eighth column computes the total LUTs, with multipliers estimated as discussed in
Section 3.
The ninth column normalizes the results with respect to the 16-bit design.
The last column lists the logic utilization, which is calculated as the ratio of the used resources to the total available resources. Looking at the trend of the logic utilization versus N in this column clearly shows that it is not possible to fit more than a 16-bit design in the FPGA.
It should be noted that reducing to (and also reducing to ), reduces resources by about 26%. However, reducing N by half (i.e., reducing to ), reduces the design resources by 46%. This means that the design exhibits excellent scalability with respect to N, meaning most of the components or resources reduce proportionally to N with only a minor fixed overhead logic. The overhead logic includes control circuits, which do not scale with N.
6.2. Timing Analysis
Timing analysis is performed based on the timing constraints presented in
Section 3.
Table 6 shows the reported maximum frequencies for different values of
N. The last column in the table normalizes the frequencies with respect to the 16-bit design. The values in
Table 6 reveal a trend: the maximum frequency tends to be slightly higher for smaller values of
N. For instance, the maximum frequency for 8-bit is roughly 2% higher than the one for 16-bit. This observation might be attributed to the efficient scalability of our design, which is a result of its well-considered parametric structure. We should mention that adjusting a few parameters in the HDL code allows for adaptation to various
N-bit designs, with the primary design changes occurring in the datapaths (longest timing paths). These alterations leverage pre-designed and optimized datapath units within the FPGA, leading to minimal timing variations (few logic levels of delay) across different designs. Additionally, the timing analysis helps us compute the throughput (i.e., processed images per second) using Equation (
6):
where:
is the time required to process one image.
represents the total number of clock cycles needed to process a single image.
refers to the duration of one clock cycle.
The throughput results of the 16-, 12-, and 8-bit designs are 328 image/second, 333 image/second, and 334 image/second, respectively.
6.3. Power and Energy Consumption
Table 7 summarizes the power results for our implemented designs of varying
N-bit, where
. Columns two through five show the power dissipation for combinational cells, registers, clock, and DSP blocks, and columns six and seven list the total power and normalized total power with respect to the 16-bit design, respectively.
Looking carefully at
Table 7, the following can be inferred.
The combined power consumption of the clock and registers, known as sequential power, accounts for only 2% of the total power, playing a minor role in overall power consumption. This is primarily because these sequential circuits occupy a smaller area compared to the more power-hungry data path logic.
The power consumption of the DSP blocks is around 5% of the total power. This indicates that the datapath resources like multipliers and adders are well-designed for low power.
The combinational cells are the primary source of power consumption, accounting for approximately 93% of the total power. This is primarily due to the presence of random logic, high routing overhead, and large data selection components like multiplexers and demultiplexers.
The final column of
Table 7 showcases the superior power saving of the 8-bit design, consuming around 41% less power compared to the 16-bit design. While the 12-bit design offers a modest 2% power saving over the 16-bit option. This unexpectedly low power saving in the 12-bit design prompted further investigation. We believe the root cause might be the combined nature of combinational cell power: it includes both block power and routing power. The routing power is the power consumed by the metal wires and the routing resources that connect the logic blocks. It increases with the wire length and complexity of routing paths. Interestingly, the 12-bit design displayed minimal change, even a slight increase in routing power compared to the 16-bit design. We suspect this anomaly might indicate an issue with the software tool’s routing algorithm, potentially favoring byte-aligned sizes (8-bit and 16-bit) and hindering efficiency for non-aligned designs like the 12-bit one. While other factors could contribute to the 12-bit power consumption,
Table 7 clearly demonstrates the scalability of power consumption with a 41% reduction achieved by halving the bit-width from 16 to 8. This power saving is achieved by 41% power reduction in the combinational cell power and 35% reduction in the DSP power.
Now, regarding the energy analysis, it is captured by Equation (
7), which shows how the energy of processing one input (i.e., an image) is being computed:
The analyzed energy results, based on Equation (
7) and presented in
Table 8 convincingly demonstrate the design’s energy scalability. By simply halving the bit-width from 16 to 8 bits, we achieved a significant 42% reduction in energy consumption as shown in the last column of
Table 8. However, the 12-bit design’s energy saving remains modest due to the previously discussed power anomaly.
8. Conclusions and Future Works
In this research, we presented a scalable quantization algorithm to reduce the CNN hardware design and estimate and model the area, power, and energy. The algorithm combines quantization training and post-training quantization techniques and it provides full model quantization without increasing the model complexity.
We implemented LeNet in Altera Stratix® IV FPGA. The algorithm was applied to quantize the model to various bit widths. We succeeded in implementing the model on the FPGA using 16-, 12-, and 8-bit quantizations. Compared to the 16-bit design, the 8-bit design offers improved resource efficiency with a 44% decrease in LUT utilization, and it achieves power and energy reductions of 41% and 42%, respectively.
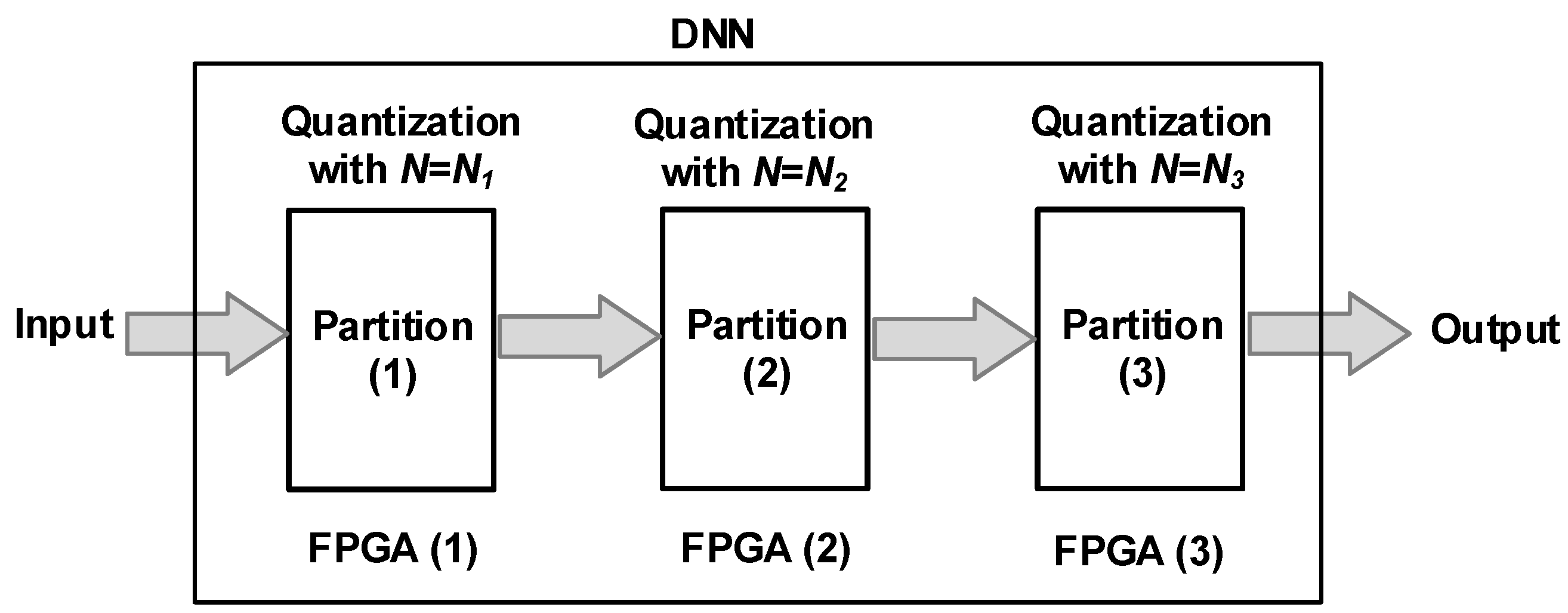
The derived models show significant value in estimating design metrics. This indicates that trading off one quantization bit yields savings of approximately 5.4 K LUTs, 4% logic utilization, 46.9 mW power, and 147 J energy. We also demonstrated the practical use of the derived models to estimate performance metrics for a sample DNN design.
Future efforts could investigate the expansion of the algorithm to handle aggressive quantization, such as 4-bit or even lower. Subsequently, modeling the metrics at these extremely low-precision levels would provide valuable insights into their effects on resources and performance. Moreover, exploring architectural options like pipelining could potentially lead to significant design savings. Also, exploring the feasibility and impact of merging computations from multiple layers into a unified layer deserves further research. Furthermore, future work can explore the impact of alternative quantization techniques and conduct a broader comparison study to optimize NN design efficiency. Finally, applying the algorithm to a recent, representative DNN architecture presents an exciting opportunity to assess its potential for substantial performance improvements. This practical evaluation could solidify the algorithm’s effectiveness and real-world impact.