Characterizing Lossy Dielectric Materials in Shock Physics by Millimeter-Wave Interferometry Using One-Dimensional Convolutional Neural Networks and Nonlinear Optimization
Abstract
:1. Introduction
- A more robust 1D-CNN is proposed to address the inverse problem of lossless/lossy shocked wavefront (ILSW-Net), which embeds information about the complex refractive index of the material at rest to boost the prediction performance. The model’s performance is empirically validated on simulated validation data, demonstrating ability to significantly reduce the prediction error.
- A physics-informed loss between the input signal and the approximated signal computed through the estimation of the velocities and the complex refractive index is introduced. Moreover, this loss is minimized using a nonlinear optimization technique, namely the Nelder–Mead algorithm, enabling estimation even in the case of experimental data in which the measured complex refractive index is unavailable. The results show out that the obtained approximated signal fits better with the original one, and the estimation error is reduced.
2. Proposed Method to Derive the Refractive Index of Lossy Dielectric Materials Subjected to Shock
2.1. Data Preprocessing
2.1.1. Normalization of the Signal Delivered by the Millimeter-Wave Interferometer during a Shock Experiment
2.1.2. Normalization of Output Variables
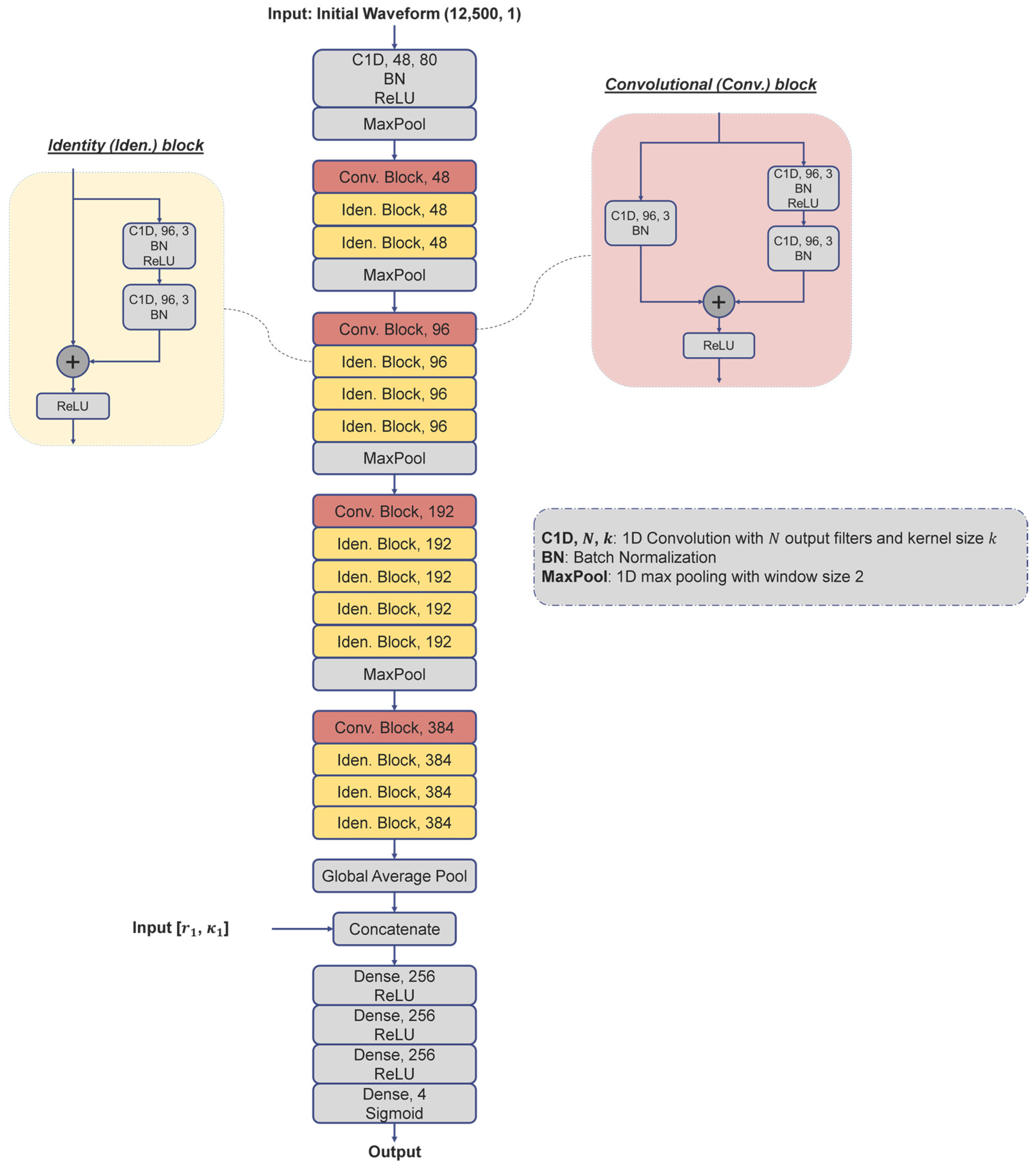
2.2. Architecture of ILSW-Net
2.3. Physics-Informed Loss and the Nelder–Mead Optimization Algorithm
3. Learning Procedure and Hyper-Parameter Setting
3.1. Learning Procedure
3.2. Hyper-Parameter Setting
4. Results and Discussions
4.1. Lossless Material
4.2. Lossy Material
4.2.1. Validation on Simulated Data
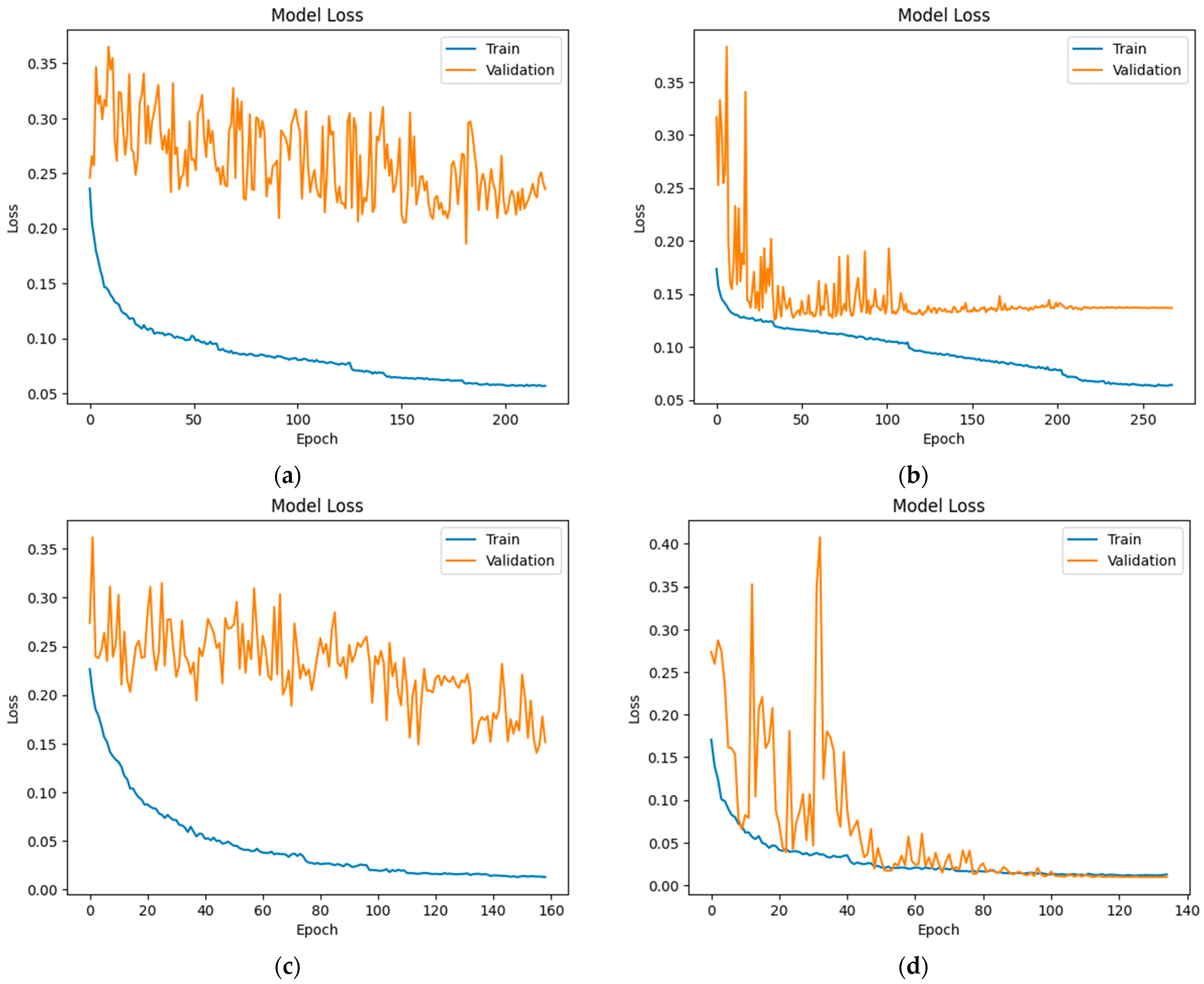
- ILSW-Net with only the waveform as input (one-input ILSW-Net);
- One-input ILSW-Net with the data normalization process;
- ILSW-Net with two inputs, namely the waveform and the complex refractive index () (two-input ILSW-Net);
- Two-input ILSW-Net with the data normalization process.
4.2.2. Application to Experimental Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luther, G.G.; Warthen, B.J. Microwave interferometry to elucidate shock properties. AIP Conf. Proc. 1994, 309, 1755–1757. [Google Scholar]
- Warthen, B.; Luther, G. A Microwave Interferometer to Measure Transient Properties; Technical Report; Los Alamos National Laboratory (LANL): Los Alamos, NM, USA, 1994. [Google Scholar]
- Hawke, R.S.; Mitchell, A.C.; Keeler, R.N. Microwave measurement of permittivity and electrical conductivity in shock compressed liquids. Rev. Sci. Instrum. 1969, 40, 632–636. [Google Scholar] [CrossRef]
- Glancy, B.C.; Krall, A.D. Microwave Interferometric Measurements of Particle and Wave Velocities in Porous Media; Technical Report; Naval Surface Warfare Center: Dahlgren, VA, USA, 1990. [Google Scholar]
- Krall, A.D.; Glancy, B.C.; Sandusky, H.W. Microwave interferometry of shock wave. I. unreacting porous media. J. Appl. Phys. 1993, 74, 6322–6327. [Google Scholar] [CrossRef]
- Glancy, B.C.; Sandusky, H.W.; Krall, A.D. Microwave interferometry of shock wave. II. reacting porous media. J. Appl. Phys. 1993, 74, 6328–6334. [Google Scholar] [CrossRef]
- Rougier, B.; Aubert, H.; Lefrançois, A.; Barbarin, Y.; Luc, J.; Osmont, A. Reflection of Electromagnetic Waves on Moving Interfaces for Analyzing Shock Phenomenon in Solids. RadioScience 2018, 53, 888–894. [Google Scholar] [CrossRef]
- Rougier, B.; Lefrançois, A.; Chuzeville, V.; Poeuf, S.; Aubert, H. Static and Dynamic Permittivity Measurement of High Explosives in the W band to investigate shock and detonation phenomena. Propellants Explos. Pyrotech. 2019, 44, 153–159. [Google Scholar] [CrossRef]
- Mapas, J.; Lefrançois, A.; Aubert, H.; Comte, S.; Barbarin, Y.; Lavayssière, M.; Rougier, B.; Dore, A. Shock Properties Characterization of Dielectric Materials Using Millimeter-Wave Interferometry and Convolutional Neural Networks. Sensors 2023, 23, 4835. [Google Scholar] [CrossRef]
- Kanakov, V.A.; Lupov, S.Y.; Orekhov, Y.I.; Rodionov, A.V. Techniques for retrieval of the boundary displacement data in gas-dynamic experiments using millimeter-waveband radio interferometers. Radiophys. Quantum Electron. 2008, 51, 210–221. [Google Scholar] [CrossRef]
- Bel’skii, V.M.; Mikhailov, A.L.; Rodionov, A.V.; Sedov, A.A. Microwave diagnostics of shockwave and detonation processes. Combust. Explos. Shock. Waves 2011, 47, 639–650. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Solovyev, R.; Vakhrushev, M.; Radionov, A.; Aliev, V.; Shvets, A. Deep Learning Approaches for Understanding Simple Speech Commands. In Proceedings of the 2020 IEEE 40th International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 22–24 April 2020; pp. 6–7. [Google Scholar]
- Takenaga, S.; Ozaki, Y.; Onishi, M. Practical initialization of the Nelder–Mead method for computationally expensive optimization problems. Optim. Lett. 2023, 17, 283–297. [Google Scholar] [CrossRef]
- Davison, L.; Graham, R.A. Shock compression of solids. Phys. Rep. 1979, 55, 255–379. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 1026–1034.
- Kingma, D.; Ba, J. ADAM: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]



| Ground Truth | Minimum Value | Maximum Value |
|---|---|---|
| ) | 1 | 2 |
| ) | 0.001 | 0.2 |
| ) | 1 | 3 |
| ) | 0.001 | 0.2 |
| ) | 2000 m/s | 6000 m/s |
| ) | 200 m/s | 600 m/s |
| Model | |||
|---|---|---|---|
| Model [9] | 2.46 | 3.59 | 0.75 |
| ILSW-Net | 0.68 | 1.37 | 0.5 |
| Method | ||||
|---|---|---|---|---|
| One-input ILSW-Net (baseline) | 14.59 | 16.2 | 13.81 | 70.65 |
| One-input ILSW-Net using norm. step | 9.49 | 9.82 | 9.22 | 136.62 |
| Two-input ILSW-Net | 4.29 | 10.38 | 2.75 | 77.62 |
| Two-input ILSW-Net using norm. step (final model) | 0.69 | 1.28 | 0.79 | 16.95 |
| HDPE | PMMA | |||
|---|---|---|---|---|
| Prediction | Accuracy (%) | Prediction | Accuracy (%) | |
| without refinement | 3616 m/s | 99.06 | 3397 m/s | 89.81 |
| with refinement | 3631 m/s | 99.47 | 3375 m/s | 90.40 |
| without refinement | 589 m/s | 85.57 | 251 m/s | 82.67 |
| with refinement | 565 m/s | 89.20 | 270 m/s | 88.93 |
| without refinement | 1.63 | 1.616 | ||
| with refinement | 1.60 | 1.614 | ||
| without refinement | 0.036 | 0.0232 | ||
| with refinement | 0.031 | 0.0224 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, N.T.; Lefrançois, A.; Aubert, H. Characterizing Lossy Dielectric Materials in Shock Physics by Millimeter-Wave Interferometry Using One-Dimensional Convolutional Neural Networks and Nonlinear Optimization. Electronics 2024, 13, 1664. https://doi.org/10.3390/electronics13091664
Pham NT, Lefrançois A, Aubert H. Characterizing Lossy Dielectric Materials in Shock Physics by Millimeter-Wave Interferometry Using One-Dimensional Convolutional Neural Networks and Nonlinear Optimization. Electronics. 2024; 13(9):1664. https://doi.org/10.3390/electronics13091664
Chicago/Turabian StylePham, Ngoc Tuan, Alexandre Lefrançois, and Hervé Aubert. 2024. "Characterizing Lossy Dielectric Materials in Shock Physics by Millimeter-Wave Interferometry Using One-Dimensional Convolutional Neural Networks and Nonlinear Optimization" Electronics 13, no. 9: 1664. https://doi.org/10.3390/electronics13091664
APA StylePham, N. T., Lefrançois, A., & Aubert, H. (2024). Characterizing Lossy Dielectric Materials in Shock Physics by Millimeter-Wave Interferometry Using One-Dimensional Convolutional Neural Networks and Nonlinear Optimization. Electronics, 13(9), 1664. https://doi.org/10.3390/electronics13091664








