A New Artificial Duroc Pigs Optimization Method Used for the Optimization of Functions
Abstract
1. Introduction to Pig Herd Optimization
- Hybrid Fuzzy-Ant Colony optimization [21].
2. Introduction to Ordered Fuzzy Numbers and Their Application
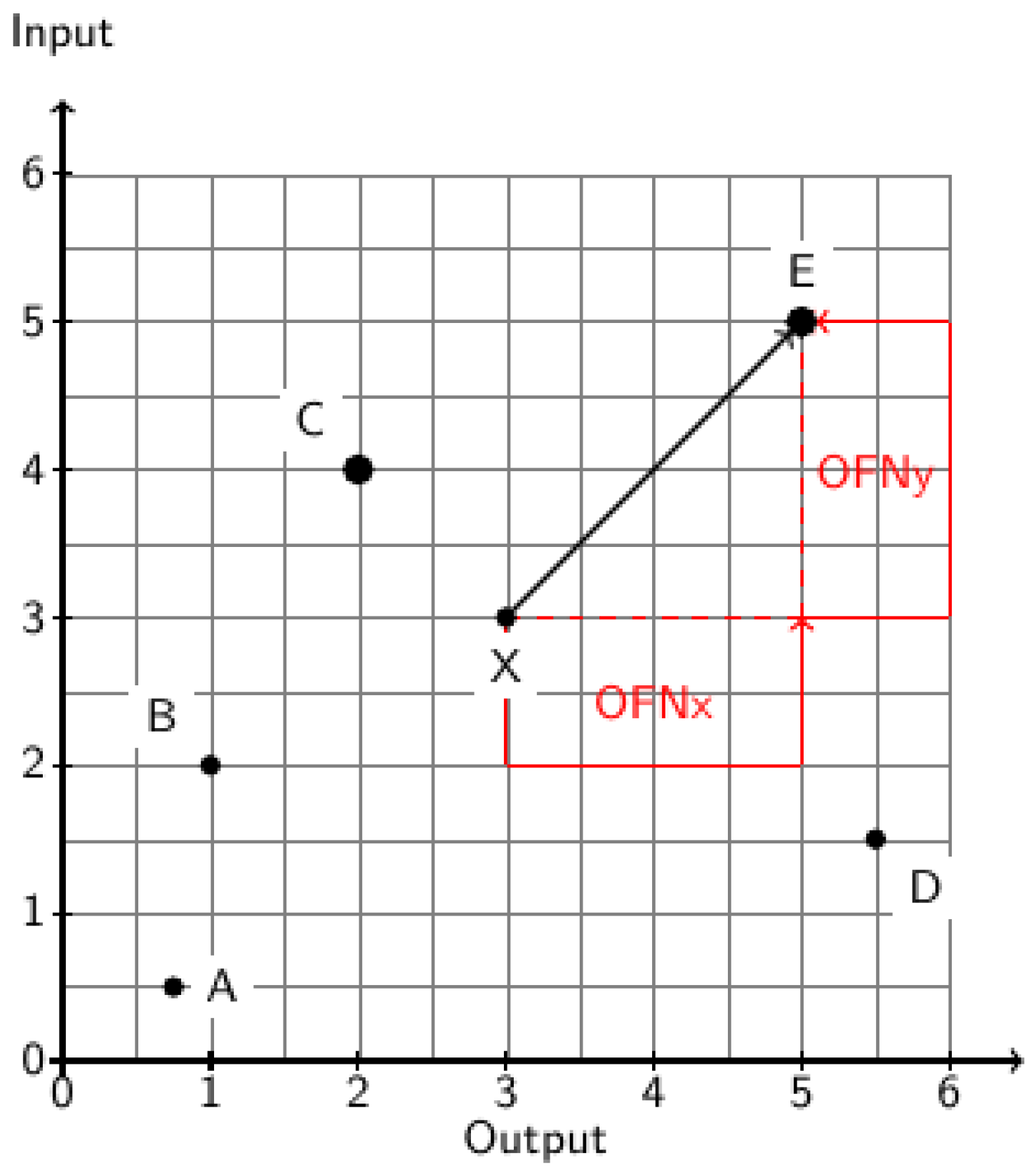
2.1. Concept of Ordered Fuzzy Numbers
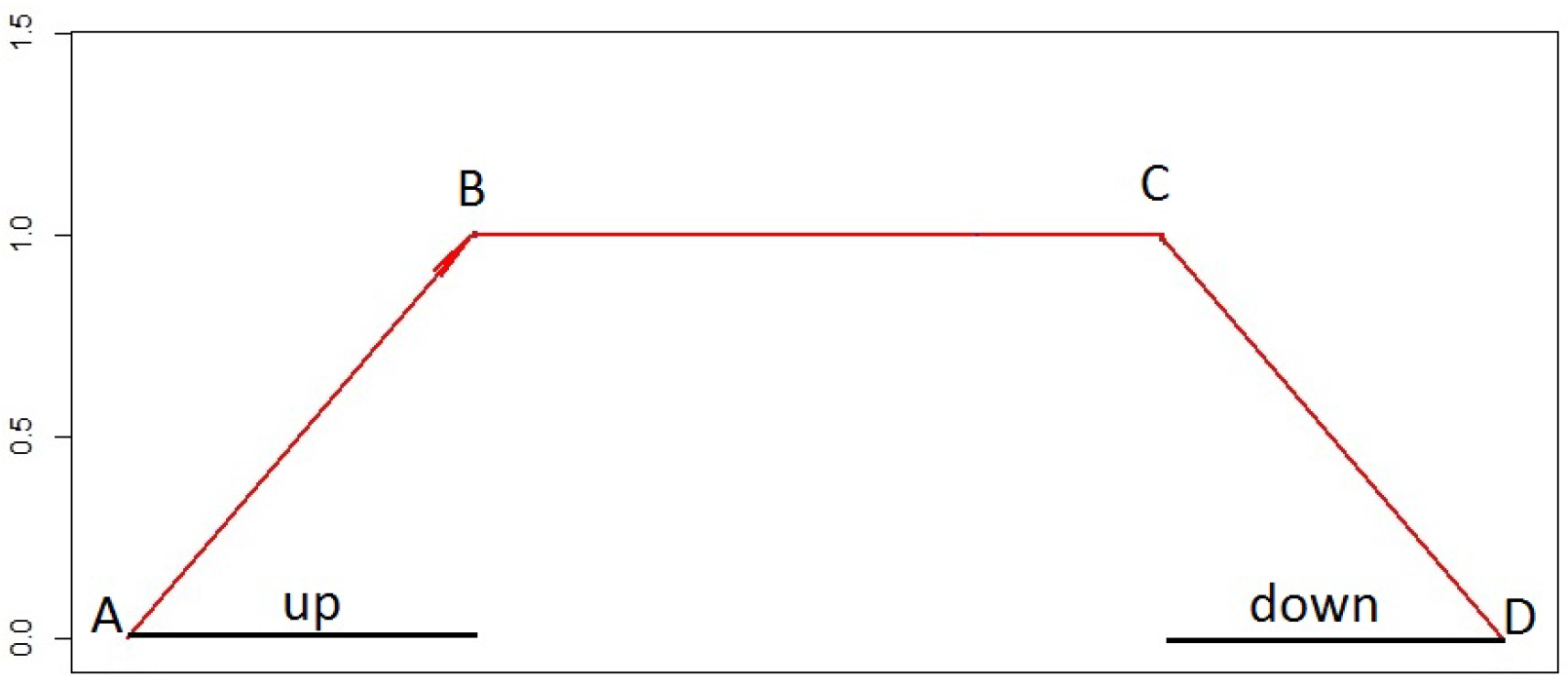
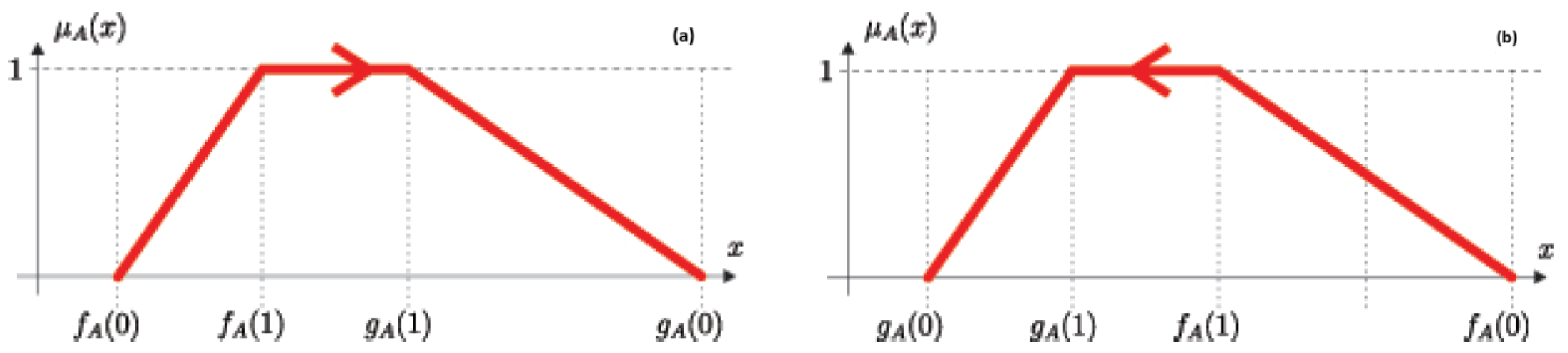
- When the directed OFN is aligned in the direction of increasing values along the X-axis, it is termed as having a positive orientation,
- Conversely, when the directed OFN is aligned in the opposite direction, it is referred to as having a negative orientation.
- Finally, a convex fuzzy number is a fuzzy set in the space of real numbers, which is normal, convex, has a bounded support, and a piecewise continuous membership function. It encompasses proper fuzzy numbers, fuzzy intervals, singleton sets, and fuzzy sets with an unbounded support.
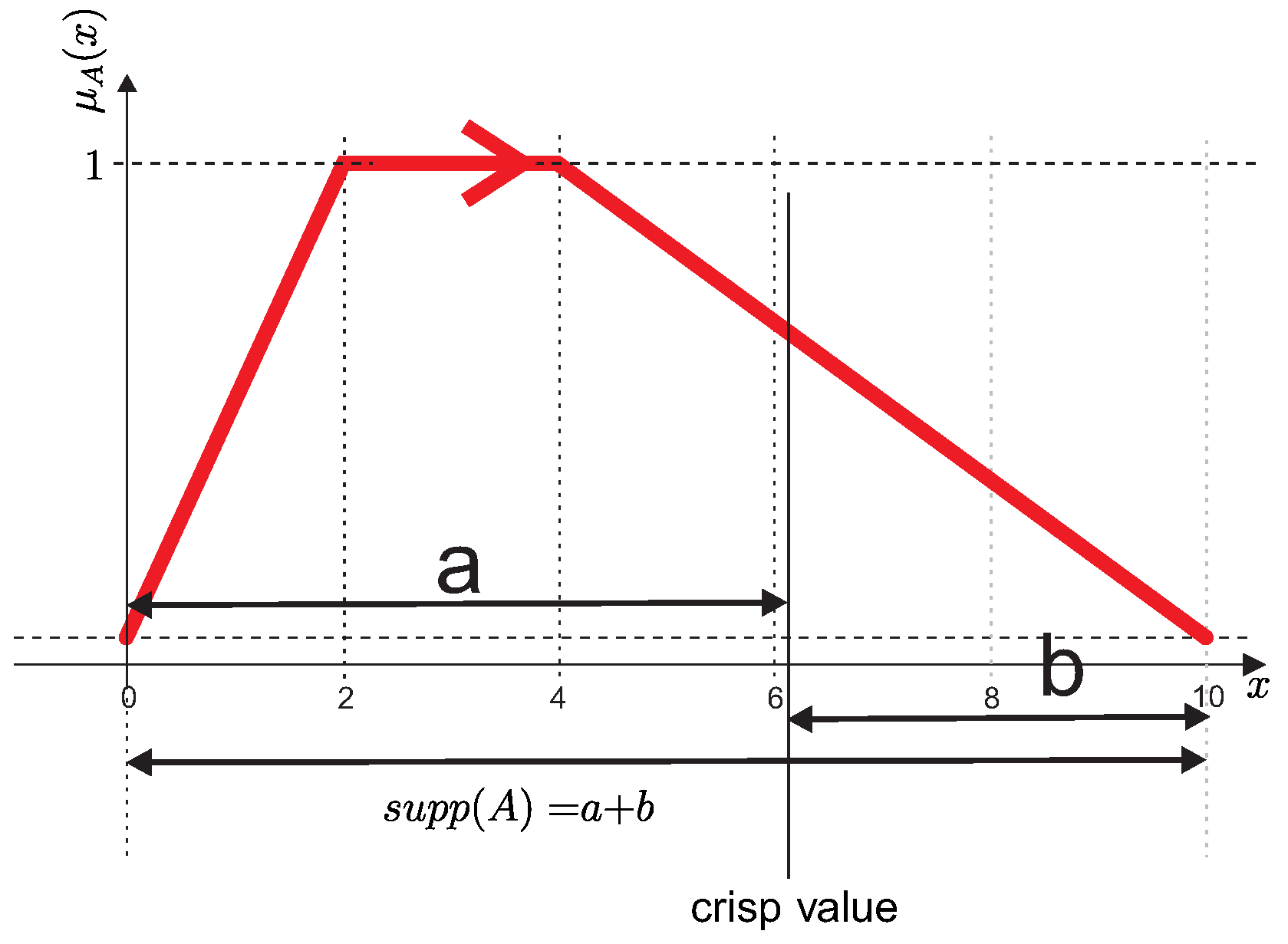
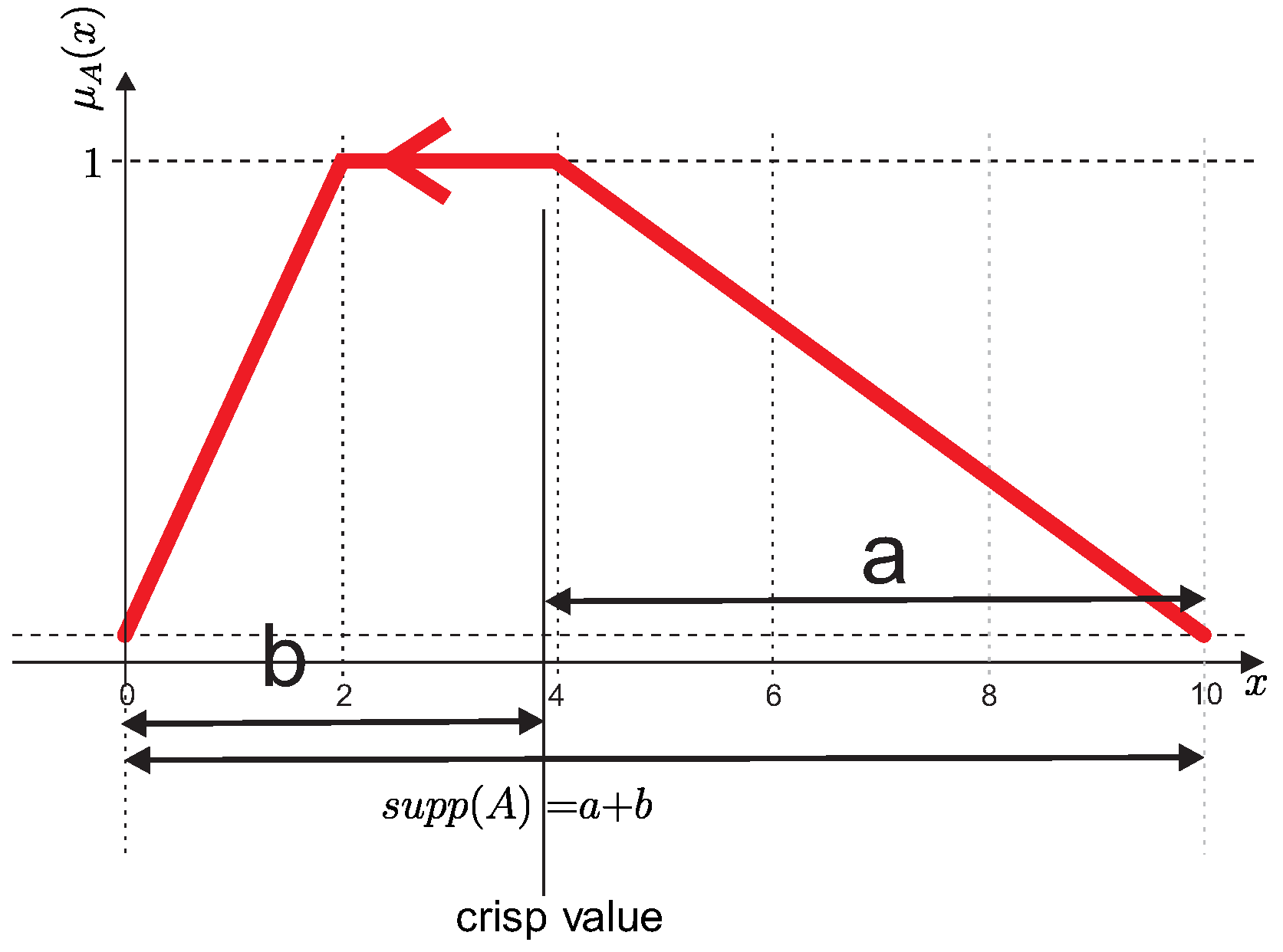
2.2. Definition of Golden Ratio-Based Defuzzyfication Operator
3. Proposed Artificial Duroc Pigs Optimization Method
- —pig number i.
- —pig number i from the subset of new individuals.
- —pig scout number i, temporary collection of solutions.
- ADPO Pseudocode:
- Number of scouting pigs—
- Number of leaders [%]—
- Number of pigs—
- A herd of scouting pigs—
- Herd of pigs—
- Solution in the form of a point
- —sending out pigs to random places,
- —sending out pig scouts to other unexplored places,
- —arranging solutions from the finest to the poorest,
- —looking for the top performer(s), constituting of the target population,
- —return of scout pigs,
- —determining the subsequent position for each member of the herd, excluding the leaders.
- —completes the sample from the + − set,
- —deleting solutions that did not fit in the
- —a function that verifies the satisfaction of the termination condition; the algorithm will conclude upon reaching the specified accuracy or the maximum number of epochs.
- step 1: SendToRandomPlaces()
- step 2: SendToUniquePlaces()
- step 3: SortGroup()
- step 4: FindLeaderPigs()
- step 5: RefillHerdPigs()
- step 6: AvoidWeakPigs()
- step 7: NextPigsPositions()
- niech i
- step 8: IfNoEnd()⟶GoTo(Step2)
- END
4. Experimental Setup
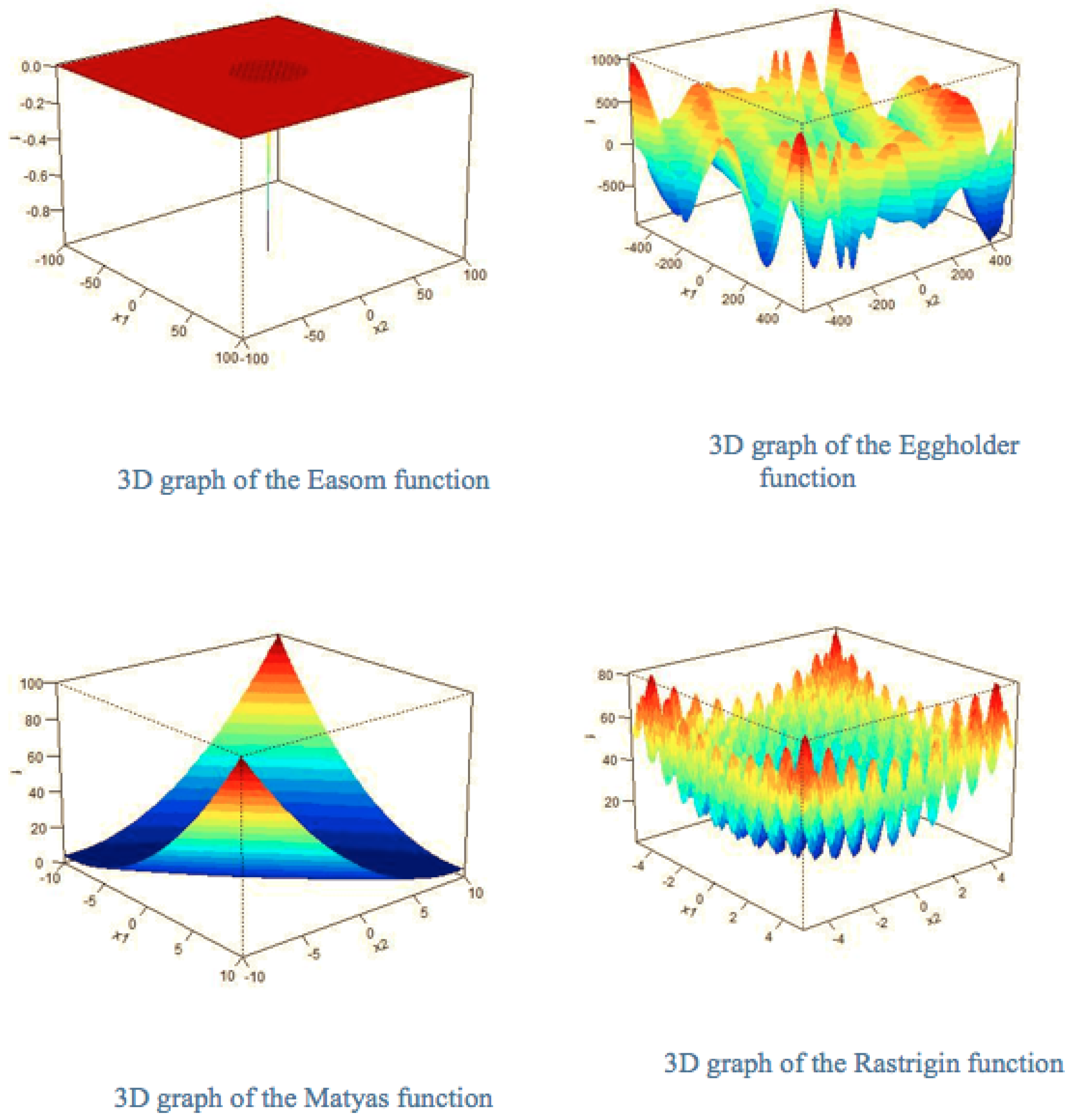
Benchmark Functions
5. Experimental Results
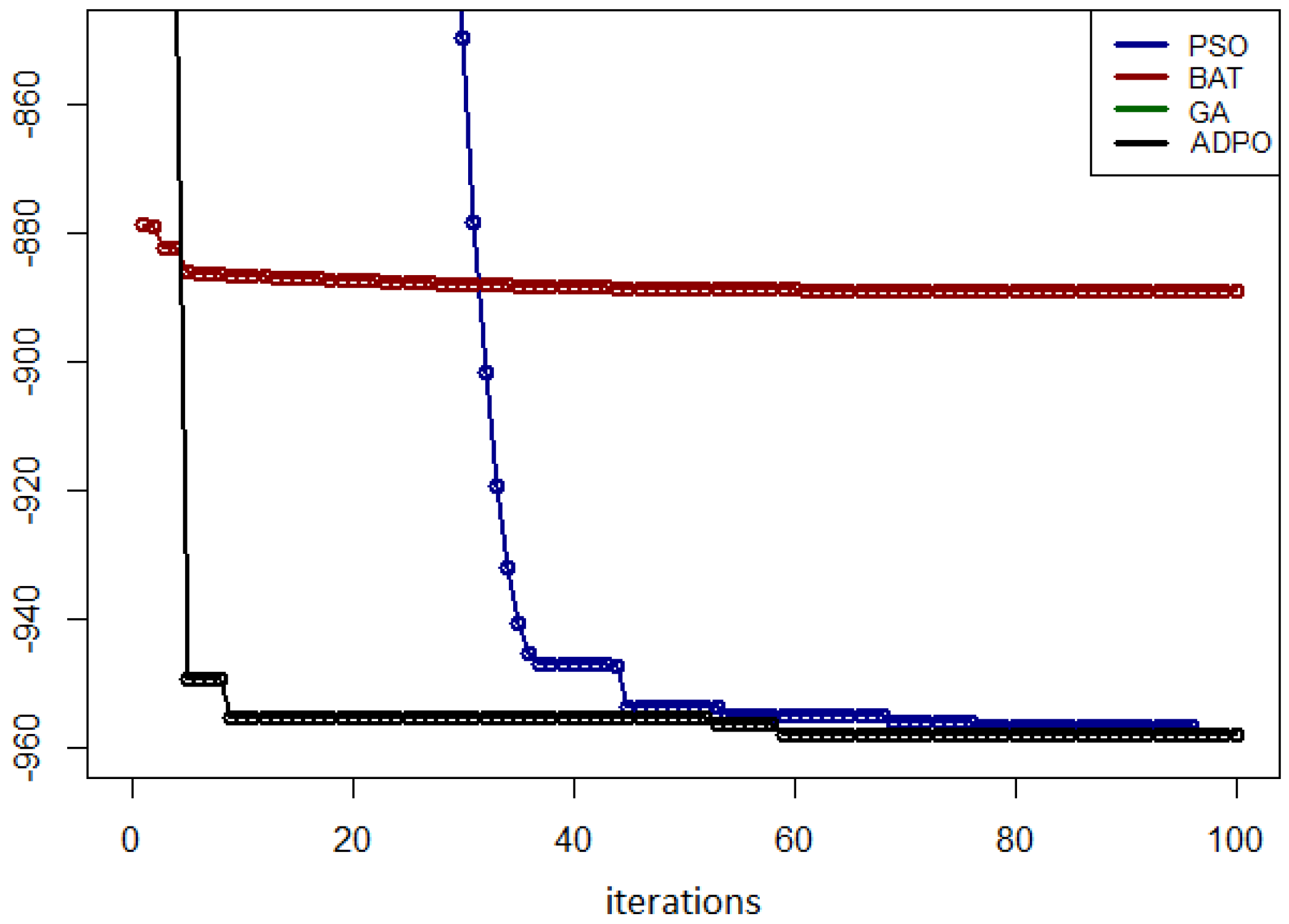
5.1. Execution Time Comparison
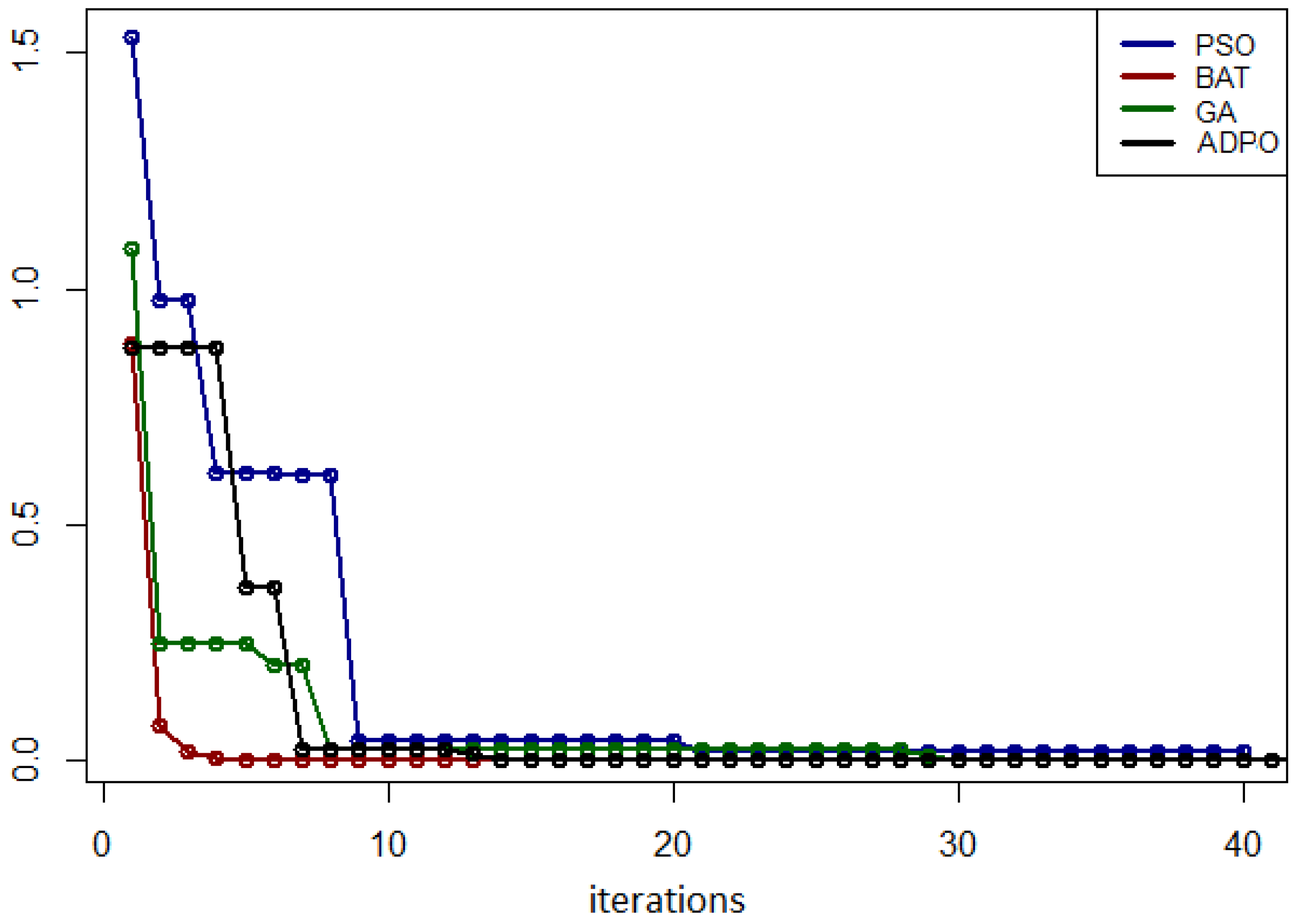
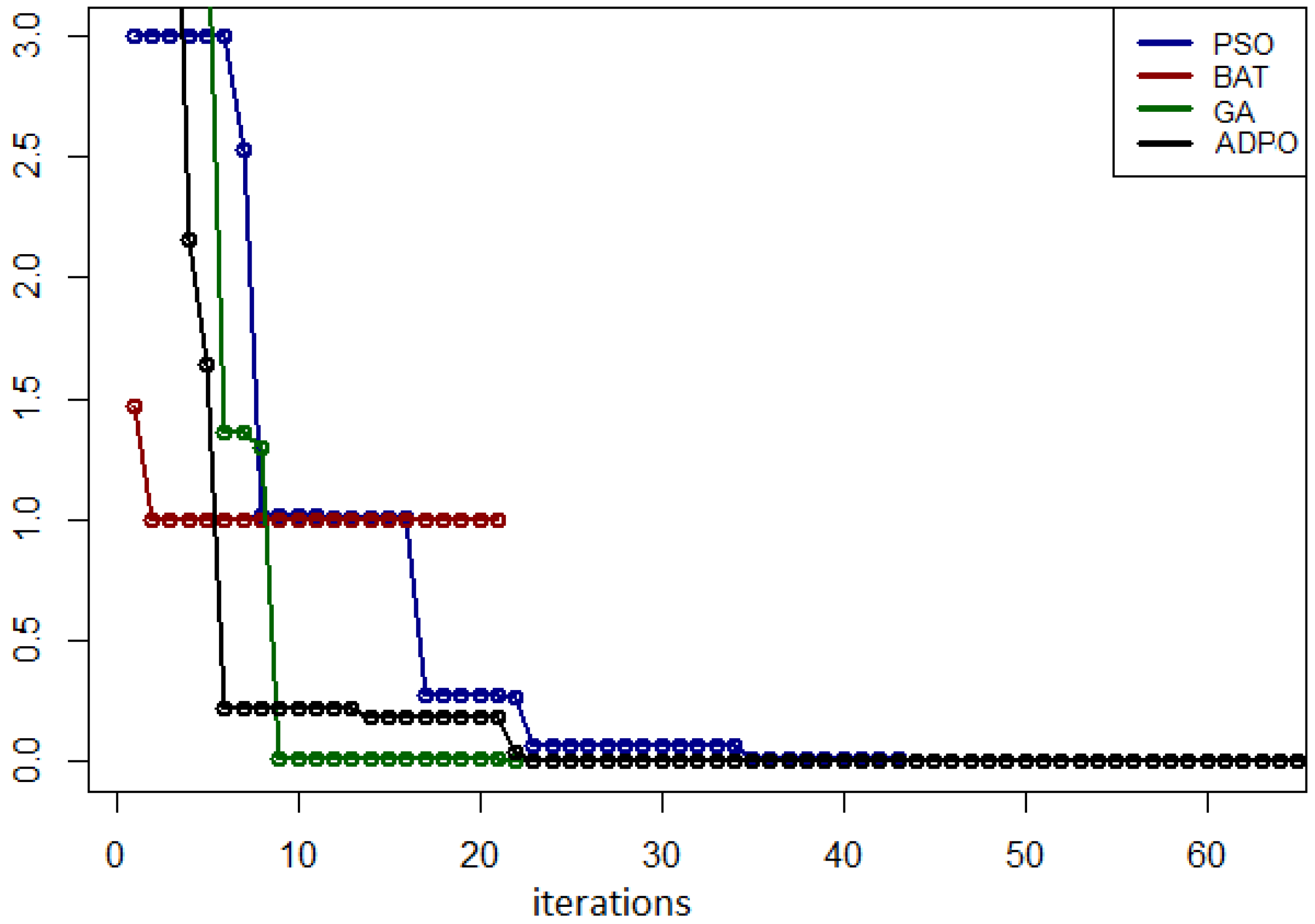
5.2. Results for the Eggholder Function
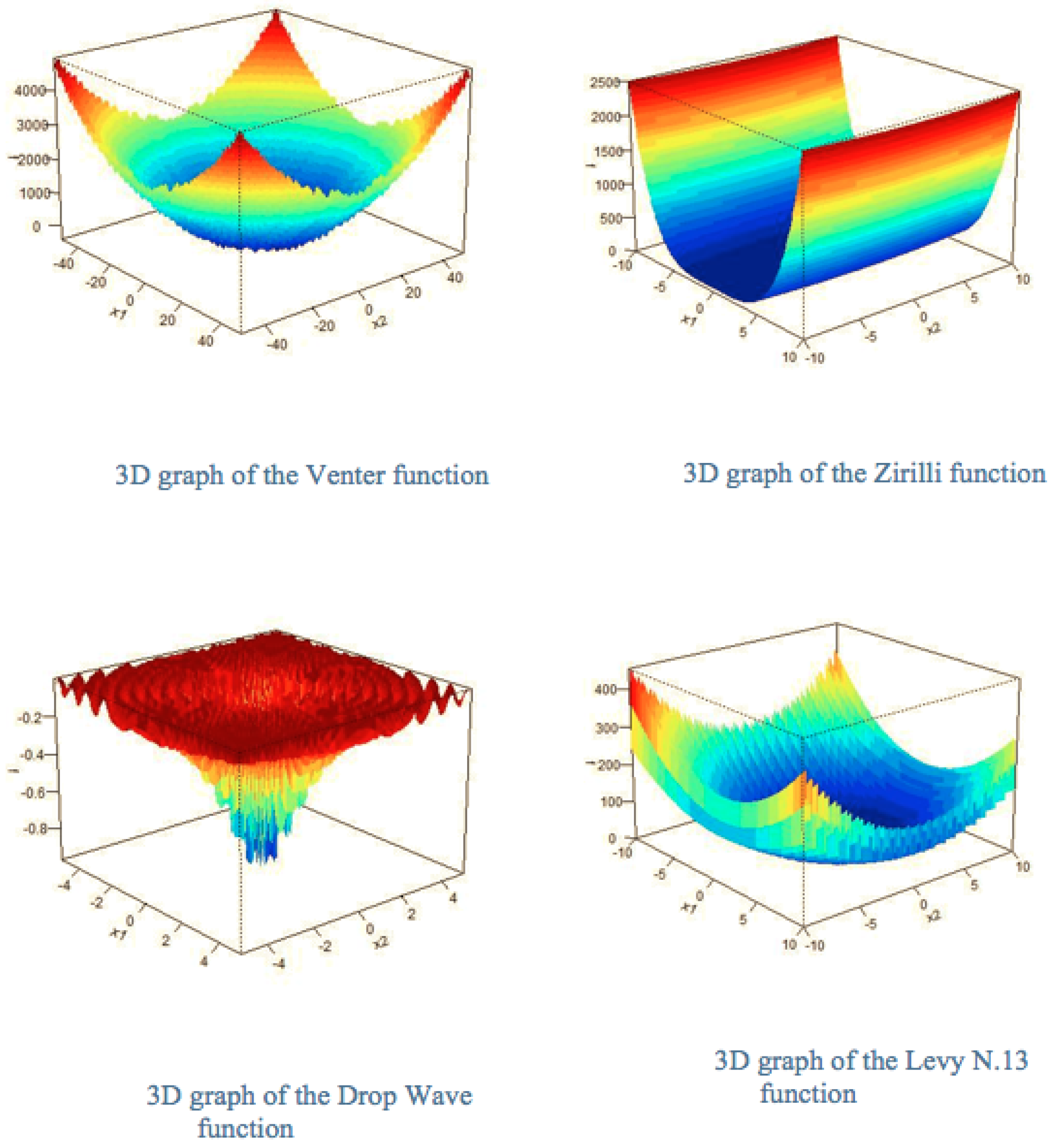
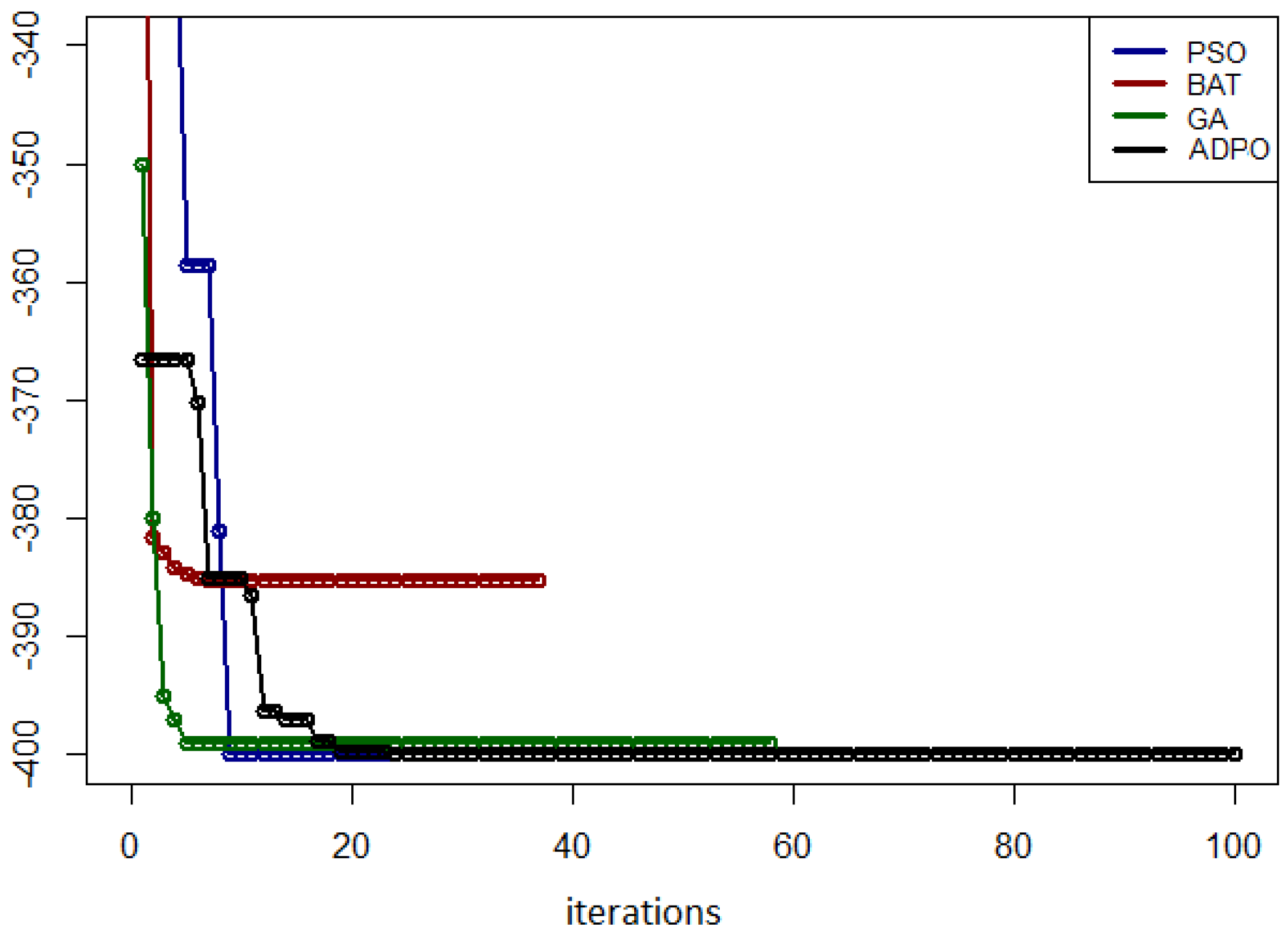
5.3. Results for the Venter Function
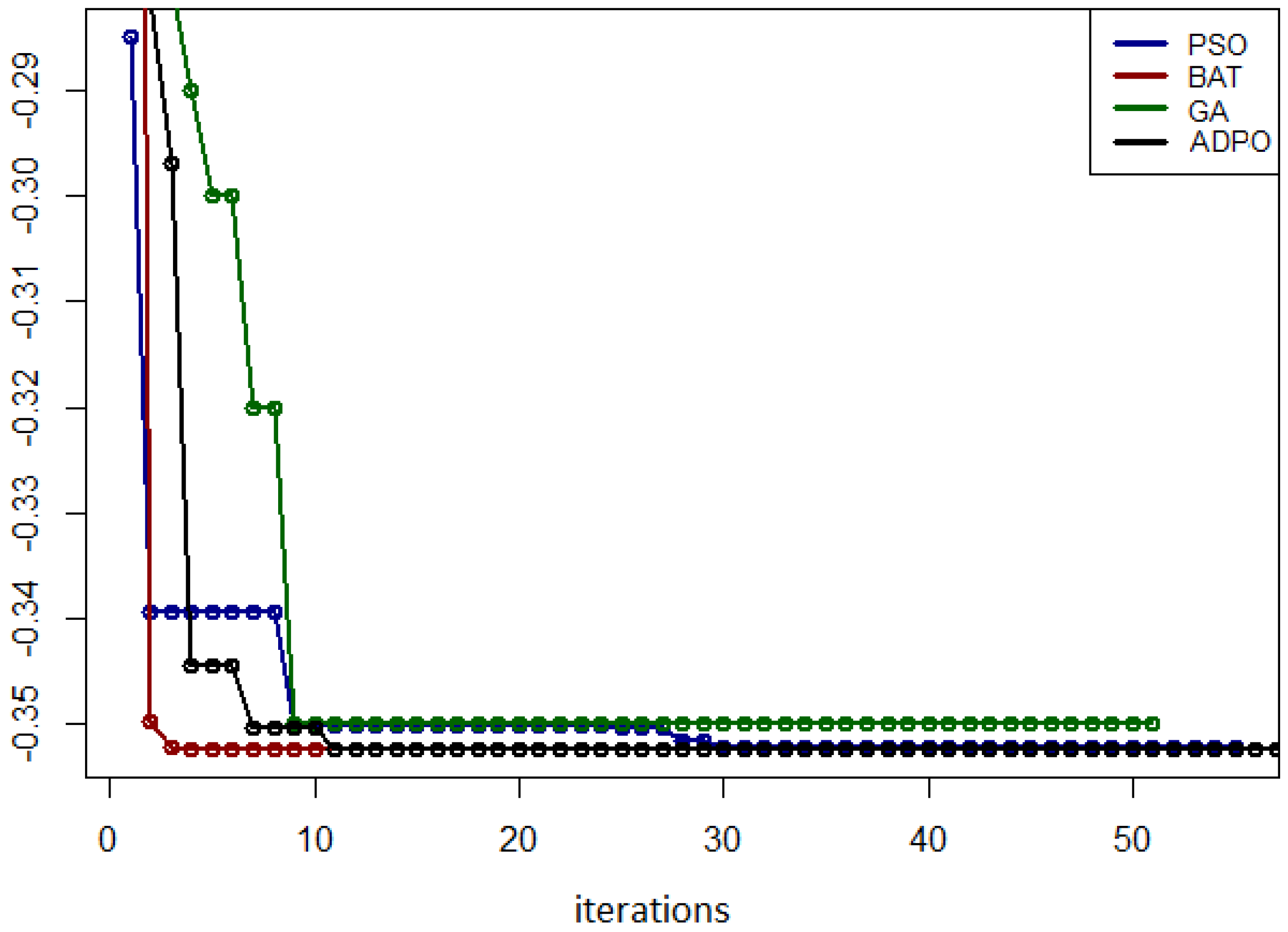
5.4. Results for the Zirilli Function
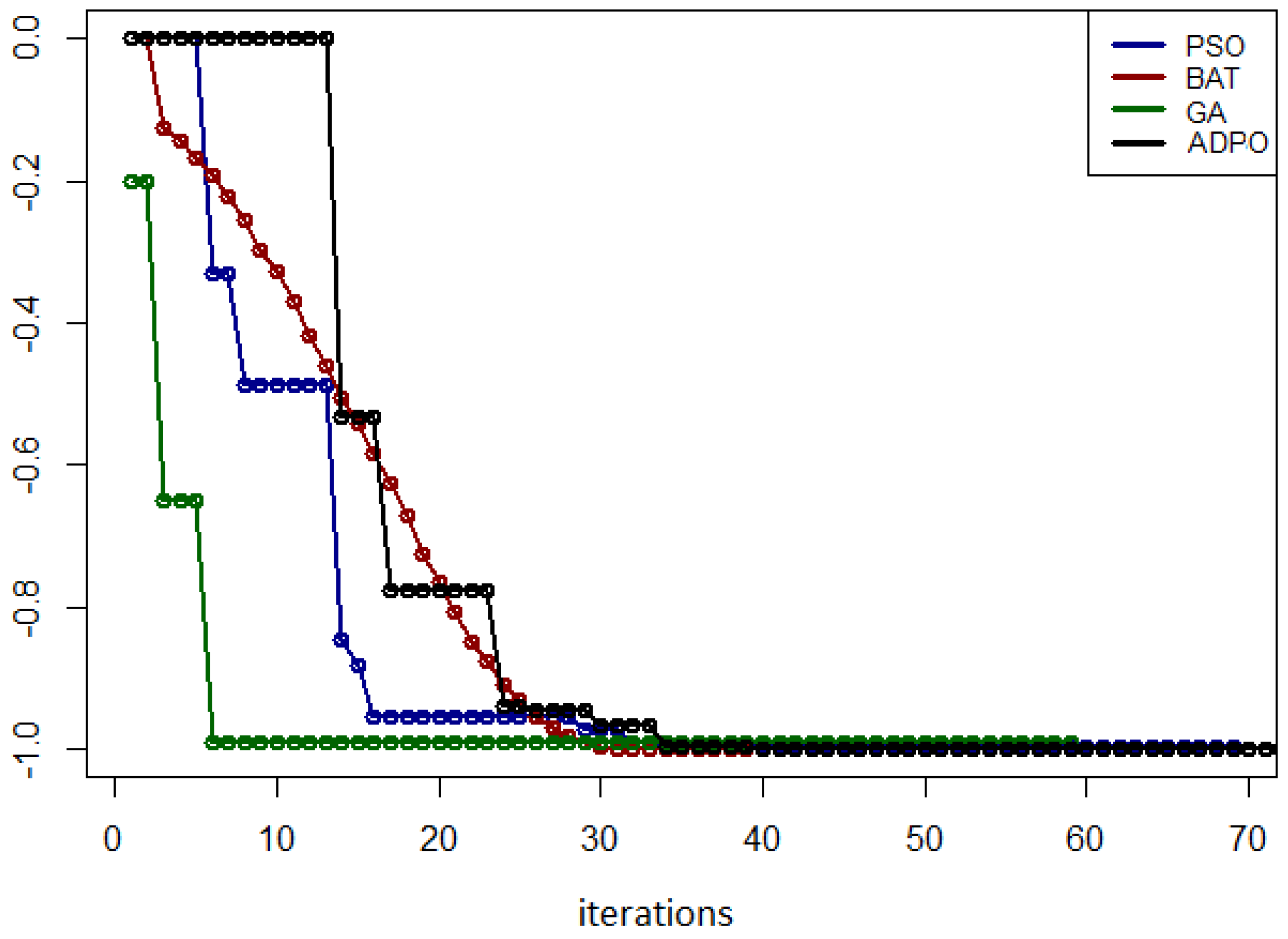
5.5. Results for the Easom Function
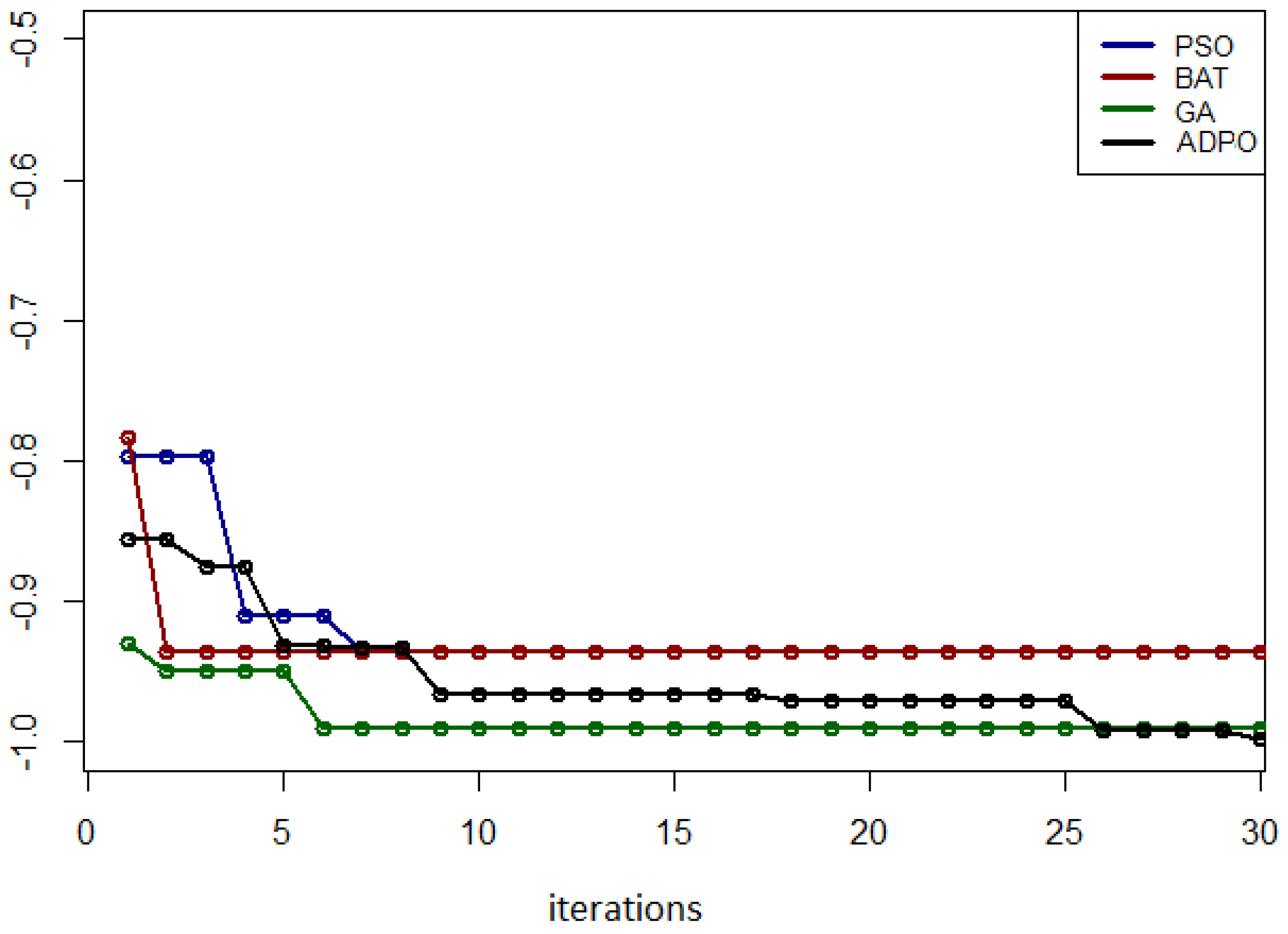
5.6. Results for the Drop Wave, Levy N.13, and Rastrigin Functions
5.7. Summary of Experimental Results
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jakšić, Z.; Devi, S.; Jakšić, O.; Guha, K. A Comprehensive Review of Bio-Inspired Optimization Algorithms Including Applications in Microelectronics and Nanophotonics. Biomimetics 2023, 8, 278. [Google Scholar] [CrossRef] [PubMed]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Fister, I.; Fister, I., Jr.; Yang, X.S.; Brest, J. A comprehensive review of firefly algorithms. Swarm Evol. Comput. 2013, 13, 34–46. [Google Scholar] [CrossRef]
- Jiang, Y.; Wu, Q.; Zhu, S.; Zhang, L. Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems. Expert Syst. Appl. 2022, 188, 116026. [Google Scholar] [CrossRef]
- Golilarz, N.A.; Gao, H.; Addeh, A.; Pirasteh, S. ORCA optimization algorithm: A new meta-heuristic tool for complex optimization problems. In Proceedings of the 2020 17th International Computer Conference on Wavelet Active Media Technology and Information Processing (ICCWAMTIP), Chengdu, China, 18–20 December 2020; IEEE: New York, NY, USA, 2020; pp. 198–204. [Google Scholar]
- Drias, H.; Drias, Y.; Khennak, I. A new swarm algorithm based on orcas intelligence for solving maze problems. In Proceedings of the Trends and Innovations in Information Systems and Technologies, Budva, Montenegro, 7–10 April 2020; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1, pp. 788–797. [Google Scholar] [CrossRef]
- Cavagna, A.; Cimarelli, A.; Giardina, I.; Parisi, G.; Santagati, R.; Stefanini, F.; Viale, M. Scale-free correlations in starling flocks. Proc. Natl. Acad. Sci. USA 2010, 107, 11865–11870. [Google Scholar] [CrossRef] [PubMed]
- Chu, H.; Yi, J.; Yang, F. Chaos particle swarm optimization enhancement algorithm for UAV safe path planning. Appl. Sci. 2022, 12, 8977. [Google Scholar] [CrossRef]
- Zamani, H.; Nadimi-Shahraki, M.H.; Gandomi, A.H. Starling murmuration optimizer: A novel bio-inspired algorithm for global and engineering optimization. Comput. Methods Appl. Mech. Eng. 2022, 392, 114616. [Google Scholar] [CrossRef]
- Oftadeh, R.; Mahjoob, M.; Shariatpanahi, M. A novel meta-heuristic optimization algorithm inspired by group hunting of animals: Hunting search. Comput. Math. Appl. 2010, 60, 2087–2098. [Google Scholar] [CrossRef]
- Adhirai, S.; Mahapatra, R.P.; Singh, P. The Whale Optimization Algorithm and Its Implementation in MATLAB. Int. J. Comput. Inf. Eng. 2018, 12, 815–822. [Google Scholar]
- Rohani, M.R.; Shafabakhsh, G.A.; Asnaashari, E. The Workflow Planning of Construction Sites Using Whale Optimization Algorithm (WOA).The Turkish Online Journal of Design, Art and Communication-TOJDAC November 2016 Special Edition 2016. Available online: http://www.tojdac.org/tojdac/VOLUME6-NOVSPCL_files/tojdac_v060NVSE207.pdf (accessed on 22 January 2024).
- Yang, X.S. Firefly Algorithms for Multimodal Optimization. In Proceedings of the Stochastic Algorithms: Foundations and Applications, Sapporo, Japan, 26–28 October 2009; pp. 169–178. [Google Scholar]
- Shadravan, S.; Naji, H.; Bardsiri, V. The Sailfish Optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems. Eng. Appl. Artif. Intell. 2019, 80, 20–34. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Suganthi, M.; Madheswaran, M. An improved medical decision support system to identify the breast cancer using mammogram. J. Med. Syst. 2012, 36, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shen, J.; Yong, J. A survey on bio-inspired algorithms for web service composition. In Proceedings of the 2012 IEEE 16th International Conference on Computer Supported Cooperative Work in Design (CSCWD), Wuhan, China, 23–25 May 2012; pp. 569–574. [Google Scholar] [CrossRef]
- Shalamov, V.; Filchenkov, A.; Shalyto, A. Heuristic and metaheuristic solutions of pickup and delivery problem for self-driving taxi routing. Evol. Syst. 2019, 10, 3–11. [Google Scholar] [CrossRef]
- Ewald, D.; Czerniak, J.M.; Paprzycki, M. A New OFNBee Method as an Example of Fuzzy Observance Applied for ABC Optimization. In Theory and Applications of Ordered Fuzzy Numbers; Springer: Berlin/Heidelberg, Germany, 2017; p. 223. [Google Scholar]
- Ewald, D.; Zarzycki, H.; Apiecionek, L.; Czerniak, J.M. Ordered fuzzy numbers applied in bee swarm optimization systems. J. Univers. Comput. Sci. 2020, 26, 1475–1494. [Google Scholar] [CrossRef]
- Ragmani, A.; Elomri, A.; Abghour, N.; Moussaid, K.; Rida, M. An improved Hybrid Fuzzy-Ant Colony Algorithm Applied to Load Balancing in Cloud Computing Environment. In Proceedings of the 10th International Conference on Ambient Systems, Networks and Technologies (ANT 2019), Leuven, Belgium, 29 April 29–2 May 2019; Volume 151, pp. 519–526. [Google Scholar] [CrossRef]
- Grandin, T.; Curtis, S.; Greenough, W. Effects of rearing environment on the behaviour of young pigs. J. Anim. Sci. 1983, 57, 137. [Google Scholar]
- McGlone, J.; Curtis, S.E. Behavior and Performance of Weanling Pigs in Pens Equipped with Hide Areas. J. Anim. Sci. 1985, 60, 20–24. [Google Scholar] [CrossRef] [PubMed]
- Mrozek, D.; Dabek, T.; Małysiak-Mrozek, B. Scalable Extraction of Big Macromolecular Data in Azure Data Lake Environment. Molecules 2019, 24, 179. [Google Scholar] [CrossRef] [PubMed]
- Grandin, T.; Curtis, S. Toy preferences in young pigs. J. Anim. Sci. 1984, 59, 85. [Google Scholar]
- Pettigrew, J.E. Essential role for simulation models in animal research and application. Anim. Prod. Sci. 2018, 58, 704–708. [Google Scholar] [CrossRef]
- de Silva Ramos-Freitas, L.C.; Torres-Campos, A.; Schiassi, L.; Yanagi-Júnior, T.; Cecchin, D. Fuzzy index for swine thermal comfort at nursery stage based on behavior. DYNA 2017, 84, 201–207. [Google Scholar] [CrossRef]
- Harris, A.; Patience, J.; Lonergan, S.; Dekkers, J.; Gabler, N. Improved nutrient digestibility and retention partially explains feed efficiency gains in pigs selected for low residual feed intake. J. Anim. Sci. 2013, 90, 164–166. [Google Scholar] [CrossRef] [PubMed]
- Held, S.; Mason, G.; Mendl, M. Using the Piglet Scream Test to enhance piglet survival on farms: Data from outdoor sows. Anim. Welf. 2007, 16, 267–271. [Google Scholar] [CrossRef]
- Patel, B.; Chen, H.; Ahuja, A.; Krieger, J.F.; Noblet, J.; Chambers, S.; Kassab, G.S. Constitutive modeling of the passive inflation-extension behavior of the swine colon. J. Mech. Behav. Biomed. Mater. 2017, 77, 176–186. [Google Scholar] [CrossRef] [PubMed]
- Dyczkowski, K. A Less Cumulative Algorithm of Mining Linguistic Browsing Patterns in the World Wide Web. In Proceedings of the 5th EUSFLAT Conference, Ostrava, Czech Republic, 11–14 September 2007. [Google Scholar]
- Stachowiak, A.; Dyczkowski, K. A Similarity Measure with Uncertainty for Incompletely Known Fuzzy Sets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013; pp. 390–394. [Google Scholar]
- Marszalek, A.; Burczynski, T. Modeling and forecasting financial time series with ordered fuzzy candlesticks. Inf. Sci. 2014, 273, 144–155. [Google Scholar] [CrossRef]
- Prokopowicz, P.; Czerniak, J.; Mikolajewski, D.; Apiecionek, L.; Slezak, D. Theory and Applications of Ordered Fuzzy Numbers. A Tribute to Professor Witold Kosińsk; Studies in Fuzziness and Soft Computing; Springer International Publishing: Cham, Switzerland, 2017; Volume 365. [Google Scholar]
- Kosinski, W.; Słysz, P. Fuzzy Numbers and Their Quotient Space with Algebraic Operations. Bull. Pol. Acad. Sci. Math. 1993, 41, 285–295. [Google Scholar]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. Fuzzy Reals with Algebraic Operations: Algorithmic Approach. In Proceedings of the IIS 2002 Symposium, Sopot, Poland, 3–6 June 2002; pp. 311–320. [Google Scholar]
- Kosinski, W. On fuzzy number calculus. Int. J. Appl. Math. Comput. Sci. 2006, 16, 51–57. [Google Scholar]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. Ordered Fuzzy Numbers. Bull. Pol. Acad. Sci. Math. 2003, 51, 327–338. [Google Scholar]
- Kosinski, W.; Frischmuth, K.; Wilczyńska-Sztyma, D. A New Fuzzy Approach to Ordinary Differential Equations. In Proceedings of the ICAISC 2010, Zakopane, Poland, 13–17 June 2010; Part I. Volume 6113, pp. 120–127. [Google Scholar]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. Algebraic Operations on Fuzzy Numbers. In Proceedings of the IIS 2003, Zakopane, Poland, 2–5 June 2003; Kłopotek, M.A., Wierzchoń, S.T., Trojanowski, K., Eds.; Advances in Soft Computing. Springer: Berlin/Heidelberg, Germany, 2003; pp. 353–362. [Google Scholar]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. Calculus with Fuzzy Numbers. In Intelligent Media Technology for Communicative Intelligence; Bolc, L., Michalewicz, Z., Nishida, T., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3490, pp. 21–28. [Google Scholar] [CrossRef]
- Kosinski, W.; Prokopowicz, P.; Kacprzak, D. Fuzziness—Representation of Dynamic Changes by Ordered Fuzzy Numbers. In Views on Fuzzy Sets and Systems from Different Perspectives: Philosophy and Logic, Criticisms and Applications; Seising, R., Ed.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2009; Volume 243, pp. 485–508. [Google Scholar]
- Kosinski, W. Evolutionary algorithm determining defuzzyfication operators. Eng. Appl. Artif. Intell. 2007, 20, 619–627. [Google Scholar] [CrossRef][Green Version]
- Kosinski, W.; Prokopowicz, P.; Slezak, D. On Algebraic Operations on Fuzzy Reals. In Neural Networks and Soft Computing, Proceedings of the Sixth International Conference on Neural Networks and Soft Computing, Zakopane, Poland, 11–15 June 2002; Rutkowski, L., Kacprzyk, J., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2003; pp. 54–61. [Google Scholar] [CrossRef]
- Czerniak, J.M.; Zarzycki, H.; Ewald, D.; Augustyn, P. Application of OFN Numbers in the Artificial Duroc Pigs Optimization (ADPO) Method. In Proceedings of the Uncertainty and Imprecision in Decision Making and Decision Support: New Challenges, Solutions and Perspectives, Warsaw, Poland, 12–14 October 2018; pp. 310–327. [Google Scholar]
- Zarzycki, H.; Apiecionek, Ł.; Czerniak, J.M.; Ewald, D. The Proposal of Fuzzy Observation and Detection of Massive Data DDOS Attack Threat. In Proceedings of the Uncertainty and Imprecision in Decision Making and Decision Support: New Challenges, Solutions and Perspectives, Warsaw, Poland, 24–28 October 2021; pp. 363–378. [Google Scholar]
- Mikolajewska, E.; Mikolajewski, D. The prospects of brain—Computer interface applications in children. Cent. Eur. J. Med. 2014, 9, 74–79. [Google Scholar] [CrossRef]
- Mikolajewska, E.; Mikolajewski, D. Wheelchair Development from the Perspective of Physical Therapists and Biomedical Engineers. Adv. Clin. Exp. Med. 2010, 19, 771–776. [Google Scholar]
- Chwastyk, A.; Pisz, I. OFN Capital Budgeting Under Uncertainty and Risk. In Theory and Applications of Ordered Fuzzy Numbers: A Tribute to Professor Witold Kosiński; Prokopowicz, P., Czerniak, J., Mikołajewski, D., Apiecionek, Ł., Ślȩzak, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 157–169. [Google Scholar] [CrossRef]
- Kacprzak, D. Input-Output Model Based on Ordered Fuzzy Numbers. In Theory and Applications of Ordered Fuzzy Numbers: A Tribute to Professor Witold Kosiński; Prokopowicz, P., Czerniak, J., Mikołajewski, D., Apiecionek, Ł., Ślezak, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 171–182. [Google Scholar] [CrossRef]
- Kacprzak, M.; Starosta, B. Two Approaches to Fuzzy Implication. In Theory and Applications of Ordered Fuzzy Numbers: A Tribute to Professor Witold Kosiński; Prokopowicz, P., Czerniak, J., Mikołajewski, D., Apiecionek, Ł., Ślȩzak, D., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 133–154. [Google Scholar] [CrossRef]
- Dobrosielski, W.; Czerniak, J.; Szczepanski, J.; Zarzycki, H. Two New Defuzzification Methods Useful for Different Fuzzy Arithmetics. In Uncertainty and Imprecision in Decision Making and Decision Support: Cross-Fertilization, New Models and Applications. IWIFSGN 2016; Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2018; Volume 559, pp. 83–101. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Shi, Y.; Kennedy, J. Swarm Intelligence. In Proceedings of the Morgan Kaufmann Series on Evolutionary Computation, 1st ed.; Morgan Kaufman: Burlington, MA, USA, 2001. [Google Scholar]
- Szmidt, E.; Kacprzyk, J. Distances between intuitionistic fuzzy sets. Fuzzy Sets Syst. 2000, 114, 505–518. [Google Scholar] [CrossRef]
- Kacprzyk, J.; Wilbik, A. Using Fuzzy Linguistic Summaries for the Comparison of Time Series: An application to the analysis of investment fund quotations. In Proceedings of the IFSA/EUSFLAT Conference, Lisbon, Portugal, 20–24 July 2009; pp. 1321–1326. [Google Scholar]
- Piegat, A.; Pluciński, M. Computing with words with the use of inverse RDM models of membership functions. Int. J. Appl. Math. Comput. Sci. 2015, 25, 675–688. [Google Scholar] [CrossRef]
- Zadrozny, S.; Kacprzyk, J. On the use of linguistic summaries for text categorization. In Proceedings of the IPMU, Perugia, Italy, 1 July 2004; pp. 1373–1380. [Google Scholar]
| Algorithm | The Size of the Population | |
|---|---|---|
| 1 | PSO | 40 |
| 2 | APDO | 30 |
| 3 | BAT | 40 |
| 4 | GA | 40 |
| No. | Function Name | Range of Values and | Searched Values of and | Searched Value of |
|---|---|---|---|---|
| 1 | Easom | [−100, 100] | (3.14, 3.14) | −1 |
| 2 | Eggholder | [−512, 512] | (512, 404) | −959 |
| 3 | Drop Wave | [−5.12, 5.12] | (0, 0) | −1 |
| 4 | Levy N.13 | [−10, 10] | (1, 1) | 0 |
| 5 | Matyas | [−10, 10] | (0, 0) | 0 |
| 6 | Rastrigin | [−5.12, 5.12] | (0, 0) | 0 |
| 7 | Zirilli | [−10, 10] | (−1.04, 0) | −0.35 |
| 8 | Venter | [−50, 50] | (0, 0) | −400 |
| No. | Function Name | PSO | APDO | BAT | GA |
|---|---|---|---|---|---|
| 1 | Eggholder | 0.0996 | 0.06 | 0.1308 | 0.122 |
| 2 | Venter | 0.06 | 0.047 | 0.06 | 0.18 |
| 3 | Matyas | 0.0748 | 0.062 | 0.0816 | 0.058 |
| 4 | Zirilli | 0.072 | 0.066 | 0.082 | 0.060 |
| 5 | Easom | 0.07 | 0.04 | 0.079 | 0.098 |
| 6 | Rastrigin | 0.073 | 0.038 | 0.076 | 0.18 |
| 7 | Levy N.13 | 0.076 | 0.04 | 0.084 | 0.187 |
| 8 | Drop Wav | 0.077 | 0.04 | 0.085 | 0.147 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czerniak, J.M.; Ewald, D.; Paprzycki, M.; Fidanova, S.; Ganzha, M. A New Artificial Duroc Pigs Optimization Method Used for the Optimization of Functions. Electronics 2024, 13, 1372. https://doi.org/10.3390/electronics13071372
Czerniak JM, Ewald D, Paprzycki M, Fidanova S, Ganzha M. A New Artificial Duroc Pigs Optimization Method Used for the Optimization of Functions. Electronics. 2024; 13(7):1372. https://doi.org/10.3390/electronics13071372
Chicago/Turabian StyleCzerniak, Jacek M., Dawid Ewald, Marcin Paprzycki, Stefka Fidanova, and Maria Ganzha. 2024. "A New Artificial Duroc Pigs Optimization Method Used for the Optimization of Functions" Electronics 13, no. 7: 1372. https://doi.org/10.3390/electronics13071372
APA StyleCzerniak, J. M., Ewald, D., Paprzycki, M., Fidanova, S., & Ganzha, M. (2024). A New Artificial Duroc Pigs Optimization Method Used for the Optimization of Functions. Electronics, 13(7), 1372. https://doi.org/10.3390/electronics13071372









