Abstract
In high-power microwave applications, the reflection of energy can be effectively reduced by adjusting the three-stub waveguide. However, most of the existing tuning algorithms do not make an arrangement for the adjustment sequence of stubs, and accurately calculating the depth of the stubs requires a great deal of time via electromagnetic (EM) simulations, which may cause large reflection in the matching process. To solve these problems, we first propose an improved calculation method that can accurately calculate the input impedance of a three-stub waveguide. Then, an impedance matching algorithm is designed based on the equivalent circuit model that can quickly and accurately calculate the optimal depth of the stubs. Finally, we present a low-reflection tuning strategy to suppress the large reflection during the adjustment of the stub process. An experimental system is built to verify the calculation method and the tuning strategy. The results show that the strategy can avoid large reflection in the case of load mutation and can maintain low reflection when the load changes continuously. The algorithm meets the needs of the industry and can be used for automatic and real-time adjustment of three-stub waveguides of different specifications.
1. Introduction
Microwave energy has been widely used in many aspects of industrial applications, such as microwave heating, microwave plasma, microwave sterilization, microwave medical treatment, and microwave chemistry [1,2,3,4,5,6]. In high-power microwave applications [7,8,9], a three-stub waveguide is often adopted between the source and the load to perform impedance matching and to reduce reflection. However, the impedance of some loads will change nonlinearly due to the influence of temperature in the processing [10], which will cause impedance mismatching. Automatic impedance tuners have been widely investigated. Long calculation time, inaccurate calculation, and direct tuning may cause large reflections, which can damage the equipment [11] and cause energy waste. An accurate calculation method and a fast impedance matching algorithm will reduce the design complexity and cost of the automatic three-stub tuner.
So far, some researchers have studied the equivalent circuit of the stub waveguide [12,13,14], and a series of tuning algorithms have been proposed [15,16,17,18,19]. In [20], a four-stub waveguide was studied and analyzed as a radio frequency circuit, and impedance matching was accomplished by adjusting the stubs to change the reflection coefficient of the port. In [21], a gradient algorithm was used to automatically adjust the stub to gradually reduce its port reflection coefficient to a minimum value. In [22], an automatic tuning method for a three-stub waveguide tuner was proposed by using the space mapping technique to solve the problem of non-uniqueness of the solution of the stub depths, and the optimal solution can be calculated by two space mapping programs. In [23], an automatic impedance matching system of a four-stub waveguide was proposed, which can make |S11| lower than −30 dB based on an iterative algorithm. In [24], a dynamic impedance matching algorithm of three-stub tuners based on equivalent circuit analysis was proposed. The S-parameters of the equivalent circuit were calculated using the analysis method of the stub waveguide, and the calculation formulas of the port reflection coefficient and external load were deduced to achieve real-time matching of dynamic loads. The above algorithms could generally achieve impedance matching effectively. However, few studies have mentioned the reflection conditions during tuning. It is likely that reflection generated by long calculation time, inaccurate calculation, and the adjustment of the stubs may also damage the components and cause the protection circuits to trip [25,26]. Thus, it is of great importance not only to study a fast and accurate calculation method but also the sequence of stub adjustment.
Focusing on the above issue that the reflection may be too large during tuning, we propose a calculation method and a low-reflection tuning strategy for a three-stub waveguide. Based on theoretical analysis, we add a correction coefficient, the input impedance formula of the stub waveguide is improved, and the influence of the stub itself on the calculation results is considered. Using the analysis method of distributed impedance matching circuit, the spacing of the stubs is designed to be a quarter wavelength of the waveguide, and the whole tuning algorithm is completed by numerical calculation. In this article, the input impedance of the three-stub waveguide is studied, and a calculation method for calculating the stub waveguide is revised, which can accurately and quickly calculate the input impedance of the waveguide port. The whole tuning process is roughly divided into three steps. First, the optimal solution of the stub depths is calculated via the impedance matching algorithm, then judging the change in load, and finally adjusting the stubs. The proposed strategy can determine the adjustment sequence of the stubs according to load impedance and quickly calculate the depth of the stubs, achieving impedance matching efficiently while avoiding high reflection during tuning.
The subsequent sections are structured as follows: Section 2 studies the input impedance of a three-stub waveguide and proposes an improved formula for calculating the input impedance. Section 3 first proposes an impedance matching algorithm to quickly calculate the optimal depth of the stubs and then proposes a low-reflection tuning strategy to suppress the increase in reflection during adjusting the stubs. Section 4 describes the experimental results and analysis. Section 5 summarizes the findings and contributions of this work.
2. Study on Input Impedance of Three-Stub Waveguide
2.1. Input Impedance of Rectangular Waveguide
The rectangular waveguide model is shown in Figure 1a. According to waveguide transmission line theory, the electromagnetic wave of each mode in the rectangular waveguide can be equivalent to an independent transmission line, as shown in Figure 1b. So, under the condition of dominant mode, in theory, we only need to know the characteristic impedance Z0 of the transmission line and load impedance ZL, and the input impedance can be calculated [27],
where β is the phase constant and l is the length of the transmission line.
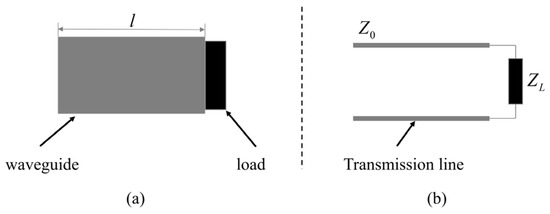
Figure 1.
Rectangular waveguide and its equivalent circuit. (a) Rectangular waveguide model. (b) Ideal equivalent circuit model.
2.2. An Improved Method Based on Input Impedance of Three-Stub Waveguide
In practical situations, the stub depth is limited to prevent the three-stub waveguide from being broken down. Therefore, the stub can be equivalent to a parallel capacitor if the depth of the stub is within a certain range [28]. In order to study the influence of the stub itself on the input impedance, a matching load is connected to the rectangular waveguide, as shown in Figure 2a. In Figure 2b, the single-stub rectangular waveguide with a matched load can be ideally equivalent to a circuit in which a capacitor is in parallel with a transmission line with a matched load. The input impedance in Figure 2b is
where Xc is impedance of equivalent capacitance.
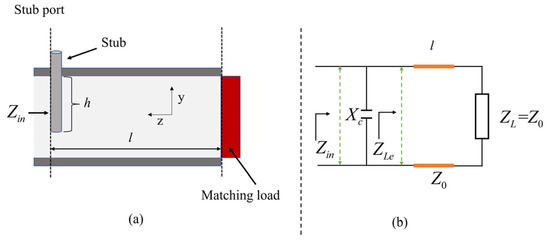
Figure 2.
(a) Single-stub waveguide model. (b) Ideal equivalent circuit model of single-stub rectangular waveguide.
In order to simplify the analysis, the input impedance is converted to the input admittance,
where C is equivalent capacitance value of the stub and ω is the angular frequency.
If the influence of the stub itself on the equivalent circuit is not considered, the real part of the input admittance in Equation (3) is theoretically a constant value. However, the ideal constant value cannot be achieved. For instance, a WR340 waveguide with a single stub is taken into consideration. The radius of the stub used is R = 3.5 mm, and the length of waveguide is l = 75 mm. When the microwave frequency f = 2.45 GHz, the phase constant β = 36.258 rad/m, and the characteristic impedance of the rectangular waveguide Z0 = 328.9 Ω. Figure 3a shows the simulated input admittance of the WR340 single-stub waveguide. It can be seen that the real parts of the input admittance with different stub depths are not fixed. The greater the stub depth, the larger the real parts of the input admittance. Therefore, due to the influence of the stub itself, the single-stub waveguide cannot be regarded as an ideal equivalent circuit as shown in Figure 2b [29]; otherwise, the calculated results may be inaccurate. One can approximate the input impedance at a waveguide port using the ratio of equivalent voltage to equivalent current. When the stub depth is 0, the equivalent load impedance ZLe can be calculated by [28]
where is the electric field at the center of the waveguide cross-section and is the magnetic field at the top of the waveguide. In this case, Equations (4) and (1) are equivalent,
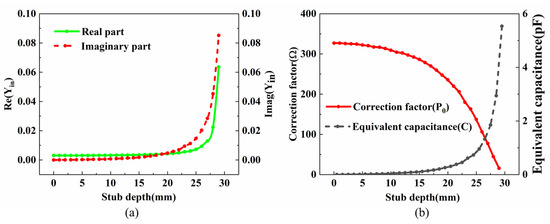
Figure 3.
Simulated parameters for single-stub waveguide. (a) Input admittance at stub port. (b) Correction factor and equivalent capacitance of the stub at different depths.
and in Equation (4) will change with the depth of the stub. Therefore, a modification to Equation (4) is needed. The corrected formula is
where h is the depth of the stub, k1(h,y) is the coefficient of change for the electric field, and k2(h,y) is the coefficient of change for the magnetic field. We make an approximation that the effect of the stub on the field at each location is the same, and we can obtain
Therefore, the approximate expression for input impedance is
Thus, the modified formula for calculating the input impedance of the waveguide with a stub at the port can be expressed by
and we define
So, Equation (9) can be written as
When the waveguide is matched, the input admittance at the stub port is
P0 is the reciprocal of the real part of the input admittance. According to the imaginary part of the input admittance, the equivalent capacitance value C of the stub at different depths can be calculated,
Figure 3b shows the equivalent capacitance value and reciprocal of the real part of the input admittance at different stub depths. It can be seen that, the greater the depth of the stub, the smaller the value of P0. The value will tend to 0 at the resonance. On the other hand, the equivalent capacitance value C increases with the stub depth, and the value will tend to infinity.
The input impedance of a three-stub waveguide can be similarly derived, as shown in Figure 4. The form of input impedance is the same as a single-stub waveguide. By obtaining the expression of , the input impedance and can be further derived as
where C1, C2, and C3 are equivalent capacitance with different stub depths, l1 is the length between the stub port and the load, l2 and l3 are the lengths between the stubs, and , , and are correction factors of stub port with different depths. The input impedance of the rectangular waveguide under different conditions can be calculated according to Equation (1), and the input impedance at the stub port can be calculated according to Equation (11). In addition, Equation (14) can realize the calculation of the input impedance at any position of the three-stub waveguide, which improves the accuracy for calculating the input impedance of the three-stub waveguide.
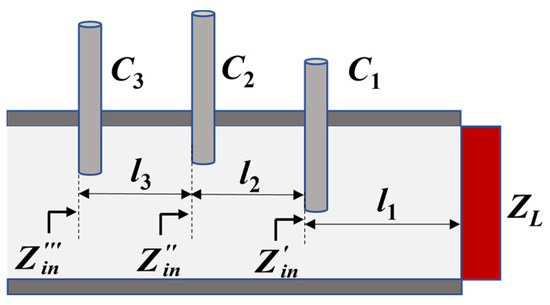
Figure 4.
Three-stub waveguide model.
3. A Low-Reflection Tuning Strategy
3.1. Impedance Matching Algorithm
The matching circuit generally has a matching forbidden zone, and the Smith chart is divided into two regions, the upper half region and the lower half region, as shown in Figure 5a and Figure 6a. For the load value in each area, a simple distributed matching circuit can be applied to complete the impedance matching [30]. Figure 5b can be used to match the load in the upper half of the Smith chart, and Figure 6b can be used to match the load in the lower half of the Smith chart. Each matching circuit contains two capacitors, and the length of each transmission line in the matching circuit is a quarter wavelength of the waveguide.
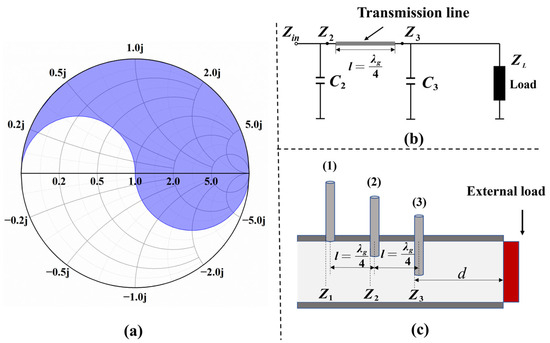
Figure 5.
(a) The upper half of the Smith chart. (b) Impedance matching circuit in the upper half area. (c) Tuning method of three-stub waveguide in the upper half area.
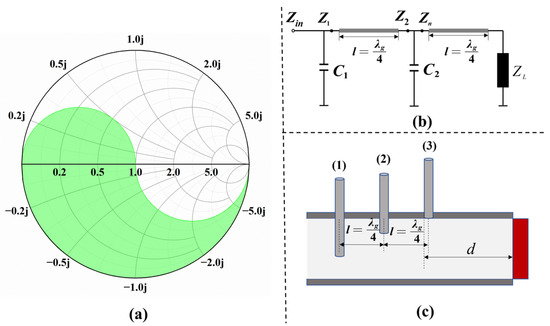
Figure 6.
(a) The lower half of the Smith chart. (b) Impedance matching circuit in the lower half area. (c) Tuning method of three-stub waveguide in the lower half area.
The matching circuit in Figure 5b is only used to match the impedance value in the upper half area of the Smith chart. The matching process is shown in Figure 7a. When performing impedance matching, the steps are as follows:
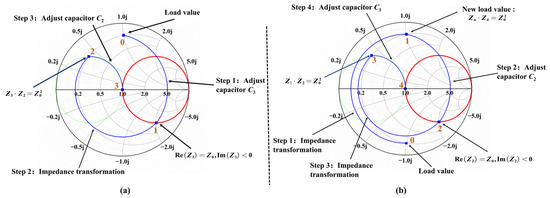
Figure 7.
(a) The impedance matching process of the upper half of the Smith chart. (b) The impedance matching process of the lower half of the Smith chart.
(1) Adjusting capacitor C3: The real part of the impedance value Z3 is made equal to the characteristic impedance of the transmission line by adjusting the capacitance, and the imaginary part of the impedance value Z3 is made less than 0.
(2) Impedance transformation: Through the quarter-impedance converter, Z3 and Z2 are exactly centrosymmetric about the matching point on the Smith chart.
(3) Adjusting capacitor C2: It only needs to adjust the capacitor C2 to a suitable value so that the value of Zin is equal to the value of the characteristic impedance of the transmission line, which completes the impedance matching.
The matching circuit in Figure 6b is only used to match the impedance value in the lower half region of the Smith chart. In Figure 6b, the load impedance will be transformed to the upper half area of the Smith chart through a transmission line, so the remaining adjustment procedure is exactly the same as that for the upper half region. The matching process is shown in Figure 7b.
Therefore, the stub spacing of the three-stub waveguide can be designed to a quarter wavelength of the waveguide. The waveguide can be equivalent to a transmission line, and the stubs have the role of capacitance. By adjusting the depth of the stubs, the functions of both circuits in Figure 5b and Figure 6b can be realized. As shown in Figure 5c, when only stub 2 and stub 3 are adjusted, it is equivalent to the function of Figure 5b. As shown in Figure 6c, when only stub 1 and stub 2 are adjusted, it is equivalent to the function of Figure 6b. Hence, as long as the load value is known, the adjustment sequence of the stubs can be known. Theoretically, it only needs to adjust two stubs for matching any external load, which simplifies the numerical calculation.
The external load and the rectangular waveguide with length d are equivalent to the equivalent load, as shown in Figure 8. According to Equation (1), the impedance is
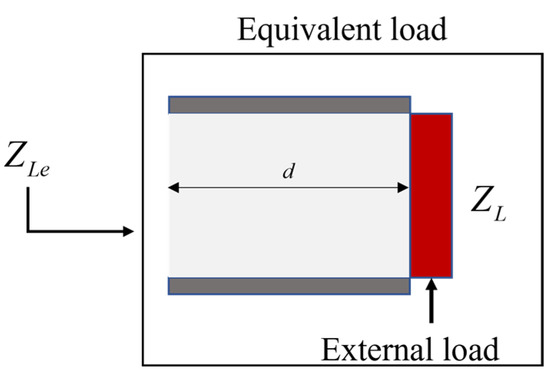
Figure 8.
The equivalent load of the external load and a length of waveguide.
The value of ZLe is used to determine whether the equivalent load is located in the upper or lower half region of the Smith chart to determine which two stubs to adjust.
Since P0 decreases with the increase in the stub depth, the change in the input impedance when increasing the stub depth is no longer a conductance circle but a shift to the inner part of the conductance circle when a matching load is connected, as shown in Figure 9a. Therefore, the division of the Smith chart should be revised, as shown in Figure 9b.
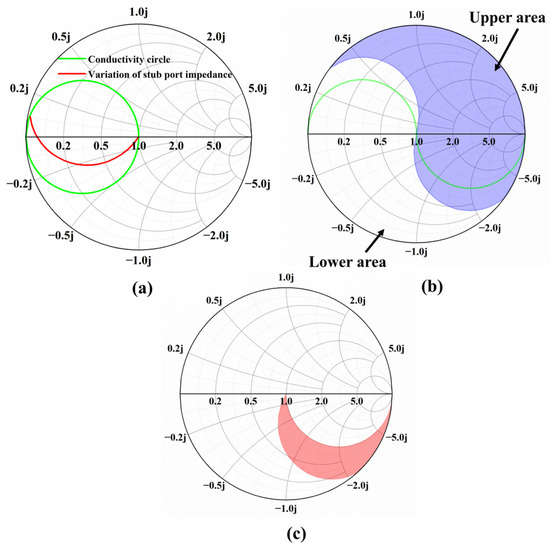
Figure 9.
The radius of the stub is 8.5 mm. (a) Variation in stub port impedance with stub depth. (b) Regional division of Smith chart. (c) The region of impedance after the first tuning.
In Figure 5c, adjusting the depth of stub 3 is required to make the real part of Z3 equal to the characteristic impedance of the waveguide. However, from Figure 9b, the real part of Z3 will be smaller than the characteristic impedance of the waveguide, and the imaginary part of Z3 is smaller than 0,
where α is a coefficient, which increases with the increase in modulus of Z3. The impedance Z3 is transformed to the lower region, as shown in Figure 9c. Therefore, there are various combinations of stub 2 and stub 3, and the criteria for selecting the optimal solution are
where and are the optimal depths of stub 2 and stub 3, and Γ is reflection coefficient. That is, a set of solutions is selected from the solution set to minimize the reflection coefficient of the energy input port. The basic procedure flowchart is as shown Figure 10.
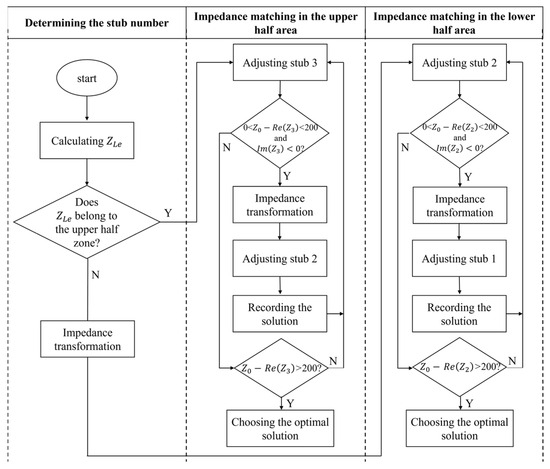
Figure 10.
Algorithm flowchart of three-stub waveguide impedance matching.
The above impedance matching algorithm is completely accomplished by numerical calculation, and the optimal solution can be obtained quickly.
3.2. Low-Reflection Tuning Strategy
After solving the optimal depth of the stubs, the first step of the tuning strategy is to judge the change in load and then adjust the other stubs in sequence; the whole tuning process can be completed quickly. We use the ideal equivalent circuit model to analyze the change in reflection when the load changes, as shown in Figure 11.
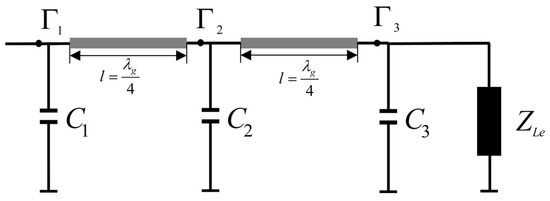
Figure 11.
An ideal equivalent circuit model for three-stub waveguides.
- a.
- Initial state tuning strategy
In the initial matching process, the initial depth of three stubs is 0. As shown in Figure 12a, when the load is in region AU (the impedance matching process is shown in Figure 7a), the reflection will first decrease and then increase in the process of only adjusting stub 3. When the load is in region BU, the reflection will increase in the process of only adjusting stub 3. We need to suppress the increase in reflection as much as possible. When the load value is in region BU, adjusting stub 3 while adjusting stub 2 can effectively suppress the increase in reflection.
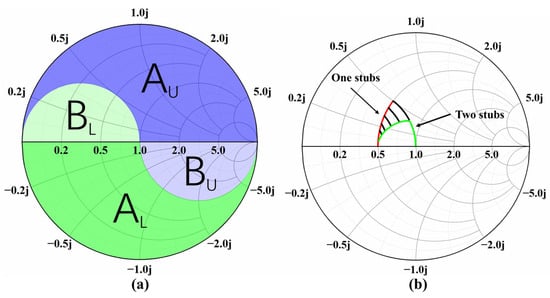
Figure 12.
(a) Region A and region B of the upper and lower half. (b) Reflection changes when two stubs are adjusted simultaneously.
Assume that the load is in the upper half area and the admittance of the load value is X + jA. When only stub 3 is adjusted, the modulus of reflection coefficient at stub 2 port is
When stub 3 and stub 2 are adjusted simultaneously, the modulus of reflection coefficient at stub 2 port is
where D = −2
ωC2(A + ωC3) + │Yin3│2ω2C22, and Yin3 is the input admittance of stub 3 port. When A ≥ 0 and the depth of stub 2 does not exceed the stub 3, it can be proved that D must be less than 0.
Due to D < 0 in small depth of the stub, obviously, |Γ1| < |Γ0. When A ≥ 0, the load value is in region BU, so the simultaneous adjustment of stub 2 and stub 3 effectively suppresses the increase in reflection. The same result can be obtained when only adjusting stub 2. As shown in Figure 12b, the simultaneous adjustment of two stubs is better than the adjustment of a single stub in this case.
Therefore, when the load value is in region AU, stub 3 needs to be adjusted first to make the imaginary part of the input impedance at the stub 3 port zero (Im(Z3) = 0). Then, stub 3 and stub 2 are adjusted simultaneously. When the load value is in region AL, stub 2 needs to be adjusted first to make the imaginary part of the input impedance at the stub 2 port zero (Im(Z2) = 0). Then, stub 2 and stub 1 are adjusted simultaneously.
When the load value is in region BU, stub 2 and stub 3 need to be adjusted at the same time. When the load value is in region BL, stub 2 and stub 1 need to be adjusted at the same time.
- b.
- Online state tuning strategy
In the real-time tuning system, external loads are constantly changing. If the stubs are adjusted randomly, it may cause large reflection. In the case of load changes, it is difficult to deduce by formula how to adjust the stubs to gradually reduce reflection, and it is necessary to analyze them in different situations and formulate corresponding strategies.
When the load changes only in the upper half area, the tuning approach is to adjust two stubs simultaneously. As both stubs 2 and 3 have a certain depth, when adjusting a single stub, the port impedance gradually moves towards the matching point, as shown in Figure 13a,b. However, when two stubs are adjusted simultaneously, under the cooperative action of two stubs, the port impedance will approach the matching point faster, which has better performance compared to single-stub adjustment. Because the upper and lower half areas are symmetrical, the adjustment mode of the lower half area is completely the same as that of the upper half area.
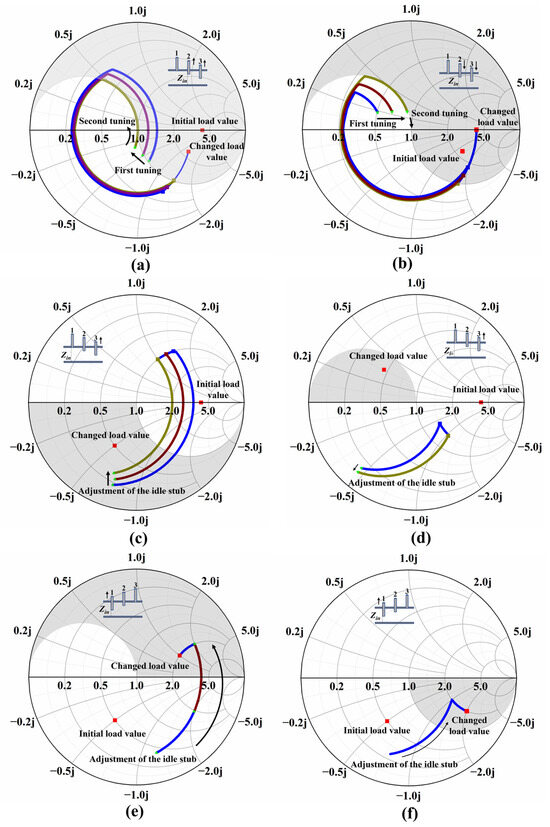
Figure 13.
The variations in reflection in dynamic matching. (a,b) Represent the tuning processes where the load value changes in the upper half. (c,d) Represent the process of adjusting the idle stub 3. (e,f) Represent the process of adjusting the idle stub 1.
When the load changes from the upper half area to the lower half area, there are two situations. As shown in Figure 13c, the reflection is decreasing in the process of adjusting the idle stub. As shown in Figure 13d, although the reflection is increasing in the process of adjusting the idle stub, the reflection changes very little. After stub 3 is adjusted to 0, since the depth of stub 1 is 0 and stub 2 has a certain depth, the port impedance value at stub 2 is considered to be in region BU and AL. In both cases, it is effective to adjust both stubs simultaneously. When the port impedance value is in region BU, it can be proved by (19). When the port impedance value is in region AL, due to the fact that stub 2 has a certain depth, its adjustment range will not be large, and the depth of stub 1 remains small after stub 2 has been adjusted to the proper position. Therefore, compared with adjusting a single stub, adjusting two stubs at the same time will not cause excessive reflection, or even reduce the reflection.
When the load changes from the lower half area to the upper half area, there are also two situations in the process of adjusting the idle stub. As shown in Figure 13e, the reflection will decrease first and then increase in the process of adjusting the idle stub. To suppress the increase in reflection, stub 3 needs to be adjusted while adjusting stub 1 to 0. Because adjusting stub 3 can move the impedance at this port to region BU, and stub 2 has a certain depth, the reflection will not increase or even decrease when adjusting stub 1. As shown in Figure 13f, the reflection is decreasing in this case. After stub 1 is adjusted to 0, stub 2 and stub 3 are adjusted at the same time. The reason remains that stub 2 has a certain depth and its adjustment range is not too large.
The initial tuning strategy and online tuning strategy proposed are shown in Figure 14a and 14b, respectively.
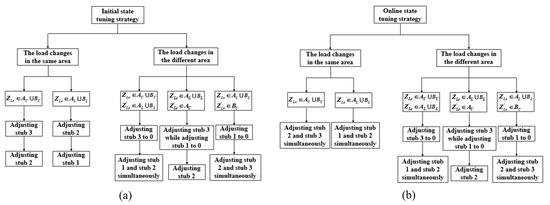
Figure 14.
A low-reflection tuning strategy. (a) Initial state tuning strategy. (b) Online state tuning strategy.
4. Experimental Verification and Discussion
4.1. Validation of Matching Algorithms
The size parameters of the three-stub waveguide model are shown in Figure 15. The distance between the stubs is 43 mm, which is approximately a quarter wavelength (43.33 mm) at 2.45 GHz. The three-stub waveguide used in the experiment is shown in Figure 16a, the waveguide calibration device is shown in Figure 16b, and the load diaphragm is shown in Figure 16c. The radius of the stub is 8.5 mm, P0 and C are calculated in the simulation, which can be derived from Equation (13), and the values of P0 and C at different stub depths are shown in Figure 17a and 17b, respectively.
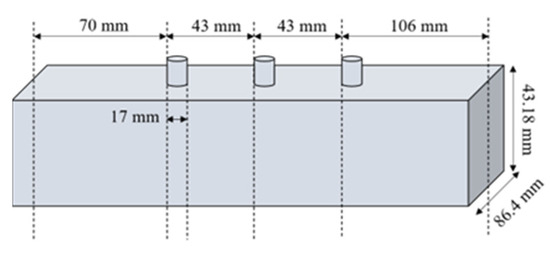
Figure 15.
Dimensions of the three-stub waveguide used in the experiment.

Figure 16.
(a) Experimental environment of three-stub waveguide. (b) Waveguide calibration device. (c) Load diaphragm.
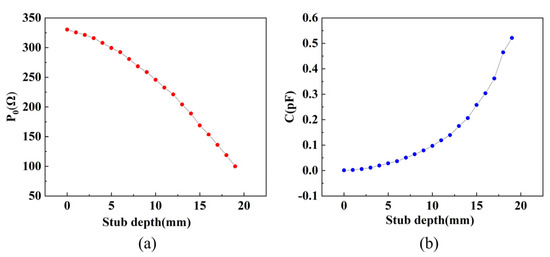
Figure 17.
The values of P0 and C at different stub depths with a stub radius of 8.5 mm. (a) The values of P0 at different stub depths. (b) The values of C at different stub depths.
When the three-stub waveguide is connected to a matching load, the S-parameter and impedance are measured using a vector network analyzer (ZVB 8, ROHDE&SCHWARZ, Munich, Germany). Only stub 1 is adjusted, and the stub depth is varied from 0 to 19 mm in a 1 mm step. The verification results for Equation (11) are shown in Figure 18. Figure 18a,b show the amplitude and phase of S11, respectively. Figure 18c,d show the real and imaginary parts of the input impedance, respectively. We define an error factor ε,
where ε is the error between the calculated value of the input impedance and the measured value, is the calculated value, and is the measured value. The experimental results of the input impedance at different stub depths basically match with the calculated results, with an error factor ε not exceeding 0.1.
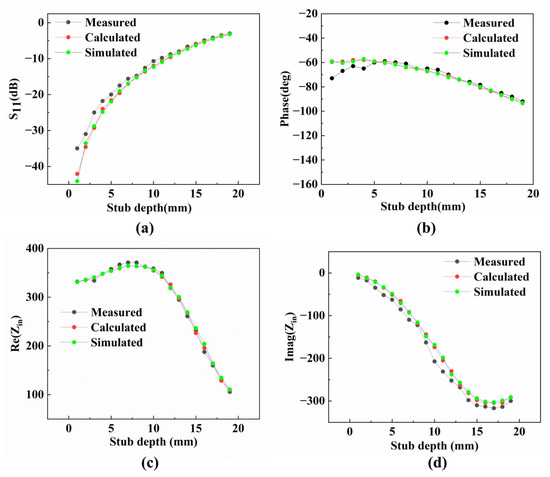
Figure 18.
(a) Magnitude of S11. (b) Phase of S11. (c) Real part of input impedance. (d) Imaginary part of input impedance.
After verifying the formula of the input impedance of the three-stub waveguide, the effectiveness of the algorithm is further verified in the impedance matching process. The impedance matching algorithm is programmed, and the depth of each movement of the stub is 0.2 mm. Loads with different impedance can be generated through different load diaphragms and external environments, and then impedance matching is carried out for these different loads.
The initial depth of the three stubs is 0 before each measurement. By measuring the magnitude and phase of S11 on the waveguide port plane, the impedance of the external load can be inversely deduced using Equation (1) so that the program can calculate the optimal solution of the stub depths, then adjust the stubs manually. The calculated stub depths for different load values and test results are shown in Table 1.

Table 1.
Matching algorithm test data.
According to test results, it can be seen that only two stubs need to be adjusted to complete the impedance matching, which is in line with the theory. It also verifies the reliability of the formula proposed in this paper. From the test results, the matching effect of the load impedance in the upper half of the Smith chart is obviously better than that in the lower half of the Smith chart; this is due to the fact that the stub spacing does not reach the ideal condition, and there is certain error in parameter measurement. However, the experiment achieved good verification effects generally, the |S11| is basically below −18 dB, and the solution of stub depths can be produced within 0.1 s by the procedure.
4.2. Validation of the Tuning Strategy
As shown in Figure 19a, we connected a cavity behind the three-stub waveguide in the simulation. A small ball with variable volumes is placed in the cavity. The small ball is set as the impedance boundary condition. When the radius of the ball changes, the impedance value of its external load changes. As shown in Figure 19b, the impedance of the external load changes with the volume.
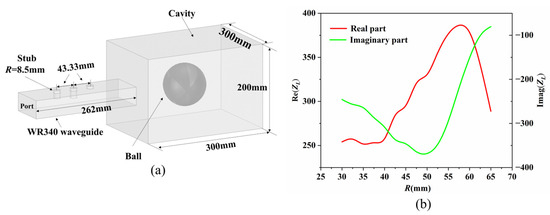
Figure 19.
(a) Simulation model. (b) Variation in external load value with ball radius.
As shown in Figure 20a, at the initial position, the stub depth is 0; that is, the first matching process is initial state matching. We can see that the reflection is basically decreasing, and there is no large reflection in this process. When load mutation occurs, it is an online state matching process, and the reflection can be gradually reduced by adjusting the stubs in sequence, avoiding the large reflection in the tuning process.
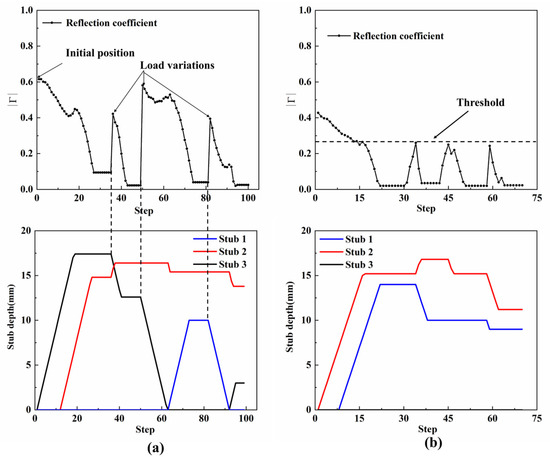
Figure 20.
Variation in reflection coefficient during tuning in simulation. (a) Load mutation. (b) Load changes continuously.
The continuous change in load value is simulated by continuously changing the radius of the ball. As shown in Figure 20b, by setting a threshold, reflection can be stabilized within the threshold when the load value continuously changes.
As shown in Figure 21, we connected a cavity behind the three-stub waveguide in the experiment. We put a paper cup with 100 mL of water inside the cavity and placed the cups in sequence in the cavity to simulate the change in load. The dimensions of the paper cup and the cavity are shown in Figure 22a,b, and the interior of the cavity is shown in Figure 22c. The sequence of movement of the paper cup inside the cavity is shown in Figure 22d. We moved the paper cup 18 times, and the external load values and equivalent load values of the paper cups at different positions are shown in Table 2. When the port reflection is greater than −15 dB, the stubs are adjusted. The experimental results are shown in Figure 23. An experimental data point is recorded every time the stubs are moved by 2 mm. It can be seen that the reflection is gradually decreasing during the tuning process.

Figure 21.
Experimental verification device of the low-reflection tuning strategy.
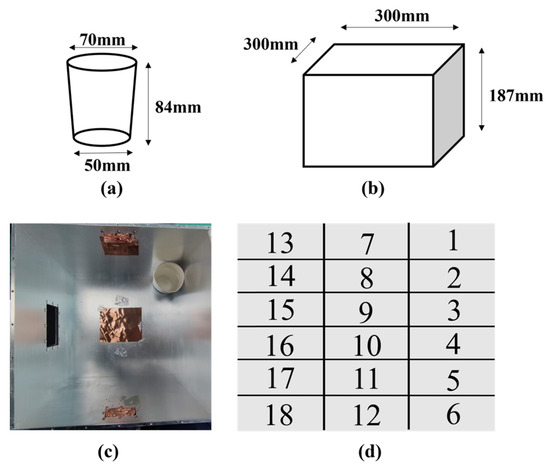
Figure 22.
(a) The size of the paper cup in the cavity. (b) Dimensions of the cavity. (c) The interior of the cavity. (d) The order of moving paper cups.

Table 2.
Measured load values.
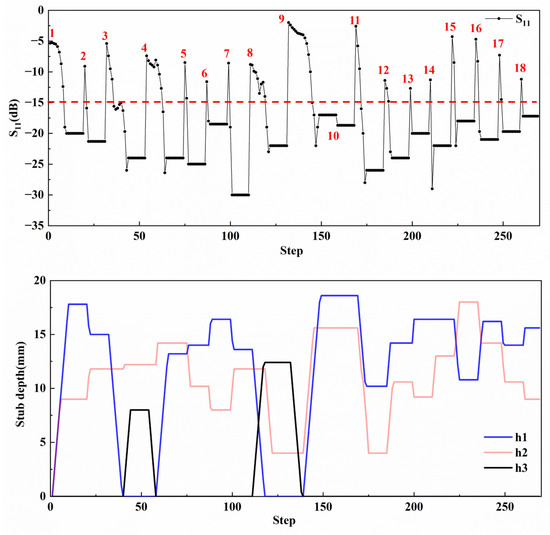
Figure 23.
Changes in S11 and the stub depths during tuning.
We compare our work with previous studies, as shown in Table 3. Due to the improvement of the calculation formula for input impedance, the proposed impedance matching algorithm can accurately calculate the depth of the stubs, thus achieving good impedance matching results without the need for iteration or finetuning of the algorithm. Although increasing the number of stubs can improve the matching effect, the production cost will also increase. In addition, this work also proposes a low-reflection strategy to suppress large reflections during the process of adjusting the stubs.

Table 3.
Comparison with previous work.
5. Conclusions
In this paper, we proposed a low-reflection adjustment strategy for a three-stub waveguide, which can effectively suppress the increase in reflection during the tuning process. We conducted an analysis from a field perspective on the impact of the stub on the input impedance of the stub port, improving the calculation accuracy for determining the input impedance of the stub port by adding a correction factor. The error between the calculated values and the measured/simulated values is relatively small, with an error factor ε not exceeding 0.1. By using the analysis method of equivalent circuits, we designed the stub spacing with the value of one-quarter of the waveguide wavelength. With this configuration, we can achieve impedance matching using two stubs, and good matching results can be obtained under different load conditions, with the |S11| being less than −15 dB. Afterward, in order to adjust the stubs and achieve a stable reduction in reflection, we divided the Smith chart into four regions and used an ideal equivalent circuit model to analyze the impact of moving stubs on reflection. By calculating the interactions between the stubs, a low-reflection adjustment strategy was proposed and analyzed. Finally, we set up an experimental system where we placed a cup of water at different positions within the cavity to simulate variations in the load. When the reflection exceeded the threshold (−15 dB), the adjustment process was initiated. Based on the experimental results, it is evident that reflection can effectively decrease during the stub adjustment process.
Author Contributions
Conceptualization, H.Z., L.D. and Y.Y.; methodology, R.L. and Y.Y.; validation, R.L., S.L. and Z.Z.; writing—original draft preparation, R.L. and Y.Y.; writing—review and editing, T.H., H.Z. and Y.Y.; project administration, Y.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (Grant number: 61971295), the Key Technology of Shunde District (Grant number: 2130218002514), National Key Project (Grant number: GJXM92579), and Nature Science Foundation of Sichuan Province (Grant number: 2022NSFSC0562).
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
We declare that we do not have any commercial or associative interests that represent a conflict of interest in connection with the work submitted.
References
- Nakano, S.; Kim, J.-H.; Hwang, T.; Kasada, R.; Nakamichi, M. Dissolution and recovery of beryllium from beryl using a novel wet process with microwave heating. Nucl. Mater. Energy 2022, 30, 101113. [Google Scholar] [CrossRef]
- Jung, S.; Kwak, J.H.; Han, S.M. Guided-wavelength-controlled dynamic microwave heating in a near-cutoff waveguide. Appl. Therm. Eng. 2021, 188, 116630. [Google Scholar] [CrossRef]
- Chi, C.; Fu, W.; Zhang, C.; Lu, D.; Han, M.; Yan, Y. Dual-Frequency Microwave Plasma Source Based on Microwave Coaxial Transmission Line. Appl. Sci. 2021, 11, 9873. [Google Scholar] [CrossRef]
- Norrawit, T.; Akira, Y.; Nobuya, H. Surface sterilization using LF-microwave hybrid plasma. Jpn. J. Appl. Phys. 2021, 60, SAAE01. [Google Scholar]
- Shevelev, O.; Petrova, M.; Smolensky, A.; Osmonov, B.; Toimatov, S.; Kharybina, T.; Karbainov, S.; Ovchinnikov, L.; Vesnin, S.; Tarakanov, A.; et al. Using medical microwave radiometry for brain temperature measurements. Drug Discov. Today 2022, 27, 881–889. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, C.; Huang, H.; Guo, W.; Yu, J.; Qiu, J. Carbon-enabled microwave chemistry: From interaction mechanisms to nanomaterial manufacturing. Nano Energy 2021, 85, 106027. [Google Scholar] [CrossRef]
- Bilik, V.; Bezek, J. Investigation of High-Power Limits of Stub Tuners by Means of Electromagnetic Simulation. In Proceedings of the 2008 14th Conference on Microwave Techniques, Prague, Czech Republic, 23–24 April 2008; pp. 1–4. [Google Scholar]
- Bilik, V.; Bezek, J. High power limits of waveguide stub tuners. J. Microw. Power Electromagn. Energy 2010, 44, 178–186. [Google Scholar] [CrossRef]
- Zhuang, Q.; Yan, F.; Jiang, Z.; Liu, M.; Xiong, Z.; Yan, C. Study and design of a contracting waveguide phase shifter for s-band high-power microwave applications. In Proceedings of the 2019 IEEE 2nd International Conference on Electronics Technology (ICET), Chengdu, China, 10–13 May 2019; pp. 162–165. [Google Scholar]
- Duan, Y.; Fu, Y.; Shi, Y.; Pang, H.; Huang, L. T-ZnOw/FCIPs with vertical-orientated structure achieving temperature-stable broadband microwave absorption. Appl. Surf. Sci. 2022, 613, 155988. [Google Scholar] [CrossRef]
- Livshits, P.; Gurfinkel, M.; Fefer, Y. VLSI MOSFETs lifetime reduction caused by impedance mismatch. Microelectron. Eng. 2011, 88, 28–31. [Google Scholar] [CrossRef]
- Ishibashi, K.; Sawado, E. Three-dimensional analysis of electromagnetic fields in rectangular waveguides by the boundary integral equation method. IEEE Trans. Microw. Theory Techn. 1990, 38, 1300–1308. [Google Scholar] [CrossRef]
- Yang, N.; Huang, Y. Analysis of a post with arbitrary cross-section and height in a rectangular waveguide. IEE Proc. Part. H. Microwaves Antennas Propag. 1991, 138, 475–480. [Google Scholar]
- Kocabas, S.E.; Veronis, G.; Miller, D.A.B.; Fan, S. Transmission Line and Equivalent Circuit Models for Plasmonic Waveguide Components. IEEE J. Quantum Electron. 2008, 14, 1462–1472. [Google Scholar] [CrossRef]
- Wyslouzil, W.; VanKoughnett, A.L. Automated Matching of Resonant Microwave Heating Systems. J. Microw. Power Electromagn. Energy 1973, 8, 89–100. [Google Scholar] [CrossRef]
- Mallorqui, J.J.; Aguasca, A.; Cardama, A.; Pagès, R.; Haro, J. Application of the conjugate gradient method to a self-matching network for industrial microwave heating antennas. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Orlando, FL, USA, 11–16 July 1999; pp. 978–981. [Google Scholar]
- Bandler, J.W.; Cheng, Q.S.; Dakroury, S.A. Space Mapping: The State of the Art. IEEE Trans. Microw. Theory Techn. 2004, 52, 337–361. [Google Scholar] [CrossRef]
- Koziel, S.; Bandler, J.W. Space Mapping with Multiple Coarse Models for Optimization of Microwave Components. IEEE Microw. Wireless Compon. Lett. 2008, 18, 1–3. [Google Scholar] [CrossRef]
- Cheng, Q.S.; Bandler, J.W.; Nikolova, N.K.; Koziel, S. A Statistical Input Space Mapping Approach for Accommodating Modeling Residuals. In Proceedings of the 2013 IEEE MTT-S International Microwave Symposium Digest (MTT), Seattle, WA, USA, 2–7 June 2013; pp. 1–3. [Google Scholar]
- Parro, V.C.; Pait, F.M. An automatic impedance matching system for a multi point power delivery continuous industrial microwave oven. In Proceedings of the 2004 IEEE International Conference on Control Applications, Taipei, Taiwan, 2–4 September 2004; pp. 143–148. [Google Scholar]
- Chtcherbakov, A.A.; Swart, P.L. Automatic microwave tuner for plasma deposition applications using a gradient search method. J. Microw. Power Electromagn. Energy 1997, 32, 28–33. [Google Scholar]
- Zhou, L.; Kuang, Y.; Li, S.; Fan, X.; Cheng, Q.S. Automatic Impedance Matching for Three-Stub Waveguide Tuner Based on Space Mapping. In Proceedings of the 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Guangzhou, China, 19–22 May 2019; pp. 1–3. [Google Scholar]
- Plaza-Gonzalez, P.J.; Penaranda-Foix, F.L.; Canos, A.J.; Catala-Civera, J.M. Microwave High-Power Four-Posts Auto-Matching System. IEEE Trans. Instrum. Meas. 2007, 56, 1006–1011. [Google Scholar] [CrossRef]
- Lai, S.; Qiao, J.; Rasool, N.; Li, K.; Zhu, H.; Yang, Y. A dynamic impedance matching algorithm of three-stub tuners based on equivalent circuit analysis. J. Microw. Power Electromagn. Energy 2020, 54, 330–347. [Google Scholar] [CrossRef]
- Bilik, V. Stub Swapping in Automatic Three-Stub Impedance Matching Systems. In Proceedings of the 2013 Conference on Microwave Techniques (COMITE), Pardubice, Czech Republic, 17–18 April 2013; pp. 192–196. [Google Scholar]
- Bilik, V. Optimizing tuning stubs motion in automatic three-stub impedance matching systems. In Proceedings of the International Conference on Microwave and High Frequency Heating, Nottingham, UK, 16–19 September 2013; pp. 222–225. [Google Scholar]
- Varan, M.; Ergüzel, A.T.; Genç, H.H.; Ulusoy, B.; Öylek, I.; Ay, M. Design and implementation of an open source transmission line impedance matching educational framework. Comput. Appl. Eng. Educ. 2020, 28, 724–736. [Google Scholar] [CrossRef]
- Marcuvitz, N. Waveguide Handbook; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Bilik, V.; Bezek, J. Experiment-based characterization of thick capacitive stub in a rectangular waveguide for vector autotuning purposes. J. Electr. Eng.-Slovak. 1998, 49, 299–305. [Google Scholar]
- Popov, M.; He, S. Design of an automatic impedance-matching device. Microw. Opt. Technol. Lett. 1999, 20, 236–240. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).