Abstract
For energy-storage-assisting conventional units to participate in the primary frequency regulation of a power system, firstly, based on the frequency regulation mechanism of virtual inertial control (VIC) and virtual droop control (VDC) of energy storage, we analyze the effect of the action timing of energy storage on the frequency deviation of the grid under two control methods and put forward a reasonable combination of the two control methods; on this basis, we also put forward hybrid energy storage adaptive VIC and VDC based on the demand of VIC and VDC on the power and capacity of energy storage. On this basis, based on the demand of VIC and VDC on the power and capacity of energy storage, a hybrid energy storage adaptive VIC and VDC coordinated control strategy based on supercapacitor–lithium batteries is proposed, whereby a high-power storage supercapacitor responds to inertial control signals to rapidly suppress a drop in frequency, and the high-capacity lithium battery responds to droop control signals to perform long-time droop control. The high-capacity lithium battery responds to the sagging control signal and is used to perform a long-time sagging power response; finally, in order to avoid the state of charge (SOC) of energy storage falling into a low/high working condition and losing the subsequent frequency regulation ability, an adaptive power control strategy of energy storage based on the improved logistic function is proposed. The simulation results show that under typical load disturbance, the SOC level of the proposed strategy increases by 19.17% and 30.16%, respectively, compared with that of the single-lithium strategy and no energy storage, and the SOC level of the supercapacitor and lithium battery increases by 29.4% and 2.1%, respectively, compared with that of logistic optimization.
1. Introduction
The growing demand for energy has aggravated environmental pollution caused by the burning of fossil fuel resources, and the development of renewable and low-carbon energy sources such as wind and hydrogen has become an inevitable trend, and our country has also put forward the “3060 goal” and incorporated it into the “14th Five-Year Plan”. However, the mismatch between source and load caused by the continuous increase in the proportion of wind and solar installations has also brought about serious challenges to the frequency adjustment of power systems. At the same time, in recent years, the rapid development of an energy storage system as a new type of power device that can be charged and discharged, with fast power response characteristics, has become an indispensable part of the security and stability of today’s power systems [1,2].
Energy storage can be widely used in various aspects of a power system due to its power flexibility [3,4], which can participate in power system peak and frequency regulation but also smooth new energy power fluctuations [5,6] to ensure the security and stability of large-scale wind and other new energy grid-connected power systems. Among them, lithium-battery-based electrochemical energy storage, due to its mature technology and high degree of scale, has been widely adopted by most experts and scholars [7]. In the field of power system frequency regulation, due to the power system frequency regulation time scale, the response time of energy storage equipment is more in line with the use of energy storage to assist the conventional unit involved in power system frequency regulation, a topic which has become the focus of many scholars. The authors of [8] constructed a mechanism model for energy storage to participate in wind power leveling, laying a theoretical foundation for energy-storage-assisted power system frequency regulation. The authors of [9] used energy storage to assist wind turbines to jointly participate in grid frequency regulation, so that the wind turbine has a similar traditional unit of primary frequency regulation ability, and they constructed a storage economy to reach the goal of establishing an optimization model so as to find the optimal capacity configuration of energy storage. The authors of [10] analyzed the characteristics of SOC that may fall into poor working conditions after energy storage is involved in one-time FR with VDC, and they proposed an energy storage SOC reconfiguration control strategy after one-time FR which can significantly improve the service life of energy storage. The authors of [11] analyzed the characteristics of wind power output and proposed an optimized VDC control strategy for energy storage participation in wind-power-containing grids, which can effectively suppress wind power fluctuations. The authors of [12], with VIC, simulated the inertial response characteristics of conventional units and energy storage because of its fast response capability to obtain a better frequency regulation effect. The authors of [13] produced a mechanism model between VIC and grid frequency for energy storage using VIC when parameter tuning and control strategy selection are used to lay a theoretical foundation. In order to overcome the problem of the frequent penetration of distributed energy in a microgrid environment, the authors of [14] proposed the concept of a virtual power plant and proposed an adaptive VDC control strategy with a remarkable frequency modulation effect.
Most of the existing strategies only consider a virtual control strategy or simply the superposition of VIC and VDC [15,16,17], which ignores the intrinsic frequency regulation mechanism of the two. The authors of [18], based on the energy storage and frequency regulation outputs of VIC and VDC, conclude that the simultaneous use of VIC and VDC before frequency deviation reaches an extreme value is beneficial to inhibit the rapid fall of frequency, while after frequency deviation reaches an extreme value, the energy storage outputs of VIC and VDC present mutual counteracting characteristics to weaken the effectiveness of part of the frequency regulation, meaning that adopting VIC and VDC before the frequency deviation reaches the extreme value is proposed, considering only the VDC energy storage output strategy after it reaches an extreme value.
However, virtual inertia control focuses on the support of system inertia, which is proportional to the rate of change in the frequency deviation; virtual sag control focuses on the frequency deviation itself, which is proportional to the size of the value of the frequency deviation, and the use of a type of energy storage to participate in FR often does not fully match the FR mechanism of the two controls. Therefore, on the basis of clarifying the action timing of energy storage, it is necessary to choose the appropriate type of energy storage to achieve the best frequency regulation effect based on the frequency regulation demand for energy storage of the two.
Therefore, this paper proposes a hybrid energy storage adaptive VIC and VDC coordinated control strategy taking into account SOC optimization for energy-storage-assisting conventional units to participate in the primary frequency regulation of the power system. Firstly, based on the energy storage output mechanism of VIC and VDC, we analyze the influence of the action timing of the two control methods on the grid frequency deviation and put forward a control method that reasonably combines the two; secondly, based on the virtual inertia and the sag control demand for energy storage power and capacity, we put forward a hybrid energy storage adaptive VIC and VDC coordination control strategy based on supercapacitor–lithium batteries and put forward a hybrid energy storage adaptive VIC and VDC coordination control strategy based on super capacitors and lithium batteries, in which the power-type power storage supercapacitor, which has high power, responds to the inertia control signal and quickly suppresses the energy storage capacity. The energy storage supercapacitor responds to the inertia control signal to quickly suppress the frequency drop, while the high-capacity lithium battery responds to the sag control signal and performs a long-duration sag power response; finally, in order to avoid the energy storage SOC from falling into the lower/higher severe operating conditions and losing the subsequent frequency regulation capability, the energy storage adaptive power control strategy based on the improved logistic function is proposed. The simulation verifies the effectiveness of the proposed strategy.
2. This Paper’s Hybrid Energy Storage FR Framework
Figure 1 shows the framework of energy storage frequency regulation under the control strategy of this paper. First, when the system generates frequency deviation Δf due to power shortage, calculate its frequency deviation change rate and input the two into the energy storage artificial setting dead zone module; then, when Δf or exceeds the deadband range, judge the positivity and negativity of the product of Δf and , if , then adopt the control strategy of superimposing the VIC and the VDC at the same time; if , then adopt the control strategy of the VDC only. In this regard, the supercapacitor with higher power density is used to assume the FR power command of the VIC, while the lithium battery with higher energy density is used to assume the FR power command of the VDC. The details will be described and analyzed in detail in Section 2 and Section 3 of this paper.
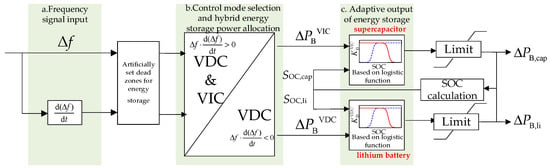
Figure 1.
The current energy storage frequency regulation framework.
3. Primary FR model of a Regional Power System with Energy Storage
3.1. Primary FR Model for Conventional Thermal Power Units
In this paper, a thermal power unit with larger capacity is taken as a conventional FR unit, the governor and reheat turbine are mainly considered in the FR process, and the corresponding FR transfer function can be expressed as [19].
3.2. Generalized Control Model for Primary FR of Energy Storage
Compared with conventional FR units, in order to reflect the fast response characteristics of energy storage, the first-order inertia link is generally used to equate its output characteristics. It has been pointed out in [20] that appropriate simplification of the energy storage model can increase the simulation speed while ensuring the simulation accuracy and its transfer function can be expressed as
In addition, in order to fully characterize the remaining FR capacity of the energy storage to reflect the advantages and disadvantages of its own state, this paper further introduces the state of charge (SOC) of the energy storage to evaluate it as
In summary, this paper combines Formulas (1) and (2) and takes into account the power and SOC constraints to construct a generalized control model for energy storage participating in primary FR as shown in Figure 2, where E0(s) is the primary FR signal accepted by the energy storage and SOC0 is the initial SOC of the energy storage.
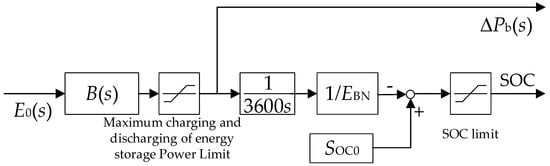
Figure 2.
General control model of energy storage and primary frequency regulation.
3.3. Dynamic Modeling of Primary Frequency Regulation of Regional Power Systems with Energy Storage
Currently, the common control methods for energy storage to participate in primary FR include VIC and VDC. When the system has a load disturbance , the system frequency will change abruptly and, at this time, the dynamic model of the primary FR of the regional power system containing energy storage can be expressed as [21]
the output power and the corresponding frequency deviation are as shown in Formulas (6) and (7), respectively, when the storage battery adopts VIC and VDC.
Combining the frequency deviation in Formulas (6) and (7), the literature [18] has analyzed the initial frequency rate of change and the steady state frequency deviation of the system under the two control modes as follows:
From Formulas (8) and (9), it can be seen that when VIC is used, the initial rate of change of frequency depends on the inertia coefficient H of the thermal unit itself and the virtual inertia coefficient of the energy storage under the system load perturbation; the steady state frequency deviation is irrelevant with . It can be seen that VIC can quickly suppress the initial rate of change of frequency but cannot improve the system steady-state frequency deviation. When VDC is used, depends only on the thermal unit’s own H; depends on both and . It can be seen that VDC can improve the steady-state frequency deviation but does not work on the initial frequency deviation rate of change.
In addition, the literature [22] also utilizes the sensitivity analysis to further conclude that the use of VDC for energy storage can effectively improve the FR effect throughout the FR cycle, while the use of VIC can only play a role in recovering the frequency deviation before the frequency reaches the lowest point but will inhibit the recovery of the frequency after the frequency deviation reaches the maximum value. Therefore, it is necessary to combine the FR characteristics of different types of energy storage and select suitable FR control methods for them to realize the control effects of and at the same time.
4. Primary FR Control Strategy for Supercapacitor–Lithium Battery Counting and SOC Optimization
4.1. Adaptive Coordinated Control of VIC and VDC Based on Supercapacitor–Lithium Battery
From the analysis in Section 3.3, it can be seen that the energy storage involved in VIC can increase the system inertia, the energy storage output is proportional to the rate of change of frequency when a sudden change in the system frequency needs to respond quickly to inhibit the change of frequency, and at the same time there is the disadvantage of inhibiting the recovery of the frequency after the frequency deviation reaches the extreme value. Energy storage involved in the VDC when the output and the frequency deviation is proportional to the frequency in the entire FR cycle can be effective in inhibiting the deterioration of the frequency, however, VDC requires energy storage to produce power for a long period of time, which requires energy storage to be configured with a higher FR capacity. It can be seen that VIC and VDC should be used before the frequency reaches the extreme value, and only VDC should be used after the extreme value point to ensure the effect of frequency regulation. However, the literature [18,19,20,21] suggests that a single energy storage to implement the above strategies at the same time cannot reflect the characteristics of the energy storage involved in the VIC and VDC at the same time, which ignores that the characteristics of the VIC and VDC for the energy storage power and capacity requirements are different, therefore, in order to give full play to the advantages of the power-type and energy-type energy storage in the two modes of FR control, this paper further puts forward a supercapacitor–lithium-battery-based adaptive VIC and VDC control. An adaptive coordinated control strategy of VIC and VDC is further proposed in this paper.
At present, the most commonly used and the most mature energy storage is based on lithium batteries as the main energy-based energy storage, which is characterized by high energy density and low power density. Supercapacitor-based power-type energy storage is less used in the field of FR, which is characterized by high power density and small energy density, which is due to the high cost and small capacity of supercapacitors, which are not suitable for today’s drastic load disturbances in systems. Table 1 demonstrates the performance comparison between the typical power-type and energy-type energy storage [14]. It can be seen that power-based energy storage is suitable for VIC due to its high power density and fast response to frequency-changing signals, while energy-based energy storage is suitable for VDC due to its high energy density, which can leave a sufficient FR margin to perform FR tasks throughout the FR cycle.

Table 1.
Comparison of power-type and energy-type energy storage performance.
In summary, in order to solve the limitations of a single control method on the frequency control effect and make full use of the complementary advantages of VIC and VDC, this paper firstly proposes an adaptive coordinated control strategy of VIC and VDC. When the system frequency changes abruptly (i.e., energy storage is needed for inertial support), since VDC can improve the frequency control effect throughout the frequency control cycle, the control strategy of superposition of VIC and VDC should be adopted at this time; when the frequency deviation reaches the maximum value, since VIC will inhibit the frequency recovery instead, only the VDC control strategy should be adopted at this time. When the frequency deviation reaches the maximum value, the VIC will inhibit the frequency recovery, and only the VDC control strategy should be adopted. Then, considering that power-based energy storage is applicable to VIC and energy-based energy storage is applicable to VDC, the output power of hybrid energy storage and its auxiliary thermal power units to participate in the primary FR of the regional grid are obtained in the dynamic model as shown in Formula (10) and Figure 3.
where and are the FR transfer functions of the supercapacitor and lithium battery, respectively.
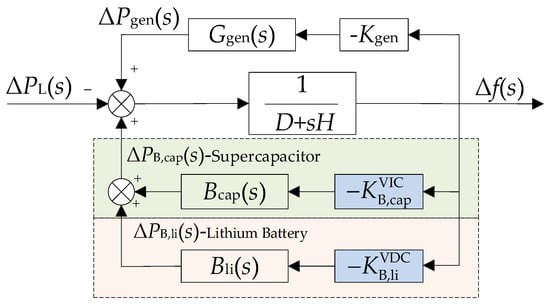
Figure 3.
Hybrid energy storage auxiliary thermal power units participate in the primary frequency regulation model of the regional power grid.
From Formula (10) and Figure 3, the frequency deviation under the control strategy of this paper is given as
Further, the initial frequency rate of change and the steady-state frequency deviation can be calculated as
4.2. Improved Generalized Logistic Function Design Method Based on Energy Storage Output Constraints
When the energy storage battery responds to the demand of system frequency regulation, if it has been operating with a given inertia/sag coefficient, it is very easy to saturate or exhaust the energy storage capacity due to the excessive frequency deviation in some time periods. In previous studies, many experts and scholars have improved the fixed inertia/sag coefficient control [22,23], and the more typical ones are the variable coefficient control [24], however, the previous control strategies focus on establishing a simple linear constraint between the storage inertia/sag coefficients and and the SOC. This alleviates the problem of overcharge and overdischarge of the energy storage battery to a certain extent, but at the same time, there are two main problems: one is weakening of the fast response characteristics of the energy storage battery, and the other is a secondary perturbation of the system frequency when its own SOC reaches the critical point.
Therefore, when introducing the variable coefficient control, it is necessary to consider that when the storage SOC is in a relatively good interval, it should be a priority to ensure the FR demand and participate in the FR control with a high inertia/sag coefficient; and when the SOC is in a relatively poor interval, the storage should be less charged and less discharged or even not charged and not discharged in order to ensure that the SOC is maintained in a reasonable range and to leave the FR margin for the subsequent cycle and reduce the storage life loss. This paper is based on a generalized logistic curve, which is often used as an S-shaped curve that mimics similar population growth, as shown in Formula (13). The curve initially grows slowly, with the fastest growth rate at the center point, and then gradually slows down, and the overall growth rate is characterized by slow–fast–slow. In this paper, the generalized logistic function is improved by combining the relationship between the energy storage output and SOC, so that the discharge/charge of the energy storage can be limited as much as possible when its SOC is small/large, i.e., its corresponding inertia/sag control coefficients are lowered, and the output of the energy storage can be unrestricted as much as possible when the SOC is in a better state.
where K is the maximum value; P0 is the initial value, affecting the logistic function slope at the maximum (hereinafter referred to as the center point) of the location, P0. The smaller the function of the center of the curve from the SOC = 0.5, the closer the curve, so this paper takes the P0 to 0.01; n represents the curve change as fast or slow (i.e., the slope of the center point); the appropriate transformation of Formula (13) can be obtained with the curve shown in Figure 4, and its expression is as follows:
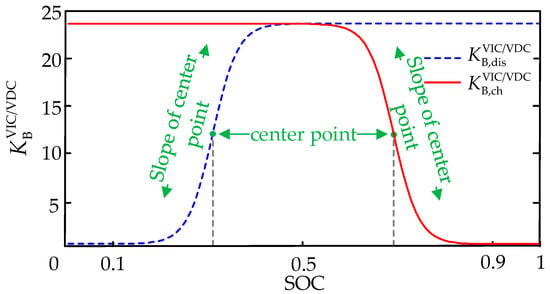
Figure 4.
Relationship between the virtual inertia/droop control coefficient of energy storage and the SOC.
In summary, the flowchart of the hybrid energy storage adaptive VIC and VDC coordinated control strategy proposed in this paper taking into account SOC optimization is shown in Figure 5.
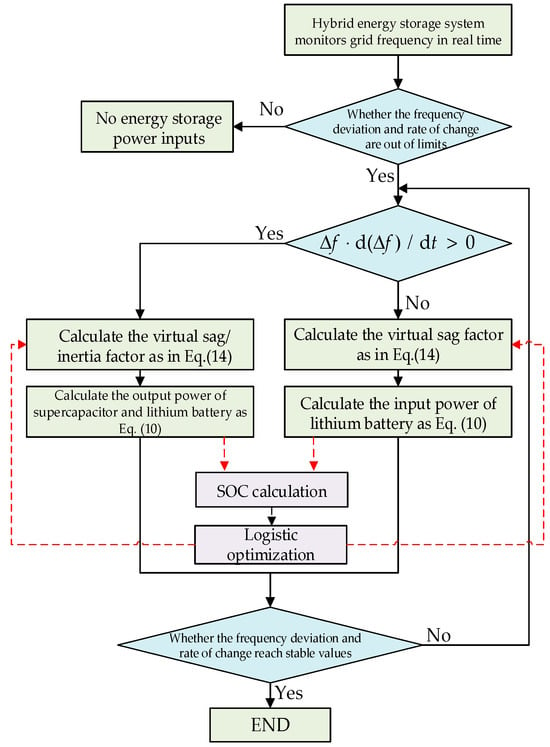
Figure 5.
Strategy flowchart of this article.
In order to quantitatively analyze the effectiveness of the strategies proposed in this paper, this paper defines the evaluation indexes of maximum frequency deviation Δfm, frequency decline rate Vm, and steady-state frequency deviation Δfs to evaluate the effectiveness of FR and the SOC of energy storage under different strategies, as follows.
- (1)
- Primary FR Effectiveness Indicators
In the typical step load disturbance, so that the initial moment is t0, the initial frequency deviation is Δf0. When the frequency deviation reaches the maximum value of the moment for the frequency deviation that at this time is set to tm, it can be defined as the frequency rate of descent for the Δfm; the frequency deviation begins to recover until it reaches the steady-state moment Vm when the steady-state frequency deviation is set to Vm = (Δf0 − Δfm)/(tm − t0). Δf0, t0 are taken to be 0. Obviously, the smaller the value of Δfm, Vm, and Δfs, the more pronounced the effect of frequency regulation.
Under continuous load disturbance, all frequency deviation values in the sampling points can be measured. So that there are n sampling points, regarding Δfi for the ith sampling point of the frequency deviation value, the root mean square value of is calculated and, obviously, a smaller value of the frequency regulation effect is better.
- (2)
- SOC Maintenance Effectiveness Indicators
In the same way as for the frequency deviation metric under continuous perturbation, the root mean square value of the SOC deviation (i.e., the degree of deviation from the optimal SOC0 = 0.5) is taken to be , and it is clear that the smaller the value, the better the SOC maintenance effect.
5. Simulation Verification
A hybrid energy-storage-assisted thermal power unit primary FR simulation model for a regional power grid is built by combining Figure 1 and Figure 2.
Among them, in order to highlight the characteristics of power-type energy storage with high power but small capacity and energy-type energy storage with low power but large capacity, after fully considering the capacity configuration range of the two types of energy storage, the economic costs of the two types of energy storage are further considered, as shown in Table 2. It can be seen from Table 2 that compared with lithium batteries, the power cost of supercapacitors is lower and the capacity cost is higher. Therefore, this paper comprehensively considers the feasibility and economy of the strategy and sets the power and capacity configuration of supercapacitors in the hybrid energy storage system as 2.5 MW and 0.5 MWh and that of lithium batteries as 1 MW and 5 MWh.

Table 2.
Comparison of the economic costs of energy storage.
In addition, in order to make the energy storage have a relatively ideal charge and discharge capacity at the initial moment, the initial energy storage SOC is generally set to 0.5, the power in the system is normalized to 100 MW, and the rest of the simulation parameters are shown in Table 3.

Table 3.
Simulation parameters.
5.1. Analysis of Load Step Disturbance FR Effect
In order to verify the effectiveness of this paper’s strategy, a step load perturbation of 0.05 p.u. is set at 2 s. The system frequency deviation, the thermal unit output, the storage output, the SOC change curves of this paper’s strategy and the single-battery control strategy proposed in the literature [10] (a common lithium battery is used in this paper, hereinafter referred to as the single-lithium strategy), and the strategy of no energy storage are shown in Figure 6, Figure 7, Figure 8 and Figure 9, and the evaluation indexes are shown in Table 4.
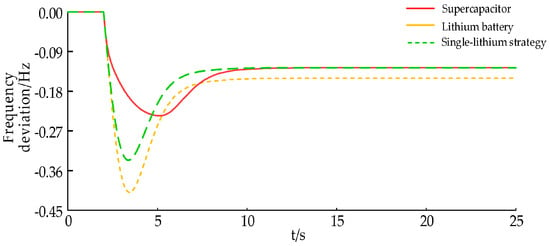
Figure 6.
System frequency deviation under step perturbation.
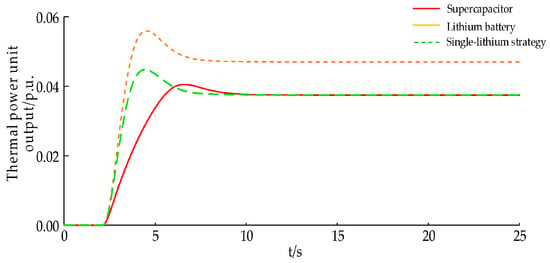
Figure 7.
Output of thermal power unit under step jump disturbance.
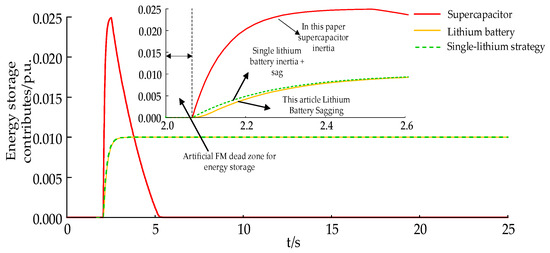
Figure 8.
Energy storage output under step-jump disturbance.
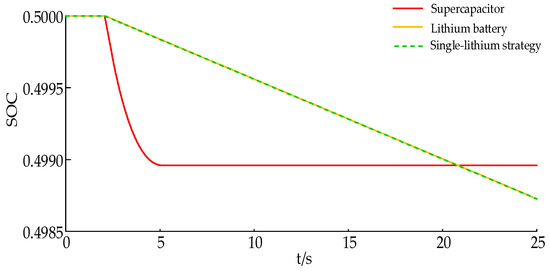
Figure 9.
Energy storage SOC under step perturbation.

Table 4.
Frequency regulation index under different strategies under step perturbation.
From Figure 6 and Figure 7, it can be seen that comparing the system frequency deviation and thermal unit output curve, the absolute value of the maximum frequency deviation under this paper’s strategy is the smallest, followed by the single-lithium strategy, and it is the worst without energy storage; for the steady-state frequency deviation, the current strategy is consistent with the single-lithium strategy, and the no energy storage is the worst. The reason for this is that in the frequency fall when the energy storage displays its fast response characteristics, in the system VIC and VDC quickly make up for the active deficit of the system and then inhibit the frequency fall, so compared with the no storage frequency regulation effect it is better and, at the same time, the improvement of the frequency regulation effect will also directly reduce the thermal power unit’s primary frequency regulation output. From Figure 8 and Figure 9, it can be seen that under the single-lithium strategy, due to the use of only lithium batteries in the VIC and VDC at the same time, it cannot effectively respond to the superimposed power command signal because of the limitation of its power amplitude. In contrast, the strategy in this paper considers the use of supercapacitor high-power short-time response to the VIC signal and the use of lithium battery high-energy long-time response to the VDC signal. When the load disturbance occurs in the 2 s system, after the energy storage set up in this paper and after the frequency regulation dead zone, the high-power supercapacitor responds quickly to the VIC signal with the rated power, the Li-ion battery only assumes the VDC signal, and the supercapacitor quits operation as the frequency deviation reaches the lowest point, which effectively avoids the supercapacitor SOC from falling into the bad state and at the same time also facilitates the restoration of the system frequency, as shown in Figure 6. The steady-state frequency deviation is consistent with the single-lithium strategy.
Analyzing from the perspective of data, in this paper, the improvement under strategy Δfm is 30.04% and 42.49% compared to the single-lithium strategy and no storage, respectively; Δfs is 15.82% compared to no storage, which is consistent with the single-lithium strategy; and Vm is 14.50% and 73.72% compared to the single-lithium strategy and no storage, respectively.
5.2. Analysis of the Effect of Continuous Load Perturbation FR
The 2 h continuous load disturbance data of a regional power grid are used as the research object, the sampling interval is 1 min, and the corresponding load disturbance curve is shown in Figure 10. In order to verify the superiority of the logistic-based variable coefficient control proposed in this paper, the strategy of this paper is compared with the no energy storage, single-lithium strategy, and the strategy of this paper with no logistic optimization (hereinafter referred to as without logistic). The system frequency deviation, storage output, and SOC variation curves under different strategies are shown in Figure 11, Figure 12 and Figure 13, and the evaluation indexes are shown in Table 5.
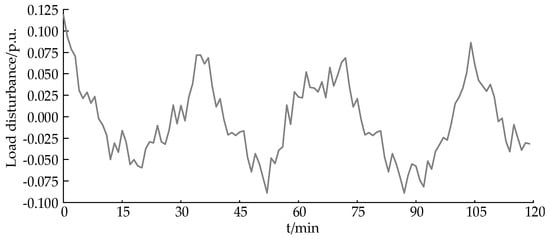
Figure 10.
A 2 h continuous load perturbation curve.
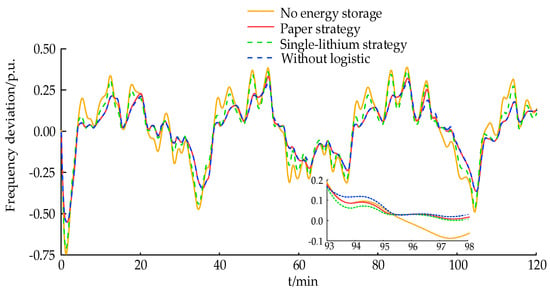
Figure 11.
System frequency deviation under continuous load disturbance.
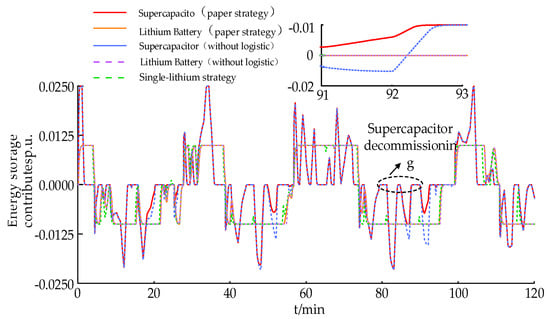
Figure 12.
Energy storage output under continuous load disturbance.
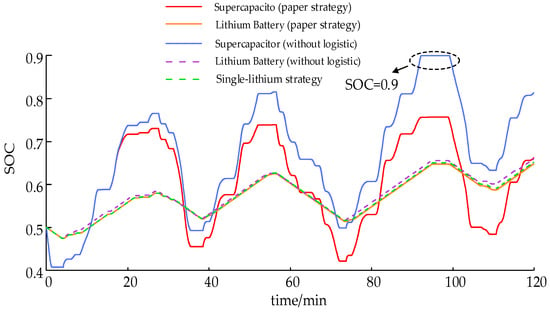
Figure 13.
Energy storage SOC under continuous load disturbance.

Table 5.
Frequency regulation index under different strategies under continuous load disturbance.
As can be seen from Figure 11, the strategy in this paper maintains the best FR effect in the continuous disturbance scenario compared with no energy storage and the single-lithium strategy. From Figure 12 and Figure 13, it can be seen that the supercapacitor under the strategy of this paper can exit the inertial response in time after the frequency reaches the frequency extreme value, while the lithium battery participates in the sagging response of the system in the whole FR cycle; compared with the strategy presented in this paper and without logistic, the SOC state of the supercapacitor and lithium battery under the strategy presented in this paper is significantly better than that of the lithium battery without logistic. If the without logistic control strategy is adopted, the SOC of the supercapacitor will fall into a bad condition of 0.1/0.9 when the load disturbance is large (e.g., 92~100 min in Figure 13) and lose the ability of the subsequent FR, which can be seen in Figure 11, and the FR effect is the worst in this time period.
Analyzing from the data point of view, compared with the single-lithium strategy and no energy storage, with the strategy in this paper the ΔfRMS improved 19.17% and 30.16%, respectively, slightly worse than the without logistic strategy, which is due to the limitation by the logistic curve in some periods of time to reduce the coefficients of storage involved in the inertia and sagging response but effectively maintaining the SOC of the energy storage, and with the supercapacitor and lithium batteries, the SOC level improved 29.4% and 2.1%, respectively.
6. Conclusions
The influence of the action timing of the two control modes on the frequency deviation of the grid based on the output mechanism of VIC and VDC is analyzed, putting forward a control method that reasonably combines the two and elaborating on the different requirements of the two control modes regarding the energy storage output characteristics.
According to the demand of VIC and VDC for energy storage output power and capacity, a hybrid energy storage adaptive VIC and VDC coordination control strategy is proposed, which will have a high-power energy storage supercapacitor responding to inertia control signal and a high-capacity lithium battery responding to sag control signal. It makes the output characteristics of VIC and VDC fit with different types of energy storage, effectively reducing frequency differences and preventing frequency deterioration. Compared with the single-lithium strategy and no energy storage, Δfm increases by 30.04% and 42.49%, respectively, under step disturbance, and ΔfRMS increases by 19.17% and 30.16%, respectively, under continuous disturbance.
In order to avoid the energy storage SOC from falling into lower/higher severe operating conditions and losing the subsequent FR capability, an adaptive output control strategy for energy storage based on an improved logistic function is proposed, which improves the SOC levels of the supercapacitor and Li-ion batteries by 29.4% and 2.1%, respectively, under continuous perturbation as compared to that of the supercapacitor and Li-ion batteries without logistic.
At present, the price of energy storage equipment is high, but with the rapid development of related technologies, its economy will be continuously improved, and the application of energy storage will be more large-scale. The price used in this paper may somewhat deviate from the current energy storage price, but its capacity allocation method and cost–benefit model are the same, which have certain reference value.
Author Contributions
Conceptualization, C.X.; methodology, J.X.; software, J.X.; validation, X.X.; formal analysis, C.X.; investigation, X.X.; resources, C.X.; data curation, X.X.; writing—original draft preparation, C.X.; writing—review and editing, X.X.; visualization, Y.C.; supervision, P.L.; project administration, Q.G.; funding acquisition, P.L. All authors have read and agreed to the published version of the manuscript.
Funding
The paper has been funded by National Key Research and Development Program (NKRDP) (2019YFE0118000); National Key Program for Basic Research and Development (973 program) (2021YFB2601504).
Data Availability Statement
All data underlying the results are available as part of the article.
Conflicts of Interest
The authors Chao Xing and Xinze Xi were employed by the company Electric Power Research Institute of Yunnan Power Grid Co., Ltd. The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Variables | |
| Δf | frequency deviation |
| t | time index |
| SOC(t) | energy storage SOC at moment t |
| one FR cycle | |
| ΔPB(t) | output power of the energy storage at moment t |
| ΔPG(s) | output power of the thermal power unit |
| ΔPB(s) | output power of the energy storage |
| output power of the supercapacitor | |
| output power of the lithium battery | |
| Parameters | |
| TG | thermal unit governor time constant |
| TCH | turbine time constant |
| TRH | heater time constant |
| FHP | heater gain |
| energy storage time constant | |
| time constants of supercapacitor | |
| time constants of lithium battery | |
| D | system damping coefficient |
| H | inertia coefficient of the thermal power unit |
| inertia coefficient when VIC is used for energy storage | |
| sag coefficient when VDC is used for energy storage | |
| EBN | total capacity of the energy storage system |
| Kgen | primary unit regulation power of the thermal power unit |
| Abbreviations | |
| VIC | virtual inertial control |
| VDC | virtual droop control |
| SOC | state of charge |
| FR | frequency regulation |
References
- Cirio, D.; Conte, F.; Gabriele, B.; Gandolfi, C.; Rapizza, S.M.M.; Silvestro, F. Fast Frequency Regulation from a Wind Farm-BESS Unit by Model Predictive Control: Method and Hardware-in-The-Loop Validation. IEEE Trans. Sustain. Energy 2023, 14, 2049–2061. [Google Scholar] [CrossRef]
- Li, C.; Li, J.; Li, J.; Zhang, X.; Hou, T. Optimization strategy of secondary Frequency regulation based on dynamic loss model of the energy storage unit. J. Energy Storage 2022, 51, 104425. [Google Scholar] [CrossRef]
- Xiao, J.; Li, P.; Mao, Z. Battery Energy Storage Participating in Secondary Frequency Regulation Based on Fuzzy Allocation Factor. Power Syst. Technol. 2023, 47, 3568–3577. [Google Scholar] [CrossRef]
- Li, B.; Li, M.; Yan, S.; Zhang, Y.; Shi, B.; Ye, J. An optimal energy storage system sizing determination for improving the utilization and forecasting accuracy of photovoltaic (PV) power stations. Front. Energy Res. 2023, 10, 1074916. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Xu, M.; Xiao, Z. Wind Power Fluctuation Smooth Strategy Based on Digital Twin Hybrid Energy Storage. Power Syst. Technol. 2021, 45, 2503–2514. [Google Scholar] [CrossRef]
- Barra, P.H.A.; de Carvalho, W.C.; Menezes, T.S.; Fernandes, R.A.S.; Coury, D.V. A review on wind power smoothing using high-power energy storage systems. Renew. Sustain. Energy Rev. 2021, 137, 110455. [Google Scholar] [CrossRef]
- Wang, L.; Tan, L.; Xu, Z.; Tan, X.; Wu, C.; Ye, H.; Li, A. Lithium battery energy storage power station primary Frequency regulation designoptimization and verification. Energy Storage Sci. Technol. 2022, 11, 3862–3871. [Google Scholar] [CrossRef]
- Xiong, L.; Xiu, L.; Wang, H.; Xu, Z. Mechanism of Energy Storage System to Suppress Grid Power Oscillations. Trans. China Electrotech. Soc. 2019, 34, 4373–4380. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, C.; Lu, X.; Xu, C. Optimization of Micro-grid Primary Frequency Regulation Reserve Capacity and Energy Storage System. Proc. CSEE 2017, 37, 4324–4332. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, L.; Huang, S.; You, H.; Li, J.; Yang, L. Research on the mixed control strategy of the battery energy storage considering frequency modulation, peak regulation, and SOC. Energy Sci. Eng. 2022, 10, 3459–3470. [Google Scholar] [CrossRef]
- Xing, W.; Wang, H.; Lu, L.; Han, X.; Sun, K.; Ouyang, M. An adaptive virtual inertia control strategy for distributed battery energy storage system in microgrids. Energy 2021, 233, 121155. [Google Scholar] [CrossRef]
- Hasan, N.S.; Rosmin, N.; Nordin, N.M.; Abd Bakar, S.; Aman, A.H.M. Dynamic response of hybrid energy storage based virtual inertial support in wind application. J. Energy Storage 2022, 53, 105181. [Google Scholar] [CrossRef]
- Xing, P.; Shi, Q.; Wang, G.; Fu, L.; Wang, Y.; Wu, Y. Response Characteristics and Mechanism Analysis About Virtual lnertia Control of Wind Generators. High Volt. Eng. 2018, 44, 1302–1310. [Google Scholar] [CrossRef]
- Gupta, S.; Mukhopadhyay, S.; Banerji, A.; Sanki, P.; Biswas, S.K. Adaptive Droop Control for Voltage and Frequency Regulation in Virtual Power Plant under Power System Contingencies. Jordan J. Electr. Eng. 2023, 9, 618–649. [Google Scholar] [CrossRef]
- Obaid, Z.A.; Cipcigan, L.M.; Muhssin, M.T.; Sami, S.S. Control of a population of battery energy storage systems for frequency response. Int. J. Electr. Power Energy Syst. 2020, 115, 105463. [Google Scholar] [CrossRef]
- Xiao, J.; Jia, Y.; Jia, B.; Li, Z.; Pan, Y.; Wang, Y. An inertial droop control based on comparisons between virtual synchronous generator and droop control in inverter-based distributed generators. Energy Rep. 2020, 6, 104–112. [Google Scholar] [CrossRef]
- Hernández, J.C.; Sanchez-Sutil, F.; Vidal, P.G.; Rus-Casas, C. Primary frequency control and dynamic grid support for vehicle-to-grid in transmission systems. Int. J. Electr. Power Energy Syst. 2018, 100, 152–166. [Google Scholar] [CrossRef]
- Tan, Z.; Li, X.; He, L.; Li, Y.; Huang, J. Primary frequency control with BESS considering adaptive SoC recovery. Int. J. Electr. Power Energy Syst. 2020, 117, 105588. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Zhang, B.; Yang, T. Energy storage peak and Frequency regulation cooperative control strategy based on multi-time-scale. Dianli Xitong Baohu Yu Kongzhi/Power Syst. Prot. Control 2022, 50, 94–105. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Q.; Zhang, H.; Li, C. Optimal sizing of hybrid energy storage system considering power smoothing and transient frequency regulation. Int. J. Electr. Power Energy Syst. 2022, 142, 108227. [Google Scholar] [CrossRef]
- Gao, S.; Li, J.; Song, H.; Ding, L.; Zhang, C. An integrated thermal power-energy storage system for improving primary frequency regulation performance of thermal power units. Power Syst. Prot. Control 2023, 51, 116–125. [Google Scholar] [CrossRef]
- Zhang, X.; Qin, S.; Zhang, Y.; Hao, S.; Wu, Q.; Zhang, J. Wind Turbine and Storage Joint Frequency regulation Control Strategy Considering Energy Storage State of Charge. High Volt. Eng. 2023, 49, 4120–4130. [Google Scholar] [CrossRef]
- Zhu, X.; Han, X. The adaptive control strategy of energy storage battery cooperating with conventional generating units to participate in primary frequency regulation. Electr. Meas. Instrum. 2023, 60, 34–42. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, C.; Tang, W.; Low, S. Profit-Maximizing Planning and Control of Battery Energy Storage Systems for Primary Frequency Control. IEEE Trans. Smart Grid 2018, 9, 712–723. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).