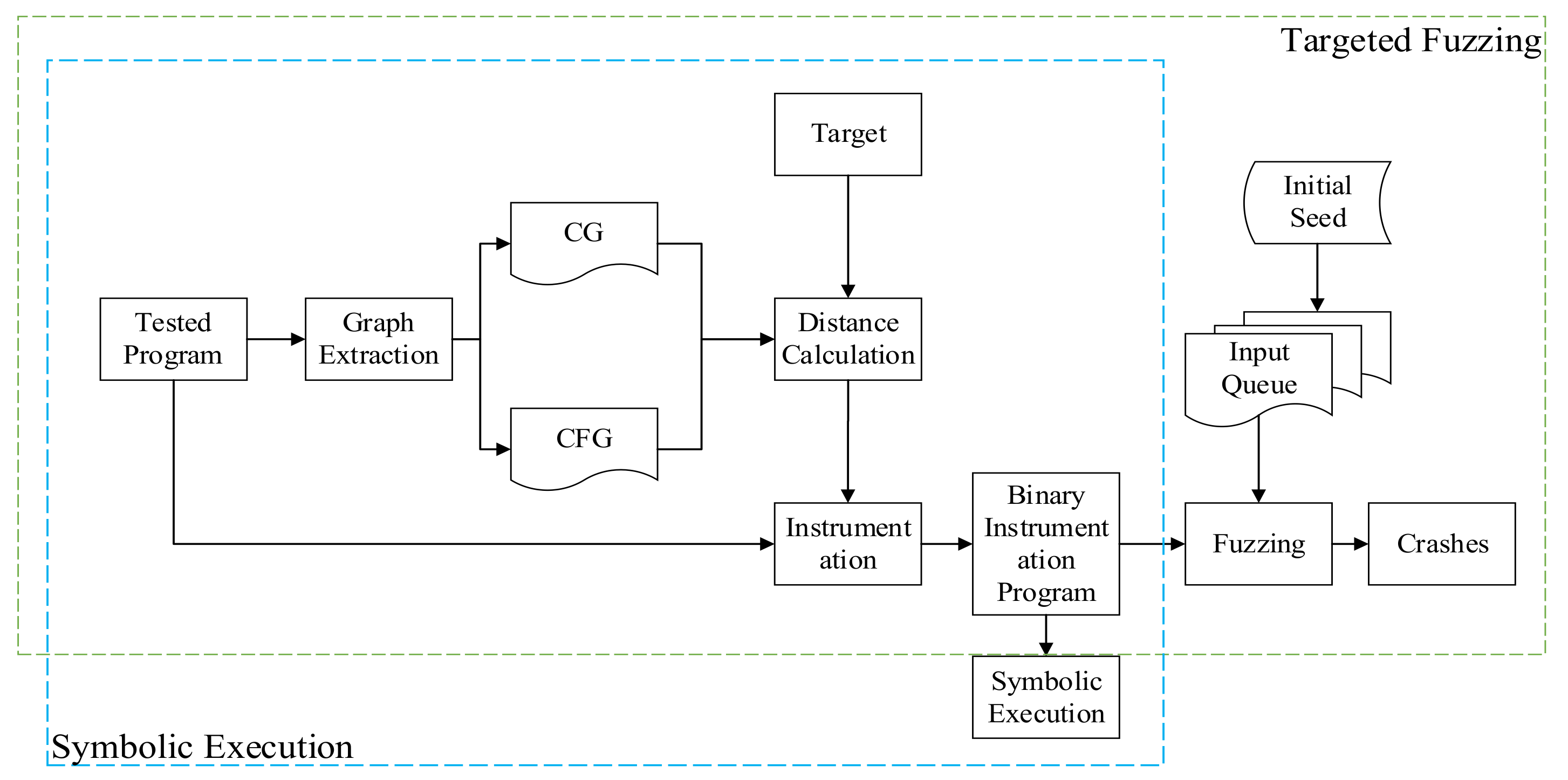
4.2. Experimental Design
As AFL++ incorporates both symbolic execution and fuzzing techniques, the optimizations implemented by AFL++ can, to some extent, increase the coverage of the target area and execution speed, effectively enhancing vulnerability discovery efficiency. The primary observed metrics include crashes (unique) and total paths, where higher values for both metrics are desirable.
During vulnerability discovery, the main objective is to identify real vulnerabilities, with a focus on observing the value of crashes. If there are no crashes, the coverage rate within a unit of time is observed for comparison. In vulnerability reproduction, the primary goal is the reproduction time, and shorter times for reproducing vulnerabilities are preferable.
Since most vulnerability discovery tools use the same LAVA-M dataset for evaluation, we also utilized this dataset for vulnerability discovery assessment. The LAVA-M dataset consists of four programs: base64, md5sum, uniq, and who, each intentionally injected with multiple vulnerabilities. The number of vulnerabilities in the LAVA-M dataset and the detailed commands are shown in
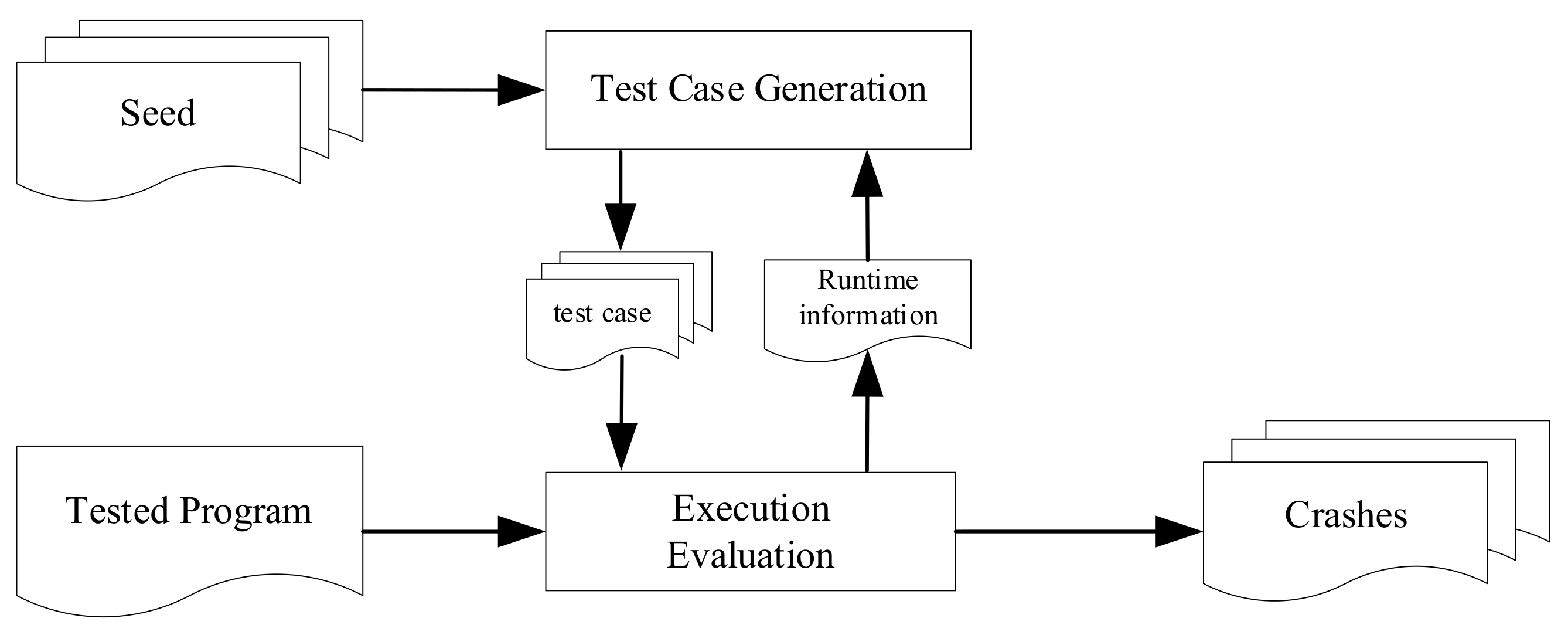
Table 3. The experimental process is shown in
Figure 2.
4.3. Vulnerability Mining Performance Evaluation
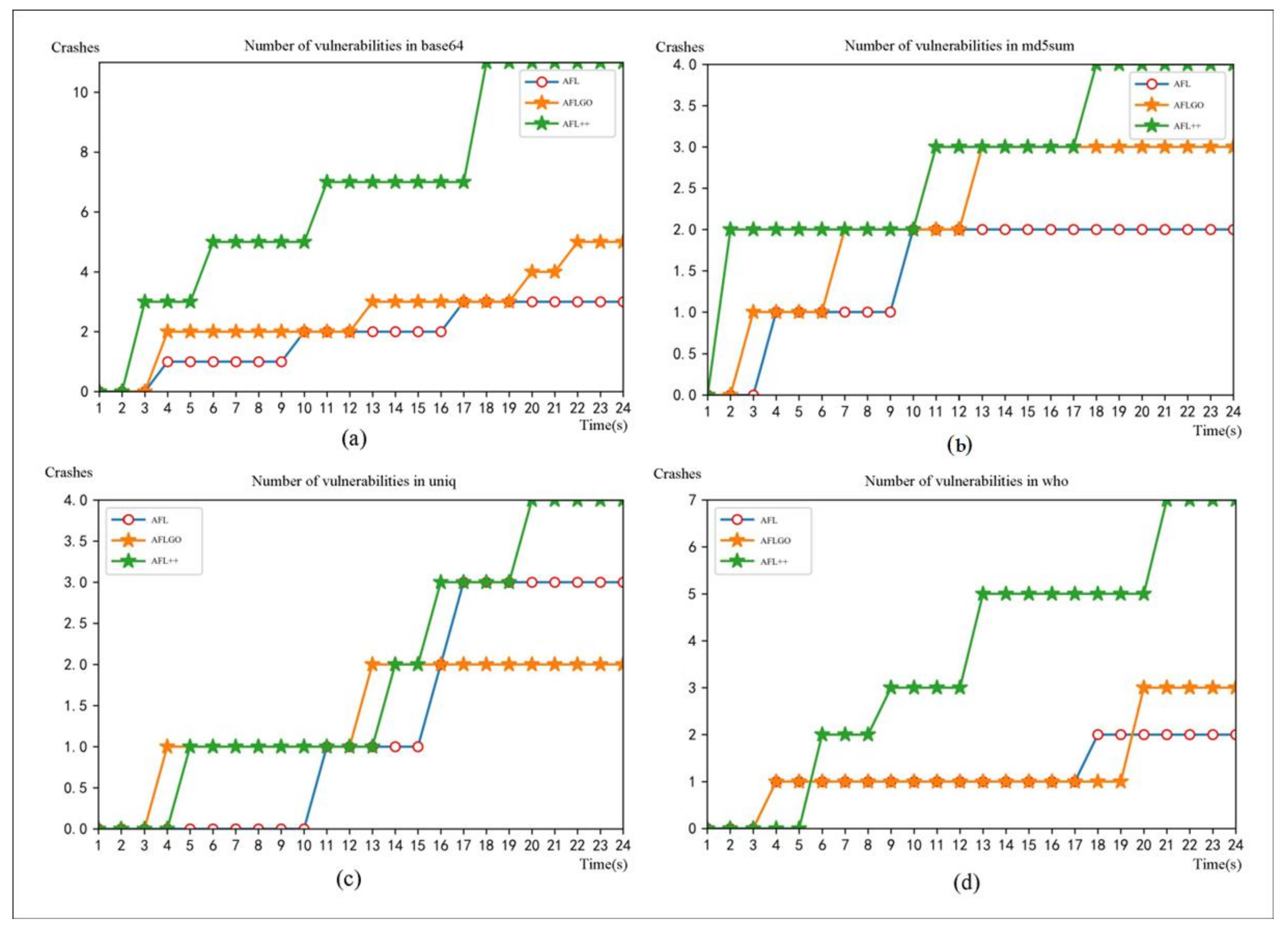
Firstly, vulnerability discovery was conducted on LAVA-M. For the purpose of controlling the variables, this study employed the same virtual machine to perform vulnerability discovery on the four programs in LAVA-M using AFL, AFLGo, and AFL++, respectively. The experiment was set to run for 24 h, and the number of crashes discovered by each tool during the process was recorded. The experimental results are presented in
Figure 3.
In
Figure 3, it can be observed that within 24 h, AFL discovered three crashes on base64, two on md5sum, three on uniq, and two on who. AFLGo found five crashes on base64, three on md5sum, two on uniq, and three on who. AFL++ identified 11 crashes on base64, four on md5sum, four on uniq, and seven on who. It can be seen that for vulnerability mining on the LAVA-M dataset, AFL++ was better. To enhance data visibility, the overall presentation is illustrated in
Table 4.
We conducted vulnerability mining evaluations on real programs. The latest version of libxml2 was first selected for vulnerability mining, and programs such as libming, xpdf, libexif, gdb, giflib, jasper, and lrzip were selected. Eight simple programs were tested for 48 h using AFL, AGLGO, and AFL++.
Among the programs, the number of total paths was as follows: AFL had 4818, 5296, 3231, 4209, 1107, 233, 1, 1151; AFLGo had 5812, 5411, 3562, 5579, 1425, 188, 163, 1403; and AFL++ had 7324, 6573, 4517, 8662, 3237, 316, 233, 2282, as shown in
Figure 4. Therefore, AFL++ resulted in increases of 52.01%, 24.11%, 39.8%, 110.54%, 192.41%, 35.62%, 233%, and 98.26%, respectively, based on AFL; based on AFLGo, the distribution increases were 26%, 21.47%, 26.81%, 55.26%, 127.15%, 68.08%, 42.94%, and 42.94%, respectively. These data are shown in
Table 5. The table clearly shows that the proposed tool outperformed AFLGo and AFL. In Jasper software (
https://github.com/mdadams/jasper, (accessed on 25 February 2024)), the number of AFL test paths was 1, and the number of tests was 1, but the test with a lower version had 200+ paths. AFL instrumentation likely had a problem, but it did not affect the results of AFL++ and AFLGo, and AFL++ was still better than AFLGo. AFL++ had the most significant advantage in libexif, with more than double that of AFL and AFLGo.
For crashes, neither AFL, AFLGo, nor AFL++ found crashes on limxml2, libexif, gdb, or jasper. When testing libming, the number of crashes and unique crashes found by AFL++ was 107 (48), which was the most. The crashes were analyzed and submitted, and a CVE was assigned: CVE-2022-44232. For xpdf, the total crashes found by AFL++ were 700 (110), that is, 700 crashes, with a total of 110 unique crashes; the total crashes found by AFLGo were 581 (71); the total crashes found by AFL were 534 (58). The crashes were aggregated into a table, as shown in
Table 6. AFL++ found eight vulnerabilities alone, which were analyzed and submitted, and seven CVEs were assigned: CVE-2023-26930, CVE-2023-26931, CVE-2023-26934, CVE-2023-26935, CVE-2023-26936, CVE-2023-26937, and CVE-2023-26938.
Table 6 shows that the number of crashes (unique) in AFL++ had an absolute ad-vantage, especially on giflib, and AFL++ found three path vulnerabilities, but neither AFL nor AFLGo found them.
The above experimental data all show that the vulnerability mining ability of AFL++ is better than that of AFL and AFLGo. This proves that the vulnerability mining framework based on directed fuzzing and symbolic execution can effectively increase the coverage rate and significantly improve the efficiency of vulnerability mining.
4.4. Vulnerability Reproduction Experiment Evaluation
We tested against some open-source programs with public vulnerabilities. We used AFL, AFLGo, and AFL++ to reproduce the vulnerability and evaluate the effectiveness of AFL++ by comparing the time and times of recurrence. Here, we mainly chose binutils and libming to reproduce the vulnerability. Since individual vulnerabilities are difficult to trigger, the time for each test was set to 12 h. To reduce the interference caused by randomness, each experiment was repeated 20 times. The reproduction results of the two vulnerabilities in libming are shown in
Table 7. TTE refers to the time from runtime to the first time a vulnerability was triggered, where m is minutes and s is seconds. It can be seen in
Table 7 that AFL++ was superior to AFL and AFLGo in the reproduction of these two vulnerabilities.
In addition, we also conducted experiments on historical vulnerabilities CVE-2016-4487 to CVE-2016-4492 in binutils. The results were compared with currently known targeted fuzzing tools. We used the target definition strategy of CVE-2016-4487 in the AFLGo script to find the target points in the stack backtracking.
Hawkeye was proposed in 2018, and it is also a classic tool in directed greybox fuzzing. AFL-Ant was proposed between 2019 and 2020, and Beacon was proposed in 2022. It is also the latest closed-source directed fuzzing tool. Beacon is based on path pruning. With the assistance of static analysis, all irrelevant paths are deleted, and only the relevant parts are kept to prevent the seeds from executing into branches that have nothing to do with the target code.
It can be seen from
Table 8 that, except for the reappearance of CVE-2016-4490, AFL++ took longer than AFL, and the rest were shorter than the AFL reappearance. AFL++ took less time to reproduce than AFLGo, AFL-Ant, and Hawkeye in all the reproduced vulnerabilities. Moreover, for the bugs that take a long time to reproduce on average, although the improved efficiency was not the greatest, the number of recurrences was significantly improved. However, it was still impossible to achieve 20 full recurrences, which may be because the path search algorithm prefers shorter paths rather than full path coverage, and the randomness of the mutation algorithm resulted in an inability to reach all node paths.
In the reproduction of CVE-2016-4487, CVE-2016-4489, and CVE-2016-4492, AFL++ took less time than the latest tool, Beacon, and in CVE-2016-4487, it only took 19 s to reproduce at the fastest time. The improvement in CVE-2016-4492 was more prominent, probably because there were multiple paths to reach the target point, and AFL++’s precise guidance and fuzz test random mutation could easily trigger one of the paths. However, in CVE-2016-4491 and CVE-2016-6131, the recurrence time was slightly higher. It may be that the time was too long due to the consumption of a large amount of resources in the AFL++ symbolic execution solution. When reproducing vulnerabilities under shallow paths, AFL++ can find vulnerabilities under shallow paths faster by using symbolic execution solutions due to fewer constraints. AFL++ needs to consume more resources when reproducing deep vulnerabilities due to more constraints. However, Beacon does not need to consider which branches are taken. That is, the mutation can hit the branch no matter what, and the factor of the recurrence time is mainly determined by the mutation algorithm. So, Beacon was slightly faster than AFL++ on deeper paths.
Overall, AFL++ has reasonable practicability and effectiveness in guided vulnerability mining.