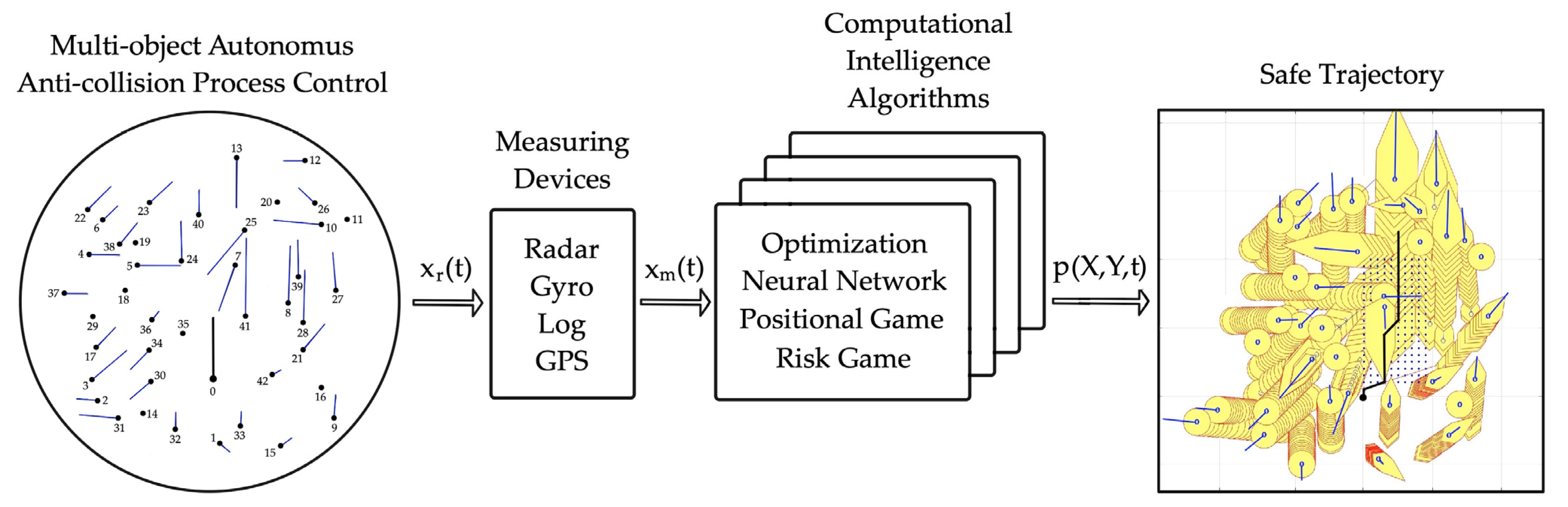
Computational Intelligence Supporting the Safe Control of Autonomous Multi-Objects
Abstract
1. Introduction
1.1. State of Knowledge
1.2. Study Objectives
- Synthesis of safe multi-object control algorithms in various degrees of object cooperation and environment complexity, using appropriately selected optimization methods, artificial intelligence, and game theory;
- Experimental comparative analysis of the effectiveness of methods using computational intelligence to determine the safe trajectories of many objects.
1.3. Article Content
2. Algorithms of Safe Multi-Object Control
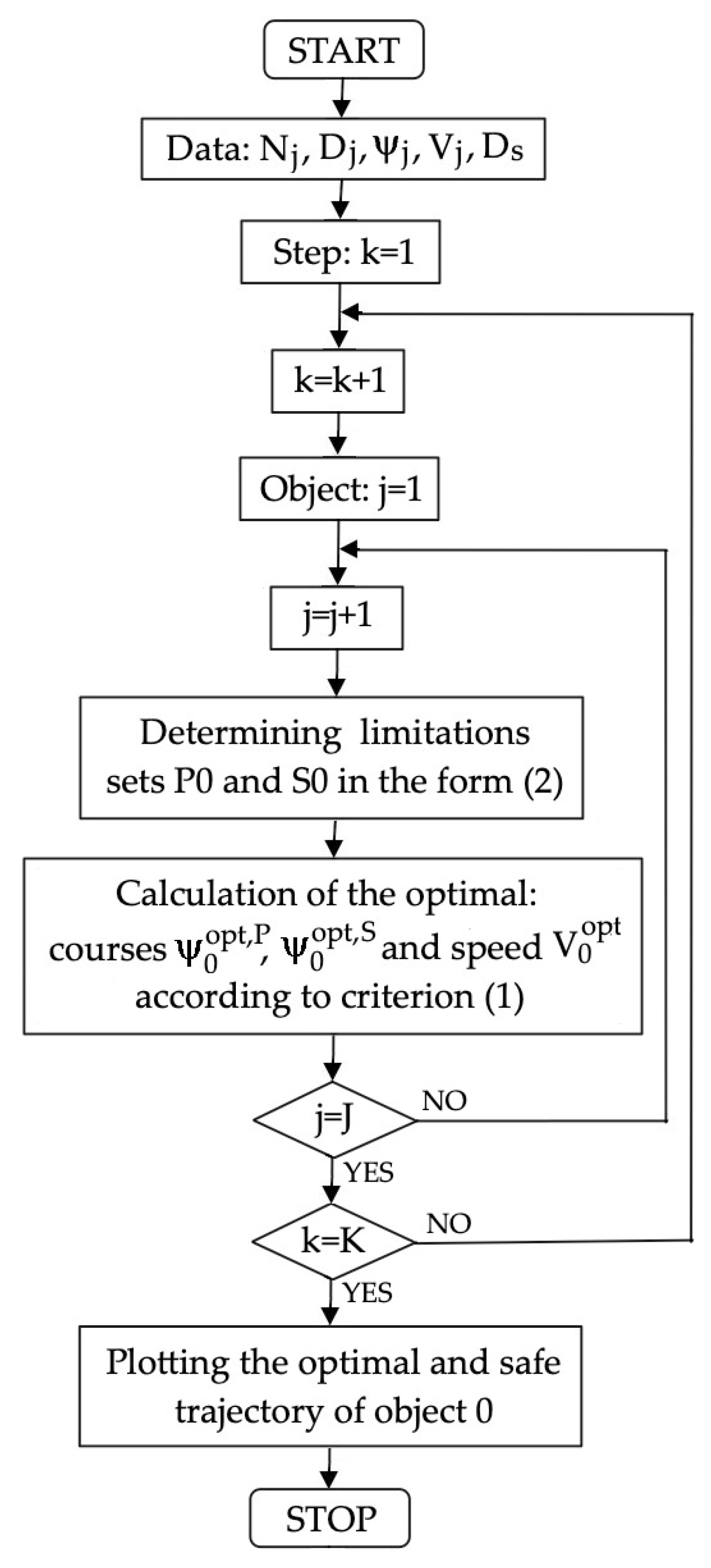
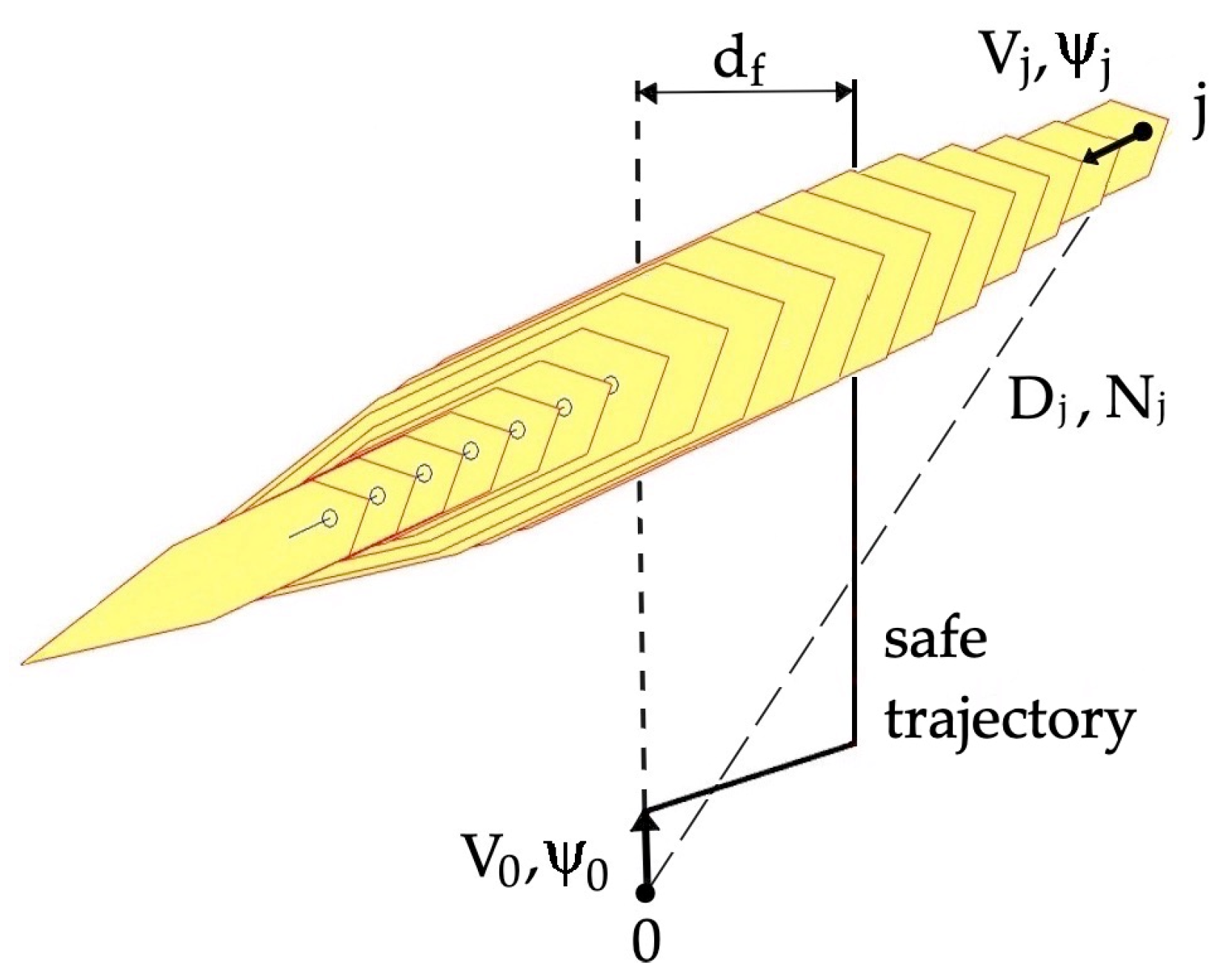
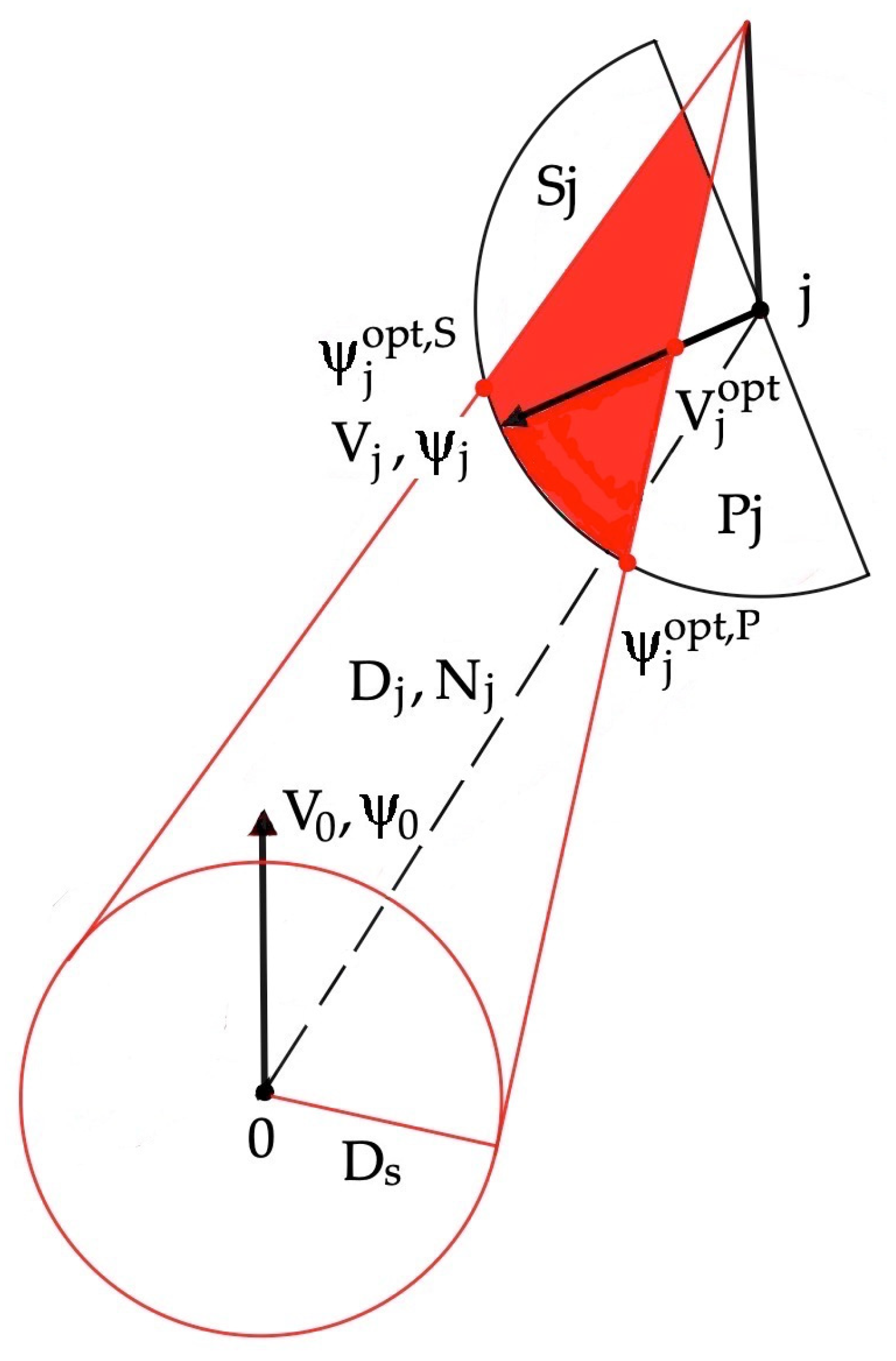
2.1. Algorithm of Optimal Control OPT
| Algorithm 1: Optimal Multi-Object Control Algorithm |
| BEGIN 1. Read Data: Nj, Dj, ψj, Vj, Ds 2. Step: k:=1 3. Object: j:=1 4. Determining limitations sets P0 and S0 in the form (2) 5. Calculation of the optimal: courses and speed according to criterion (1) IF not j = J THEN (j:=j + 1 and GOTO 4) ELSE k:=K IF not k = K THEN (k:=k + 1 and GOTO 3) ELSE Plotting the optimal and safe trajectory of object 0 END |
2.2. Algorithm of Artificial Neural Network AI-NN
| Algorithm 2: Artificial Neural Network Algorithm |
| BEGIN 1. Read Data: Nj, Dj, ψj, Vj, Ds 2. Step: k:=1 3. Object: j:=1 4. Determining the size of neural domain of object j IF not j = J THEN (j:=j + 1 and GOTO 4) ELSE Node: n:=1 6. Choosing the minimum-time of object 0 path in Bellman dynamic programming IF not n = N THEN (n:= n + 1 and GOTO 6) ELSE k:=K IF not k = K THEN (k:=k + 1 and GOTO 3) ELSE Plotting the time-optimal and safe trajectory of object 0 END |
2.3. Algorithm of Positional Game AI-PG
- The determination of the optimal control of object 0 in relation to each object j ();
- The determination of the optimal cooperative control (AI-PGc algorithm) or non-cooperative control (AI-PGnc algorithm) of individual objects j ();
- The determination of the optimal control of object 0 in relation to all objects j ().
| Algorithm 3: Positional Game Algorithm |
| BEGIN 1. Read Data: Nj, Dj, ψj, Vj, Ds 2. Step: k:=1 3. Object: j:=1 4. Determining optimal maneuvers of object 0: in relation to each object j 5. Triple programming 6. Algorithm AI-PGc max max max 7. Choosing cooperative maneuvers of object j: 8. Algorithm AI-PGnc max min max 9. Choosing non-cooperative maneuvers of object j: IF not j = J THEN (j:= j + 1 and GOTO 4) ELSE Determining optimal maneuvers of object 0: in relation to each object j IF not k = K THEN (k:= k + 1 and GOTO 3) ELSE Plotting the optimal and safe trajectory of object 0 END |
2.4. Algorithm of Risk Game AI-RG
| Algorithm 4: Risk Game Algorithm |
| BEGIN 1. Read Data: Nj, Dj, ψj, Vj, Ds 2. Step: k:=1 3. Object: j:=1 4. Calculation of optimal collision risk IF not j = J THEN (j:=j + 1 and GOTO 4) 6. Creation of collision risk matrix 7. Dual linear programming 9. Algorithm AI-RGc min min 10. Algorithm AI-RGnc min max IF not k = K THEN (k:= k + 1 and GOTO 3) ELSE Plotting the optimal and safe trajectory of object 0 END |
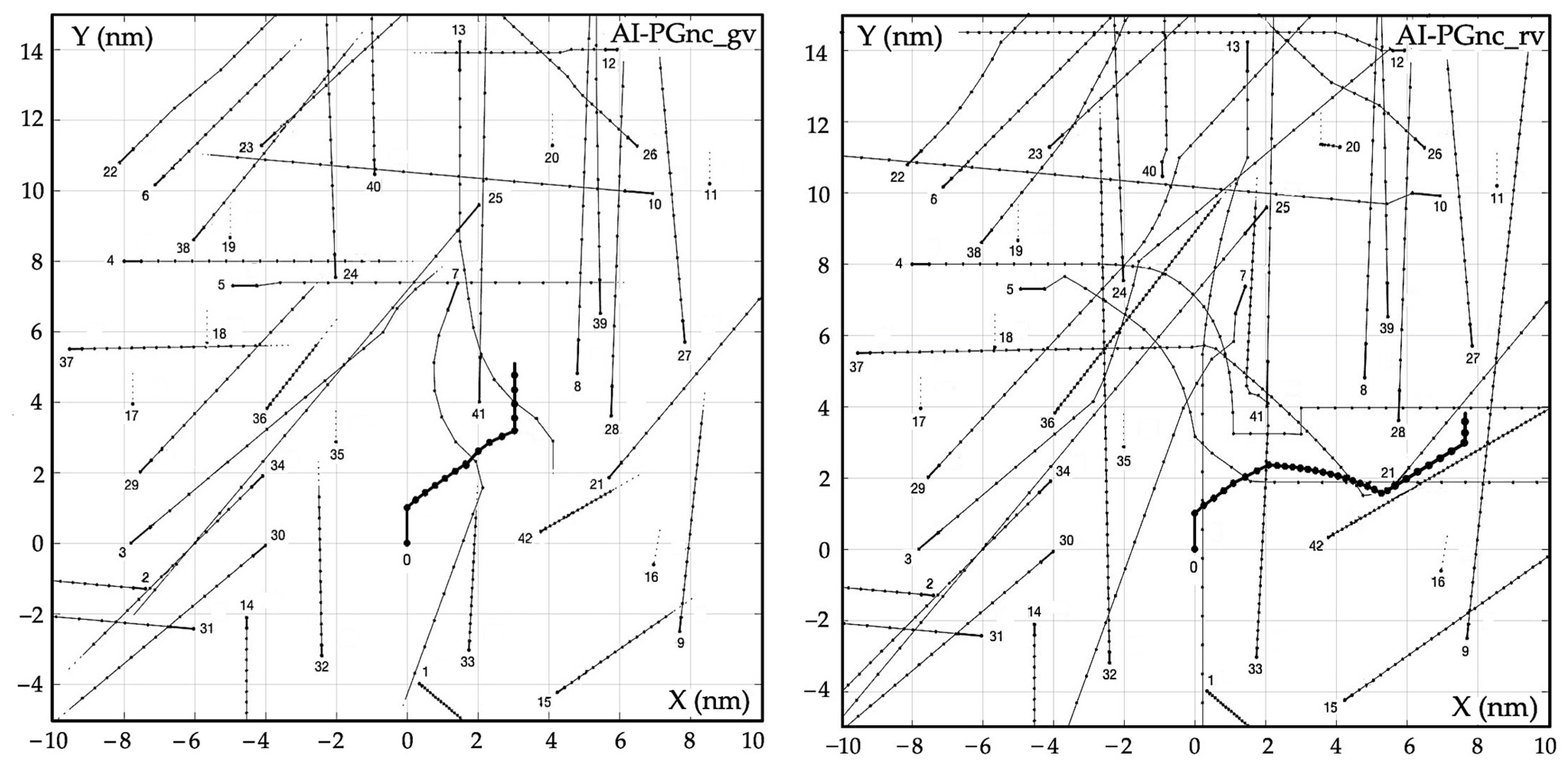
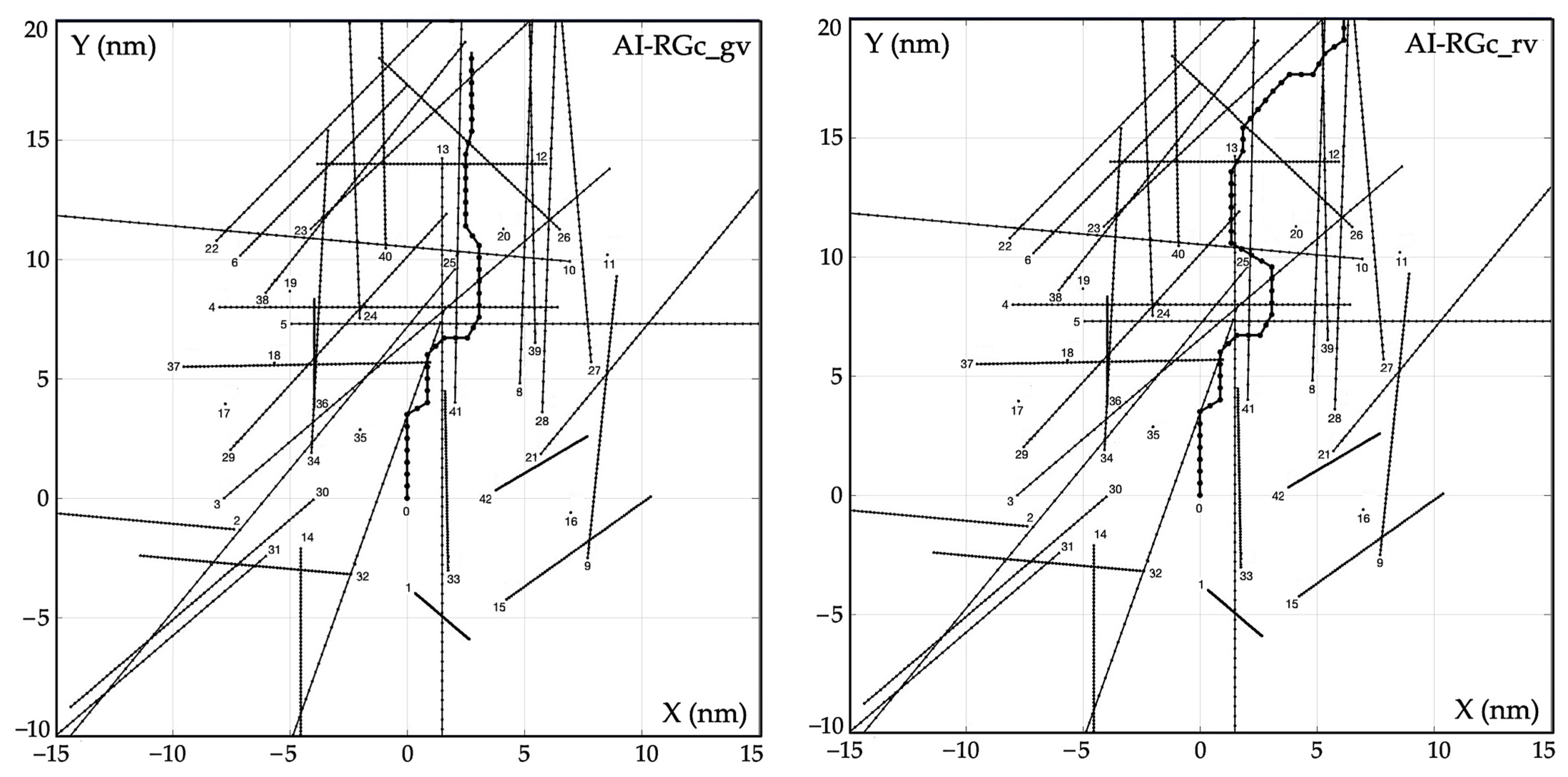
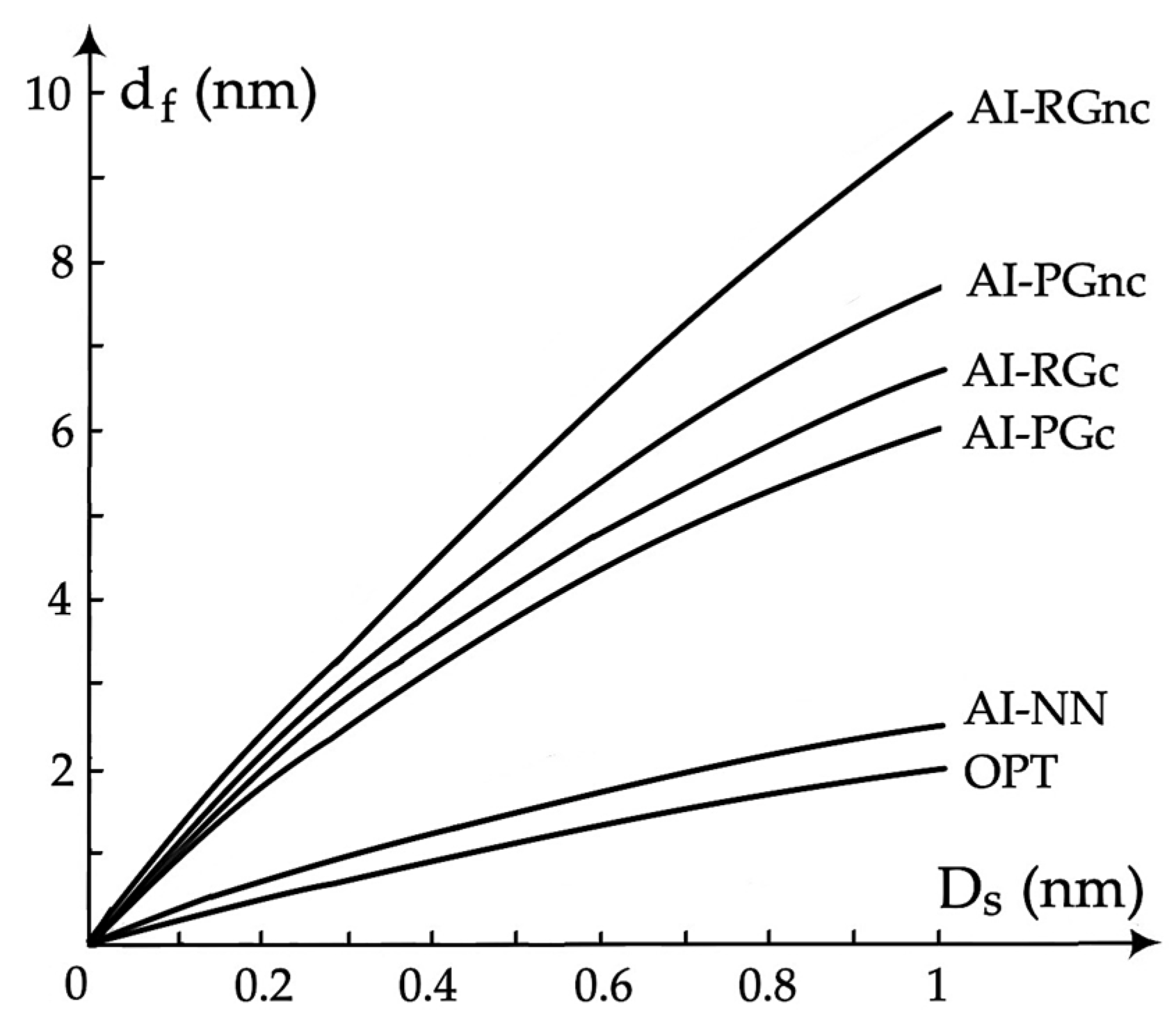
3. Experimental Comparative Analysis of Algorithms
4. Conclusions
- The object-domain neural network model supported by dynamic programming allows for the elements of the subjective assessment of the navigation situation to be taken into account;
- The positional game model supported by triple linear programming enables the cooperative and non-cooperative safe control of a group of many encountered objects;
- The collision-risk matrix game model is supported by dual linear programming and provides a solution to the problem of safe multi-object cooperative and non-cooperative control.
- The use of cooperative game algorithms reduces the final path deviation from 10 to 30% compared to non-cooperative game algorithms;
- The use of an artificial neural network in the AI-NN algorithm allows for an adequate representation of subjectivity in the assessment of the navigation situation, resulting in an increase in the final path deviation by only 10% compared to the OPT algorithm without artificial intelligence elements;
- In the situation in which object 0 passed only one object 1, the characteristics of the final path df deviation of the AI-RGc and AI-PGc algorithms would be below the characteristics of the NN and OPT algorithms due to the lack of other objects interacting with each other and indirectly with object 0.
- Use of real situation data from radar, log, and gyrocompass;
- Adequate selection of simulation parameters in the form of the values of the safe passing distance and the maneuver advance time needed for calculations and making a maneuvering decision.
- To take into account the uncertainty of the process model, the fuzzy-neural control method can be used;
- In order to achieve lower computational complexity, the use of particle swarm methods can be considered, for example in the form of the ant algorithm;
- In order to adapt to the real tasks of navigation of objects moving in unrestricted and restricted areas, it is necessary to provide the determination of a safe trajectory with the final condition in the form of a given final position or a given final course.
Funding
Data Availability Statement
Conflicts of Interest
References
- Engel, E.A.; Kovalev, I.V.; Engel, N.E.; Brezitskaya, V.V.; Prohorovich, G.A. Intelligent control system of autonomous objects. In Proceedings of the IOP Conference Series: Materials Science and Engineering, V International Workshop on Mathematical Models and their Applications, Krasnoyarsk, Russia, 7–9 November 2016; Volume 173. [Google Scholar]
- Bathla, G.; Bhadane, K.; Singh, R.K.; Kumar, R.; Aluvalu, R.; Krishnamurthi, R.; Kumar, A.; Thakur, R.N.; Basheer, S. Autonomous Vehicles and Intelligent Automation: Applications, Challenges and Opportunities. Hindawi Mob. Inf. Syst. 2022, 2022, 7632892. [Google Scholar] [CrossRef]
- Macrae, C. Learning from the Failure of Autonomous and Intelligent Systems: Accidents, Safety, and Sociotechnical Sources of Risk. Risk Anal. 2022, 42, 1893–2124. [Google Scholar] [CrossRef] [PubMed]
- Tselentis, D.I.; Papadimitriou, E.; Gelder, P. The usefulness of artificial intelligence for safety assessment of different transport modes. Accid. Anal. Prev. 2023, 186, 107034. [Google Scholar] [CrossRef] [PubMed]
- Xin, P. Multi-Objects Tracking Based on 3D Lidar and Bi-Directional Recurrent Neural Networks under Autonomous Driving. Ph.D. Thesis, School of Graduate Studies Electronic, Rutgers University, New Brunswick, NJ, USA, 18 January 2020. [Google Scholar] [CrossRef]
- Razmjooei, H.; Shafiei, M.H.; Palli, G.; Arefi, M.M. Non-linear Finite-Time Tracking Control of Uncertain Robotic Manipulators Using Time-Varying Disturbance Observer-Based Sliding Mode Method. J. Intell. Robot. Syst. 2022, 104, 36. [Google Scholar] [CrossRef]
- Lee, J.; Laskey, M.; Fox, R.; Goldberg, K. Constraint Estimation and Derivative-Free Recovery for Robot Learning from Demonstrations. arXiv 2018, arXiv:1801.10321. [Google Scholar]
- Azar, A.T.; Koubaa, A. Artificial Intelligence for Robotics and Autonomous Systems Applications, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2023; ISBN 978-3031287145. [Google Scholar]
- Soori, M.; Arezoo, B.; Dastres, R. Artificial intelligence, machine learning and deep learning in advanced robotics, a review. Cogn. Robot. 2023, 3, 54–70. [Google Scholar] [CrossRef]
- Schwarting, W.; Alonso-Mora, J.; Rus, D. Planning and Decision-Making for Autonomous Vehicles. Annu. Rev. Control. Robot. Auton. Syst. 2018, 1, 187–210. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, Z.; Yang, H.; Yang, L. Artificial intelligence applications in the development of autonomous vehicles: A survey. IEEE/CAA J. Autom. Sin. 2020, 7, 315–329. [Google Scholar] [CrossRef]
- Priyanka, G.; Rajanika, D.; Dharavi, C.; Lakshika, B.; Neha, B. Role of Artificial Intelligence in Autonomous Vehicle. In Proceedings of the International Conference on Innovative Computing & Communication (ICICC), Delhi, India, 20–21 February 2021. [Google Scholar]
- Alabdulkreem, E.; Alzahrani, J.S.; Nemri, N.; Alharbi, O.; Mohamed, A.; Marzouk, R.; Hilal, A.M. Computational Intelligence with Wild Horse Optimization Based Object Recognition and Classification Model for Autonomous Driving Systems. Appl. Sci. 2022, 12, 6249. [Google Scholar] [CrossRef]
- Naz, N.; Ehsan, M.K.; Amirzada, M.R.; Ali, M.Y.; Qureshi, M.A. Intelligence of Autonomous Vehicles: A Concise Revisit. J. Sens. 2022, 2022, 2690164. [Google Scholar] [CrossRef]
- Ming, G. Exploration of the intelligent control system of autonomous vehicles based on edge computing. PLoS ONE 2023, 18, e0281294. [Google Scholar] [CrossRef]
- Sana, F.; Azad, N.L.; Raahemifar, K. Autonomous Vehicle Decision-Making and Control in Complex and Unconventional Scenarios—A Review. Machines 2023, 11, 676. [Google Scholar] [CrossRef]
- Perera, L.P. Autonomous Ship Navigation Under Deep Learning and the Challenges in COLREGs. In Proceedings of the 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 17–22 June 2018. [Google Scholar]
- Martelli, M.; Virdis, A.; Gotta, A.; Cassarà, P.; Di Summa, M. An Outlook on the Future Marine Traffic Management System for Autonomous Ships. IEEE Access 2021, 9, 157316–157328. [Google Scholar] [CrossRef]
- Veitch, E.; Alsos, O.A. A systematic review of human-AI interaction in autonomous ship systems. Saf. Sci. 2022, 152, 105778. [Google Scholar] [CrossRef]
- Guan, W.; Cui, Z.; Zhang, X. Intelligent Smart Marine Autonomous Surface Ship Decision System Based on Improved PPO Algorithm. Sensors 2022, 22, 5732. [Google Scholar] [CrossRef]
- Johansen, T.; Blindheim, S.; Torben, T.R.; Utne, I.B.; Johansen, T.A.; Sørensen, A.J. Development and testing of a risk-based control system for autonomous ships. Reliab. Eng. Syst. Saf. 2023, 234, 109195. [Google Scholar] [CrossRef]
- Yussupova, N.I.; Gonchar, L.E.; Rembold, U. Path Planning Algorithm of a Lot of Mobil Autonomous Objects in Unknown Constrained Environment. In Proceedings of the ISARC’99 International Symposium on Automation and Robotics in Construction, Madrid, Spain, 22–24 September 1999; pp. 403–407. [Google Scholar] [CrossRef]
- Arnold, R.D.; Yamaguchi, H.; Tanaka, T. Search and rescue with autonomous flying robots through behavior-based cooperative intelligence. Int. J. Humanit. Action 2018, 3, 18. [Google Scholar] [CrossRef]
- Kotenko, I.; Stankevitch, L. The control of teams of autonomous objects in the time-constrained environments. In Proceedings of the 2002 IEEE International Conference on Artificial Intelligence Systems (ICAIS 2002), Divnomorskoe, Russia, 5–10 September 2002; pp. 158–163. [Google Scholar] [CrossRef]
- Li, S.; Wang, Y.; Zhou, Y.; Jia, Y.; Shi, H.; Yang, F.; Zhang, C. Multi-UAV Cooperative Air Combat Decision-Making Based on Multi-Agent Double-Soft Actor-Critic. Aerospace 2023, 10, 574. [Google Scholar] [CrossRef]
- Muzahid, A.J.M.; Kamarulzaman, S.F.; Rahman, M.A.; Murad, S.A.; Kamal, M.A.S.; Alenezi, A.H. Multiple vehicle cooperation and collision avoidance in automated vehicles: Survey and an AI-enabled conceptual framework. Sci. Rep. 2023, 13, 603. [Google Scholar] [CrossRef] [PubMed]
- Dey, S.; Xu, H. Intelligent Distributed Swarm Control for Large-Scale Multi-UAV Systems: A Hierarchical Learning Approach. Electronics 2023, 12, 89. [Google Scholar] [CrossRef]
- Thie, P.R.; Keough, G.E. An Introduction to Linear Programming and Game Theory; Wiley: Hoboken, NJ, USA, 2008; ISBN 978-0-470-23286-6. [Google Scholar]
- Lew, A.; Mauch, H. Dynamic Programming—A Computational Tool; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-37014-7. [Google Scholar]
- Faigle, U. Mathematical Game Theory, 1st ed.; World Scientific: Singapore, 2022; ISBN 978-981-1246-70-8. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V. Algorithmic Game Theory; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-87282-9. [Google Scholar]





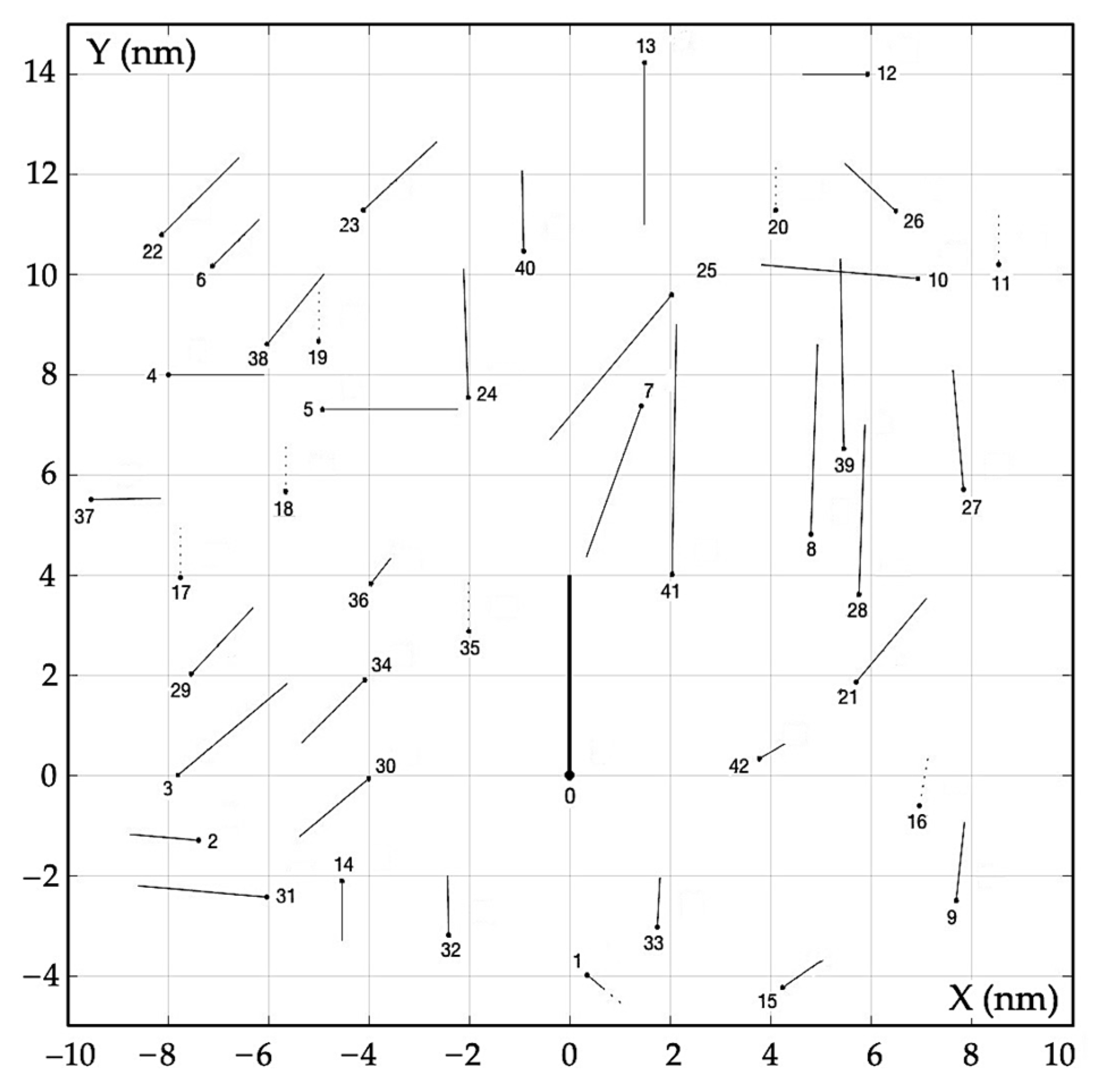
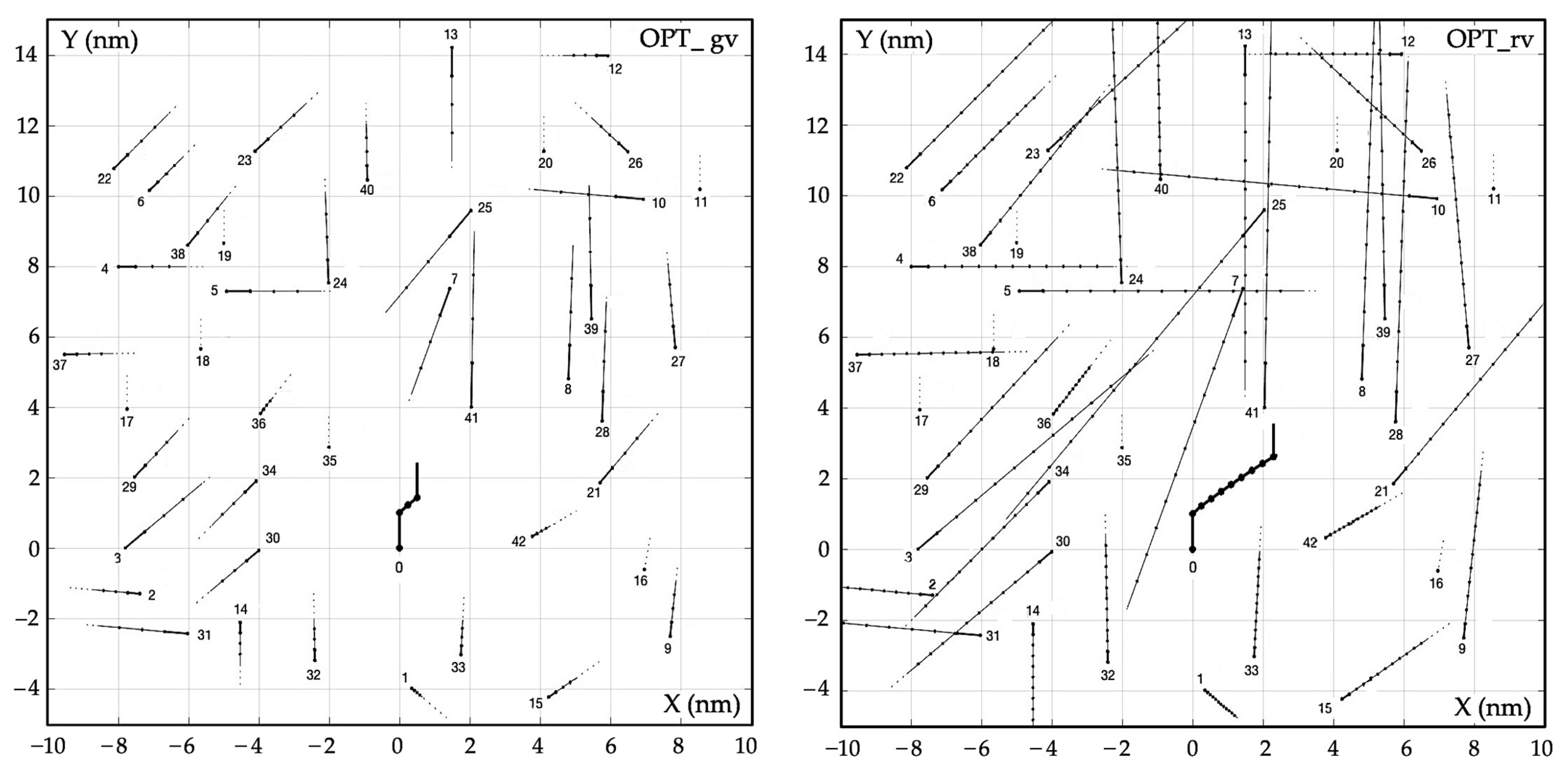
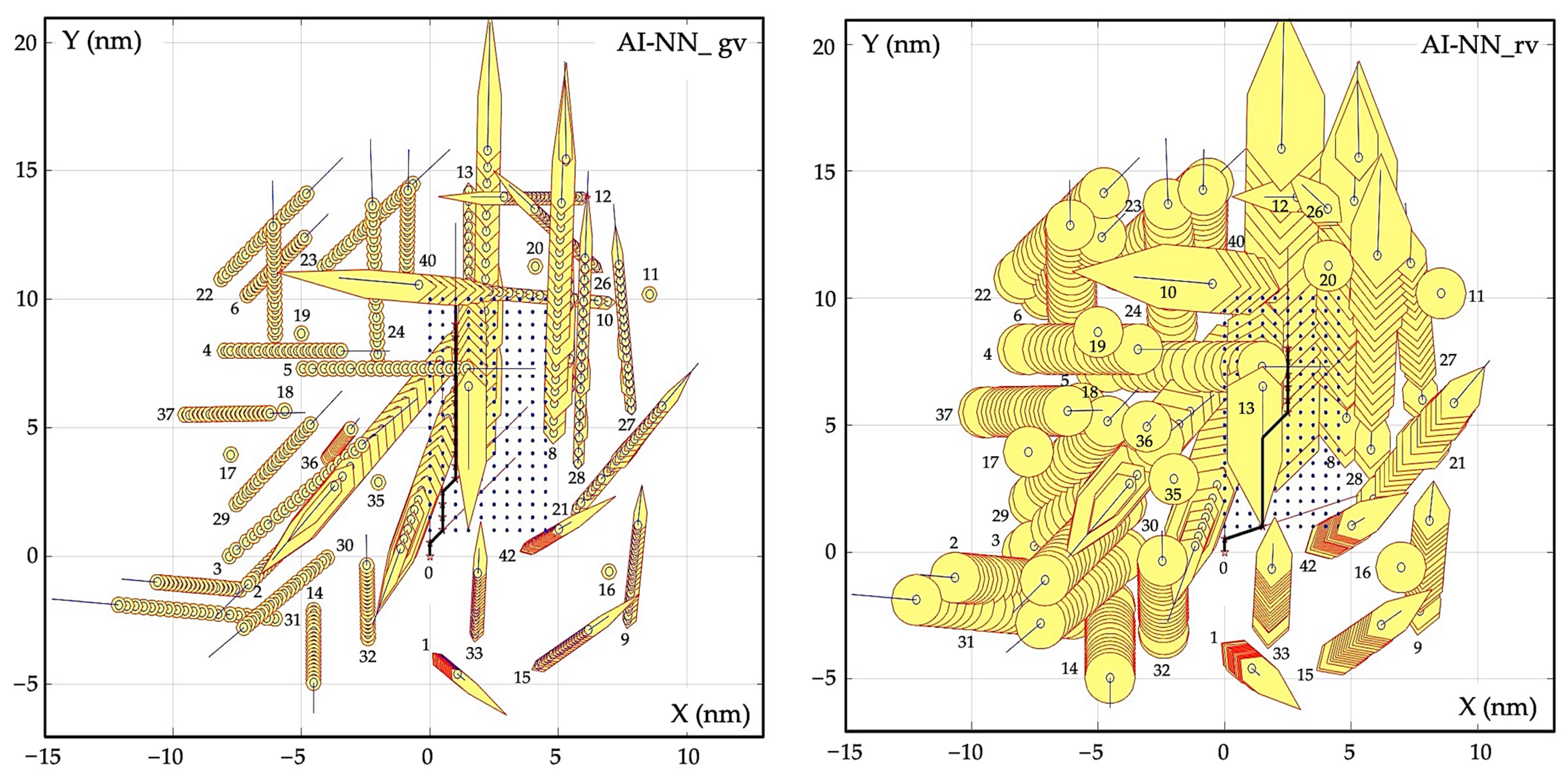
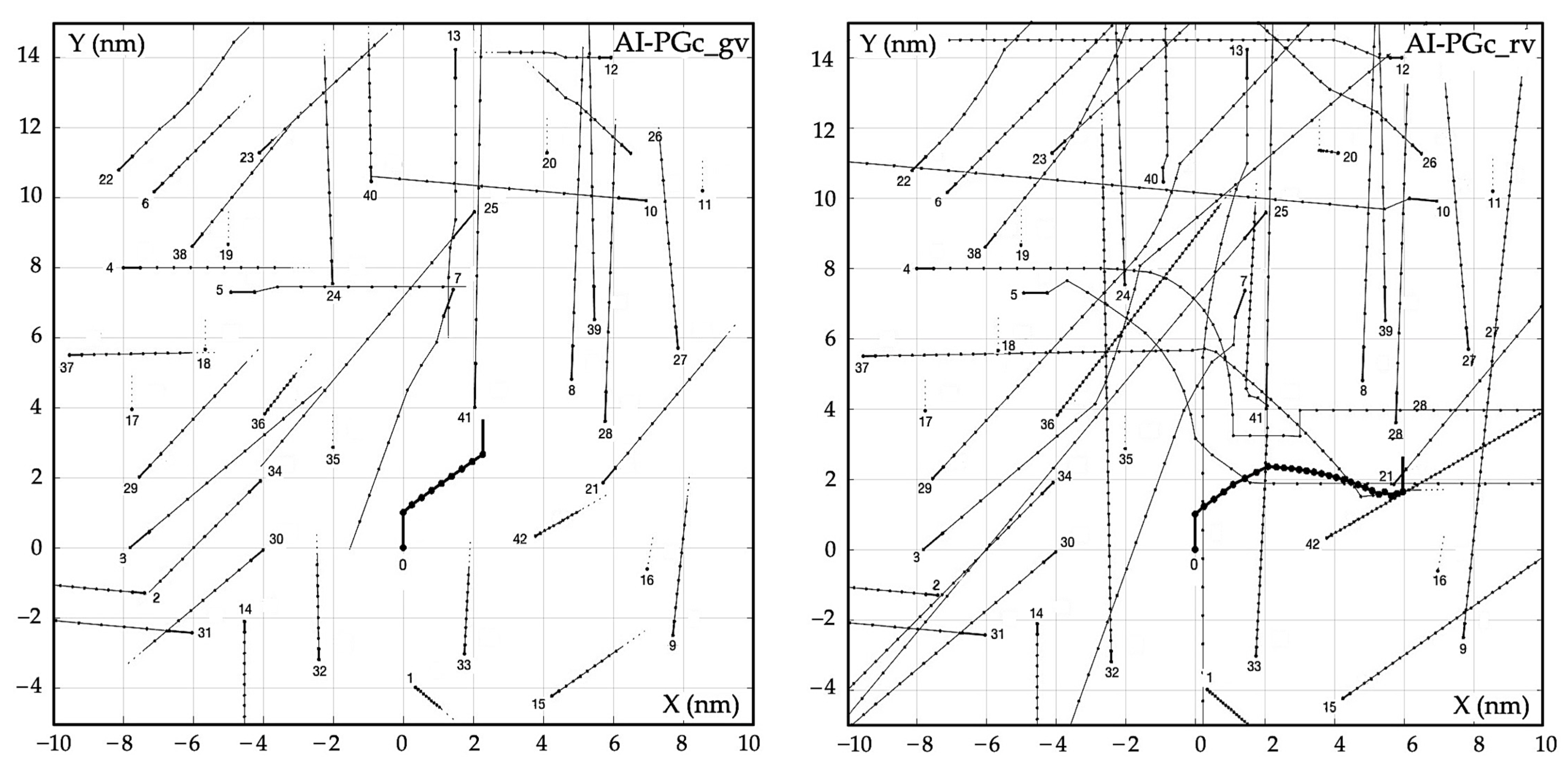

| Object j | Distance Dj (nm) | Bearing Nj (deg) | Speed Vj (kn) | Course ψj (deg) |
|---|---|---|---|---|
| 0 | - | - | 20.0 | 0 |
| 1 | 4.0 | 175 | 2.0 | 130 |
| 2 | 7.5 | 260 | 6.9 | 275 |
| 3 | 7.8 | 270 | 14.3 | 50 |
| 4 | 11.3 | 315 | 9.6 | 90 |
| 5 | 8.8 | 326 | 13.5 | 90 |
| 6 | 12.4 | 325 | 6.7 | 45 |
| 7 | 7.5 | 11 | 16.0 | 200 |
| 8 | 8.8 | 45 | 19.0 | 2 |
| 9 | 8.1 | 108 | 7.9 | 6 |
| 10 | 12.1 | 35 | 15.7 | 275 |
| 11 | 13.3 | 40 | 0 | 0 |
| 12 | 15.2 | 23 | 6.5 | 270 |
| 13 | 14.3 | 6 | 16.2 | 180 |
| 14 | 5.0 | 245 | 6.0 | 180 |
| 15 | 6.0 | 135 | 5.0 | 55 |
| 16 | 7.0 | 95 | 0 | 0 |
| 17 | 8.7 | 297 | 0 | 0 |
| 18 | 8.0 | 315 | 0 | 0 |
| 19 | 10.0 | 330 | 0 | 0 |
| 20 | 12.0 | 20 | 0 | 0 |
| 21 | 6.0 | 72 | 11.0 | 40 |
| 22 | 13.5 | 323 | 11.0 | 45 |
| 23 | 12.0 | 340 | 10.0 | 47 |
| 24 | 7.8 | 345 | 13.0 | 358 |
| 25 | 9.8 | 12 | 19.0 | 220 |
| 26 | 13.0 | 30 | 7.0 | 313 |
| 27 | 9.7 | 54 | 12.0 | 355 |
| 28 | 6.8 | 58 | 17.0 | 2 |
| 29 | 7.8 | 285 | 9.0 | 43 |
| 30 | 4.0 | 269 | 9.0 | 230 |
| 31 | 6.5 | 248 | 13.0 | 275 |
| 32 | 4.0 | 217 | 6.0 | 359 |
| 33 | 3.5 | 150 | 5.0 | 3 |
| 34 | 4.5 | 295 | 9.0 | 225 |
| 35 | 3.5 | 325 | 0 | 0 |
| 36 | 5.5 | 314 | 3.0 | 38 |
| 37 | 11.0 | 300 | 7.0 | 89 |
| 38 | 10.5 | 325 | 9.0 | 39 |
| 39 | 8.5 | 40 | 19.0 | 359 |
| 40 | 10.5 | 355 | 8.0 | 359 |
| 41 | 4.5 | 27 | 25.0 | 1 |
| 42 | 3.8 | 85 | 3.0 | 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisowski, J. Computational Intelligence Supporting the Safe Control of Autonomous Multi-Objects. Electronics 2024, 13, 780. https://doi.org/10.3390/electronics13040780
Lisowski J. Computational Intelligence Supporting the Safe Control of Autonomous Multi-Objects. Electronics. 2024; 13(4):780. https://doi.org/10.3390/electronics13040780
Chicago/Turabian StyleLisowski, Józef. 2024. "Computational Intelligence Supporting the Safe Control of Autonomous Multi-Objects" Electronics 13, no. 4: 780. https://doi.org/10.3390/electronics13040780
APA StyleLisowski, J. (2024). Computational Intelligence Supporting the Safe Control of Autonomous Multi-Objects. Electronics, 13(4), 780. https://doi.org/10.3390/electronics13040780






