Sum Rate Optimization for Multi-IRS-Aided Multi-BS Communication System Based on Multi-Agent
Abstract
1. Introduction
- We develop a large-scale communication system with multi-BS assisted by multi-IRS to serve multi-UE. We formulate a comprehensive optimization problem aimed at maximizing the data rates of served UEs. The joint optimization encompasses BSs’ transmit powers, IRSs’ passive beamforming, and the design of BS–UE–IRS associations, all subject to the system and UEs’ QoS requirements.
- Addressing the inherent non-convexity of the original optimization problem, we propose a MADRL-based algorithm under continuous and discrete phases of the IRS scenarios. The optimization problem is modeled as an MAMDF, where the agents are designed by integrating DDPG and DQN algorithms to learn a joint policy. This approach enables the system to dynamically adapt to changing environmental conditions and maximize the long-term total system utility.
- We analyze the convergence, computational complexity, and implementation efficiency of the proposed MADRL-based algorithm, integrated with the DRL algorithms. Our numerical results not only showcase the superior performance of our algorithm over benchmark schemes (e.g., the successive refinement-based approach), but also demonstrate its efficiency in terms of implementation runtime, thus validating its practical feasibility. Moreover, the achieved rate in the IRS-aided system exhibits substantial improvements as the number of reflecting elements increases, highlighting the scalability and effectiveness of the proposed approach.
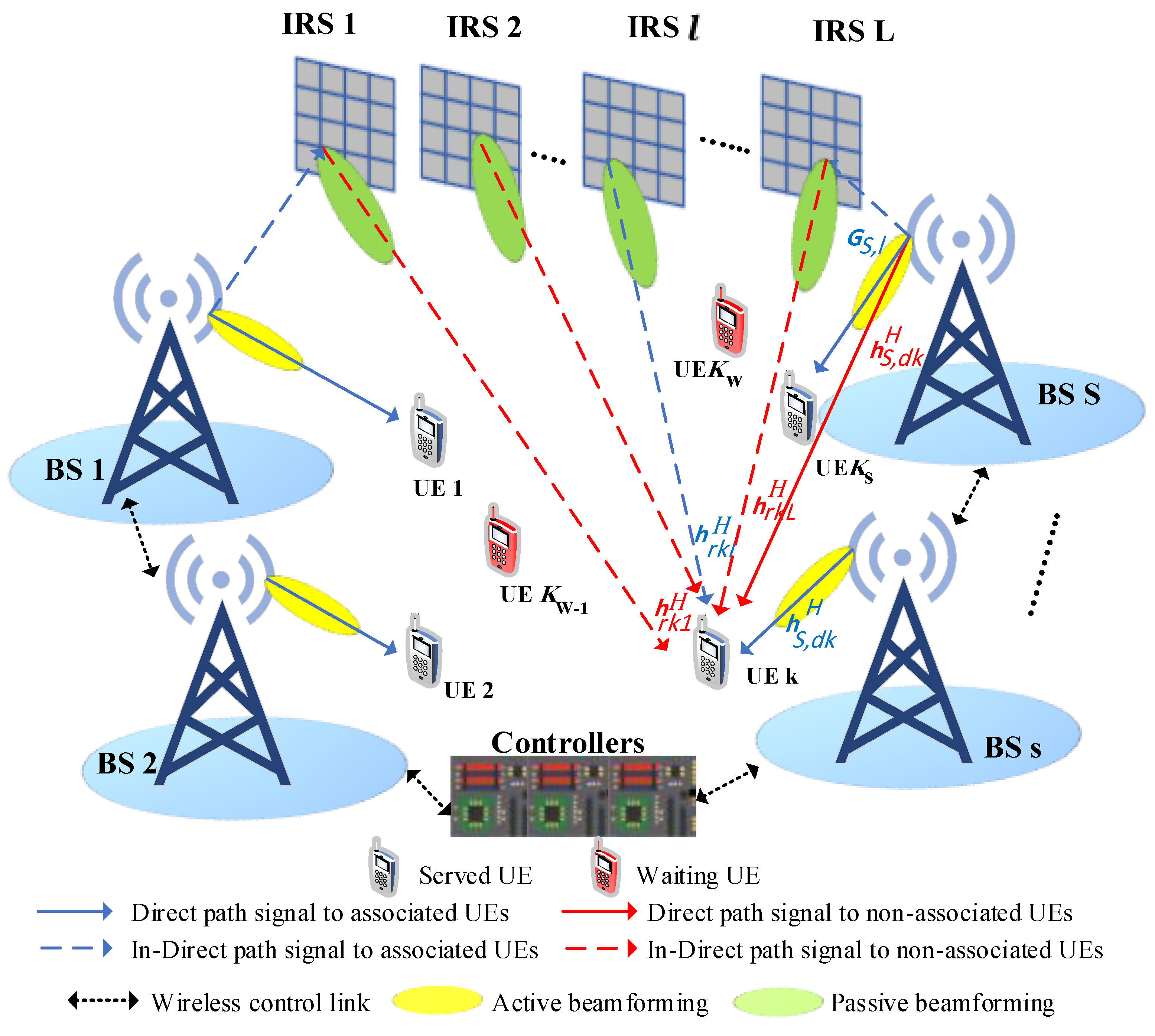
2. System Model
3. Formulation of the Optimization Problem
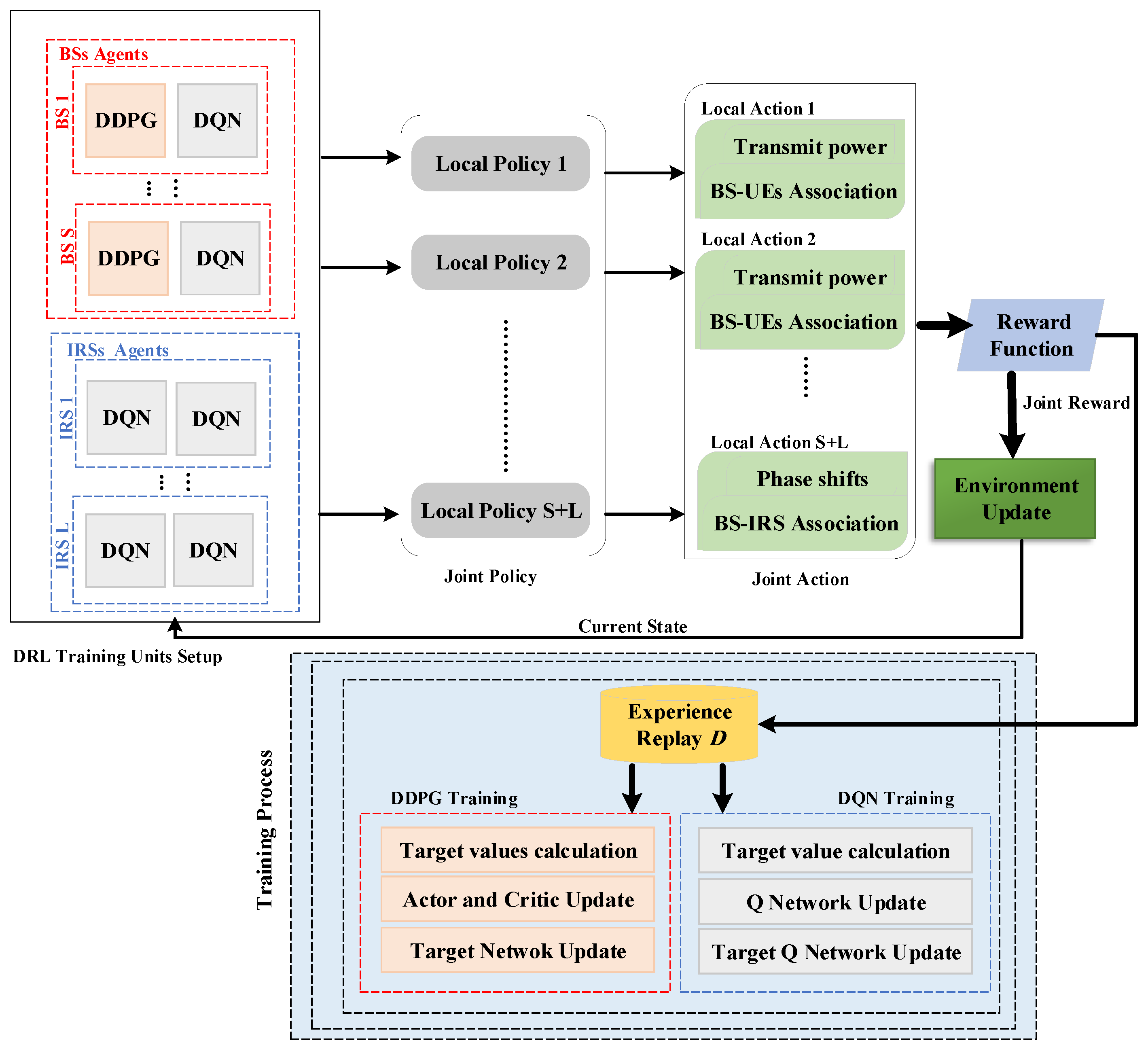
4. Proposed MADRL-Based Algorithm
4.1. MAMDP Formulation of the Optimization Problem
- States: For each BS agent , we define its state as the current active beamforming at time step t, , the previous transmit power at time step , , the previous BS–UE associations vector at time step , , the previous BS-IRSs associations vector at time step , , and the current position to the served UE, , which is mathematically given by:whose dimension is . The term , determined by the CSI, serves as a surrogate for the CSI in at time t to capture variations in wireless channel conditions. Note that directly integrating the channel estimates among all system nodes into the local observation may not be feasible due to the impracticality of handling high-dimensional feedback, while for each IRS agent , we define its state as the previous passive beamforming vector at time step , , which is defined as:whose dimension is .
- Actions: For each BS agent , its action includes the transmit power, , BS–UE association vector, , and BS-IRSs associations vector, . However, in order to handle constraint (11e) and reduce the action space of the BS–IRS associations from to L, we shift the BS-IRSs associations as a subfunction to IRS agents, where each IRS has to choose one BS. Moreover, in order to reduce the infeasible BS–UE association actions and handle constraints (11c) and (11d) during training, a centralized DRL element for all BS–UE associations is trained at one BS, and then a copy is delivered to all BSs. Consequently, the action of each BS agent j is denoted by:where is the index of the served k-th UE by the s-th BS. Correspondingly, the dimension is simply 2, and the action space of BS–UE associations equals K, while for each IRS agent , we define its action as the current passive beamforming, , and BS-IRS association index element, , where is the index of the chosen j-th BS for l-th IRS. For example, if at time step t, the agent IRS l chose to associate with the fourth BS, then in the BS–IRS associations matrix. The action of each IRS agent l is denoted by:which outputs a dimension of and an action space of BSs-IRS associations of S.
- Rewards: As the objective function of the optimization problem is to maximize the sum rate of served UEs, establishing a connection between the reward and the objective function drives the realization of the MMDP goal to augment long-term rewards. Noting that each agent with a separate reward may behave selfishly, therefore hindering the global optimal solution. Thus, we assume all agents have the same reward after the joint action is performed. The environment sets the instant reward for all cooperative agents in this framework as the total sum rate achieved. Note that all the constraints in (P1) are handled above, except the constraint (11b), which considers the minimum QoS requirements constraints. If the resulting joint action fails to satisfy the minimum data rates of the UEs, agents are penalized to encourage them to modify inappropriate actions. The reward function includes a penalty value, which is represented by the difference between the minimum achieved rate and the specified constraint rate. Thus, the agents will receive a negative penalty if the minimum QoS is not satisfied for the UEs. Otherwise, all agents will receive positive rewards represented by the total utility achieved. Here, we set such a penalty value instead of zero to limit the sparsity of the rewards and reflect how far the agents are from achieving the minimum QoS. Therefore, each agent can receive an instant reward, determined as follows:where represents the minimum achieved data rate of all the served UEs at the t-th time step.
- Policies: In the proposed MADRL framework, effective collaboration hinges on creating an optimal joint policy, denoted as . This joint policy plays a pivotal role in guiding collective decision-making among agents, directing them to choose actions that enhance cumulative rewards in the dynamic multi-agent environment. The process of learning and contributing to this joint policy is iterative and adaptive for each agent. In response to ever-changing environmental states, agents continually adjust their local policies by evaluating the outcomes of their actions based on observed states. Reinforcement signals aid this learning process, guiding agents toward actions that maximize system utility over the long term through reward-based feedback. Further sections will provide a closer look at how agents refine their local policies, contributing to the overall success of the collaborative MADRL framework.
4.2. The Implementation of the Proposed MADRL-Based Algorithm
4.2.1. MADRL-Based Algorithm under Continuous Phases Case
| Algorithm 1 The proposed MADRL-based algorithm. |
|
4.2.2. MADRL-Based Algorithm under Discrete Phases Case
4.3. Analysis of the Proposed MADRL-Based Algorithm
4.3.1. Convergence Analysis
4.3.2. Computational Complexity Analysis
- Action selection complexity: Let denote the input dimension, n represent the number of nodes in the hidden layer, and indicate the output dimension. Specifically, denotes the size of the action space in the DQN algorithms and the dimension of the continuous action in the DDPG algorithms [28]. The complexity of a single decision for one three-layer DNN is approximately:In our system, we have S BSs and L IRSs acting as agents, all sharing the same state. Thus, the states, actions, and related complexities under continuous and discrete cases can be defined as follows:where B represents the quantization level with .
- Training process complexity: The computational complexity of backpropagation in the DQN and DDPG algorithms for fully connected DNN (FC-DNN) per training step is approximated as:where is determined based on the types of actions. Thus, the training complexity of all DNNs is approximated as:Here, the total complexity is approximated as the backpropagation training complexity, which has a higher order than the action selection complexity.
4.3.3. Implementation Complexity Analysis
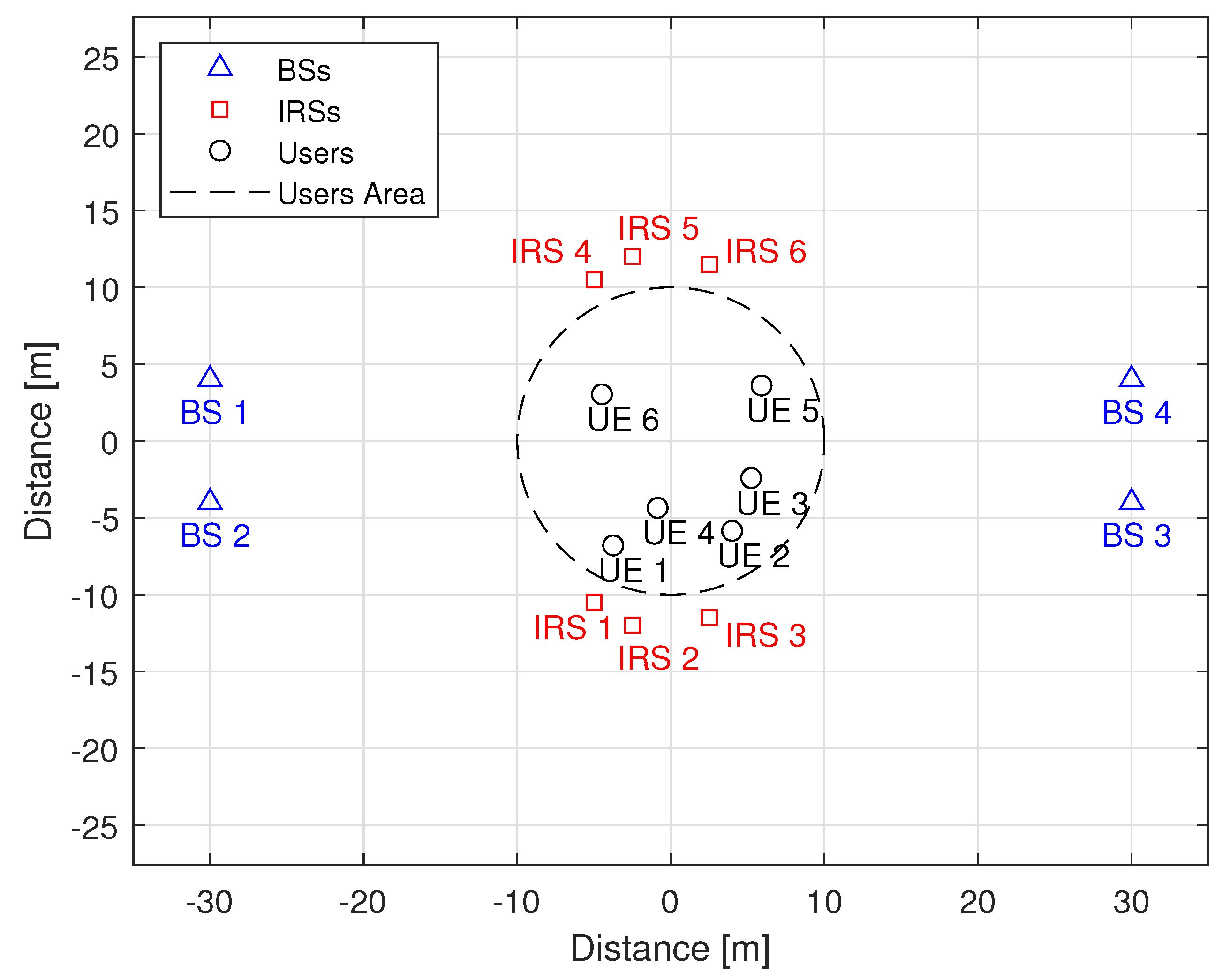
5. Simulation Results
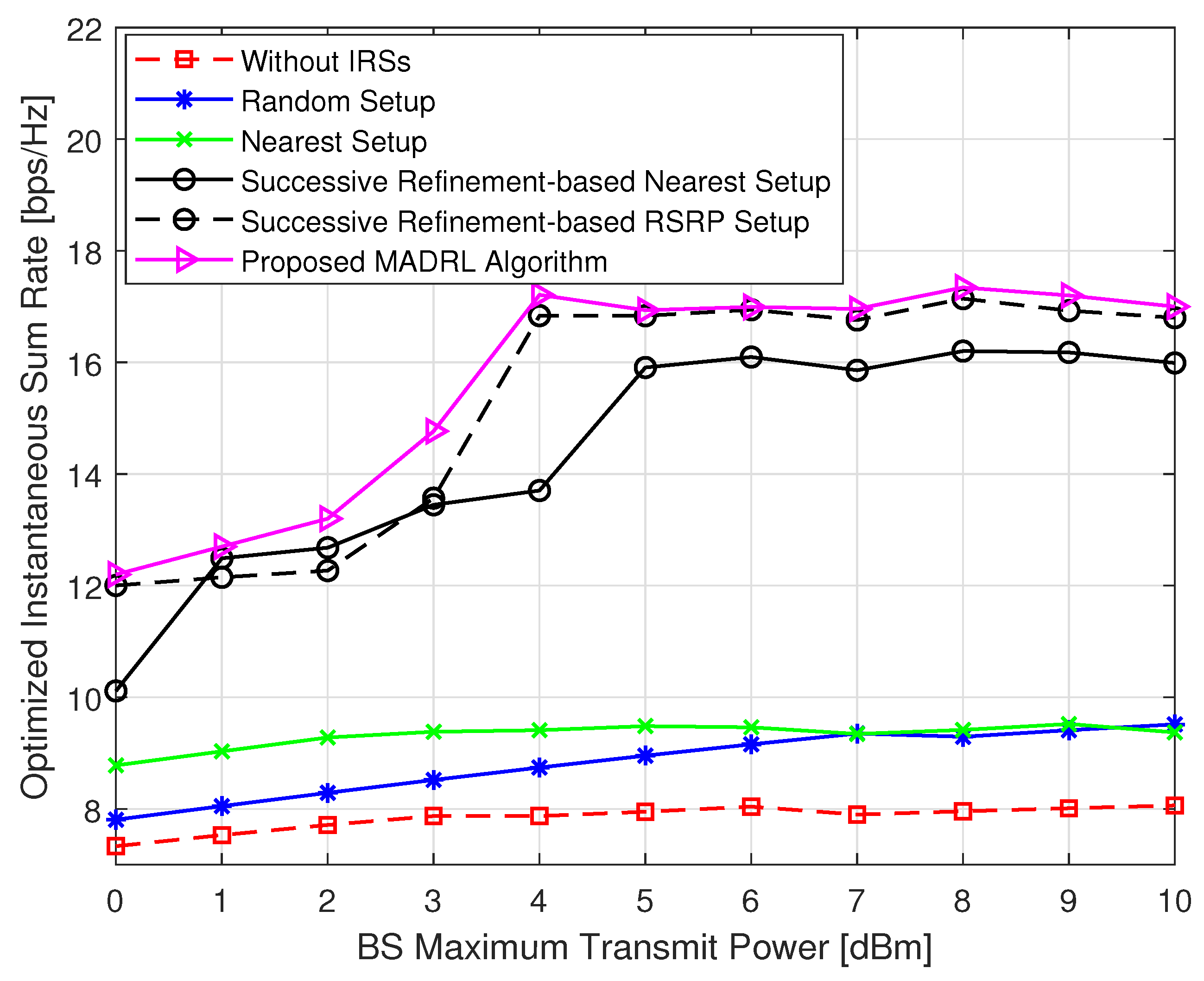
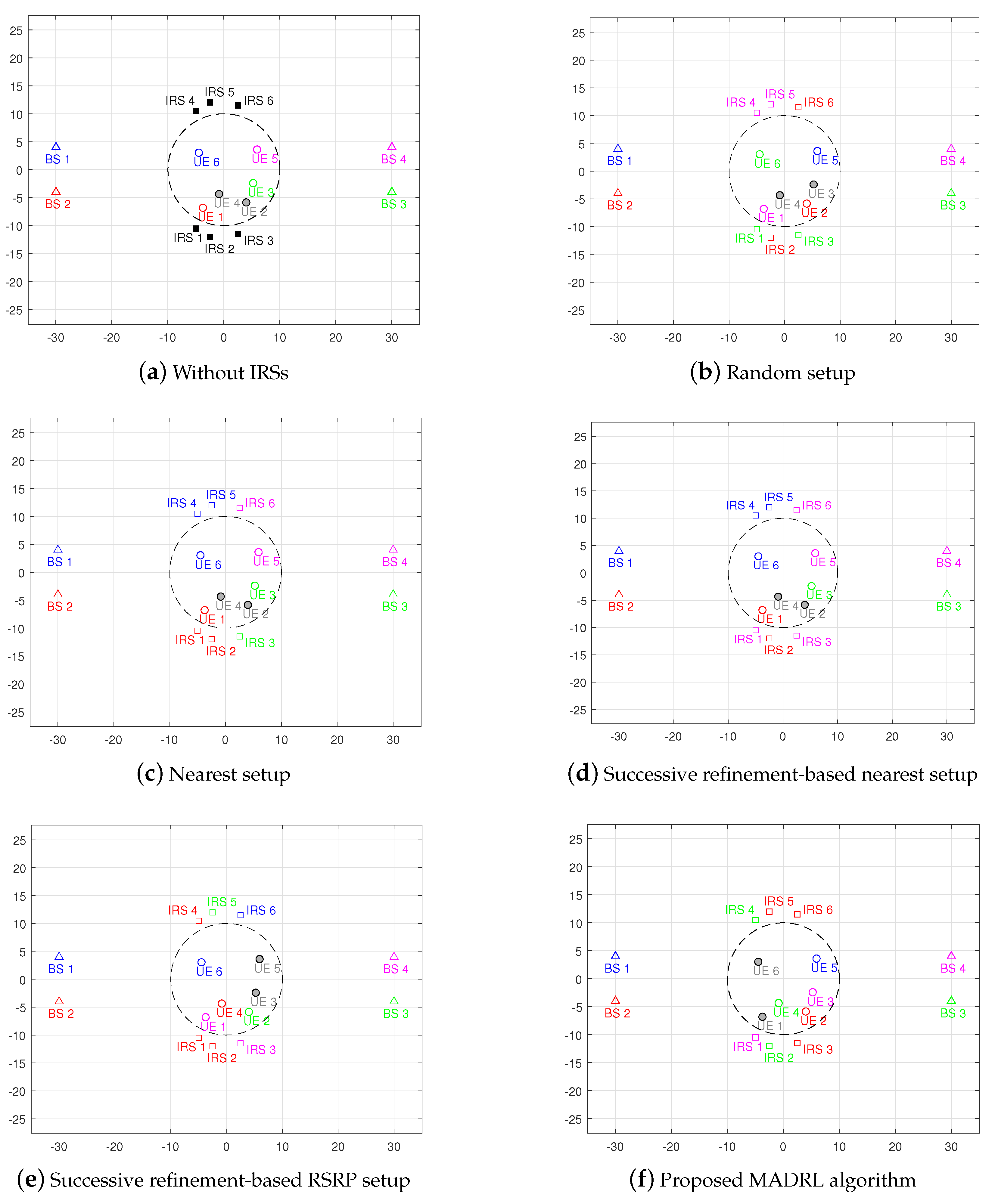
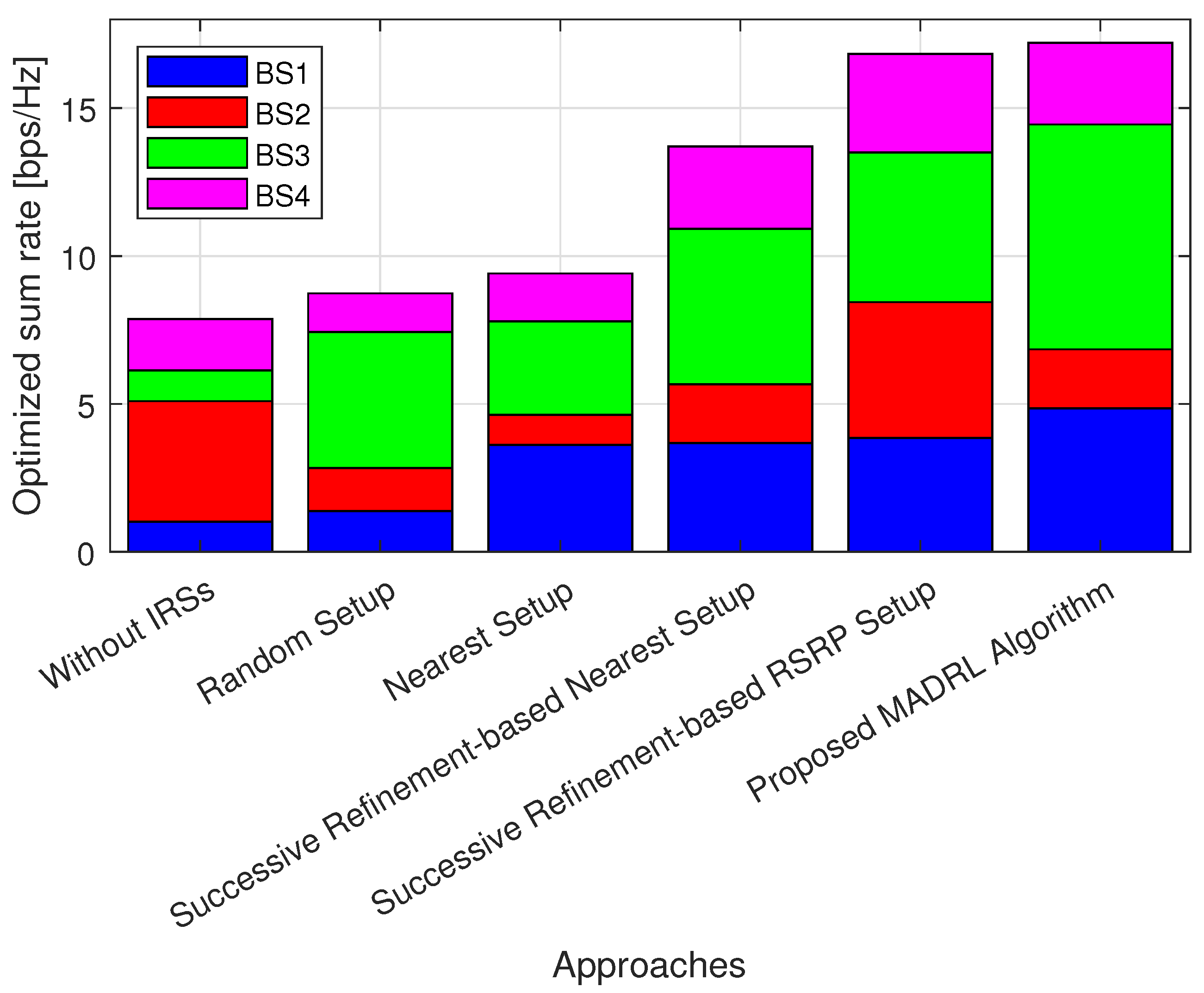
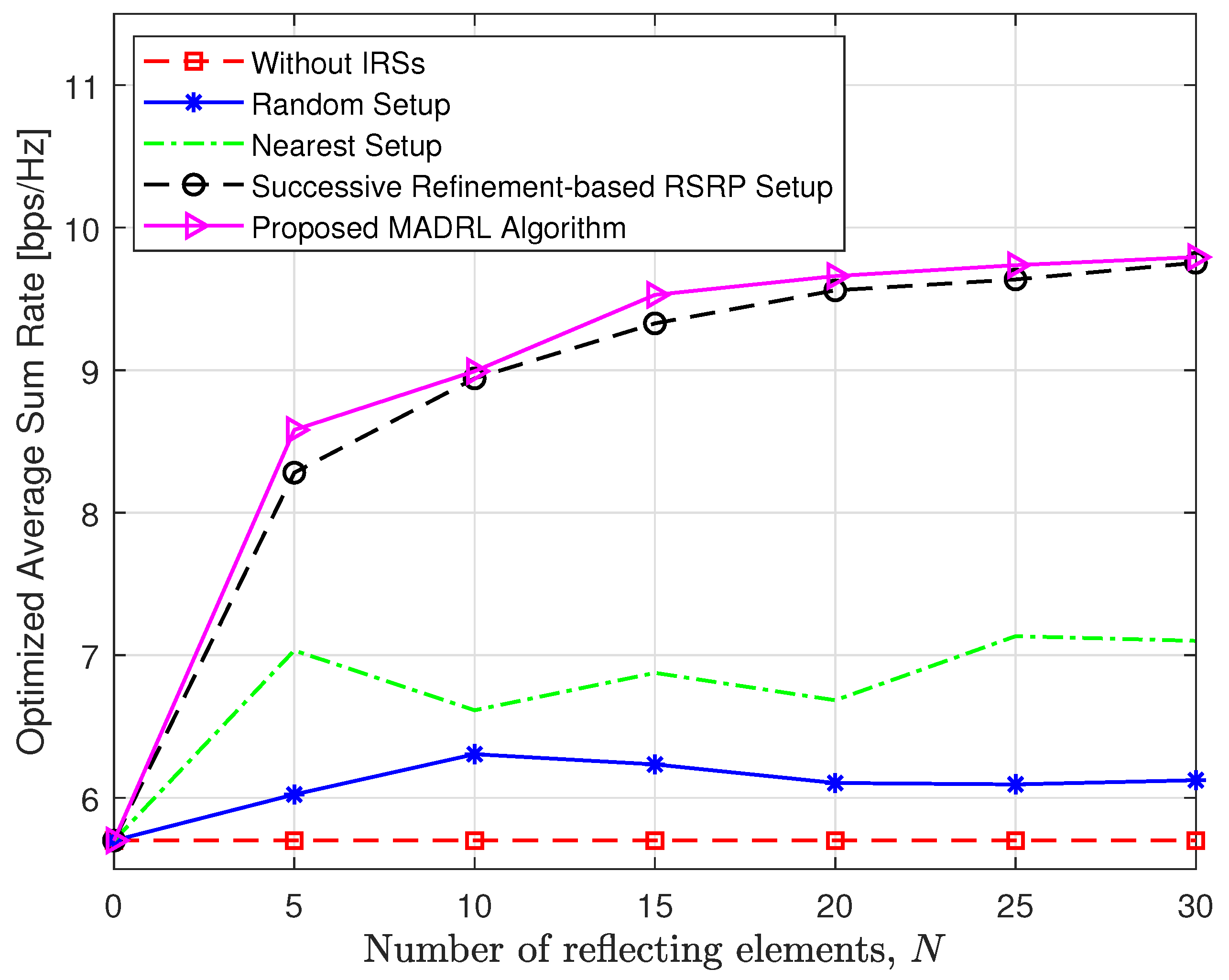
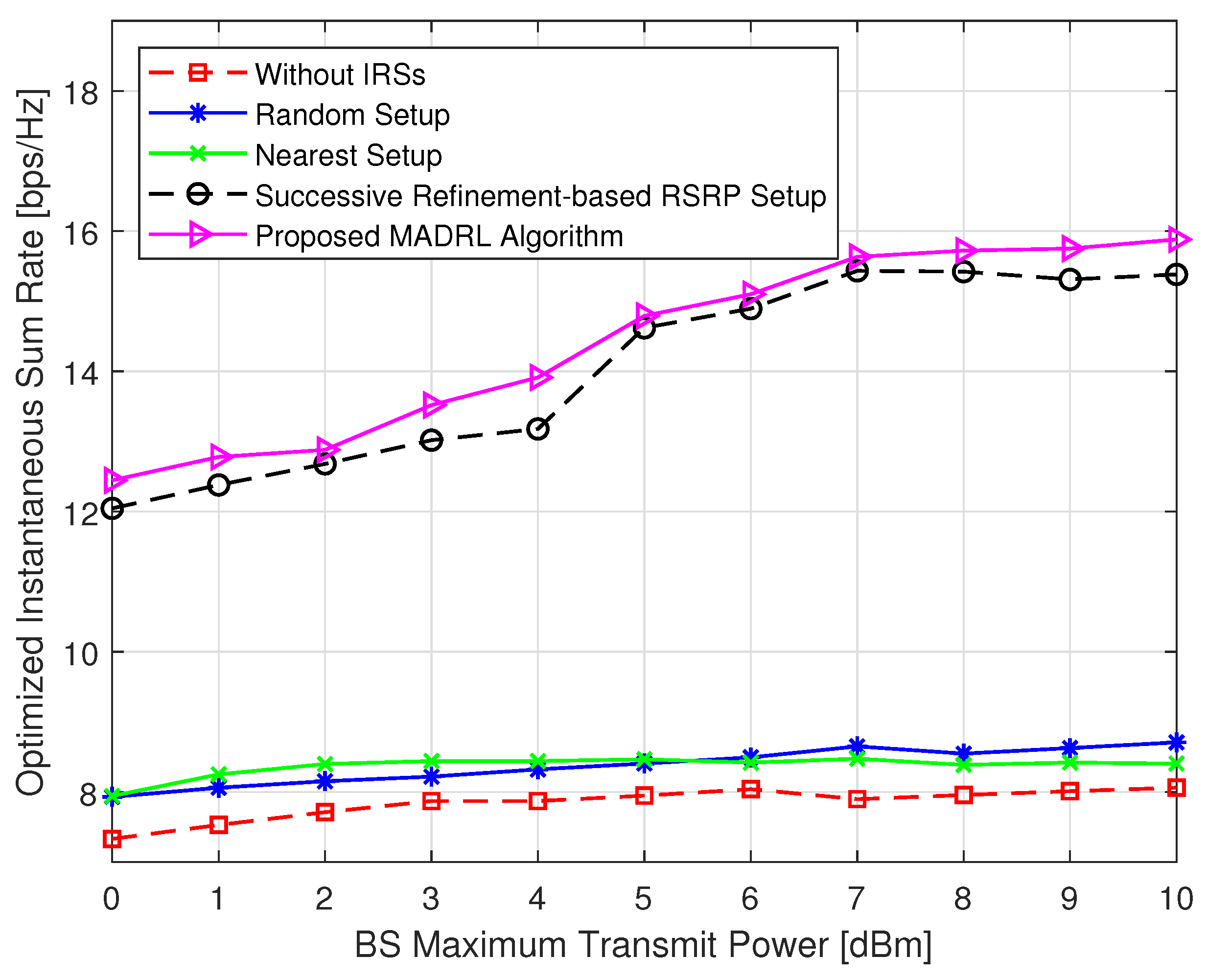
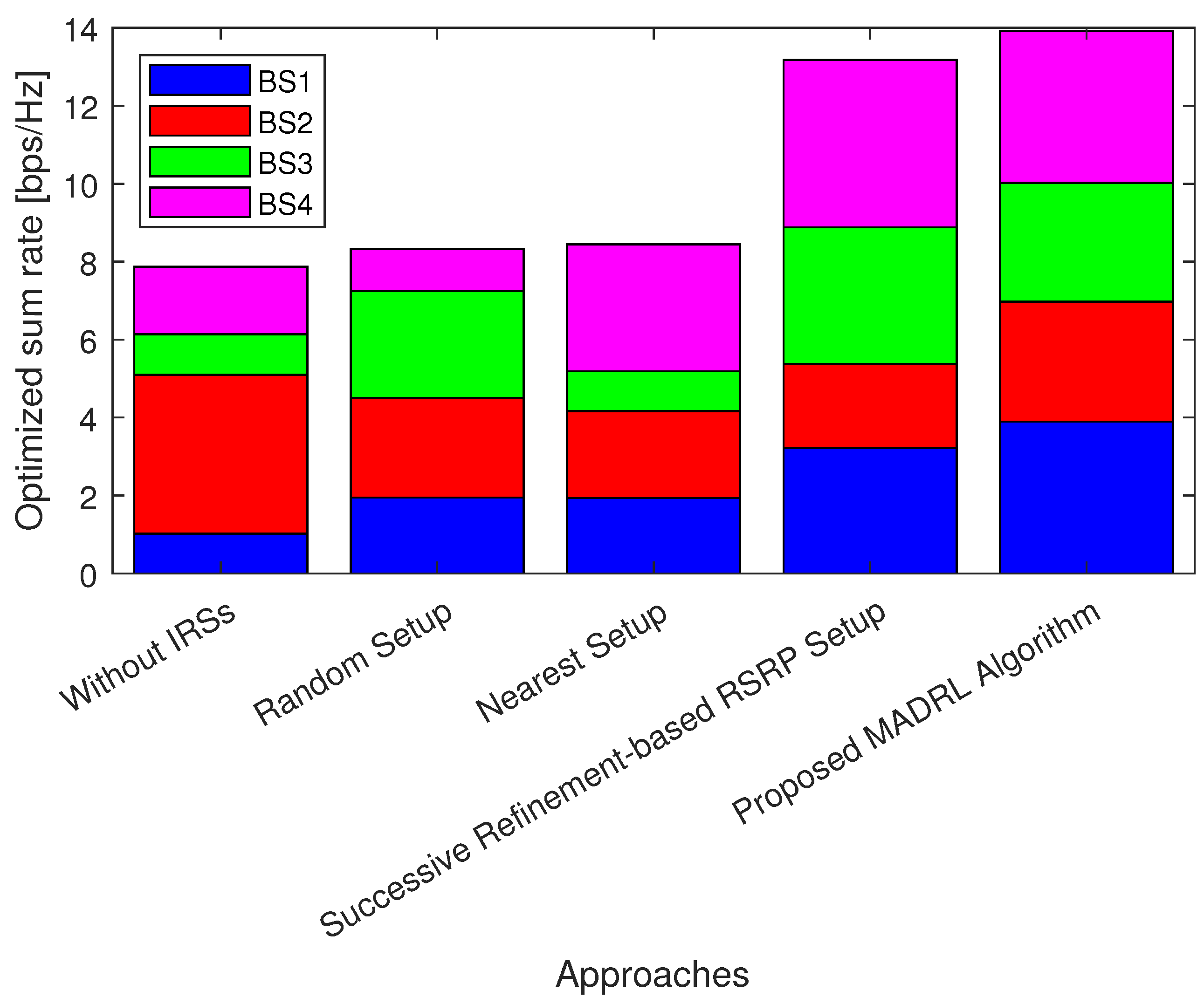
- Without IRSs: conventional system without IRSs aid, i.e., switch off all the deployed IRSs and no related associations.
- Random setup: system with the BS–IRS–UE associations are set up randomly.
- Nearest setup: system with the BS–IRS–UE associations are set up based on the nearest association rule.
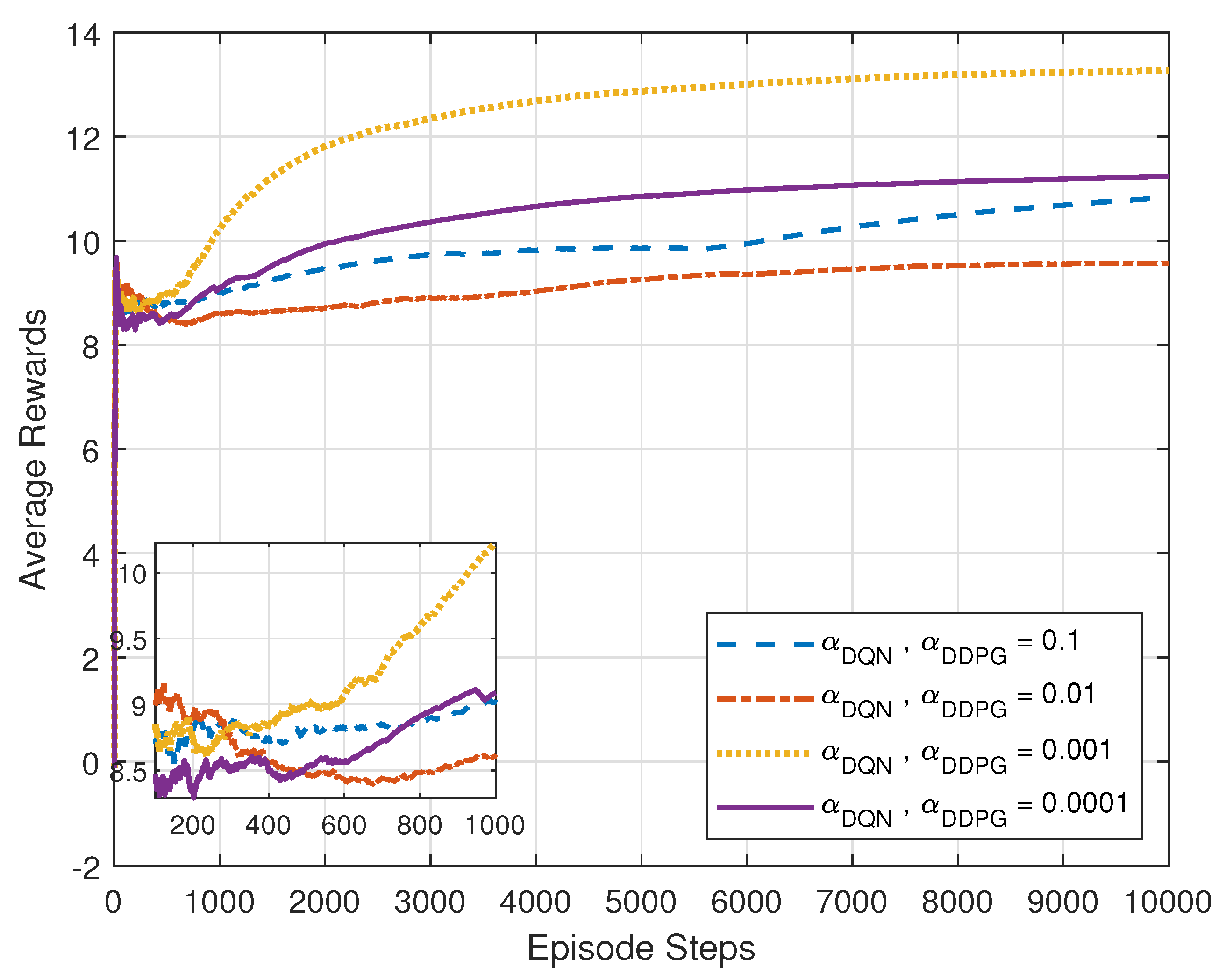
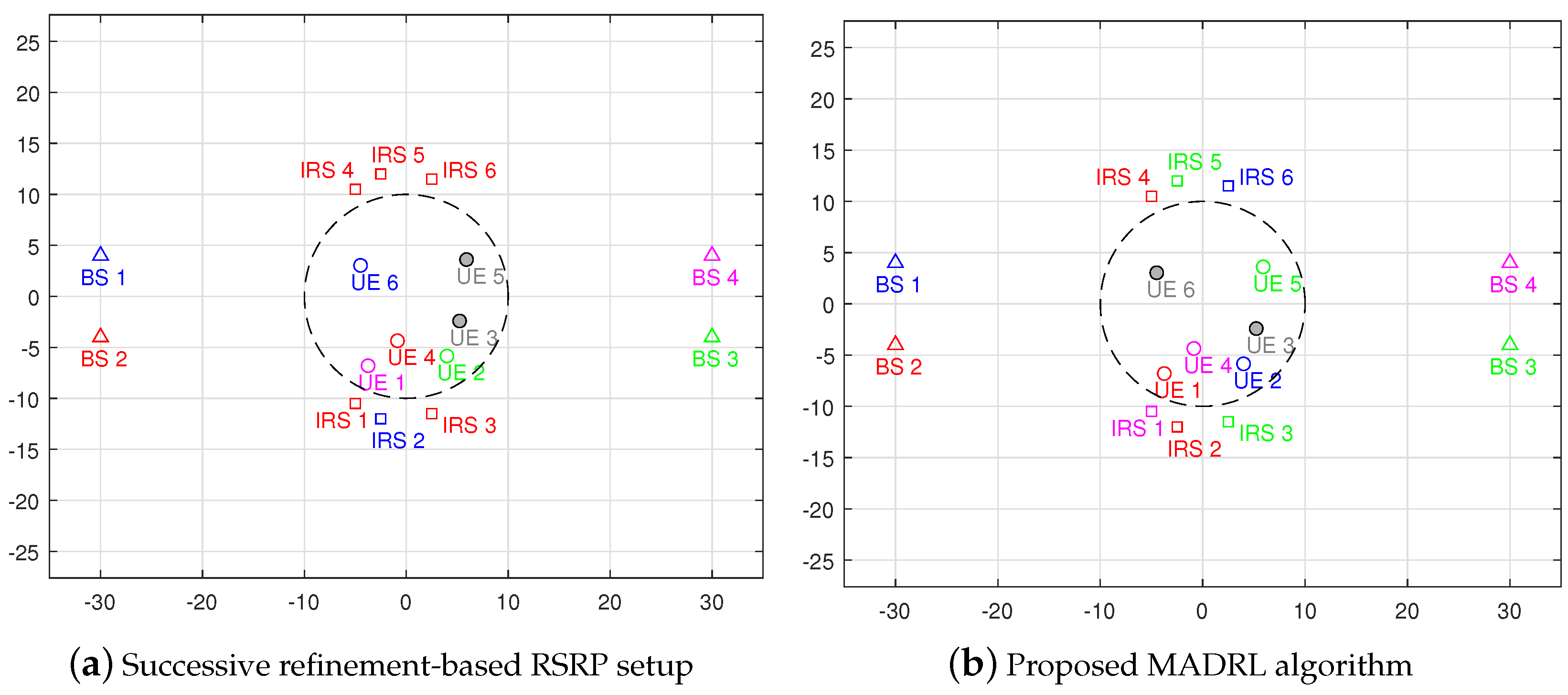
5.1. Performance Analysis of the Proposed MADRL-Based Algorithm
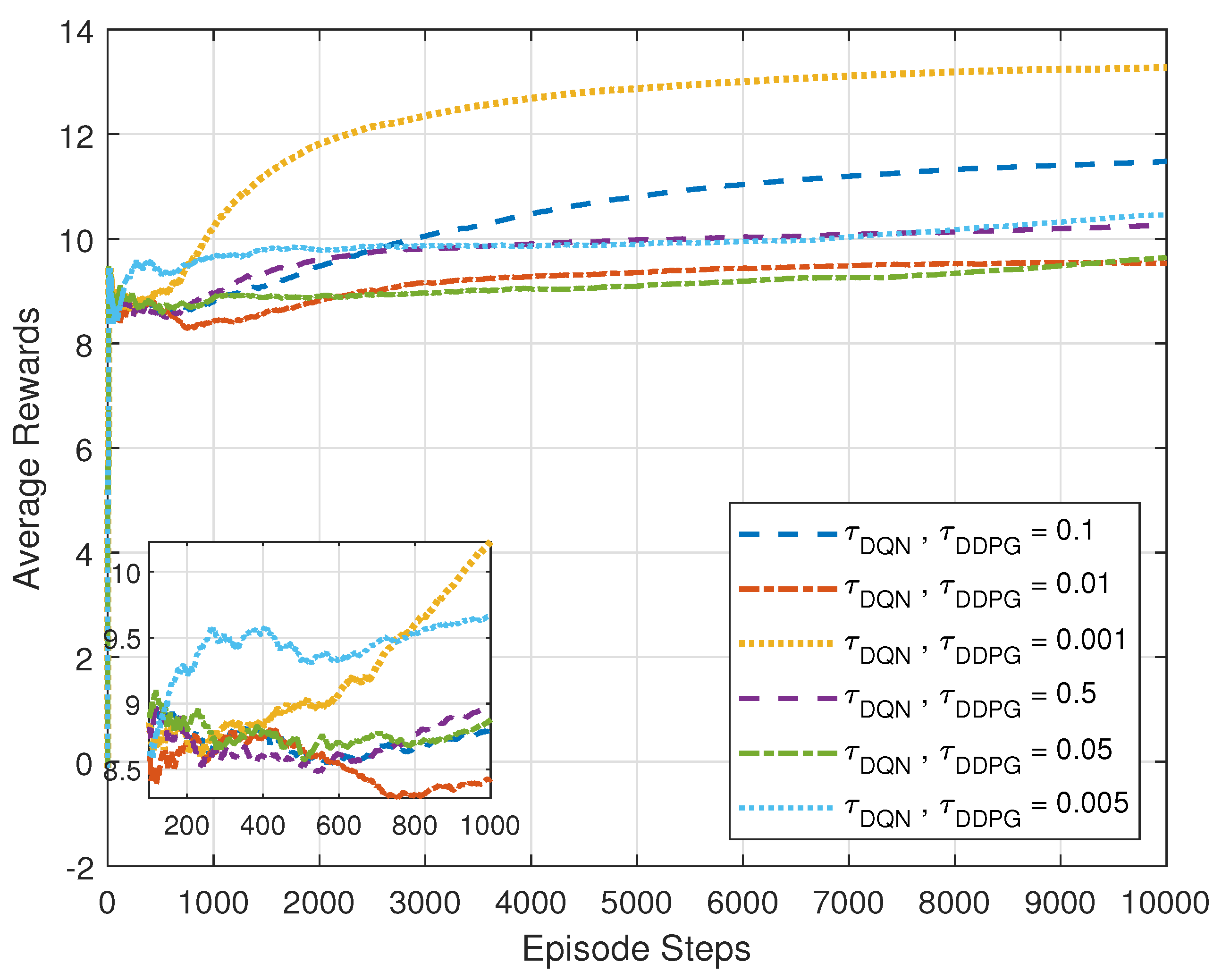
5.2. Performance Comparison of the Proposed MADRL-Based Algorithm under the Continuous Phases Case
5.3. Performance Comparison of the Proposed MADRL-Based Algorithm under the Discrete Phases Case
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Gong, S.; Lu, X.; Hoang, D.T.; Niyato, D.; Shu, L.; Kim, D.I.; Liang, Y.C. Toward smart wireless communications via intelligent reflecting surfaces: A contemporary survey. IEEE Commun. Surv. Tutor. 2020, 22, 2283–2314. [Google Scholar] [CrossRef]
- Di Renzo, M.; Debbah, M.; Phan-Huy, D.T.; Zappone, A.; Alouini, M.S.; Yuen, C.; Sciancalepore, V.; Alexandropoulos, G.C.; Hoydis, J.; Gacanin, H.; et al. Smart radio environments empowered by reconfigurable AI meta-surfaces: An idea whose time has come. EURASIP J. Wirel. Commun. Netw. 2019, 2019, 129. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, R. Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Trans. Wirel. Commun. 2019, 18, 5394–5409. [Google Scholar] [CrossRef]
- Hu, S.; Rusek, F.; Edfors, O. Beyond massive MIMO: The potential of data transmission with large intelligent surfaces. IEEE Trans. Signal Process. 2018, 66, 2746–2758. [Google Scholar] [CrossRef]
- Fu, M.; Zhou, Y.; Shi, Y. Intelligent reflecting surface for downlink non-orthogonal multiple access networks. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Waikoloa, HI, UA, 9–13 December 2019; IEEE: New York, NY, USA, 2019; pp. 1–6. [Google Scholar]
- Huang, C.; Zappone, A.; Alexandropoulos, G.C.; Debbah, M.; Yuen, C. Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Guo, H.; Liang, Y.C.; Chen, J.; Larsson, E.G. Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks. IEEE Trans. Wirel. Commun. 2020, 19, 3064–3076. [Google Scholar] [CrossRef]
- Li, Z.; Hua, M.; Wang, Q.; Song, Q. Weighted sum-rate maximization for multi-IRS aided cooperative transmission. IEEE Wirel. Commun. Lett. 2020, 9, 1620–1624. [Google Scholar] [CrossRef]
- Han, P.; Zhou, Z.; Wang, Z. Joint user association and passive beamforming in heterogeneous networks with reconfigurable intelligent surfaces. IEEE Commun. Lett. 2021, 25, 3041–3045. [Google Scholar] [CrossRef]
- Alwazani, H.; Nadeem, Q.U.A.; Chaaban, A. Performance Analysis under IRS-User Association for Distributed IRSs Assisted MISO Systems. arXiv 2021, arXiv:2111.02531. [Google Scholar]
- Zhao, D.; Lu, H.; Wang, Y.; Sun, H. Joint passive beamforming and user association optimization for IRS-assisted mmWave systems. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Mei, W.; Zhang, R. Joint base station-IRS-user association in multi-IRS-aided wireless network. In Proceedings of the GLOBECOM 2020—2020 IEEE Global Communications Conference, Taipei, Taiwan, 7–11 December 2020; IEEE: New York, NY, USA, 2020; pp. 1–6. [Google Scholar]
- Mei, W.; Zhang, R. Performance analysis and user association optimization for wireless network aided by multiple intelligent reflecting surfaces. IEEE Trans. Commun. 2021, 69, 6296–6312. [Google Scholar] [CrossRef]
- Zhao, D.; Lu, H.; Wang, Y.; Sun, H.; Gui, Y. Joint power allocation and user association optimization for IRS-assisted mmWave systems. IEEE Trans. Wirel. Commun. 2021, 21, 577–590. [Google Scholar] [CrossRef]
- Taghavi, E.M.; Alizadeh, A.; Rajatheva, N.; Vu, M.; Latva-aho, M. User association in millimeter wave cellular networks with intelligent reflecting surfaces. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Virtual Event, 25–28 April 2021; IEEE: New York, NY, USA, 2021; pp. 1–6. [Google Scholar]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; Al-Dhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Taha, A.; Zhang, Y.; Mismar, F.B.; Alkhateeb, A. Deep reinforcement learning for intelligent reflecting surfaces: Towards standalone operation. In Proceedings of the 2020 IEEE 21st International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Atlanta, GA, USA, 26–29 May 2020; IEEE: New York, NY, USA, 2020; pp. 1–5. [Google Scholar]
- Taha, A.; Alrabeiah, M.; Alkhateeb, A. Enabling large intelligent surfaces with compressive sensing and deep learning. IEEE Access 2021, 9, 44304–44321. [Google Scholar] [CrossRef]
- Zhang, Q.; Saad, W.; Bennis, M. Millimeter wave communications with an intelligent reflector: Performance optimization and distributional reinforcement learning. IEEE Trans. Wirel. Commun. 2021, 21, 1836–1850. [Google Scholar] [CrossRef]
- Huang, C.; Mo, R.; Yuen, C. Reconfigurable intelligent surface assisted multiuser MISO systems exploiting deep reinforcement learning. IEEE J. Sel. Areas Commun. 2020, 38, 1839–1850. [Google Scholar] [CrossRef]
- Yang, H.; Xiong, Z.; Zhao, J.; Niyato, D.; Xiao, L.; Wu, Q. Deep reinforcement learning-based intelligent reflecting surface for secure wireless communications. IEEE Trans. Wirel. Commun. 2020, 20, 375–388. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Chen, Y.; Poor, H.V. RIS enhanced massive non-orthogonal multiple access networks: Deployment and passive beamforming design. IEEE J. Sel. Areas Commun. 2020, 39, 1057–1071. [Google Scholar] [CrossRef]
- Fathy, M.; Fei, Z.; Guo, J.; Abood, M.S. Machine-Learning-Based Optimization for Multiple-IRS-Aided Communication System. Electronics 2023, 12, 1703. [Google Scholar] [CrossRef]
- Fathy, M.; Abood, M.S.; Guo, J. A Generalized Neural Network-based Optimization for Multiple IRSs-aided Communication System. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; IEEE: New York, NY, USA, 2021; pp. 480–486. [Google Scholar]
- Ahsan, W.; Yi, W.; Qin, Z.; Liu, Y.; Nallanathan, A. Resource allocation in uplink NOMA-IoT networks: A reinforcement-learning approach. IEEE Trans. Wirel. Commun. 2021, 20, 5083–5098. [Google Scholar] [CrossRef]
- Zhang, Y.; Mou, Z.; Gao, F.; Jiang, J.; Ding, R.; Han, Z. UAV-enabled secure communications by multi-agent deep reinforcement learning. IEEE Trans. Veh. Technol. 2020, 69, 11599–11611. [Google Scholar] [CrossRef]
- Zhong, R.; Liu, X.; Liu, Y.; Chen, Y. Multi-agent reinforcement learning in NOMA-aided UAV networks for cellular offloading. IEEE Trans. Wirel. Commun. 2021, 21, 1498–1512. [Google Scholar] [CrossRef]
- Omidshafiei, S.; Pazis, J.; Amato, C.; How, J.P.; Vian, J. Deep decentralized multi-task multi-agent reinforcement learning under partial observability. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; PMLR: Baltimore, MA, USA, 2017; pp. 2681–2690. [Google Scholar]
- Nasir, Y.S.; Guo, D. Multi-agent deep reinforcement learning for dynamic power allocation in wireless networks. IEEE J. Sel. Areas Commun. 2019, 37, 2239–2250. [Google Scholar] [CrossRef]
- Chen, J.; Guo, L.; Jia, J.; Shang, J.; Wang, X. Resource allocation for IRS assisted SGF NOMA transmission: A MADRL approach. IEEE J. Sel. Areas Commun. 2022, 40, 1302–1316. [Google Scholar] [CrossRef]
- Huang, C.; Chen, G.; Wong, K.K. Multi-agent reinforcement learning-based buffer-aided relay selection in IRS-assisted secure cooperative networks. IEEE Trans. Inf. Forensics Secur. 2021, 16, 4101–4112. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Elkashlan, M.; Nallanathan, A.; Wang, J.; Hanzo, L. Intelligent reflecting surface aided MIMO broadcasting for simultaneous wireless information and power transfer. IEEE J. Sel. Areas Commun. 2020, 38, 1719–1734. [Google Scholar] [CrossRef]
- Jiang, T.; Cheng, H.V.; Yu, W. Learning to reflect and to beamform for intelligent reflecting surface with implicit channel estimation. IEEE J. Sel. Areas Commun. 2021, 39, 1931–1945. [Google Scholar] [CrossRef]
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.2. 2020. Available online: http://cvxr.com/cvx/ (accessed on 22 January 2024).
- 3GPP TR 38.901. Study on Channel Model for Frequencies from 0.5 to 100 GHz. 2017. Available online: https://portal.3gpp.org/desktopmodules/Specifications/SpecificationDetails.aspx?specificationId=3173 (accessed on 20 March 2023).
- Sutton, R.S.; Barto, A.G. Introduction to Reinforcement Learning; BooksRun: Philadelphia, PA, USA, 2018. [Google Scholar]
- Sur, S.N.; Singh, A.K.; Kandar, D.; Silva, A.; Nguyen, N.D. Intelligent Reflecting Surface Assisted Localization: Opportunities and Challenges. Electronics 2022, 11, 1411. [Google Scholar] [CrossRef]
- Melo, F.S. Convergence of Q-Learning: A Simple Proof; Technical Report; Institute of Systems and Robotics, 2001; pp. 1–14. Available online: https://www.academia.edu/download/55970511/ProofQlearning.pdf (accessed on 20 March 2023).
- Timofte, V.; Timofte, A.; Khan, L.A. Stone–Weierstrass and extension theorems in the nonlocally convex case. J. Math. Anal. Appl. 2018, 462, 1536–1554. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Y.; Chen, Y.; Al-Dhahir, N. Machine learning for user partitioning and phase shifters design in RIS-aided NOMA networks. IEEE Trans. Commun. 2021, 69, 7414–7428. [Google Scholar] [CrossRef]
- Burkard, R.; Dell’Amico, M.; Martello, S. Assignment Problems: Revised Reprint; SIAM: Philadelphia, PA, USA, 2012. [Google Scholar]





| Approach | Complexity |
|---|---|
| Exhaustive Approach | |
| Graph-theoretic Algorithm | [42] |
| Successive Refinement Algorithm | [13,14] |
| Proposed MADRL Algorithm (continuous) | |
| Proposed MADRL Algorithm (discrete) |
| N | 5 | 10 | 15 | 20 | |
|---|---|---|---|---|---|
| Algorithm | |||||
| Successive Refinement Algorithm | 44.6637 | 78.5485 | 120.3662 | 153.0799 | |
| Proposed MADRL Algorithm | 0.4372 | 0.4380 | 0.4424 | 0.4669 | |
| N | 5 | 10 | 15 | 20 | |
|---|---|---|---|---|---|
| Algorithm | |||||
| Successive Refinement Algorithm | 80.8549 | 94.6200 | 101.2413 | 134.2253 | |
| Proposed MADRL Algorithm | 0.4478 | 1.2505 | 38.9429 | 1050 | |
| Hyper-Parameter | Setting |
|---|---|
| Learning rates , | 0.001 |
| Discount factor | 0.95 |
| Buffer size C | 200,000 |
| Mini-batch size | 16 |
| Probability threshold | 1 |
| Min Probability threshold | 0.01 |
| Decay rate | 0.0050 |
| Target smooth factors | 0.001 |
| Target update frequency U | 1 |
| Sampling time | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathy, M.; Fei, Z.; Guo, J.; Abood, M.S. Sum Rate Optimization for Multi-IRS-Aided Multi-BS Communication System Based on Multi-Agent. Electronics 2024, 13, 735. https://doi.org/10.3390/electronics13040735
Fathy M, Fei Z, Guo J, Abood MS. Sum Rate Optimization for Multi-IRS-Aided Multi-BS Communication System Based on Multi-Agent. Electronics. 2024; 13(4):735. https://doi.org/10.3390/electronics13040735
Chicago/Turabian StyleFathy, Maha, Zesong Fei, Jing Guo, and Mohamed Salah Abood. 2024. "Sum Rate Optimization for Multi-IRS-Aided Multi-BS Communication System Based on Multi-Agent" Electronics 13, no. 4: 735. https://doi.org/10.3390/electronics13040735
APA StyleFathy, M., Fei, Z., Guo, J., & Abood, M. S. (2024). Sum Rate Optimization for Multi-IRS-Aided Multi-BS Communication System Based on Multi-Agent. Electronics, 13(4), 735. https://doi.org/10.3390/electronics13040735






