Hyperbolic-Embedding-Aided Geographic Routing in Intelligent Vehicular Networks
Abstract
1. Introduction
2. Background and Related Works
2.1. Background
2.2. Related Works
3. Hyperbolic-Embedding-Aided Geographic Routing Strategy
3.1. Preliminaries
- (1)
- , which is equal to half of the average node degree;
- (2)
- , defining the power-law degree distribution exponent ;
- (3)
- , which controls the network clustering;
- (4)
- , where K is the curvature of the hyperbolic plane. Since changing rescales the node radial coordinates and this does not influence the network topology structure, we set without loss of generality.
3.2. Algorithm Design
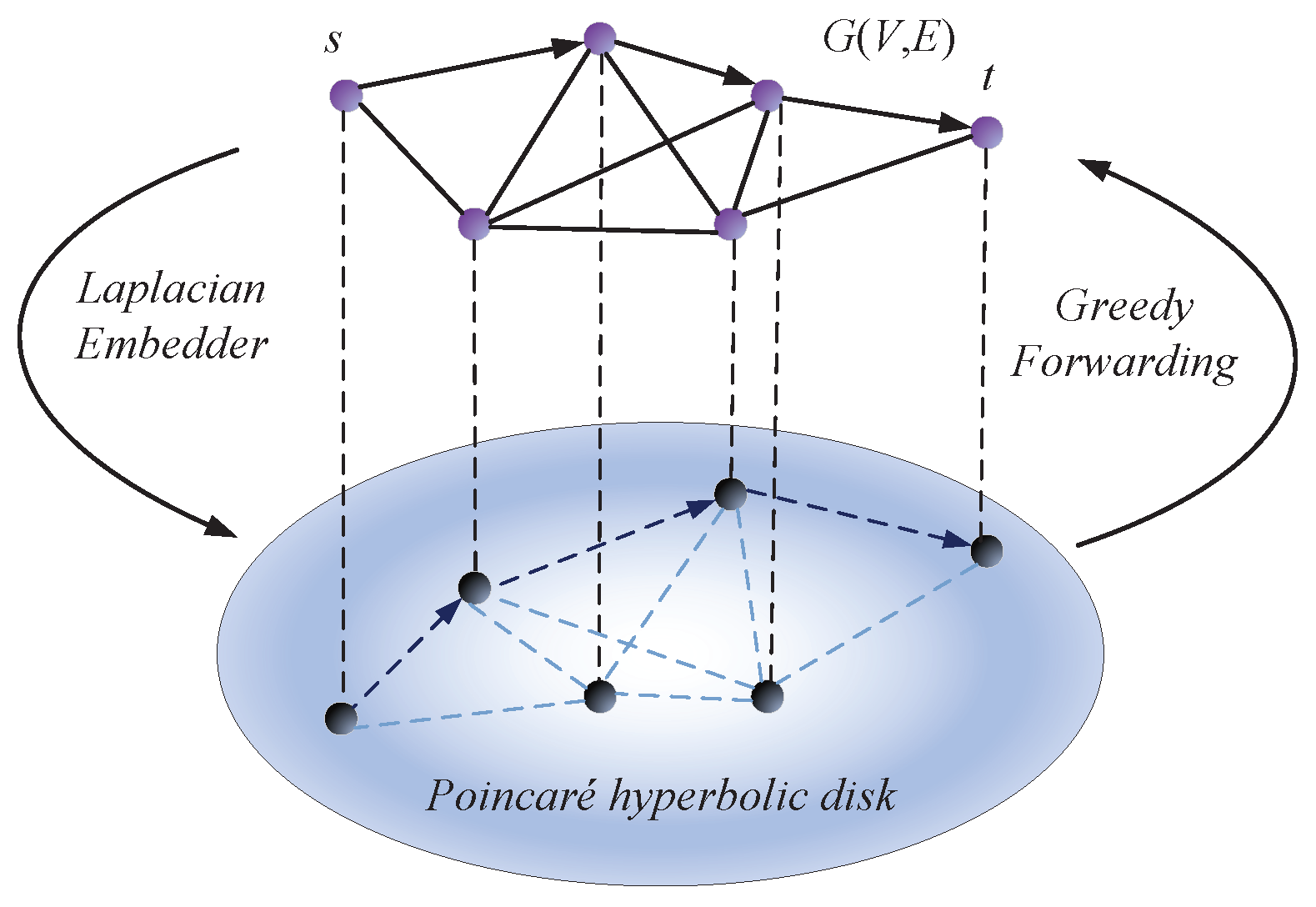
3.2.1. Laplacian-Based Hyperbolic Embedding
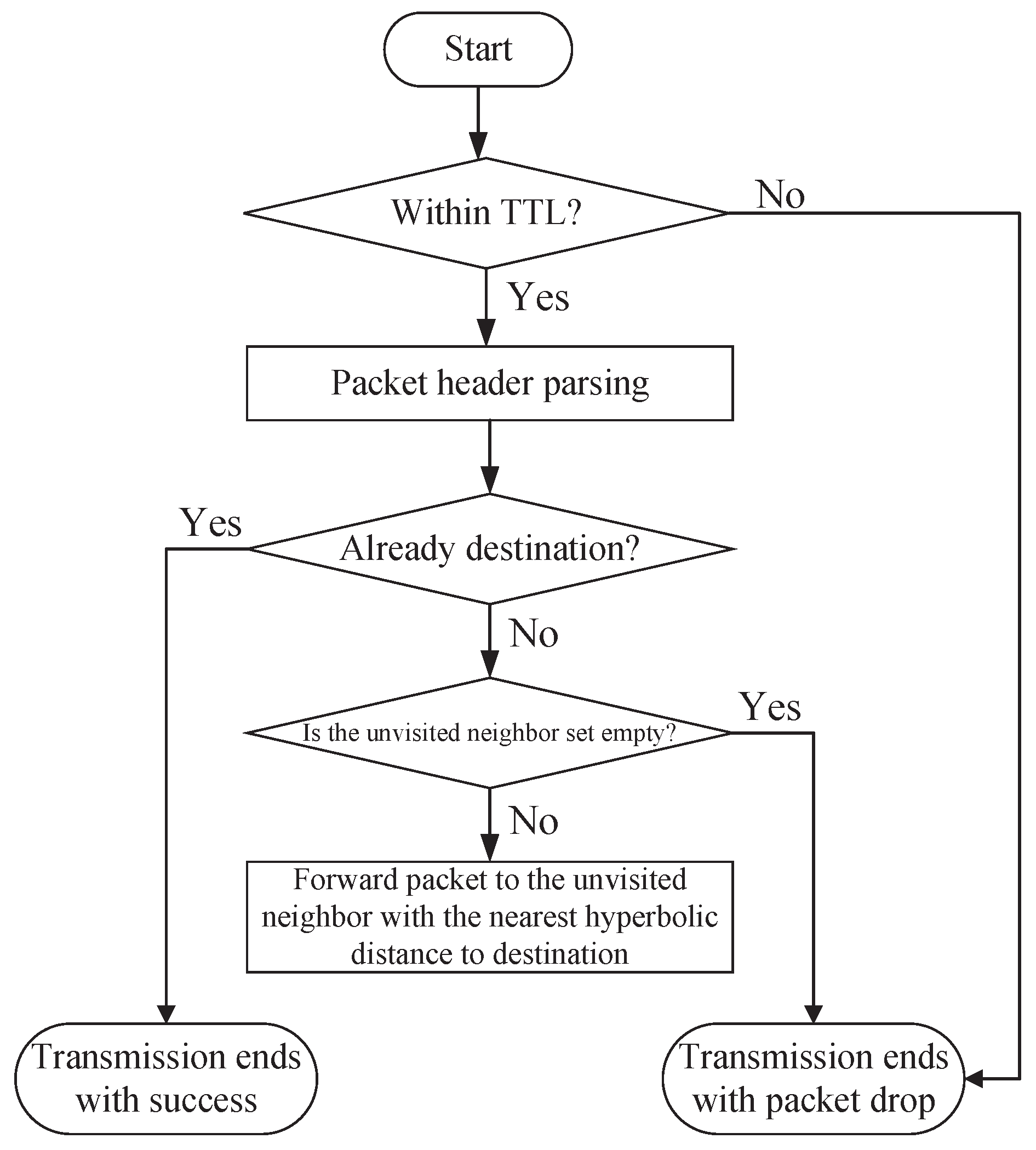
3.2.2. Hyperbolic Greedy Forwarding
4. Performance Evaluation
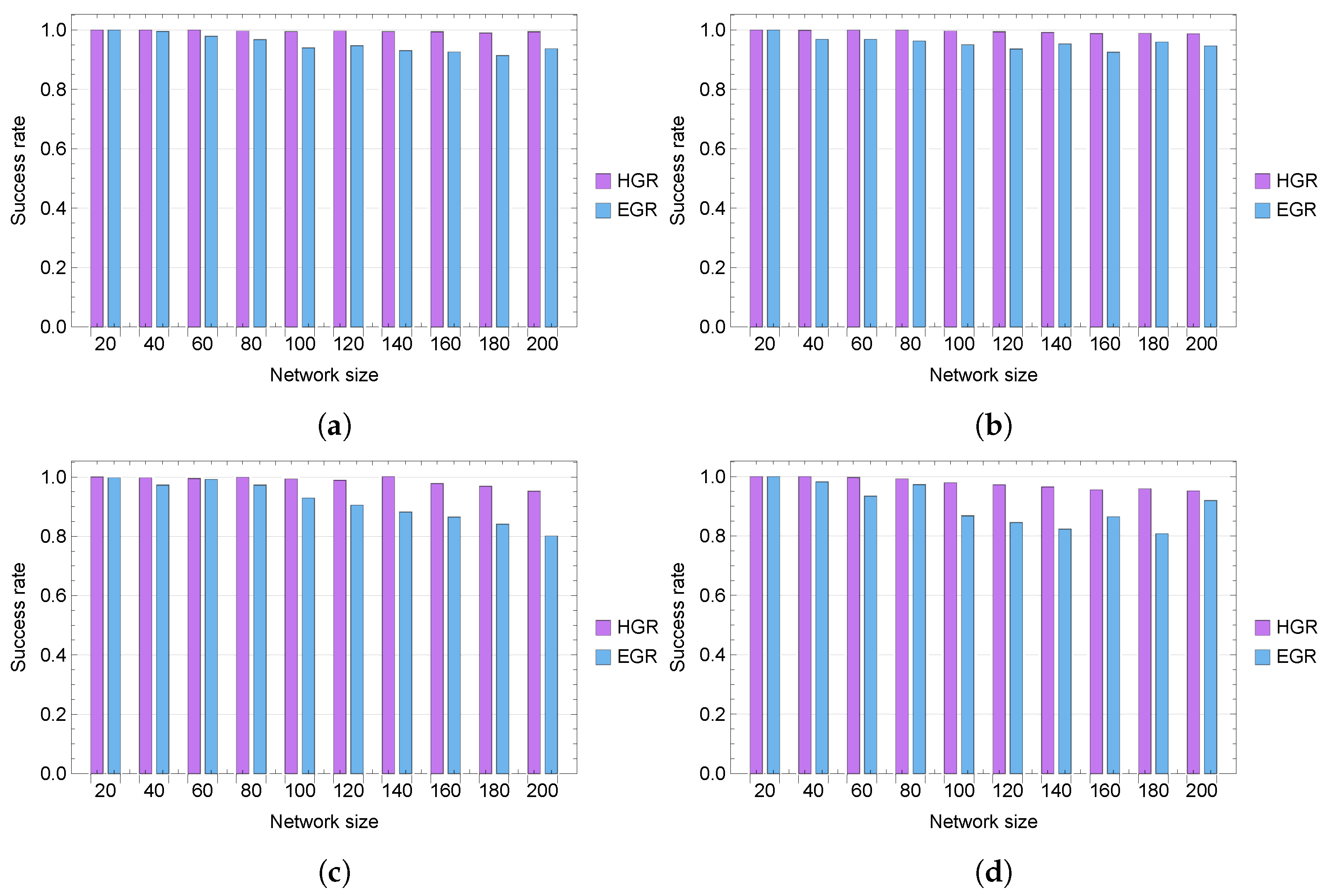
4.1. Routing Success Rate
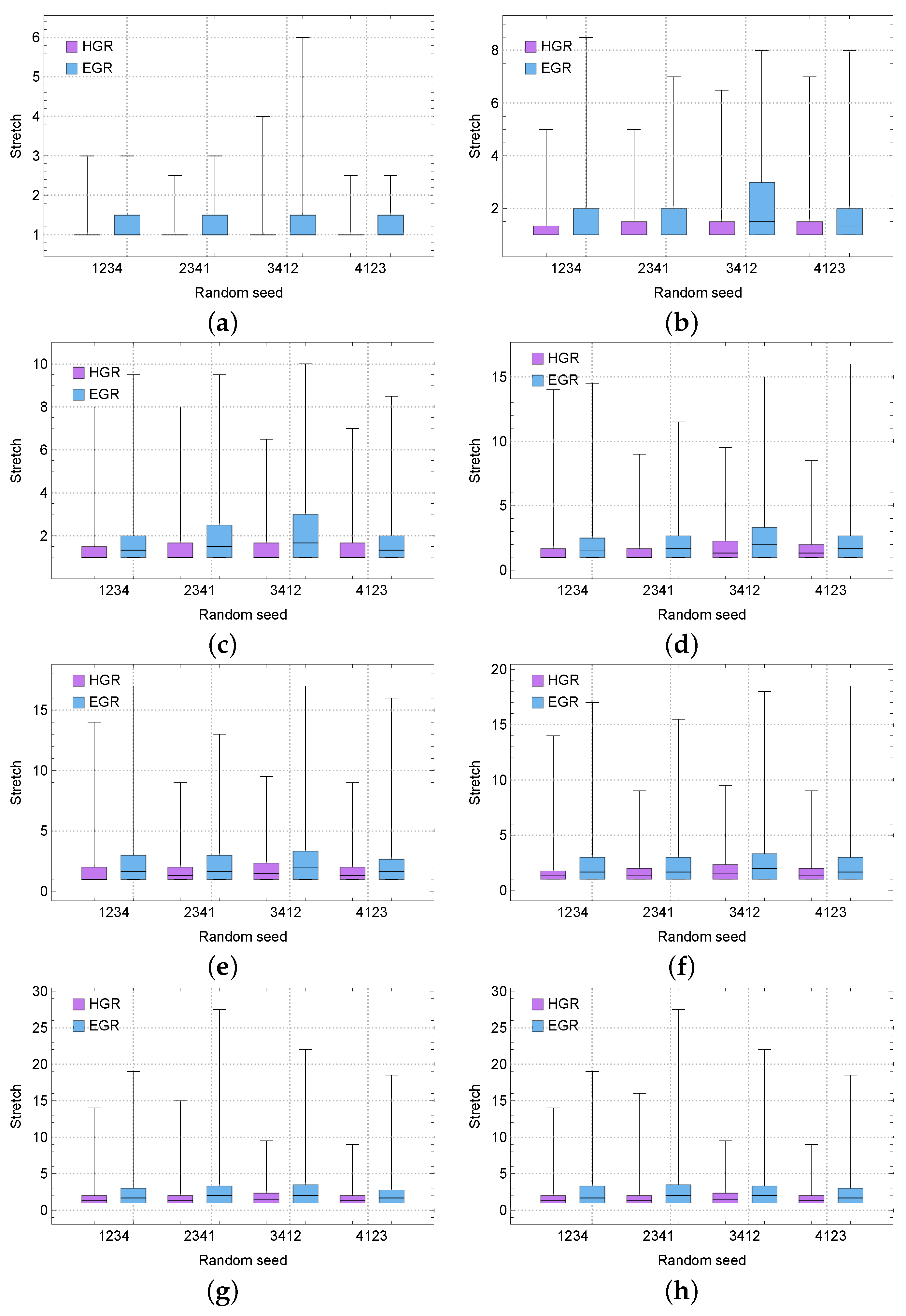
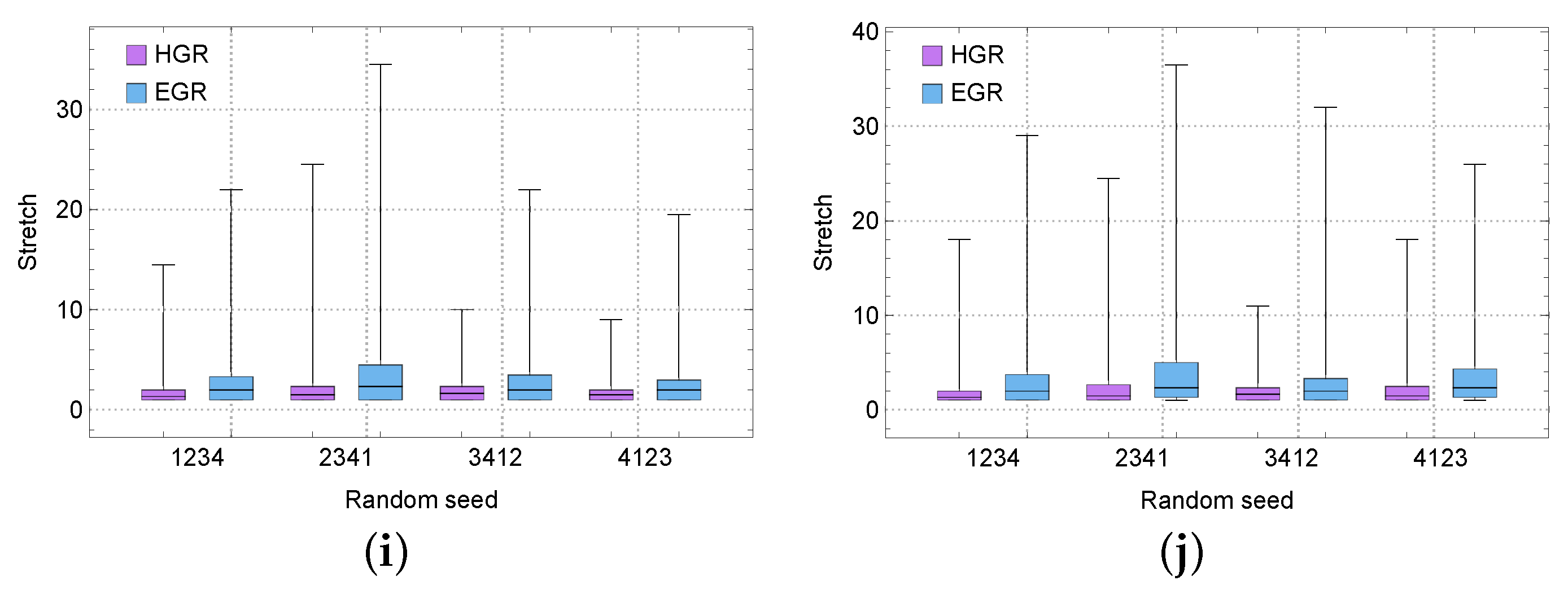
4.2. Routing Stretch
4.3. Scalability
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cheng, X.; Chen, C.; Zhang, W.; Yang, Y. 5G-Enabled Cooperative Intelligent Vehicular (5GenCIV) Framework: When Benz Meets Marconi. IEEE Intell. Syst. 2017, 32, 53–59. [Google Scholar] [CrossRef]
- Fu, H.; Guan, J.; Jing, F.; Wang, C.; Ma, H. A real-time multi-vehicle tracking framework in intelligent vehicular networks. China Commun. 2021, 18, 89–99. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Wang, B.; Zhou, Y.; Pei, Q. An Efficient and Reliable QoF Routing for Urban VANETs with Backbone Nodes. IEEE Access 2019, 7, 38273–38286. [Google Scholar] [CrossRef]
- Zhao, L.; Bi, Z.; Lin, M.; Hawbani, A.; Shi, J.; Guan, Y. An intelligent fuzzy-based routing scheme for software-defined vehicular networks. Comput. Netw. 2021, 187, 107837. [Google Scholar] [CrossRef]
- Fatemidokht, H.; Rafsanjani, M.K.; Gupta, B.B.; Hsu, C.H. Efficient and Secure Routing Protocol Based on Artificial Intelligence Algorithms with UAV-Assisted for Vehicular Ad Hoc Networks in Intelligent Transportation Systems. IEEE Trans. Intell. Transp. Syst. 2021, 22, 4757–4769. [Google Scholar] [CrossRef]
- Ma, B.; Ren, Z.; Cheng, W. Traffic Routing-Based Computation Offloading in Cybertwin-Driven Internet of Vehicles for V2X Applications. IEEE Trans. Veh. Technol. 2022, 71, 4551–4560. [Google Scholar] [CrossRef]
- Chen, C.; Liu, L.; Qiu, T.; Jiang, J.; Pei, Q.; Song, H. Routing with Traffic Awareness and Link Preference in Internet of Vehicles. IEEE Trans. Intell. Transp. Syst. 2022, 23, 200–214. [Google Scholar] [CrossRef]
- Li, P.; Zeng, Y.; Li, C.; Chen, L.; Wang, H.; Chen, C. A Probabilistic Broadcasting Scheme for Emergent Message Dissemination in Urban Internet of Vehicles. IEEE Access 2021, 9, 113187–113198. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connection with Graphs. Numer. Math. 1959, 1, 269–271. [Google Scholar] [CrossRef]
- Bang-Jensen, J.; Gutin, G. Section 3.3.4: The Bellman-Ford-Moore algorithm. In Digraphs: Theory, Algorithms and Applications, 2nd ed.; Springer: London, UK, 2010; pp. 97–99. [Google Scholar]
- Floyd, R.W. Algorithm 97: Shortest Path. Commun. ACM 1962, 5, 345. [Google Scholar] [CrossRef]
- Wahid, I.; Tanvir, S.; Ahmad, M.; Ullah, F.; AlGhamdi, A.S.; Khan, M.; Alshamrani, S.S. Vehicular Ad Hoc Networks Routing Strategies for Intelligent Transportation System. Electronics 2022, 11, 2298. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Ren, Z.; Qiu, T.; Song, H. A Connectivity Aware Transmission Quality Guaranteed Geographic Routing in Urban Internet of Vehicles. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Ren, Z.; Yu, F.R. An Intersection-Based Geographic Routing with Transmission Quality Guaranteed in Urban VANETs. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, C.; Li, H.; Li, X.; Zhang, J.; Wei, H.; Wang, H. A geographic routing protocol based on trunk line in VANETs. Digit. Commun. Netw. 2021, 7, 479–491. [Google Scholar] [CrossRef]
- Liu, L.; Chen, C.; Ren, Z.; Qiu, T.; Yang, K. A Delay-Aware and Backbone-Based Geographic Routing for Urban VANETs. In Proceedings of the 2018 IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Jiang, S.; Huang, Z.; Ji, Y. Adaptive UAV-Assisted Geographic Routing with Q-Learning in VANET. IEEE Commun. Lett. 2021, 25, 1358–1362. [Google Scholar] [CrossRef]
- Luo, L.; Sheng, L.; Yu, H.; Sun, G. Intersection-Based V2X Routing via Reinforcement Learning in Vehicular Ad Hoc Networks. IEEE Trans. Intell. Transp. Syst. 2022, 23, 5446–5459. [Google Scholar] [CrossRef]
- Al-Subhi, T.; Arafeh, B.; Alzeidi, N.; Day, K.; Touzene, A. A Void Avoidance Scheme for Grid-Based Multipath Routing in Underwater Wireless Sensor Networks. Wirel. Sens. Netw. 2018, 10, 131–156. [Google Scholar] [CrossRef][Green Version]
- Denardin, G.W.; Barriquello, C.H.; Campos, A.; Prado, R.N.D. A geographic routing hybrid approach for void resolution in wireless sensor networks. J. Syst. Softw. 2011, 84, 1577–1590. [Google Scholar] [CrossRef]
- Ullah, A.; Yao, X.; Shaheen, S.; Ning, H. Advances in Position Based Routing Towards ITS Enabled FoG-Oriented VANET—A Survey. IEEE Trans. Intell. Transp. Syst. 2020, 21, 828–840. [Google Scholar] [CrossRef]
- Boguñá, M.; Bonamassa, I.; Domenico, M.D.; Havlin, S.; Krioukov, D.V.; Serrano, M.Á. Network geometry. Nat. Rev. Phys. 2020, 3, 114–135. [Google Scholar] [CrossRef]
- Krioukov, D.V.; Papadopoulos, F.; Kitsak, M.; Vahdat, A.; Boguñá, M. Hyperbolic Geometry of Complex Networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2010, 82 Pt 2, 036106. [Google Scholar] [CrossRef]
- Boguñá, M.; Papadopoulos, F.; Krioukov, D.V. Sustaining the Internet with Hyperbolic Mapping. Nat. Commun. 2010, 1, 62. [Google Scholar] [CrossRef]
- Sarkar, R. Low Distortion Delaunay Embedding of Trees in Hyperbolic Plane. In Proceedings of the International Symposium Graph Drawing and Network Visualization, Eindhoven, The Netherlands, 21–23 September 2011. [Google Scholar]
- Almagro, P.; Boguñá, M.; Serrano, M.Á. Detecting the ultra low dimensionality of real networks. Nat. Commun. 2021, 13, 6096. [Google Scholar] [CrossRef]
- Kleinberg, R.D. Geographic Routing Using Hyperbolic Space. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Anchorage, AK, USA, 6–12 May 2007; pp. 1902–1909. [Google Scholar]
- Cvetkovski, A.; Crovella, M. Hyperbolic Embedding and Routing for Dynamic Graphs. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 1647–1655. [Google Scholar]
- Zheng, Z.; Bashir, A.K. Graph-Enabled Intelligent Vehicular Network Data Processing. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4726–4735. [Google Scholar] [CrossRef]
- Zhu, L.; Gu, W.; Yi, J.; Luan, T.H.; Li, C. On Mobility-Aware and Channel-Randomness-Adaptive Optimal Neighbor Discovery for Vehicular Networks. IEEE Internet Things J. 2021, 8, 6828–6839. [Google Scholar] [CrossRef]
- Yin, X.; Ma, X.; Trivedi, K.S. An Interacting Stochastic Models Approach for the Performance Evaluation of DSRC Vehicular Safety Communication. IEEE Trans. Comput. 2013, 62, 873–885. [Google Scholar] [CrossRef]
- Aldecoa, R.; Orsini, C.; Krioukov, D.V. Hyperbolic graph generator. arXiv 2015, arXiv:1503.05180. [Google Scholar] [CrossRef]
- Papadopoulos, F.; Boguñá, M.; Krioukov, D.V. Popularity versus similarity in growing networks. Nature 2011, 489, 537–540. [Google Scholar] [CrossRef] [PubMed]
- Bläsius, T.; Friedrich, T.; Krohmer, A.; Laue, S. Efficient Embedding of Scale-Free Graphs in the Hyperbolic Plane. IEEE/ACM Trans. Netw. 2018, 26, 920–933. [Google Scholar] [CrossRef]
- Wu, Z.; Di, Z.; Fan, Y. An Asymmetric Popularity-Similarity Optimization Method for Embedding Directed Networks into Hyperbolic Space. Complexity 2020, 2020, 8372928. [Google Scholar] [CrossRef]
- Alanis-Lobato, G.; Mier, P.; Andrade, M. Efficient embedding of complex networks to hyperbolic space via their Laplacian. Sci. Rep. 2016, 6, 30108. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Li, L.; Zeng, Y.; Fan, J.; Shen, L. Low-Complexity Hyperbolic Embedding Schemes for Temporal Complex Networks. Sensors 2022, 22, 9306. [Google Scholar] [CrossRef]
- Muscoloni, A.; Thomas, J.M.; Ciucci, S.; Bianconi, G.; Cannistraci, C.V. Machine learning meets complex networks via coalescent embedding in the hyperbolic space. Nat. Commun. 2017, 8, 1615. [Google Scholar] [CrossRef]
- García-Pérez, G.; Allard, A.; Serrano, M.Á.; Boguñá, M. Mercator: Uncovering faithful hyperbolic embeddings of complex networks. New J. Phys. 2019, 21, 123033. [Google Scholar] [CrossRef]
- Jankowski, R.; Allard, A.; Bogun’a, M.; Serrano, M.Á. The D-Mercator method for the multidimensional hyperbolic embedding of real networks. Nat. Commun. 2023, 14, 7585. [Google Scholar] [CrossRef] [PubMed]
- Nie, Q.; Jiang, H.; Zhong, S.D.; Wang, Q.; Wang, J.J.; Wang, H.; Wu, L.H. Joint Detection of Community and Structural Hole Spanner of Networks in Hyperbolic Space. Entropy 2022, 24, 894. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, Z.; Zhang, J.; Wang, F.; Du, Y.; Su, S.; Yu, P.S. PERFECT: A Hyperbolic Embedding for Joint User and Community Alignment. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 501–510. [Google Scholar] [CrossRef]
- Kitsak, M.; Voitalov, I.; Krioukov, D. Link prediction with hyperbolic geometry. Phys. Rev. Res. 2020, 2, 043113. [Google Scholar] [CrossRef]
- Moshiri, M.; Safaei, F. Application of hyperbolic geometry of multiplex networks under layer link-based attacks. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 021105. [Google Scholar] [CrossRef] [PubMed]
- Heszberger, Z. Hyperbolic trees for efficient routing computation. J. Supercomput. 2022, 78, 15250–15268. [Google Scholar] [CrossRef]
- Stai, E.; Sotiropoulos, K.; Karyotis, V.; Papavassiliou, S. Hyperbolic Embedding for Efficient Computation of Path Centralities and Adaptive Routing in Large-Scale Complex Commodity Networks. IEEE Trans. Netw. Sci. Eng. 2017, 4, 140–153. [Google Scholar] [CrossRef]
- Bläsius, T.; Friedrich, T.; Katzmann, M.; Krohmer, A. Hyperbolic Embeddings for Near-Optimal Greedy Routing. J. Exp. Algorithmics (JEA) 2020, 25, 1–18. [Google Scholar] [CrossRef]
- Sulyok, B.; Palla, G. Greedy routing optimisation in hyperbolic networks. Sci. Rep. 2023, 13, 23026. [Google Scholar] [CrossRef]


| Network Size | Random Seed | Max | 75% | Median | 25% | Min | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HGR | EGR | HGR | EGR | HGR | EGR | HGR | EGR | HGR | EGR | ||
| 1234 | 3.00 | 3.00 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 2.50 | 3.00 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 4.00 | 6.00 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 2.50 | 2.50 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 5.00 | 8.50 | 1.33 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 5.00 | 7.00 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 6.50 | 8.00 | 1.50 | 3.00 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 7.00 | 8.00 | 1.50 | 2.00 | 1.00 | 1.33 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 8.00 | 9.50 | 1.50 | 2.00 | 1.00 | 1.33 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 8.00 | 9.50 | 1.67 | 2.50 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 6.50 | 10.00 | 1.67 | 3.00 | 1.00 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 7.00 | 8.50 | 1.67 | 2.00 | 1.00 | 1.33 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.00 | 14.50 | 1.67 | 2.50 | 1.00 | 1.50 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 9.00 | 11.50 | 1.67 | 2.67 | 1.00 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 9.50 | 15.00 | 2.25 | 3.33 | 1.33 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 8.50 | 16.00 | 2.00 | 2.67 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.00 | 17.00 | 2.00 | 3.00 | 1.00 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 9.00 | 13.00 | 2.00 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 9.50 | 17.00 | 2.33 | 3.33 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 9.00 | 16.00 | 2.00 | 2.67 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.00 | 17.00 | 1.75 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 9.00 | 15.50 | 2.00 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 9.50 | 18.00 | 2.33 | 3.33 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 9.00 | 18.50 | 2.00 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.00 | 19.00 | 2.00 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 15.00 | 27.50 | 2.00 | 3.33 | 1.33 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 9.50 | 22.00 | 2.33 | 3.50 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 9.00 | 18.50 | 2.00 | 2.75 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.00 | 19.00 | 2.00 | 3.33 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 16.00 | 27.50 | 2.00 | 3.50 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 3412 | 9.50 | 22.00 | 2.33 | 3.33 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 9.00 | 18.50 | 2.00 | 3.00 | 1.33 | 1.67 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 14.50 | 22.00 | 2.00 | 3.33 | 1.33 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 24.50 | 34.50 | 2.33 | 4.50 | 1.50 | 2.33 | 1.00 | 1.33 | 1.00 | 1.00 | |
| 3412 | 10.00 | 22.00 | 2.33 | 3.50 | 1.67 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 9.00 | 19.50 | 2.00 | 3.00 | 1.50 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 1234 | 18.00 | 29.00 | 2.00 | 3.75 | 1.33 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 2341 | 24.50 | 36.50 | 2.67 | 5.00 | 1.50 | 2.33 | 1.00 | 1.33 | 1.00 | 1.00 | |
| 3412 | 11.00 | 32.00 | 2.33 | 3.33 | 1.67 | 2.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| 4123 | 18.00 | 26.00 | 2.50 | 4.33 | 1.50 | 2.33 | 1.00 | 1.33 | 1.00 | 1.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, Y.; Lyu, N. Hyperbolic-Embedding-Aided Geographic Routing in Intelligent Vehicular Networks. Electronics 2024, 13, 661. https://doi.org/10.3390/electronics13030661
Pan Y, Lyu N. Hyperbolic-Embedding-Aided Geographic Routing in Intelligent Vehicular Networks. Electronics. 2024; 13(3):661. https://doi.org/10.3390/electronics13030661
Chicago/Turabian StylePan, Ying, and Na Lyu. 2024. "Hyperbolic-Embedding-Aided Geographic Routing in Intelligent Vehicular Networks" Electronics 13, no. 3: 661. https://doi.org/10.3390/electronics13030661
APA StylePan, Y., & Lyu, N. (2024). Hyperbolic-Embedding-Aided Geographic Routing in Intelligent Vehicular Networks. Electronics, 13(3), 661. https://doi.org/10.3390/electronics13030661






