Abstract
Real-time collision risk prediction is essential for improving highway safety and reducing traffic accidents. However, previous studies have mainly used crash data and associated spatially discrete and temporally continuous traffic data, overlooking the potential of vehicle trajectory data, which provides comprehensive spatio-temporal information to characterize traffic near a specific location. Moreover, researchers have typically focused on either traffic flow characteristics or inter-vehicle microscopic kinematic characteristics for real-time risk prediction, with a dearth of studies integrating these two aspects. Given that risk events transpire more frequently than accidents and exhibit a strong correlation with them, it is imperative to concentrate more on risk events to proactively diminish crash probabilities. This study introduces a novel approach that extracts traffic flow and inter-vehicle kinematic features from risk events. It also provides a comparative analysis of the effectiveness of five machine-learning methods (Logistic Regression, K-Nearest Neighbors, eXtreme Gradient Boosting, Random Forests, and Multilayer Perceptron) and two data-processing strategies (oversampling and undersampling) in addressing risk identification and prediction issues. The results showed that (1) the synergistic use of traffic flow and inter-vehicle kinematic features surpasses the use of a single feature in identifying and predicting risks; (2) The eXtreme Gradient Boosting model, trained on the undersampled dataset, emerges as the optimal model for risk identification, boasting an Area Under the Receiver Operating Characteristic Curve (AUC) of 0.976 and an F1 score of 0.604; (3) The RF model exhibits commendable performance under both risk prediction conditions (5 s ahead prediction and 10 s prediction), demonstrating the highest performance with F1 scores of 0.377 and 0.374, respectively. Additionally, it was discovered that the resampling strategy does not always prove effective in developing risk analysis models and should be chosen based on the model’s characteristics and target metrics. This offers valuable insights into the selection of data-processing strategies when handling unbalanced data. Finally, the study’s limitations and potential enhancements are discussed.
1. Introduction
Highways, a crucial component of transportation systems, are often sites of frequent traffic accidents. The World Health Organization (WHO) reports that road traffic accidents claim over 1.4 million lives and cause approximately 50 million injuries annually [1]. A significant proportion of these accidents occur on highways, which are often characterized by higher mortality rates and a propensity for chain accidents. In response to this situation, the WHO urges all nations to implement measures aimed at reducing road traffic casualties by at least 50% by 2030 [2].
To enhance highway safety and decrease traffic accident incidence, it is imperative to perform real-time risk monitoring and assessment of highway vehicles. This allows for the early identification of collision risks and the implementation of preventive measures [3,4]. With the advancement of traffic sensor technology, the acquisition of real-time traffic operation data has become increasingly convenient, which has also promoted the research interest in real-time risk analysis [5,6]. Researchers are exploring the relationship between collision probability and pre-collision traffic operating conditions, with the aim of reducing collision likelihood through proactive traffic control strategies [7]. In addition, real-time risk analysis also has application potential in autonomous driving within vehicle networks, which places higher requirements on data resolution and accuracy of collision risk analysis [8].
From a data usage standpoint, current real-time risk analysis research primarily relies on collision data and corresponding spatially discrete, temporally continuous traffic data [9,10] (e.g., loop detector, video detection system data) to develop traffic risk identification and prediction models. A common approach involves using extracted upstream and downstream traffic flow parameters (e.g., average speed, speed standard deviation, traffic volume) from the collision site to build a collision risk assessment and prediction model of the statistical relationship between collision risk and traffic flow state [11]. However, as collisions and traffic conflicts frequently occur at specific intermediate locations on the road, traffic flow data summarized at the road segment level inadequately reflects traffic changes near the collision location. This necessitates vehicle-level traffic data that provides comprehensive coverage of road traffic conditions. Owing to continuous advancements in transportation technology, the latest generation of traffic sensing data acquisition technologies (e.g., drones [12], distributed vehicle trajectory acquisition systems [13]) and the application of intelligent Internet-connected vehicles have enabled the collection of individual-level vehicle trajectory data. This paves the way for real-time traffic risk analysis and prediction using micro-level vehicle trajectory information, which holds significant potential for enhancing road traffic safety.
Moreover, numerous researchers have used crashes as the subject of risk identification in their studies. However, collisions are low-probability events, and gathering data with sufficient collision events is time-consuming, resource-intensive, and potentially accompanied by inaccurate data recording [14]. Consequently, trajectory data containing collisions are relatively scarce, prompting some studies to construct accident detection and classification models based on simulated collision trajectory data generated in a simulation environment [15]. In contrast, practical traffic safety management systems prioritize the identification and warning of more frequently occurring risk events, given the strong correlation between the frequency of risk events and traffic accidents [16]. Therefore, implementing risk prediction models through surrogate safety measures (e.g., TTC, MTTC, etc.) by identifying risk events from vehicle trajectory datasets offers significant potential to uncover collision occurrence mechanisms and enhance road traffic safety. Additionally, most collision risk studies typically employ either traffic flow features or microscopic kinematic features between neighboring vehicles for real-time risk prediction [17,18]. However, clear evidence to demonstrate whether these two feature types can jointly predict risk occurrence is lacking, which is the focus of this study.
To address the above research gaps, this study aims to establish a real-time identification and prediction model for risk events in road traffic using traffic flow features and kinematic features between vehicles in trajectory datasets. The primary contributions and innovations of this study include:
- The proposal of a risk-event-based method for extracting traffic flow features and inter-vehicle kinematic features designed to analyze collision risk on highways.
- The development of machine-learning-based risk identification and prediction models, specifically the Risk Identification Model, Risk Prediction Model-5s, and Risk Prediction Model-10s. These models were used to compare the performance of five distinct machine-learning approaches under various data-processing strategies.
- An exploration of the impacts of traffic flow features and inter-vehicle kinematic features on risk events, confirming the effectiveness of joint prediction using these two features.
The following remainder of this paper is organized as follows. Section 2 provides a review of prior research on risk event identification and real-time traffic risk identification and prediction methods. Section 3 details the data preparation process, while Section 4 outlines the methodology employed. Section 5 presents the results and associated discussion. Finally, Section 6 offers a summary and discussion of the work.
2. Background
2.1. Identification of Risk Events
The identification of risk events in trajectory data is a crucial step in the development of risk identification and prediction models. Risk events are typically identified in two primary ways: (1) by using the vehicle’s own kinematic parameters to detect the occurrence of an emergency event and (2) by employing a surrogate safety measure (SSM) to evaluate the severity of a traffic conflict. The first method involves recognizing a risky event by comparing the vehicle’s kinematic parameters with a pre-established reasonable range threshold (e.g., longitudinal acceleration ≥ 0.6 g, lateral acceleration ≥ 0.7 g [19]). This method is relatively straightforward to implement, as it only requires the vehicle’s motion information. However, it can result in high false alarm rates and does not effectively quantify risk severity. The second method necessitates the use of measures (e.g., time to collision (TTC), deceleration to avoid collision (DRAC), and post-encroachment time (PET) [20]) to identify risky events in road traffic. This is achieved by considering the motion information and positional relationship between the target vehicle and surrounding traffic participants. Such methods can decrease the false alarm rate of risk identification and aid in further classifying risk levels.
Specifically, SSM can be classified into three categories: deceleration-based SSM, energy-based SSM, and time-based SSM [21]. DRAC is a commonly employed method in deceleration-based SSM. It evaluates the potential risk level between a vehicle and the vehicle in front of it in the target lane by calculating the minimum deceleration required for the vehicle to match the speed of the vehicle in front during a lane change [22]. DeltaV, a key component of energy-based SSM, calculates the change in speed of the vehicles due to a collision to evaluate the propensity to collide and the potential collision severity of a traffic conflict [23]. TTC is the most popular method in time-based SSM, which represents the remaining time before a collision occurs if a front and a rear vehicle continues to travel at their current speed and on a consistent path [24]. However, it is important to note that this method is only applicable when the speed of the rear vehicle is faster than the speed of the vehicle in front, and it cannot identify the potential collision risk in other cases. To overcome this limitation, Modified Time to Collision (MTTC) was proposed, which takes into account the speed, acceleration, and relative distance of the potentially colliding vehicles [25], and has been demonstrated to cover all collision scenarios and to be effective in identifying risky events [26]. Therefore, MTTC is used as a metric to identify risky events in this study.
2.2. Real-Time Traffic Risk Identification and Prediction Methods
This section reviews research on real-time risk identification and prediction methods, focusing on three aspects: data source, feature selection, and classification model.
2.2.1. Data Source
From the perspective of data sources, the existing real-time traffic risk identification and prediction methods can be roughly divided into three categories: the methods based on macro traffic flow data, the methods based on single-vehicle attitude data, and the methods based on trajectory data.
The methods based on macro traffic flow data use data acquisition equipment, such as loop detectors, to identify risks by analyzing the changes in traffic flow characteristics over time. This approach generally has two types: rule-based and machine-learning-based. Pirdavani A et al. [27] developed a rule-based real-time collision Risk Prediction Model by pruning part of the decision tree and using characteristics such as traffic volume, average speed, and speed standard deviation at the 5-min aggregation level. Xu C et al. [9] designed a sequential logic model to link collision probability with traffic flow characteristics and to predict the likelihood of accidents of different severities. In summary, the risk prediction method based on macro traffic flow data is widely used in practice because of its accessibility and robustness. However, this method has some limitations, especially in detection ability, as it can only provide lane-level aggregated traffic flow characteristics and cannot obtain the driving data of individual vehicles. Therefore, the differential behavior of individual vehicles cannot be incorporated into the risk modeling process.
At present, researchers have applied the attitude data of vehicles to identify traffic accidents and set the threshold values of variables, such as speed, acceleration, and angular velocity of a single vehicle, to detect the risk. Bhatti F et al. [28] designed an accident detection and reporting system that collects vehicle operation data through the pressure sensor, noise sensor, and accelerometer of mobile phones and uses the threshold method to detect and report accidents. Khan A et al. [29] used a similar method with Android applications and mobile phone accelerometers to achieve accident detection and rescue. The risk identification method based on bicycle attitude data has the advantages of high real-time and low cost, but it cannot perceive the running state of surrounding vehicles well, limiting the accuracy of risk identification.
Real-time risk prediction based on trajectory data uses the position, speed, acceleration, and other information of the vehicle to predict the risks that the vehicle may encounter according to its motion state and the surrounding environment. Yu R et al. [17] achieved short-term prediction of high-risk events and analysis of influencing factors using random parameter logistic regression model and random effects logistic regression model. Yuan C et al. [18] proposed a two-step framework that employs statistical models and various machine-learning models to analyze the feature interpretability of trajectory data and construct a Risk Prediction Model. Compared with other data sources, trajectory data have the following advantages: (1) Large amount of data, wide coverage, and ability to reflect more traffic scenarios and conditions; (2) High real-time data, frequent updates, and responsiveness to changes in traffic status. However, trajectory data also has some limitations, such as (1) high data dimensions and complex features that require effective reduction and feature extraction, (2) high difficulty in data analysis and mining, which requires consideration of the spatio-temporal correlation, nonlinearity, and other characteristics of trajectory data, and adoption of more advanced models and algorithms.
2.2.2. Feature Selection
The most widely used features in real-time risk identification and prediction models are the mean values of flow, speed, and occupancy and other statistical variables of these three basic traffic parameters, such as standard deviation and coefficient of variation [10]. Differential features, such as the difference in traffic parameters between upstream and downstream and between lanes [9], have been gradually incorporated into risk prediction modeling. Feature sensitivity analysis confirmed that the model with lane differential features performed better than the model with only single lane features [18]. Moreover, the occurrence of risk depends not only on the traffic state but also on various complex factors, such as people, vehicles, road conditions, and the environment. The interaction and influence degree among these factors are often hard to quantify and predict, making the establishment of an effective real-time collision Risk Prediction Model a challenging task.
Furthermore, some scholars use micro-kinematic characteristics between adjacent vehicles for real-time risk prediction [17]. In general, previous studies tend to use two types of features for real-time risk prediction: traffic flow features, which reflect the macro traffic conditions of the road section, and micro-kinematic characteristics, which reflect the micro motion characteristics and driving behavior of vehicles. Each type of feature has its own pros and cons. However, there is no clear evidence on whether these two types of features can jointly predict the occurrence of risk or whether they have complementary or redundant effects. Therefore, exploring the relationship between different feature types and their impact on the model is a problem for further study.
2.2.3. Classification Model
The real-time identification and prediction of traffic risks is a classification problem that aims to differentiate the risk level of traffic operation status based on precursors of risk events. To achieve this, researchers have proposed various methods, primarily classified into two categories: statistical models and machine-learning models. Statistical models, the earliest methods used for traffic risk analysis, primarily utilize crash data and traffic flow data to establish statistical relationships between risk and traffic flow features. Common methods include Bayesian logistic regression models [30], probabilistic models with random parameters and random effects [31,32], and correlated random parameters models [33,34], which have been recently found to be more effective. These methods can elucidate the correlation between traffic flow states and the probability of collision occurrence. However, statistical models struggle with the nonlinearity and high dimensionality of data when dealing with real-time traffic collision risk prediction, and they require high-quality and well-distributed data. Consequently, machine-learning models have been extensively used in traffic risk analysis in recent years, effectively addressing these issues. For instance, machine-learning models such as Support Vector Machines (SVMs) [35], Random Forest (RF) [36], eXtreme Gradient Boosting (XGBoost) [37], and Neural Networks [38] have proven effective in solving the classification problem in real-time safety analysis.
Additionally, the selection of the classification threshold becomes a significant issue when dealing with the classification problem of unbalanced data. Real-time risk identification and prediction exemplify such a problem, as the number of non-risk situations in real traffic significantly outweighs the risk situations. The selection of classification thresholds involves adjusting these thresholds at the output level to bias the prediction results towards a certain category [39,40]. In traditional binary classification problems, “0.5” is typically chosen as the classification threshold, and accuracy is used as the primary performance metric of the model. However, this approach is not applicable to risk prediction where the sample distribution is severely unbalanced [41,42]. This is particularly evident in extreme cases where all risky events are incorrectly classified as non-risky, yet the prediction model still maintains high prediction accuracy. Furthermore, the trade-off between the precision and recall of the model must be considered, as adjusting the threshold can cause these two metrics to change in opposite directions. Consequently, it is essential to select an appropriate metric to evaluate the model’s performance in risk identification and prediction to determine the optimal classification threshold. Therefore, in this study, the model’s performance and the determination of the classification threshold were evaluated using the F1 score, which considers both the precision and recall of the model.
3. Data Preparation
3.1. Trajectory Dataset
This study utilizes the HIGHD [12] (“The Highway Drone Dataset”), a naturalistic vehicle trajectory dataset that documents vehicle movements on German motorways. As shown in Table 1, the dataset employs a drone to record six distinct motorway scenarios, encompassing various lane counts and speed limit conditions and spanning a broad spectrum of traffic operating conditions (e.g., smooth and congested). As shown in Figure 1, the drone covers a road with a record range of 420 m, collecting vehicle driving trajectory images at a high resolution of 4 K and a frame rate of 25 fps. Each trajectory frame in the dataset comprises structured information such as vehicle position, speed, acceleration, and surrounding vehicles. Moreover, owing to its low typical positioning error (less than 10 cm), the HIGHD dataset has found extensive application in traffic simulation modeling analysis and validation of technologies related to automated driving [43,44].

Table 1.
Information about the HIGHD dataset.
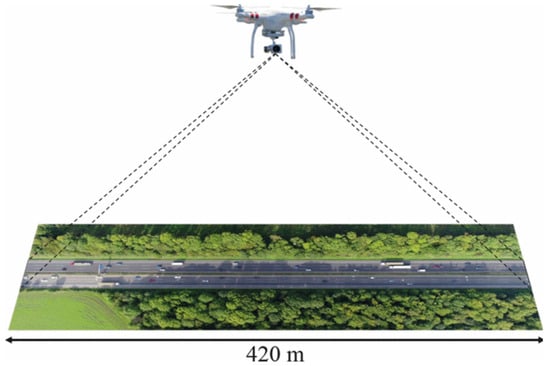
Figure 1.
Using drone to record highway vehicle trajectory information [12].
3.2. Identification of Risk and Non-Risk Events
3.2.1. MTTC-Based Risk Event Identification
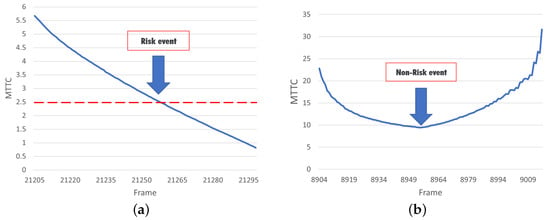
As previously mentioned, this study selected MTTC as the metric to evaluate the operating status of vehicles in the trajectory dataset, therefore identifying risky and non-risky events. Various methods for selecting thresholds for SSM have been proposed in earlier studies, such as those based on the type of vehicle ahead [45], dynamic calculation methods grounded in the driving environment [46], and statistically based methods [47]. The objective of using MTTC in this study is to expect more identification of risky vehicle operating conditions. Hence, a threshold of 2.5 s is selected for risky event identification [48,49]. As shown in Figure 2, in the typical car following scenario, the MTTC value of the following vehicle can be calculated as:
where represent the speed, acceleration, and longitudinal position of the preceding vehicle, respectively; represent the speed, acceleration, and longitudinal position of the following vehicle, respectively; D represents the relative distance between the two vehicles; l represents the length of the preceding vehicle. Consequently, the MTTC value for any frame of the vehicle in the trajectory data can be computed using Equations (1)–(3). A risk event is identified if the MTTC value is less than 2.5 s.
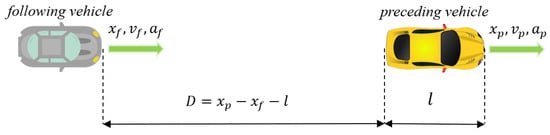
Figure 2.
Typical car following scenario.
3.2.2. Risk Event and Non-Risk Event Extraction
To analyze the precursors of traffic risks and their influencing factors, it is necessary to extract risky and non-risky events from the trajectory dataset for comparison of traffic conditions in both scenarios. In the HIGHD dataset, the vehicle trajectory data are composed of consecutive frames of data, from which a series of MTTC values are computed. As shown in Figure 3, in the identification and extraction of events, the moment when a vehicle’s MTTC reaches 2.5 s in trajectories is considered to be the occurrence of the risky event. For the remaining vehicle trajectories where the MTTC never reaches 2.5 s, the moment of the non-risky event is set to the time with the lowest MTTC. Thus, only one risk event or non-risk event is extracted for each vehicle trajectory. Specifically, to eliminate the potential influence of risky events on the traffic features of non-risky events, non-risky events occurring within 30 s before and after the risky event were excluded, based on a previous study [18]. Ultimately, 865 risk events and 46,821 non-risk events were obtained.
3.3. Traffic Flow Features and Inter-Vehicle Kinematic Feature Extraction
In crash-based traffic risk prediction studies, researchers can obtain the corresponding traffic flow features directly from nearby fixed sensors (such as loop detectors and automatic vehicle recognition detectors) [9,35] once they have identified the crash data and its time of occurrence. However, effectively characterizing traffic features remains a challenge when using trajectory data to construct risk identification and prediction models based on risk events, despite the comprehensive road operational state information contained in trajectory data. To address this challenge, methods such as time-slice traffic feature extraction for trajectory data [17] and the virtual detectors [18] method for obtaining cross-sectional traffic data have been proposed. Moreover, most current traffic risk studies use either traffic flow features or inter-vehicle kinematic features aggregated at the road segment level to characterize the precursor features of risk. This approach leaves a gap in risk analysis studies that combine both traffic features. This study presents a method for extracting traffic flow and inter-vehicle kinematic features from trajectory data. The aim is to investigate the effects of traffic flow variations and micro-interactions of conflicting vehicles on risk events. To achieve this, 18 traffic flow features and seven inter-vehicle kinematic features were computed for risk identification and prediction modeling.
3.3.1. Temporal Range
Given that the features used for risk identification and prediction vary in their temporal range, it is essential to delineate the corresponding feature extraction ranges for Risk Identification Model, Risk Prediction Model-5s, and Risk Prediction Model-10s, as shown in Figure 4. For the Risk Identification Model, the temporal extraction range for traffic flow features is within 30 s prior to the event, and the temporal extraction range for inter-vehicle kinematic features is within 1 s prior to the event, whereas for the Risk Prediction Model-5s and Risk Prediction Model-10s, the temporal extraction ranges of the traffic features are 5 s and 10 s in advance with respect to the event, respectively.
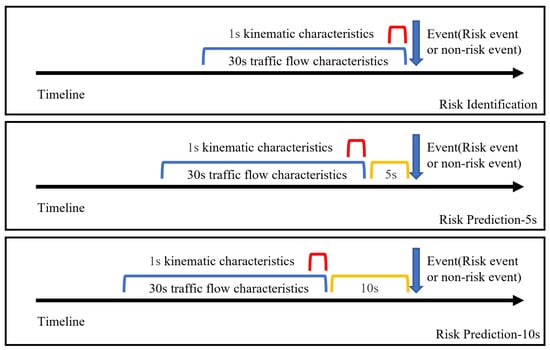
Figure 4.
Temporal range for feature extraction.
3.3.2. Feature Variable Extraction
Upon defining the temporal range for feature extraction, it becomes necessary to consider the methods for extracting traffic flow features and inter-vehicle kinematic features within this temporal range. As shown in Figure 5, the blue dashed line, and the red dashed line represent the spatial extraction ranges of these two features on the road, respectively. Consequently, the two traffic features for each event are extracted as follows: For the lane-level aggregated traffic flow features, parameters such as average speed, speed standard deviation, and flow features of the vehicles passing at upstream and downstream locations on the road are calculated. These calculations are based on the first frame of data after the vehicle enters the road (the vehicle arrives at the upstream location) and the last frame of data before the vehicle departs from the road (the vehicle arrives at the downstream position), collected within the delineated 30 s temporal range. For the inter-vehicle kinematic features, parameters within the same lane, such as maximum longitudinal speed and maximum longitudinal speed gap, among others, are calculated within the delineated 1 s temporal range. It should be noted that both features are extracted in the event lane.
Figure 5.
Spatial range for feature extraction.
Moreover, prior studies suggest that the factors contributing to the occurrence of risky events are not confined to the current lane’s traffic operating status. An increase in the inter-lane differences in operating status can also escalate the likelihood of conflict situations [50,51]. Consequently, a more comprehensive consideration of inter-lane differences in traffic flow features is warranted. Since the HIGHD dataset encompasses both 2-lane and 3-lane road sections, it is necessary to establish selection rules for the main and adjacent lanes of an event. These rules will guide the extraction of inter-lane difference features of traffic flow: (1) The lane where the event occurs is always considered the main lane; (2) If the main lane is situated at the edge of the road, its nearest lane is deemed the adjacent lane; (3) If the main lane is located in the middle of the road and the current vehicle has changed lanes, the lane prior to the lane change is selected as the adjacent lane. Otherwise, the inter-lane difference feature of the traffic flow is calculated as the average difference between the main lane and the two adjacent lanes. Ultimately, 25 traffic feature variables were computed for modeling, as shown in Table 2. Some examples of trajectory data and detailed steps about the process of data preparation can be found in the “Appendix A” section.

Table 2.
Description and statistics of traffic flow features and inter-vehicle kinematic features.
4. Methodology
The identification and prediction of road traffic risk events constitute a typical classification problem, aiming to analyze the probability of risk event occurrence and their influencing factors. To achieve real-time risk identification and prediction, it is essential to employ effective machine-learning methods for traffic state classification. This study utilizes five machine-learning methods widely used in traffic risk studies: Logistic Regression (LR) [9], K-Nearest Neighbors (KNN) [52], eXtreme Gradient Boosting (XGBoost) [53], Random Forests (RF) [35], and Multilayer Perceptron (MLP) [54]. These five methods fall into three categories of machine-learning classification methods: single classifier, integrated learning, and deep learning. Specifically, LR and KNN are distance-based single-classifier methods that use a log-odds function and Euclidean distance, respectively, to measure sample similarity. XGBoost and RF are integrated learning methods based on decision trees, each with distinct generative processes and combinations. XGBoost, a boosting method, generates multiple classifiers sequentially. The weights and division points of each classifier are adjusted according to the error of the previous classifier, and finally, all the classifiers are summed according to their weights to obtain the final result. RF, a bagging method, generates multiple classifiers in parallel, each drawing a portion of the samples from the original dataset randomly and retrospectively. Finally, all the classifiers are voted on or averaged to obtain the final result. MLP, on the other hand, belongs to the deep learning methods, utilizing a multilayer neural network structure trained and optimized by a back-propagation algorithm. All five selected methods have a wide range of applications and demonstrate efficient performance in classification problems.
To assess the performance of the chosen method in identifying and predicting risk events, several widely used metrics are employed, particularly due to the high degree of data imbalance. These metrics include accuracy, precision, recall, and the F1 score, as defined in Table 3 and Equations (4)–(7). The F1 score [55] is the harmonic mean of precision and recall, which measures both the precision and completeness of the model in classifying positive and negative samples. The F1 score varies from 0 to 1, where a higher value indicates a better balance between precision and recall. The F1 score depends on the classification threshold and is thus useful for assessing the model performance under a specific threshold, especially when the positive sample has more significance than the negative sample.

Table 3.
Confusion matrix.
Additionally, the Area Under the Receiver Operating Characteristic Curve (AUC) was employed as a metric to evaluate the prediction accuracy of the model [56]. The AUC, which ranges from 0 to 1, reflects the model’s classification ability. A larger value indicates superior classification ability, translating to higher prediction accuracy for risk. The AUC reflects the prediction probability instead of the prediction category and thus remains unaffected by the threshold. Moreover, the AUC is appropriate for assessing the model’s overall performance, particularly when the positive and negative samples are imbalanced.
In prior studies, the precision and false alarm rate of risk prediction has been considered as two crucial evaluation metrics [9,18]. A risk warning system that frequently intervenes in road traffic due to low precision or high false alarm rates can reduce road efficiency and may result in drivers ignoring high-frequency warning messages. Conversely, an excessive focus on high precision or low false alarm rates can lead to the neglect of many real risk events, which is unacceptable in a highly risk-sensitive road safety warning scenario. Consequently, this study places greater emphasis on the F1 score to balance the precision and completeness of risk prediction.
5. Results and Discussion
5.1. Variable Importance
The importance of a variable is estimated based on the Random Forest algorithm by monitoring how much the Gini index decreases after splitting each time the tree is built [57]. The algorithm constructed 100 trees and used five candidate variables () for each split. Table 4 shows the results of the importance estimation of variables in the Risk Identification Model, Risk Prediction Model-5s, and Risk Prediction Model-10s, respectively, based on the MeanDecreaseGini criterion. Overall, the top six important variables of each model comprised traffic flow features and inter-vehicle kinematic features, demonstrating the significance of these two features for risk identification and prediction. In the Risk Identification Model, the most important factors in the inter-vehicle kinematic feature were the minimum distance between the vehicle (Min_D), the maximum difference of longitudinal acceleration (Max_Diff_XA), and the maximum lateral acceleration (Max_YA). In contrast, the Risk Prediction Model-5s and the Risk Prediction Model-10s focused more on the traffic flow feature, especially the difference in average downstream velocity between main lane and adjacent lane (Diff_AvgV_D) and the difference in average upstream velocity between main lane and adjacent lane (Diff_AvgV_U). This indicates that the traffic characteristics of both lanes should be considered in real-time risk prediction.

Table 4.
Random forests provide the normalized MeanDecreaseGini of variables. The top six important variables in each of the three models are shown.
5.2. Risk Identification Model
To thoroughly evaluate the performance of the machine-learning approach in risk identification and prediction, a five-fold cross-validation technique was employed for model training and testing. As a result, the average of the five model performance metrics was adopted as the final modeling result to represent the model’s overall performance more accurately. This method ensures the fairness and precision of the evaluation results. Simultaneously, to ensure that the non-risk events in the training and test sets accurately mirror the distribution of MTTC values in real traffic, the non-risk events were divided into three groups based on the MTTC values at the time of extraction. Stratified random sampling was then conducted proportionally when partitioning the data, as shown in Figure 6.
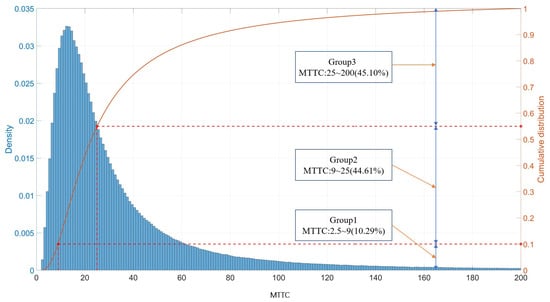
Figure 6.
Probability density and stratified sampling grouping of non-risk events.
Additionally, given the low probability of risky events occurring compared to non-risky events, resampling techniques are utilized to address the significant imbalance in the dataset [58,59]. Two strategies, specifically oversampling and undersampling, are compared in the experiments, using the original training dataset as a benchmark. The Synthetic Minority Oversampling Technique (SMOTE) is a traditional oversampling strategy that balances the dataset by generating synthetic samples from minority classes using the k-nearest neighbors algorithm and linear interpolation [60]. This technique has been extensively used in real-time crash prediction studies [61,62]. Conversely, the undersampling strategy balances the class proportions by removing samples from the majority class [17,42]. The Repeated Edited Nearest Neighbors (RENN) algorithm is employed in the experiments, which enhances the boundaries of the minority class samples and improves the classification performance by iteratively removing some majority class samples that are confused with the minority class using the KNN algorithm. It is important to note that the resampling technique is applied exclusively to the training dataset, while the test dataset retains the original unbalanced proportions for evaluation.
The modeling results of the Risk Identification Model are shown in Table 5. Overall, the XGBoost model demonstrated the highest F1 scores of 0.596, 0.592, and 0.604 for all data-processing methods (original dataset, SMOTE, and RENN), indicating superior classification results and generalization ability for unbalanced data. The XGBoost model, trained on the RENN dataset, emerged as the best model with the highest F1 score, successfully identifying 53.9% of risk events with a correct risk identification rate of 66.9%. In comparison, the Random Forest (RF) model yielded an F1 score of 0.594, slightly lower than the XGBoost model, when using the original dataset. Both integrated learning models exhibited robust risk identification capabilities. Additionally, the Multilayer Perceptron (MLP) model, trained on the RENN dataset, achieved an F1 score of 0.536. Despite MLP-based models not outperforming XGBoost and RF in terms of metrics, they are still considered viable alternatives for risk identification models, particularly in addressing the issue of model updating and migration [63,64], therefore circumventing the time-consuming process of retraining the entire model.

Table 5.
Modeling results of the Risk Identification Model.
In relation to the resampling technique, it is evident that both SMOTE and RENN influence the performance of the models, albeit differently. With respect to the overall performance of the models, all machine-learning models achieved AUC values that were comparable to or higher than those of the original dataset using the resampling technique, suggesting an enhancement in the models’ overall classification capabilities. However, most models that employed the resampling technique exhibited a decrease in F1 scores, implying a reduction in their ability to balance the precision and completeness of risk identification. The only exceptions were the XGBoost model and the MLP model when RENN was used. This indicates that one should not indiscriminately apply a resampling strategy when developing a Risk Identification Model. Instead, an appropriate resampling strategy should be chosen based on the characteristics of the model and the target metrics to prevent degradation of model performance due to overfitting and information loss.
To explore the correlation between the performance of the Risk Identification Model and the traffic flow features as well as the inter-vehicle kinematic features, the XGBoost and the RF were used for risk identification modeling on datasets with three different combinations of the features: the traffic flow features (18 variables), inter-vehicle kinematic features (7 variables), and complete features (25 variables). The results of feature sensitivity analysis are shown in Table 6. It is obvious from the table that both traffic flow features and inter-vehicle kinematic features significantly impact the performance of the risk identification models. The F1 scores and AUC values of risk identification models trained on different features by XGBoost and RF models differ, and both models achieve optimal performance when using complete features. This suggests that the combined use of both features for risk analysis can enhance the accuracy and robustness of the models. Furthermore, the comparison results of the two features reveal that the model using inter-vehicle kinematic features outperforms the model using traffic flow features in both F1 scores and AUC values. This indicates that inter-vehicle kinematic features possess a stronger discriminative ability and differentiation for risk identification.

Table 6.
Feature sensitivity analysis of risk identification models.
5.3. Risk Prediction Model
Furthermore, risk prediction is considered to be more forward-looking and proactive than risk identification in the context of actual road traffic accident prevention. Such a model can provide drivers with more adjustment time and more effective decision support for risk management. By extracting features within the specific temporal range, a dataset for constructing a Risk Prediction Model can be generated. Consequently, two new models are developed:
- Risk Prediction Model-5s: This model utilizes the currently extracted traffic flow features and inter-vehicle kinematic features to predict the risk situation 5 s later.
- Risk Prediction Model-10s: This model employs the currently extracted traffic flow features and inter-vehicle kinematic features to predict the risk situation 10 s later.
The modeling results of the Risk Prediction Model are shown in Table 7. Generally, due to the advancement of the feature extraction temporal range, both the F1 scores and AUC values of the Risk Prediction Model have decreased compared to the Risk Identification Model, indicating a weakened classification ability of the model. Specifically, the RF model displays the highest F1 scores of 0.377 and 0.370 for both risk prediction conditions. This suggests that the RF model can predict 25.8% of the risk events with 74.9% precision 5 s in advance and 25.7% of the risk events with 72.0% precision 10 s in advance. Moreover, the XGBoost model also exhibits strong risk prediction ability, with F1 values of 0.356 and 0.361, respectively. This indicates that both integrated learning models possess robust risk identification and prediction capabilities. These results imply that both risk prediction models can provide timely early warnings to drivers and active traffic management systems without excessively affecting driver alertness or limiting road capacity, therefore contributing to the reduction of risky events.

Table 7.
Modeling results of the Risk Identification Model.
The effects of traffic flow features and inter-vehicle kinematic features on risk prediction were further investigated. Specifically, the RF model was employed to perform two risk prediction models on three datasets with different feature combinations, and the results of the sensitivity analysis are shown in Table 8. It is obvious from the table that, unlike risk identification, where inter-vehicle kinematic features play a dominant role, the Risk Prediction Model using traffic flow features significantly outperforms the model using inter-vehicle kinematic features in both F1 scores and AUC values. This implies that traffic flow features are more predictive of the occurrence of risk events. Moreover, both risk prediction models achieved optimal performance when utilizing the complete features. This further substantiates that the combination of traffic flow features and inter-vehicle kinematic features for risk prediction can facilitate earlier detection of risk events.

Table 8.
Feature sensitivity analysis of risk prediction models.
Additionally, the models developed in this study were compared with previous work that utilized trajectory data, and the results are shown in Table 9. Yu et al. [17] constructed a high-risk event prediction model based on the kinematic characteristics of the vehicle in front for a brief period prior to the risk occurrence, using a case-control dataset with a fixed scale (1:4). The experimental results demonstrated that the AUC values of both models exceeded 0.96. Yuan et al. [18] predicted real-time conflict risk using traffic flow characteristics 30 s before the risk occurrence, with the model achieving an F1 score of 0.447 and an AUC value of 0.871. Katrakazas et al. [14] constructed an SVM model for real-time conflict prediction based on the speed, flow, and acceleration characteristics of the 5 min before the risk occurrence, achieving an F1 score of 0.335. Compared with the previous research works presented in the table, the model construction process in this study gives greater consideration to the imbalance between risky and non-risky conditions in real traffic environments. The proposed risk identification and prediction model shows promising results in terms of accuracy, robustness, and applicability.

Table 9.
Comparison of collision risk identification and prediction models based on trajectory data.
6. Conclusions
Real-time risk prediction plays a crucial role in enhancing highway safety, reducing traffic accident incidence, and facilitating proactive identification and prevention of collision risks. In this study, a method for extracting traffic flow features and inter-vehicle kinematic features based on risk events is proposed using the HIGHD trajectory dataset as empirical data, and a risk identification and prediction model is established. First, surrogate safety measures with MTTC less than 2.5 s are used to obtain risky events and non-risky events in the trajectory dataset. Subsequently, 30 s of traffic flow features and 1 s of inter-vehicle kinematic features are extracted within a delimited temporal range to cater to the needs of risk identification and prediction. Then, a comparative study of five machine-learning methods (Logistic Regression, K-Nearest Neighbors, eXtreme Gradient Boosting, Random Forests, and Multilayer Perceptron) and two data-processing strategies (SMOTE and RENN) was conducted using a five-fold cross-validation approach.
The modeling results reveal that the developed models exhibit robust risk identification and prediction performance. The main findings are as follows:
- The XGBoost model trained on the RENN dataset emerges as the superior model for risk identification, with an F1 score of 0.604, and can identify 53.9% of risk events with a 66.9% correct risk identification rate. However, it is important to note that the resampling strategy is not always effective when developing risk analysis models and a decision on whether to adopt a resampling strategy and to select an appropriate resampling technique needs to be made based on the characteristics of the model and the target metrics.
- The RF model demonstrated optimal performance under both risk prediction conditions, with precision and recall of 0.749 and 0.258 for the 5-s-advance scenario and 0.720 and 0.257 for the 10-s-advance scenario, respectively. In addition, the XGBoost model also achieved a strong risk prediction capability with F1 values of 0.356 and 0.361, indicating that the integrated learning model has strong fitting and generalization performance in the identification and prediction of risk.
- In the sensitivity analysis of traffic features, the model using complete features achieved higher F1 scores and AUC values compared to the model using traffic flow features or inter-vehicle kinematics features alone, indicating that the combined use of traffic flow features and inter-vehicle kinematics features yields the best.
Although this study has made considerable progress, there is still potential for further improvement. First, comprehensive and high-resolution vehicle trajectory data remain limited. The empirical data used in this study covers only six scenarios on German motorways and includes records with a total duration of 16.5 h. This may not sufficiently reflect the diversity of different traffic operating conditions and risky events. Therefore, it is necessary to validate the proposed method on datasets with larger sample sizes and greater diversity to assess their validity and generalization capabilities. This could involve applying trajectory data from different countries, traffic scenarios, and weather conditions. Second, MTTC is used as a surrogate safety measure in the identification of risk events in this study. However, it can only reflect the risk of collision between vehicles, not the risk of collision between vehicles and roads or other obstacles, nor the risk arising from the driver’s poor condition. Therefore, it is necessary to consider the use of a combination of multiple surrogate safety measures or accident risk coefficients that take into account driver factors [65] to improve the accuracy and coverage of risk identification.
Author Contributions
Conceptualization, S.H. and H.Z.; methodology, S.H. and H.C.; software, S.H.; validation, S.H. and X.W.; formal analysis, H.Z.; investigation, S.H.; resources, H.Z.; writing—original draft preparation, S.H. and H.C.; writing—review and editing, S.H. and X.W.; visualization, S.H. and X.W.; funding acquisition, H.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Restrictions apply to the availability of these data. Data were obtained from the Institute for Automotive Engineering (ika) of RWTH Aachen University and are available from at https://levelxdata.com/highd-dataset/ (accessed on 1 December 2023) with the permission of the Institute for Automotive Engineering (ika) of RWTH Aachen University.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SSM | Surrogate safety measure |
| TTC | Time to collision |
| MTTC | Modified Time to Collision |
| DRAC | Deceleration to avoid collision |
| PET | Post-encroachment time |
| HIGHD | The Highway Drone Dataset |
| LR | Logistic Regression |
| KNN | K-Nearest Neighbors |
| XGBoost | eXtreme Gradient Boosting |
| RF | Random Forests |
| MLP | Multilayer Perceptron |
| AUC | Area Under the Receiver Operating Characteristic Curve |
| SMOTE | Synthetic Minority Oversampling Technique |
| RENN | Repeated Edited Nearest Neighbors |
Appendix A
The detailed steps of the data preparation process are shown below, using the data and parameters in Table A1 as an example:
- Refer to Section 3.2.2 to identify whether each trajectory contains risk events or non-risk events in turn, and obtain the frame time of event occurrence. For example, the trajectory with id 76 contains the risk event, which occurs at frame time 1509.
- Refer to Section 3.3.1 to calculate the time range for extracting traffic flow features and inter-vehicle kinematic features. Taking the above risk event as an example, the time range of feature extraction for traffic flow for risk identification is 760 to 1509 frames, and the time range of feature extraction for inter-vehicle kinematic features is 1485 to 1509 frames.
- Refer to Section 3.3.2 to calculate the traffic flow features and inter-vehicle kinematic features of the corresponding samples of events. For the traffic flow features, first, trajectory data within the time range of traffic flow feature extraction is found, and parts in the same direction are screened out. Then, the traffic flow features are calculated using the frame data that belong to the first entry or exit of the road during this period. For the inter-vehicle kinematic features, first, trajectory data within the time range of inter-vehicle kinematic feature extraction is found, and the parts in the same direction and lane are screened out. Then, the inter-vehicle kinematic features are calculated. Table A2 shows the feature extraction results of risk events in the complete dataset.

Table A1.
HIGHD data set trajectory data example (only some features in the original data are shown). Frame is the current number of frames, id is the number of the track, width is the length of the vehicle, x is the longitudinal position of the vehicle, laneId is the lane in which the vehicle is located, and laneId “2” and “3” are adjacent lanes in the same direction; precedingId is the number of the vehicle in front.
Table A1.
HIGHD data set trajectory data example (only some features in the original data are shown). Frame is the current number of frames, id is the number of the track, width is the length of the vehicle, x is the longitudinal position of the vehicle, laneId is the lane in which the vehicle is located, and laneId “2” and “3” are adjacent lanes in the same direction; precedingId is the number of the vehicle in front.
| Frame | Id | Width | x | LaneId | PrecedingId | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1507 | 76 | 7.48 | 334.66 | 2 | −27.82 | 0.82 | −0.38 | 0.46 | 74 | 2.55 |
| 1508 | 76 | 7.48 | 333.54 | 2 | −27.84 | 0.84 | −0.37 | 0.45 | 74 | 2.51 |
| 1509 | 76 | 7.48 | 332.42 | 2 | −27.85 | 0.87 | −0.36 | 0.45 | 74 | 2.47 |
| 1507 | 74 | 8.49 | 314.94 | 2 | −23.65 | −0.11 | 0.2 | −0.03 | 72 | 21.15 |
| 1508 | 74 | 8.49 | 313.98 | 2 | −23.64 | −0.11 | 0.2 | −0.02 | 72 | 19.88 |
| 1509 | 74 | 8.49 | 313.01 | 2 | −23.63 | −0.11 | 0.2 | −0.01 | 72 | 19.86 |
| 1507 | 77 | 4.45 | 309.41 | 3 | −40.88 | 0.02 | 1.15 | 0.08 | 69 | 7.03 |
| 1508 | 77 | 4.45 | 307.79 | 3 | −40.84 | 0.02 | 1.15 | 0.08 | 69 | 7.02 |
| 1509 | 77 | 4.45 | 306.16 | 3 | −40.79 | 0.03 | 1.14 | 0.08 | 69 | 7.02 |

Table A2.
Examples of feature extraction results for risk events in the complete dataset.
Table A2.
Examples of feature extraction results for risk events in the complete dataset.
| AvgV_U | AvgV_D | DiffV_UD | StdV_U | StdV_D | CvV_U | CvV_D | Vo_U | Vo_D |
|---|---|---|---|---|---|---|---|---|
| 35.20 | 35.35 | 0.14 | 1.71 | 3.96 | 0.04 | 0.11 | 12.00 | 8.00 |
| DiffVo_DU | Diff_AvgV_U | Diff_AvgV_D | Diff_StdV_U | Diff_StdV_D | Diff_CvV_U | Diff_CvV_D | Diff_Vo_U | Diff_Vo_D |
| 4.00 | 8.56 | 6.35 | 2.25 | 0.98 | 0.10 | 0.05 | 5.00 | 1.00 |
| Max_XV | Max_Diff_XV | Max_YV | Max_XA | Max_Diff_XA | Max_YA | Min_D | ||
| 37.61 | 4.55 | 0.30 | 0.86 | 0.17 | 0.08 | 29.10 |
References
- WHO. Road Traffic Injuries. 2022. Available online: https://www.who.int/news-room/fact-sheets/detail/road-traffic-injuries (accessed on 20 June 2022).
- WHO. Global Plan for the Decade of Action for Road Safety 2021–2030. 2021. Available online: https://www.who.int/publications/m/item/global-plan-for-the-decade-of-action-for-road-safety-2021-2030 (accessed on 20 October 2021).
- Flannagan, C.; LeBlanc, D.; Bogard, S.; Nobukawa, K.; Narayanaswamy, P.; Leslie, A.; Kiefer, R.; Marchione, M.; Beck, C.S.; Lobes, K. Large-scale field test of forward collision alert and lane departure warning systems. Natl. Acad. Sci. 2016, 01605729. [Google Scholar]
- FHWA. Highway Safety Improvement Program (HSIP). 2020. Available online: https://safety.fhwa.dot.gov/hsip/hsip.cfm (accessed on 11 February 2023).
- Yasmin, S.; Eluru, N.; Wang, L.; Abdel-Aty, M. A joint framework for static and real-time crash risk analysis. Anal. Methods Accid. Res. 2018, 18, 45–56. [Google Scholar] [CrossRef]
- Yuan, J.; Abdel-Aty, M. Approach-Level Real-Time Crash Risk Analysis for Signalized Intersections. Accid. Anal. Prev. 2018, 119, 274–289. [Google Scholar] [CrossRef]
- Lu, Q.L.; Yang, K.; Antoniou, C. Crash risk analysis for the mixed traffic flow with human-driven and connected and autonomous vehicles. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 1233–1238. [Google Scholar]
- Dan Chia, W.M.; Loong Keoh, S.; Michala, A.L.; Goh, C. Real-time Recursive Risk Assessment Framework for Autonomous Vehicle Operations. In Proceedings of the 2021 IEEE 93rd Vehicular Technology Conference (VTC2021-Spring), Helsinki, Finland, 25–28 April 2021; pp. 1–7. [Google Scholar]
- Xu, C.; Tarko, A.P.; Wang, W.; Liu, P. Predicting crash likelihood and severity on freeways with real-time loop detector data. Accid. Anal. Prev. 2013, 57, 30–39. [Google Scholar] [CrossRef]
- Chen, Z.; Qin, X. A novel method for imminent crash prediction and prevention. Accid. Anal. Prev. 2019, 125, 320–329. [Google Scholar] [CrossRef]
- Liu, M.; Chen, Y. Predicting real-time crash risk for urban expressways in China. Math. Probl. Eng. 2017, 2017, 6263726. [Google Scholar] [CrossRef]
- Krajewski, R.; Bock, J.; Kloeker, L.; Eckstein, L. The highD Dataset: A Drone Dataset of Naturalistic Vehicle Trajectories on German Highways for Validation of Highly Automated Driving Systems. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018. [Google Scholar]
- Wang, J.; Fu, T.; Xue, J.; Li, C.; Song, H.; Xu, W.; Shangguan, Q. Realtime wide-area vehicle trajectory tracking using millimeter-wave radar sensors and the open TJRD TS dataset. Int. J. Transp. Sci. Technol. 2023, 12, 273–290. [Google Scholar] [CrossRef]
- Katrakazas, C.; Quddus, M.; Chen, W.H. A simulation study of predicting real-time conflict-prone traffic conditions. IEEE Trans. Intell. Transp. Syst. 2018, 19, 3196–3207. [Google Scholar] [CrossRef]
- Yang, D.; Wu, Y.; Sun, F.; Chen, J.; Zhai, D.; Fu, C. Freeway accident detection and classification based on the multi-vehicle trajectory data and deep learning model. Transp. Res. Part C Emerg. Technol. 2021, 130, 103303. [Google Scholar] [CrossRef]
- Guo, F.; Klauer, S.G.; McGill, M.T.; Dingus, T.A. Evaluating the Relationship between Near-Crashes and Crashes: Can Near-Crashes Serve as a Surrogate Safety Metric for Crashes? 2010. Available online: https://api.semanticscholar.org/CorpusID:6401904 (accessed on 11 February 2023).
- Yu, R.; Han, L.; Zhang, H. Trajectory data based freeway high-risk events prediction and its influencing factors analyses. Accid. Anal. Prev. 2021, 154, 106085. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Li, Y.; Huang, H.; Wang, S.; Sun, Z.; Li, Y. Using traffic flow characteristics to predict real-time conflict risk: A novel method for trajectory data analysis. Anal. Methods Accid. Res. 2022, 35, 100217. [Google Scholar] [CrossRef]
- Dingus, T.A.; Klauer, S.G.; Neale, V.L.; Petersen, A.; Lee, S.E.; Sudweeks, J.; Perez, M.A.; Hankey, J.; Ramsey, D.; Gupta, S.; et al. The 100-Car Naturalistic Driving Study, Phase II-Results of the 100-Car Field Experiment; Department of Transportation, National Highway Traffic Safety Administration: Washington, DC, USA, 2006.
- Allen, B.L.; Shin, B.T.; Cooper, P.J. Analysis of Traffic Conflicts and Collisions. Transp. Res. Rec. 1978, 67–74. [Google Scholar]
- Wang, C.; Xie, Y.; Huang, H.; Liu, P. A review of surrogate safety measures and their applications in connected and automated vehicles safety modeling. Accid. Anal. Prev. 2021, 157, 106157. [Google Scholar] [CrossRef] [PubMed]
- Cooper, D.F.; Ferguson, N. Traffic studies at T-Junctions. 2. A conflict simulation Record. Traffic Eng. Control. 1976, 17, 306–309. [Google Scholar]
- Shelby, S.G. Delta-V as a measure of traffic conflict severity. In Proceedings of the 3rd International Conference on Road Safety and Simulati, Indianapolis, IN, USA, 14–16 September 2011. [Google Scholar]
- Hayward, J.C. Near miss determination through use of a scale of danger. In Proceedings of the 51st Annual Meeting of the Highway Research Board, Washington, DC, USA, 17–21 January 1972. [Google Scholar]
- Ozbay, K.; Yang, H.; Bartin, B.; Mudigonda, S. Derivation and validation of new simulation-based surrogate safety measure. Transp. Res. Rec. 2008, 2083, 105–113. [Google Scholar] [CrossRef]
- Yang, H. Simulation-Based Evaluation of Traffic Safety Performance Using Surrogate Safety Measures. Ph.D. Thesis, Rutgers, The State University of New Jersey, Newark, NJ, USA, 2012. [Google Scholar]
- Pirdavani, A.; De Pauw, E.; Brijs, T.; Daniels, S.; Magis, M.; Bellemans, T.; Wets, G. Application of a rule-based approach in real-time crash risk prediction model development using loop detector data. Traffic Inj. Prev. 2015, 16, 786–791. [Google Scholar] [CrossRef]
- Bhatti, F.; Shah, M.A.; Maple, C. A novel internet of things-enabled accident detection and reporting system for smart city environments. Sensors 2019, 19, 2071. [Google Scholar] [CrossRef]
- Khan, A.; Bibi, F.; Dilshad, M.; Ahmed, S.; Ullah, Z.; Ali, H. Accident detection and smart rescue system using Android smartphone with real-time location tracking. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 341–355. [Google Scholar] [CrossRef]
- Wang, L.; Abdel-Aty, M.; Shi, Q.; Park, J. Real-time crash prediction for expressway weaving segments. Transp. Res. Part C Emerg. Technol. 2015, 61, 1–10. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M.; Ahmed, M. Bayesian random effect models incorporating real-time weather and traffic data to investigate mountainous freeway hazardous factors. Accid. Anal. Prev. 2013, 50, 371–376. [Google Scholar] [CrossRef]
- Fu, C.; Sayed, T. Random parameters Bayesian hierarchical modeling of traffic conflict extremes for crash estimation. Accid. Anal. Prev. 2021, 157, 106159. [Google Scholar] [CrossRef]
- Hou, Q.; Tarko, A.P.; Meng, X. Analyzing crash frequency in freeway tunnels: A correlated random parameters approach. Accid. Anal. Prev. 2018, 111, 94–100. [Google Scholar] [CrossRef]
- Caliendo, C.; Guida, M.; Postiglione, F.; Russo, I. A Bayesian bivariate hierarchical model with correlated parameters for the analysis of road crashes in Italian tunnels. Stat. Methods Appl. 2022, 31, 109–131. [Google Scholar] [CrossRef]
- Yu, R.; Abdel-Aty, M. Analyzing crash injury severity for a mountainous freeway incorporating real-time traffic and weather data. Saf. Sci. 2014, 63, 50–56. [Google Scholar] [CrossRef]
- Jiang, H.; Deng, H. Traffic incident detection method based on factor analysis and weighted random forest. IEEE Access 2020, 8, 168394–168404. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Cheng, H.; Zhang, J.; Wang, Q.; Zhu, H. Deep learning-based prediction of traffic accidents risk for Internet of vehicles. China Commun. 2022, 19, 214–224. [Google Scholar] [CrossRef]
- Pawar, K.; Attar, V. Deep learning based detection and localization of road accidents from traffic surveillance videos. ICT Express 2022, 8, 379–387. [Google Scholar] [CrossRef]
- Karim, M.M.; Li, Y.; Qin, R.; Yin, Z. A dynamic spatial-temporal attention network for early anticipation of traffic accidents. IEEE Trans. Intell. Transp. Syst. 2022, 23, 9590–9600. [Google Scholar] [CrossRef]
- Yang, K.; Yu, R.; Wang, X.; Quddus, M.; Xue, L. How to determine an optimal threshold to classify real-time crash-prone traffic conditions? Accid. Anal. Prev. 2018, 117, 250–261. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Li, C.; Wang, K.; Gao, Z.; Yu, R. Examining imbalanced classification algorithms in predicting real-time traffic crash risk. Accid. Anal. Prev. 2020, 144, 105610. [Google Scholar] [CrossRef] [PubMed]
- Kurtc, V. Studyg car-following dynamics on the basis of the HighD dataset. Transp. Res. Rec. 2020, 2674, 813–822. [Google Scholar] [CrossRef]
- Schneider, P.; Butz, M.; Heinzemann, C.; Oehlerking, J.; Woehrle, M. Scenario-based threat metric evaluation based on the highd dataset. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 213–218. [Google Scholar]
- Das, S.; Maurya, A.K. Defining time-to-collision thresholds by the type of lead vehicle in non-lane-based traffic environments. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4972–4982. [Google Scholar] [CrossRef]
- Nadimi, N.; NaserAlavi, S.S.; Asadamraji, M. Calculating dynamic thresholds for critical time to collision as a safety measure. Proc. Inst. Civ. Eng.-Transp. 2022, 175, 403–412. [Google Scholar] [CrossRef]
- Jin, S.; Qu, X.; Wang, D. Assessment of expressway traffic safety using Gaussian mixture model based on time to collision. Int. J. Comput. Intell. Syst. 2011, 4, 1122–1130. [Google Scholar]
- Essa, M.; Sayed, T. Full Bayesian conflict-based models for real time safety evaluation of signalized intersections. Accid. Anal. Prev. 2019, 129, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Yang, D.; Xie, K.; Ozbay, K.; Zhao, Z.; Yang, H. Copula-based joint modeling of crash count and conflict risk measures with accommodation of mixed count-continuous margins. Anal. Methods Accid. Res. 2021, 31, 100162. [Google Scholar] [CrossRef]
- Lee, C.; Saccomanno, F.; Hellinga, B. Analysis of crash precursors on instrumented freeways. Transp. Res. Rec. 2002, 1784, 1–8. [Google Scholar] [CrossRef]
- Yu, R.; Wang, X.; Yang, K.; Abdel-Aty, M. Crash risk analysis for Shanghai urban expressways: A Bayesian semi-parametric modeling approach. Accid. Anal. Prev. 2016, 95, 495–502. [Google Scholar] [CrossRef]
- Xiao, J. SVM and KNN ensemble learning for traffic incident detection. Phys. A Stat. Mech. Its Appl. 2019, 517, 29–35. [Google Scholar] [CrossRef]
- Qu, Y.; Lin, Z.; Li, H.; Zhang, X. Feature recognition of urban road traffic accidents based on GA-XGBoost in the context of big data. IEEE Access 2019, 7, 170106–170115. [Google Scholar] [CrossRef]
- Zhu, W.; Wu, J.; Fu, T.; Wang, J.; Zhang, J.; Shangguan, Q. Dynamic prediction of traffic incident duration on urban expressways: A deep learning approach based on LSTM and MLP. J. Intell. Connect. Veh. 2021, 4, 80–91. [Google Scholar] [CrossRef]
- Huang, J.; Ling, C.X. Using AUC and accuracy in evaluating learning algorithms. IEEE Trans. Knowl. Data Eng. 2005, 17, 299–310. [Google Scholar] [CrossRef]
- Sokolova, M.; Japkowicz, N.; Szpakowicz, S. Beyond accuracy, F-score and ROC: A family of discriminant measures for performance evaluation. In Proceedings of the Australasian Joint Conference on Artificial Intelligence, Hobart, Australia, 4–8 December 2006; pp. 1015–1021. [Google Scholar]
- Han, H.; Guo, X.; Yu, H. Variable selection using mean decrease accuracy and mean decrease gini based on random forest. In Proceedings of the 2016 7th IEEE International Conference on Software Engineering and Service Science (Icsess), Beijing, China, 26–28 August 2016; pp. 219–224. [Google Scholar]
- Parsa, A.B.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Real-time accident detection: Coping with imbalanced data. Accid. Anal. Prev. 2019, 129, 202–210. [Google Scholar] [CrossRef]
- Abou Elassad, Z.E.; Mousannif, H.; Al Moatassime, H. A proactive decision support system for predicting traffic crash events: A critical analysis of imbalanced class distribution. Knowl.-Based Syst. 2020, 205, 106314. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Elamrani Abou Elassad, Z.; Mousannif, H.; Al Moatassime, H. Class-imbalanced crash prediction based on real-time traffic and weather data: A driving simulator study. Traffic Inj. Prev. 2020, 21, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Mehrannia, P.; Bagi, S.S.G.; Moshiri, B.; Al-Basir, O.A. Deep representation of imbalanced spatio-temporal traffic flow data for traffic accident detection. IET Intell. Transp. Syst. 2023, 17, 606–619. [Google Scholar] [CrossRef]
- Man, C.K.; Quddus, M.; Theofilatos, A. Transfer learning for spatio-temporal transferability of real-time crash prediction models. Accid. Anal. Prev. 2022, 165, 106511. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Zhang, D.; Wang, D. Deeprisk: A deep transfer learning approach to migratable traffic risk estimation in intelligent transportation using social sensing. In Proceedings of the 2019 15th International Conference on Distributed Computing in Sensor Systems (DCOSS), Santorini, Greece, 29–31 May 2019; pp. 123–130. [Google Scholar]
- Gürbüz, H.; Buyruk, S. Improvement of safe stopping distance and accident risk coefficient based on active driver sight field on real road conditions. IET Intell. Transp. Syst. 2019, 13, 1843–1850. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).