Visual Analysis Method for Traffic Trajectory with Dynamic Topic Movement Patterns Based on the Improved Markov Decision Process

Abstract

The visual analysis of trajectory topics is helpful for mining potential trajectory patterns, but the traditional visual analysis method ignores the evolution of the temporal coherence of the topic. In this paper, a novel visual analysis method for dynamic topic analysis of traffic trajectory is proposed, which is used to explore and analyze the traffic trajectory topic and evolution. Firstly, the spatial information is integrated into trajectory words, calculating the dynamic trajectory topic model based on dynamic analysis modeling and, consequently, correlating the evolution of the trajectory topic between adjacent time slices. Secondly, in the trajectory topic, a representative trajectory sequence is generated to overcome the problem of the trajectory topic model not considering the word order, based on the improved Markov Decision Process. Subsequently, a set of meaningful visual codes is designed to analyze the trajectory topic and its evolution through the parallel window visual model from a spatial-temporal perspective. Finally, a case evaluation shows that the proposed method is effective in analyzing potential trajectory movement patterns.

1. Introduction

Visual exploration of traffic trajectory data is constrained by the limited capacity for visual information and the lack of interactive guidance. Traffic trajectories record the historical travel of vehicles, with visual information and potential features at spatial-temporal levels. Exploring traffic trajectories through visualization can intuitively obtain visual information about the trajectories and mine the potential movement patterns. However, drawing the traffic trajectory directly on a map will be limited by the information capacity and will cause problems such as visual occlusion. The most intuitive method to help the visual exploration of traffic trajectory is to reduce the visual density by computing the trajectory features. Liu et al. [1] effectively reduce the visual density of Origin to Destinatin (OD) flow by dividing and exploring urban functional areas. Liu et al. [2] employ a tensor decomposition algorithm to segment multi-dimensional spatiotemporal data and reduce the number of visualization elements on the same screen. Zhou et al. [3] propose a visual exploration system to reduce the visual clutter and strengthen the relevance of OD flows. Deng et al. [4] provide an efficient visual presentation design of temporal events by abstracting the workflow of temporal and spatial interaction association analysis. Andrienko et al. [5] designed a method to abstract the characteristics of spatio-temporal OD mobility to reduce the intersection and occlusion of the trajectory flow graph. Unfortunately, these methods calculate trajectory patterns at the data feature level and do not provide enough semantic guidance for the analyst. In addition, analysts usually need to manually select and iterate different motion data slices to search for hidden patterns in trajectory data, making it difficult to deeply analyze potential trajectory movement patterns from a spatial-temporal perspective. We address these issues and propose a set of meaningful visual encodings. This visualization model establishes a parallel window model. The model presents the trajectory topic characteristics from the spatial and temporal perspectives, which is helpful in reducing visual interference and providing guidance for visual interactive exploration.

The dynamic topic information in the trajectory topic model reflects the evolution of the topic. A topic model, which provides topic guidance for trajectory analysis by applying the topic model to trajectory data analysis, is a kind of statistical model. Most of the existing methods that apply topic models to trajectory modeling are based on Latent Dirichlet Allocation (LDA) [6], Non-negative Matrix Factorization (NMF) [7], and other unsupervised topic algorithms, focusing on optimizing topic extraction strategies. Specifically, Chu et al. [8] introduce the LDA to infer hidden patterns of moving taxi populations. Liu et al. [9] transform the traffic data into a document library to capture latent traffic semantic patterns based on the NMF model. Liu et al. [10] employ the bigram topic model to analyze textualized trajectories. Tao et al. [11] introduce a hierarchical topic model H-NMF to extract multi-granularity traffic topics to capture mobility patterns. Traffic trajectory is dynamic, and the corresponding trajectory topic constantly evolves. However, the trajectory topic analysis based on the above modeling methods only considers the trajectory spatial information. It does not consider the temporal dynamic evolution of the trajectory topic, resulting in the loss of trajectory topic evolution information.

Trajectory features are described by trajectory semantics [12]. Trajectory order is an essential part of the semantics of trajectory topics. The topic model describes the topic content by counting word frequency but does not consider the ordinal relationship between words. Traffic trajectories are sequentially connected trajectory segments with a sequential relationship. Trajectory sequence information is necessary for trajectory topic modeling. However, applying the topic model to the topic modeling of traffic trajectory is challenging and needs to overcome the influence of the topic model not containing word sequence information on the interpretability of trajectory topics. In summary, there needs to be more trajectory order semantics and topic evolution information in existing work on trajectory topics. This implies the need for visual encodings that provide sufficient semantic guidance to analyze trajectory topic evolution.

To solve these problems, a visual analysis method is proposed to analyze the dynamic topics of trajectories. This method considers the evolution information of trajectory topics and overcomes the problem of missing word sequence information in probabilistic models. Firstly, the dynamic topic model (DTM) [13] for a trajectory is established to analyze the trajectory topic evolution fitted by parameter distribution. Secondly, by calculating the thematic entropy, we can quantify the informational content of the trajectory topics, which indicates meaningful thematic time segments, thereby reducing the time required for the manual repetitive selection of data slices. Subsequently, we employ Markov chains to represent trajectory words and address the issue of topic models not retaining word order information. Based on the Markov chains, we utilize an improved Markov Decision Process (MDP) to generate trajectory sequences that represent the topics, which aids in analyzing the topic content. Moreover, we introduce a meaningful visual encoding scheme, presenting trajectory topic visualizations separately through parallel views from both abstract maps and thematic information perspectives. Lastly, a case study based on a real dataset was conducted to demonstrate the efficacy of the methodology proposed in this paper in exploring dynamic trajectory topics. In summary, the primary contributions of this work are as follows:

• A trajectory dynamic topic model is proposed. This model considers the topic evolution and is used to process traffic trajectory data. This model helps to obtain trajectory dynamic topics and capture their evolution. The topic entropy is calculated to represent the volume of information in trajectory topics and is utilized to analyze the evolution of the topic.
• The improved Markov Decision Process is proposed to generate representative trajectory sequences of a topic. This method aims to overcome the problem of probabilistic models which often lose word sequence information.
• The visual models, featured with the parallel and regular arrangement, are designed to help users explore the trajectory dynamic topics and related indicators.
• Experimental studies based on the publicly available dataset demonstrate the effectiveness of this method in trajectory dynamic topic exploration.

2. Related Works

2.1. Trajectory Topic Modeling

The basic idea of topic modeling is to vectorize a given corpus by term frequency or inverse document frequency. Topic modeling decomposes a document-term matrix into document-topic and topic-word subsets, subsequently optimizing these subsets using probabilistic or decomposition techniques. The clustering of implicit semantic structures in documents obtained through topic modeling can be applied to the discovery of trajectory semantic structures and trajectory topics. Trajectory topic modeling aims to describe motion patterns by calculating sub-trajectory frequency information, thereby further extracting the content of trajectory topics. Commonly used topic models include LDA [6], NMF [7], and others.

As common topic computing methods, LDA and NMF are widely used in topic modeling. LDA computes the posterior distribution of the data based on Bayesian algorithms, whereas NMF produces deterministic outcomes from matrix decomposition, not probabilistic values. Current efforts in topic modeling largely revolve around modifications or advancements of the LDA and NMF methodologies. For instance, Liao et al. [14] established a trajectory topic model based on LDA to unearth latent driving patterns and analyze a driver’s travel intentions. Huang et al. [15] employed LDA to explore hidden ship mobility patterns from the trajectory document corpus. In contrast, Liu et al. [2] applied tensor decomposition to multi-dimensional spatiotemporal data to extract regional patterns. Addressing the challenge of selecting an optimal number of topics, Liu et al. [9] proposed an interactive trajectory topic modeling method based on a semi-supervised non-negative matrix factorization (SS-NMF) for trajectory data. Similarly, Tao et al. [11] presented a hierarchical topic analysis approach to balance the analyses of varying granularities of movement patterns. Notably, NMF’s performance degrades with more significant numbers of topics, whereas LDA exhibits more robust modeling results.

Beyond using LDA and NMF for trajectory topic modeling, Liu et al. [10] adopted the Biterm Topic Model (BTM) [16] to model trajectory movement patterns, leveraging the Apriori algorithm for sub-trajectory extraction and using sub-trajectory sequences to indicate directionality. Originating for short-text analysis, BTM differs from LDA in that its word generation is corpus-wide. Without a document hierarchy, BTM primarily retrieves word probabilities related to topics, making it challenging to obtain document-specific topic probabilities. However, different trajectory topics are implied in trajectory datasets. Analyzing trajectory data deeply and obtaining specific topic probabilities using BTM is difficult.

These topic modeling methods, including LDA, NMF, and BTM, calculate the trajectory topic within the time interval and do not calculate the trajectory topic evolution between time slices at the model level. Dynamic topic modeling adds a time factor, and the topic content changes with time. Corresponding Dynamic topic versions exist for NMF and LDA, namely, Dynamic NMF [7] and DTM [13]. Dynamic NMF [17] uses the state space to represent the NMF time dependence. The dynamic NMF first divides the corpus into time slices and then runs the NMF algorithm on the time window to obtain the topic of each time slice. After finding topics in each time slice, the dynamic NMF classifies semantically similar topics as dynamic topics. DTM is based on LDA but uses variational methods to connect topic variations in different time slices. Compared with Dynamic NMF, DTM has more continuity between adjacent time slices.

A significant limitation of these methods is their focus on trajectory topics within specific time intervals without accounting for temporal evolution at the model level. Dynamic topic modeling introduces time as a variable, allowing topic content to evolve. NMF and LDA have their dynamic counterparts, specifically Dynamic NMF and DTM. Dynamic NMF represents NMF’s temporal dependencies using state spaces, segments the corpus into temporal slices, and then runs the NMF algorithm over these time windows. After identifying topics within each time slice, semantically similar topics are categorized as dynamic topics. On the other hand, DTM, grounded in LDA, employs variational methods to link topic variations across distinct temporal slices, offering enhanced continuity compared to Dynamic NMF. Yao et al. [18], leveraging non-trajectory data from social media, developed a DTM for spatiotemporal sequence analysis. Specifically, they achieved dynamic topic analysis by covering adjacent temporal slices with radii from social media locational points. This approach bypasses trajectory point connections and computes trajectory topics at the individual point level.

In general, there is an issue of weak continuity in trajectory topics across slices when establishing a trajectory topic model. To address this problem, this paper introduces DTM into the analysis of dynamic trajectory topics for the first time, continuously tracking the evolution of trajectory topics through DTM. Additionally, by improving the Monte Carlo method to represent transition probabilities between trajectory segments, it constructs trajectory segment sequence information, providing more details for describing the evolution of trajectory topics.

2.2. Visual Analysis of Trajectory Topic

Visual analysis is often used to explore the inherent features and patterns encoded in trajectory data, because of the connection between humans and computers provided by interactive visual interfaces [19,20]. Topic visualization primarily revolves around the interrelationships among topic sets, encompassing the temporal evolution of topics and the static relations between them. The Theme River [21], an early visualization approach, is well-suited for analyzing topic evolution. While the fluid visual characteristics of the Theme River facilitate capturing change trends over time, its river-like curve metaphor poses challenges for quantitative analysis of topic attributes. In addition, Sankey diagrams are another standard visualization tool. They use rectangles to quantify topic evolution but can become crowded and complex when there is a multitude of topics. To overcome the above problems, the parallel matrix heatmap is employed for quantitative analysis of topic evolution, enabling the identification of trends in topic evolution. The visual feature of its neat arrangement allows for a clear and intuitive interpretation of visual information.

Methods for trajectory topic visual analysis merge geographical and visualization views, offering multi-level spatial information for trajectory topic pattern analysis. He et al. [22] incorporated LDA into trajectory topics to depict spatio-temporal topic variations, harnessing visual filters to mine spatio-temporal text data. Similarly, Chu et al. [8] employed LDA to dissect vast amounts of taxi trajectory data within cities, unveiling concealed knowledge through visualization. Similarly, Gao et al. [23] leveraged LDA to extract topics related to road cyclists’ behavior and movement semantics, adopting clustering and interactive visualization techniques to identify further clusters of similar cyclists and road segments within the city. By visualizing and retrieving taxi trajectory data, AL-Douhuki et al. [24] provide a semantic management approach for taxi trajectory data. Ali et al. [25] proposed a topic modeling approach grounded in LDA based on ontology, extracting topics and features by retrieving traffic content from social networks. Gao et al. [23] used LDA to extract the topics of cyclist behavior semantics and moving semantics on roads. Then, they implemented multiple interactive visual interfaces to facilitate the interpretation for analysts. Yan et al. [26] utilized a BTM to unearth latent topics within trajectories and subsequently analyze these topics via visualization.

Concerning trajectory points, Zhou et al. [27] and Liu et al. [1] implemented sampling strategies to reduce visual clutter, facilitating the discovery of trajectory patterns. Recognizing the large-scale nature of trajectory data, Zhou et al. [3] designed visual representations of Origin-Destination (OD) flows, iteratively probing OD movement patterns. Andrienko et al. [5] aggregated data to identify spatial similarities in trajectories and abstracted spatio-temporal features to delve into trajectory flows. Wang et al. [28] introduced a multi-scale geographical area data visualization method predicated on spatial attribute associations, enhancing visual perception of both global and detailed features. While these methodologies provide visual optimization at the trajectory point and line levels, investing considerable effort in visually exploring trajectory features, they fall short in contrasting spatial trajectory topic information and topic features between temporal slices.

In summary, to effectively explore the evolution of trajectory topics from different perspectives of trajectory points, trajectory lines, and trajectory topics using visual components, this paper proposes a multi-entity cascade visual analysis method under parallel views. This method aims to further reveal the potential patterns of dynamic trajectory topics by presenting the topic features through parallel abstract graphs and parallel heat matrices containing time series information. The parallel view overcomes the challenges of quantitatively analyzing topic river graphs and dealing with the complexity of crowded Sankey diagrams by organizing visual elements in a parallel layout and cascading the analysis of topic semantics. This study studies the construction and characteristics of dynamic spatio-temporal trajectory graphs to comprehend the evolution of dynamic trajectory topics.

3. Methods

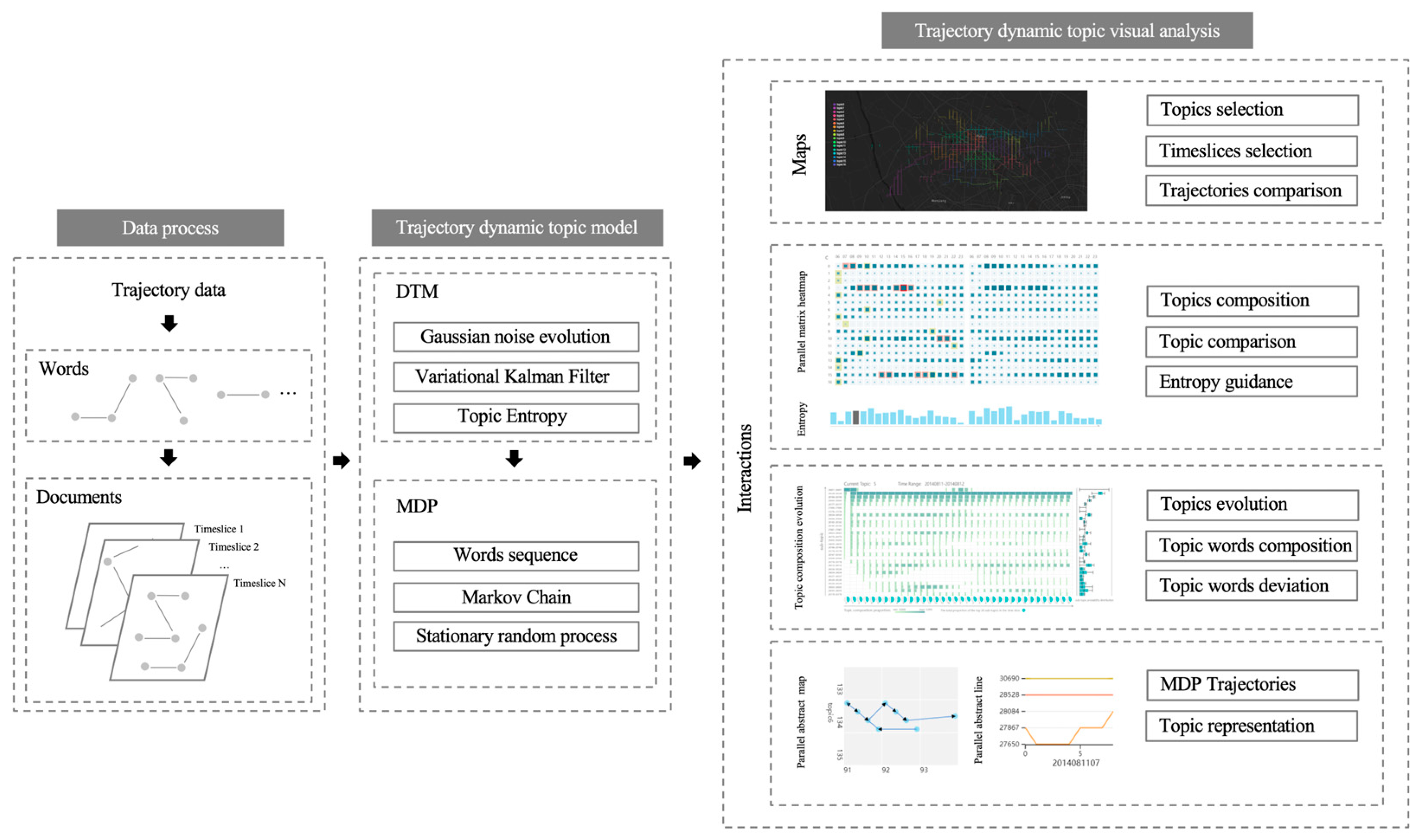
3.1. Overview

One of the challenges in trajectory topic modeling and analysis is effectively integrating both temporal and spatial information into the topic computation. To address these intricacies, our study employed three specific strategies.

First, concerning temporal information, we utilized trajectory segments partitioned based on specific time intervals to model dynamic trajectory topics. Given that the starting and ending points of trajectory segments are fixed, there is no ambiguity in trajectory words, meaning each trajectory word has a singular interpretation. Furthermore, the MDP generates trajectory sequences within the collection of trajectory segments representing a trajectory topic, ensuring that spatially discrete trajectory segments are interconnected. By leveraging these three strategies, we can efficiently compute trajectory topics imbued with both temporal and spatial dimensions. In the following sections of this chapter, we will delve deeper into these methodologies, providing a comprehensive exposition of their intricacies and applications.

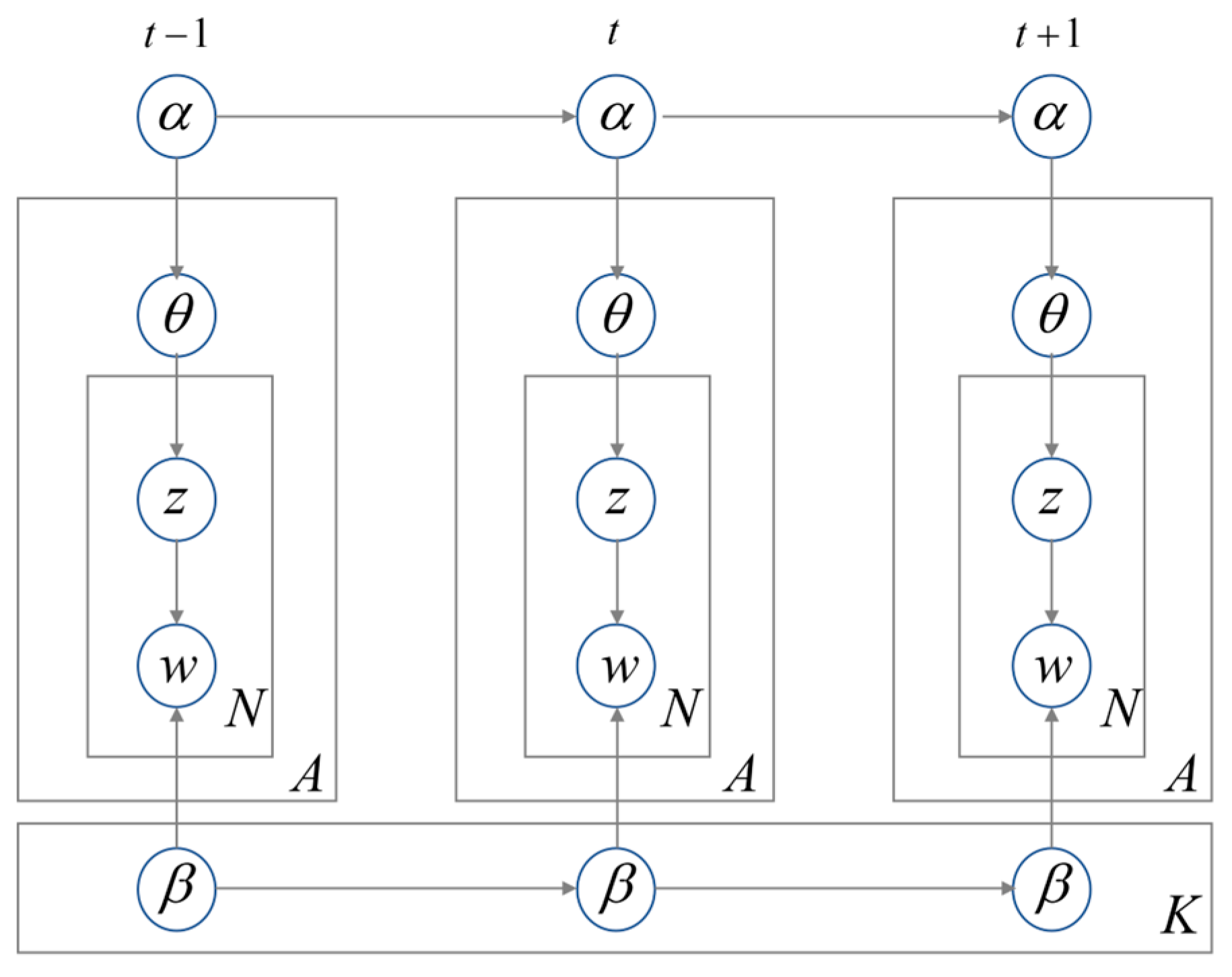
3.2. Trajectory Dynamic Topic Modeling

Topic modeling employs statistical methods to discern abstract topics within documents. When applied to trajectory information, it facilitates the extraction of abstract trajectory topics. The DTM, in contrast to conventional topic models such as LDA and NMF, incorporates temporal sequence information, making it particularly well-suited to the temporal variability inherent in trajectories. A study closely aligned with our approach is [9], where the authors employed NMF to topic-model trajectories across different time periods. However, such an approach lacks temporal coherence in trajectory topics. Compared to NMF, DTM offers superior coherence and yields more robust and flexible fitting results.

DTM treats the posterior distribution of the model parameters in the current time window as the conditional distribution for the parameters in the subsequent time window. Building upon the foundation of LDA by integrating a temporal dimension, DTM becomes especially adept at analyzing topic evolution. However, being a probabilistic model, DTM overlooks word order during its computational process. Such an oversight can be problematic, given that word order mirrors the sequential nature of trajectory segments. Our study addresses this limitation through an enhanced MDP, which we will delve into comprehensively in Section 3.3.

The trajectory DTM describes the trajectory motion pattern with time. In the DTM of traffic trajectory, we take the trajectory segment as a word and integrate the trajectory spatial information into the word. The trajectory data is divided according to time slices, with the latter moment evolving from the previous moment. Since the Dirichlet distribution is not suitable for use in time series models, as shown in Equation (1), a Gaussian noise evolved state space model is used to connect the natural parameter $\beta$ about the trajectory topic to sample the word distribution $\mathsf{\Phi }\left(Z\left(d_n\right)\right)$ about the trajectory topic $\mathrm{Z}\left(d_n\right)$. In Equation (2), the natural parameter $\alpha$ about the trajectory topic ratio is also connected using the Gaussian noise evolution state-space model to sample the trajectory topic distribution $\mathsf{\Theta }\left(d\right)$ of the generated trajectory document $d$. In the DTM model, the prior probabilities $\alpha$ for document topics and the distribution $\beta$ for topics are dynamically iterated.

$${\beta }_{t+1,k}|{\beta }_{t,k}\sim N({\beta }_{t,k},{\sigma }^{2}I)$$

(1)

$${\alpha }_{t+1,k}|{\alpha }_{t,k}\sim N({\alpha }_{t,k},{\delta }^{2}I)$$

(2)

Equations (1) and (2) link the natural parameters ${\beta }_t$ and ${\alpha }_t$ for each topic, where ${\beta }_t$ and ${\alpha }_t$ are the Gaussian noise natural parameters for time slice $t$ and topic $k$. $\sigma$ and $\delta$ are the variance parameters. After linking both the trajectory topic and its proportion distribution, we sequentially bind the collection of trajectory topic models. The corpus generation process for the trajectory DTM is as follows: Within time slice $t$, a possible word (trajectory segment) distribution $\beta$ for trajectory topic $k$ is first sampled. Then, a potential topic distribution $\alpha \left(t\right)$ for each document (a collection of trajectory segments) is sampled. For each document within time slice $t$, the topic distribution $\eta$ for document $d$ is obtained. For every word in the document during time slice $t$, the possible topic $z(t,d,n)$ for the nth word in document d is sampled, and the corresponding word $w(t,d,n)$ is generated. The number of topics is determined using an algorithm that identifies the optimal topic count based on perplexity. This generation process’s graphical model is illustrated in Figure 1. Both $\alpha$ and $\beta$ at time $t$ are generated based on $\alpha$ and $\beta$ at time $t-1$. Using time dynamics, the $k$th topic at slice $t$ smoothly evolves from the $k$th topic at slice $t-1$. When the horizontal arrow is removed, the graphical model is reduced to a set of separate topic models.

The goal of the trajectory DTM is to calculate the posterior distribution. The objective of the variational method is to optimize the free parameters of the distribution over latent variables, making the distribution closely approximate the true posterior in terms of Kullback–Liebler (KL) divergence and subsequently substituting it for the genuine posterior. Within DTM, a variational approach based on the variational Kalman filter approximation is utilized to compute the posterior distribution [13]. Entropy measures the average amount of information expressed in every allocation of a random variable, depicting the system’s level of disorder. We posit that when the system exhibits a low level of disorder, the trajectory topic is relatively stable. Conversely, with high disorder levels, the trajectory topics are relatively diverse. We compute the information entropy concerning topic probabilities within each time slice to provide information quantity across varying time slices, assisting in the subsequent selection of representative time slices for further analysis. The topic entropy at time $t$ can be expressed as in Equation (3), where $p$ represents the topic probability distribution at moment $t$.

$$H\left(t\right)=-{\sum }_{t=1}^K\left[p\right(t\left)\log p\left(t\right)\right]$$

(3)

3.3. Trajectory Dynamic Topic Generating

3.3.1. Sub-Trajectory Modeling

The trajectory dynamic topic consists of sub-trajectory sets that adhere to Markovian properties. Extracting representative trajectory sequences from these sub-trajectory sets embodies the trajectory topic. Trajectory segments illustrate transitions between states. Following a particular policy, the MDP can generate trajectory sequences within the dynamic topic sub-trajectory sets that adhere to the Markovian properties, representing the trajectory topic. A Markov chain depicts the random process of transitioning from one state to another and is a mathematical construct composed of a set of random variables. Sub-trajectory sets describe inter-regional transitions, fundamentally representing state transitions. We can characterize the transition relationships within these sub-trajectory sets using Markov chains. The trajectory topic is composed of the sub-trajectory set $E=\left\{e_1,e_2,\cdots ,e_n\right\}$. The set of areas for trajectory transitions form the state space $S=\left\{s_1,s_2,\cdots s_n\right\}$. A sub-trajectory $x_i$, transitioning from region $s_i$ to another region $x_j$, exhibits frequency characteristics. According to Markovian properties, the probability of moving from the current state to the next is only dependent on the current state, and not on prior locations, adhering to the following Equation (4):

$$\mathrm{P}\mathrm{r}\left(X_{n+1}=x|X_1=x,X_2=x_2,\cdots ,X_n=x_n\right)=\mathrm{P}\mathrm{r}(X_{n+1}=x|X_n=x)$$

(4)

where $\left\{X_1,X_2,\cdots ,X_n\right\}$ represents the random state sequence comprised of state space $S$. $P_r(X_{n+1}=x|X_n=x)$ represents the probability of the current state $X_n$ transitioning to the next state $X_{n+1}$. Given that the random process of the trajectory topic is a mathematical construct regarding the set of random variables of the sub-trajectory combinations, we can derive representative trajectories within the trajectory topic by constructing a Markov chain related to the sub-trajectory topic.

The Markov chain uses a probabilistic automaton to display transition probabilities between states, resulting in the transition matrix $P$. This matrix is a series of directed graphs, with edges representing the probability of transitioning from $S_n$ to $S_{n+1}$. Each state in the state space is included once as a row and a column, with the matrix indicating the probability of moving from a row state to a column state and the probabilities of each row summing up to 1. The steady-state distribution of the Markov chain, regarding the sub-trajectory set, aids in generating consistent trajectory sequences. Within the sub-trajectory set, the time-invariant Markov chain $\left\{X_n,n\ge 0\right\}$ of the transition matrix $P$ has its initial state space $S_i$, conforming to the probability distribution $\varnothing =\{{\varnothing }_0,{\varnothing }_1,\dots ,{\varnothing }_n\}$, satisfying the matrix Equation (5):

$$\varnothing =\varnothing P$$

(5)

where $\varnothing$ represents the steady-state distribution of the Markov chain, meaning a time-invariant Markov chain is wholly described by its initial state space $S_i$ and its transition matrix $P$. We simulate the trajectory topic’s initial state probability distribution ${\varnothing }_i$ and transition matrix against matrix Equation (5). As illustrated in Figure 2, the initial state of the sub-trajectories within the topic satisfies the stationary distribution, which can make the Markov process of the trajectory topic a stationary random process. As shown in Figure 2, the vertical axis is the probability of sub-trajectory state, and the horizontal axis is the number of iterations. Different colored line segments represent different trajectory segments. After approximately 60 simulation steps, a steady state is achieved under the action of the transition matrix $P$, with the distribution beginning to converge to a stable distribution at a certain point. Hence, the initial state of the sub-trajectory collection concerning the trajectory topic complies with the steady-state distribution. This implies that no matter the initial state of the trajectory, the equilibrium distribution will always be the same, achieving a stable initialization. The MDP concerning the sub-trajectory becomes a stationary stochastic process, meaning its finite-dimensional distributions are translation-invariant. This can further generate stable Markov sequences that represent the trajectory topic.

3.3.2. Trajectory Sequence Generating

The MDP elucidates the decision-making aspect of state transitions within Markov sequences. Within the sub-trajectory sets of the trajectory topic, transitions between sub-trajectories adhere to Markovian properties. Representative trajectory sequences within the trajectory topic can be generated using the MDP. This sequentially decided representative Markov sequence can serve as a succinct representation of the trajectory topic.

Formally, the MDP concerning the sub-trajectory set can be represented by the tuple $<S,A,R,P,\pi >$. The state $S={\{s}_{1,}{s}_2,\cdots ,s_n\}$ signifies the set of regions for trajectory transitions. The action space $A=\left\{a_1,a_2,\cdots ,a_n\right\}$ depicts transitions between states, essentially forming the starting point $S_i$ and endpoint $S_j$ of a sub-trajectory. The reward $R$ reflects the reward achievable when transitioning from one state to another within the action space. As illustrated by Equation (6):

$$R=\left(1+k\right)P-k{L}_p$$

(6)

the reward value $R$ is composed of two components, specifically the transition probability $P$ and the penalty term $\mathsf{\Phi }$. The penalty term $\mathsf{\Phi }$ is composed of hyperparameters $k$ and $L_p$. Our aspiration is for the target sub-trajectory segment to maintain a relatively consistent speed, fluctuating within a certain speed range. As presented in Equation (7):

$$L_p=|V-V_{bm}|\times {\left({\sum }_{i=0}^N{v}_i-v_{{bm}_i}\right)}^{-1}$$

(7)

the objective of establishing the penalty term $L_p$ is to curtail trajectory segments with substantial speed deviations. Consequently, we obtain the time slices of the trajectory dynamic topic and the preset number of trajectory segments $N$ to compute the baseline speed $V_{bm}$. Subsequently, trajectory segments with significant deviations are penalized. The transition probability $P:S\times A\times S\to \left[\mathrm{0,1}\right]$ expresses the probability of an action transitioning from one state to another. The essence of the policy $\mathsf{\pi }$ is to maximize the reward for each action. Specifically, $\mathsf{\pi }$ commences from a stable steady-state initial condition. During each trajectory transition, it randomly selects actions based on the transition probability, conducts finite dynamic lookups, and eventually attains the Markov sequence representing the trajectory topic.

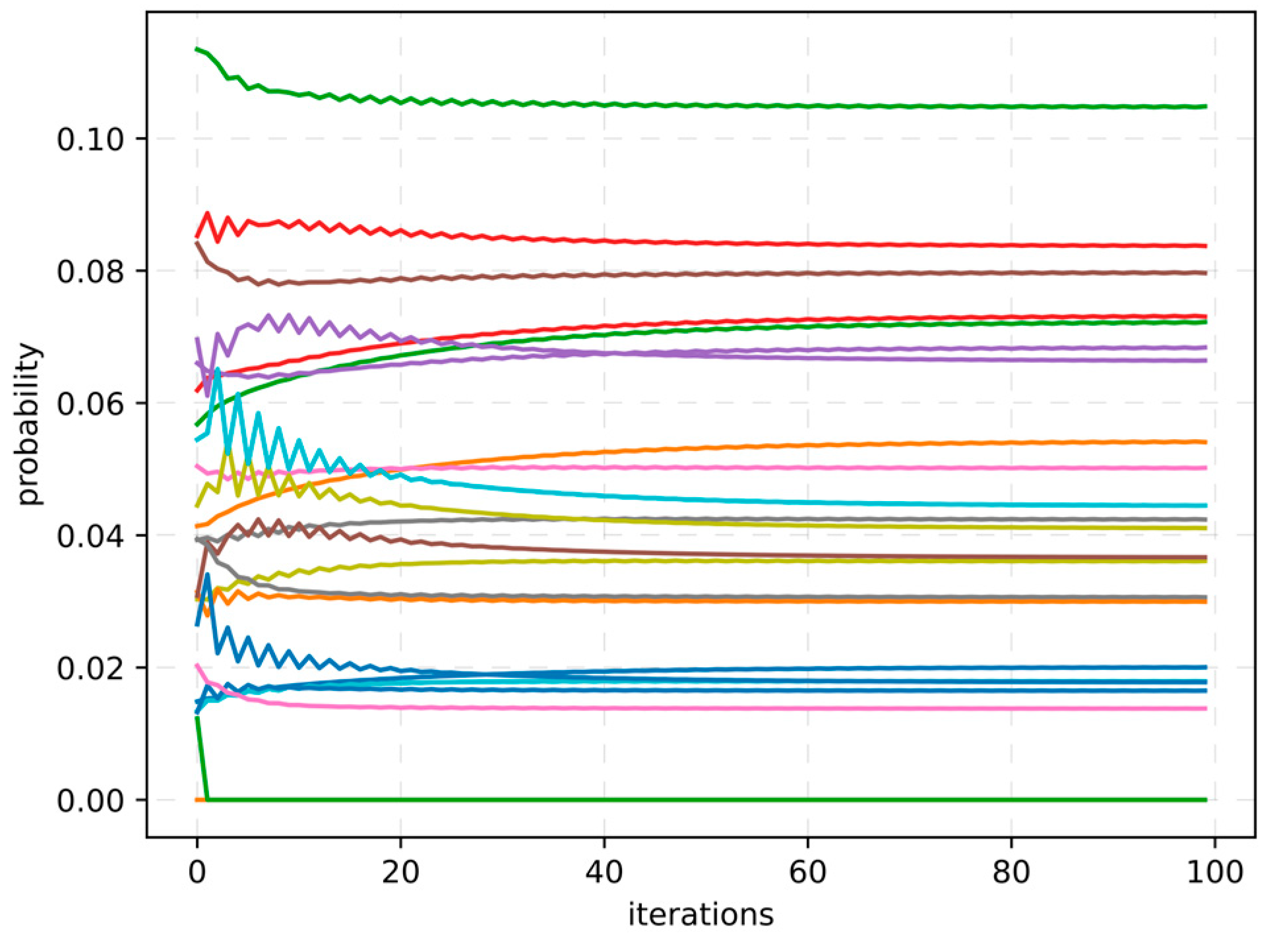
3.4. Data Set and Hyperparameter Settings

We chose taxi trajectory data from Chengdu as our experimental dataset for our study. This dataset comprises approximately 14,000 taxi-formatted trajectories commonly used for trajectory research. The dataset includes vehicle ID, latitude, longitude, passengers, date, and time attributes from 3 August 2014, to 30 August 2014 [29]. Before running the trajectory dynamic topic modeling, we calculated, on an hourly basis, the hyperparameters suitable for the DTM on this data. We employed perplexity and coherence to guide the acquisition of the optimal topic number. A lower perplexity indicates better topic performance. Coherence computation measures the consistency of words constituting a topic. A higher coherence score means topic words reinforce each other, enhancing the interpretability of the topic. Figure 3 describes the consistency score results of the experimental dataset. After evaluating the performance of all measurement metrics, we settled on 17 as the number of topics to be computed.

4. Visual Design

From a spatiotemporal perspective, we aim to dissect the composition and evolution of trajectory topics. The visual analysis of dynamic trajectory topics presents challenges. First, the dynamism of trajectory topics requires an intuitive representation through visualization, showcasing sequential changes across time and space. Secondly, given that dynamic trajectory topics are expressed as a series of trajectory word sets, a need arises to envisage the three-dimensional sequential evolution information linking time intervals, trajectory topics, and topic words.

We introduce the Parallel Viewport Visualization method for dynamic trajectory topic analysis to address these challenges. This technique provides a clear depiction of the dynamic shifts in trajectory topics through its parallel temporal visualization module and abstract map correlation module. This section delves deeper into the visualization technique for analyzing dynamic trajectory topic models.

4.1. Trajectory Dynamic Topic Time Evolution Analysis

The evolution of trajectory topics necessitates a compelling portrayal of their progression over time, offering a visual glance of the topic components. The information regarding the evolution of dynamic trajectory topics is embedded across multiple temporal slices, spanning various topics, each bearing its temporal evolution of topic words. This calls for an efficient visualization encompassing the three-dimensional data related to time, topic, and topic words. We calculated the topic distribution for each time slice and the evolution of specific topics between different time slices. We further assessed the information content of time slices and topics using entropy calculations. As illustrated in Figure 4, trajectory dynamic topic calculation consists of three parts. First, the original trajectory data is processed into a time-slice document composed of trajectory words, and then the trajectory dynamic topic is obtained by DTM and improved by MDP. Finally, the spatial and temporal evolution information of the trajectory dynamic topic is analyzed through the map view, parallel abstract map, and parallel matrix heatmap.

While topic river plots are a conventional tool to visualize topic transitions, their curve estimations can introduce visual uncertainties. Thus, it becomes essential to sidestep visual biases stemming from visual encoding. To overcome these problems, we adopted the parallel matrix heatmap on cascade analysis. Comprising two parallel heatmaps and associated components, it facilitates efficient visual searches of dense three-dimensional information within a visually organized layout.

Figure 5C’s topic evolution heatmap and Figure 5E’s topic word heatmap form the parallel matrix heatmap, offering a concise and intuitive representation of time-topic and time-topic word information. The hierarchical construction of the time-topic and time-topic word cascade analysis allows for interaction across different hierarchical levels. In Figure 5C’s heatmap, the x-axis denotes time, and the y-axis represents topics, with rectangle sizes encoding the composition of trajectory topics for corresponding time slices. To optimize exploration, we outlined rectangles with the highest probabilities in each row and column to swiftly pinpoint representative sub-topics. To reduce user interaction time when selecting the target trajectory’s time slice, we computed the entropy of topics for each time slice, aiding users in choosing meaningful topic time slices, and displayed entropy values using bar charts on the right side of the heatmap. Similarly, the entropy of each topic was computed for target topic selection and was represented by using bar charts above the heatmap.

Within the dynamic trajectory topic, topic words constituting the topic would evolve over time. As depicted in Figure 5E’s topic word heatmap, the evolution of the topic components is described by the changing proportions of topic words. Specifically, the heatmap elements were shifted from the center-expanding rectangles to left-aligned, right-expanding rectangles to facilitate clearer vertical comparisons among topic words within the same category. Typically, the x-axis of the topic word heatmap represents time, and the y-axis represents the topic words constituting the topic. For this study, we chose to display the top 35 topic words based on probability rankings, with their respective proportions among all topic words represented by a pie chart below. One can select topics of interest from the topic evolution heatmap to update the topic word heatmap, thus achieving cascade analysis concerning time, topics, and topic words.

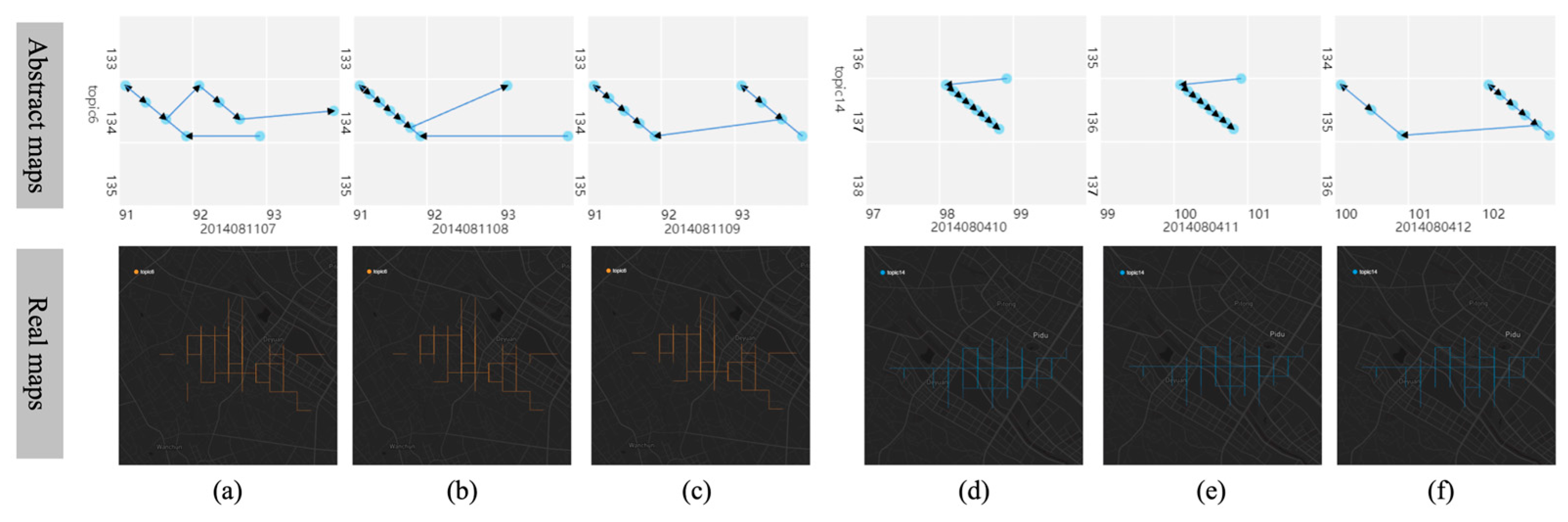
4.2. Spatial Evolution Analysis of Trajectory Dynamic Topic

Exploring trajectory topics through maps provides a spatial perspective on the features inherent to such trajectories. A trajectory topic is not just a solitary line but also a complex mosaic comprising numerous sub-trajectory segments. It is much like deciphering the narrative of a tale that unfolds across different periods in time, spotting the changes in topics between time slices, and comparing the alterations within these sub-trajectory segments. In our quest to extract the essence of these trajectory topics, we have crafted parallel abstract maps. Just imagine running the MDP on sub-trajectory segments within time slices. This allows us to gauge transition probabilities, eventually leading us to a trajectory sequence that truly captures the spirit of the overarching trajectory topic. This spatial data is about geographical coordinates and the sequence in which they are arranged. Abstract maps convey the trajectory topics by depicting the spatial relative positions of trajectory points. Utilizing parallel windows in abstract maps allows for presenting the evolutionary information of trajectory topics from both temporal and spatial dimensions. This offers an intuitive comparison of representative trajectory sequences across different periods and topics.

As illustrated in Figure 5D’s parallel abstract map, the horizontal axis represents time, while the vertical axis signifies topics. Users can select their areas of interest in the topic evolution heatmap to update the parallel abstract map, facilitating an analysis of trajectory topic evolution. This multi-instance comparison of spatial information effectively highlights the differences among trajectory sequences. Furthermore, to counteract the loss of spatial sequence information due to the overlapping trajectories on the map, we utilize a topic trajectory segment line chart to represent the trajectory topic sequence details. This chart conveys the order and composition of trajectory segments related to specific topics, offering insights into the relationship between trajectory sequences and their corresponding topics. Additionally, users can select topics of interest within the parallel abstract map to refresh the actual map, delving deeper into the detailed information of the trajectory topics.

5. Case Study

In the process of modeling transportation trajectory data, we adopted a trajectory DTM that considers topic evolution. This facilitates the extraction of dynamic trajectory topics and their subsequent evolutions. The target audience for this dynamic trajectory topic analysis includes those keen on understanding regional vehicle traffic patterns, such as urban planners and optimization specialists.

To demonstrate the efficacy of our methodology in the domain of dynamic trajectory topic analysis, we conducted a case study based on taxi data from Chengdu. This data spans 28 days, yielding 5,184,637 trajectory sequences after data cleaning. The granularity of analysis is correlated with the number of topics; the greater the number of topics, the finer the details within each topic. For this case, we defined 17 topics, with a minimum of 6 iterations for LDA, and set $\alpha$ to 0.01 to compute the dynamic trajectory topics.

5.1. Trajectory Topic Evolution Analysis

There are noticeable differences in trajectory topics within the same time slice. A single time frame encompasses multiple trajectory topics, each exhibiting varying intensities. Figure 5B illustrates the trajectory topic map at 7 a.m. on 11 August 2014, where most topics exhibit localized distributions. Having discerned the spatial distribution of trajectory topics, it is imperative to delve deeper into topic evolution over time.

5.1.1. Spatial Evolution of Trajectory Topics

There are significant differences between the trajectory segments that form trajectory topics at different time slices in the map. Before comparing the spatial evolution characteristics of the trajectory topics, we need to determine the target time slice. In Figure 5C, the topic evolution heatmap offers a vertical perspective, revealing different topic probabilities within identical time slices. The entropy for time slices 07 and 23 on 11 August 2014, is relatively low, signifying minimal differentiation among the topic probabilities and, consequently, a smaller information content. In contrast, the entropy for time slices 11 and 15 on the same date is markedly higher, with apparent disparities in topic probabilities, translating to more extensive information content.

The composition and location of trajectory segments within different trajectory themes vary across time slices. Based on the discussion above about the entropy of time slices, we select the 07 time slice to examine the spatial evolution of trajectory topics. As depicted in Figure 6, a comparative analysis of topics 3 and 12 over consecutive time frames demonstrates an uptrend in trajectory segment count with increasing topic probability.

5.1.2. Trajectories Topic Time Evolution

The information entropy of trajectory topics shows distinct differences across different time slices. One can examine the evolution of specific topics by observing Figure 5C’s heatmap from a horizontal perspective. The bar chart on the right of Figure 5C shows the information entropy of topic evolution. Topic entropy is used to indicate the amount of trajectory topic information. Topic 8 can be seen to have the smallest information entropy because topic 8 has the smallest probability and little evolutionary difference. Topics 3 and 15 have high entropy due to the significant change in topic probability during the evolution of these topics. Further, we can analyze the trajectory topic evolution at the topic word level. Figure 7 shows the composition evolution of trajectory words between trajectory topic 8 and trajectory topic 10 from “20140811” to “20140812”. The topic entropy of trajectory topic 8 is smaller than that of trajectory topic 10. That is, the change degree of topic words of trajectory topic 8 is smaller than that of trajectory topic 10. This also indicates that the number of trajectory words required to form trajectory topic 8 is smaller than those required for trajectory topic 10.

5.2. Trajectory Topic Sequence Analysis

The trajectory sequence reflects the movement patterns within the trajectory topics. The trajectory sequence is generated through the improved MDP, incorporating the spatial information of trajectory words, and represents the most representative trajectory sequences within the trajectory topics. In computing trajectory topics, the trajectory sequences have been simplified by partitioning the map into grids. Concentrating trajectories within these grids facilitates the generation of trajectory sequences. This method transforms trajectory sequences into movements within a grid and between grids. We believe that movements within a grid are significant because, in the original data entries, a vehicle might not travel a great distance, and not in all records does a vehicle’s movement span across grids. Figure 8 displays the representative trajectory topics generated through an enhanced MDP, presenting an overview of the topics using an abstract map approach. Due to scenarios in the computational data where vehicles move within a single grid, sequences of movements within a single grid arise, as illustrated in Figure 8d,e. This reflects real situations present in the trajectory data. Additionally, trajectory sequences generated over time in topics 6 and 12 can supplement the trajectory direction information on the map, indicating the most probable movement patterns under that time’s trajectory topic.

6. Discussion

The core of the dynamic trajectory topic model is the evolution of trajectory topics. Compared to previous works on trajectory topic computation [2,9,11,14,18], this study introduces a method for the temporal evolution of topics. This method facilitates dynamic trajectory topic analysis by connecting the model parameters to the topic models of adjacent windows. It is more suited to real-world scenarios than matrix factorization-based trajectory topic analysis methods such as NMF.

The order of topic words is an essential component of the semantic structure in dynamic trajectory topics. Moreover, while the topic model is a probabilistic model regarding the composition of topic words, previous works did not consider the relationships between topic words, that is, the sequence of trajectory segments. In this study, an enhanced MDP, grounded on the probabilities of topic words, is introduced for generating representative trajectory sequences under specific trajectory topics. Our approach preserved the original data characteristics without imposing intricate feature constraints on the applied trajectory dataset. We hope this method can inspire similar research to focus on the inherent features of trajectory data and the continuity of trajectory information in the real world. However, there are certain limitations to our study. During the computation of dynamic trajectory topics, due to computational constraints inherent to the LDA model, a significant number of computational resources is required when fitting the LDA. Furthermore, there is a need to explore new trajectory point aggregation methods to compress the original trajectory point data for more efficient sequences.

7. Conclusions

A dynamic topic analysis approach for traffic trajectory data was proposed in response to the issue of existing trajectory visualization analysis methods overlooking the temporal evolution of trajectory topics. This facilitates the visual exploration and analysis of traffic trajectory topics and their evolution. Initially, the DTM is employed to characterize the dynamic topics of trajectories, seamlessly integrating both temporal and spatial information into the DTM. Subsequently, we propose an enhanced Markov decision process to generate topic trajectory sequences, thereby incorporating trajectory sequence information into the trajectory topics. Following this, visual views designed based on parallel windows are introduced for exploring the evolution of trajectory topics. The objective is to convey information about dynamic trajectory topics through concise and intuitive visualization components. Ultimately, the efficacy of our methodology is illustrated through a case study focusing on the evolution of trajectory topics.

Since the trajectory dynamic topic model algorithm is based on a variational method to fit a posteriori distribution, there is room to enhance its computational efficiency. In the future, we plan to improve the efficiency of the dynamic trajectory topic model algorithm by adopting distributed learning algorithms, such as federated learning. Moreover, future research could explore the patterns and relationships of dynamic trajectory topics within and outside grids under various grid partitioning methods and investigate efficient and compact visualizations of spatiotemporal trajectory features.