Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling
Abstract
1. Introduction
- Calculating the largest estimated domain of attraction (LEDA) based on the linear matrix inequality (LMI) method and optimization modeling, which accurately characterizes the system’s stability boundary.
- Applying parameter sensitivity analysis to the LEDA, thereby revealing the influence of parameter variations on system stability. Based on this, a parameter optimization design method is proposed, where the LEDA is used to determine the parameter range that ensures system stability.
2. The Modeling of Grid-Connected RPGS
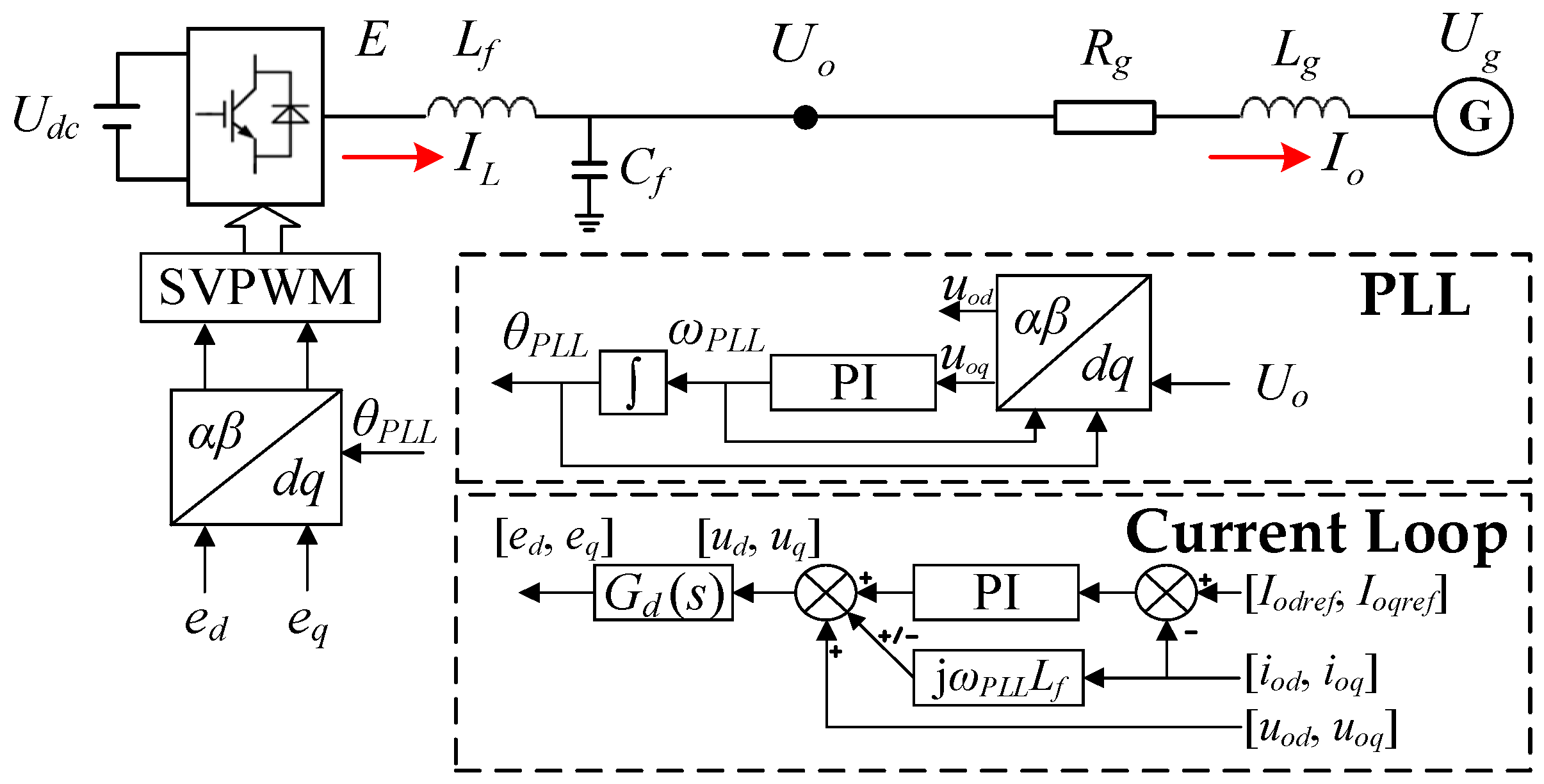
2.1. System Structure and Parameters
2.2. State–Space Modeling of the Grid-Connected RPGS
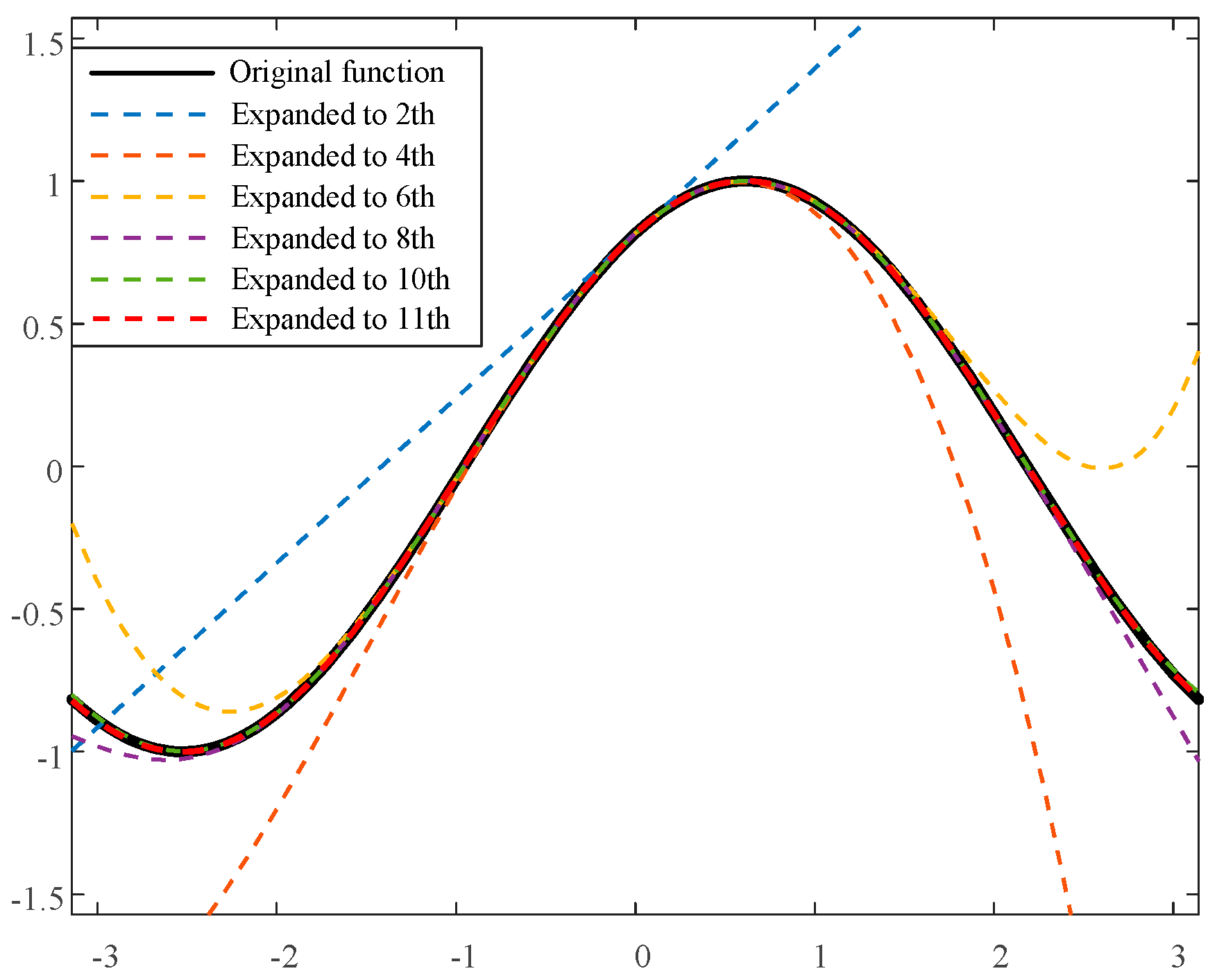
2.3. Model Order Reduction and Accuracy Analysis
Reduced-Order Model
- The non-critical influencing factors, such as LC filters, control delays, and feed-forward effects, are neglected.
- The bandwidth of the PLL is much smaller than that of the current loop. Hence, it is assumed that [Iod, Ioq] approximately tracks the current loop set values [Iodref, Ioqref] in real time.
3. Transient Stability Analysis of Grid-Connected RPGS
3.1. Construction of LEDA Based on LMI Optimization Method
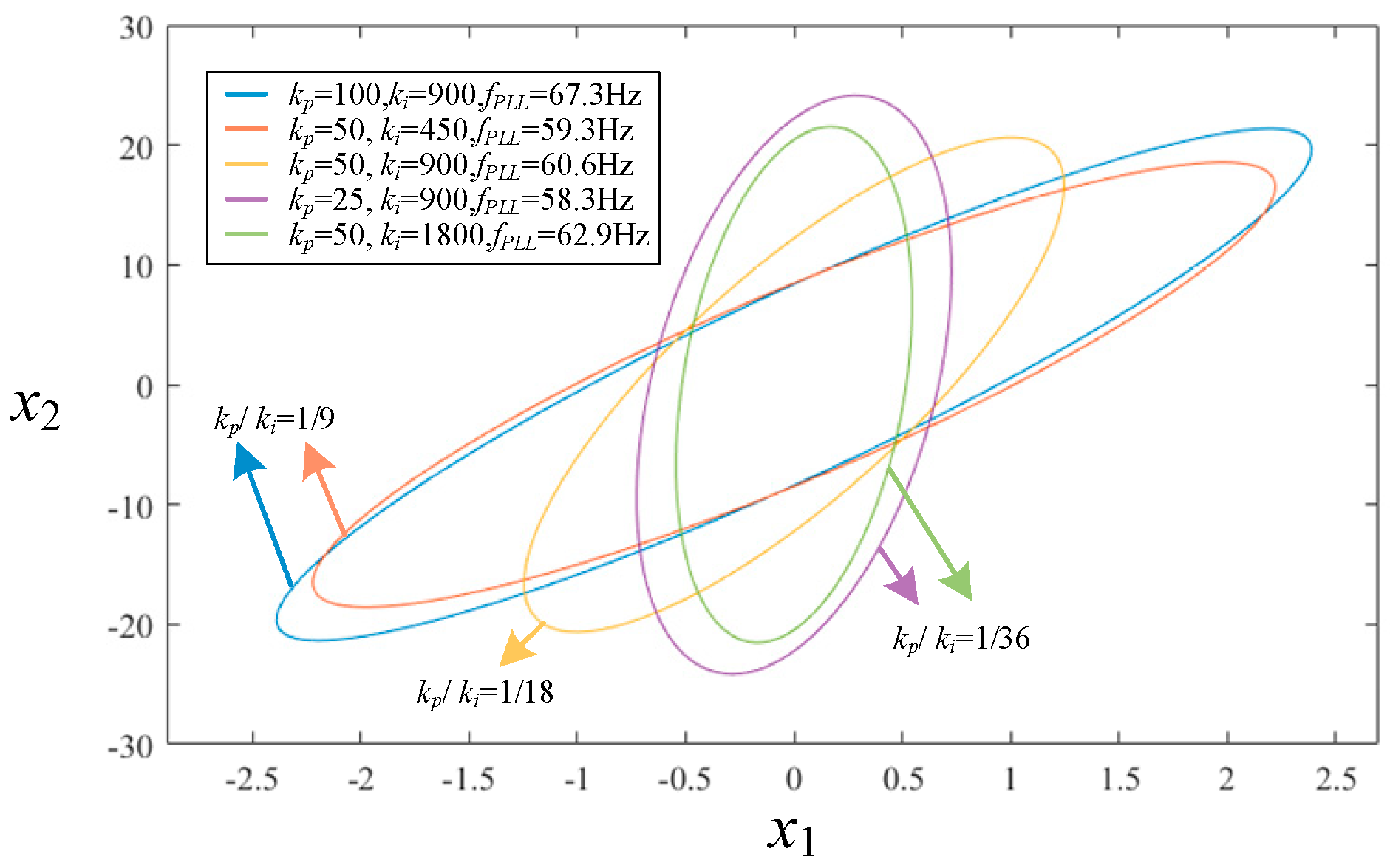
3.2. Analysis of the Correlation of LEDA and System Parameters
3.3. Verification of the Correlation of LEDA and Parameters
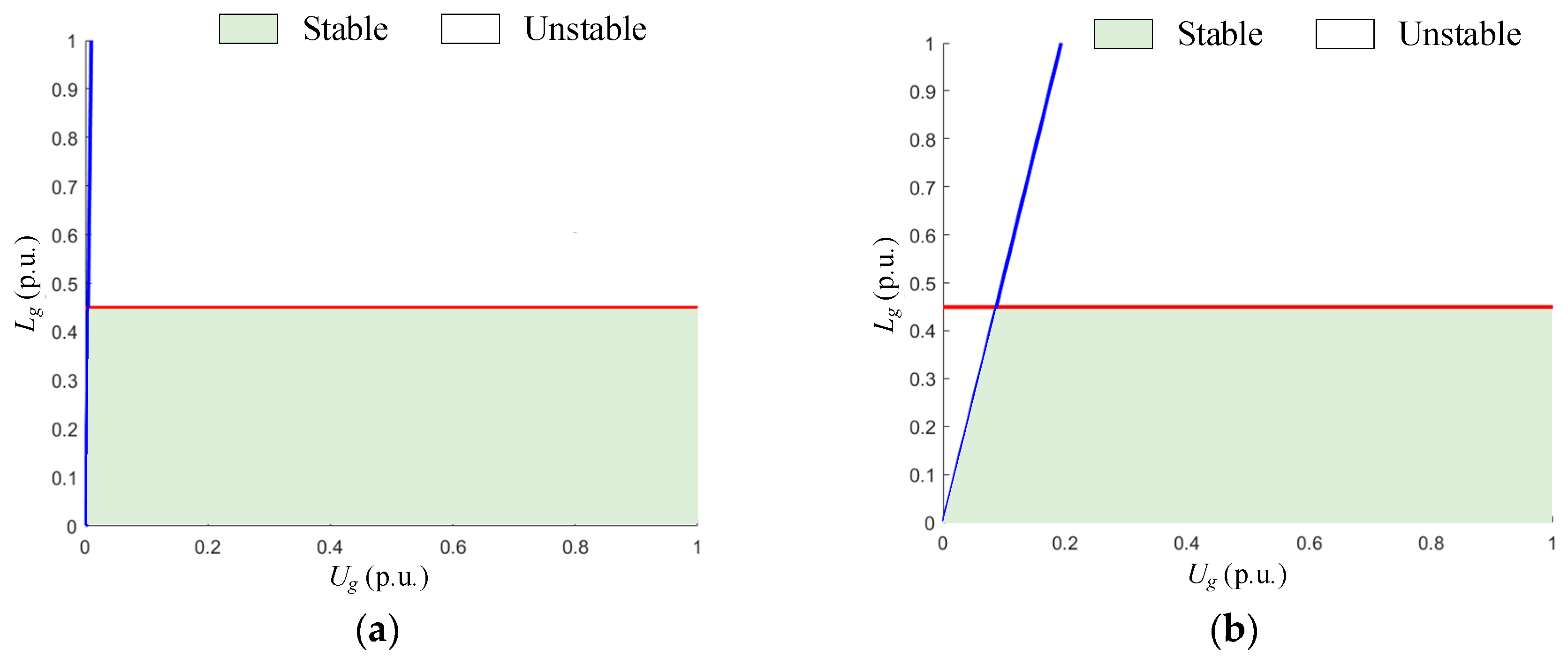
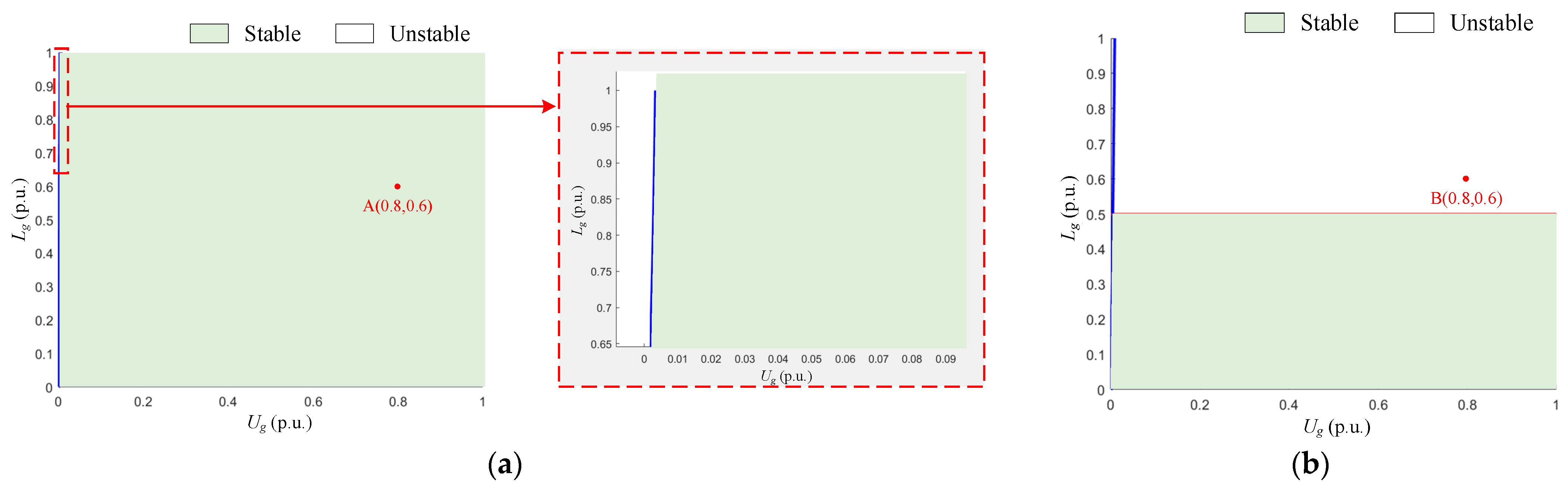
3.3.1. Line Inductance Lg
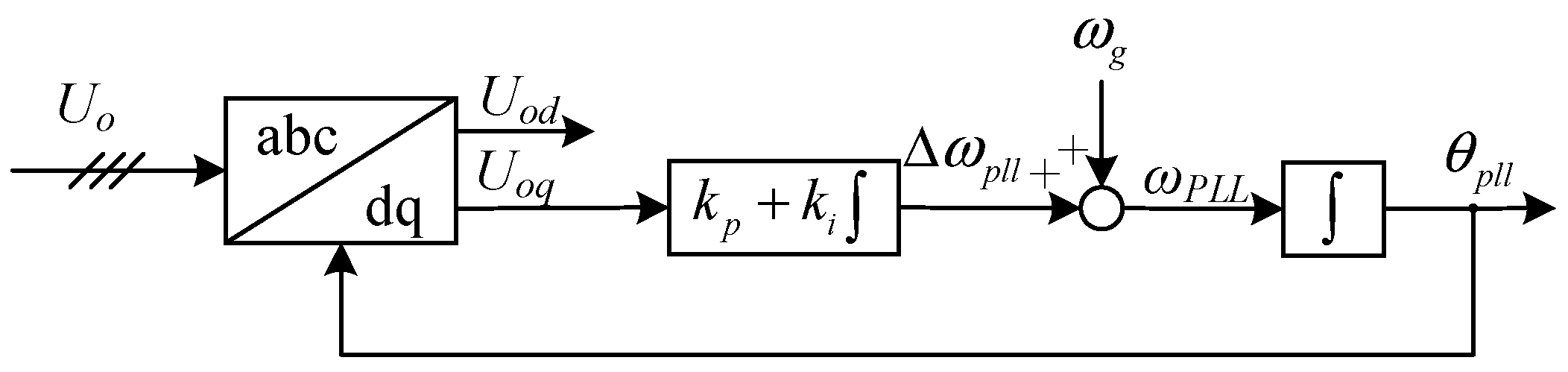
3.3.2. Control Parameters of PLL
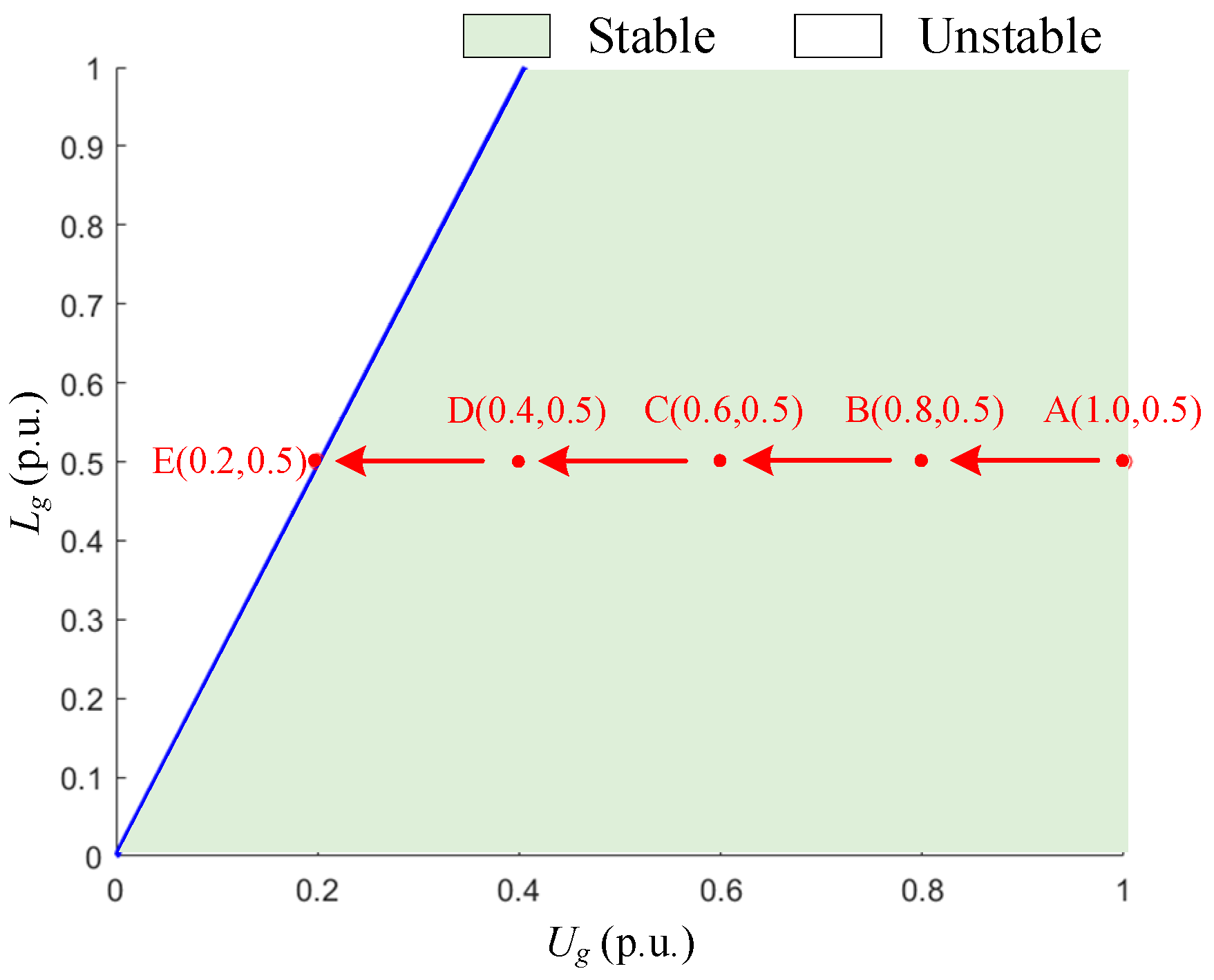
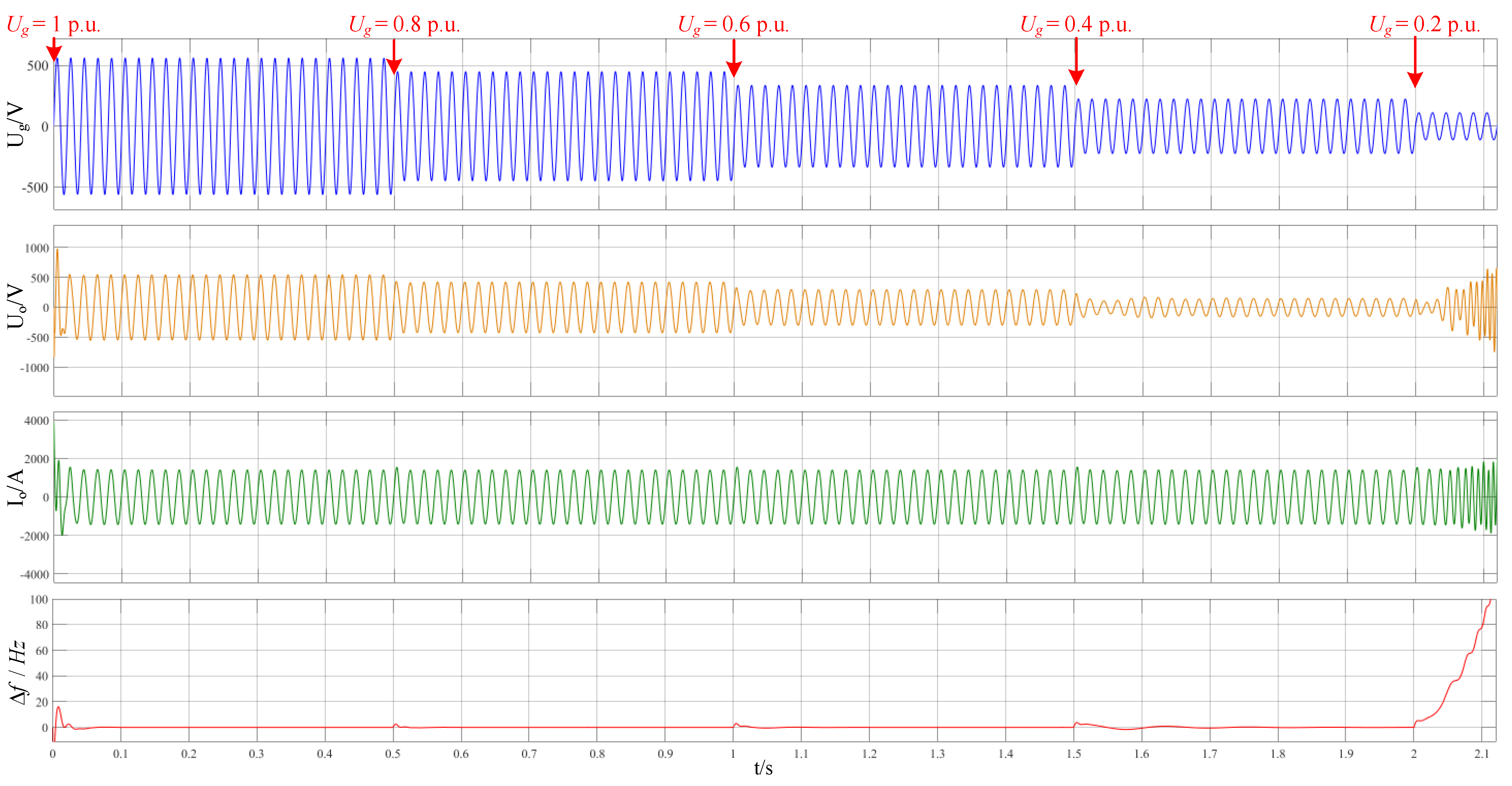
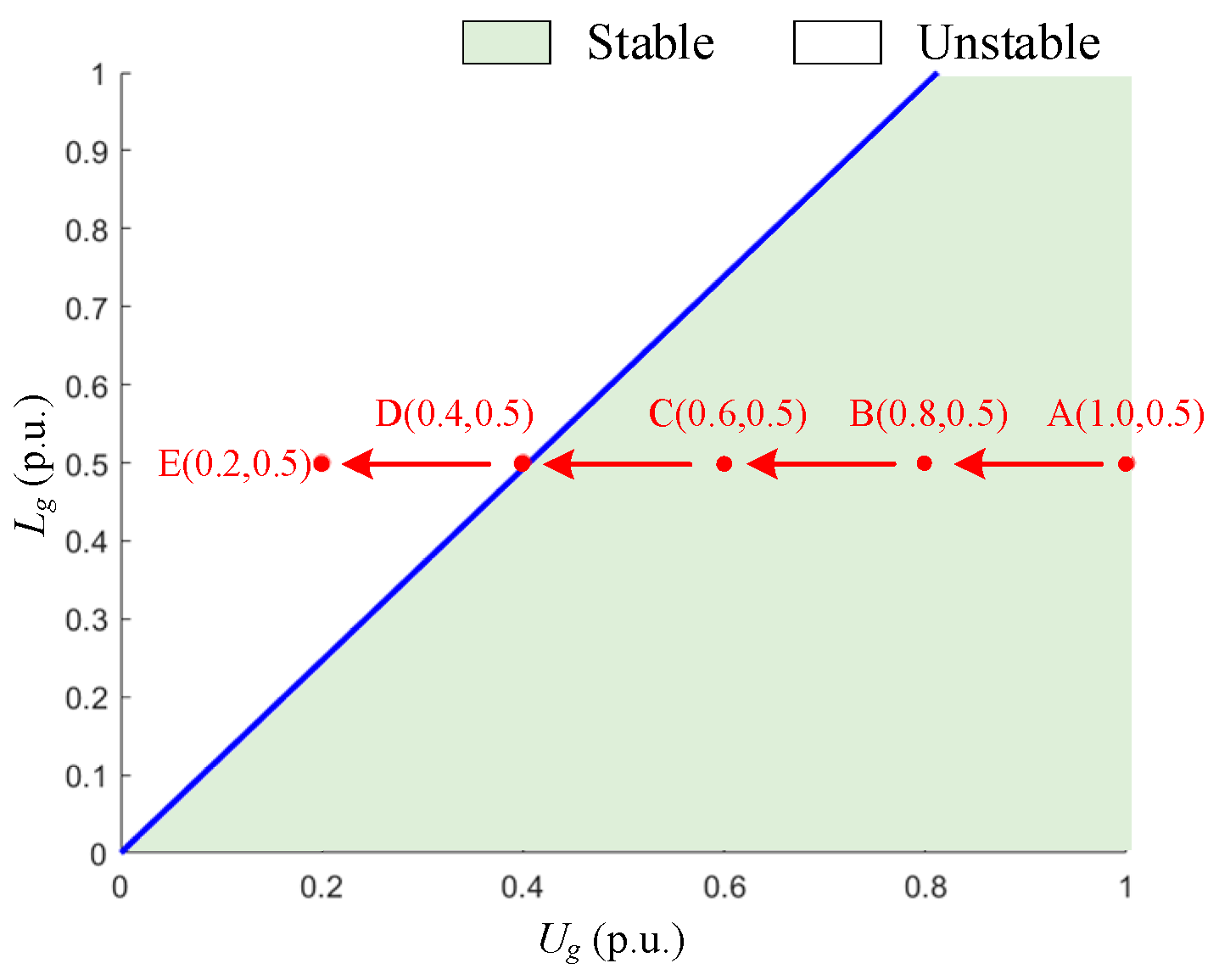
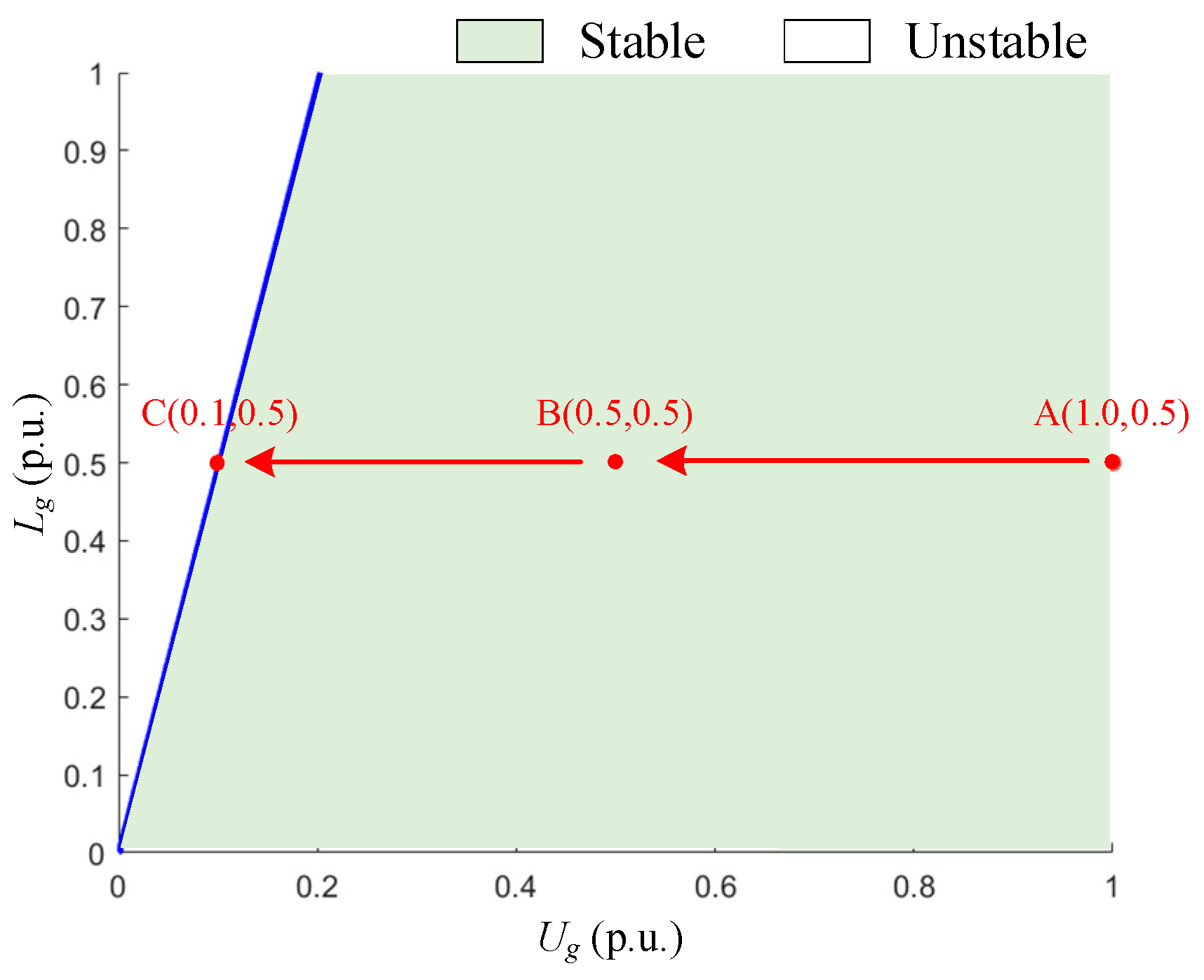
3.3.3. Grid Voltage Ug
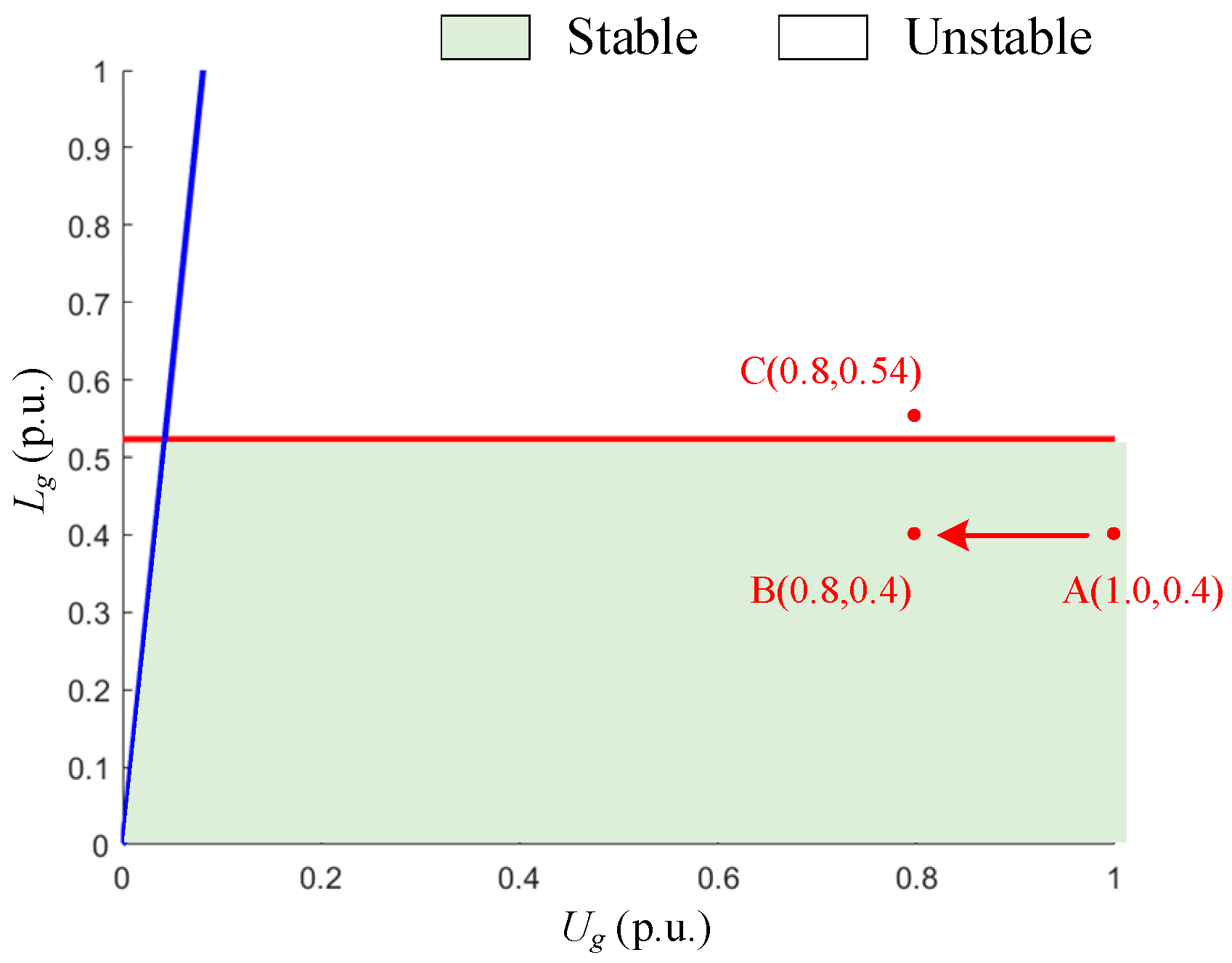
3.4. Analysis of Feasible Region of Parameters
4. Real-Time Simulation Study
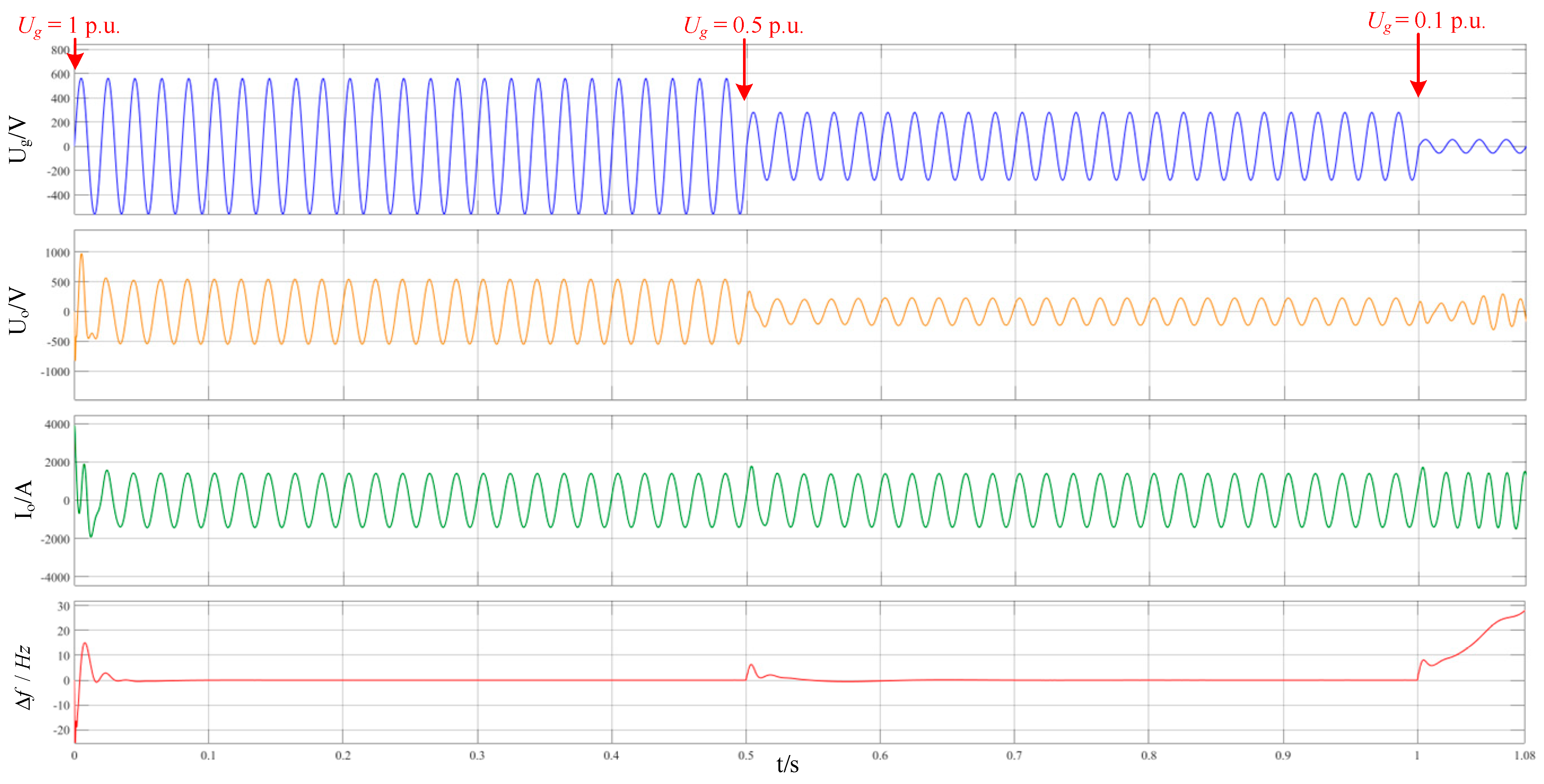
4.1. HIL Simulation Analysis Under Grid Voltage Drop
4.2. HIL Simulation Analysis of Different PLL Proportional Coefficients
4.3. HIL Simulation Analysis of Different PLL Integral Coefficients
4.4. HIL Simulation Analysis Under Different Grid Line Impedance
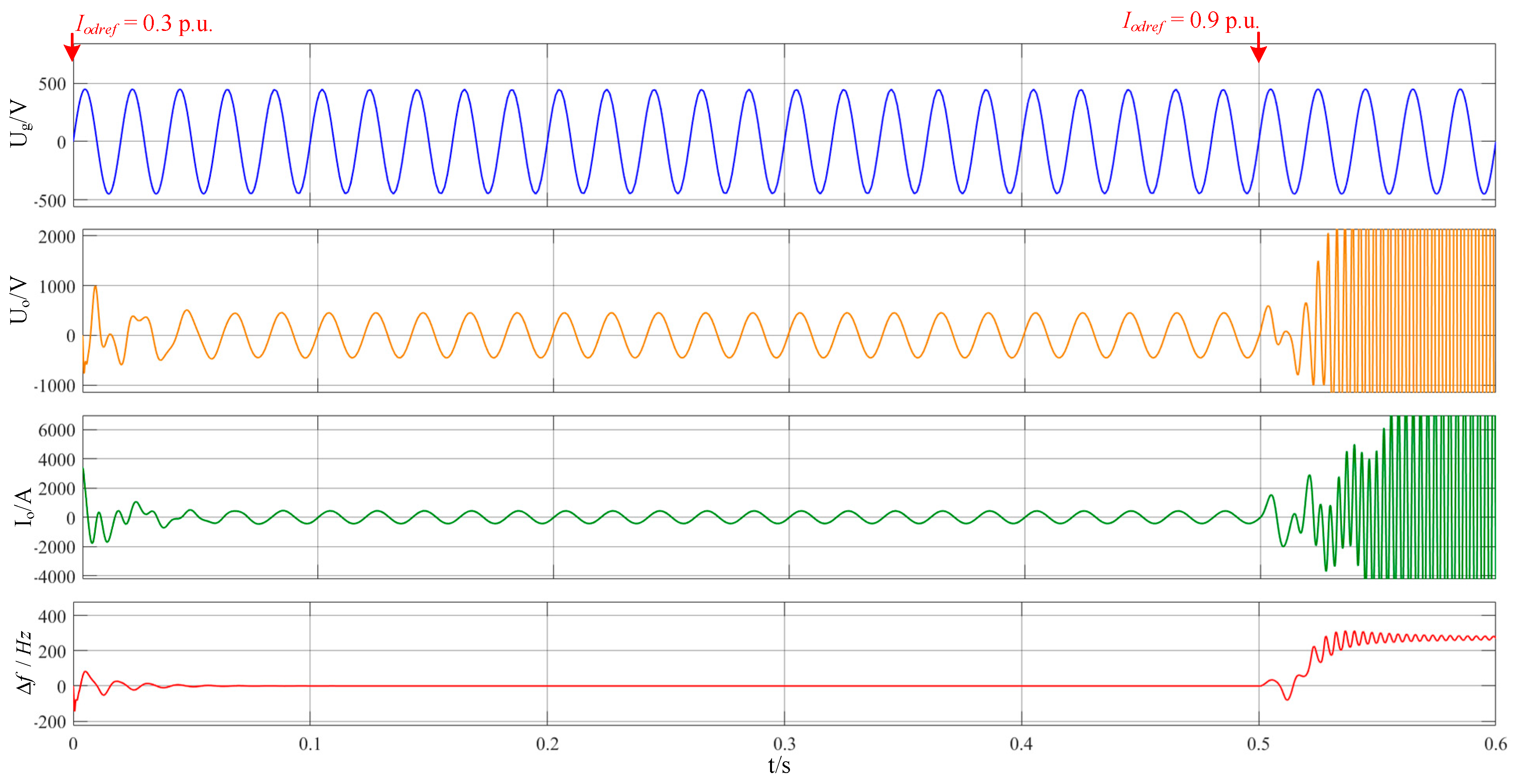
4.5. HIL Simulation Analysis of Different d-Axis Current References at the Grid Connection Point
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Sn | Rated capacity |
| Un | Rated voltage |
| fn | Rated frequency |
| Tv | Filter time constant |
| Td | Controller delay |
| Gd(s) | Control delay transfer function |
| Udc | DC-side voltage of the inverter |
| E | Port voltage of the inverter |
| Uo | Grid connection point voltage |
| Ug | Grid voltage |
| Io | Grid connection point current |
| IL | Inductive current |
| Lf | Inductance of the LC filter |
| Cf | Capacitance of the LC filter |
| Rg | Equivalent resistance between the grid connection point and the grid |
| Lg | Equivalent inductance between the grid connection point and the grid |
| θPLL | Phase angle determined by the PLL |
| θg | Grid phase angle |
| Δω | Difference between the phase angle of the PLL and the grid |
| ωPLL | PLL angular frequency |
| ΔωPLL | Difference between the angular frequency of the PLL and the grid |
| ωg | Grid angular frequency |
| fPLL | PLL bandwidth |
| ξ | Damping ratio of PLL |
| ωn | Undamped natural frequency of PLL |
| [uod, uoq] | dq-Axis components of the output voltage |
| [ed, eq] | dq-Axis components of the current loop output |
| [Iodref, Ioqref] | dq-Axis components of the current loop set values |
| [igd, igq] | dq-Axis components of the grid current |
| [iod, ioq] | dq-Axis components of the output current |
| [iLd, iLq] | dq-Axis components of the filter output current |
| [kp, ki] | PI coefficient of the PLL |
| [kpc, kic] | PI coefficient of the current loop |
| xfull | State variables |
| A | Jacobian of the polynomial system |
| W | Positive definite symmetric matrix |
| De | Damping of the system |
| He | Energy function |
References
- Cepeda, J.C.; Rueda, J.L.; Colomé, D.G.; Echeverría, D.E. Real-time Transient Stability Assessment Based on Centre-of-inertia Estimation from Phasor Measurement Unit Records. IET Gener. Transm. Distrib. 2014, 8, 1363–1376. [Google Scholar] [CrossRef]
- Azmy, A.M.; Erlich, I. Impact of Distributed Generation on the Stability of Electrical Power Systems. In Proceedings of the IEEE Power Engineering Society General Meeting, San Francisco, CA, USA, 12 June 2005; pp. 1337–1344. [Google Scholar]
- Ndreko, M.; Rüberg, S.; Winter, W. Grid Forming Control Scheme for Power Systems with up to 100% Power Electronic Interfaced Generation: A Case Study on Great Britain Test System. IET Renew. Power Gener. 2020, 14, 1268–1281. [Google Scholar]
- Poulose, A.; Kim, S. Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids. Energies 2023, 16, 2495. [Google Scholar] [CrossRef]
- Zhang, Q.; Mao, M.; Ke, G.; Zhou, L.; Xie, B. Stability Problems of PV Inverter in Weak Grid: A Review. IET Power Electron. 2020, 13, 2165–2174. [Google Scholar] [CrossRef]
- Tian, X.; Zhang, Y.; Xu, Y.; Zheng, L.; Zhang, L.; Yuan, Z. Transient Synchronous Stability Modeling and Comparative Analysis of Grid-Following and Grid-Forming New Energy Power Sources. Electronics 2024, 13, 3308. [Google Scholar] [CrossRef]
- Sajadi, A.; Rañola, J.A.; Kenyon, R.W.; Hodge, B.-M.; Mather, B. Dynamics and Stability of Power Systems with High Shares of Grid-Following Inverter-Based Resources: A Tutorial. IEEE Access 2023, 11, 29591–29613. [Google Scholar]
- Song, J.; Zhou, X.; Zhou, Z.; Wang, Y.; Wang, Y.; Wang, X. Review of Low Inertia in Power Systems Caused by High Proportion of Renewable Energy Grid Integration. Energies 2023, 16, 6042. [Google Scholar] [CrossRef]
- Du Plessis, A.A.; Strauss, J.M.; Rix, A.J. Short-term solar power forecasting: Investigating the ability of deep learning models to capture low-level utility-scale Photovoltaic system behaviour. Appl. Energy 2021, 285, 116395. [Google Scholar] [CrossRef]
- Hong, L.; Tang, R.; Jiang, Q.; Xie, X.; Zhu, Y. Admittance-Based Stability Analysis of LCL-type Grid-connected Inverter Considering AC-side and AC-DC Frequency Coupling Effects. IEEE Trans. Power Deliv. 2024, 39, 1351–1363. [Google Scholar]
- Ding, N.; Lu, Z.; Qiao, Y.; Min, Y. Simplified equivalent models of large-scale wind power and their application on small-signal stability. J. Mod. Power Syst. Clean Energy 2013, 1, 58–64. [Google Scholar] [CrossRef][Green Version]
- Patrao, I.; Liberos, M.; González-Medina, R.; Torán, E.; Figueres, E.; Garcerá, G. Small-Signal Model of the NPC+ GCC Multilevel Transformerless Inverter in Single-Phase Photovoltaic Power Systems. Electronics 2023, 12, 3545. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, C.; Xing, X.; Chi, S.; Liu, C.; Fang, J. Modeling and attenuation of common mode resonance current for improved LCL-type parallel inverters in PV plants. IEEE Trans. Ind. Inform. 2023, 20, 5193–5205. [Google Scholar] [CrossRef]
- Wang, F.; Feng, X.; Zhang, L.; Du, Y.; Su, J. Impedance-based analysis of grid harmonic interactions between aggregated flyback micro-inverters and the grid. IET Power Electron. 2018, 11, 453–459. [Google Scholar] [CrossRef]
- Zhou, W.; Torres-Olguin, R.E.; Wang, Y.; Chen, Z. A gray-box hierarchical oscillatory instability source identification method of multiple-inverter-fed power systems. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 3095–3113. [Google Scholar] [CrossRef]
- Chen, Q.; Bu, S.; Chung, C.Y. Small-Signal Stability Criteria in Power Electronics-Dominated Power Systems: A Comparative Review. J. Mod. Power Syst. Clean Energy 2024, 12, 1003–1018. [Google Scholar]
- Mazumder, S.K.; Acharya, K. Multiple Lyapunov Function Based Reaching Condition for Orbital Existence of Switching Power Converters. IEEE Trans. Power Electron. 2008, 23, 1449–1471. [Google Scholar] [CrossRef]
- Ilić, M.D.; Xie, L.; Khan, U.A.; Moura, J.M.F. Modeling of Future Cyber–Physical Energy Systems for Distributed Sensing and Control. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2010, 40, 825–838. [Google Scholar] [CrossRef]
- Kim, H.-S.; Jung, H.-S.; Sul, S.-K. Discrete-Time Voltage Controller for Voltage Source Converters with LC Filter Based on State-Space Models. IEEE Trans. Ind. Appl. 2019, 55, 529–540. [Google Scholar] [CrossRef]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient Stability of Voltage-Source Converters with Grid-Forming Control: A Design-Oriented Study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Systematic Approach for Transient Stability Evaluation of Grid-Tied Converters during Power System Faults. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), Baltimore, MD, USA, 29 September–3 October 2019; pp. 5191–5198. [Google Scholar]
- Reza, M.; Sudarmadi, D.; Viawan, F.A.; Kling, W.L.; Van Der Sluis, L. Dynamic Stability of Power Systems with Power Electronic Interfaced DG. In Proceedings of the 2006 IEEE PES Power Systems Conference and Exposition, Atlanta, GA, USA, 29 October 2006–1 November 2006; pp. 1423–1428. [Google Scholar]
- Khalil, H.K. Nonlinear Systems, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Ma, R.; Li, J.; Kurths, J.; Cheng, S.; Zhan, M. Generalized Swing Equation and Transient Synchronous Stability with PLL-Based RPGS. IEEE Trans. Energy Convers. 2022, 37, 1428–1441. [Google Scholar] [CrossRef]
- Shakerighadi, B.; Ebrahimzadeh, E.; Blaabjerg, F.; Leth Bak, C. Large-Signal Stability Modeling for the Grid-Connected RPGS Based on the Lyapunov Method. Energies 2018, 11, 2533. [Google Scholar] [CrossRef]
- Goksu, O.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjaer, P.C. Instability of Wind Turbine Converters During Current Injection to Low Voltage Grid Faults and PLL Frequency Based Stability Solution. IEEE Trans. Power Syst. 2014, 29, 1683–1691. [Google Scholar] [CrossRef]
- Lamarque, C.-H.; Touzé, C.; Thomas, O. An Upper Bound for Validity Limits of Asymptotic Analytical Approaches Based on Normal Form Theory. Nonlinear Dyn. 2012, 70, 1931–1949. [Google Scholar] [CrossRef]
- Fotopoulou, M.; Rakopoulos, D.; Petridis, S.; Drosatos, P. Assessment of smart grid operation under emergency situations. Energy 2024, 287, 129661. [Google Scholar] [CrossRef]
- Edrah, M.; Lo, K.L.; Anaya-Lara, O. Impacts of High Penetration of DFIG Wind Turbines on Rotor Angle Stability of Power Systems. IEEE Trans. Sustain. Energy 2015, 6, 759–766. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. Large Signal Lyapunov-Based Stability Studies in Microgrids: A Review. IEEE Trans. Smart Grid 2017, 8, 2287–2295. [Google Scholar] [CrossRef]
- Shair, J.; Li, H.; Hu, J.; Xie, X. Power System Stability Issues, Classifications and Research Prospects in the Context of High-Penetration of Renewables and Power Electronics. Renew. Sustain. Energy Rev. 2021, 145, 111111. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Cai, X.; Qiu, W.; Zhao, X. Transient Grid-synchronization Stability Analysis of Grid-tied Voltage Source Converters: Stability Region Estimation and Stabilization Control. Proc. CSEE 2022, 42, 7871–7884. [Google Scholar]









| System Parameters | Actual Value/ Per Unit Value (p.u.) | Control Parameters | Actual Value/ Per Unit Value (p.u.) |
|---|---|---|---|
| Rated capacity Sn | 2 MW/1 | d-Axis current reference Iodref | 2367 A/1 |
| Rated voltage Un | 0.69 kV/1 | q-Axis current reference Ioqref | 0 A/0 |
| Rated frequency fn | 50 Hz | PI coefficient of PLL | kp: 0.09/50 ki: 1.6/900 |
| Filter inductance Lf | 0.076 mH/0.1 | PI coefficient of current loop | kpc: 0.165/0.4 kic: 1.65/4 |
| Filter capacitance Cf | 535 μF/0.04 | Filter time constant Tv | 1 ms |
| Line inductance Lg | 0.3 mH/0.4 | Controller delay Td | 200 μs |
| Parameter | Description | System Damping De | Transient Stability |
|---|---|---|---|
| kp | Proportional coefficient of PLL | ↑ (De increase) | ↑ (Stability increase) |
| ki | Integral coefficient of PLL | ↓(De decrease) | ↓ (Stability decrease) |
| Ug | Grid voltage | ↑ | ↑ |
| Lg | Line impedance | ↓ | ↓ |
| Iodref | Current reference on d-axis | ↓ | ↓ |
| Ioqref | Current reference on q-axis | ↓ | ↓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Li, B.; Hou, S.; Shao, X.; Yu, H. Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling. Electronics 2024, 13, 5052. https://doi.org/10.3390/electronics13245052
Tang W, Li B, Hou S, Shao X, Yu H. Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling. Electronics. 2024; 13(24):5052. https://doi.org/10.3390/electronics13245052
Chicago/Turabian StyleTang, Wenzuo, Bo Li, Shuaicheng Hou, Xianqi Shao, and Hongjie Yu. 2024. "Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling" Electronics 13, no. 24: 5052. https://doi.org/10.3390/electronics13245052
APA StyleTang, W., Li, B., Hou, S., Shao, X., & Yu, H. (2024). Transient Stability Analysis for Grid-Connected Renewable Power Generation Systems Based on LMI Optimization Modelling. Electronics, 13(24), 5052. https://doi.org/10.3390/electronics13245052





