Abstract
Trajectory planning in tight spaces presents a significant challenge due to the complex maneuvering required under kinematic and obstacle avoidance constraints. When obstacles are densely distributed near the target state, the limited connectivity between the feasible states and terminal state can further decrease the efficiency and success rate of trajectory planning. To address this challenge, we propose a novel Dual-Stage Motion Pattern Tree (DS-MPT) algorithm. DS-MPT decomposes the trajectory generation process into two stages: merging and posture adjustment. Each stage utilizes specific heuristic information to guide the construction of the trajectory tree. Our experimental results demonstrate the high robustness and computational efficiency of the proposed method in various parallel parking scenarios. Additionally, we introduce an enhanced driving corridor generation strategy for trajectory optimization, reducing computation time by 54% to 84% compared to traditional methods. Further experiments validate the improved stability and success rate of our approach.
1. Introduction
Unmanned systems are becoming increasingly prevalent in various applications, such as intelligent transportation and emergency search and rescue. Trajectory planning, a core module in unmanned systems, involves generating collision-free, smooth, and optimal (e.g., shortest or energy-efficient) trajectories for controlled objects. While trajectory planning has been extensively studied for various platforms like drones and autonomous vehicles, navigating narrow spaces remains a challenging task. The limited connectivity between feasible states in such environments often leads to reduced planning efficiency and increased risk of collisions. Typical examples include parallel parking for autonomous vehicles [1] and agile flight through narrow gaps for drones [2].
Parallel parking poses significant challenges due to narrow terminal constraints. Drivers often need to carefully maneuver their vehicles within limited space to complete the pull-in or pull-out process, increasing the risk of accidents. Autonomous driving technology offers a solution to alleviate the stress of parking and potentially reduce accidents and traffic congestion related to parking.
To effectively improve the computational efficiency and planning success rate of the joint spatial–temporal trajectory planning method in narrow parallel parking scenarios, this work analyzes the dual-stage characteristics of the parking process and designs a novel trajectory planning method. The main contributions are outlined as follows: (1) A trajectory generation method called dual-stage motion pattern tree (DS-MPT) is proposed, which significantly improves the computational efficiency and robustness of initial trajectory generation in narrow scenes. (2) A trajectory optimization method is proposed based on an enhanced driving corridor generation strategy, which reduces the time consumption required to construct driving corridors and improves the success rate of trajectory optimization.
The remaining chapters are structured as follows: Section 2 reviews the literature on trajectory planning methods applied to narrow spaces, especially parking scenarios. Section 3 examines the parallel parking trajectory planning problem from a dual-stage perspective and provides a brief explanation of the framework proposed in this article. Section 4 introduces the proposed DS-MPT method. Section 5 illustrates the modeling of the trajectory optimization problem. Section 6 discusses the experimental results. Section 7 offers a summary and prospects for future studies.
2. Related Works
The core task of trajectory planning is to calculate a sequence of geometric poses, along with their corresponding temporal profiles. Current methods can be divided into two categories: spatial–temporal coupling and spatial–temporal decoupling. In the former approach, trajectory planning is modeled as two sequential optimization problems: path generation and speed planning, as in [3]. Path generation methods are categorized into curve-based, sampling–searching-based, and machine learning-based approaches. Curve-based generation methods offer rapid generation and customizable path shapes through a parametric configuration. Arc curves and straight lines, widely used in the generation of parking paths [3], often encounter issues of discontinuity in curvature. Therefore, smoother curve forms such as polynomial curves [4], clothoid-like curves [5,6,7,8], and spline curves [3,9,10] are used to improve trajectory tracking accuracy in parking planning. Typically, sampling-searching-based methods formulate path generation as a tree-search problem. Common methods include A*-based [11,12,13,14] and rapid-exploring random tree (RRT)-based [10,15,16,17] methods. Sampling–searching-based methods have the characteristics of high flexibility and strong generalizability. Therefore, they are frequently used to provide initial estimates for optimization-based methods. Learning-based methods learn mapping functions to match the corresponding paths in a path library with different parking tasks [18,19] or predict a path based on a parking scenario description [17]. Learning-based methods possess extensive parameters and a higher theoretical potential for algorithmic performance [20]. However, the actual generalizability of these methods remains unconfirmed due to the complexity of real-world parking scenarios. Once the initial path is established, speed planning is required to derive a trajectory with temporal data. Speed planning is typically modeled as an optimization problem [21,22,23,24]. Current speed planning research is mainly oriented towards structured road scenarios, with less emphasis on the parking process.
The spatial–temporal decoupling approach simplifies the original problem, making it easier to solve. However, since the trajectory essentially represents a manifold in three-dimensional space, the solution derived from decoupling might only achieve local optimality. In contrast to related works in on-road scenarios [25,26], which typically considers dynamic interactions between agents, existing parking trajectory planning methods often simplify the problem by assuming a static environment. However, the vehicle’s non-holonomic kinematics constraints imply that decoupling overlooks the integral relationship between path and speed. Therefore, employing a decoupling strategy may result in trajectories that fail to meet the vehicle’s kinematic constraints. In narrow parking scenarios, such trajectories can lead to tracking challenges and potential parking failures.
Therefore, many scholars have studied methods for joint spatial–temporal trajectory planning. Such methods typically model trajectory planning as an optimal control problem (OCP) and use optimization methods for solutions. Li et al. [27] proposed a lightweight iterative framework that contains a comprehensive initial trajectory generation method and simplifies the complexity of obstacle constraints by constructing corridors. Addressing the non-convexity problem of obstacle constraints, Liu et al. proposed the convex feasible set (CFS) algorithm [28] that transforms a problem with non-convex constraints into a sequence of convex optimization problems. Guo et al. [29] proposed a lightweight initialization strategy based on CFS, facilitating faster optimal trajectory identification by gradient-based solvers. In constructing obstacle constraints, Zhang et al. [30] proposed the optimization-based collision avoidance (OBCA) method, offering precise expression of obstacle constraints based on hyperplane segmentation. This approach avoids the approximation errors caused by constructing safe corridors, which improves the accuracy of obstacle constraint expressions. Generally, an OCP is discretized and converted into Non-Linear Programming (NLP) for solution [31,32]. While the discretized model brings solution convenience, it can result in potential collision violations between adjacent trajectory points. To address this issue, Zhang et al. [33] used a visual protection frame and a magnification parameter in optimization modeling, ensuring the effectiveness of discretized obstacle constraints on continuous trajectories. Li et al. [34] proposed an embedded-footprint theoretical model, where the embedded footprint of finite collocation points guarantees collision-free intervals between adjacent collocation points. Learning-based methods [35,36,37,38,39,40,41] have also been applied to spatial–temporal coupled trajectory planning problems.
The weak connectivity of narrow spaces presents challenges for trajectory planning tasks. In recent years, much literature has focused on the issue of parking trajectory planning in narrow scenarios [42,43,44]. Generally, optimization-based methods are considered more suitable for trajectory planning in narrow spaces. These methods can directly apply explicit constraints on obstacle avoidance and vehicle dynamics, providing strong interpretability and stability. However, the obstacle avoidance constraints often result in a non-convex constraint for the optimization problem, making the solution highly dependent on the quality of the initial guess. Obtaining a high-quality initial solution in narrow spaces is not an easy task and can be even more challenging than solving the optimization problem itself. For instance, common sampling–searching-based warm-up methods exhibit polynomial increases in computational complexity as the space scale grows. In narrow scenarios, only a sufficiently high spatial discretization resolution can ensure a successful solution, leading to high initial trajectory computation times. Moreover, poorly designed heuristic functions can incur additional computational costs. In existing research, the multi-stage characteristics of the parking process have received some attention [5,6,18,35,45]. Current findings indicate that parallel parking involves two stages: merging into the parking space and adjusting posture near it. Yang et al. [6] identified scenarios that require repeated posture adjustments based on the width of the parking space. Vorobieva et al. [5] divided parallel parking into three different maneuver categories and specified path planning strategies. Liu et al. [18] divided trajectory planning into two sub-processes, employing different resolutions for trajectory sampling. Li et al. [45] used this objective knowledge to simplify the obstacle constraints in the posture adjustment stage. Tang et al. [35] introduced a segmented parking training framework, decomposing the parking process into posture adjustment and parking tasks. This approach enhanced the algorithm’s ability to navigate crowded and confined spaces effectively. However, current approaches often neglect the potential presence of unstructured obstacles in the environment, limiting the applicability of multi-stage strategies in more complex scenarios.
3. Problem Formulation
In this section, we begin by analyzing the dual-stage nature of trajectory planning under narrow terminal constraints. We then present the proposed computational framework.
3.1. Analysis of Merging Stage and Posture Adjustment Stage
The parallel parking process of human drivers can be divided into two stages: merging and posture adjustment, as shown in Figure 1. Taking the pull-in process as an example, during the merging stage, vehicles primarily maneuver outside the parking spot, and the main task is to move the vehicle near the parking spot. During the posture adjustment stage, the drivable space near and inside the parking spot is primarily utilized, with the main objective of parking the vehicle in the desired posture. During this process, the vehicle needs to make precise adjustments in the limited space. The same principle applies to the pull-out process. Drawing inspiration from the dual-stage characteristics, we contemplated the factors that hinder the efficiency and success rate of trajectory planning methods in tight parking spaces, as summarized in the following three points.
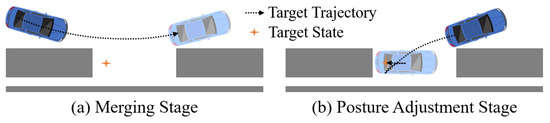
Figure 1.
Illustration of (a) merging stage and (b) posture adjustment stage for a pull-in process.
Firstly, we define a candidate node () and the target node (). Current sampling–searching-based trajectory generation methods usually employ the Minkowski distance, as indicated in (1), as the heuristic information.
When , is also referred to as Euclidean distance. When , is also known as Manhattan distance. In the merging stage, this heuristic design can offer valuable guidance. However, during the posture adjustment stage, the expansion of the trajectory tree does not always prioritize proximity to the target node. Potentially optimal nodes may deviate from or move away from the target node because they provide a larger space for maneuvering. Using the distance from the target pose as heuristic information cannot accurately capture this process, leading to reduced efficiency in trajectory tree expansion during the posture adjustment stage. As shown in Figure 2, the candidate states in (a) and (b) are generated by moving straight backward or executing a right turn behind. If the heuristic function calculates the Euclidean distance between the target state and the candidate state, then (a) is considered superior. However, during the posture adjustment stage, the candidate state in (b) can lead to faster convergence of the trajectory tree.
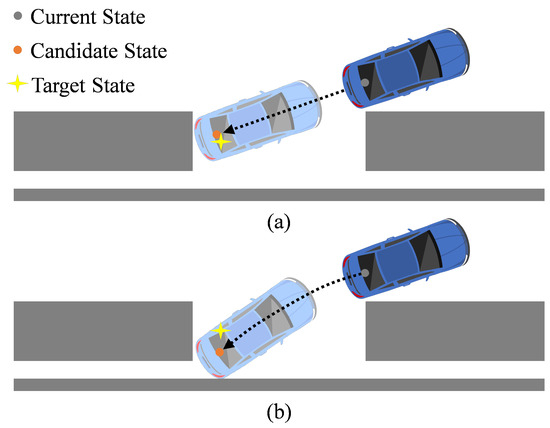
Figure 2.
Illustration of (a) the optimal candidate state under Euclidean distance metric and (b) actual optimal candidate state at the posture adjustment stage.
Secondly, in terms of speed profile planning, there are distinctions between the merging stage and the posture adjustment stage. The speed planning during the merging stage resembles that of on-road scenarios, primarily focusing on longitudinal kinematics. The maximum operating speed is a crucial component of the objective function to ensure efficient completion of the maneuver. During the posture adjustment stage, the trajectory comprises frequent forward and backward movement switches. We define as a single traveling-direction trajectory segment in the posture adjustment phase. Its length is , and the front wheel-angle change that needs to be completed is , where refers to the distance from to and refers to the difference from to . Under the premise of satisfying vehicle kinematic constraints, the time required to complete may be longer than the time required to complete .
To the best of our knowledge, in current research, velocity planning primarily considers longitudinal kinematics and curvature constraints. However, the aforementioned issues have not been adequately considered.
Thirdly, during the trajectory optimization stage, modeling obstacle constraints in terms of driving corridors offers several advantages. On one hand, the driving corridor effectively separates the feasible space from obstacles, and the scale of obstacle constraints remains independent of the number of obstacles in the environment. As a result, the number of obstacle constraints is only related to the number of optimization variables, which improves the stability of the solution time. On the other hand, expressing obstacle constraints as box constraints within the driving corridor reduces the nonlinearity of the constraints. However, it is important to note that constructing driving corridors requires additional time. Typically, to ensure the integrity of obstacle constraints, a driving corridor needs to be created for each trajectory point. In narrow parking scenarios, many trajectory points are in close proximity to each other in space, particularly during the posture adjustment stage. Calculating drivable corridors individually for each trajectory point would result in unnecessary computational overhead.
We incorporated the above considerations into the design of our method. Firstly, we design the DS-MPT method, in which different heuristic functions are designed for the merging stage and posture adjustment stage. Secondly, a trajectory resampling strategy is designed that considers the time required for steering angle changes.. Thirdly, an improved driving corridor generation method is designed to improve computing efficiency. The overall computing framework is described as follows.
3.2. Framework
The goal of trajectory planning is to find a state variable sequence and control variable sequence between the starting state and target state without collision with obstacles. These state and control variable sequences must adhere to the vehicle’s kinematic constraints. Here, denotes the midpoint along the rear-wheel axis, denotes the heading angle with respect to the x axis, v represents the velocity of , a refers to the acceleration, represents the steering angle of the front wheels, refers to the corresponding angular velocity, and represents the time sequence corresponding to each trajectory point. The total number of trajectory points is denoted by n. Some geometric and kinematic parameters of the vehicle are illustrated in Figure 3, in which L denotes the vehicle length, denotes the length of the front overhang, denotes the length of the rear overhang, denotes the length of the wheelbase, and W denotes the vehicle width.
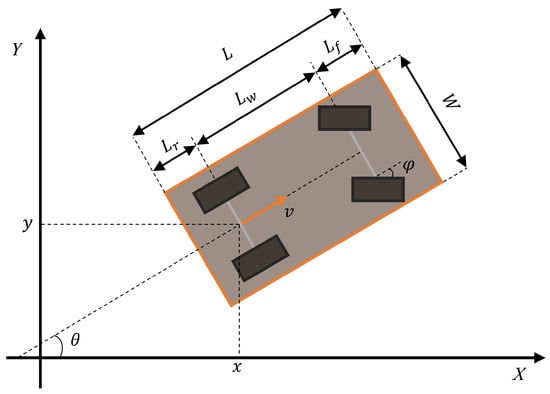
Figure 3.
Illustration of vehicle geometric parameters and kinematic parameters.
The framework of the trajectory planning method proposed in this article is shown in Figure 4, which includes two modules: trajectory generation and trajectory optimization. The trajectory generation module uses the DS-MPT method to calculate the trajectory, including full state variables with a fixed time resolution. Subsequently, the trajectory resampling module fine-tunes the trajectory in the time dimension, leaving enough time for forward and backward movement switching and steering-angle transformation. At the same time, the initial value of the control variable is calculated through time differentiation. Finally, we design a trajectory optimization module with an improved driving corridor generation method. The trajectory generation method is described in Section 4, and the details of the trajectory optimization method are described in Section 5.
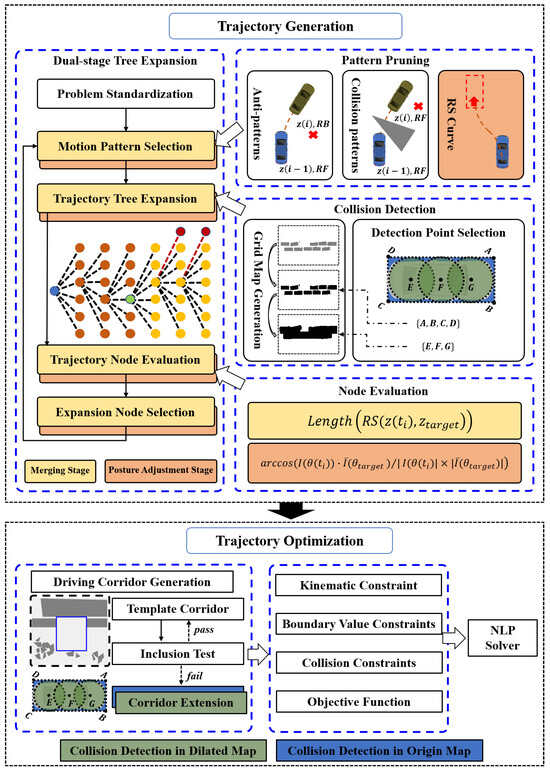
Figure 4.
Illustration of the framework.
4. Dual-Stage Motion Pattern Tree
In this paper, we propose a joint spatial–temporal trajectory generation method called dual-stage motion pattern tree (DS-MPT). In DS-MPT, the trajectory generation problem is modeled as a multi-step motion pattern decision problem. A discrete state variable set () and action variable set () are used to represent the trajectory of the vehicle from the initial state to the target state. represents the pose of the vehicle at the end of each decision-making step. represents the action performed during and , which is set to six fixed motion patterns.
In the solution process, the first step is to standardize the problem by primarily converting the coordinates of the map elements and aligning the target state with the coordinate origin [0, 0, 0], thereby improving data stability. Secondly, irrespective of the pull-in or pull-out process, DS-MPT leverages the end posture within the parking lot as the initial state. This choice offers several advantages. Firstly, it facilitates the definition of the transition from the posture adjustment stage to the merging stage. Additionally, the collision probability of the Reeds–Shepp curve in the merging stage is lower, which is beneficial to improve the solution efficiency. However, in the case of the pull-in process, this approach leads to a reversed trajectory. Nevertheless, we can rectify this by reversing the order of trajectory nodes and adjusting the direction of to obtain the correct trajectory.
The complete algorithm flow is illustrated in Algorithm 1. The algorithm consists of two stages: lines 1–10 for the posture adjustment stage and lines 11–21 for the merging stage. The trajectory expansion in each stage includes three main functions: optimal node selection (lines 3 and 14), motion pattern pruning (lines 4 and 15), and trajectory tree extension (lines 6 and 17).
| Algorithm 1: Dual-Stage Motion Pattern Tree |
 |
4.1. Trajectory Tree Extension via Motion Pattern
We define as the set of motion patterns that the vehicle may choose at each step (), representing moving straight forward, moving straight backward, left turning forward, right turning forward, left turning backward, and right turning backward, respectively. Each movement pattern () is given a unique speed () and front-wheel angle value (). The state transition function () for the trajectory generation problem is shown in (2). In order to prioritize solution efficiency, the constraints of acceleration (a) and angular velocity () are disregarded in this process.
In each decision-making step, the execution time of each can be calculated by . Where is a preset hyperparameter that specifies the maximum expansion time of the motion pattern and refers to the minimum time required to collide with an obstacle when expanding under . It is important to note that this method does not add a node to the trajectory tree after each forward simulation step via . Instead, it only adds the final expanded node within each motion pattern via , as shown in Figure 5. When a node is selected as an expansion node, the intermediate nodes are re-introduced into the trajectory to enhance its time resolution. Unlike the interpolation encrypted method, the intermediate nodes undergo collision detection, providing a stronger safety guarantee. In this article, is set to 1 s, and is set to 0.05 s.
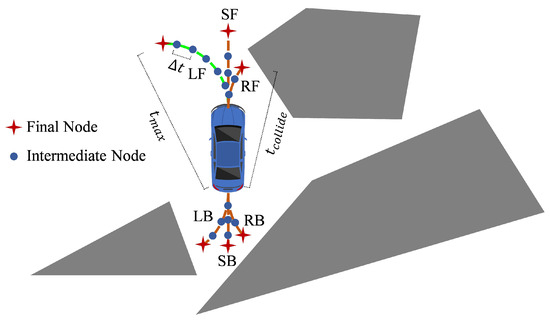
Figure 5.
Illustration of trajectory tree extension.
Another important consideration during the expansion process is determining the criteria for exiting the posture adjustment stage. This article provides a determination formula based on the difference between the heading angle of the extended node () and the heading angle of the terminal state in the parking space ():
where is a predefined hyperparameter that refers to the angle threshold used to switch the planning stage. The trajectory tree is expanded with the terminal state in the parking space as the initial node, so in initial. In the posture adjustment stage, we select the node whose heading angle is biased towards the direction of the -normal vector as the expansion node. As a result, the difference between and gradually increases until it surpasses the specified threshold (). At that point, the extension process is considered to have completed the posture adjustment stage and transitioned into the merging stage. In this article, is set to .
The selection range for expansion nodes in each round does not include the entire trajectory tree but only the children nodes expanded in the previous round. Additionally, the relationship between children and parent nodes is determined strictly based on the expansion steps.
4.2. Node Evaluation
This paper introduces two heuristic cost functions for evaluating motion patterns in the merging stage and posture adjustment stage. In the merging stage, the heuristic calculates the non-holonomic kinematic distance to the end state, which is approximated using the length of the RS curve [46]. In the posture adjustment stage, the heuristic is determined by the angle between the current vehicle heading and the normal vector of the target-state heading.
where represents the Reeds–Shepp curve between and , represents the length of the curve, represents the unit direction vector corresponding to , and represents the normal vector of I.
4.3. Tree Pruning Strategy
As shown in Figure 6, this paper prunes the trajectory tree by removing invalid motion patterns. Three situations are considered. Firstly, when is extended from and , the optimal motion pattern in is extended until it collides with an obstacle. If continues to expand in motion mode , it will be invalid. Secondly, the motion patterns in M are opposite movements to each other, and are opposite movements to each other, and and are opposite movements to each other, as are and . Let represent a pair of reverse motion patterns. If state is expanded from via , then has a greater probability returning to if it continues to expand via . The trajectory tree pruning strategy is expressed by the following formula:
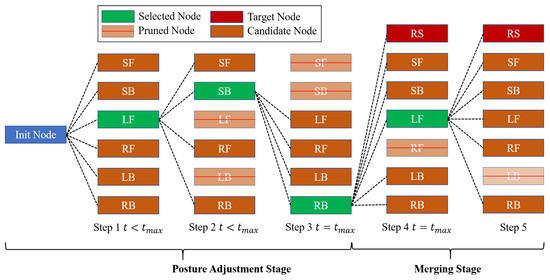
Figure 6.
Illustration of trajectory tree pruning.
Thirdly, during motion pattern tree expansion in the merging stage, each step expansion attempts to establish a connection with the end node using the RS curve. If the connected curve does not result in a collision, the initial trajectory is considered successfully generated.
4.4. Collision Detection
The geometric space is denoted as , the obstacle space as , and the available geometric space as . In the trajectory generation process, obstacles are expressed in the form of a grid map, and the obstacle constraints are expressed as follows:
where represents the grid occupied by the vehicle envelope at time .
In the parallel parking task, the vehicle envelope’s corner points are prone to collisions. Using an approximate representation that ignores the corner points (e.g., inscribed circles) reduces computational complexity but simultaneously compromises the quality of the solution. Considering calculation efficiency and detection accuracy, this paper combines two envelope forms, namely disk approximations and an oriented bounding box (OBB), to simplify the representation of the vehicle shape. we sampled the four corner points of the OBB and the three disk center points. As shown in Figure 7, A, B, C, and D perform collision detection in the original obstacle grid map, and E, F, and G perform collision detection in the dilated grid map. represents the radius of the inscribed circles. The coordinate calculation formula for each detection points is expressed as follows:
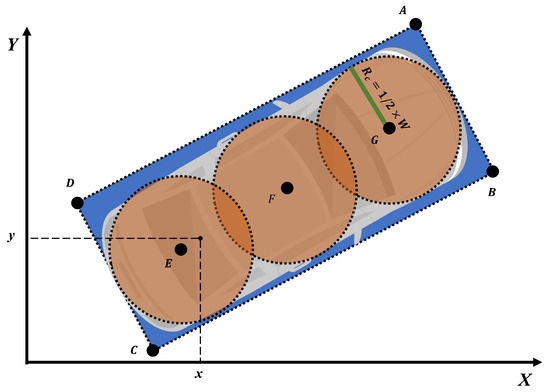
Figure 7.
Illustration of vehicle shape approximation.
The above text presents the core content of the DS-MPT algorithm. Once the trajectory tree is constructed for each stage, the initial trajectory can be obtained through backtracking, and the final trajectory can be obtained by concatenating the trajectories from both stages.
4.5. Trajectory Resample
The trajectory computed by DS-MPT incorporates state quantities ( and ). However, due to the omission of acceleration and angular velocity constraints, abrupt changes occur in both and . To mitigate this issue, we employ a trajectory resampling strategy. The central approach of resampling is re-planning of the velocity profile. We formulate the issue as a quadratic programming (QP) problem.
The initial trajectory is divided into several segments according to the gear switching. Each segment of the initial trajectory is represented by the following multi-segment n-order polynomial:
In the formula, m is the number of segments of the trajectory curve, and is the parameter vector of the n-th polynomial curve. Then, the velocity (), acceleration (), and jerk () of the trajectory point can be expressed as follows:
and are given by the initial trajectory. Since the vehicle switches gears at the end of the trajectory segment, and are set to zero. The continuity of , , , and constitutes equality constraints. At the same time, and must meet the vehicle motion restrictions in (22). Based on the above analysis, this paper models speed planning as a QP problem:
where , , , , is the parameter of the equality and inequality constraints proposed above.
In solving the aforementioned problem, it is necessary to provide the predetermined execution time (T) for each trajectory segment. As described in Section 3, in the posture adjustment stage, the trajectory segments are typically short in distance, and adjusting the steering wheel angle can be more time-consuming than longitudinal travel. Therefore, we use the following function to schedule execution time:
where represents the time required for longitudinal movement and represents the time required to complete front-wheel angle adjustment. represents the total steering-angle change during the trajectory segment. and are relaxation factors.
5. Trajectory Optimization
5.1. Trajectory Optimization Problem Definition
In this section, the vehicle state quantities are defined as , and the vehicle control quantities are defined as . The relationship between and can be described by the following differential equation: . The vehicle’s occupation of the geometric space at time t is defined as . The goal of trajectory optimization is to find the optimal state sequence () and corresponding control sequence () that will avoid collision with obstacles and achieve the minimum value of the objective function. represents the completion time of the entire parking process. The trajectory optimization problem is formulated as follows:
5.2. Objective Function
The objective function of trajectory optimization indicates the expectations for parking efficiency and comfort. In this article, the objective function is defined as follows:
where refers to the initial trajectory points calculated by DS-MPT. The objective function comprises two components. The first component aims to minimize the acceleration and front-wheel steering speed during the parking process. The second component aims to maximize the proximity of the optimized trajectory to the initial trajectory.
5.3. Constraints
5.3.1. Kinematic Equality Constraints
Since the parking process is a low-speed movement, we use a discretization kinematic single-track model [47] to describe the equality constraints () in (19).
where defines the time interval of the trajectory optimization process.
5.3.2. Kinematic Inequality Constraints
The mechanical characteristics of the vehicle limit the range of state variables and control variables. The relevant constraints( and ) after discretization are expressed as follows:
5.3.3. Boundary Value Constraints
The boundary value constraints are implemented to ensure that the starting and ending nodes of the trajectory meet the requirements of the planning task. The starting-point constraints () are expressed as follows:
The constraints on the trajectory’s end node differ from those on the start node. Firstly, a slight deviation from the target state is permitted for the end state, which facilitates the solving process. Secondly, in order to avoid incorrectly fixing the phase difference between and , the constraints of refer to the construction method proposed in [27].
and
5.3.4. Collision Avoidance Constraints
In trajectory optimization, obstacles avoidance constraints are implicitly enforced by confining trajectory nodes within specified driving corridors:
where k represents the number of key points on the vehicle envelope for collision detection.
Driving corridors build boxes along each discrete point. The box generation method is the same as that reported in [48]. Since the generation of boxes requires polling and expansion in all directions at specified steps, it is time-consuming. As described in Section 3, the vehicle pose in the posture adjustment stage is usually located in the same rectangular area. Therefore, we pre-generate a bounding box around the parking plot with the target position as the center. Before polling and expansion, the algorithm first determines whether the envelope sampling points are all located within this rectangular area. If the conditions are met, the bounding box is directly used as a constraint to avoid repeated generation. Detailed calculation steps are illustrated in Algorithm 2.
| Algorithm 2: Enhanced Driving Corridor Generation Algorithm |
 |
6. Experimental Setups, Results, and Analysis
6.1. Experimental Scenarios and Parameters
The simulation experiments were conducted in Matlab R2020b and executed on an AMD Ryzen 9 4900HS CPU with 16 GB RAM. The trajectory optimization problem defined in our method is solved by IPOPT through the AMPL interface. The parameters used in this experiment are shown in Table 1.

Table 1.
Experimental Parameters.
This paper conducts simulation experiments in sixteen parallel parking scenarios. Among them, Cases 1–6 are derived from the typical parallel parking scenes provided in the Trajectory Planning Competition for Automated Parking (TPCAP) [49]. Cases 7–11 represent typical parallel parking scenarios with narrow passages, where the passage widths are 4.667 m, 4.278 m, 3.890 m, 3.501 m, and 3.113 m, respectively. Cases 12–16 are typical parallel parking scenes with a narrow lot area in which the length ranges of the parking lot are 5.639 m, 5.546 m, 5.452 m, 5.358 m, and 5.264 m, respectively. The experiments are divided into four parts. Firstly, comparative experiments are conducted to evaluate different trajectory generation methods. Secondly, the effectiveness of the enhanced driving corridor generation method is demonstrated through experiments. Thirdly, comparative experiments are conducted to demonstrate the superiority of our method over different trajectory planning methods. Finally, to evaluate the robustness of our method, we conduct experiments with randomly sampled initial states in Case 16 and introduce random obstacles in Case 6.
6.2. Experiments for Trajectory Generation Methods
In this section, this paper selects CPU time (), the number of solution iterations (), trajectory length (), the number of switching maneuvers (), and point density () as evaluation metrics. We selected Fault-tolerant Hybrid A* (FTHA) for comparison, which was proposed in [27] and enhances the completeness of the Hybrid A* method. Another comparison method is based on a spatial–temporal decomposition strategy (STD) [45]. STD uses the two-stage characteristics of parallel parking like DS-MPT. The difference is that STD is solved based on the optimization method, while DS-MPT is based on the sampling and searching method. STD relies on structured scene descriptions and is not applicable to unstructured scenes in TPCAP cases. Therefore, in Case 1 to Case 6, we only compare the FTHA method with the DS-MPT method. In Case 7 to Case 16, we uniformly compare the performance of the three methods.
The corresponding statistical indicators are summarized in Table 2, while the planning results of DS-MPT are presented in Figure 8. Across all test scenarios, the DS-MPT method exhibits superior execution efficiency compared to the other methods, except for Case 1. This superiority is evident through and . Compared to FTHA, the DS-MPT method exhibits a longer CPU time per iteration (DS-MPT: 0.022 vs. FTHA: 0.015) due to the necessity of multiple high-resolution sampling and collision detection executions. Nonetheless, with the aid of precise two-stage heuristic information and efficient tree pruning strategies, DS-MPT achieves more accurate selection of expansion nodes. Consequently, it demands fewer iterations, thereby establishing an advantage in terms of execution efficiency. Furthermore, when considering and in different scenarios, the DS-MPT method demonstrates remarkable numerical stability, exhibiting low sensitivity to changes in the number of obstacles and parking space narrowness. The standard variance of and for the entire scenarios is significantly lower for the DS-MPT method compared to FTHA and STD, which can be seen in Table 3.

Table 2.
Experimental results for trajectory generation methods.
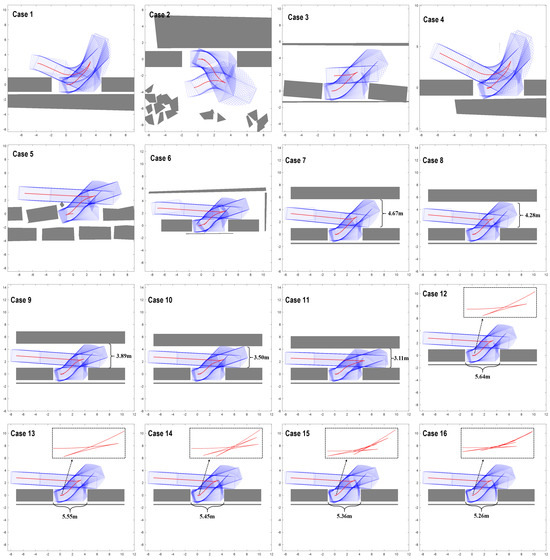
Figure 8.
Experimental results for the DS-MPT algorithm.

Table 3.
Metric statistics for trajectory generation experiments.
In terms of trajectory quality metric, the FTHA method performs better. Specifically, FTHA achieves the best index in 9 out of the 16 scenarios. Similarly, in terms of , FTHA performs better than other methods in 11 out of the 16 scenes. We analyze the reasons for this result. On one hand, the heuristic function employed by the DS-MPT algorithm during the posture adjustment stage prioritizes the transformation of the vehicle’s heading angle. This, coupled with the node extension strategy relying on collisions with the environment, potentially leads to local optimal solutions in not very narrow scenarios. Additionally, for the sake of completeness, the FTHA method incorporates the A* algorithm to connect the end point when the maximum number of iterations is reached. However, the trajectory generated by A* does not account for vehicle kinematics. As a result, while the FTHA method may exhibit favorable metrics in terms of and , its resulting trajectory may deviate further from the true optimal safe trajectory. Figure 9 illustrates the trajectories planned by DS-MPT and FTHA. In Cases 1, 2, and 4, notable differences are observed in the maneuver points generated by the two methods. In Case 3, FTHA reaches the maximum iteration limit and directly connects the target state to the nearest optimal node, potentially violating kinematic and obstacle constraints. Compared with the STD method, it can be found that the trajectory length generated by DS-MPT is relatively close to the trajectory length calculated by STD, and the length of the former is always slightly shorter than that of the latter. In terms of , DS-MPT achieves performance better than or equal to that of STD in 70% of scenarios.
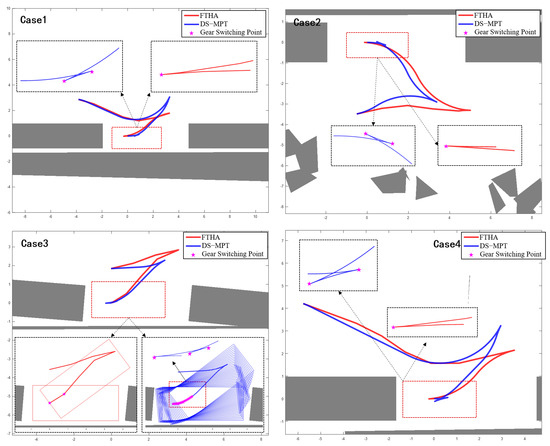
Figure 9.
Comparison of planning results of DS-MPT and the FTHA algorithm.
Another noteworthy metric is the density of trajectory points. As shown in Table 2 and Table 3, the DS-MPT method not only exhibits superior solving efficiency but also achieves a higher density of trajectory points, averaging eight points per meter. It is important to emphasize that the higher trajectory-point density in DS-MPT is not attained through simple interpolation. Rather, collision detection is performed for each node in the trajectory, ensuring a more reliable and safer trajectory. However, FTHA and STD can also improve the trajectory point density by adjusting parameters, for example, by choosing a smaller expansion step size for the FTHA method or increasing the number of optimized subsequences for the STD method, although this means a longer solution time.
6.3. Experiments for Enhanced Driving Corridors Generation Strategy
We measure the computational efficiency of the two driving corridor generation strategies. The origin corridor generation method is cited from [48]. The experiment assesses the utilization of the original method for generating driving corridors with three inner-circle center points, as well as the utilization of both the original strategy and the enhanced strategy for generating driving corridors with seven envelope sampling points. The experimental results are shown in Figure 10. When generating corridors for seven sampling points, the enhanced strategy can significantly reduce the calculation time by 54–84% compared to the original strategy. Importantly, the calculation time is lower than or comparable to that of the original method, which calculates the driving corridor using three inner-circle center points.
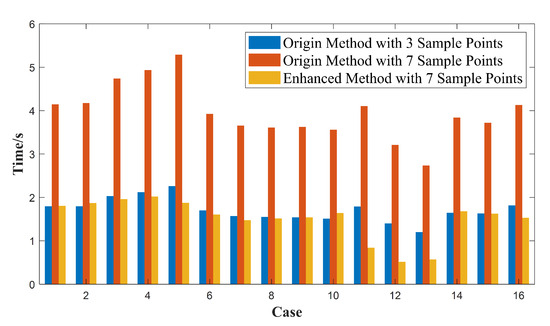
Figure 10.
Experimental results for driving corridor generation strategies.
6.4. Experiments for Trajectory Planning Methods
We compared our proposed trajectory planning method with the approaches presented in [27,30,45]. The method proposed in [27] utilizes the aforementioned FTHA method for trajectory discovery and introduces a lightweight iterative framework called LIOM. In LIOM, the nonlinear equalities in the optimization problem are softened using external penalty functions and incorporated into the objective function. An iterative update strategy for driving corridors is additionally adopted. This method demonstrates strong advantages in terms of algorithmic execution efficiency and completeness. The STD method proposed in [45] uses the two-stage characteristics as a kind of expert knowledge to reduce the complexity of obstacle avoidance constraints, with a high solution success rate in narrow scenarios. The H-OBCA method proposed in [30] proposes a method to accurately model obstacle constraints without approximation errors caused by driving corridors. Therefore, H-OBCA has great potential in narrow scenarios. We compare above methods and our method in Case 7 to Case 16.
The experimental results are shown in Table 4 and Table 5, in which represents the time required for initial trajectory generation, represents the time required for trajectory optimization (CPU time in IPOPT), represents a summary of and , represents the number of iterations required for trajectory optimization, represents the optimal trajectory length, and represents the number of maneuvers in the optimal trajectory.

Table 4.
Experimental results for trajectory planning methods.

Table 5.
Statistics for trajectory planning experiments.
In terms of efficiency indexes and success rate, our method performs better than other methods on the index. It not only takes less time, on average, but also shows stronger stability. Furthermore, considering the average total calculation time, our method ranks second after the FTHA + LIOM method. However, it is worth noting that our method exhibits a higher solution success rate compared to FTHA + LIOM. In all cases, both our method and the STD method achieve a 100% solution success rate. We analyze the cases where the solution fails. The main reason for this is either the failure of the initial solution or the unacceptable quality of the initial solution. As a result, the DS-MPT method proposed in this article shows significant potential in enhancing computational efficiency and success rates for other trajectory optimization methods.
In terms of trajectory quality indicators, both the STD method and our method exhibit excellent performance in terms of . Our method produces the shortest trajectory in four scenarios, while the STD method outperforms in the remaining six scenarios. For the indicator, there are significant differences among the four methods. The reason is that all the methods used in the experiments transform the continuous-time trajectory planning problem into a finite, nonlinear program with constraints applied at finite collocation points. However, potential violations between adjacent collocation points can occur. Because of this, some trajectories find exactly two feasible collocation points that cross the obstacle. In this situation, although the trajectory has a lower value, it is actually not feasible. To be honest, our method does not solve this problem. However, since the initial speed profile considers the two-stage characteristics, more points in the initial trajectory are concentrated near the parking area. The optimal obtained trajectory is relatively better in terms of safety. Figure 11 shows the trajectories obtained by H-OBCA and our method under Case 12.
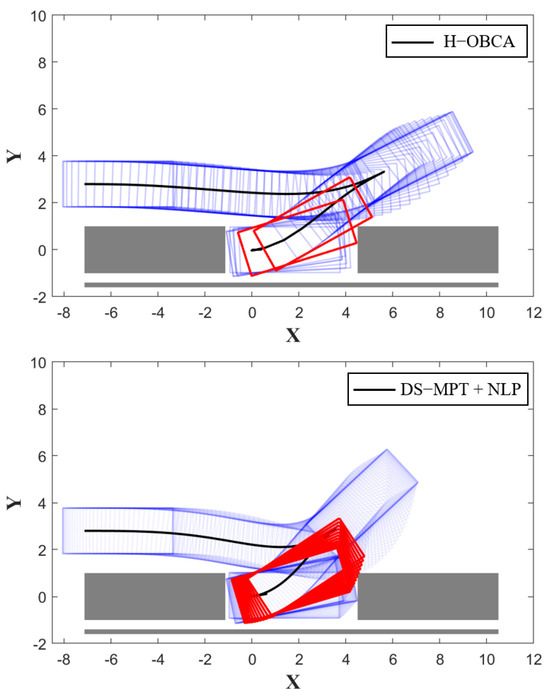
Figure 11.
The optimal trajectories in Case 12 with the local trajectory in the posture adjustment stage highlighted in red.
In order to further analyze the optimality of the trajectories obtained by our method, we calculate the standard deviations of the differentials of four quantities in the optimal trajectories obtained from three cases, the results of which are shown in Table 6. Figure 12, Figure 13 and Figure 14 present the curves of state variables and control variables in the optimal trajectories. The results indicate that the optimal trajectories obtained using our method do not exhibit abrupt changes in the state variables or control variables . By comparing the extreme values in the figures, we can conclude that the solved trajectories satisfy the vehicle kinematic constraints stated in Equation (22).

Table 6.
Standard deviations of the optimal states/control variables.
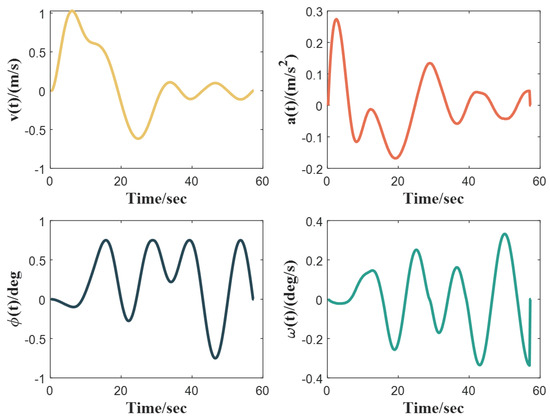
Figure 12.
Optimized control/state profiles in Case 14.
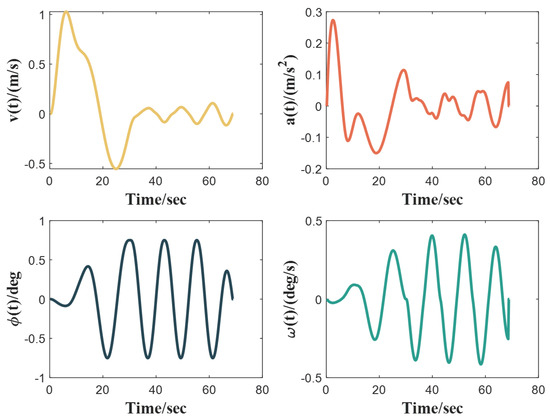
Figure 13.
Optimized control/state profiles in Case 15.
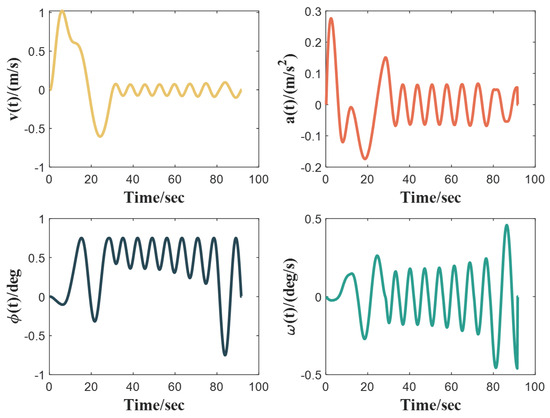
Figure 14.
Optimized control/state profiles in Case 16.
6.5. Robustness Analysis
To further analyze the robustness of the proposed trajectory planning method, we conducted two additional experiments. First, a random experiment was performed for parking Case 16, involving 200 Monte Carlo trials. The initial conditions of the vehicle were varied, with the random initialization data summarized in Table 7. In the second experiment, 20 scenarios were generated based on Case 6 by randomly adding obstacles. The parameters of these random obstacles are detailed in Table 8.

Table 7.
Stochastic initial state generation parameters.

Table 8.
Stochastic obstacles generation parameters.
Our four performance indicators are listed in Table 9: the times of successful solution (), the times of infeasible solution (), the average total solve time (), and the standard deviation of total solve time (). The DS-MPT method was successfully solved in all random situations, and the average time consumption was relatively stable, but the success rate of back-end trajectory optimization was reduced. The success rate in 200 experiments was 92.5%, and the standard deviation of the solve time was larger. This is because the trajectories generated by DS-MPT under random conditions have different lengths and the number of trajectory points is also different, leading to uncertainty in the scale of the optimization problem. Longer trajectories increase the size of the optimization variables, prolonging the solution time. Table 10 presents the experimental results under conditions with random obstacles. The algorithm’s success rate and computation time remained consistent despite the increasing complexity of the obstacle distribution, demonstrating strong robustness.

Table 9.
Convergence results with random initial states.

Table 10.
Convergence results with random obstacles.
7. Discussion
This paper investigated the problem of trajectory planning under narrow terminal constrains. A novel trajectory generation approach called DS-MPT was structured to plan parking maneuvers with higher computational efficiency and robustness. Subsequently, a trajectory optimization method was introduced, along with an enhanced driving corridor generation strategy.
Based on the experimental simulation results, we found that trajectory planning under narrow terminal constrains has dual-stage characteristics. The heuristic functions designed for the two stages better guide the expansion of the trajectory tree, thereby improving the calculation efficiency. At the same time, the speed re-planning method and the driving corridor generation strategy based on the dual-stage characteristics further improve the trajectory quality, reduce the time consumption of optimization, and improve the success rate of trajectory optimization.
In future work, we will explore strategies to enhance the algorithm’s generalization capabilities, such as by incorporating dual-stage strategies and learning-based techniques. We will also investigate more efficient trajectory optimization methods to reduce computational cost. Furthermore, we aim to develop a general-purpose trajectory planner for unmanned systems operating in narrow, unstructured environments.
Author Contributions
Conceptualization, Y.C. and B.L.; methodology, Y.C.; software, Y.C.; validation, Y.C. and X.G.; formal analysis, Z.D.; investigation, Y.C.; data curation, Y.C.; writing—original draft preparation, Y.C.; writing—review and editing, B.L. and Z.D.; visualization, Y.C.; supervision, B.L.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key R&D Program of Hubei Province (No. 2023BAB146).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
Yongxing Cao would like to thank Lin Zhao from National University of Singapore for their support during this study.
Conflicts of Interest
Author Xiaomin Guo was employed by the company Dongfeng USharing Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Qiu, D.; Qiu, D.; Wu, B.; Gu, M.; Zhu, M. Hierarchical Control of Trajectory Planning and Trajectory Tracking for Autonomous Parallel Parking. IEEE Access 2021, 9, 94845–94861. [Google Scholar] [CrossRef]
- Xie, Y.; Lu, M.; Peng, R.; Lu, P. Learning agile flights through narrow gaps with varying angles using onboard sensing. IEEE Robot. Autom. Lett. 2023, 8, 5424–5431. [Google Scholar] [CrossRef]
- Zhang, J.; Shi, Z.; Yang, X.; Zhao, J. Trajectory planning and tracking control for autonomous parallel parking of a non-holonomic vehicle. Meas. Control 2020, 53, 1800–1816. [Google Scholar] [CrossRef]
- Zhang, D.; Li, S.; Yang, Q.; Liu, L. Optimization based trajectory planning of parallel parking with multiple constraints. SAE Int. J. Passeng. Cars-Electron. Electr. Syst. 2015, 8, 413–418. [Google Scholar] [CrossRef]
- Vorobieva, H.; Glaser, S.; Minoiu-Enache, N.; Mammar, S. Automatic parallel parking in tiny spots: Path planning and control. IEEE Trans. Intell. Transp. Syst. 2014, 16, 396–410. [Google Scholar] [CrossRef]
- Yi, Y.; Lu, Z.; Xin, Q.; Jinzhou, L.; Yijin, L.; Jianhang, W. Smooth path planning for autonomous parking system. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 167–173. [Google Scholar]
- Tazaki, Y.; Okuda, H.; Suzuki, T. Parking trajectory planning using multiresolution state roadmaps. IEEE Trans. Intell. Veh. 2017, 2, 298–307. [Google Scholar] [CrossRef]
- Cai, L.; Guan, H.; Zhou, Z.Y.; Xu, F.L.; Jia, X.; Zhan, J. Parking Planning Under Limited Parking Corridor Space. IEEE Trans. Intell. Transp. Syst. 2022, 24, 1962–1981. [Google Scholar] [CrossRef]
- Gómez-Bravo, F.; Cuesta, F.; Ollero, A.; Viguria, A. Continuous curvature path generation based on β-spline curves for parking manoeuvres. Robot. Auton. Syst. 2008, 56, 360–372. [Google Scholar] [CrossRef]
- Jeong, Y.; Kim, S.; Jo, B.R.; Shin, H.; Yi, K. Sampling based vehicle motion planning for autonomous valet parking with moving obstacles. Int. J. Automot. Eng. 2018, 9, 215–222. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Dolgov, D.; Thrun, S.; Montemerlo, M.; Diebel, J. Practical search techniques in path planning for autonomous driving. Ann. Arbor. 2008, 1001, 18–80. [Google Scholar]
- Yang, H.; Xu, X.; Hong, J. Automatic Parking Path Planning of Tracked Vehicle Based on Improved A* and DWA Algorithms. IEEE Trans. Transp. Electrif. 2023, 9, 283–292. [Google Scholar] [CrossRef]
- Wang, Y.; Hansen, E.; Ahn, H. Hierarchical Planning for Autonomous Parking in Dynamic Environments. IEEE Trans. Control Syst. Technol. 2024, 32, 1386–1398. [Google Scholar] [CrossRef]
- Lian, J.; Ren, W.; Yang, D.; Li, L.; Yu, F. Trajectory planning for autonomous valet parking in narrow environments with enhanced hybrid a* search and nonlinear optimization. IEEE Trans. Intell. Veh. 2023, 8, 3723–3734. [Google Scholar] [CrossRef]
- Tang, Z.; Chen, B.; Lan, R.; Li, S. Vector field guided rrt* based on motion primitives for quadrotor kinodynamic planning. J. Intell. Robot. Syst. 2020, 100, 1325–1339. [Google Scholar] [CrossRef]
- Zheng, D.; Tsiotras, P. Accelerating Kinodynamic RRT* Through Dimensionality Reduction. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September 2021–1 October 2021; pp. 3674–3680. [Google Scholar] [CrossRef]
- Shan, Y.; Zhong, Z.; Fan, L.; Kai, H. DeepParking: Deep Learning-Based Planning Method for Autonomous Parking. In Proceedings of the International Conference on Spatial Data and Intelligence, Nanchang, China, 13–15 April 2023; Springer: Cham, Switzerland, 2023; pp. 21–33. [Google Scholar]
- Liu, W.; Li, Z.; Li, L.; Wang, F.Y. Parking like a human: A direct trajectory planning solution. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3388–3397. [Google Scholar] [CrossRef]
- Lembono, T.S.; Paolillo, A.; Pignat, E.; Calinon, S. Memory of motion for warm-starting trajectory optimization. IEEE Robot. Autom. Lett. 2020, 5, 2594–2601. [Google Scholar] [CrossRef]
- Teng, S.; Hu, X.; Deng, P.; Li, B.; Li, Y.; Ai, Y.; Yang, D.; Li, L.; Xuanyuan, Z.; Zhu, F.; et al. Motion Planning for Autonomous Driving: The State of the Art and Future Perspectives. IEEE Trans. Intell. Veh. 2023, 8, 3692–3711. [Google Scholar] [CrossRef]
- Fan, H.; Zhu, F.; Liu, C.; Zhang, L.; Zhuang, L.; Li, D.; Zhu, W.; Hu, J.; Li, H.; Kong, Q. Baidu apollo em motion planner. arXiv 2018, arXiv:1807.08048. [Google Scholar]
- Zhang, Y.; Sun, H.; Zhou, J.; Hu, J.; Miao, J. Optimal trajectory generation for autonomous vehicles under centripetal acceleration constraints for in-lane driving scenarios. In Proceedings of the 2019 IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, 27–30 October 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 3619–3626. [Google Scholar]
- Liu, C.; Zhan, W.; Tomizuka, M. Speed profile planning in dynamic environments via temporal optimization. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 154–159. [Google Scholar]
- Zhang, Y.; Chen, H.; Waslander, S.L.; Yang, T.; Zhang, S.; Xiong, G.; Liu, K. Toward a more complete, flexible, and safer speed planning for autonomous driving via convex optimization. Sensors 2018, 18, 2185. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, W.; Sun, C.; Chu, D.; Huang, T.; Li, W.; Yu, C.; Pirani, M.; Cao, D.; Khajepour, A. Eliminating Uncertainty of Driver’s Social Preferences for Lane Change Decision-Making in Realistic Simulation Environment. IEEE Trans. Intell. Transp. Syst. 2024. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, W.; Huang, T.; Sun, C.; Zhong, J.; Khajepour, A. Social Predictive Intelligent Driver Model (SPIDM) for Autonomous Driving Simulation. Automot. Innov. 2024. [Google Scholar] [CrossRef]
- Li, B.; Acarman, T.; Zhang, Y.; Ouyang, Y.; Yaman, C.; Kong, Q.; Zhong, X.; Peng, X. Optimization-based trajectory planning for autonomous parking with irregularly placed obstacles: A lightweight iterative framework. IEEE Trans. Intell. Transp. Syst. 2021, 23, 11970–11981. [Google Scholar] [CrossRef]
- Liu, C.; Lin, C.Y.; Tomizuka, M. The convex feasible set algorithm for real time optimization in motion planning. SIAM J. Control Optim. 2018, 56, 2712–2733. [Google Scholar] [CrossRef]
- Guo, Y.; Yao, D.; Li, B.; Gao, H.; Li, L. Down-sized initialization for optimization-based unstructured trajectory planning by only optimizing critical variables. IEEE Trans. Intell. Veh. 2022, 8, 709–720. [Google Scholar] [CrossRef]
- Zhang, X.; Liniger, A.; Borrelli, F. Optimization-based collision avoidance. IEEE Trans. Control Syst. Technol. 2020, 29, 972–983. [Google Scholar] [CrossRef]
- Lee, S.; Lim, W.; Sunwoo, M. Robust parking path planning with error-adaptive sampling under perception uncertainty. Sensors 2020, 20, 3560. [Google Scholar] [CrossRef]
- Chen, C.; Wu, B.; Xuan, L.; Chen, J.; Wang, T.; Qian, L. A trajectory planning method for autonomous valet parking via solving an optimal control problem. Sensors 2020, 20, 6435. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Lu, S.; Xie, L.; Su, H.; Li, D.; Wang, Q.; Xu, W. A guaranteed collision-free trajectory planning method for autonomous parking. IET Intell. Transp. Syst. 2021, 15, 331–343. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Zhang, T.; Acarman, T.; Ouyang, Y.; Li, L.; Dong, H.; Cao, D. Embodied Footprints: A Safety-Guaranteed Collision-Avoidance Model for Numerical Optimization-Based Trajectory Planning. IEEE Trans. Intell. Transp. Syst. 2024, 25, 2046–2060. [Google Scholar] [CrossRef]
- Tang, X.; Yang, Y.; Liu, T.; Lin, X.; Yang, K.; Li, S. Path Planning and Tracking Control for Parking via Soft Actor-Critic Under Non-Ideal Scenarios. IEEE/CAA J. Autom. Sin. 2024, 11, 181–195. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, H.; Song, S.; Hu, F. Reinforcement learning-based motion planning for automatic parking system. IEEE Access 2020, 8, 154485–154501. [Google Scholar] [CrossRef]
- Song, S.; Chen, H.; Sun, H.; Liu, M. Data efficient reinforcement learning for integrated lateral planning and control in automated parking system. Sensors 2020, 20, 7297. [Google Scholar] [CrossRef] [PubMed]
- Chai, R.; Liu, D.; Liu, T.; Tsourdos, A.; Xia, Y.; Chai, S. Deep Learning-Based Trajectory Planning and Control for Autonomous Ground Vehicle Parking Maneuver. IEEE Trans. Autom. Sci. Eng. 2023, 20, 1633–1647. [Google Scholar] [CrossRef]
- Chai, R.; Tsourdos, A.; Savvaris, A.; Chai, S.; Xia, Y.; Chen, C.P. Design and implementation of deep neural network-based control for automatic parking maneuver process. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1400–1413. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Chen, Z.; Liu, M.; Piao, C.; Wan, K.; Huang, H. Vertical Parking Trajectory Planning With the Combination of Numerical Optimization Method and Gradient Lifting Decision Tree. IEEE Trans. Consum. Electron. 2023, 70, 1845–1856. [Google Scholar] [CrossRef]
- Jiang, M.; Li, Y.; Zhang, S.; Wang, C.; Yang, M. HOPE: A Reinforcement Learning-based Hybrid Policy Path Planner for Diverse Parking Scenarios. arXiv 2024, arXiv:2405.20579. [Google Scholar]
- Guo, P.; Sun, C.; Li, Q. Obstacle Avoidance Path Planning in Unstructured Environment With Narrow Passages. IEEE Trans. Intell. Veh. 2023, 8, 4632–4643. [Google Scholar] [CrossRef]
- Zhao, M.; Shen, T.; Wang, F.; Yin, G.; Li, Z.; Zhang, Y. APTEN-Planner: Autonomous Parking of Semi-Trailer Train in Extremely Narrow Environments. IEEE Trans. Intell. Transp. Syst. 2024, 25, 4116–4132. [Google Scholar] [CrossRef]
- Hu, J.; Feng, Y.; Li, S.; Wang, H.; So, J.; Zheng, J. Mirroring the Parking Target: An Optimal-Control-Based Parking Motion Planner with Strengthened Parking Reliability and Faster Parking Completion. IEEE Trans. Intell. Transp. Syst. 2024, 25, 16157–16170. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y.; Shao, Z. Spatio-temporal decomposition: A knowledge-based initialization strategy for parallel parking motion optimization. Knowl.-Based Syst. 2016, 107, 179–196. [Google Scholar] [CrossRef]
- Reeds, J.; Shepp, L. Optimal paths for a car that goes both forwards and backwards. Pac. J. Math. 1990, 145, 367–393. [Google Scholar] [CrossRef]
- Althoff, M.; Koschi, M.; Manzinger, S. CommonRoad: Composable benchmarks for motion planning on roads. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 11–14 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 719–726. [Google Scholar]
- Li, B.; Acarman, T.; Peng, X.; Zhang, Y.; Bian, X.; Kong, Q. Maneuver planning for automatic parking with safe travel corridors: A numerical optimal control approach. In Proceedings of the 2020 European Control Conference (ECC), St. Petersburg, Russia, 12–15 May 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1993–1998. [Google Scholar]
- Li, B.; Fan, L.; Ouyang, Y.; Tang, S.; Wang, X.; Cao, D.; Wang, F.Y. Online competition of trajectory planning for automated parking: Benchmarks, achievements, learned lessons, and future perspectives. IEEE Trans. Intell. Veh. 2022, 8, 16–21. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).