A High-Speed Train Traction Motor State Prediction Method Based on MIC and Improved SVR

Abstract

The traction motor realizes the mutual conversion of electrical energy and mechanical energy during the train traction and braking process and is a key component of high-speed trains. The normal operation of the motor is directly related to the safety of high-speed train operation. Changes in temperature signals can reflect faults in the traction motor. By analyzing the internal and external influencing factors of temperature signals, a multi-factor prediction model for traction motors is established based on the maximal information coefficient and improved support vector regression. In this model, highly relevant features selections are performed based on time-delayed sequences and the maximal information coefficient. Using the adaptive particle swarm algorithm to optimize the improved support vector regression algorithm can enhance its accuracy and efficiency. Furthermore, using the K-nearest neighbor algorithm for error prediction will yield more accurate results. By comparing the $RMSE$, $MBE$, $MAE$, and other evaluation metrics of different algorithms under various working conditions, the results show that the prediction method proposed in this paper performs well across different working conditions. This method demonstrates greater adaptability to varying conditions and is more suitable for applications involving high-speed trains.

1. Introduction

The high-speed rail system is a complex system consisting of multiple subsystems, including traction, braking, bogies, and passenger services, among other key subsystems. The traction system is a key part of the high-speed rail train and provides traction and drives the train. As the core component of the traction system, the traction motor is responsible for converting electrical energy into mechanical energy to drive the train [1]. When the traction motor is working, it will be affected by various external and internal factors, such as season, region, operating speed, and the status of related components. These factors will affect the status of the motor [2]. Therefore, real-time monitoring and prediction of the status of the traction motor and its influencing factors are of great significance to ensure the safe operation of high-speed railways.

Prognostics health management (PHM) proposes a new approach to managing health status, which focuses on monitoring, predicting, and managing the health status of complex engineering projects to reduce the economic losses caused by equipment failures [1,3]. PHM plays a key role in the industrial field. It can help companies reduce equipment maintenance costs and improve equipment availability and efficiency, enhancing competitiveness and achieving sustainable development [4]. In recent years, research on PHM has involved multiple disciplines [5]. A PHM system should have functions such as data management, condition monitoring, fault prediction, fault diagnosis, health assessment, and operation and maintenance analysis [6].

Fault prediction methods are divided into physical model-based, data-driven, and hybrid methods [7,8]. Physical model-based fault prediction methods are common in industrial applications and can identify detailed fault characteristics and the requirements for experimental measurement and data analysis to obtain the required information [8,9]. However, some of the physical model-based fault prediction methods make it difficult to construct an accurate degradation model, and the prediction accuracy is not high [7,10]. Data-driven methods are more effective than physical model-based methods in complex equipment [11] and are widely used in PHM for equipment monitoring, fault prediction, maintenance optimization, etc., which can improve equipment reliability, reduce maintenance costs, and provide accurate data support and visual analysis for decision-makers [12].

There are complex nonlinear relationships between the factors affecting the temperature of traction motors. It is necessary to obtain enough information from valid data to explore the correlation between the data and further improve the accuracy and reliability of temperature prediction. Currently, many machine learning methods can make full use of existing data for accurate prediction. Hong et al. [13] proposed a model joint prediction strategy using long short-term memory (LSTM) and the multivariate linear regression algorithm, which can obtain an accuracy benchmark and flexibly control the prediction steps of LSTM. Liu et al. [14] proposed a hybrid model. The approach comprises three steps: first, the raw oil temperature data are preprocessed using a secondary decomposition method. Second, a reinforcement learning-based algorithm selects important features for each sub-series. Finally, forecasting models are created with a simple recurrent unit network to generate the final forecasts. Chen et al. [15] proposed a health state estimation method based on temperature prediction and gated recurrent neural networks. Zhang et al. [16] proposed a mechanical fault diagnosis method based on improved complete ensemble empirical mode decomposition (ICEEMD) and the adaptive whale optimization algorithm (AWOA) optimized extreme learning machine (ELM). The signal of the mechanical equipment was decomposed by the ICEEMD method, and the mixed entropy of the screened intrinsic mode function (IMF) was used as the feature vector to improve the accuracy of fault information extraction. Currently, a large amount of production data contains many outliers and missing values. Wang et al. [17] proposed a short-term wind power forecasting method based on data cleaning and feature reconstruction that can detect and delete outliers embedded in multivariate variables through local density.

This study proposes a prediction method based on the maximal information coefficient (MIC) and improved support vector regression (SVR). The main contributions are as follows:

(1)

Using time-delayed sequences and MIC for feature selection can transform three feature variables into multiple feature variables. Each feature variable has a high correlation with the target variable, which enables the algorithm to mine more data associations and improve the accuracy and robustness of the algorithm. In the past, there was no error reduction step after algorithm model training. This method utilizes the K-nearest neighbor (KNN) algorithm to reduce errors while effectively mitigating the impact of noise and irrelevant data on the model, thereby enhancing its prediction accuracy.

(2)

Using adaptive particle swarm optimization (APSO) to optimize the SVR regression prediction algorithm can improve the algorithm’s prediction accuracy while improving the algorithm’s efficiency and reducing the time spent on prediction. This method can predict the future temperature of the traction motor using external temperature, train speed, time, and initial motor temperature. It enables accurate predictions of the temperature signals of the traction motor under various operating conditions, with the goals of optimizing train operation schedules, ensuring the safety of train operations, reducing energy consumption, and lowering operational costs.

The paper is organized as follows. Section 1 introduces the necessity of high-speed rail traction motor state prediction and reviews the related research works. Section 2 presents a high-speed train traction motor status prediction method based on MIC and an improved SVR approach. In Section 3, a case study is conducted using real data to verify the proposed prediction method. Section 4 analyzes and discusses the prediction results. Finally, the conclusion is in Section 5.

2. Methodology

2.1. Prediction Model

During the operation of high-speed trains, accurate prediction models are crucial for system monitoring and maintenance [18]. In this paper, the state prediction model of a high-speed railway traction motor is the main research object. Traction motors are affected by a variety of factors. The operating environment, such as filter blockage, hard object impact, and fan duct blockage, will affect the integrity and heat dissipation of the motor and cause motor failures. Instances of improper maintenance, such as oil contamination, misalignment of installation, and cooling fan failures, can also adversely affect the condition of the motor; in addition, poor motor manufacturing quality caused by the supplier will also affect the motor state and cause motor failure. Most faults can be reflected by changes in the motor temperature signal [19]. Relevant data show that in China, in 2020, failures caused by abnormal temperatures in the traction motors of high-speed trains accounted for 73.3% of the total failure data. Therefore, in this paper, it is feasible and necessary to use temperature signals to predict the state of traction motors.

SVR has attracted widespread attention due to its excellent generalization and powerful nonlinear modeling ability [20]. The fundamental concept behind the SVR model involves mapping the initial data points from the input space onto a higher, or potentially infinite-dimensional, space. Its primary benefit lies in its ability to handle high-dimensional data sets while preserving robust predictive accuracy, a capability that is particularly advantageous when dealing with small sample sizes [21,22]. By constructing time-delayed sequences, we can reveal the dynamic changes and trends in the data, laying the foundation for subsequent feature selection and model optimization. At the same time, the MIC method is used to select input features. MIC can capture the linear and nonlinear correlations between variable pairs, which is more suitable for feature selection of complex systems. After feature selection, this study uses the SVR model optimized by the APSO algorithm to reduce the prediction error and improve the model’s generalization ability. Finally, KNN optimizes the residual. The process of this method is shown in Figure 1.

2.2. Constructing Time-Delayed Sequences

The time-delayed sequences on the data set are established and can transform the time-series data into the data sets of supervised learning problems so that the prediction model can extract information from it and make the prediction more accurate. The high-speed train state parameters, including the outside temperature, train speed, time, and initial motor temperature, are divided into training and test sets. As shown in Equation (1), $r$ time-delayed sequences $x_{n-1},x_{n-2},\dots \dots ,x_{n-r}$ are constructed, and the high-speed train traction motor temperature is used as the response variable $y$, as shown in Equation (2).

$$x_{n-k}=\left(\begin{array}{cccc}{a}_{\left(m-k\right)1}& a_{\left(m-k\right)2}& \cdots & a_{\left(m-k\right)p}\\ a_{\left(m-k+1\right)1}& a_{\left(m-k+1\right)2}& \cdots & a_{\left(m-k+1\right)p}\\ ⋮& ⋮& \cdots & ⋮\\ a_{\left(n-k\right)1}& a_{\left(n-k\right)2}& \cdots & a_{\left(n-k\right)p}\end{array}\right)$$

(1)

$$y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_{\left(n-m+1\right)}\end{array}\right)$$

(2)

Here, $n$, $m$ represents the sequence index, satisfying $r+1\le n$ and $r+1\le m$. $k$ and $r$ represent the lagged time nodes, satisfying $1\le r$ and $1\le k\le r$; $p$ represents the number of constructed time-delayed sequence feature sets; $1\le p$, $a_{ij}$ represents the specific eigenvalue of the delay sequence set vector $x_{n-k}$; and $y_q$ represents the specific eigenvalue of the response variable $y$, satisfying $\left(m-1\right)\le i\le \left(n-m+1\right),1\le j\le p,1\le q\le \left(n-m+1\right)$.

2.3. State Prediction Model Based on APSO-SVR

The model is constructed as shown in Equations (3) and (4):

$$f\left(a\right)=⟨w,a⟩+b$$

(3)

$$\underset{w,b,\xi ,{\xi }^{*}}{min} {\displaystyle \frac{1}{2}}\parallel w{\parallel }^2+C\sum _{i=1}^N \left({\xi }_i+{\xi }_i^{*}\right)$$

(4)

where $f\left(a\right)$ represents the objective of SVR, $w$ represents the weight vector, $b$ represents the intercept term, $C$ represents the regularization parameter, and ${\xi }_i$ and ${\xi }_i^{*}$ represent slack variables and satisfy $1\le i\le l$.

The constructed SVR model [23] should satisfy the constraints of Equation (5):

$$\begin{array}{ll}& y-⟨w,a_i⟩-b\le \epsilon +{\xi }_i\\ & ⟨w,a_i⟩+b-y\le \epsilon +{\xi }_i^{*}\\ & {\xi }_i,{\xi }_i^{*}\ge 0\end{array}$$

(5)

$\epsilon$ represents tolerance, and $a_i$ is the explanatory variable, $1\le i\le l$.

Since the grid search method is slow and has an average effect, this paper uses APSO to train the parameters of SVR. The flow chart is shown in Figure 2.

As shown in Equation (6), the APSO algorithm is used to optimize the parameters of the SVR model. This paper mainly uses it to find the optimal regularization parameter $C_1$ and tolerance ${\epsilon }_1$:

$$\begin{array}{l}{V}_i\left(t+1\right)=\omega \cdot V_i\left(t\right)+c_1\cdot r_1\cdot \left(P_i\left(t\right)-X_i\left(t\right)\right)+c_2\cdot r_2\cdot \left(G\left(t\right)-X_i\left(t\right)\right)\hfill \\ { X}_i\left(t+1\right)=X_i\left(t\right)+V_i\left(t+1\right)\hfill \end{array}$$

(6)

Here, $t$ represents the number of iterations. $\omega$ represents the inertia weight; $V_i$ represents the initialization speed; $c_1$ and $c_2$ represent the acceleration factors, which will change continuously during the training of the model; $r_1$ and $r_2$ represent random numbers; $P_i\left(t\right)$ represents the individual best position of particle $i$ at the $t$-th iteration; $X_i=\left(C_i,{\epsilon }_i\right)$ represents the particle initialization position; and $G\left(t\right)$ represents the global best position of the particle swarm at the $t$-th iteration.

Using $C_1$ and ${\epsilon }_1$ as SVR hyperparameters for model training, we can obtain the preliminary prediction result $y_1$.

2.4. Maximal Information Coefficient

The maximal information coefficient is a method for measuring the correlation between variables. MIC can identify extensive correlations between a pair of variables [24]. Taking each of the constructed time-delayed sequences $x_{n-1},x_{n-2},\dots \dots ,x_{n-r}$ as a unit, the MIC value of each set of time-delayed sequences and the high-speed train traction motor temperature $y$ is calculated as shown in Equations (7) and (8).

$$I\left(x_{n-k};y\right)=H\left(x_{n-k}\right)-H\left(\left.x_{n-k}\right|y\right)$$

(7)

where $I\left(x_{n-k};y\right)$ is the mutual information between $x_{n-k}$ and $\mathrm{y}$, $H\left(x_{n-k}\right)$ is the marginal entropy of $x_{n-k}$, and $H\left(\left.x_{n-k}\right|y\right)$ is the conditional entropy and satisfies $1\le k\le r$.

$$MIC\left(x_{n-k},y\right)={\displaystyle \frac{I\left(x_{n-k};y\right)}{\sqrt{H\left(x_{n-k}\right)\cdot H\left(y\right)}}}$$

(8)

where $x_{n-k}$ represents the $\mathrm{k}$th time-delayed sequence, $MIC\left(x_{n-k},y\right)$ represents the $\mathrm{M}\mathrm{I}\mathrm{C}$ value of the $\mathrm{k}$th time-delayed sequence and $y$, and $I\left(x_{n-k};y\right)$ is the mutual information between $x_{n-k}$ and $y$. $H\left(x_{n-k}\right)$ and $H\left(y\right)$ represent the entropy of $x_{n-k}$ and $y$, respectively, satisfying $1\le k\le r$.

Take the $l$ group of time-delayed sequences $a_1,a_2,\dots \dots ,a_l$ with larger $MIC$ values in the time-delayed sequences set as the explanatory variables.

2.5. Residual Prediction Method Based on KNN

The KNN algorithm is used to predict the error, which can make the prediction result more accurate. The KNN algorithm is an instance-based learning method whose core function is to perform prediction by evaluating the feature similarity between the new sample and a set of labeled training samples. In KNN, the similarity distance between the new sample and each training sample is first calculated, and then the prediction analysis is performed based on the data of the K training samples closest to the new sample [25].

First, the residual $∆y$ between the prediction result $y_1$ and the response variable $y$ is calculated, and $\mathrm{K}\mathrm{N}\mathrm{N}$ is used for residual prediction, as shown in Equations (9)–(11), and the residual prediction result $∆y_1$ is obtained.

$$∆y=y-y_1$$

(9)

$$d\left(a,a_i\right)=\sqrt{\sum _{j=1}^n {\left(a_j-a_{i,j}\right)}^2}$$

(10)

$$∆y_1={\displaystyle \frac{1}{K}}\sum _{i=1}^K ∆y_i$$

(11)

Here, $∆y_1$ is the predicted value, $∆y_i$ represents the target value of the $i$th neighbor, $K$ represents the nearest $K$th neighbor, $d\left(a,a_i\right)$ represents the distance between the new sample $a$ and $a_i$, and $i$ represents the number of actual parameters.

As calculated in Equation (12), the residual prediction result and the preliminary prediction result are combined to obtain the final high-speed train traction motor temperature prediction result $\hat{y}$.

$$\hat{y}=y_1+∆y_1$$

(12)

3. Experimental Verification

3.1. Data Set Introduction

A real traction motor state parameter data set and a traction motor fault data set during operation are established. The state parameter data set contains a large amount of real-time temperature data and train status data, covering the changes in motor temperature under different external temperatures and speeds. The fault data set contains the fault information of the traction system, which can be used to analyze the factors affecting the temperature.

3.1.1. Traction Motor Temperature and Related Parameter Data Set

Each carriage of the electric multiple units (EMUs) studied in this paper has two bogies, and each bogie is equipped with two traction motors, as shown in Figure 3. The data of this model have traction motor parameters corresponding to four axles in each carriage. The temperature prediction method for the EMU traction motor is studied based on the data collected by the bearing temperature sensor at the drive-end of the train traction motor, the bearing temperature sensor at the non-drive-end of the motor, the stator temperature sensor of the motor, the external temperature sensor, and the train speed sensor. The location of the traction motor temperature measurement point is shown in Figure 3. The data transmission method is shown in Figure 4. Various sensors installed on the train collect data, transmit the collected data to the transmission platform, and then package and transmit them to the server. After unpacking, the data are transmitted to the wireless data transmission device system (WTDS). The data format is shown in

Table 1. Original state parameter data.

Train Unit Number	Timestamp	Train Carriages	Parameter Name	Parameter Value	Time
7595	1943501402	8	Axis 1 motor non-drive-end bearing temperature	89	31 January 2023 21:43
7595	1943501402	8	Axis 2 motor non-drive-end bearing temperature	43	31 January 2023 21:43
7595	1943501402	8	Axis 3 motor non-drive-end bearing temperature	29	31 January 2023 21:43
7595	1943501402	8	Axis 4 motor non-drive-end bearing temperature	86	31 January 2023 21:43
7595	1943501402	8	Axis 1 motor drive-end bearing temperature	40	31 January 2023 21:43
7595	1943501402	8	Axis 2 motor drive-end bearing temperature	30	31 January 2023 21:43
7595	1943501402	8	Axis 3 motor drive-end bearing temperature	92	31 January 2023 21:43
7595	1943501402	8	Axis 4 motor drive-end bearing temperature	43	31 January 2023 21:43
7595	1943501402	8	Axis 1 motor stator temperature	29	31 January 2023 21:43
7595	1943501402	8	Axis 2 motor stator temperature	88	31 January 2023 21:43
7595	1943501402	8	Axis 3 motor stator temperature	42	31 January 2023 21:43
7595	1943501402	8	Axis 4 motor stator temperature	31	31 January 2023 21:43
7595	1943501402	8	Motor current	352	31 January 2023 21:43
7595	1943501402	5	External temperature	15	31 January 2023 21:43
7595	1943501402	0	Train speed	295	31 January 2023 21:43

, where carriage number 0 represents the parameters of the whole train, carriage numbers 1–4 represent the parameters of dividing the train into two units (for example, indoor temperature), the carriage numbers 5–12 represent the parameters corresponding to the carriages, and their serial number minus 4 represents the actual number of corresponding carriages, such as the carriage 8 in Table 1, which is the fourth train carriage.

3.1.2. Traction Motor Fault Data Set

The traction motor fault data set contains all the fault data obtained from manual inspection and sensor detection. The relevant factors affecting the traction motor temperature can be mined according to its records and time. The traction motor fault original data set includes 13 parameters: train model, train unit number, train number, discovery time, fault description, kilometers traveled, processing status, processing method, processing detailed description, processing time, processing repair process, date of completion, and function classification name. Its format is shown in

Table 2. Original fault data.

Serial Number	Parameter Name	Example
1	Train type	CRH3/CRH5/CRH380
2	Train unit number	8234
3	Train number	G4511
4	Discovery time	2023-1-1 1:11 (The time when the fault was discovered)
5	Fault description	One-axis traction motor dust cap damaged
6	Train mileage	3876315 (as of the time the fault was detected)
7	Processing status	Processed/Unprocessed/To be processed
8	Processing method	Replace/Repair/Supplement/Cleaning/Other
9	Processing detailed description	(Fill in the content by relevant personnel according to the specific situation)
10	Processing time	2023-1-1 1:11 (The time when the fault was dealt with)
11	Processing repair process	First-level repair/Third-level repair/First-level overhaul
12	Date of completion	2023-1-1 1:13 (The time when the fault was completely handled)
13	Function classification name	Traction motor

.

After analysis and processing, the multidimensional data set (partial) used by the method in this paper is screened out, as shown in

Table 3. Data sets used (partial).

Time	Stator Temperature	Drive-End Bearing Temperature	Non-Drive-End Bearing Temperature	Electric Current	External Temperature	Speed	Initial Bearing Temperature
10:34:00	123	68	54	424	41	294	68
10:35:00	123	69	55	264	41	293	68
10:36:00	125	70	55	248	41	293	68
10:37:00	125	70	56	280	41	292	68
10:38:00	126	71	56	232	41	294	68
10:39:00	126	72	56	304	42	292	68

. The data are time, stator temperature, drive-end bearing temperature, non-drive-end bearing temperature, current value, external temperature, speed, and initial bearing temperature.

3.2. Data Analysis

As shown in Figure 5, the sensor data for a complete cycle can be divided into four parts. Since the train does not operate continuously for 24 h but the sensor collects data throughout the entire day, analyzing this full-day data set allows us to accurately identify the specific time periods we need to predict and determine which parameters will be used to forecast abnormal conditions.

The data of S1 segment are from 00:00 to 03:00. As shown in the figure, the train running speed is 0, and the train remains in an inactive state during this period. At this time, the temperature of the motor bearings and stator is mainly affected by the external environment, and the basic trend changes with the change of external temperature.

The data for segment S2 are from 03:00 to 05:00, during which the train speed fluctuates twice. This stage is mainly the testing phase before the train runs, and the temperature of the motor bearings and stator fluctuates slightly due to the influence of train speed. At this time, the temperature of the motor bearings is more affected by the ambient temperature compared to the stator temperature, but it may also fluctuate due to the train starting. During the phase of increasing train speed, the values of various temperature sensors of the motor change.

The data of S3 segment are from 05:00 to 21:00, which is the stage of train operation. The sensors are affected by the running speed and ambient temperature. When stopping at the station, if t is 690 and the train speed is 0, the axle temperature and stator sensor temperature will have a decreasing trend over time.

The data for S4 segment are from 21:10–24:00. At this time, the train stops at the station with a running speed of 0. The temperature of the motor bearings and stator gradually approaches room temperature. After a period of time, like S1 segment, it is mainly affected by the external environment.

After dividing the train operation phase into four sections, the correlation between each parameter in each section will be analyzed in detail.

This article uses methods such as correlation coefficient, scatter plot, and correlation coefficient table to analyze the correlation between the data. The use of matrix scatter plots can visually display the relationships between variables and help us further understand the distribution of data. The correlation coefficient table provides detailed correlation information, which helps screen parameters and prepare for predicting the temperature of traction motors in the future. Figure 5 shows the segmentation results of data from a certain day in August.

In this article, the Pearson correlation coefficient is used to calculate the correlation between various parameters.

(1)

S1 and S2 segments:

Due to the fact that the S1 and S2 segments are mainly affected by environmental temperature and are not significantly affected by other temperatures, they were analyzed together. From the matrix scatter plot and correlation coefficient graph in Figure 6, it can be seen that the linear relationship between the parameters in this segment is not strong. There is a certain correlation between the stator, drive-end, and non-drive-end bearing temperatures of the traction motor. The reason may be that all three parameters are affected by outdoor temperature during this stage, so the trend of change is roughly the same. The correlation coefficient between train speed and motor current is relatively large, but the linear correlation is not obvious. At this stage, the train has not yet started running, so it is impossible to accurately determine the precise relationship between various factors.

(2)

S3 segment:

From the matrix scatter plot and correlation coefficient graph in Figure 7, it can be seen that there is a linear correlation and strong correlation between the stator, drive-end bearing, and non-drive-end bearing temperatures of the traction motor. The reason may be that all three parameters are greatly affected by speed during this stage, and their trend changes with speed. The correlation coefficient between the external temperature and non-drive-end bearing temperature during this stage is relatively large, and the temperature of the non-drive-end bearing may be more affected by external temperature than the temperature of the drive-end bearing. The stator may be affected by external temperature.

(3)

S4 section:

From the matrix scatter plot and correlation coefficient graph in Figure 8, it can be seen that some parameters have a clear linear relationship with time. There is a strong correlation between the temperature and time of the stator, drive-end bearing, and non-drive-end bearing of the traction motor. The reason may be that at this stage, when the train stops at the station, the temperature of the motor gradually decreases to the outdoor temperature, so there is a negative correlation with time.

As can be seen from the sections above, the time when the traction motor experiences temperature abnormalities is generally in section S3, which is the stage of train operation, and may be affected by various factors that may cause abnormal temperature of the traction motor, thereby affecting its state. Therefore, the data from section S3 will be selected for subsequent prediction.

3.3. Method Validation

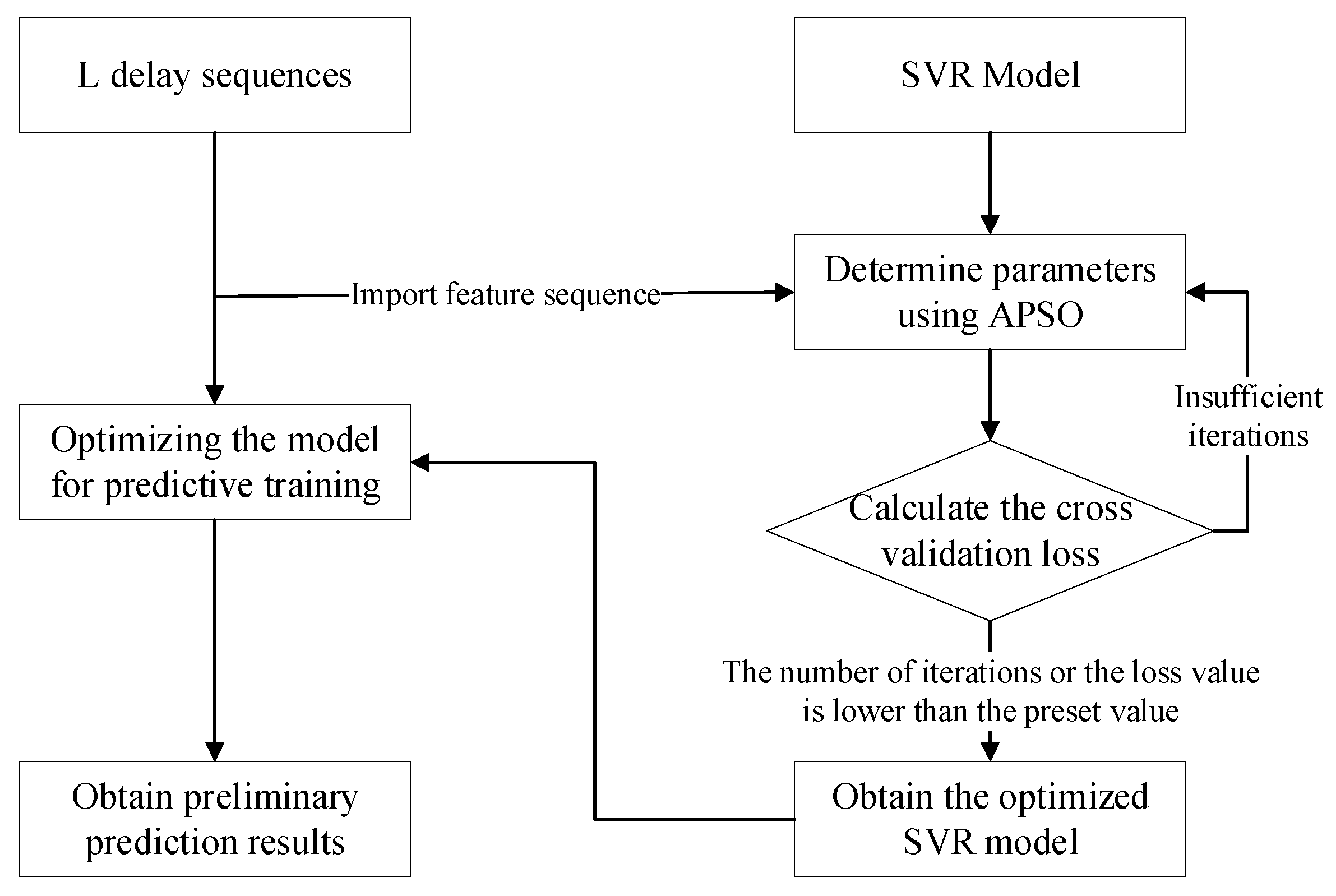
In order to verify the feasibility and accuracy of the algorithm in this paper, the high-speed train data set in Section 2.1 was divided into a training set and a test set according to a ratio of 7:3. The influence of external and internal factors on the state of the traction motor was considered. Time, external temperature, train speed, and initial bearing temperature of the traction motor were selected as inputs to verify the algorithm in this paper. First, the data shown in Table 3 were used to construct the time-delayed sequences, as shown in Figure 9.

A time-delayed sequence was constructed for each input parameter of the traction motor, and the MIC value was calculated in relation to the target signal. Here, the temperature signal of the traction motor drive-end was taken as the target temperature signal. The calculated partial MIC value results are shown in

Table 4. MIC values of the bearing temperature at the drive-end corresponding to different state parameters of the traction motor.

MIC Value	The MIC Value of Time and the Target Parameter	The MIC Value of the External Temperature and the Target Parameter	The MIC Value of the Initial Bearing Temperature and the Target Parameter
Delay time 1	0.632	0.485	0.439
Delay time 2	0.642	0.485	0.453
Delay time 3	0.635	0.484	0.464

. It can be seen that the MIC value of time is the largest, followed by the external temperature, train speed, and the initial bearing temperature of the traction motor.

Equations (13)–(18) provide the calculation methods for the mean square error $MSE$, root mean square error $RMSE$, mean absolute error $MAE$, mean bias error $MBE$, mean absolute percentage error $MAPE$, and $R^2$, and the results of calculating the parameters above based on the predicted values of the traction motor temperature and its true values are shown in

Table 5. The prediction error of this model.

Error Value	$\mathit{M}\mathit{S}\mathit{E}$	$\mathit{R}\mathit{M}\mathit{S}\mathit{E}$	$\mathit{M}\mathit{A}\mathit{E}$	$\mathit{M}\mathit{B}\mathit{E}$	$\mathit{M}\mathit{A}\mathit{P}\mathit{E}$	${\mathit{R}}^2$
Our model	1.525	1.235	0.991	0.353	0.075	0.980

.

$$MSE={\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(y_i-\widehat{y_i}\right)}^2$$

(13)

$$RMSE=\sqrt{{\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(y_i-\widehat{y_i}\right)}^2}$$

(14)

$$MAE={\displaystyle \frac{1}{m}}\sum _{i=1}^m\left|y_i-\widehat{y_i}\right|$$

(15)

$$MBE={\displaystyle \frac{1}{m}}\sum _{i=1}^m\left(y_i-\widehat{y_i}\right)$$

(16)

$$MAPE={\displaystyle \frac{100\%}{m}}\sum _{i=1}^m\left|{\displaystyle \frac{{\widehat{y_i}-y}_i}{y_i}}\right|$$

(17)

$$R^2=1-{\displaystyle \frac{SSR}{SST}}=1-{\displaystyle \frac{\sum _{i=1}^m{\left({\widehat{y_i}-y}_i\right)}^2}{\sum _{i=1}^m{\left({\overline{y}-y}_i\right)}^2}}$$

(18)

where $m$ is the number of prediction samples, $y_i$ is the true value, $\widehat{y_i}$ is the predicted value, $SSR$ is the variation explained by the regression model, and $SST$ is the total variation of the dependent variable.

The residual prediction result using KNN is shown in Figure 10, and the final prediction result of the prediction method based on MIC and improved SVR is shown in Figure 11.

From the residual prediction results of KNN in Figure 10, it can be seen that the predicted value has the same positive and negative signs as the true value. Using KNN for residual prediction can reduce some prediction errors. From Figure 11, it can be seen that after prediction using the method proposed in this paper, the predicted value of the traction motor temperature signal output is closer to its true temperature value, and when the temperature fluctuates, the method in this paper can still make predictions, and the model fitting effect is good.

4. Prediction Results and Analysis

4.1. The Impact of Parameter Selection on This Method in This Experiment

4.1.1. Comparison of Different Search Parameter Methods

Grid search is one of the methods for determining the best model hyperparameters in machine learning. Its advantage is that it can ensure that the global optimal solution in a given grid is found, avoiding excessive errors [26]. However, when the hyperparameter space is large, the search process may become time-consuming because each set of parameters needs to be trained and evaluated. To speed up the hyperparameter search process, other optimization algorithms or techniques can be considered. For example, this paper uses the APSO optimization algorithm, which has higher search efficiency and smaller errors. Figure 12 shows the change in prediction error value during APSO iteration.

Table 6. Performance comparison of two search optimization methods.

Error Value	APSO Search	Grid Search
Search parameter quantity	1048,576.00	287.00
Search time	67.99	235.95
$RMSE$	1.20306205	2.23

compares the two search methods. It can be seen that APSO optimization reduces a lot of search time and shows better results in this paper’s data set.

4.1.2. Comparison of Different $r$ (Delay Time Points) and $l$ (Selected Time Series)

Selecting different delay time points for the time-delayed sequences and selecting different time series will affect the prediction results. The results of discussing the impact of different $r$ and $l$ on the loss value are shown in

Table 7. Loss results for different $r$/l.

$\mathit{r}$$\text{}\mathit{l}$	4	5	6	7	8	9	10	11	12	13	14
3	1.18	1.12	1.22	1.20	1.22
4	1.34	1.25	1.35	1.05	1.14	1.23	1.24	1.23
5	2.42	1.35	1.21	1.40	1.40	1.17	1.8	1.2	1.98	1.48	1.38

and Figure 13.

As can be seen from Table 7 and Figure 13, different $r$ (delay time point) and $l$ (selected time series) will affect the predicted loss value. It is necessary to calculate and select the optimal delay time point $r$ and time series $l$ for prediction to ensure the minimum error and achieve the purpose of optimizing the prediction effect. When using grid search, the best parameters $r$ are 5, and $l$ are 14. It can be seen from the figure that as $r$ increases, the $MSE$ decreases steadily. At the same $r$ level, the larger the $l$, the smaller the $MSE$ is, and the $MSE$ value gradually converges to a stable value.

4.1.3. The Impact of This Optimization Method on the Prediction Results

This paper uses MIC to select feature sequences and KNN to optimize SVR prediction results, as shown in

Table 8. The impact of optimization methods on prediction results.

	$\mathbf{Our}\mathbf{Method}\mathit{R}\mathit{M}\mathit{S}\mathit{E}$	$\mathbf{The}\mathit{R}\mathit{M}\mathit{S}\mathit{E}$ Without Using the MIC	$\mathbf{The}\mathit{R}\mathit{M}\mathit{S}\mathit{E}$ Without Using KNN
Train unit A	1.25	2.80	1.32
Train unit B	1.29	2.48	1.36

and Figure 14. Using the data of the two train units for analysis, the optimization methods used in this paper have optimized the prediction results.

4.2. Effects of Different Working Conditions and Components on This Method

Under different ambient temperatures, the initial and outside temperatures of the traction motor are different. Temperature variations in traction motors may also vary when trains are operated under different conditions. This paper selects the traction motor temperature prediction results of the trains on the same route in different months. Due to the different locations of different sensor measurement points and the different influences of external factors, the temperature changes are different. In order to verify the universality of the method in this paper for motor temperature prediction, this paper predicts different measurement points. The results are shown in

Table 9. Prediction results under different working conditions and different measuring points ($RMSE$).

	Non-Drive-End Bearing Temperature in August	Drive-End Bearing Temperature in August	Non-Drive-End Bearing Temperature in January	Drive-End Bearing Temperature in January
Train unit A	1.21	1.29	1.30	1.29
Train unit B	1.27	1.11	1.22	1.33

and Figure 15. The results show that the model in this paper has good prediction results for the non-drive-end bearing temperature measurement points and the drive-end bearing temperature measurement points, and the prediction results for different seasons are also similar. The method in this paper has a certain universality under different working conditions.

4.3. Comparison of Experimental Results with Other Algorithms

In order to verify the advantages of the proposed method, this section compares the errors of the prediction results of the proposed method with those of other prediction algorithms. As shown in

Table 10. Evaluation index results of different prediction methods.

	Our Method	SKRR	ELM	Random Forest	CNN	SVR	BP
$RMSE$	1.23	2.29	2.72	3.22	3.89	4.22	4.73
$R^2$	0.98	0.96	0.92	0.57	0.87	0.78	0.74
$MAE$	0.99	1.38	1.65	2.34	2.77	3.59	3.45
$MBE$	0.02	−0.08	0.21	0.46	0.47	1.55	0.14

and Figure 16, the results show that the proposed method has the smallest $RMSE$, $MAE$, and $MBE$, indicating that the deviation between the predicted value and the true value of the traction motor temperature signal by the proposed method is small, and the prediction result is more accurate and stable.

5. Conclusions

An offline prediction method for traction motor temperature signals is proposed based on MIC and improved SVR. Time-delayed sequences were constructed for the traction motor feature set, and the MIC value based on motor temperature signal was calculated. The time-delayed sequences were screened based on this value, the traction motor temperature signal was predicted using APSO-SVR, and the residual was calculated. The residual was predicted using KNN, and the final prediction result of the traction motor temperature signal was obtained by combining the prediction results of the two. Some conclusions can be obtained as follows:

(1)

The offline prediction method of traction motor temperature signal based on MIC and improved SVR proposed by our research institute was validated on the high-speed train data set, and the method is feasible. The experimental results indicate that, compared to other comparative models, the prediction model proposed in this paper, based on MIC and the improved SVR, achieves higher prediction accuracy and lower $MAE$ and $RMSE$ values. This suggests that the predicted values obtained using this method deviate less from the actual values of the traction motor temperature signal, making the predictions more accurate and stable. Consequently, this model can more effectively ensure the efficiency and safety of high-speed train operations.

(2)

This method uses the time-delayed sequences and MIC for feature selection and expands the three feature variables into multiple (up to $r\ast l$) feature variables. This feature selection method can give each feature sequence a high correlation with the target variable, thereby improving the accuracy and robustness of the prediction.

(3)

This method introduces the KNN algorithm to reduce the error after the APSO-SVR model is trained, effectively reducing the model’s interference factors and improving the model’s prediction accuracy.

In summary, the prediction technology proposed in this study integrates the advantages of APSO-SVR and KNN algorithms and has high prediction accuracy and reliability, which can meet the high standard requirements of actual equipment fault prediction. However, considering the limitations of this technology in predicting time spans and the extremely strict standards for prediction accuracy required by the safety requirements of high-speed railway equipment, a future study will continue to delve into the field of long-term prediction and strive to further improve and enhance existing technologies.