Design Oriented Analysis of Overhead Line Magnetic Energy Harvesters with Passive and Active Rectifiers
Abstract
1. Introduction
2. Methodology
2.1. OLMEH with Passive Rectifier
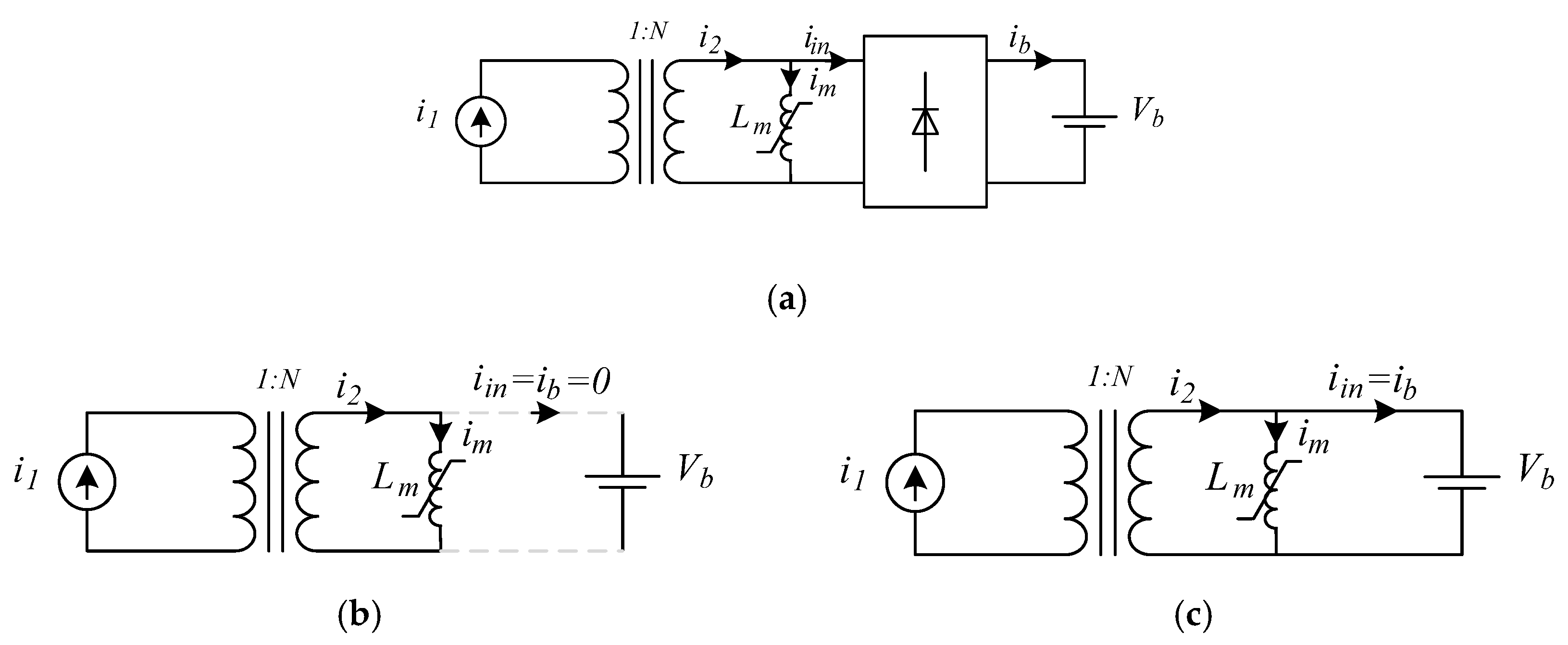
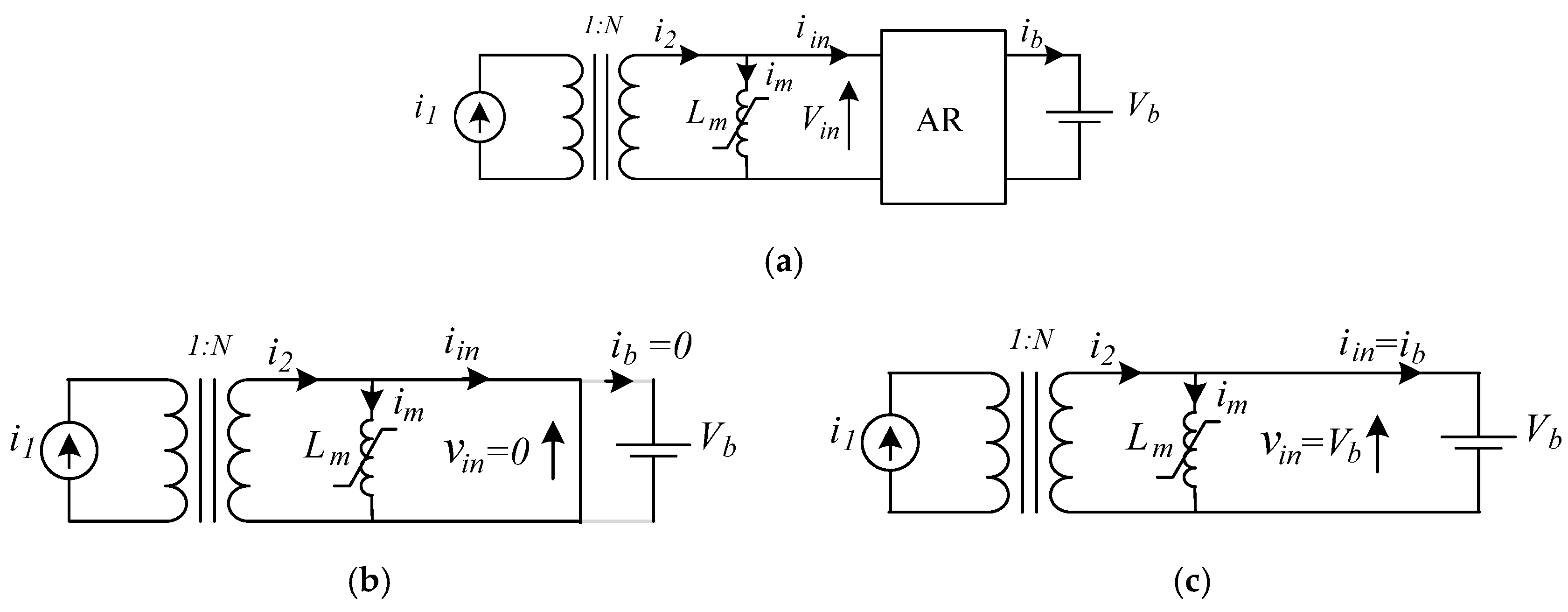
2.1.1. Basic Assumptions and Equivalent Circuits
- (a)
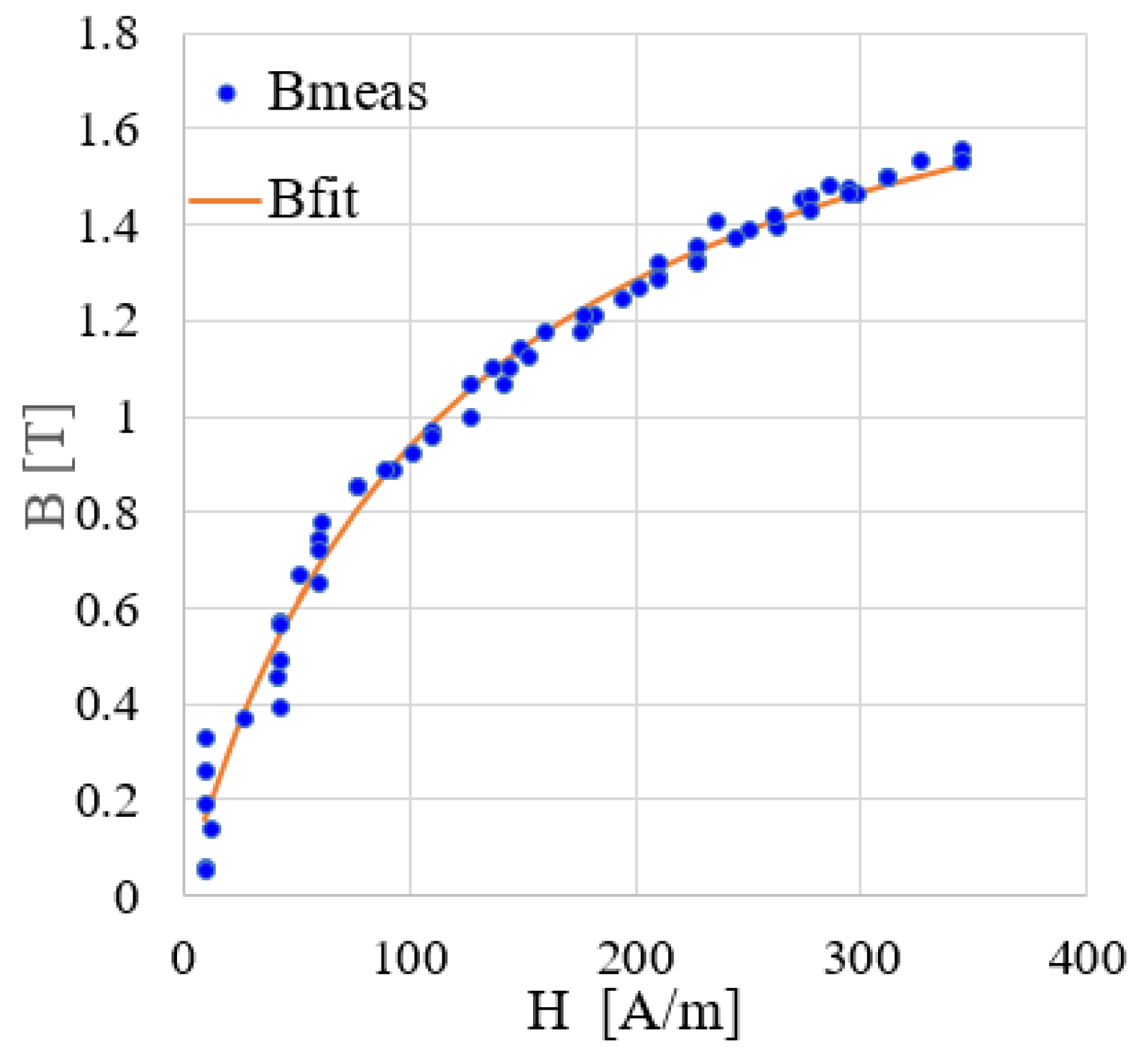
- The hysteresis of the core material is neglected.
- (b)
- The core BH characteristic is approximated by a piecewise linear function.
- (c)
- A simplified cantilever model is used to represent the OLMEH magnetic circuit with the saturable magnetizing inductance, Lm, placed on the secondary winding, whereas the leakage inductance is neglected.
- (d)
- Lossless rectifiers are assumed.
2.1.2. State Analysis of OLMEH with a Passive Rectifier
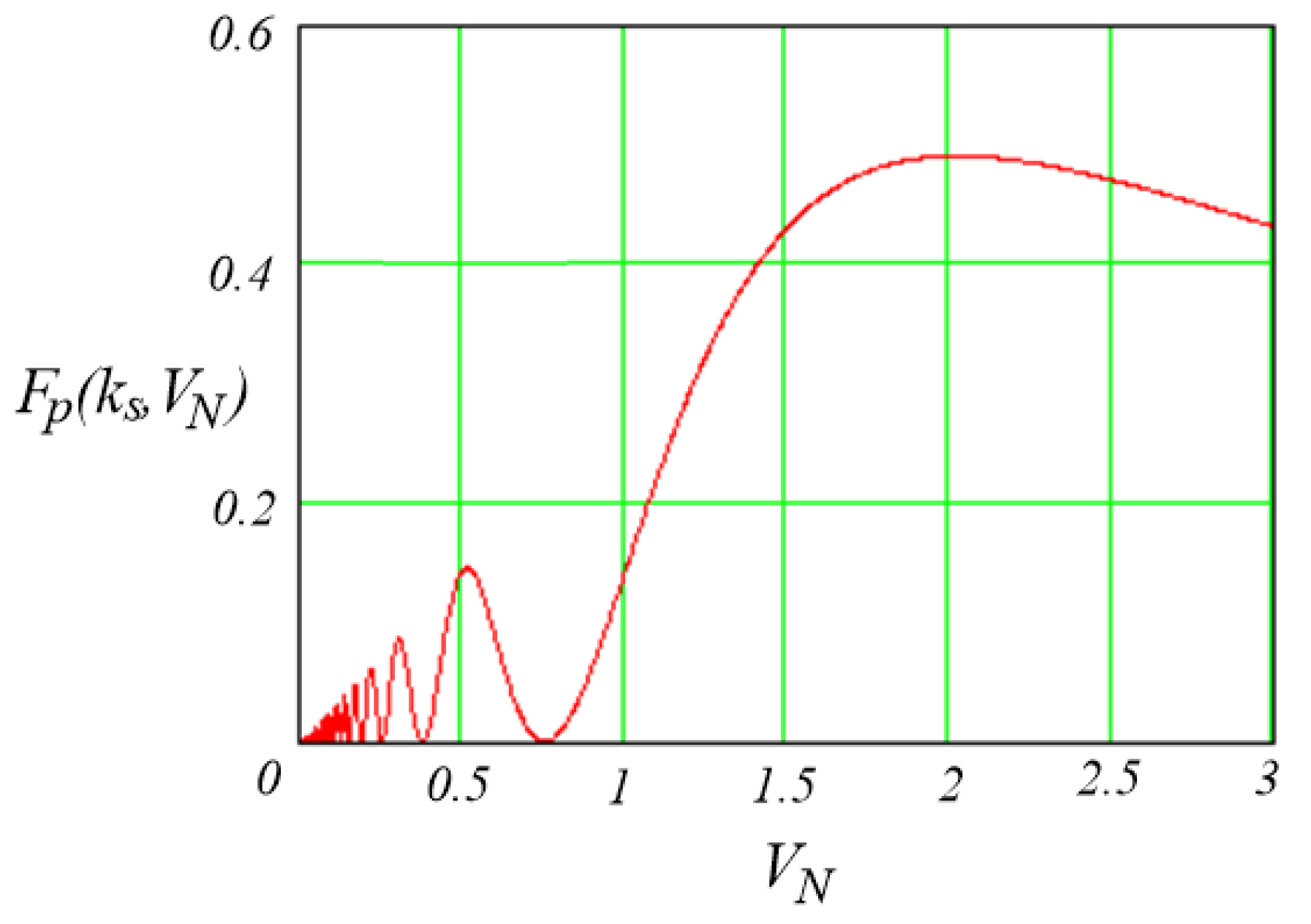
2.1.3. Design Guidelines of an OLMEH with a Passive Rectifier
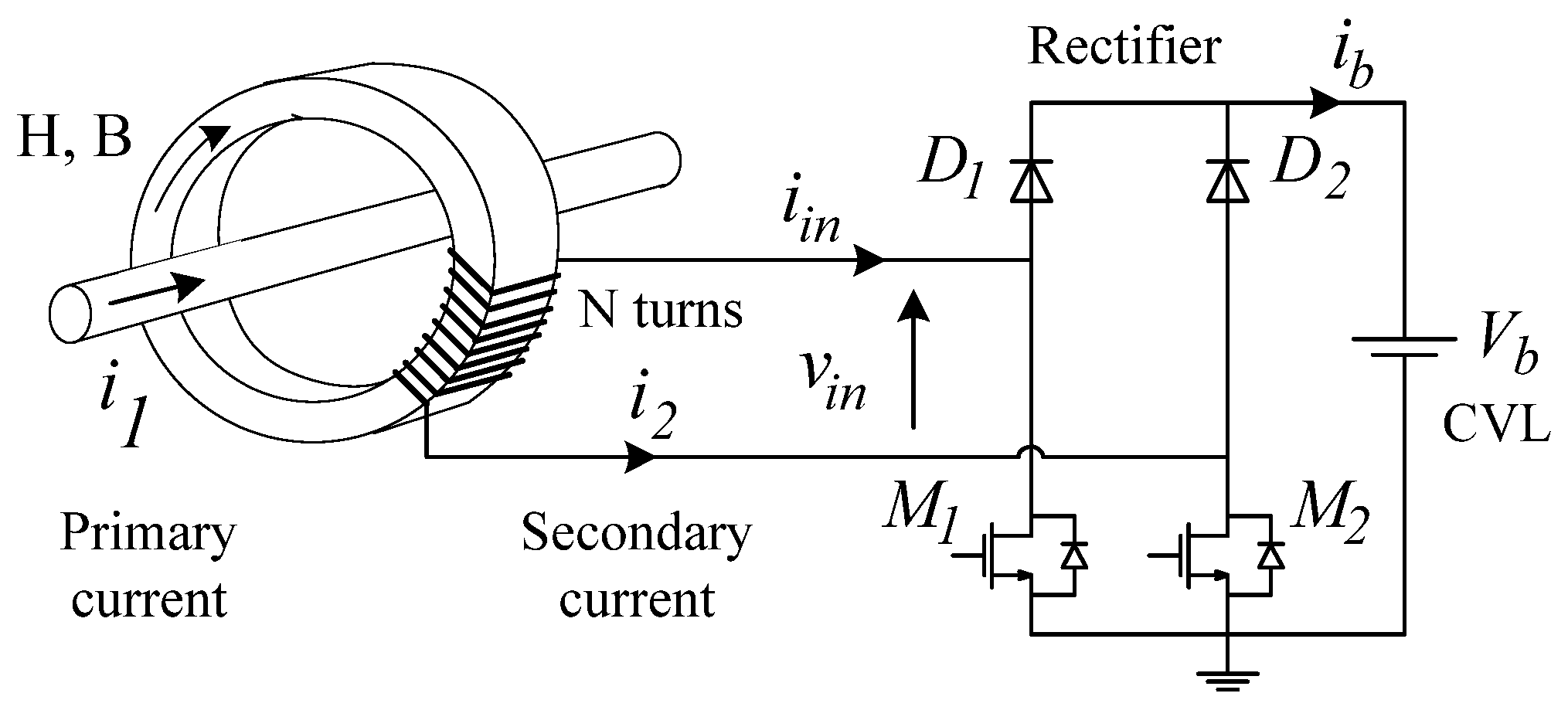
2.2. OLMEH with Active Rectifier
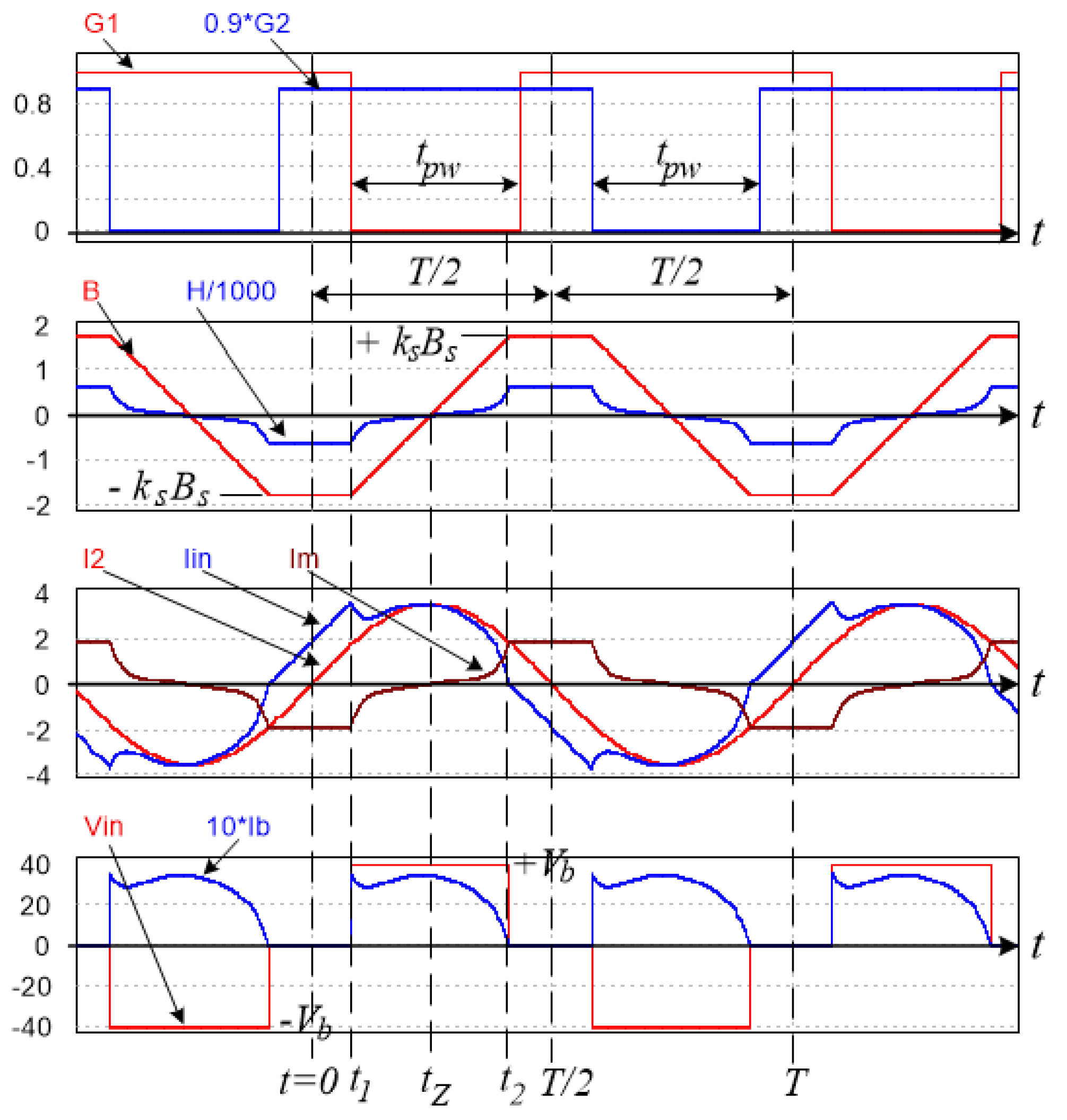
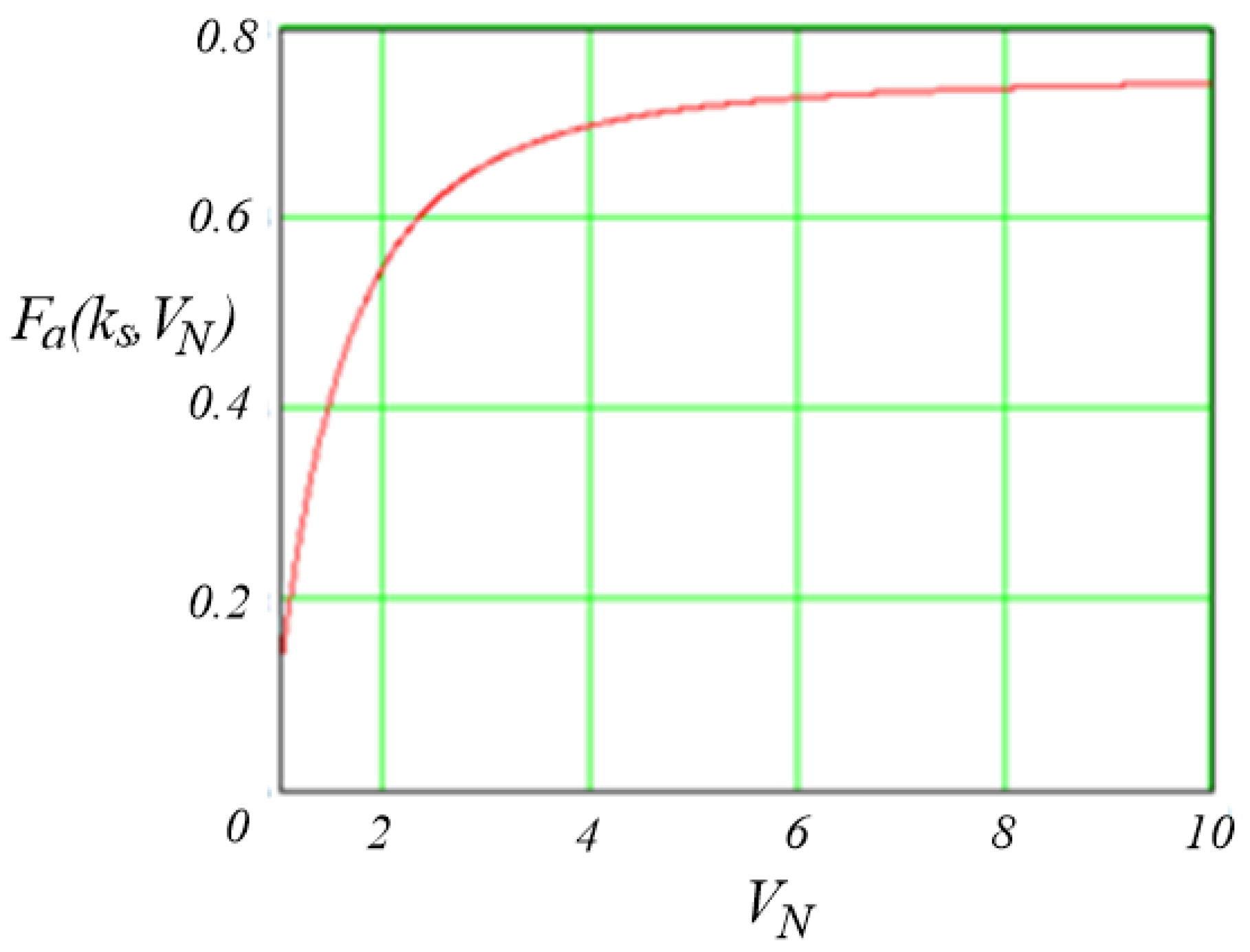
2.2.1. State Analysis of OLMEH with Active Rectifier
2.2.2. Design Guidelines for OLMEH with an Active Rectifier
2.3. Design Examples
2.3.1. Design Example 1: OLMEH with a Passive Rectifier
2.3.2. Design Example 2: OLMEH with an Active Rectifier
2.3.3. Design Example 3: OLMEH with an Active Rectifier
3. Validation and Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| t | Time (continuous): |
| t1 | State 1 termination instant |
| t2 | State 2 termination instant |
| tZ | Flux density zero crossing instant |
| Power line angular frequency | |
| Flux density: | |
| Bs | Saturation flux density |
| Field intensity: | |
| Hs | Saturation field intensity |
| a, b | Froelich coefficients: |
| N | Number of turns |
| lc | Magnetic path length |
| Ac | Magnetic core area |
| i1(t) | Line (primary) current instantaneous |
| I1m | Line (primary) current amplitude |
| i2(t) | Secondary current instantaneous |
| I2m | Secondary current amplitude |
| im(t) | Magnetizing current, (instantaneous) |
| Rectifiers’ input (AC side) voltage | |
| Rectifiers’ input (AC side) current | |
| Vb | CVL voltage |
| CVL current | |
| Po | Average output power |
References
- Enayati, J.; Asef, P. Review and Analysis of Magnetic Energy Harvesters: A Case Study for Vehicular Applications. IEEE Access 2022, 10, 79444–79457. [Google Scholar] [CrossRef]
- Olszewski, O.Z.; Houlihan, R.; Blake, A.; Mathewson, A.; Jackson, N. Evaluation of vibrational PiezoMEMS harvester that scavenges energy from a magnetic field surrounding an AC current-carrying wire. J. Microelectromech. Syst. 2017, 26, 1298–1305. [Google Scholar] [CrossRef]
- Zorlu, Ö.; Topal, E.T.; Külah, H. A vibration-based electromagnetic energy harvester using mechanical frequency up-conversion method. IEEE Sens. J. 2011, 11, 481–488. [Google Scholar] [CrossRef]
- Deng, Z.; Dapino, M.J. Review of magnetostrictive vibration energy harvesters. Smart Mater. Struct. 2017, 26, 103001. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, X.; Liu, H.; Yang, J. Magnetostrictive biomechanical energy harvester with a hybrid force amplifier. Int. J. Mech. Sci. 2022, 233, 107652. [Google Scholar] [CrossRef]
- Bibo, A.; Masana, R.; King, A.; Li, G.; Daqaq, M.F. Electromagnetic ferrofluid-based energy harvester. Phys. Lett. A 2012, 376, 2163–2166. [Google Scholar] [CrossRef]
- Liu, Q.; Alazemi, S.F.; Daqaq, M.F.; Li, G. A ferrofluid based energy harvester: Computational modeling analysis and experimental validation. J. Magn. Magn. Mater. 2018, 449, 105–118. [Google Scholar] [CrossRef]
- Wu, S.; Luk, P.C.K.; Li, C.; Zhao, X.; Jiao, Z. Investigation of an electromagnetic wearable resonance kinetic energy harvester with ferrofluid. IEEE Trans. Magn. 2017, 53, 4600706. [Google Scholar] [CrossRef]
- Kanno, I. Piezoelectric MEMS for energy harvesting. J. Phys. Conf. Ser. 2015, 660, 012001. [Google Scholar] [CrossRef]
- Wang, Q.; Kim, K.-B.; Woo, S.; Sung, T. Magnetic Field Energy Harvesting with a Lead-Free Piezoelectric High Energy Conversion Material. Energies 2021, 14, 1346. [Google Scholar] [CrossRef]
- Xiao, H.; Peng, H.; Yuan, J. A Coil Connection Switching Strategy for Maximum Power Delivery in Electromagnetic Vibration Energy Harvesting System. In Proceedings of the 2021 IEEE Energy Conversion Congress and Exposition (ECCE), Vancouver, BC, Canada, 10–14 October 2021; pp. 5867–5872. [Google Scholar]
- Moon, J.; Leeb, S.B. Power Electronic Circuits for Magnetic Energy Harvesters. IEEE Trans. Power Electron. 2016, 31, 270–279. [Google Scholar] [CrossRef]
- Yuan, S.; Huang, Y.; Xu, Q.; Zhou, J.; Song, C.; Thompson, P. Magnetic Field Energy Harvesting Under Overhead Power lines. IEEE Trans. Power Electron. 2015, 30, 6191–6202. [Google Scholar] [CrossRef]
- Chang, K.; Kang, S.; Park, K.; Shin, S. Electric Field Energy Harvesting Powered Wireless Sensors for Smart Grid. J. Electr. Eng. Technol. 2012, 7, 75–80. [Google Scholar] [CrossRef]
- Bader, S.; Oelmann, B. Enabling Battery-Less Wireless Sensor Operation Using Solar Energy Harvesting at Locations with Limited Solar Radiation. In Proceedings of the 4th International Conference on Sensor Technologies and Applications (SENSORCOMM), Venice, Italy, 18–25 July 2010; pp. 602–608. [Google Scholar]
- Tan, Y.; Panda, S. Self-Autonomous Wireless Sensor Nodes with Wind Energy Harvesting for Remote Sensing of Wind-Driven Wildfire Spread. IEEE Trans. Instrum. Meas. 2011, 60, 1367–1377. [Google Scholar] [CrossRef]
- Zhu, M.; Baker, P.C. Alternative Power Sources for Autonomous Sensors in High Voltage Plant. In Proceedings of the 2009 IEEE Electrical Insulation Conference, Montreal, QC, Canada, 31 May–3 June 2009; pp. 36–40. [Google Scholar]
- Abramovitz, A.; Shvartsas, M.; Kuperman, A. On the maximum power of passive magnetic energy harvesters feeding constant voltage loads under high primary currents. IEEE Trans. Power Electron. 2024, 39, 12076–12080. [Google Scholar] [CrossRef]
- Abramovitz, A.; Shvartsas, M.; Kuperman, A. Enhanced maximum power point reaching method for passive magnetic energy harvesters operating under low primary currents. IEEE Trans. Power Electron. 2024, 39, 6619–6623. [Google Scholar] [CrossRef]
- Abramovitz, A.; Shvartsas, M.; Orfanoudakis, G.I.; Kuperman, A. Output Characteristics of Passive Magnetic Energy Harvester Feeding a Constant-Voltage-Type Load. IEEE J. Emerg. Sel. Top. Power Electron. 2024. [Google Scholar] [CrossRef]


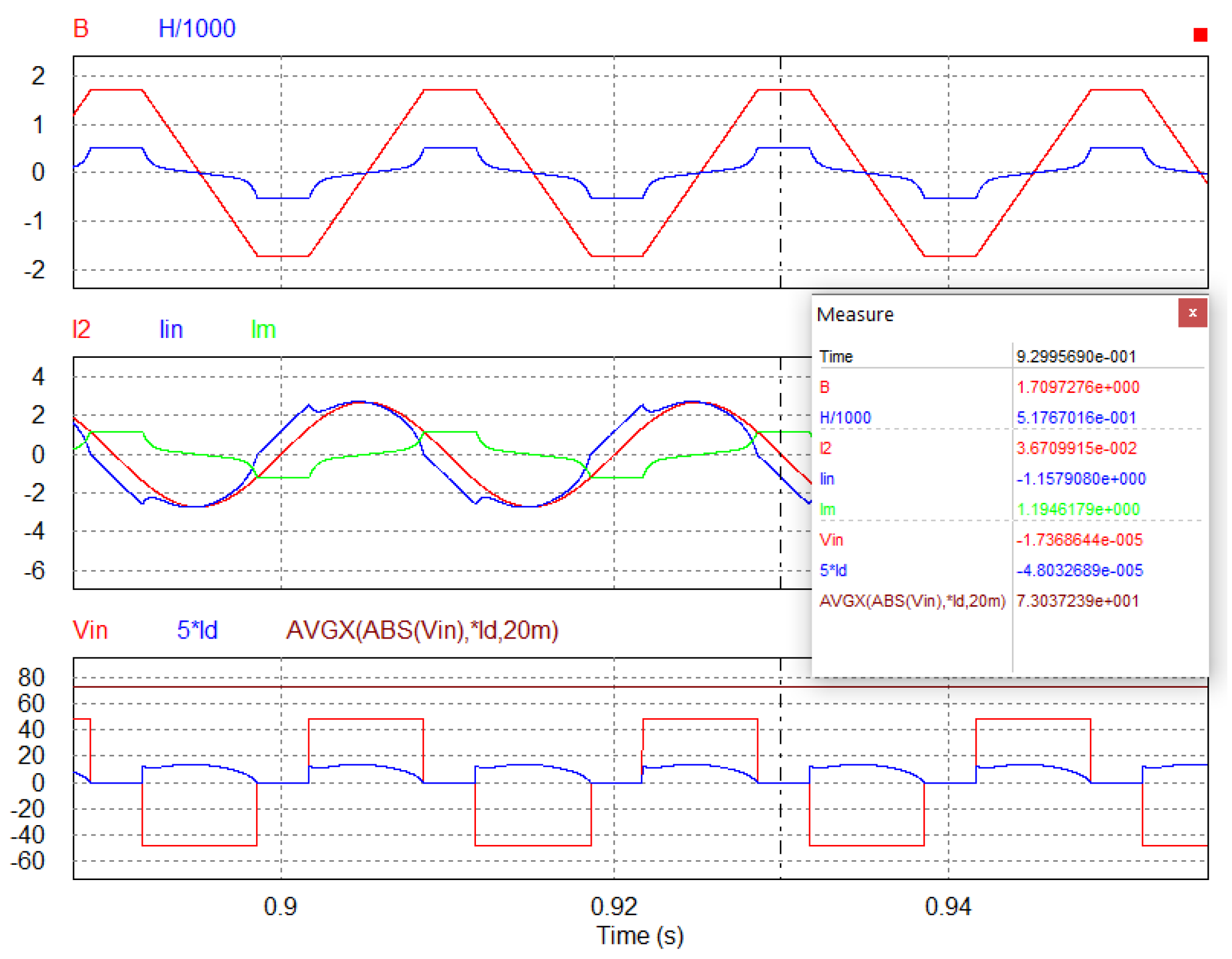


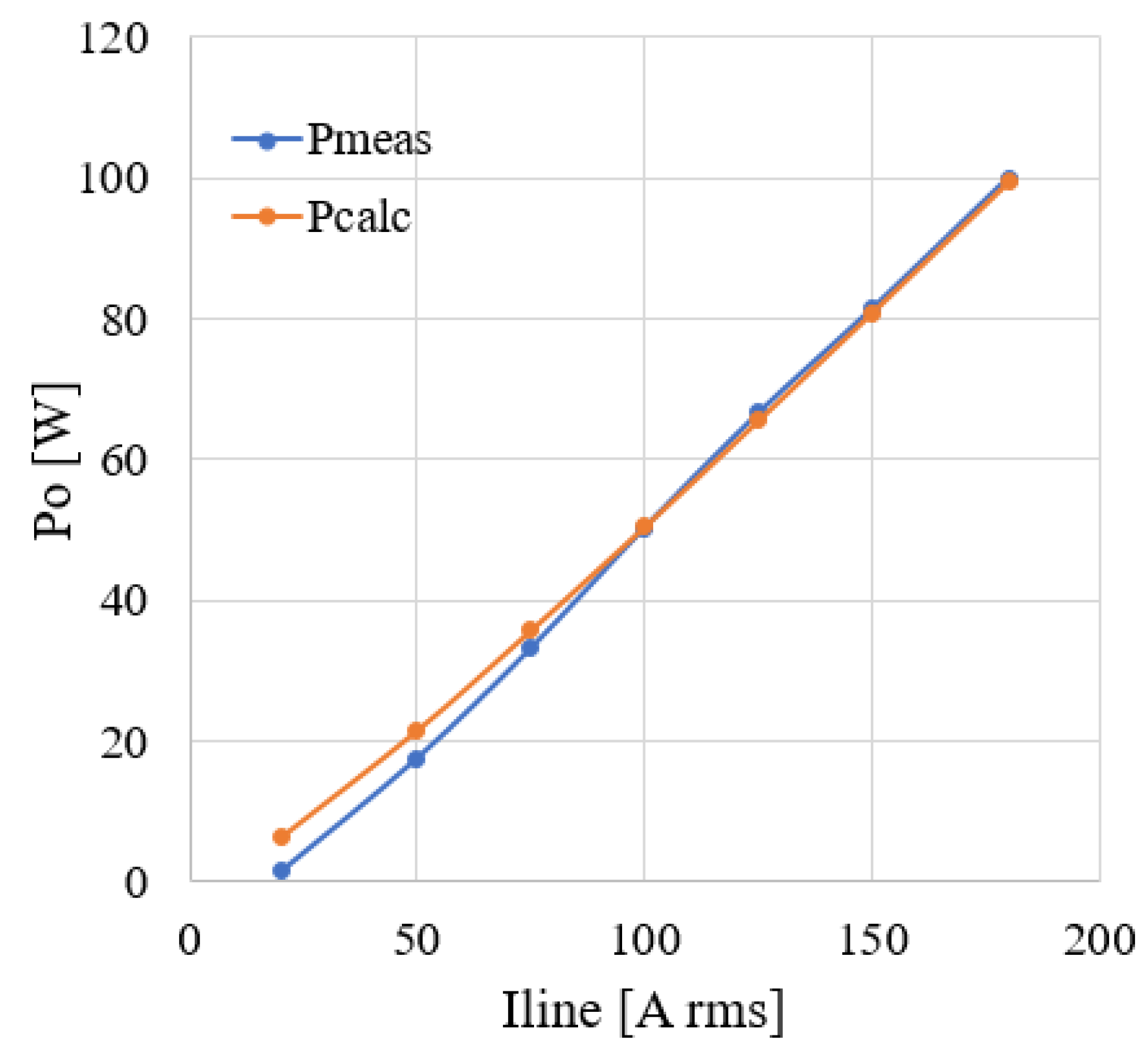


| Param. (eq.) | (23) | (29) | (30) | |
|---|---|---|---|---|
| Calculated | 75 (goal) | 0.8 | 1.6 | 2.5 (goal) |
| Simulated | 80 | 0.9 | 1.7 | 2.4 |
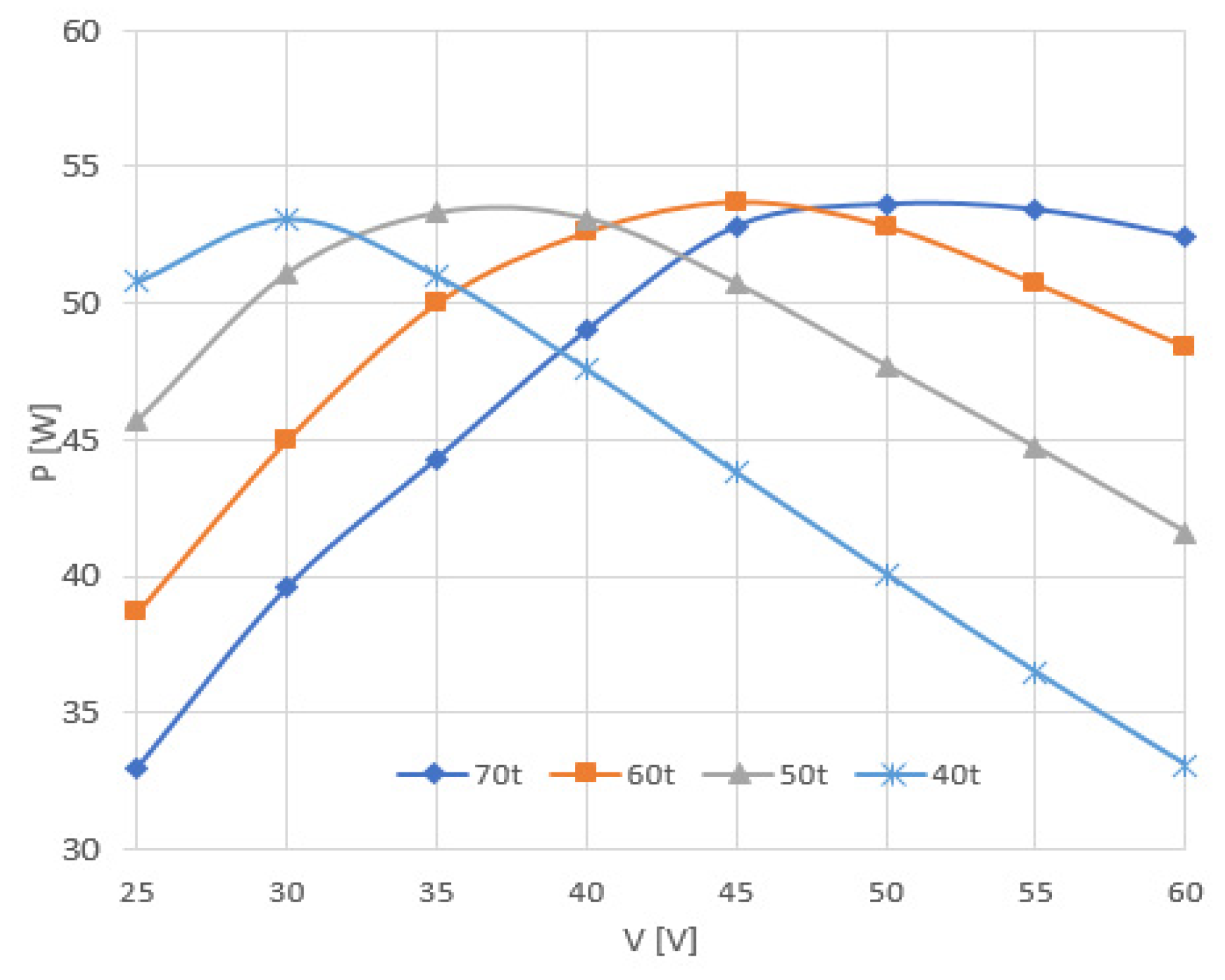
| N [Turn] | 40 | 50 | 60 | 70 |
|---|---|---|---|---|
| [V] predicted | 26.9 | 34.3 | 41.8 | 49.2 |
| [V] experimental | 30 | 37 | 45 | 51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abramovitz, A.; Shvartsas, M.; Kuperman, A. Design Oriented Analysis of Overhead Line Magnetic Energy Harvesters with Passive and Active Rectifiers. Electronics 2024, 13, 4904. https://doi.org/10.3390/electronics13244904
Abramovitz A, Shvartsas M, Kuperman A. Design Oriented Analysis of Overhead Line Magnetic Energy Harvesters with Passive and Active Rectifiers. Electronics. 2024; 13(24):4904. https://doi.org/10.3390/electronics13244904
Chicago/Turabian StyleAbramovitz, Alexander, Moshe Shvartsas, and Alon Kuperman. 2024. "Design Oriented Analysis of Overhead Line Magnetic Energy Harvesters with Passive and Active Rectifiers" Electronics 13, no. 24: 4904. https://doi.org/10.3390/electronics13244904
APA StyleAbramovitz, A., Shvartsas, M., & Kuperman, A. (2024). Design Oriented Analysis of Overhead Line Magnetic Energy Harvesters with Passive and Active Rectifiers. Electronics, 13(24), 4904. https://doi.org/10.3390/electronics13244904







