1. Introduction
The advent of quantum computers breaks classical public key cryptosystems such as RSA [
1] using Shor’s algorithm [
2]. As a result, the development of post-quantum cryptography (PQC) has become crucial. The National Institute of Standards and Technology (NIST) has initiated a standardization process for PQC [
3], with many candidates based on lattice cryptography.
Lattice-based cryptography heavily relies on modular arithmetic, particularly modular polynomial multiplication, which constitutes a significant computational bottleneck. The number theoretic transform (NTT) reduces the complexity of modular polynomial multiplication from to by leveraging component-wise multiplication. Despite this, modular reduction within the NTT remains computationally expensive.
This paper proposes
LazyNTT, a method designed to reduce the number of Montgomery multiplications [
4] in the NTT computation, which is an efficient workaround for naive modular reduction but is still more expensive than the standard integer multiplication. By replacing some of them with standard multiplications at intermediate stages of the NTT computation, we achieve significant computational complexity improvements.
1.1. Contributions
In this paper, we propose a new variant of the NTT with a faster runtime by reducing the number of Montgomery multiplications. The detailed contributions are given as follows:
1.2. Related Works
Extensive research has been conducted on the NTT due to its critical role in cryptography. In the hardware domain, efficient implementations of the NTT on FPGA have been presented in [
12,
13]. They optimized memory access patterns and minimized the latency of the NTT computation. Additionally, the performance improvement of polynomial multiplication using the NTT by employing a unified butterfly unit has been presented in [
14]. In the software domain, performance improvements have been achieved using the Harvey butterfly structure in the radix-4 NTT [
15] and optimizing cyclic convolution operations to speed up the NTT [
16]. In the context of PQC, efficient NTT implementations using a hardware accelerator and instruction set for Kyber [
7,
8], parallelism with FPGA for Dilithium [
9,
10], and twiddle factor generation for Falcon [
11,
17] have been presented. In the field of homomorphic encryption (HE), some have focused on efficiently implementing the NTT using GPUs [
18,
19,
20]. Specialized hardware designs to optimize the NTT for HE also have been proposed in [
21,
22]. Previous works are summarized in
Table 1 for better clarity.
Our work builds on these advancements by specifically addressing the computational load of modular reduction within the NTT. To the best of our knowledge, a direction focusing on replacing only the type of multiplications used in the NTT has not been explored before. Additionally, previous works on the NTT have been developed across various platforms and cryptosystems, making it difficult to compare them under the same criterion. Therefore, we use the official implementation code of Falcon as a reference, which is selected as the PQC standard by NIST. We believe that comparing computational complexity with this reference code is appropriate for demonstrating the meaningful results of LazyNTT. By replacing some Montgomery multiplications with standard multiplications without modular reduction, we achieve a notable computational complexity gain, which complements existing optimization in both hardware and software implementations.
1.3. Organization
The structure of this paper is as follows:
Section 2 introduces the basic notations and preliminaries needed for understanding Montgomery multiplication and the NTT. It also includes a detailed explanation of the radix-2 NTT, which is the primary focus of the proposed method.
Section 3 describes the proposed Standard–Montgomery version (
SM-LazyNTT) and Standard–Standard–Montgomery version (
SSM-LazyNTT) algorithms. Their designs, operational principles, and generalization are also included in this section.
Section 4 provides the implementation results and an analysis of the improved computational complexity achieved by
SM-LazyNTT and
SSM-LazyNTT compared to the original NTT.
Section 5 concludes the paper with a summary of the proposed method and suggestions for future works.
2. Preliminaries
2.1. Notations
A ciphertext modulus is denoted as
q, and
n represents both the length of the polynomial and the NTT. Throughout this paper, we assume that
n is a power of two. For a polynomial
, let
denote the
i-th coefficient of the polynomial. Vectors are indicated as bold letters, for example
, and it represents a vector containing all the coefficients of
, i.e.,
. We denote the
j-th component of the vector
as
. We use
to indicate a value in Montgomery space and similarly use
to denote a vector containing values in Montgomery space. The NTT of the polynomial
is denoted as
.
R is a scaling factor used in Montgomery multiplication. The integer ring is denoted as
and the polynomial ring with the modulus is
. For a polynomial
, we define the quotient ring
. Standard multiplication is denoted by · and Montgomery multiplication is denoted by ∗. Component-wise multiplication between two vectors,
and
, is denoted as
, which means that each element in the same index is multiplied as
. When the context is clear, we may omit the modular reduction notation,
. Let
be a primitive
n-th root of unity, and let
be a primitive
-th root of unity in
, such that
with
and
for any integers
and
, respectively.
2.2. Montgomery Multiplication
In integer modular arithmetic, while there are simple constant-time methods for addition and subtraction, multiplication is more complex due to the division by the modulus
q required in the modular reduction step. Montgomery multiplication [
4] is a widely used technique in cryptography for efficient modular multiplication. It allows the modulo multiplication of integers without directly performing division by the modulus, which is computationally expensive. Instead, it first transforms the numbers into a special domain called Montgomery space by multiplying them with a constant,
R, and taking the result modulo
q as
This transformation enables more efficient modular arithmetic operations by replacing the division by q with cheaper operations such as multiplication, addition, and bit-shifting.
An element,
a, in
is mapped to Montgomery space as
. Addition and subtraction in Montgomery space are defined as in
, such that
. However, multiplication doubles the factor
R, and thus Montgomery multiplication
is defined as follows:
To implement the steps of multiplying
and reducing modulo
q efficiently, we use the extended Euclidean algorithm. Algorithm 1 describes the whole procedures. Unlike Montgomery multiplication, which multiplies two values in Montgomery space, we use the standard multiplication in this paper to refer to the multiplication between one value in Montgomery space and the other value in standard space.
| Algorithm 1 Montgomery Multiplication |
Require:
Ensure:
Pre-computation:
1:
2: ▹
3: ▹
Montgomery Multiplication:
4:
5:
6:
7: if
then
8:
9: end if
10: return u |
2.3. Number Theoretic Transform
The NTT is a specialized form of the discrete Fourier transform (DFT) that operates in an integer ring. Unlike the DFT, which handles complex numbers, the NTT utilizes integer modular arithmetic, making it suitable for error-free and efficient computations in cryptography and polynomial multiplication. For efficient NTT computation, a structure analogous to the fast Fourier transform (FFT) [
23] can be employed.
Let be the n-th cyclotomic polynomial, whose roots are the primitive n-th roots of unity, and . The NTT can be defined as a ring homomorphism that maps a polynomial in to . Here, the product of the quotient ring can be considered an integer vector , which is the vector of evaluations at the powers of a primitive root of unity.
Considering a polynomial multiplication over the quotient ring
for two polynomials,
and
the result
has coefficients such that
This requires multiplication complexity using a direct convolution approach. However, modular polynomial multiplication using the NTT achieves complexity with the following steps:
- (1)
Calculating the NTT of two polynomials.
- (2)
The component-wise multiplication of two NTTs.
- (3)
Calculating the inverse NTT of the result.
For the NTT, using
enhances efficiency due to the presence of the roots of unity
for
and
for
. These roots of unity enable a structured and cyclic approach to polynomial multiplication, allowing the use of FFT structure that breaks down the problem into smaller subproblems, leading to
complexity. Moreover, the cyclic nature imposed by
allows for efficient modular arithmetic operations, ensuring that the polynomial degree is maintained within
n, thereby simplifying modular reduction steps. For the quotient rings
and
, the former is known as positive wrapped convolution (PWC) [
24] and the latter as negative wrapped convolution (NWC) [
25].
In the context of PQC, the NTT usually refers to the NWC version. For example, in Falcon and Dilithium, is used for the NTT. To perform polynomial multiplication using the NTT, the modulus is chosen to ensure that the primitive -th root of unity exists in such that . Two examples are as follows:
- -
Falcon uses
for
or 512 [
5].
- -
Dilithium uses
for
[
26].
In Kyber, the parameters and are used, but a primitive 512-th root of unity does not exist in . Therefore, Kyber does not use the NWC-based NTT. Instead, during the NTT, the polynomial is converted into 128 polynomials with a degree of 1 rather than 256 integers. Although this paper focuses on NWC, the proposed method can be naturally extended to the PWC environment and works similarly well.
The NTT using NWC transforms a polynomial to its evaluations at points for . Since is also a n-th root of unity, we only consider , which is a primitive -th root of unity.
2.4. Radix-2 NTT Using FFT Structure
In the context of the NTT, radix-2 refers to a processing step, where two terms are handled together in a structure commonly known as a butterfly operation. By leveraging the divide-and-conquer strategy inherent in the FFT, the radix-2 NTT recursively splits the polynomial into smaller sub-NTTs, each half the size of the previous one, and applies the butterfly operation to combine the results. We will refer to this single iteration as a “stage”. Within a stage, we refer to each spot according to the index as a “position”. The butterfly operation involves the pairwise addition and subtraction of polynomial coefficients where one of them is multiplied by a power of the root of unity. This recursive structure ensures a significant reduction in computational complexity, making the transform efficient in both time and space, as in Algorithm 2.
In Algorithm 2, refers to the vector that stores all odd powers of the root of unity for , which are converted into Montgomery space. The first “for” loop (line 3) shows that there are a total of stages, with each iteration representing the computation of one stage. The second “for” loop (line 5) handles the computation of the m butterfly structure sets, with each structure using a different element of in that stage. The third “for” loop (line 7) processes h butterfly structures using the same element of .
Generally, the radix-2 NTT is calculated using following steps.
Divide all coefficients into two sets.
Perform the NTT of each half.
Recursively divide the coefficients in each NTT until a 2-point NTT is reached.
Combine the results to compute the final n-point NTT.
This process is conducted recursively, until the 2-point NTT is obtained.
| Algorithm 2 Radix-2 NTT |
Require: , , , q, and R
1:
2:
3: for to n do
4:
5: for to do
6:
7: for to do
8:
9:
10:
11:
12:
13:
14:
15: end for
16: end for
17:
18:
19: end for |
3. Lazy Modular Reduction for NTT
All multiplications during the NTT computation are carried out using Montgomery multiplication. Although Montgomery multiplication performs integer modular reduction efficiently, it still involves several multiplications, additions, and bit-shift operations. Notably, we observe that the NTT computation can proceed to subsequent stages without completing modular reduction in every intermediate stage. We propose a method, LazyNTT, where some of the Montgomery multiplications in intermediate stages of the NTT are replaced with standard multiplications without modular reduction. Although the results in intermediate stages are not reduced modulo, q, our goal is to ensure that the final NTT result is reduced modulo, q, not necessarily in every stage. Therefore, by increasing the value of the parameter R used in Montgomery multiplication, standard multiplications can replace some of the Montgomery multiplications required in the NTT computation. Since the algorithm occasionally skips modular reduction during the NTT computation, we refer to the proposed method as LazyNTT.
In this paper, we propose two versions of
LazyNTT. The first version replaces one out of two Montgomery multiplications with a standard multiplication, using both in an alternating manner during the NTT computation. Based on the order of the standard (S) and Montgomery (M) multiplications used, we refer to this version as
SM-LazyNTT. The second version replaces the first two of three Montgomery multiplications with standard multiplications. We similarly refer to this version as
SSM-LazyNTT. Although this paper focuses only on the SM and SSM versions of
LazyNTT, the approach can be easily generalized to replace more Montgomery multiplications. The generalization technique is described in
Section 3.5.
3.1. SM-LazyNTT
A polynomial,
, of the length
can be expressed in radix-2 form as below.
For the above polynomial , we can count the number of required multiplications as follows.
Remark 1. A total of multiplications are required for the NTT computation of .
From the radix-2 butterfly structure, it is clear that the number of multiplications required in each stage is exactly half of the length, .
For any , there are sub-NTTs in the ith stage, each of size . For each sub-NTT, a butterfly operation is applied to pairs of elements, which involves one multiplication by a power of the root of unity.
Since there are elements in each sub-NTT, the number of multiplications required per sub-NTT is .
Thus, multiplications are required in the ith stage. In total, multiplications are required for the entire NTT computation with k stages.
In (
1), the
ith coefficient
is multiplied by
in the innermost bracket first, corresponding to the first stage. In the second stage, it is multiplied by
, and this continues until it is finally multiplied by
. As we unfold the brackets through all
k stages, the exponent of
x accumulates to the value
, which is equal to the coefficient index
i. This corresponds to the binary representation of
i, indicating that each bit is from
to
. Therefore, throughout the NTT computation,
encounters Montgomery multiplications with modular reduction when
for
. On the other hand, when
, there is no multiplication and no modular reduction.
These multiplications can be computed using the proposed SM-LazyNTT algorithm based on the following principles:
The last multiplication encountered in each index is always performed using a Montgomery multiplication.
The second-to-last multiplication, i.e., the one immediately preceding the Montgomery multiplication, is replaced with a standard multiplication.
The multiplication preceding the standard multiplication is again performed using a Montgomery multiplication, ensuring that standard and Montgomery multiplications alternate, with the multiplication sequence always ending in a Montgomery multiplication.
We can make the following claim, which is the condition for the replacement of a Montgomery multiplication with a standard multiplication in SM-LazyNTT.
Claim 1. To replace a Montgomery multiplication with a standard multiplication, the condition should be satisfied, and there should be at least one Montgomery multiplication in the subsequent stages of the NTT computation.
Proof. In the original Montgomery multiplication, R is set to be a power of two greater than the modulus q, performing modular reduction within every multiplication.
In Montgomery multiplication, the result of the multiplication of two values in
should be less
. As described in
Section 2.2, this ensures the correct result by subsequent conditional addition. For
SM-LazyNTT, one standard multiplication will make the value be within the range of
, since it is performed without modular reduction. Then, if this value is multiplied by another element in
using Montgomery multiplication, the result should be less than
. This leads to the condition that
, which implies that
.
After a Montgomery multiplication is replaced by a standard multiplication without modular reduction, there should be at least one Montgomery multiplication remaining in the subsequent stages to ensure that the result is properly reduced modulo, q. Clearly, the last multiplication of each coefficient throughout the NTT should be conducted using Montgomery multiplication to perform modular reduction in the end. At the point of the multiplication just before the last Montgomery multiplication, modular reduction can be skipped because following Montgomery multiplication involves modular reduction.
□
Also, the number of replaceable positions in SM-LazyNTT can be determined by the following claim.
Claim 2. Out of a total of Montgomery multiplications, can be replaced with standard multiplications.
Proof. From the Remark 1, there are multiplications for each stage.
The replaceable positions among all these Montgomery multiplications depend on whether there are any Montgomery multiplications in the subsequent stages.
We count the number of replaceable multiplications starting from the final stage. In the final kth stage, all multiplications are performed using Montgomery multiplication to ensure that the multiplication results are correctly reduced modulo, q. In the preceding th stage, half of the Montgomery multiplications (that is, ) can be replaceable, since they are followed by Montgomery multiplications in the next kth stage. Thus, in the th stage, the indices with Montgomery multiplication are partitioned exactly in half, depending on whether there is subsequent Montgomery multiplication in the kth stage or not. Only for the indices with subsequent Montgomery multiplication, modular reduction can be skipped and standard multiplication can be used instead of Montgomery multiplication.
Similarly, in the th stage, Montgomery multiplications out of the total can be replaceable, since there are remaining Montgomery multiplications in the following th and kth stages.
Thus, for every stage except the final one, half of the required multiplications can be replaced with standard multiplications. As a result, a total of Montgomery multiplications out of can be replaced, achieving asymptotically half-reduced multiplicative complexity.
□
The proposed
SM-LazyNTT algorithm is given in Algorithm 3. The input
is the coefficient vector of
. The input
stores all odd powers of the primitive
-th root of unity,
, in Montgomery space, as in Algorithm 2. The input
stores all odd powers of the primitive
-th root of unity, but they are in standard space. In lines 11, 37, and 53 (blue colored) of Algorithm 3, Montgomery multiplications are used. However, in lines 21 and 43 (red colored), standard multiplications are used, providing modular reduction-free multiplication. Unlike the original NTT, where computations proceed sequentially with indices increasing by 1 (as in the “for” loop in line 7 of Algorithm 2), the proposed
SM-LazyNTT requires specifying the positions of standard and Montgomery multiplications. To determine these positions, the index jumping vector
is used. Details about
are described in
Section 3.3. The two for-loops starting in lines 33 and 49 correspond to the second-to-last stage and the final stage, respectively. In the second-to-last stage, each sub-NTT contains one standard multiplication and one Montgomery multiplication, and thus the jumping index is not used. Additionally, in the final stage, only Montgomery multiplications are performed, which is why a separate loop is created for it.
In
SM-LazyNTT, larger intermediate values can arise. These larger values are subsequently reduced to the range of
through Montgomery multiplication. After one standard multiplication, the resulting values range from 0 to
. By using the subtraction part in a butterfly operation, the result ranges from
to
. The conditional addition (line 8 of Algorithm 1) in Montgomery multiplication is performed to the value but uses
instead of
q, ensuring that the final result remains in the range from 0 to
.
| Algorithm 3
SM-LazyNTT |
Require: , , , , , q
1:
2: for to do
3:
4:
5:
for to do
6:
7: for to do
8:
9:
10:
11: ▹ Montgomery multiplication
12:
13:
14:
15:
16: end for
17: for to do
18:
19:
20:
21: ▹ Standard multiplication
22:
23:
24:
25:
26: end for
27:
28:
end for
29:
30:
31: end for
32:
33: for to do
34:
35:
36:
37:
▹ Montgomery multiplication
38:
39:
40:
41:
42:
43:
▹ Standard multiplication
44:
45:
46:
47: end for
48:
49: for to do
50:
51:
52:
53:
▹ Montgomery multiplication
54:
55:
56:
57: end for |
3.2. SSM-LazyNTT
Building on the previous section about SM-LazyNTT, we can further consider a method that replaces one more Montgomery multiplication. That is, up to two consecutive preceding multiplications before Montgomery multiplication can be replaced with standard multiplications. In this case, we can state the condition for the replacement as follows.
Claim 3. To replace up to two consecutive Montgomery multiplications with standard multiplications, the condition should be satisfied, and there should be at least one Montgomery multiplication in the subsequent stages of the NTT computation.
Proof. From the Claim 1, we know that the result of a Montgomery multiplication should be less than .
After two consecutive standard multiplications without modular reduction, the result lies in the range . To perform the next Montgomery multiplication with an element in , the condition should be satisfied, which implies that .
Similarly, there should be at least one Montgomery multiplication in the subsequent NTT stages to ensure that the computed result is properly modular reduced.
□
For a polynomial,
, in (
1), the number of standard multiplications and Montgomery multiplications in the
SSM-LazyNTT algorithm are counted by the following claim, where
represents the Hamming weight of
i.
Claim 4. In the proposed SSM-LazyNTT algorithm, the number of Montgomery multiplications isand the number of standard multiplications is Proof. We know that multiplication is performed in the positions where the bit is 1 in the binary representation of an index, i.
Since the final multiplication of each index should be performed by Montgomery multiplication, the possible patterns of the multiplications are combinations of M, S-M, and S-S-M.
Since Montgomery multiplication is only performed in the last of every three multiplications, the number of Montgomery multiplications required in each index i is given by . The remaining multiplications are performed as standard multiplications, and, thus, the number of replaceable multiplications in each index is .
□
The proposed
SSM-LazyNTT algorithm is presented in Algorithm 4. It is similar to Algorithm 3, but with some key differences. First, unlike in
SM-LazyNTT, where standard and Montgomery multiplications are equally partitioned, here, there are more standard multiplications. Therefore, we define the vectors
and
, specifying the number of multiplications required in each stage. Second, unlike in
SM-LazyNTT, where a single jumping vector
is sufficient to indicate both positions of the standard multiplication and Montgomery multiplication, here, the separate index jumping vectors
and
for standard and Montgomery multiplication are required, respectively.
| Algorithm 4
SSM-LazyNTT |
Require: , , , , , q
1:
2:
3:
4: for to do
5:
6:
7: for to do
8:
9: for to do
10:
11:
12:
13: ▹ Montgomery multiplication
14:
15:
16:
17:
18: end for
19: for to do
20:
21:
22:
23: ▹ Standard multiplication
24:
25:
26:
27:
28: end for
29:
30: end for
31:
32: end for
33:
34: for to do
35:
36:
37:
38: ▹ Montgomery multiplication
39:
40:
41: for to 3 do
42:
43:
44:
45: ▹ Standard multiplication
46:
47:
48: end for
49:
50: end for
51:
52: for to do
53:
54:
55:
56: ▹ Montgomery multiplication
57:
58:
59:
60:
61:
62: ▹ Standard multiplication
63:
64:
65: end for
66:
67: for to do
68:
69:
70:
71: ▹ Montgomery multiplication
72:
73:
74:
75: end for |
However, since these jumping vectors are determined deterministically once the size of the NTT, n, is fixed, they can be precomputed and stored before the algorithm begins, and, thus, this does not pose any issue.
Similarly, the third-to-last, second-to-last, and final stages are also separated into their own for-loops. In the for-loop starting in line 34, i.e., the third-to-last stage, there is only one Montgomery multiplication per sub-NTT, and, thus, the jumping vector is not used here.
In SSM-LazyNTT, larger intermediate values can arise, as in SM-LazyNTT. A notable point is that the ranges of values differ after the first and second standard multiplications; the first standard multiplication results in values ranging from 0 to , while the second results in values ranging from 0 to . To ensure that these values remain positive and within correct ranges, different conditional additions (adding and , respectively) are applied for each case. This ensures that the results are always positive and modularly reduced during subsequent Montgomery multiplications.
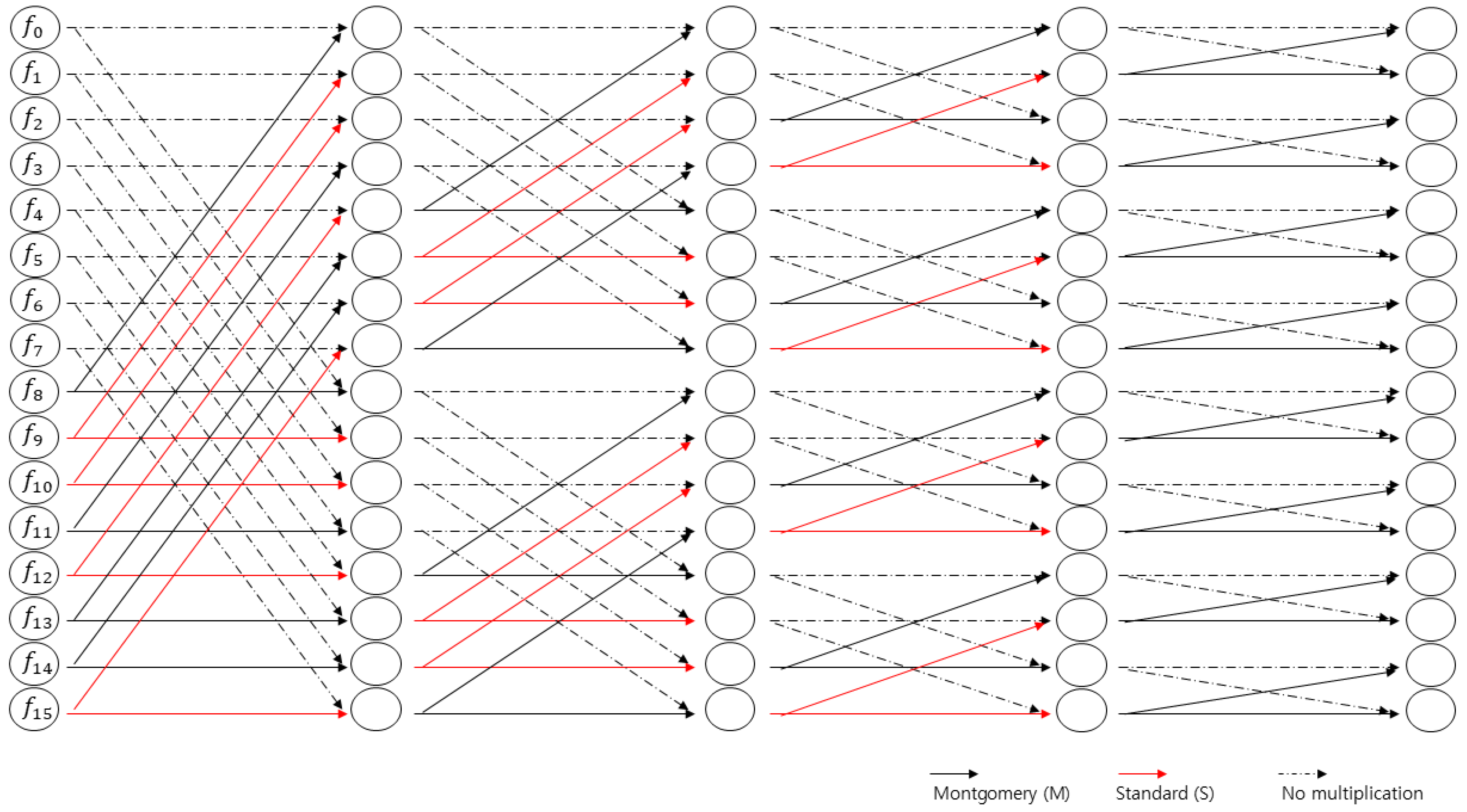
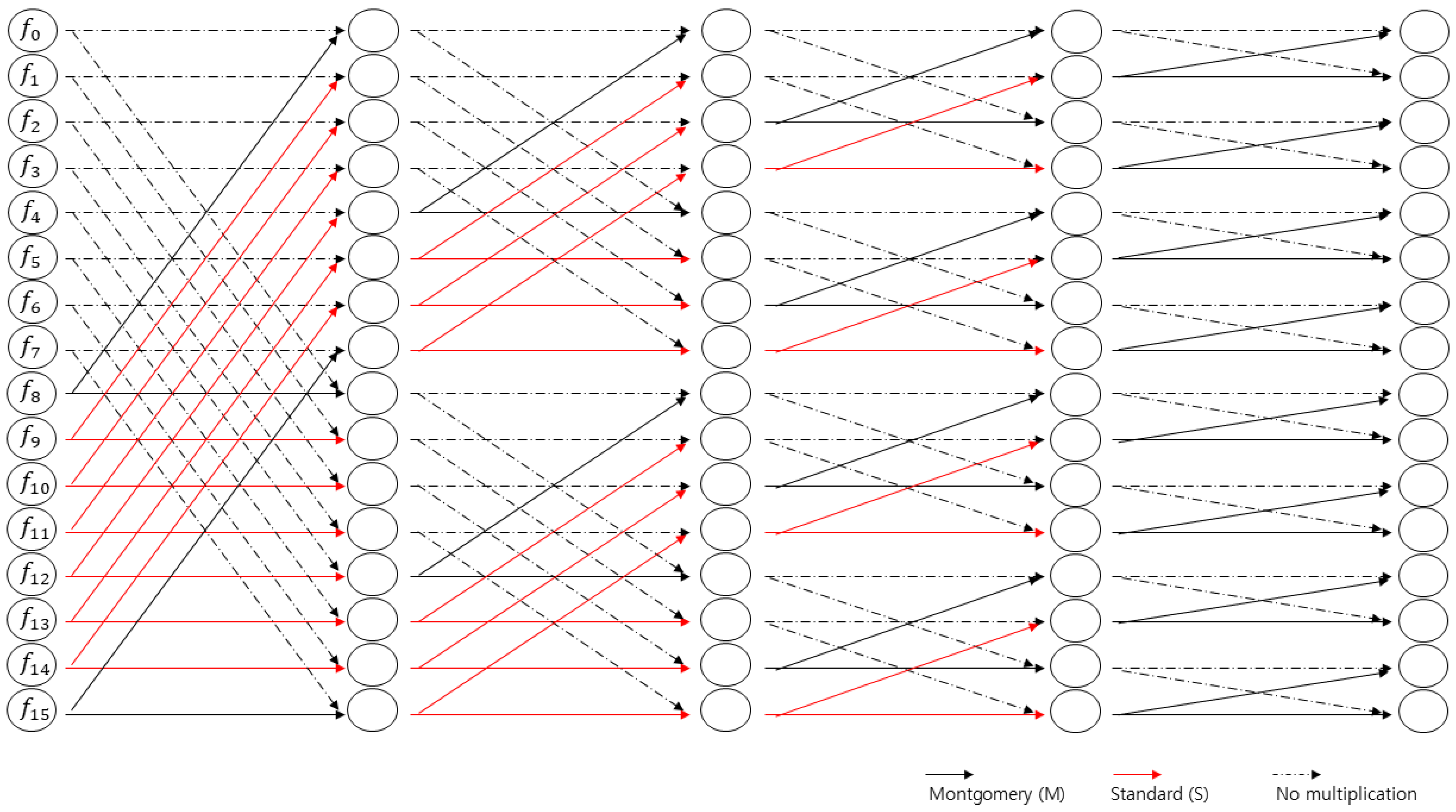
3.3. Jumping Vector
Unlike the original NTT, which uses only Montgomery multiplication, the proposed algorithms mix standard multiplication and Montgomery multiplication. Therefore, it is necessary to determine in each stage which indices use standard multiplication and which use Montgomery multiplication. In Algorithms 3 and 4, the jumping vectors , and indicate in which indices standard or Montgomery multiplication should be applied. These vectors are deterministic and can be predetermined once the NTT size, n, is defined.
As shown in
Figure 1 and
Figure 2, by considering Montgomery and standard multiplications from the final stage, we can determine all the multiplications to be performed as either Montgomery multiplications or standard multiplications. Red lines represent standard multiplications, black lines represent Montgomery multiplications, and dashed lines represent no multiplication. Clearly, we do not generate or compute these vectors in each execution. Instead, they can be precomputed and stored for use.
3.4. Memory Usage Analysis
LazyNTT may produce larger intermediate values compared to the original NTT and requires slightly more memory, as it utilizes not only , the powers of the root of unity in Montgomery space, but also , those in standard space. However, the additional memory consumption is not expensive. For cases where 12,289 or , a 16-bit variable is used, requiring a total of bits. Furthermore, since the jumping index values range from 1 to 3 for SM-LazyNTT and from 1 to 7 for SSM-LazyNTT with a length of , eight-bit variables are sufficient to store the indices. This requires bits in software implementation, but two or three bits are actually enough, respectively. In Algorithm 4, the arrays M and S are needed to store the number of standard and Montgomery multiplications for running multiplications for loops of varying lengths. In summary, the additional memory required compared to the original NTT is not substantial, and this trade-off of using a small amount of additional memory to achieve speed improvement is quite meaningful.
3.5. Generalization
The proposed LazyNTT algorithm is not limited to only one or two replacements of Montgomery multiplication but can be extended to more replacements. When multiplying a total of elements in , we can proceed with standard multiplications instead of Montgomery multiplications. We apply Montgomery multiplication only in the final tth multiplication to ensure that the result is in the range of . The condition for this to hold is , since the result x should satisfy .
In general, for an algorithm that uses standard multiplications out of a total of t required multiplications, referred to as -LazyNTT, the following claim holds.
Claim 5. In the -LazyNTT algorithm, the number of Montgomery multiplications isand the number of standard multiplications is Proof. Similarly to Claim 4, we know that Montgomery multiplication is only performed in the last of all consecutive multiplications in each index. Thus, the number of required Montgomery multiplications in each index, i, is given by . The remaining multiplications can be performed by standard multiplications, and, thus, the number of replaceable multiplications in each index is . □
In Falcon [
5], the prime modulus and Montgomery scaling factor are
12,289 and
. In the original Falcon implementation [
27], since each multiplication is performed using Montgomery multiplication,
R only needs to be a power of two larger than
q. However, to apply the proposed
SM-LazyNTT and
SSM-LazyNTT algorithms, given that the size of
q is 14 bits,
R should be at least
and
, respectively. For the Kyber parameter
, given that the size of
q is 12 bits,
R should be at least
and
, respectively.
In the original NTT, modular reduction is performed after each multiplication, ensuring that no value exceeds the modulus q. However, in the proposed algorithm, modular reductions are skipped in some of the intermediate stages, requiring the storage of larger values, which sometimes necessitates a 64-bit variable. For SM-LazyNTT with 12,289, after one standard multiplication, the result can reach up to , which corresponds to a maximum of 28 bits. To perform the subsequent Montgomery multiplication of this value, a variable capable of holding up to 42 bits is required. In the case of SSM-LazyNTT, after two standard multiplications, the value can reach up to 42 bits, and to perform the subsequent Montgomery multiplication, a variable capable of holding up to 56 bits is necessary.
M-LazyNTT can be the generalized version of the proposed LazyNTT; however, there are some practical obstacles for its implementation. First, variables larger than 64 bits are required for going beyond SSM-LazyNTT. For example, in SSSM-LazyNTT, R should be for 12,289 to perform three consecutive standard multiplications, and following Montgomery multiplication would demand a variable capable of bits for its computation. Thus, while it is theoretically possible to extend the algorithm, the need for higher bit-width processing may introduce overhead, potentially diminishing the performance benefits. Additionally, memory usage would increase accordingly to store these larger values. These are more seriously considered in both hardware and software implementations of the generalized version of LazyNTT.
5. Discussion and Conclusions
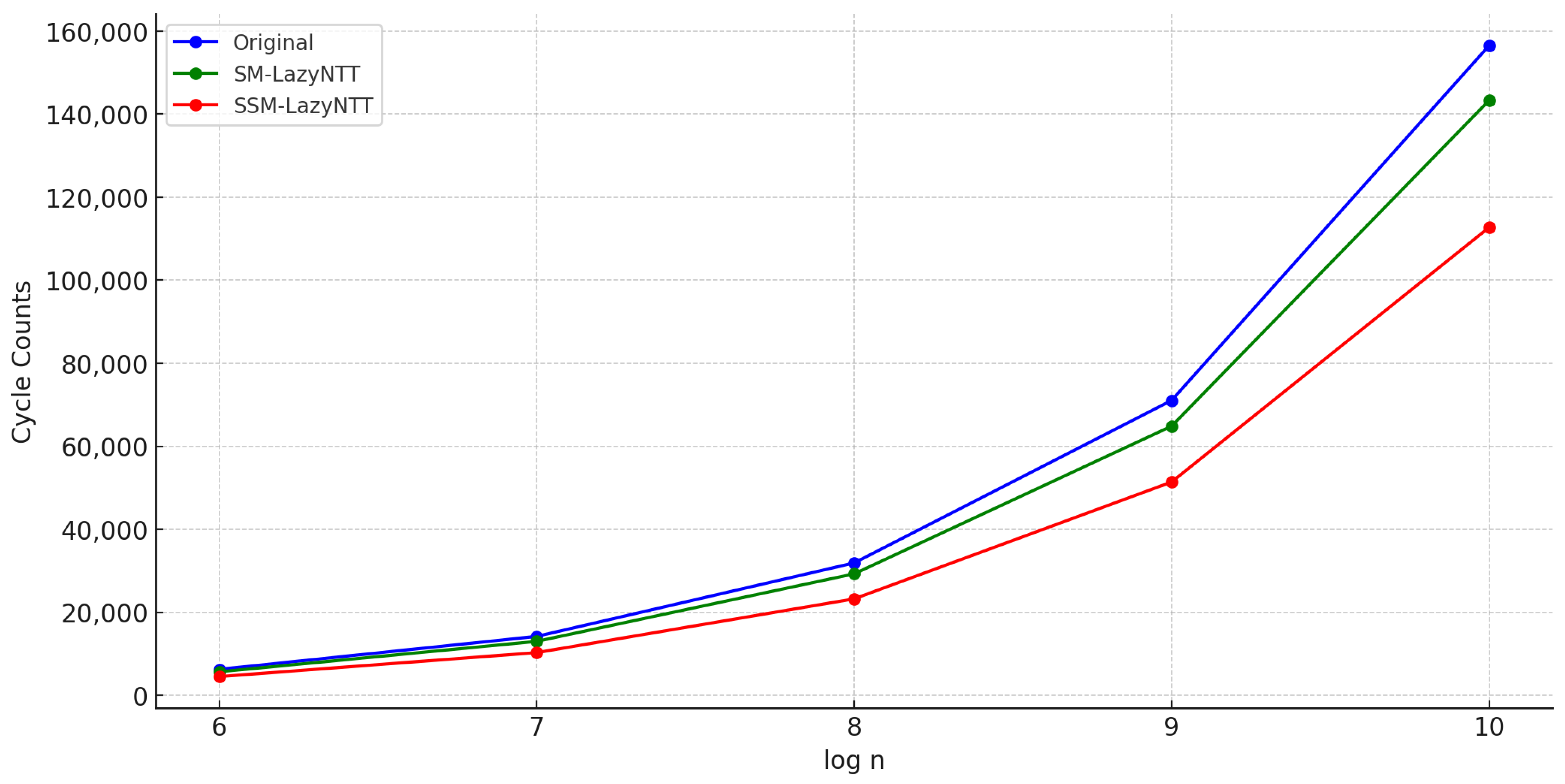
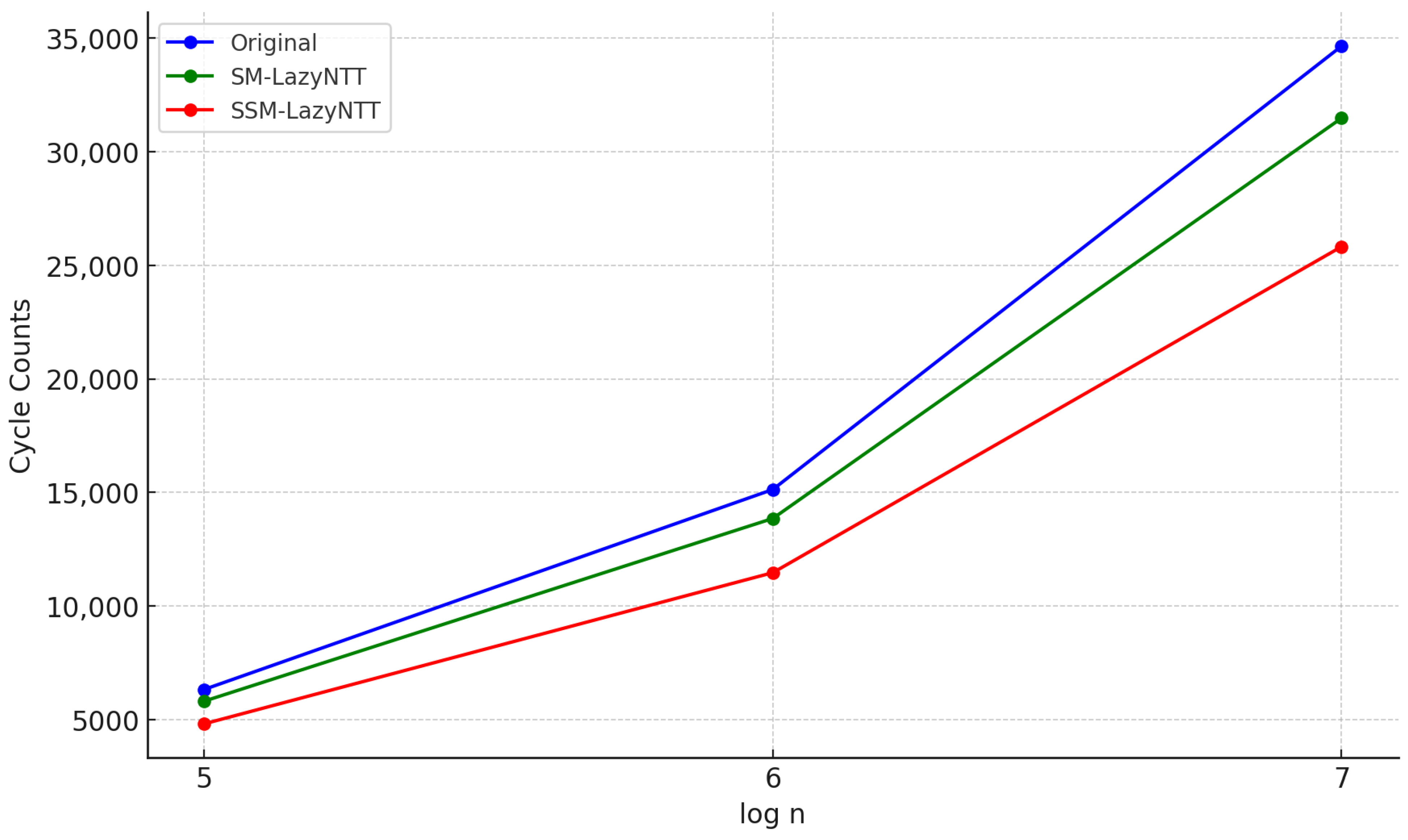
As the NTT plays an important role in lattice-based cryptosystems, reducing its computational load can be an important contribution. We proposed a new and faster NTT algorithm, LazyNTT, and its two versions of implementation. The implementation results showed that SSM-LazyNTT and SM-LazyNTT were practically efficient, improving the runtime of the NTT by up to and , respectively. Moreover, the proposed technique could be naturally generalized to replace more than two Montgomery multiplications with standard integer multiplications. Even with the replacement of just one or two multiplications, we observed meaningful computational complexity improvements compared to the original NTT and confirmed the proper functionality of the proposed methods. Furthermore, the proposed LazyNTT only replaces some Montgomery multiplications with standard multiplications, without changing any other structures of the NTT; the runtime improvement can be achieved without compromising security.
In this paper, LazyNTT was implemented for PQC parameters, especially Falcon and Kyber. However, it can also be extended to other cryptographic schemes, such as HE. For example, HE typically employs larger parameters and longer NTT lengths compared to PQC. Consequently, LazyNTT could replace a larger number of multiplications, potentially leading to a higher reduction in the number of cycles. Furthermore, when implementing software with large parameters requiring 128-bit variables or more, although there may be additional costs, improved speed with LazyNTT compensates the costs and introduces a suitable implementation for homomorphic encryption.
Some future works can be considered in the following directions. First, implementing the generalized version of the proposed LazyNTT can be a promising research topic. Second, this approach can be extended not only to the radix-2 NTT but also by mixing NTTs that use various sizes of radix. Third, this technique can be applied to the inverse NTT, thereby improving the overall polynomial multiplication process. Fourth, it can be applied to various lattice-based cryptographic schemes, such as digital signatures, homomorphic encryption, and zero knowledge proofs. Finally, implementing LazyNTT on various platforms, such as GPUs or FPGAs, can be a research direction for broader applications.