ENSG: Enhancing Negative Sampling in Graph Convolutional Networks for Recommendation Systems

Abstract

In the field of recommendation, negative samples that are close to positive samples are referred to as “hard negative samples”. These hard negative samples are more likely to be incorrectly recommended to users. Therefore, researching how to enhance the ability to identify hard negative samples and thereby improve recommendation accuracy is an important direction in the field of recommendation systems. To address this issue, we propose a new model named Enhancing Negative Sampling in Graph Convolutional Networks for Recommendation Systems (ENSG). Firstly, part of the information in the positive sample was injected into the negative sample, and the high-quality, difficult negative sample was selected by the inner product method. Secondly, a lightweight graph convolutional network is used for feature extraction to obtain node representations for both users and items. Then, contrastive learning is used to maximize the similarity between the hard negative samples and the positive samples, so that the hard negative samples are as close to the positive samples as possible in the feature space. Ultimately, the model is trained by taking hard negative samples as input and minimizing the loss function to optimize model parameters; the recommendation accuracy of the model is enhanced. To validate the effectiveness of our approach, we conducted comparative evaluations utilizing three publicly accessible datasets. The experimental outcomes indicate that our proposed model surpasses the baseline model in terms of performance. On three public datasets, the algorithm proposed in this paper achieved the highest improvements of 16.27% and 12.72% in the evaluation metrics Recall@20 and NDCG@20, respectively.

1. Introduction

With the continuous evolution of the digital era, the amount of information shows explosive growth, and it becomes more and more difficult for people to find the required content in the huge amount of information. Recommender systems have successfully alleviated this issue [1]. Traditional recommendation algorithms can be categorized into content-based, collaborative filtering, and hybrid selection, and all have a specific technical basis and technical means to complete the recommendation task. The collaborative filtering algorithm is a widely used algorithm in recommender systems, which is based on the historical behavioral data between users and items, and by analyzing and comparing the similar characteristics between users or items, it can predict the interest of the items that users have not touched, so as to speculate the degree of their preference for these items [2,3,4].

In recent years, in order to further improve the embedding quality and mitigate the effects of data sparsity, an important research direction has been to utilize the non-Euclidean structure of graph convolutional networks (GCNs) to characterize the nodes [5]. Graph Convolutional operations are able to aggregate information within a node’s neighborhood to learn an embedded representation of each node that contains not only attribute information about users and items but also incorporates information about their structure in the graph [6,7,8]. In this way, the algorithm is able to understand user preferences and item properties more comprehensively, thus generating more accurate recommendations and alleviating the data sparsity problem to a certain extent. Contrastive learning is an effective unsupervised learning method that learns feature representations by comparing positive and negative samples so that similar samples are closer in the feature space and different samples are further away [9,10]. In recommendation algorithms, the application of comparative learning is mainly reflected in improving the performance of recommendation systems by learning the interaction features between users and items [11]. In this way, contrastive learning not only improves the accuracy and efficiency of the recommender system but also enhances its robustness and generalization ability [12].

In graph convolutional network recommendation, a common practice when training a recommender system model is to use items that users have actually interacted with as positive samples while selecting items that users have not interacted with as negative samples. These positive and negative samples are then used to optimize the loss function of the model, which in turn learns embedding vectors that accurately represent the characteristics of the user and the item and finally completes the model training process. Although existing recommendation methods have achieved certain results, there are still some shortcomings:

(1)

In the field of recommendation, existing negative sampling techniques often struggle to mine hard negative samples, which can lead to models overemphasizing simple samples during training and neglecting the truly challenging hard negative samples. This, in turn, affects the model’s recommendation accuracy.

(2)

Research has found that hard negative samples have a significant impact on the recommendation accuracy of models. In existing studies, after obtaining hard negative samples, there has not been consideration of how to further improve their quality based on these hard negative samples, thereby enhancing the recommendation model’s ability to distinguish between positive and negative samples.

To address the above problems, we propose a new model named ENSG. The main contributions of the algorithm are as follows:

(1)

A new negative sampling strategy is proposed; firstly, the original negative samples are randomly selected; secondly, the positive sample embedding information is randomly introduced into the original negative samples using the interpolated multivariate technique; and then the final difficult negative samples are synthesized by using the inner-product method selection strategy in the process of aggregation in the graph convolutional network to lay the foundation for the subsequent model training.

(2)

Introducing the contrast learning method, by mining more feature information in the positive samples and the difficult negative samples, the difficult negative samples are made closer to the positive samples in the feature space, which further improves the model’s ability to recognize the boundary of the positive and negative samples.

(3)

In order to validate the overall performance of the collaborative filtering recommendation algorithm based on multivariate sampling for graphical convolutional networks, the experimental results comparing it with a variety of state-of-the-art algorithms on three publicly available datasets, Yelp2018, Alibaba, and Gowalla, are conducted, significantly demonstrating that the proposed model has a significant performance enhancement with respect to the baseline model. This improvement not only validates the effectiveness of the multivariate negative sampling module but also confirms the positive role of the contrast learning module in the model.

2. Related Work

2.1. Recommendation Model Based on GCN

Compared with traditional deep learning methods, graph convolutional networks (GCNs) show unique advantages in processing non-Euclidean structured data, and these advantages have led to a wide range of applications in various fields, such as computer vision and recommender systems. Chen et al. [13] proposed Linear Residual Graph Convolutional Collaborative Filtering (LR-GCCF), utilizing residual network structure to alleviate the over-smoothing problem. Wang et al. [14] proposed Neural Graph Collaborative Filtering (NGCF). They apply GCNs to collaborative filtering algorithms for the first time and explicitly learn the high-dimensional information of user–item interactions through message passing. He et al. [15] simplify the traditional GCN framework for the collaborative filtering by omitting the feature transformations and nonlinear activation steps and construct a Light graph convolution network (LightGCN) to provide a more effective and efficient collaborative filtering algorithm. This simplified version of the GCN model shows higher accuracy in recommender system applications and has significant performance improvement compared with models such as NGCF.

2.2. Negative Sampling Strategy

In the field of recommender systems, most of the collected data belong to the implicit feedback category, and these forms of feedback include user behaviors such as clicking, browsing, favoriting, and purchasing [16]. Given that users usually interact with only a limited number of items, an intuitive and efficient strategy is to consider the items that the user directly interacts with as positive samples, which directly reflect the user’s interests and preferences. Pan et al. [17] proposed Random Negative Sampling (RNS), which randomly selects samples from all non-interacted samples as negative samples according to a uniform distribution. Perozzi et al. [18] proposed the Online Representation Learning Algorithms for Graph Node Embedding (DeepWalk), in which a degree-based negative sampling method has been proposed to accelerate model training, which samples according to the popularity distribution. Yang et al. [19] suggest that about 95% of negative samples belong to the category of easy negative samples, which are not similar to positive samples in terms of features. Therefore, just relying on these easily negative samples to train the model is not enough to obtain a model with superior performance. Ying et al. [20] proposed the graph convolutional neural networks for Web-Scale Recommender Systems (PinSage), in which strong negative samples are constructed by finding samples similar to positive samples. Ma et al. [21] proposed multi-dimensional graph convolutional networks (MGCNs), which dynamically select negative samples from the ranking list generated by the current prediction model and iteratively update the model. This approach not only reduces training time but also significantly enhances performance.

2.3. Contrast Learning

Contrast learning, as an effective self-supervised learning method, mainly relies on comparing the differences between positive and negative examples in the feature space in order to capture the consistency of feature representations across different views. Wu et al. [22] proposed self-supervised graph learning for recommendation (SGL), a model that employs three graph-based data augmentation techniques, leveraging multi-view information, and then conducts contrastive learning to increase the differences between different node representations. This data augmentation and pre-training approach helps to mine more supervisory signals from the original graph data. Yu et al. [23] proposed Simple Graph Contrastive Learning for Recommendation (SimGCL) that adds uniform noise to the embedding null to create a contrasting view, which implicitly mitigates popularity bias and smoothly adjusts the uniformity of the learned representations by learning a more uniform representation of the user or item to make recommendations. Chuang et al. [24] improved on the Contrastive Estimation of Neural Entropy model (Infonce) by proposing the Robust Contrastive Learning against Noisy Views model (RINCE), which is robust to noise and does not require explicit estimation of noise, further enhanced performance.

3. Algorithm Design

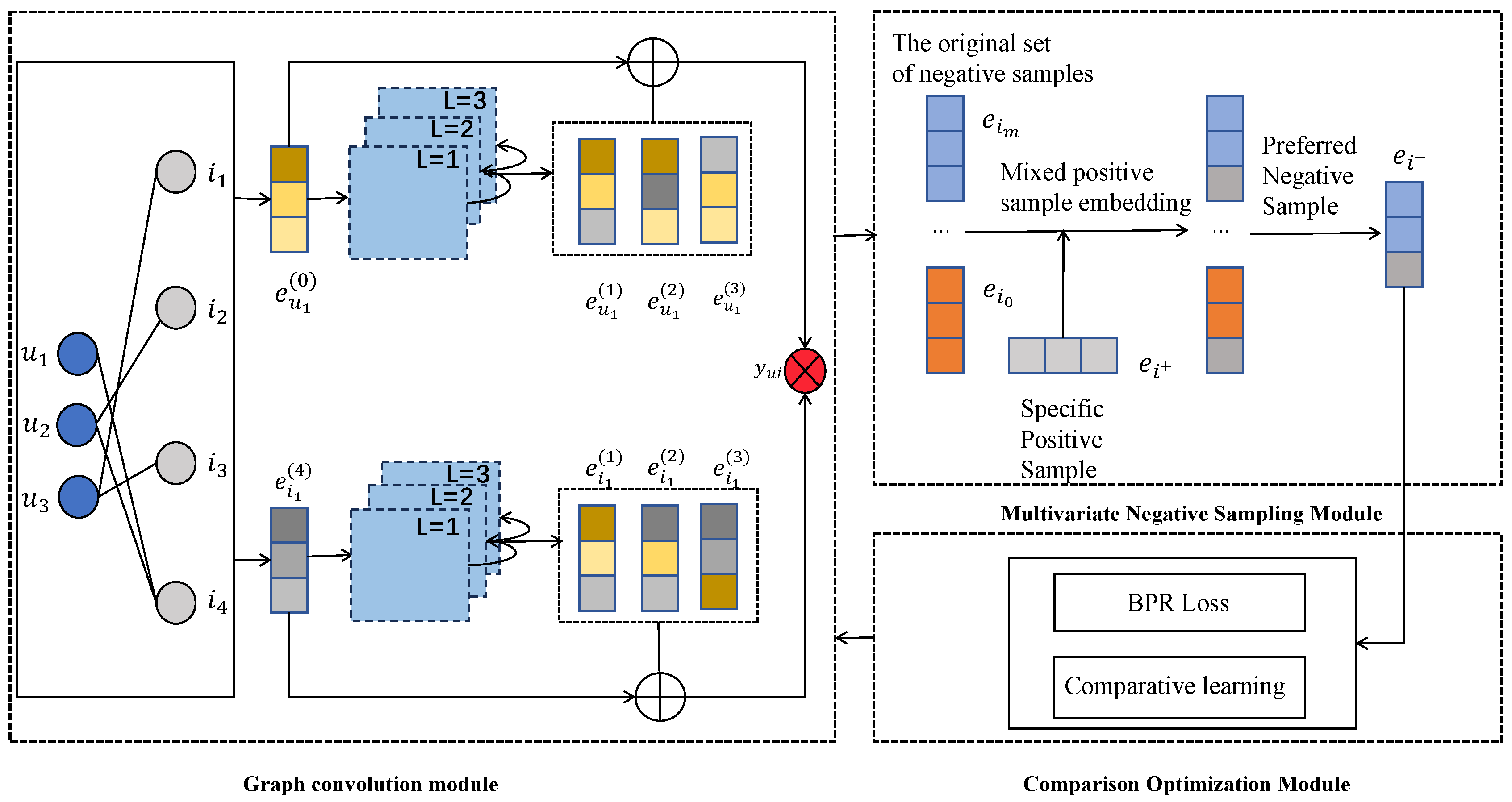
3.1. Overall Framework

The recommendation model framework of a graph convolutional network based on multivariate sampling is shown in Figure 1. It can be mainly divided into three major modules:

(1)

Multivariate negative sampling module: the primary recommendation task employs a multivariate negative sampling strategy during the negative sampling phase, generating challenging negative samples by integrating information across different nodes.

(2)

Graph convolutional network module: the multivariate negative sampling module provides the difficult negative sample data required for model training, and the graph convolutional network module performs feature extraction based on the graph structure and the sample data obtained from sampling.

(3)

Optimization module: the positive samples and the obtained difficult negative samples are compared and learned as sample pairs so as to narrow the distance between the difficult negative samples and the positive samples in the semantic feature space, and the model parameters are optimized by minimizing the BPR loss function.

3.2. Multivariate Negative Sampling

In the model training phase, in order to learn user preferences, the model receives both positive and negative samples as input. By adjusting the loss function, the model is trained to amplify the difference between positive and negative samples. The traditional approach is to directly utilize the samples that are real and have been identified as negative for training. However, this paper proposes a new strategy of artificially constructing those hard negative samples that are challenging for the model in a continuous embedding space. This strategy helps the model to capture and distinguish user preferences more accurately during training. The method is divided into two main steps: generating enhanced candidate negative samples and sample preference aggregation.

3.2.1. Generate an Augmented Negative Sample Candidate Set

The first step of this method generates an enhanced negative sample candidate set by introducing positive sample information into the original negative samples. In an l-layer graph convolutional network, each item generates l + 1 embedding vectors; each embedding vector $e_i^{\left(l\right)}$ integrates the information of the previous layer. Firstly, m negative samples are randomly drawn from an original set of negative samples to form a candidate set $\epsilon =\left\{e_{i_m^{-}}^{\left(l\right)}\right\}$. Inspired by the Mixup method proposed in [25,26], this paper further randomly injects the positive sample information $e_{i^{+}}$ into the original set of candidate negative samples$e_{i_m^{-}}^{\left(l\right)}$. Finally, new hard negative sample embeddings ${\widehat{e}}_{i_m^{-}}^{\left(l\right)}$ are generated as follows:

$${\widehat{e}}_{i_m^{-}}^{\left(l\right)}={\alpha }^{\left(l\right)}{e}_{i^{+}}^{\left(l\right)}+\left(1-{\alpha }^{\left(l\right)}\right)e_{i_m^{-}}^{\left(l\right)},{\alpha }^{\left(l\right)}\in \left(\mathrm{0,1}\right)$$

(1)

Here, ${\widehat{e}}_{i_m^{-}}^{\left(l\right)}$ is the newly-generated augmented candidate negative sample; a negative sample set represented as $\widehat{\epsilon }=\left\{{\widehat{e}}_{i_m^{-}}^{\left(l\right)}\right\}$ is generated. ${\alpha }^{\left(l\right)}$ is the mixing coefficient used to regulate the amount of positive sample information injected into the model. $e_{i^{+}}^{\left(l\right)}$ represents the positive sample embeddings in the graph convolutional network at layer l. In order to reduce the potential impact of this coefficient on the generalization ability of the model, its value is selected uniformly in the range of (0, 1) in each layer by randomization, thus ensuring that the introduction of this coefficient does not bias a particular data distribution or pattern. The identification ability of the model is enhanced by injecting information from the positive samples into the negative samples, thus making it more difficult for the model to distinguish between decision boundaries.

3.2.2. Sample Optimization and Aggregation

The step of Sample Optimization and Aggregation primarily utilizes the hierarchical aggregation features of GCN by sampling from candidate negative sample embeddings at various layers and combining these embeddings to synthesize hard negative samples. In the l-th layer of the graph convolutional network, the set of hard negative samples generated at each layer is denoted as ${\widehat{\epsilon }}^{\left(l\right)}$. Firstly, inspired by multi-dimensional graph convolutional networks (MGCNs), this paper employs a hard negative sample selection strategy that approximates the positive sample distribution using inner products, sampling hard negative sample embeddings from ${\widehat{\epsilon }}^{\left(l\right)}$. Then, the aforementioned embeddings are synthesized to obtain the final hard negative sample embedding, which is generated as follows:

$$e_{i^{-}}=f_{pool}\left({\widehat{e}}_{i_m^{-}}^{\left(0\right)},\dots ,{\widehat{e}}_{i_m^{-}}^{\left(l\right)}\right)$$

(2)

Here, $e_{i^{-}}$ represents the final hard negative sample embedding that has been aggregated,$f_{pool}$ is the aggregation function to synthesize the final embedding, and ${\widehat{e}}_{i_m^{-}}^{\left(l\right)}$ represents the hard negative sample embeddings sampled from the l layer.

3.3. Graph Convolutional Network

The collaborative filtering algorithm based on graph convolutional networks identifies user behavior patterns by aggregating information and passing messages. Let $u$ and $i$ represent users and items, respectively. Let $\mathcal{U}$ and $I$ represent user sets and item sets, respectively. The interaction between users and items is defined as follows:

$${\mathcal{O}}^{+}=\{y_{ui}|u\in \mathcal{U},i\in I\}$$

(3)

Here, ${\mathcal{O}}^{+}$ the set of positive sample pairs. $y_{ui}$ indicates that there has been an interaction between user $u$ and item $i$. The core of GCN lies in updating the embedding of a target node by aggregating the embeddings of its neighboring nodes. This process can be represented as follows:

$${\mathit{E}}^l=F({\mathit{E}}^{l-1},\mathcal{G}),l=\{0,1,\cdots ,L\}$$

(4)

Here, ${\mathit{E}}^l$ represents the node representation at the$l$ layer, ${\mathit{E}}^{l-1}$ is the representation from the previous layer, and $\mathcal{G}$ represents a bipartite graph of all users and items. The function F represents the neighborhood aggregation function, which can be described in vector form as

$$e_u^l=f_{\mathrm{com}}(e_u^{l-1},f_{\mathrm{agg}}(\{e_i^{l-1}|i\in {\mathcal{N}}_{\mathcal{U}}\}))$$

(5)

Here, $e_u^l$ is the updated embedding of user node$u$at layer$l$, $e_i^{l-1}$ represents the updated embedding of item node i at layer l−1, and $f_{\mathrm{com}}$ and $f_{\mathrm{agg}}$ are the combination function and neighborhood aggregation function, respectively. It first aggregates the embeddings of the neighbors ${\mathcal{N}}_{\mathcal{U}}$ from layer $l-1$ and then combines them with its own embedding $e_u^{l-1}$.

After obtaining the representations at layer $l,$ a final representation for prediction is generated through a readout function $f_{read}$.

$$e_u=f_{\mathrm{read}}(e_u^l|l=\{0,1,\cdots ,L\})$$

(6)

Here, $e_u$ represents the user feature representation, and $l$ is the number of graph convolutional layers.

The preference of user $u$ for item$i$ is predicted using the inner product of their final embeddings:

$${\widehat{y}}_{ui}=e_u^{\mathrm{T}}{e}_i$$

(7)

Here, ${\widehat{y}}_{ui}$ represents the predicted score of users’ preferences for items, $e_u$ represents the user feature representation, and $e_i$ represents the item feature representation.

3.4. Contrastive Learning

In the multivariate sampling stage, due to the use of linear interpolation of the positive sample information randomly injected into the negative sample, which will lead to the generation of difficult negative samples, semantic features will have a certain bias, and difficult negative samples in the semantic features of the positive samples biased away from the negative samples can improve the model’s recognition and classification ability. To address this problem, based on the work in [24], this paper further uses augmented robustness comparison learning. After multivariate sampling to obtain the difficult negative samples, the positive samples and the difficult negative samples are regarded as positive pairs, and the negative samples and the difficult negative samples are regarded as negative pairs. The distance between the positive samples and the hard negative samples in the feature space is further narrowed through the augmented robustness comparison learning, which can better train the model and enhance its ability to distinguish between positive and negative samples.

This paper leverages the concept of contrastive learning, treating positive samples and hard negative samples as positive pairs and hard negative samples and easy negative samples as negative pairs, which encourages the hard negative samples to get closer to the positive samples in the semantic space. The contrastive loss function used is RINCE, with the loss function given by

$$\begin{array}{c}{\mathcal{L}}_{RINCE}^{\lambda ,q}\left(\mathit{s}\right)={\displaystyle \frac{-{\mathit{e}}^{q\cdot s^{+}}+{\left(\lambda \cdot \left({\mathit{e}}^{s^{+}}+{{\displaystyle \sum }}_{i=\mathbf{1}}^K{\mathit{e}}^{s^{-}}\right)\right)}^q}{q}}\end{array}$$

(8)

Here, λ, q are the hyperparameters,$k$ represents the sample size, $s^{+}$ positive sample pairs of scores, and $s^{-}$ negative sample pairs of scores.

3.5. Optimize Model Parameters

After negative sampling with mixing, in order to further leverage the role of hard negative samples, this model uses the Bayesian Personalized Ranking (BPR) loss function to optimize the model by comparing positive and negative samples and iteratively updating model parameters using gradient descent to enhance the ranking of items preferred by users.

$${\mathcal{L}}_{\mathrm{BPR}}=\sum _{(u,i^{+})\in {\mathcal{O}}^{+},i^{-}\sim f_M(u,i)}-\log \sigma ({\widehat{\mathit{y}}}_{u{i}^{+}}-{\widehat{\mathit{y}}}_{u{i}^{-}})$$

(9)

Here, ${\mathcal{O}}^{+}$ represents the set of positive sample pairs, $i^{-}\sim f_M\left(u,i\right)$ represents the hard negative samples obtained through mixed negative sampling, and ${\widehat{y}}_{u{i}^{+}}$ and ${\widehat{y}}_{u{i}^{-}}$ respectively represent the user’s predicted scores for positive and negative items.

The pseudocode for the ENSG algorithm is shown in Algorithm 1:

Algorithm 1: Enhancing Negative Sampling in Graph Convolutional Networks for Recommendation Systems (ENSG)

Input: user set $\mathcal{U}$, item set$I$, user–item interaction set ${\mathcal{O}}^{+}$. Output: Each $u\in \mathcal{U}$ returns a list of recommended items. (1) Construct an interaction view, $G^O$. (2) For $u\in \mathcal{U}$, do. (3) Based on Equations (4)–(6), calculate the user representation $e_u$ and the positive sample representation $e_{i^{+}}$. (4) Based on Equations (1) and (2), generate the embedding representations of hard negative samples in the continuous space for set $e_{i^{-}}$. (5) Optimize the quality of hard negative samples according to Equation (8). (6) Calculate the predicted scores for users on items based on Equation (7) for set ${\widehat{y}}_{ui}$. (7) Calculate the BPR loss according to Equation (9) and optimize the parameters. (8) End for. (9) Return a list of recommended items for each user.

4. Experiments and Analysis of Results

4.1. Datasets and Evaluation Indicators

In this paper, three public datasets Yelp2018, Alibaba, and Gowalla are used, and the datasets are divided into training, validation, and testing sets for comparative experiments according to the ratio of 7:1:2, and the detailed information of the datasets is shown in

Table 1. Data information of Yelp 2018, Alibaba, and Gowalla.

Dataset Name	Number of Users	Number of Products	Number of Interactions	Data Density
Yelp2018	31,668	38,048	1,561,406	0.00130
Alibaba	106,042	53,591	907,407	0.00130
Gowalla	29,858	40,981	1,027,370	0.00084

.

In this paper, based on a popular top-K recommendation algorithm, Recall@K and NDCG@K, which are widely recognized in the industry, are chosen as the core evaluation metrics in order to evaluate the performance of the recommender system. In accordance with the convention in the field of recommender systems, the value of K is set to 20 to conform to the conventional setting for the length of recommendation lists in the field.

Recall@K is one of the important metrics for evaluating the performance of recommender systems. It measures how many of all truly relevant positive samples are correctly predicted or recognized by the recommender system. NDCG@K is a key metric for measuring the performance of recommender systems, which focuses specifically on the relevance of the recommendations to the user’s preferences and the ordering of these recommendations in the list.

4.2. Benchmarking Model

In order to evaluate the performance of the ENSG recommendation model in a more comprehensive way, this paper selects the better-performing models for comparison tests, and the comparison models are as follows:

(1)

BPRMF [27]: a classic collaborative filtering algorithm optimized using matrix factorization.

(2)

NGCF [14]: graph convolutional neural network is applied to the collaborative filtering recommendation task by constructing a bipartite graph of user–item interactions in order to capture high-dimensional interactions between users and items.

(3)

LightGCN [15]: discarded the traditional complete graph convolution process and removed the feature transformation and nonlinear activation steps. Reduces the computational complexity of the model.

(4)

RNS [17]: a negative sampling module is added to the traditional network to select un-interacted items as negative examples to enrich the training data and improve the model performance.

(5)

PinSage [19]: the core idea is to learn the embedded representations of the nodes in the graph through efficient random wandering and graph convolution operations to capture high-dimensional interactions between users and items.

(6)

SGL [20] adding an auxiliary self-supervised task to the classical supervised recommendation task to enhance node representation learning through self-recognition.

(7)

SimGCL [22]: a simple contrastive learning strategy has been proposed, forgoing complex graph enhancement techniques and instead introducing uniform noise into the embedding space to create comparative views.

4.2.1. Experimental Environment and Parameter Settings

In order to validate the model performance, experiments were conducted using the PyTorch machine learning framework in PyCharm 2020, NVIDIA GeForce GTX 3090, and Python 3.6. In the experiments, the embedding size is set to 64, the learning rate is set to 0.001, the batch size is 2048, the graph convolution layer l is set to 3, the hyperparameters q = 0.5, λ = 0.025, the parameters are initialized using Xavier, and the optimizer is set to Adam.

4.2.2. Analysis of Experimental Results

The results of the comparison between the model proposed in this paper and the six base models on the public dataset are shown in

Table 2. Experimental results comparing ENSG and baseline models.

Dataset Name Model Name	Yelp2018		Alibaba		Gowalla
	Recall@20	NDCG@20	Recall@20	NDCG@20	Recall@20	NDCG@20
BPRMF	0.0433	0.0332	0.0351	0.0112	0.1389	0.0921
NGCF	0.0543	0.0443	0.0426	0.0197	0.1573	0.1332
LightGCN	0.0637	0.0531	0.0585	0.0275	0.1822	0.1543
PinSage	0.0470	0.0392	0.0411	0.0232	0.1380	0.1195
RNS	0.0625	0.0516	0.0506	0.0332	0.1532	0.1319
SGL	0.0675	0.0553	0.0688	0.0338	0.1611	0.1398
SimGCL	0.0676	0.0555	0.0450	0.0336	0.1871	0.1589
ENSG	0.0733	0.0603	0.080	0.0381	0.2002	0.1696
Improve/%	8.43%	8.64%	16.27%	12.72%	7.0%	6.73%

, where underlining is used to indicate the best performance achieved by the baseline model, bolding denotes the optimal results, and the Improve/% of enhancement of the model proposed in this paper with respect to the optimal baseline model in each of the metrics.

Through meticulous analysis of the experimental results, we can draw the following conclusions:

(1)

Recommendation algorithms that employ graph convolutional networks, such as NGCF, demonstrate significant advantages compared with traditional algorithms like BPRMF that do not utilize this technology. This finding strongly supports the exceptional performance of graph convolutional networks in enhancing the effectiveness of recommendation systems.

(2)

Recommendation models based on graph contrastive learning, such as SimGCL, SGL, and ENSG, outperform NGCF and LightGCN in terms of performance, which confirms the effectiveness of contrastive learning in recommendation tasks.

(3)

The proposed model demonstrates significant advantages in all performance indicators, especially in the key indicator of Recall@20. Compared with the best baseline model, the proposed model achieves 8.43%, 16.27%, and 7.0% performance improvement on the three datasets, respectively. This significant performance improvement fully verifies the validity and superiority of the proposed model in this paper, which is mainly due to the following aspects:

(a)

ENSG adopts a multivariate sampling method, which can generate hard negative samples with higher quality and lay a good foundation for subsequent improvement.

(b)

ENSG employs the idea of contrastive learning to further explore the hidden features of samples based on obtaining higher-quality hard negative samples. It brings the hard negative samples closer to the positive samples in the feature space, thereby enhancing the quality of the hard negative samples and further improving the model’s ability to recognize them.

4.2.3. Ablation Experiment

In order to deeply investigate the practical effects of the multivariate negative sampling module and contrast learning module proposed in this paper, three ablation models, ENSG-R, ENSG-P, and ENSG, are designed for experiments, where ENSG-R denotes the removal of the contrast learning module and the use of traditional random sampling for model training, ENSG-P denotes the substitution of the traditional random sampling into the multivariate sampling mechanism for model training, and ENSG denotes adding the contrast learning module to ENSG-P for model training. The experimental results on the three public datasets are shown in Figure 2:

From the experimental results, it can be seen that both the multivariate sampling module and the contrast learning module in this model play an optimization role for the model. Taking the Yelp 2018 dataset as an example, the ENSG-P improves by 11.6% on the basis of the ENSG-R, and the ENSG-P improves by 3.5% on the basis of the ENSG-P. The enhancement of the experimental results is mainly due to the fact that the multivariate negative sampling mechanism proposed in this paper is able to utilize the graphical convolutional network structure to generate hard negative samples with higher quality, and then on the basis of this, the contrast learning idea is used to maximize the similarity between hard negative samples and positive samples to further improve the model’s ability to identify the boundaries of positive and negative samples.

4.2.4. Hyperparametric Analysis

In order to achieve better performance, the parameters l and hyperparameter q, which affect the effect of the model, are tuned. In the process of parameter tuning, a stepwise optimization strategy is used, i.e., one of the parameters (e.g., l) is first fixed, and the optimal value of the other parameter (e.g., q) is determined through experiments. Then, based on the optimal q value that has been found, q is fixed again, and the search for the optimal setting of parameter l continues. For the parameter l, three possible values of 1, 2, and 3 were considered, while for the parameter q, five different values between 0.1 and 0.5 were evaluated. In order to assess the impact of these parameters on the model performance, a sensitivity parameter analysis was performed on the Yelp 2018 dataset. The experimental results are shown in

Table 3. Effect of number of layers l and hyperparameters q of a graphical convolutional network on Recall@20.

q/l	1	2	3
0.1	0.0706	0.0710	0.0716
0.2	0.0709	0.0712	0.0720
0.3	0.0710	0.0715	0.0723
0.4	0.0712	0.0716	0.0727
0.5	0.0713	0.0718	0.0733

and

Table 4. Effect of number of layers l and hyperparameters q of a graphical convolutional network on NDCG@20.

q/l	1	2	3
0.1	0.0581	0.0583	0.0596
0.2	0.0582	0.0585	0.0598
0.3	0.0585	0.0586	0.0600
0.4	0.0587	0.0588	0.0602
0.5	0.0588	0.0589	0.0603

.

From Table 3 and Table 4, it can be obtained that the number of graph convolutional network layers l and hyperparameters q have a certain impact on the performance of the recommendation model. In general, by increasing the number of layers of the GCN, the model can explore the association between nodes in the graph structure as well as the relationship between users and items more deeply, so as to better capture the patterns and information hidden in the graph. The hyperparameter q mainly controls the degree of attention to positive and negative samples in the learning process. When the hyperparameter is larger, the model will pay more attention to those difficult-to-distinguish pairs of samples, i.e., those pairs of samples with similarity scores close to each other, which will help the model to improve the accuracy of distinguishing between positive and negative samples in the noisy environment. Recall@20 and NDCG@20 achieve the best results when l = 3 and q = 0.5.

5. Conclusions

In this paper, we propose a new model called ENSG that employs a hybrid sampling method instead of directly sampling from the original negative samples. This approach generates hard negative samples that contain information about positive samples, thereby producing higher-quality hard negative samples. After obtaining high-quality hard negative samples, to further improve sample quality, the model introduces robust contrastive learning. It treats hard negative samples and positive samples as positive pairs, further mining hidden features and reducing the semantic space distance between the two, thereby enhancing the quality of hard negative samples. Finally, by taking hard negative samples as input and minimizing the loss function to optimize model parameters, the model strengthens its ability to judge positive and negative samples, improving recommendation accuracy.

In order to further improve the accuracy and personalization level of recommendation, the introduction of auxiliary information as a means of enhancement is considered in the next step of the work so as to provide more accurate and personalized recommendation services.