Optimizing Transmit Power for User-Cooperative Backscatter-Assisted NOMA-MEC: A Green IoT Perspective

Abstract

Non-orthogonal multiple access (NOMA) enables the parallel offloading of multiuser tasks, effectively enhancing throughput and reducing latency. Backscatter communication, which passively reflects radio frequency (RF) signals, improves energy efficiency and extends the operational lifespan of terminal devices. Both technologies are pivotal for the next generation of wireless networks. However, there is little research focusing on optimizing the transmit power in backscatter-assisted NOMA-MEC systems from a green IoT perspective. In this paper, we aim to minimize the transmit energy consumption of a Hybrid Access Point (HAP) while ensuring task deadlines are met. We consider the integration of Backscatter Communication (BackCom) and Active Transmission (AT), and leverage NOMA technology and user cooperation to mitigate the double near–far effect. Specifically, we formulate a transmit energy consumption minimization problem, accounting for task deadline constraints, task offloading decisions, transmit power allocation, and energy constraints. To tackle the non-convex optimization problem, we employ variable substitution and convex optimization theory to transform the original non-convex problem into a convex one, which is then efficiently solved. We deduce the semi-closed form expression of the optimal solution and propose an energy-efficient algorithm to minimize the transmit power of the entire wireless powered MEC. The extensive simulation results demonstrate that our proposed scheme significantly reduces the HAP transmit power by around 8% compared to existing schemes, validating the effectiveness of our approach. This study provides valuable insights for the design of green IoT systems by optimizing the transmit power in NOMA-MEC networks.

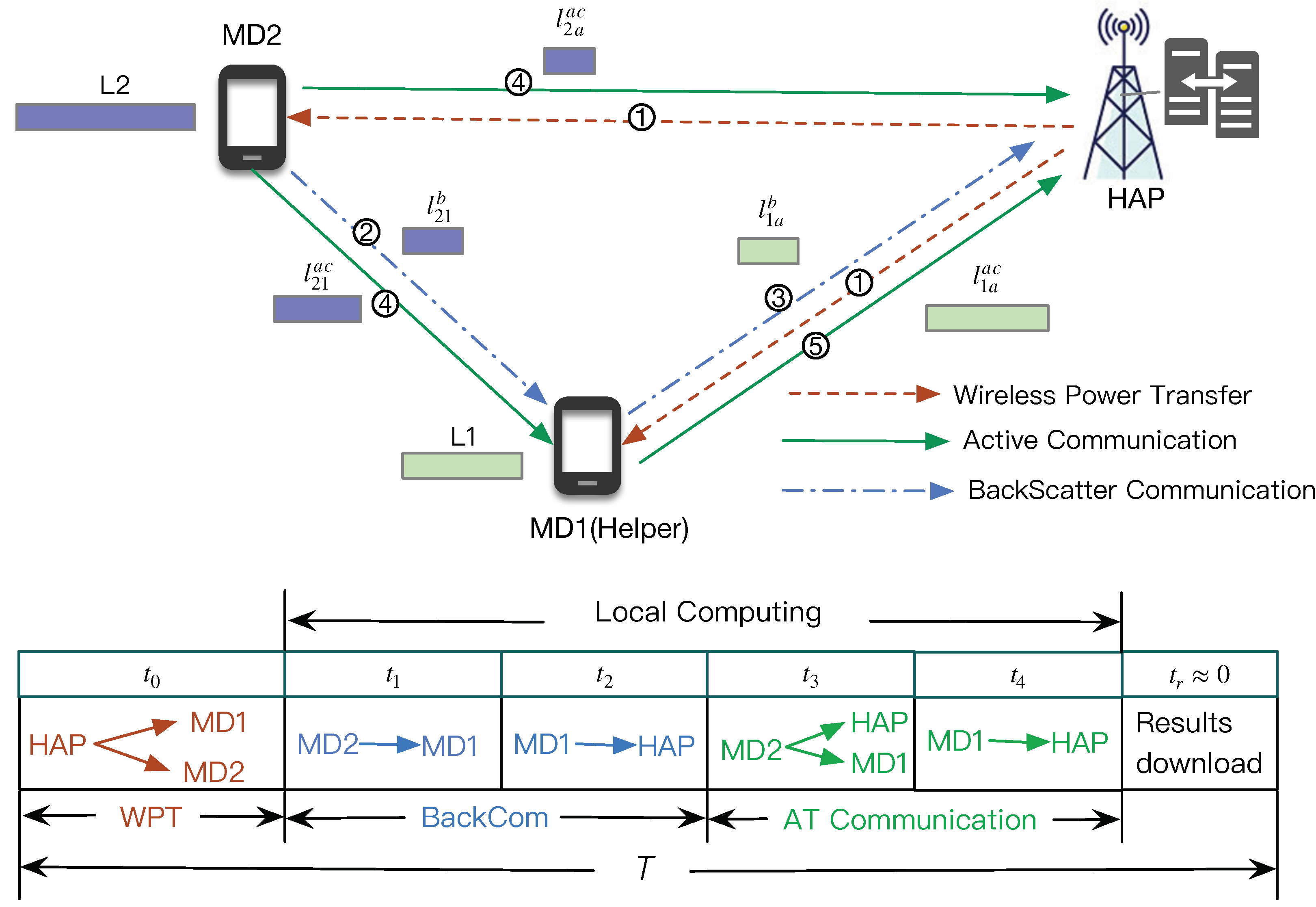
1. Introduction

The rapid development of the Internet of Things (IoT) has driven an increasing demand for efficient data processing and low-latency communication in mobile devices such as autonomous vehicles, facial recognition systems, virtual reality (VR) devices, and electronic health monitors [1]. To address the limitations in computational power and battery life of these devices, Mobile Edge Computing (MEC) technology offloads computationally intensive tasks to servers deployed at the network’s edge, such as base stations, thereby effectively enhancing the devices’ computational capacity and response speed [2,3]. Additionally, Wireless Power Transmission (WPT) [4] technology collects energy remotely through radio frequency (RF) signals, further extending the battery life of devices. Leveraging the advantages of MEC and WPT networks, numerous studies have been conducted to explore the potential of Wireless-Powered MEC (WPMEC) systems, and a multitude of efficient algorithms have been proposed to address the joint allocation of communication and computational resources.

However, to address the challenges of serving the massive number of devices in future wireless networks, relying solely on MEC may not suffice to meet service demands. Beyond computational and battery limitations, the double near–far effect can severely impact network performance, especially for devices that are far from Hybrid Access Points (HAPs) and often in poor channel conditions [5]. This effect leads to a significant difference in rates between distant users and nearby users due to the dual impact of signal propagation loss. It not only reduces the efficiency of energy harvesting but also affects the distance-based path loss compensation in Wireless Information Transmission (WIT). To overcome these challenges, researchers have proposed a collaborative computing model. By allowing user devices to collaborate, near-end users can act as relays for far-end users. This cooperation helps to strengthen the signal received by the far-end users and reduces the interference caused by the proximity of near-end users to the HAP. The relaying of signals from near-end to far-end users can overcome the path loss and interference, ensuring a more balanced signal strength distribution among all users. This approach not only increases the efficiency with which distant users offload tasks to access points but also makes full use of idle computing resources in the network through Device-to-Device (D2D) [6,7] communication and User Collaboration (UC) [8] mechanisms, optimizing resource allocation, effectively improving energy efficiency, and addressing the challenges posed by geographical disparities.

The integration of Non-Orthogonal Multiple Access (NOMA) technology into WPMEC systems has been identified as a means to enhance overall performance [9,10]. This approach allows for the shared use of time-frequency resources among users, leveraging power domain multiplexing and multiuser detection techniques such as Successive Interference Cancellation (SIC) [11]. The adoption of these techniques not only improves spectral efficiency but also substantially increases system capacity and coverage, which is particularly beneficial in frequency-constrained or densely populated urban scenarios.

Backscatter Communication (BackCom) technology has emerged as a promising approach in mobile communication due to its low energy footprint [12,13,14,15,16,17]. This technology facilitates the transmission of information through the passive reflection of radio frequency signals, concurrently harvesting energy to power circuit operations. When compared to the traditional active transmission (AT) model, which follows the Harvest-then-Transmit (HTT) protocol, BackCom dramatically minimizes energy usage, typically requiring only a few microwatts to hundreds of microwatts, despite offering comparatively lower transmission rates. To optimize the trade-off between energy harvesting and data transmission, and to concurrently enhance system throughput and energy efficiency (EE) [18], BackCom can be strategically combined with AT. This dual-mode approach capitalizes on the complementary strengths of both communication methods.

Extensive research [19,20,21,22,23] has explored the use of BackCom and NOMA to improve the efficiency of wireless spectrum utilization and wireless energy transfer. In NOMA systems, near-end users with superior channel conditions receive lower power allocations to decode signals for far-end users, who transmit at higher power to reduce interference. Backscatter communication further conserves energy and enhances spectrum efficiency through signal reflection. However, research on the synergy between backscatter communication and NOMA in cooperative scenarios remains underexplored. Additionally, the majority of existing work on energy optimization in WPMEC systems has focused on energy consumption at the mobile device (MD) level. However, since the energy for MDs is entirely harvested from the RF signals emitted by the HAP, the energy transmitted by the HAP constitutes the total energy budget of the WPMEC system. Therefore, optimizing the energy consumption of HAP transmissions is of significant practical importance.

In this paper, we consider a transmit energy minimization (TEM) problem within a three-node wireless powered NOMA-MEC network, integrating BackCom and AT communication modes. In a three-node network, the far-end user faces poor channel conditions and significant double near–far effects due to the long distance from the HAP. We employ NOMA technology to facilitate user cooperation, allowing the far-end user to delegate tasks to the near-end user and AP. After receiving and processing the signals, the near-end user computes some tasks locally and forwards the rest to the AP, thereby enhancing the communication quality of the far-end user and mitigating the double near–far effect. We jointly optimize the WPT time fraction, backscatter time fraction, task offloading time fraction, transmit power allocation of the MD node, and backscatter reflection coefficients, aiming to minimize the total transmit power of the HAP while meeting task latency constraints. We formulate the mathematical model for the TEM problem, which is strongly non-convex. Due to signal interference in NOMA communication, there is a coupling between transmission power allocation decisions, and the coupling between BackCom communication and AC communication introduces additional coupling in the offloading of data, posing significant challenges in solving the problem. To address this highly non-convex TEM problem, we employ variable substitution techniques and convex optimization theory to convert it into a convex problem, allowing for efficient solutions. Extensive numerical simulations are conducted to verify the performance and effectiveness of our proposed scheme.

The primary contributions are summarized as follows:

• Proposing an innovative energy optimization model for a WPMEC system from a green IoT perspective. We formulate a TEM problem for HAP under task delay constraints, while leveraging the NOMA technique, integrating BackCom with AT communication, and employing user cooperation to alleviate the impact of the double near–far effect. Furthermore, our model focuses on the optimization of the overall energy consumption in WPMEC networks, rather than solely considering the energy expenditure of mobile nodes. The model has practical application value for reducing carbon emissions in WPMEC and promoting the development of green IoT technologies.
• Applying variable substitution and convex optimization theory to convert the non-convex TEM problem into a convex one. Through a meticulous analysis of the problem’s structure, we have developed a low-complexity algorithm to solve it and derived a semi-closed-form expression for the optimal solution.
• Evaluating the performance of our scheme through extensive simulations. The experimental results demonstrate that our proposed scheme surpasses the state-of-the-art methods, with an approximate improvement of 8%.

The remainder of this paper is organized as follows: Section 2 provides an overview of the related works in the field. In Section 3, we details the model of the Backscatter-Aided wireless powered NOMA-MEC system. In Section 4, formulates the transmit power optimization problem, presenting the mathematical formulation. Section 5, we develop a low-complexity algorithm designed to solve the optimization problem. Section 6 offers a comprehensive evaluation of the proposed algorithm’s performance through extensive simulations. In Section 7, we conclude the paper by summarizing the key findings and contributions, and suggest potential directions for future research.

2. Related Work

In order to increase the data computation capability and decrease the task processing delay, the resource management in WPT assisted MEC network has been extensively studied [24]. Zhang et al. [25] presented a mobility-aware hierarchical MEC framework for IoT, employing a game theoretic approach to enhance energy efficiency and reduce latency in computation offloading. Dinh et al. [26] introduced a semidefinite relaxation (SDR)-based approach for task offloading from a mobile device to multiple edge devices, aiming to minimize execution latency through joint task allocation and CPU frequency optimization in both fixed and elastic CPU frequency scenarios. Moreover, energy consumption as a determining factor of network performance has been widely explored in MEC networks. Wang et al. [27] proposed a modified-cutting-plane (MCP) algorithm and a pivoting-and-subgradient (PS) algorithm to minimize total energy consumption in a multicell MEC system. Mei et al. [28] explored a dynamic energy-efficient task offloading algorithm for a multidevice single-MEC system, leveraging Lyapunov optimization to minimize energy consumption while maintaining system stability. Chen et al. [29] introduced a polling callback energy-saving offloading strategy for MEC systems to address asynchronous data transmission and task processing times, and employs a game-learning algorithm combining DDQN and distributed LSTM to optimize energy consumption. However, most of the aforementioned research has focused on optimizing the energy consumption of mobile nodes in MEC networks, without considering the optimization of the total energy consumption of radio frequency (RF) from the HAP in WPT-MEC systems. Since the mobile nodes in WPT-MEC network harvest their energy from the RF emitted by the HAP base station, optimizing the total RF energy consumption of the HAP is of more practical significance.

Researchers have extensively adopted user cooperation mechanism to mitigate the double near–far effect and optimize resource utilization in MEC systems [30,31,32]. Sun et al. [30] introduced an iterative algorithm designed to minimize end-to-end latency in IoT environment, jointly optimizing user association and resource allocation in a three-phase operation protocol. Lyu et al. [31] considered user-cooperation schemes in different communication modes, Backscatter and HTT, improving network communication capability and energy efficiency by optimizing time and power allocation and energy beamforming. Li et al. [8] employed a multiuser cooperation scheme to enhance computation performance in a WPMEC system, focusing on maximizing the weighted sum computation rate by jointly optimizing collaboration, time, and data allocation among IoT devices and an HAP. Huang et al. [32] introduced a NOMA-assisted cooperative computing scheme with user cooperaration in a three-node MEC system to leverage idle mobile device resources, optimizing energy consumption and offloading data through joint communication and computation resource allocation. Our previous research [33] addressed the challenge of energy management in WPT-MEC networks with user cooperation by proposing a multistage stochastic optimization approach, introducing Lyapunov optimization technique to ensure sustainability and stability in the dynamic IoT environment. Although prior research has effectively mitigated the impact of the near–far double effect on data transmission for distant nodes through user collaboration communication, it has not adequately consider the simultaneous utilization of NOMA and Backscatter, two advanced communication technologies in 5G and Beyond (B5G), to further enhance energy efficiency and communication efficiency in WPT-MEC systems.

NOMA and Backscatter, as advanced communication technologies in 5G and 6G, are gradually being widely applied in WPT-MEC networks to enhance network communication efficiency and improve the energy utilization of wireless radio frequency charging [34,35]. Toro et al. [36] provided a comprehensive survey on BackCom for green IoT, examining its operating principles, applications in various domains, and addressing operational and security challenges. Shi et al. [37] introduced a hybrid approach combining Harvest-Then-Transmit (HTT) with Backscatter communication aimed at maximizing the weighted sum of computation bits within a WPT-MEC network, taking into account a realistic non-linear energy harvesting (EH) model. Additionally, Khan et al. [35] explored the integration of 6G communications, specifically NOMA and Backcom, to enhance energy efficiency and data sharing in Automotive Industry 5.0, proposing a multicell optimization framework for backscatter-enabled NOMA vehicular networks. Fang et al. [38] proposed an energy-efficient optimization scheme for a multiuser NOMA-MEC network, employing a bilevel programming method to derive optimal solutions for a one-user two-base station (BS) scenario and extends it to a low-complexity algorithm for the multiuser and multi-BS case. Shi et al. [39] presented a NOMA-based millimeter-wave (mmW) MEC mechanism to minimize the average delay of MEC offloading by jointly optimizing beamwidth, user equipment scheduling, and transmit power, employing alternative optimization and matrix control algorithms to enhance accessing efficiency. However, the aforementioned research did not take into account the latency constraints of computational task processing and the energy consumption optimization of the HAP.

Different from the above research, this paper aims to reduce carbon emissions in MEC networks by investigating the minimization of HAP wireless radio frequency transmission energy consumption in WPT-MEC networks under user collaboration communication, while ensuring the latency of computational task processing, with the goal of achieving green communication. We have also considered the hybrid communication mode of Backscatter (e.g., BackCom and AC) and utilized the advanced communication technology of NOMA to further enhance the communication efficiency of the nodes.

3. System Model

3.1. Communication Model

We consider a user-cooperative wireless-powered MEC system, comprising a user node, a helper node, and a HAP, as illustrated in Figure 1. The HAP is equipped with an RF energy transmitter and is directly connected to an edge server. The user node, denoted as ${\mathrm{MD}}_1$, is located at a greater distance from the HAP, while the helper node, ${\mathrm{MD}}_2$, is positioned closer to the HAP. Both ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ have individual computation tasks that must be completed within a specified latency constraint. Additionally, both nodes are equipped with a BackCom circuit and an AT circuit, allowing them to select between backscatter communication and active communication modes.

In this three-node model, both ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ have their own data processing tasks with data-size $L_1$ and $L_2$ that need to be completed within a specified time T. ${\mathrm{MD}}_1$ is positioned between ${\mathrm{MD}}_2$ and the HAP, allowing it not only to process its own data but also to assist ${\mathrm{MD}}_2$ in relaying data offloaded to the edge server. The system employs a NOMA communication scheme, which allows ${\mathrm{MD}}_2$ to offload data simultaneously to both ${\mathrm{MD}}_1$ and the HAP. We focus on a zero-power IoT system, where the energy for mobile nodes ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ is entirely derived from wireless power transfer by the HAP. By using wireless charging, ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ eliminate the additional costs associated with battery replacement.

The system adopts a partial offloading model, allowing computational tasks to be fragmented and offloaded to the edge server. Here, we consider the allocation of time slice resources within a time slot of length T, which includes six parts: $t_0$ to $t_4$ and $t_r$. The communication process of the system is as follows. (1) Initially, at time $t_0$, ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ receive wireless energy transmitted by the HAP’s RF equipment, which is used to process their respective computational tasks, denoted as $L_1$ and $L_2$. (2) Since the system employs a hybrid transmission mode combining BackCom and AC, data offloading begins with BackCom. At time $t_1$, ${\mathrm{MD}}_2$ partially offloads its data to ${\mathrm{MD}}_1$ using BackCom, with the offloaded data size denoted as $l_{21}^b$. (3) Subsequently, during the $t_2$ time slot, ${\mathrm{MD}}_1$ offloads its data to the HAP via BackCom, with the offloaded data size denoted as $l_{1a}^b$. (4) Next, task offloading proceeds using the AT mode. During the $t_3$ time slot, ${\mathrm{MD}}_2$, utilizing NOMA technique, simultaneously offloads data to both ${\mathrm{MD}}_1$ and the HAP, with data sizes denoted as $l_{21}^{ac}$ and $l_{2a}^{ac}$, respectively. (5) In the $t_4$ time slot, ${\mathrm{MD}}_1$ offloads its data to the edge server connected to the HAP, with the offloaded data size denoted as $l_{1a}^{ac}$. (6) Finally, during the $t_r$ time slot, the computation results are downloaded from the edge server. Because the computation result data are typically small, the time required for this step can be considered negligible.

The primary symbols and definitions used are listed in

Table 1. Key notations and definitions.

Notation	Definition
T	The time block
$t_0$	The time for WPT
$t_1{t}_2$	The time for offloading by Backcom of ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$
$t_3,t_4$	The time for offloading by AC of ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$
$L_i$	the amount of computational tasks of ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$
$h_i$	The WPT channel gain between ${\mathrm{MD}}_i$ and HAP
$g_{12}$,$g_{2a}$	The offloading channel gain between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$, ${\mathrm{MD}}_2$ and HAP
$P_0$,$P_1$,$P_{21}$,$P_{2a}$	The transmit power by AC at HAP, ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$
$P_i^{\mathrm{b}}$	The circuit power by Backcom at ${\mathrm{MD}}_i$
$l_i^{\mathrm{loc}}$	The amount of tasks processed locally at ${\mathrm{MD}}_i$
$l_{1a}^b$,$l_{21}^b$	The amount of tasks offloaded by Backcom at ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$
$l_{1a}^{\mathrm{ac}}$, $l_{2a}^{\mathrm{ac}}$, $l_{21}^{\mathrm{ac}}$	The amount of tasks offloaded by AC at ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$
$e_i^{\mathrm{loc}}$	The energy consumed by processing tasks locally at ${\mathrm{MD}}_i$
$e_i^{\mathrm{b}}$	The energy consumed by offloading tasks by Backcom at ${\mathrm{MD}}_i$
$f_i$	The local CPU frequency at ${\mathrm{MD}}_i$
${\varphi }_i$	The CPU cycles required to compute one bit task at ${\mathrm{MD}}_i$
${\beta }_i^t$	The reflection coefficient of ${\mathrm{MD}}_i$ at slot t
$\mu$	The energy conversion efficiency
${\kappa }_i$	The computing energy efficiency of ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$
B	The channel bandwidth
${\sigma }^2$	The additive white Gaussian noise

.

3.2. Wireless Powered Transfer Model

During both the WPT charging phase and the BackCom communication phase, the MD can harvest RF energy from the HAP’s RF transmitter. This harvested energy is used for both local computation and task offloading. Let $P_0$ denote the RF transmit power of the HAP, and $\mu (0<\mu <1)$ represents the energy conversion efficiency. The amount of harvested energy of ${\mathrm{MD}}_2$ is given by [17]:

$$E_2=\mu h_2{P}_0\left(t_0+t_2\right)$$

(1)

where $h_2$ represents the channel gain from the HAP to ${\mathrm{MD}}_1$, which remain constant within the T time period. Similarly, the amount of harvested energy of ${\mathrm{MD}}_1$ is as follows:

$$E_1=\mu h_1{P}_0\left(t_0+t_1\right)$$

(2)

where $h_1$ represents the channel gain from the HAP to ${\mathrm{MD}}_1$.

3.3. Computing Model

Upon the arrival of a task at a mobile node, a portion of the task may be offloaded to the edge server, while the remaining part is processed locally. Let the CPU frequencies of ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ be denoted as $f_1$ and $f_2$, respectively, and let the number of CPU cycles required to process one bit of data be represented by ${\varphi }_1$ and ${\varphi }_2$. The amount of task data processed locally at ${\mathrm{MD}}_2$ is $(L_2-l_{21}^b-l_{2a}^{ac}-l_{21}^{ac})$. Thus, the corresponding energy consumption for local computing can be expressed as [17]:

$$e_2^{loc}={\kappa }_2(L_2-l_{21}^b-l_{2a}^{ac}-l_{21}^{ac}){\varphi }_2{(f_2)}^2$$

(3)

where ${\kappa }_2$ represents the computing energy efficiency parameter of ${\mathrm{MD}}_2$ [17].

The local computing latency constraint for ${\mathrm{MD}}_2$ is as follows:

$${\displaystyle \frac{(L_2-l_{21}^b-l_{2a}^{ac}-l_{21}^{ac}){\varphi }_2}{f_2}}\le T-t_0$$

(4)

For ${\mathrm{MD}}_1$, which is responsible for forwarding ${\mathrm{MD}}_2$’s data to HAP without performing local computation on ${\mathrm{MD}}_2$’s data. Therefore, we have the following data constraint:

$$l_{1a}^b+l_{1a}^{ac}\ge l_{21}^b+l_{21}^{ac}$$

(5)

Similarly, the amount of task data that is processed locally on ${\mathrm{MD}}_1$ is equal to $L_1+l_{21}^b+l_{21}^{ac}-l_{1a}^b-l_{1a}^{ac}$, and the energy consumption for local computing at ${\mathrm{MD}}_1$ is as follows:

$$e_1^{loc}={\kappa }_1(L_1+l_{21}^b+l_{21}^{ac}-l_{1a}^b-l_{1a}^{ac}){\varphi }_1{(f_1)}^2$$

(6)

where ${\kappa }_1$ denotes the computing energy efficiency parameter of ${\mathrm{MD}}_1$ [17].

The local computing latency constraint for ${\mathrm{MD}}_2$ is as follows:

$${\displaystyle \frac{(L_1+l_{21}^b+l_{21}^{ac}-l_{1a}^b-l_{1a}^{ac}){\varphi }_1}{f_1}}\le T-t_0$$

(7)

where ${\kappa }_i$ denotes the computing energy efficiency parameter of ${\mathrm{MD}}_1$ [17].

3.4. Task Offloading Model

3.4.1. Offloading Task by BackCom

During time slot $t_1$, ${\mathrm{MD}}_2$ offloads tasks to ${\mathrm{MD}}_1$ by using Backscatter communication. We denote the reflection coefficient of BackCom at ${\mathrm{MD}}_2$ as ${\beta }_1,0\le {\beta }_2\le 1$, which plays a crucial role for a balance between energy harvesting and communication performance. Thus, there is ${\beta }_1$ proportion of energy utilized as a carrier to transfer data, and $(1-{\beta }_1)$ proportion of incident power that is absorbed by ${\mathrm{MD}}_2$ [13]. According to Shannon’s theorem [40], the amount of tasks offloaded from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ is as follows:

$$l_{21}^b=t_{1}B{log}_2\left(1+{\displaystyle \frac{\zeta {\beta }_2{P}_0{h}_2{g}_{21}}{{\sigma }^2}}\right)$$

(8)

where $\zeta$ represents the performance gap reflecting real modulation of BackCom [14], $g_{21}$ denotes the channel gain from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$, and ${\sigma }^2$ is the noise power.

The corresponding energy consumption for task offloading by BackCom is as follows:

$$e_2^{\mathrm{b}}=P_2^{\mathrm{b}}{t}_1$$

(9)

where $P_2^{\mathrm{b}}$ is the circuit power consumption of ${\mathrm{MD}}_2$ by BackCom, which is a constant value depending on the circuit structure. In BackCom communication, a node can simultaneously reflect the signal and harvest RF energy. The energy harvested by ${\mathrm{MD}}_2$ during the BackCom communication at time $t_1$ is expressed as follows:

$$E_2^b=\mu h_2{P}_0{t}_1\left(1-{\beta }_2\right)$$

(10)

After receiving the tasks offloaded by ${\mathrm{MD}}_2$, ${\mathrm{MD}}_1$ will act as a relay and forward a portion of these tasks to the HAP. Additionally, ${\mathrm{MD}}_2$ will offload its own tasks to the HAP. At time $t_2$, the task data transmitted by ${\mathrm{MD}}_2$ via BackCom are subject to the following constraints:

$$l_{1a}^b=t_{2}B{log}_2\left(1+{\displaystyle \frac{\zeta {\beta }_1{P}_0{h}_1{g}_{1a}}{{\sigma }^2}}\right)$$

(11)

where ${\beta }_1$ is the reflection coefficient of the BackCom at ${\mathrm{MD}}_1$ and $g_{1a}$ represents the channel gain from ${\mathrm{MD}}_1$ to the HAP. The corresponding energy consumption for task offloading by BackCom is as follows:

$$e_1^b=P_1^b{t}_2$$

(12)

where $P_2^b$ is the circuit power consumption of ${\mathrm{MD}}_2$ by BackCom. The energy harvested of ${\mathrm{MD}}_1$ by Backcom during $t_2$ is as follows:

$$E_1^b=\mu h_1{P}_0{t}_2\left(1-{\beta }_1\right)$$

(13)

3.4.2. Offloading Task by NOMA-Aided AC Communication

In the AC transfer mode, we adopt the NOMA technique improve the task transmission efficiency. In time slot $t_3$, ${\mathrm{MD}}_2$ simultaneously offload task to ${\mathrm{MD}}_1$ and the HAP with data size $l_{21}^{ac}\in {\mathbb{R}}_{\ge 0}$ and $l_{2a}^{ac}\in {\mathbb{R}}_{\ge 0}$, respectively. In the NOMA transmission process, the transmit allocation allocated for task offloading to ${\mathrm{MD}}_1$ and the HAP are denoted as $p_{21}\in {\mathbb{R}}_{\ge 0}$ and $p_{2a}\in {\mathbb{R}}_{\ge 0}$. ${\mathrm{MD}}_2$ transmits a linear superposition signal to ${\mathrm{MD}}_1$ and the HAP. We suppose that the global channel state information (CSI) of network can be obtained. After receiving the signal, ${\mathrm{MD}}_1$ first decodes the ${\mathrm{MD}}_2$’s signal and subtracts it from the received signal by leveraging the successive interference cancellation (SIC) technique. We convert the channel coefficients from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ and the HAP as $g_{21}$ and $g_{2a}$, respectively. Therefore, the task offloading rate from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ and the HAP can be expressed as follows:

$$R_{21}^{ac}=B{log}_2\left(1+h_{21}{p}_{21}\right)$$

(14)

$$R_{2a}^{ac}=B{log}_2\left(1+{\displaystyle \frac{h_{2a}{p}_{2a}}{1+h_{2a}{p}_{21}}}\right)$$

(15)

where $h_{21}:={|g_{21}|}^2/{\sigma }^2$ and $h_{2a}:={|g_{2a}|}^2/{\sigma }^2$ represent the effective channel gain to the noise power ratio (ECGNR) from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ and the HAP, respectively.

During the time slot $t_3$, the amount of offloaded task from ${\mathrm{MD}}_2$ offloading to ${\mathrm{MD}}_1$ and the HAP are define to be:

$$l_{21}^{ac}=R_{21}^{ac}{t}_3$$

(16)

$$l_{2a}^{ac}=R_{2a}^{ac}{t}_3$$

(17)

The energy consumption of task offloading from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ and the HAP via NOMA are obtained as $p_{21}{t}_3$ and $p_{2a}{t}_3$.

At the $t_4$ time slot, ${\mathrm{MD}}_1$ offloads computation task to HAP by utilizing the AC mode, which includes tasks offloaded from ${\mathrm{MD}}_2$ and task native to ${\mathrm{MD}}_1$. The amount of task offloading from ${\mathrm{MD}}_1$ to the HAP is as follows:

$$l_{1a}^{ac}=t_{4}B{log}_2\left(1+h_{1a}{p}_1\right)$$

(18)

where $0\le p_1^t\le P_1^{\max }$ represents the transmit power allocated to AC at ${\mathrm{MD}}_1$ [17], $h_{1a}:={|g_{1a}|}^2/{\sigma }^2$ represents ECGNR from ${\mathrm{MD}}_1$ to the HAP, and $g_{1a}$ represents the channel coefficients from ${\mathrm{MD}}_1$ to the HAP.

The energy consumption for offloading task from ${\mathrm{MD}}_1$ to the HAP is $P_1{t}_4$.

4. Problem Formulation

In this paper, we consider a computation task offloading algorithm to minimize the carbon footprint for a green IoT network with NOMA-Backscatter assisted under user cooperation. We make joint decisions on time slot allocation $\mathit{t}=[t_0,t_1,t_2,t_3,t_4]$, power allocation $\mathit{p}=\left[p_{21},p_{2a},p_1\right]$, Backscatter reflection coefficients $\mathit{\beta }=\left[{\beta }_1,{\beta }_2\right]$, and the size of offloading tasks $\mathit{l}=[l_{21}^b,l_{1a}^b,l_{21}^{ac},l_{2a}^{ac},l_{1a}^{ac}]$ to minimize the total transmit power of HAP subjected to common latency constraints. The HAP’s transmit power minimization (TPM) problem can be defined as follows:

$$\begin{array}{cc}\hfill (P1):\underset{\mathit{t},\mathit{p},\mathit{\beta },\mathit{l}}{min}& P_0(t_0+t_1+t_2)\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& t_0+t_1+t_2+t_3+t_4\le T,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & P_2^b{t}_1+p_{21}{t}_3+p_{2a}{t}_3+e_2^{loc}\le E_2+E_2^b,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & P_1^b{t}_2+p_1{t}_4+e_1^{loc}\le E_1+E_1^b,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & p_{21}+p_{2a}<P_2^{max},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & p_1\le P_1^{max},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & l_{21}^{ac}+l_{2a}^b\le l_{1a}^b+l_{1a}^{ac},\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{(L_2-l_{21}^b-l_{2a}^{ac}-l_{21}^{ac}){\varphi }_2}{f_2}}\le T-t_0,\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{(L_1+l_{21}^b+l_{21}^{ac}-l_{1a}^b-l_{1a}^{ac}){\varphi }_1}{f_1}}\le T-t_0,\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill & \mathit{p}\in {\mathbb{R}}_{\ge 0},\mathit{\beta }\in {\mathbb{R}}_{\ge 0},\mathit{l}\in {\mathbb{R}}_{\ge 0},\mathit{t}\in {\mathbb{R}}_{\ge 0},\hfill \end{array}$$

(28)

where constraint (20) specifies the time slot allocation, constraints (21) and (22) set the energy consumption limits for ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$, respectively, constraints (23) and (24) govern the transmit power allocation for ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$, respectively, constraint (25) ensures that the task offloaded from ${\mathrm{MD}}_2$ to ${\mathrm{MD}}_1$ is relayed to the HAP within the specified time T, constraints (26) and (27) impose the task processing latency requirements for ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$, respectively, and constraint (28) defines the feasible domain for the decision variables.

Note that Problem (P1) is a non-convex optimization problem due to the nonconvex objective function and nonconvex constraints (21) and (22). This characteristic precludes the use of traditional convex optimization methods for its direct solution. Therefore, through in-depth analysis of the problem’s structure and careful design, we employ the variable substitutions to solve Problem P1.

5. Optimal Solution for the TPM Problem

Problem P1 is a non-convex optimization problem due to the non-convexity of constraints (21) and (22), and the presence of the coupling decision variables $\mathit{p}$ and $\mathit{l}$. To address this, we first rewrite $p_{21}$ and $p_{1a}$ based on Equations (14) and (18) as follows:

$$\begin{array}{c}\hfill p_{21}={\displaystyle \frac{1}{h_{21}}}f\left({\displaystyle \frac{l_{21}^{ac}}{B{t}_3}}\right)\end{array}$$

(29)

$$\begin{array}{c}\hfill p_1={\displaystyle \frac{1}{h_{1a}}}f\left({\displaystyle \frac{l_{1a}^{ac}}{B{t}_4}}\right)\end{array}$$

(30)

where the function f is define as $f:\mathbb{R}\to \mathbb{R},x\mapsto 2^x-1$ for all $x\in \mathbb{R}$.

Lemma 1.

The sum of the transmit power $p_{21}$ and $p_{2a}$ can be expressed as:

$$\begin{array}{ccc}\hfill p_{21}+p_{2a}& =& {\displaystyle \frac{1}{h_{21}}}f\left({\displaystyle \frac{l_{21}^{ac}+l_{2a}^{ac}}{B{t}_3}}\right)+\left({\displaystyle \frac{1}{h_{2a}}}-{\displaystyle \frac{1}{h_{21}}}\right)f\left({\displaystyle \frac{l_{2a}^{ac}}{B{t}_3}}\right)\hfill \end{array}$$

(31)

Proof. 

See Appendix A.    □

To address the non-convexity of constraints (21) and (22), we introduce auxiliary variable ${\psi }_1$ and ${\psi }_2$, where ${\psi }_1=t_2{\beta }_1$, ${\psi }_2=t_1{\beta }_2$ and $l_2^{ac}=l_{21}^{ac}+l_{2a}^{ac}$. Additionally, based on Lemma 1, we replace the decision variables $\mathit{p}$ with $\mathit{l}$ and introduce decision variables set $\mathit{\psi }=\{{\psi }_1,{\psi }_2\}$. We define ${\mathit{l}}^{\prime }=[l_{21}^b,l_{1a}^b,l_2^{ac},l_{2a}^{ac},l_{1a}^{ac}]$ as the amount of task processing locally and offloading for both ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$. Meanwhile, to simplify the mathematical expression, we denote some constants $C_1$, $C_2$, $C_3$. $C_1=\left({\displaystyle \frac{1}{h_{2a}}}-{\displaystyle \frac{1}{h_{21}}}\right)$, $C_2={\kappa }_2{\varphi }_2{(f_2)}^2$ and $C_3={\kappa }_1{\varphi }_1{(f_1)}^2$. Therefore, problem P1 can be transformed into problem P2, as follows:

$$\begin{array}{cc}\hfill (P2):\underset{\mathit{t},\mathit{\psi },{\mathit{l}}^{\prime }}{min}& P_0(t_0+t_1+t_2)\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.& t_0+t_1+t_2+t_3+t_4\le T\hfill \end{array}$$

(33)

$$\begin{array}{cc}\hfill & P_2^b{t}_1+{\displaystyle \frac{t_3}{h_{21}}}f\left({\displaystyle \frac{l_2^{ac}}{B{t}_3}}\right)+t_3{C}_{1}f\left({\displaystyle \frac{l_{2a}^{ac}}{B{t}_3}}\right)+C_2(L_2-l_{21}^b-l_2^{ac})\hfill \end{array}$$

(34)

$$\begin{array}{c}\hfill \le \mu h_2{P}_0\left(t_0+t_2+t_1-{\psi }_2\right)\end{array}$$

$$\begin{array}{cc}\hfill & P_1^b{t}_2+{\displaystyle \frac{t_4}{h_{1a}}}f\left({\displaystyle \frac{l_{1a}^{ac}}{B{t}_4}}\right)+C_3(L_1+l_{21}^b+l_2^{ac}-l_{2a}^{ac}-l_{1a}^b-l_{1a}^{ac})\hfill \end{array}$$

(35)

$$\begin{array}{c}\hfill \le \mu h_1{P}_0\left(t_0+t_2+t_1-{\psi }_1\right)\end{array}$$

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{h_{21}}}f\left({\displaystyle \frac{l_2^{ac}}{B{t}_3}}\right)+C_{1}f\left({\displaystyle \frac{l_{2a}^{ac}}{B{t}_3}}\right)\le P_2^{max}\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{1}{h_{1a}}}f\left({\displaystyle \frac{l_{1a}^{ac}}{B{t}_4}}\right)\le P_1^{max}\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill & l_{21}^{ac}+l_{2a}^b\le l_{1a}^b+l_{1a}^{ac}\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{(L_2-l_{21}^b-l_2^{ac}){\varphi }_2}{f_2}}\le T-t_0\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{(L_1+l_{21}^b+l_2^{ac}-l_{2a}^{ac}-l_{1a}^b-l_{1a}^{ac}){\varphi }_1}{f_1}}\le T-t_0\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill & 0\le {\psi }_1\le t_2,0\le {\psi }_2\le t_{1}and(28)\hfill \end{array}$$

(41)

Problem P2 can be proven to be a convex optimization problem according to the following Lemma.

Lemma 2.

Problem P2 is convex and can be efficiently solved using optimization tools such as CVX.

Proof. 

See Appendix B.    □

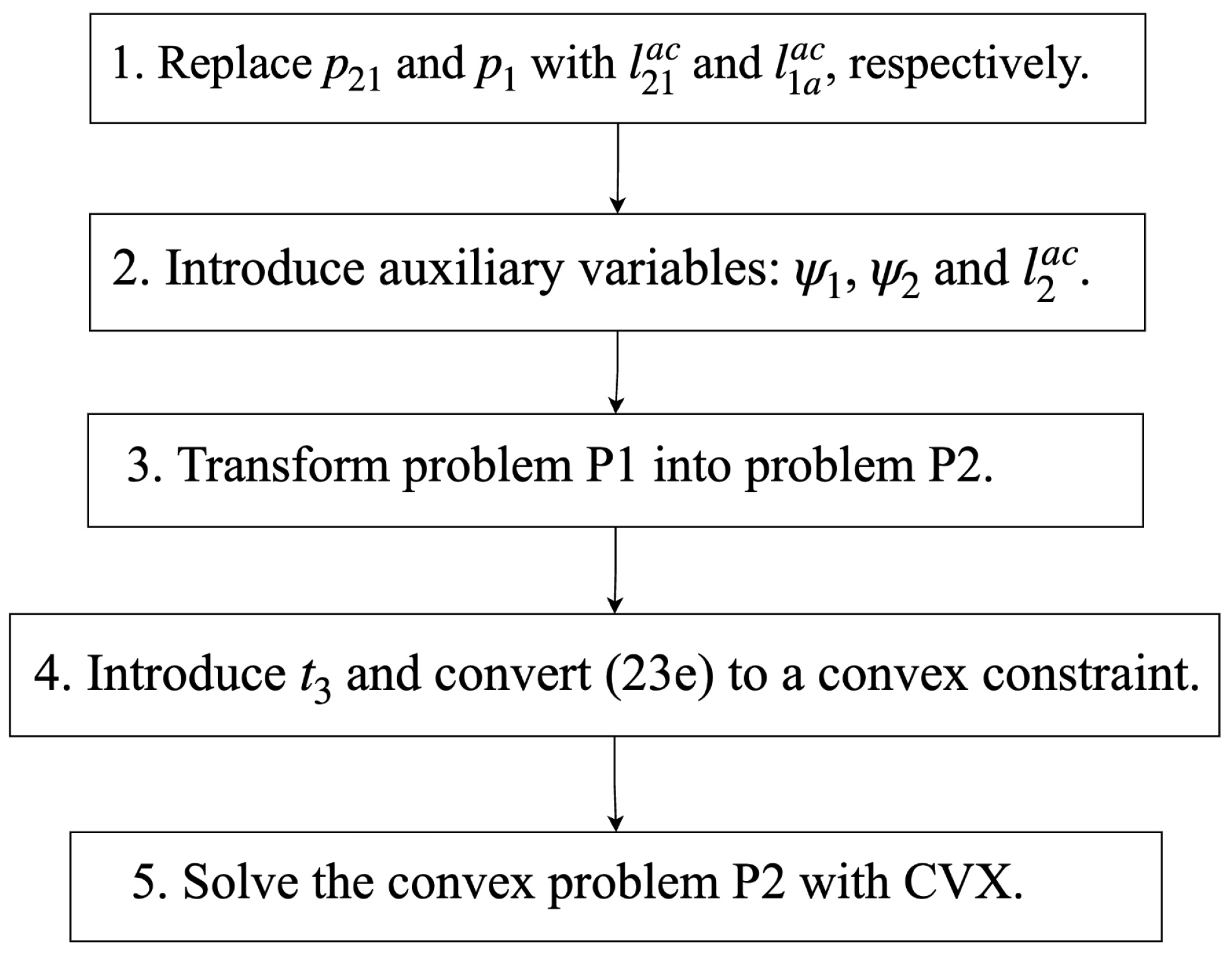
In summary, the process of convexifying Problem P1 is shown in Figure 2. By solving the convex optimization problem P2, we can obtain the global optimal solution to the original problem.

Besides, by using the Lagrange multiplier technique, we derive valuable insights into the characteristics of the optimal solution with the following theorem.

Theorem 1.

Given non-negative Lagrange multipliers ${\lambda }_i$, $i=1,2,\dots ,10$, the optimal power allocation $\mathit{l}=\left[l_2^{ac},l_{2a}^{ac},{\mathrm{ł}}_{1a}^{ac}\right]$ must fulfill certain conditions:

$$\begin{array}{cc}\hfill & l_2^{ac,*}=\left\{\begin{array}{cc}0,\hfill & if{t}_3=0\hfill \\ {\left[B{t}_3{log}_2\left({\displaystyle \frac{-{\lambda }_7\frac{{\varphi }_2}{f_2}B{t}_3-{\lambda }_2{C}_2+{\lambda }_3{C}_3-{\lambda }_8\frac{{\varphi }_1}{f_1}B{t}_3}{{\lambda }_2\frac{t_3}{h_{21}}+{\lambda }_4\frac{1}{h_{21}}ln2}}\right)\right]}^{+},\hfill & \mathrm{others}\hfill \end{array}\right.\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & l_{2a}^{ac,*}=\left\{\begin{array}{cc}0,\hfill & if{t}_3=0\hfill \\ {\left[B{t}_3{log}_2\left({\displaystyle \frac{-{\lambda }_3{C}_3-{\lambda }_8\frac{{\varphi }_1}{f_1}B{t}_3}{{\lambda }_2{C}_1\frac{t_3}{h_{21}}+{\lambda }_4{C}_1\frac{1}{h_{21}}ln2}}\right)\right]}^{+},\hfill & \mathrm{others}\hfill \end{array}\right.\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill & {\mathrm{ł}}_{1a}^{ac,*}=\left\{\begin{array}{cc}0,\hfill & if{t}_4=0\hfill \\ {\left[B{t}_4{log}_2\left({\displaystyle \frac{-{\lambda }_3{C}_3-{\lambda }_8\frac{{\varphi }_1}{f_1}B{t}_4}{{\lambda }_3\frac{t_4}{h_{1a}}+{\lambda }_5\frac{1}{h_{1a}}ln2}}\right)\right]}^{+},\hfill & \mathrm{others}\hfill \end{array}\right.\hfill \end{array}$$

(44)

Proof. 

See Appendix C.    □

According to this theorem, we can deduce that in the process of wireless radio frequency energy transfer, increasing the value of B will motivate ${\mathrm{MD}}_2$ and ${\mathrm{MD}}_1$ entities to offload data more, which correspondingly reduces the computational tasks they perform locally. Specifically, when $-{\lambda }_7{\displaystyle \frac{{\varphi }_2}{f_2}}B{t}_3-{\lambda }_2{C}_2+{\lambda }_3{C}_3-{\lambda }_8{\displaystyle \frac{{\varphi }_1}{f_1}}B{t}_3>{\lambda }_2{\displaystyle \frac{t_3}{h_{21}}}+{\lambda }_4{\displaystyle \frac{1}{h_{21}}}ln2$, the ${\mathrm{MD}}_2$ is more inclined to offload tasks through the AT mode. For the ${\mathrm{MD}}_1$, a similar conclusion can be drawn.

The process of solving the original TEP problem, denoted as (P1), is encapsulated within Algorithm 1.

Algorithm 1: User-Assisted Dynamic Resource Allocation Algorithm.

Input: the task arrical $L_i$; the channel gain $\{h_i$, $g_{12}$, $g_{2a}\}$. 1  Variable substitution is conducted based on (29), (30), (A3); 2  Calculate $C_1,C_2,C_3$ based on P1.1.1; 3  cvx_begin 4   Minimize P2 5   Subject to (33)–(41) 6  cvx_end 7  Calculate ${\mathit{\beta }}^{*}$ based on ${\psi }_1=t_2{\beta }_1$, ${\psi }_2=t_1{\beta }_2$; 8  Calculate ${\mathit{p}}^{*}$ based on (29), (30), (A3);  Output: Obtain the optimal resource allocation $\left\{{\mathit{t}}^{*},{\mathit{p}}^{*},{\mathit{\beta }}^{*},{\mathit{l}}^{*}\right\}$;

Algorithm Complexity Analysis

After transformation, the non-convex problem P1 is converted into a convex optimization problem P2, which involves a total of 12 variables. P2 can be solved using existing mature convex optimization algorithms, such as the interior-point method, with a time complexity of $O(n^{3.5}log(1/ϵ))$, where n is the number of decision variables. For P2, due to its small scale of variables, it can be solved quickly. Here, we use the open-source CVX toolbox for solving it.

In practical applications, our algorithm can be implemented using a master–slave architecture. The MEC server periodically gathers data regarding the computational tasks’ size from the MD nodes and the wireless network’s channel status, which are used as inputs for problem P2. CVX is then employed to determine the most efficient time slicing and resource allocation strategy. Given the small size of this data, it has a negligible effect on network traffic. Furthermore, the MEC server can swiftly solve problem P2 due to the limited number of decision variables, ensuring that regular data processing is not interrupted. The operation of the algorithm does not require any additional conditions or data.

6. Simulation Results

In this section, we assess the performance of our proposed scheme through comprehensive numerical simulations. Our high-performance experimental setup leverages a 2.10 GHz Intel(R) Xeon(R) Silver 4116 CPU with 48 cores, paired with two GeForce RTX 4070 GPUs, to ensure efficient simulation processing. This configuration is complemented by 64 GB of RAM, which is essential for handling the memory-intensive tasks of our simulations. The software environment consists of Python 3.12, integrated with the convex optimization library CVXPY 1.5, all running on an Ubuntu 22.04 LTS operating system. We define the following parameters: $A_d$ for antenna gain, $f_c$ for carrier frequency, $d_e$ for the path loss exponent, and $d_i$ for the distance between nodes. We employ a free-space path loss model to simulate signal propagation, with the average channel gain $\overline{h}=A_d{({\displaystyle \frac{3\times {10}^8}{4\pi f_c{d}_i}})}^{d_e}$. Additionally, we incorporate a Rayleigh fading model to account for channel gains. The simulation parameters are summarized in

Table 2. Simulation parameters.

Symbol	Value
Transmit power of the AP $P_0$	1 W
Bandwidth W	$1.2$ MHz
Noise power ${\sigma }^2$	${10}^{-3}$ W
The circuit consumption of the BackCom $p_1^{ba}$ and $p_2^{ba}$	$0.01$ W
The distance between ${\mathrm{MD}}_1$, ${\mathrm{MD}}_2$ and HAP	130 m, 180 m
The distance between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$	80 m
CPU frequency of ${\mathrm{MD}}_1$ $f_1$	250 MHz
CPU cycles to compute 1 bit task of ${\mathrm{MD}}_1$ ${\varphi }_1$	250 cycles/bit
CPU frequency of ${\mathrm{MD}}_2$ $f_2$	250 MHz
CPU cycles to compute 1 bit task of ${\mathrm{MD}}_2$ ${\varphi }_2$	150 cycles/bit
Equal computing efficiency parameter of ${\mathrm{MD}}_1$ ${\kappa }_1$	${10}^{-8}$
Equal computing efficiency parameter of ${\mathrm{MD}}_2$ ${\kappa }_2$	${10}^{-8}$
The antenna gain $A_d$	3
The carrier frequency $f_c$	915 Mhz
The path loss exponent $d_e$	3

[6].

To verify the performance of our proposed algorithm, we consider the following three representative benchmarks:

(1) UC With NOMA scheme [32]: By introducing NOMA technology without BackCom, ${\mathrm{MD}}_1$ offloads tasks to ${\mathrm{MD}}_2$ and HAP simultaneously.

(2) UC with BackCom scheme [17]: Users opt to complete computational tasks exclusively via the BackCom mode. Specifically, the HAP continuously broadcasts RF energy to the users throughout the time slot.

(3) Integrated BackCom and NOMA Without UC scheme [37]: The remote users directly offload computation tasks to the MEC server without the assistance of the nearby node.

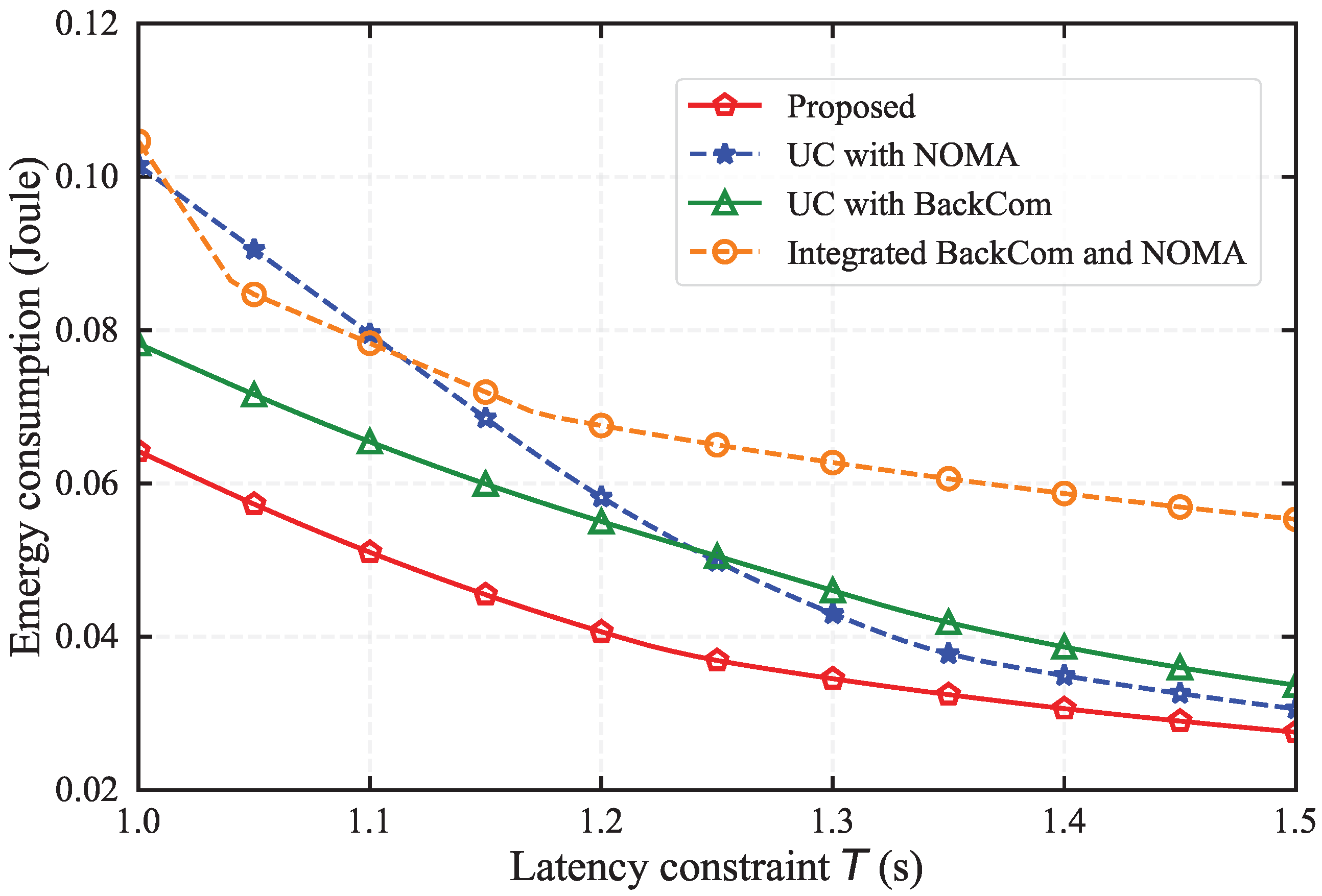
Figure 3 illustrates the comparative analysis of energy consumption across different schemes under various latency constraint T, with parameters defined as $\zeta =-20\mathrm{dB}$, $p_0=1\mathrm{W}$, and $W=1.2\mathrm{MHz}$. The results indicate a consistent decline in energy consumption for all four schemes, with our proposed algorithm demonstrating the lowest energy expenditure at any task processing latency constraints. Our proposed algorithm outperforms the other three schemes by reducing energy consumption by 20%, 40%, and 40%, respectively, when $T=1$ s. From Figure 3, it can be observed that as the task execution delay constraint becomes tighter, our scheme achieves greater energy savings. Our algorithm outperforms the current state-of-the-art methods by approximately 8% under the same network configuration. This improvement underscores the algorithm’s efficiency in energy utilization, as a result of effectively integrating multiple communication technologies, such as BackCom and NOMA.

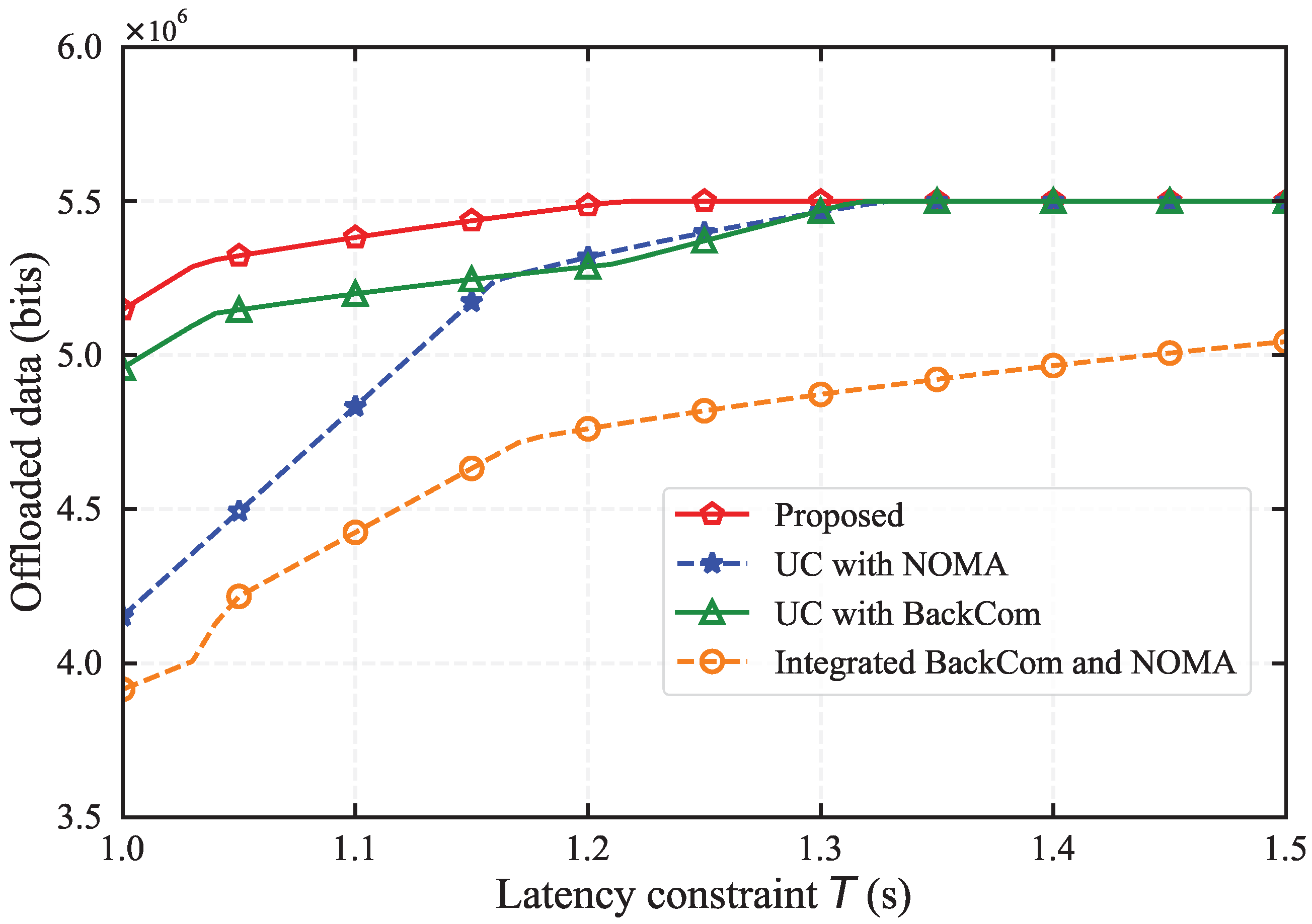
Figure 4 illustrates the amount of data processed by task offloading across various schemes with the latency constraint T ranging from 1.0 s to 1.5 s. The proposed algorithm is observed to consistently facilitate higher data offloading as the latency constraint T increases. It can be observed that the gap in offloaded data between the proposed algorithm and the other schemes widens when the latency constraint T is small, highlighting the algorithm’s robustness and effectiveness under time-sensitive conditions. This trend indicates the algorithm’s adeptness at managing task offloading within tight time constraints, suggesting the capability to utilize constraint resources in real-life scenarios. In contrast, the without UC scheme, in which ${\mathrm{MD}}_1$ directly offloads tasks to the HAP, suffers from the poor channel condition between ${\mathrm{MD}}_1$ and HAP and exhibits the lowest data offloading capability.

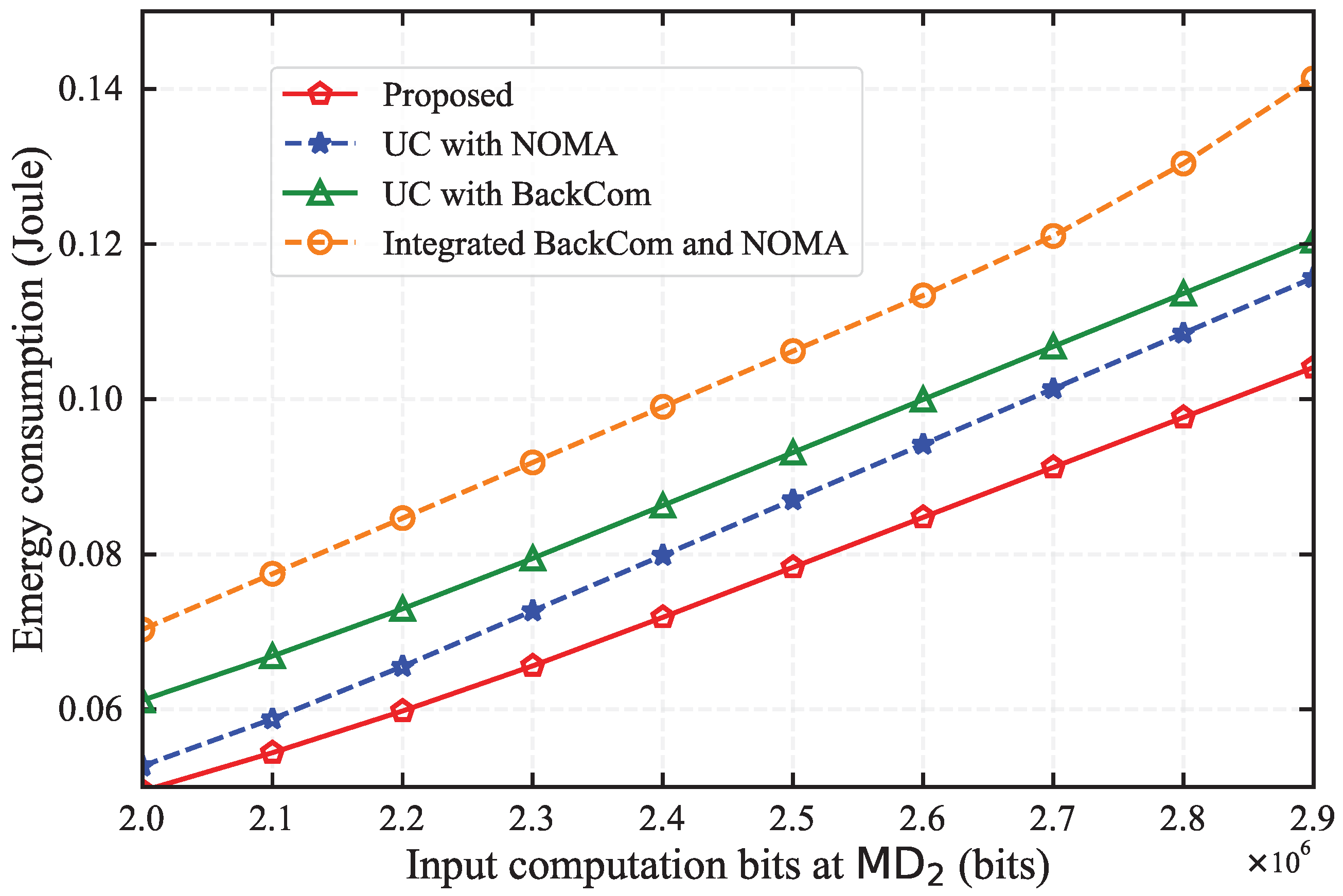
Figure 5 illustrates the impact of input computation bits at ${\mathrm{MD}}_1$ on energy consumption. It can be observed that our proposed algorithm achieves an average energy reduction of approximately 30% compared to other benchmark schemes. Notably, as the input computation bits escalate, the disparity in energy consumption between the proposed algorithm and the other three schemes becomes more pronounced. This divergence can be attributed to the algorithm’s ability to optimize resource allocation and leverage advanced communication techniques, such as BackCom and NOMA, which become more beneficial under higher computational input. This experiment underscores the robustness of our proposed algorithm across various levels of input computation bits, suggesting its superior adaptability in diverse scenarios.

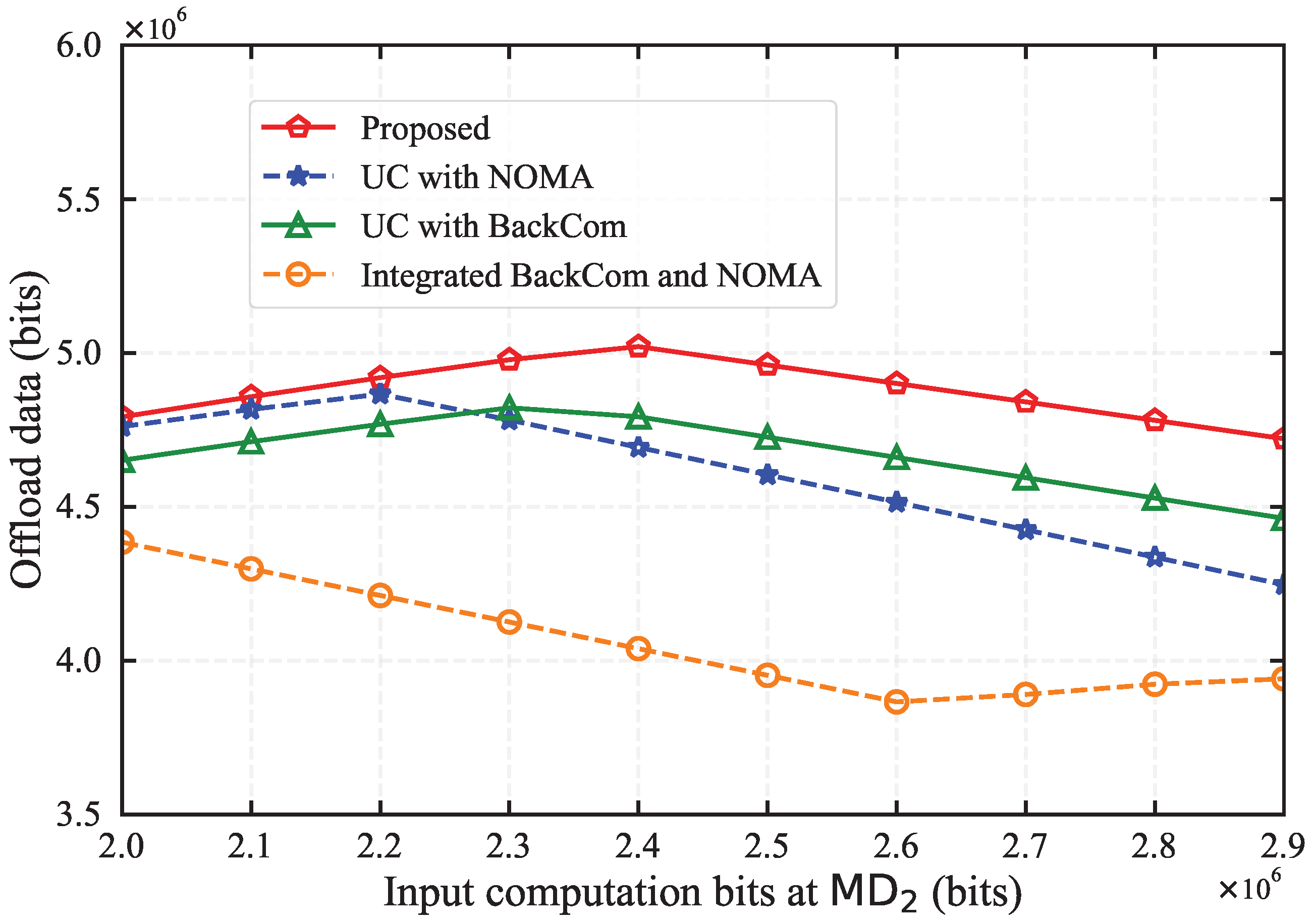
Figure 6 illustrates the task offloading capabilities across four schemes. It is clear that the proposed algorithm consistently achieves the largest amount of data processed by task offloading, indicating its enhanced transmit capability. With an increase in the input computation bits, the performance gap between the proposed scheme and the benchmark schemes widens. The proposed algorithm demonstrates a notable advantage of 7%, 12%, and 17% over the other schemes. This advantage can be attributed to the integration of advanced communication techniques and the efficient allocation of resources. Furthermore, at an input computation bit value of 2.4 Mbits, the proposed algorithm reaches its peak performance, suggesting that an optimal balance has been achieved among the various communication techniques employed.

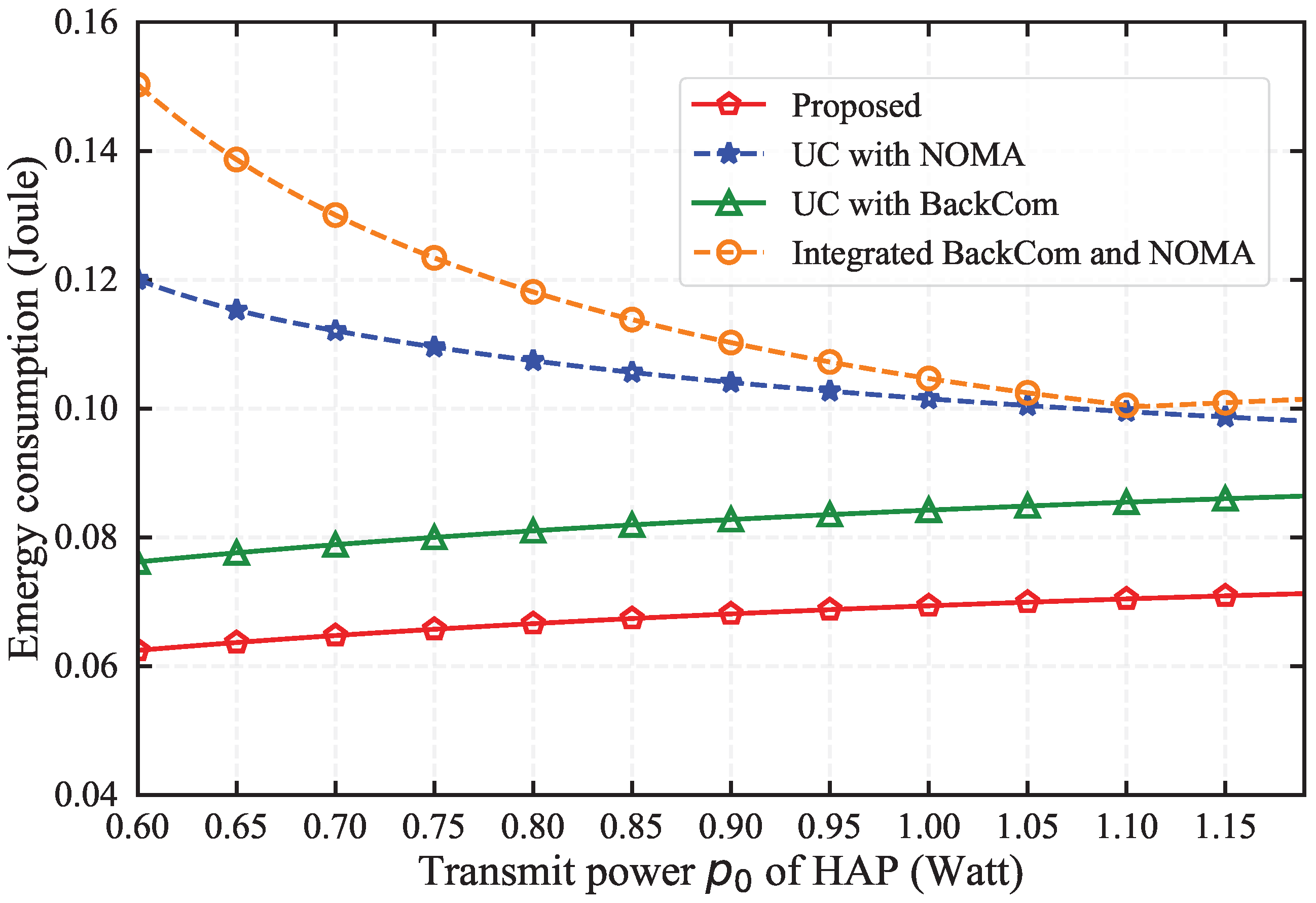
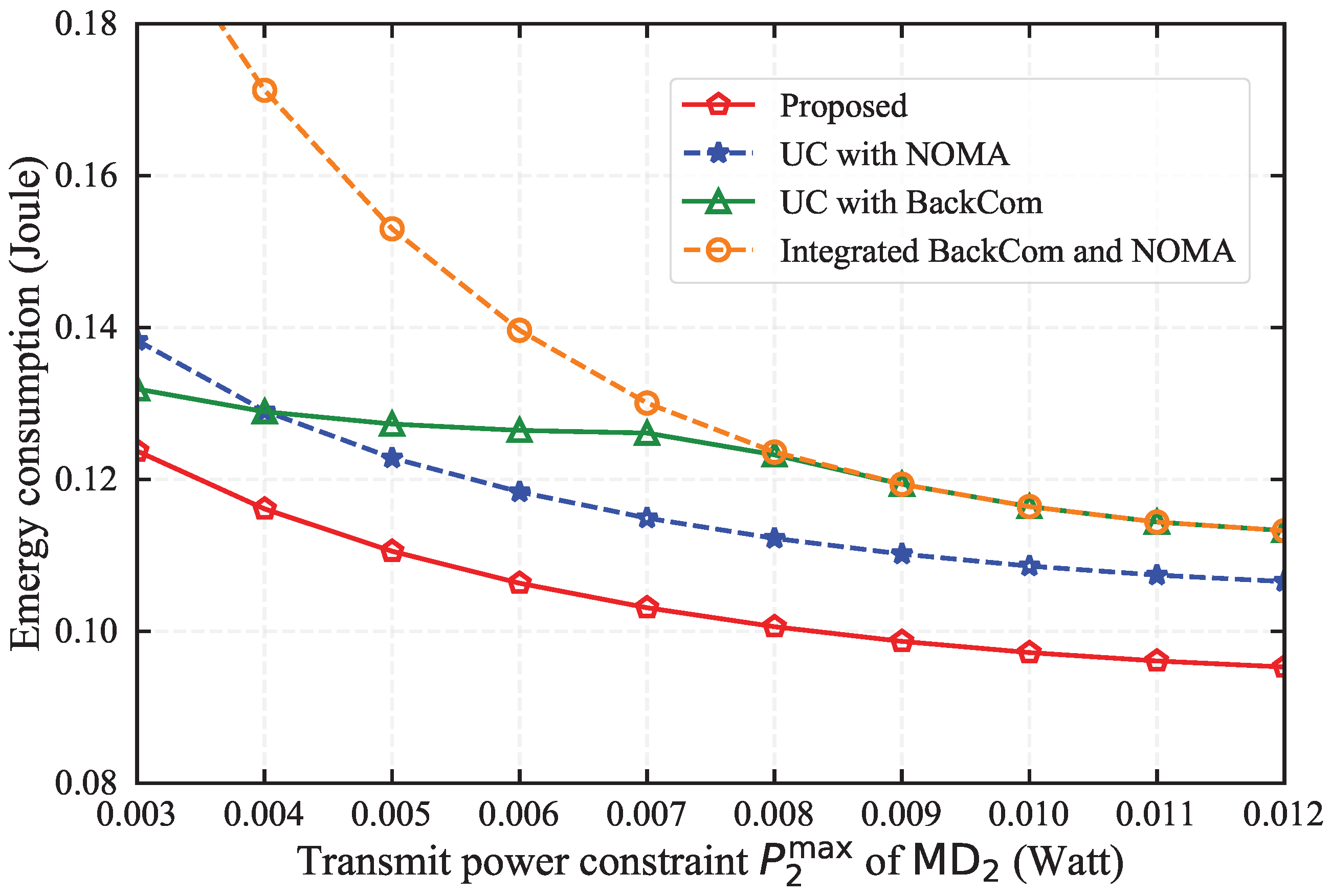
Figure 7 compares the energy consumption of four different algorithms under varying transmit power levels of the HAP, which in turn affects the energy harvested by MDs. It is evident that the our proposed algorithm consistently exhibits the lowest energy consumption of approximately 0.06 J across the entire spectrum of transmit power levels. The UC with BackCom scheme exhibits slightly higher energy consumption attributable to its less effective task offloading capability in the absence of NOMA’s assistance. Moreover, the UC with NOMA and Integrated BackCom and NOMA without UC schemes demonstrates a steady decrease in energy consumption as the transmit power increases. This is because their restricted transmission modes cannot process enough tasks when energy is insufficient. This suggests that the proposed algorithm can adapt well to the variations in energy supplies in different scenarios. The suboptimal performance of benchmark schemes also indicates that the integration of BackCom and NOMA significantly enhances the energy efficiency and robustness of the system.

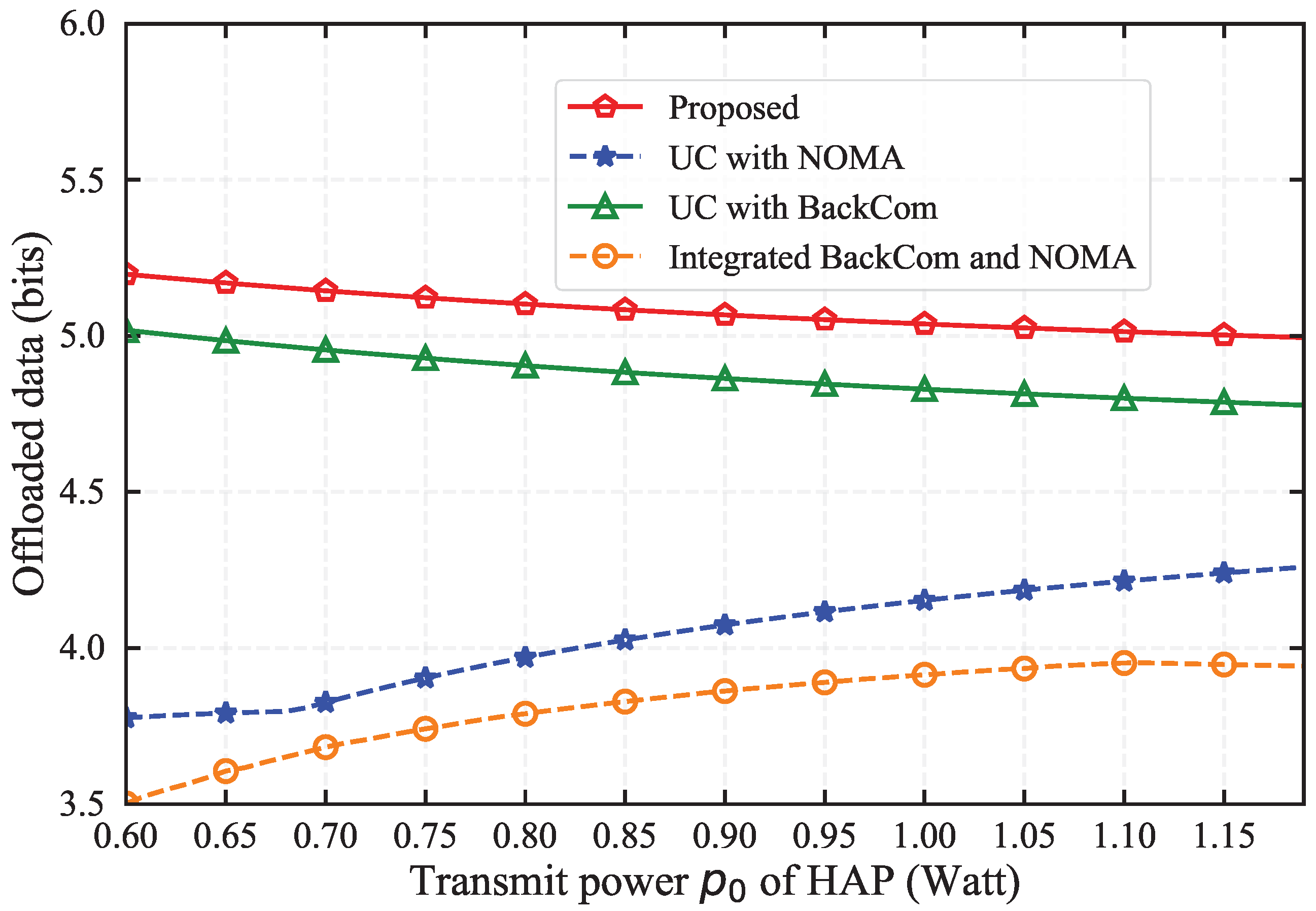
Figure 8 compares the offloaded data of four schemes under different transmit power of the HAP. Notably, the proposed algorithm offloads largest amount of data whatever $p_0$ is, suggesting that MDs prefer to process tasks by task offloading. This is due to the strong task offloading capability of the proposed algorithm, coming from the integrated communication techniques. The UC with BackCom, without the NOMA technique, exhibits less favorable performance, with the UC with BackCom and Integrated BackCom and NOMA performing the worst. The Proposed UC with NOMA’s ability to maintain high offloaded data levels even at lower power settings is particularly noteworthy. This indicates its robustness and adaptability, enabling efficient data offloading even under constrained energy conditions.

In Figure 9, we evaluate the energy consumption of the four schemes under different offloading power constraint of ${\mathrm{MD}}_1$. It is evident that the proposed algorithm consistently demonstrates the lowest energy consumption across the entire range of power constraints, indicating its superior efficiency. Interestingly, at lower power constraints for ${\mathrm{MD}}_1$, the without UC with integrated BackCom and AC scheme performs extremely poorly. This underscores the critical role of user collaboration in energy-efficient task offloading. Meanwhile, the UC with BackCom scheme performs relatively better among benchmark schemes, suggesting that BackCom technology can significantly enhance task offloading efficiency when ${\mathrm{MD}}_1$’s power is constrained. Overall, this simulation highlights the benefits of integrating multiple communication techniques, especially UC and BackCom, into the proposed algorithm.

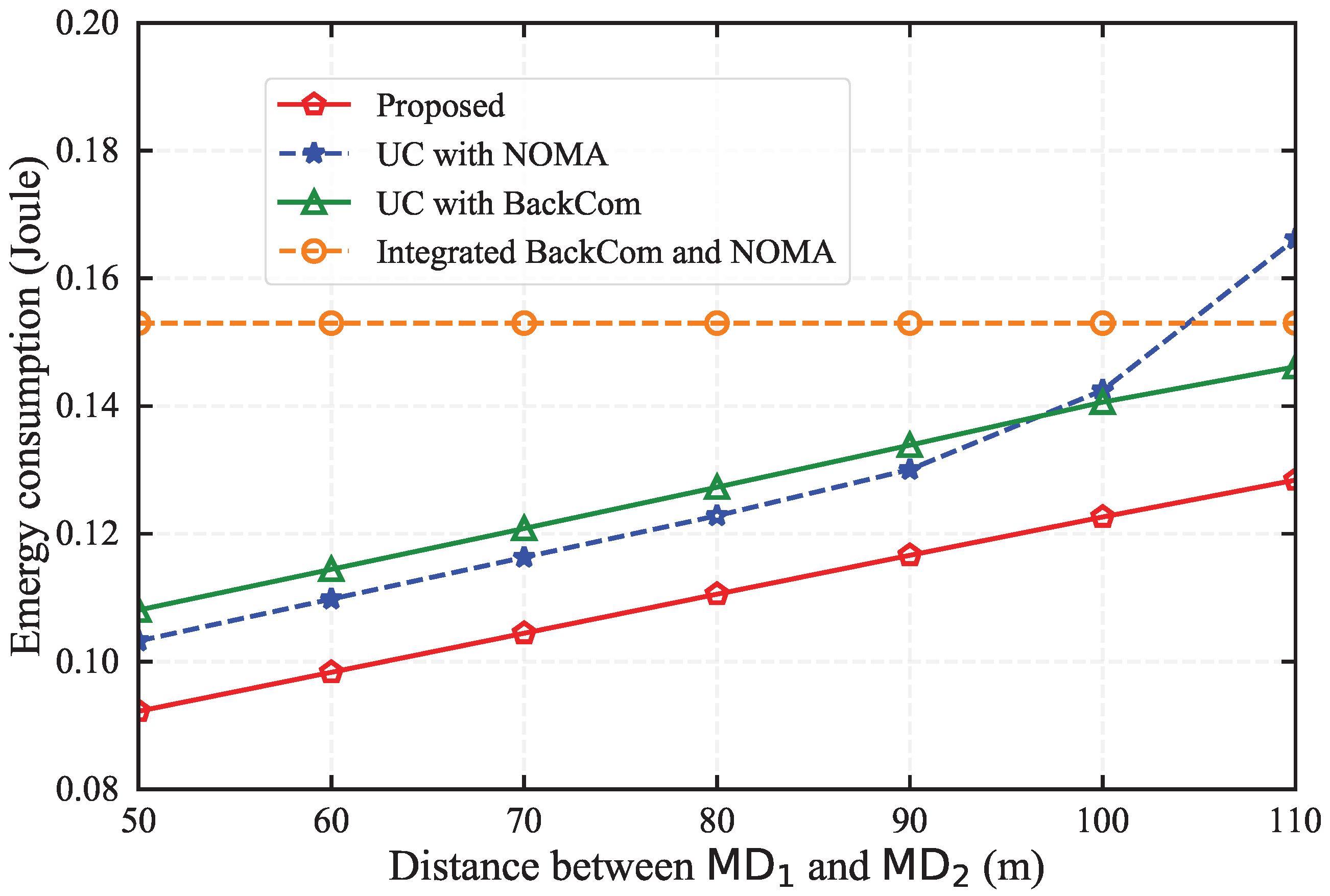
Figure 10 illustrates the energy consumption patterns under varying distances between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ from 50 to 110 m. It is observed that the energy consumption for the proposed scheme, as well as the schemes incorporating UC with NOMA and UC with BackCom, all exhibit a decline as the distance grows. This decrease can be attributed to the reduction in channel gain with distance, which in turn requires more time and higher power to offload tasks, consequently increasing energy consumption. The scheme without UC but with integrated BackCom and NOMA does not show variation with distance, as it does not rely on task offloading between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$. This observation underscores the practical deployment consideration that the proper choice of helper devices should be maintained within an optimal range to prevent a sharp deterioration in network performance. The analysis not only quantifies the impact of distance on energy consumption, but also highlights the critical role of user cooperation in efficient network architectures.

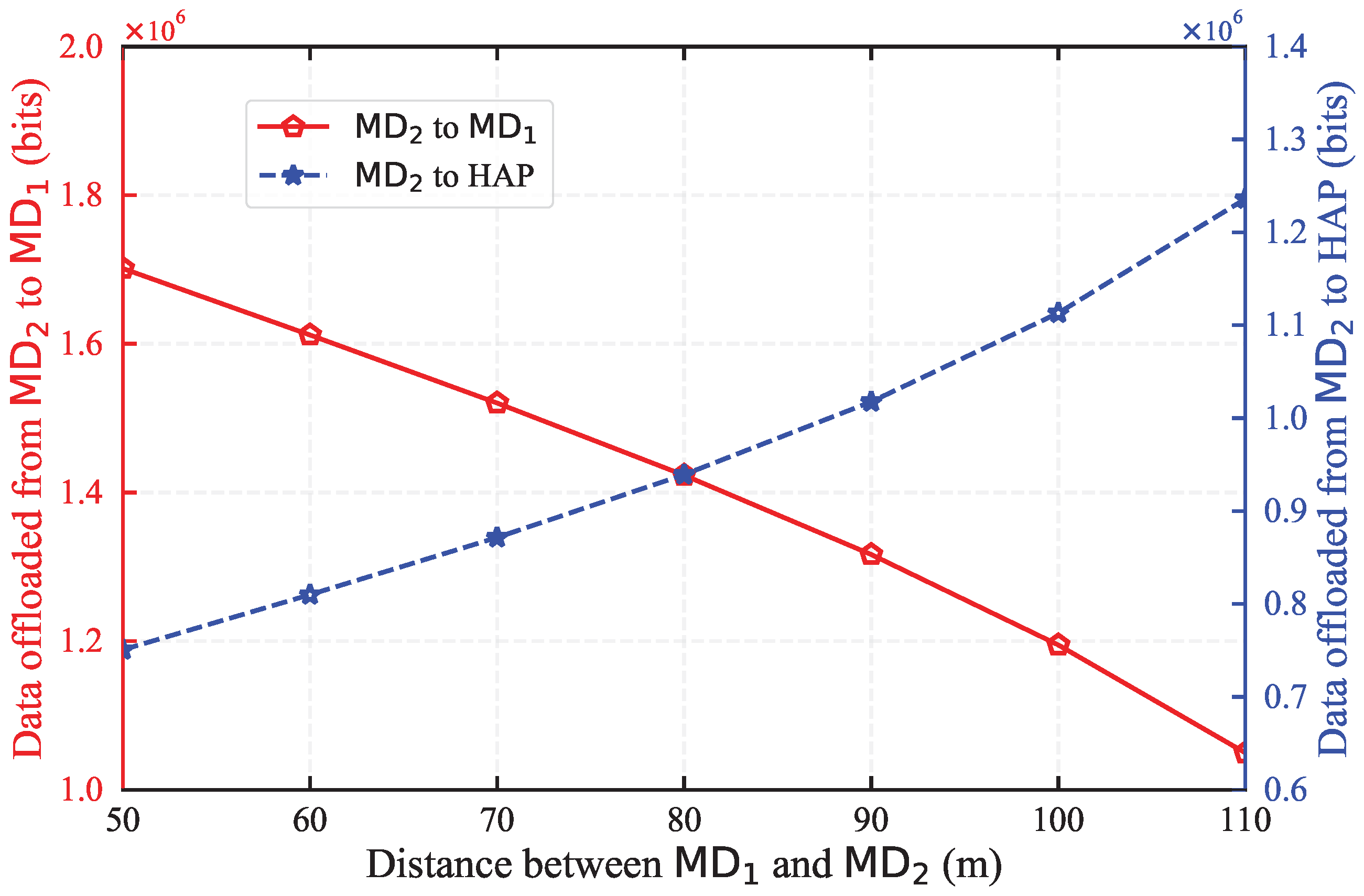
Figure 11 evaluates the task offloading strategy from ${\mathrm{MD}}_1$ as the distance between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ varies. As the distance between ${\mathrm{MD}}_1$ and ${\mathrm{MD}}_2$ increases, offloading tasks via UC to ${\mathrm{MD}}_2$ becomes less efficient, prompting ${\mathrm{MD}}_1$ to offload tasks directly to the HAP rather than relying on UC. This observation indicates that the proposed algorithm effectively adapts to network topological changes, such as the distance between mobile devices. By strategically diverting offloaded tasks to the HAP when UC is less efficient, the algorithm enhances overall network performance and minimizes energy consumption. In conclusion, the offloading strategy illustrated in Figure 11 demonstrates the algorithm’s adaptability and efficiency in managing data flow, underscoring its capability to enhance network performance and energy efficiency in real-world scenarios.

7. Conclusions

This paper explores the HAP transmission energy minimization problem in the WPT-MEC network via user cooperative communication. We take into account the processing delay constraints of computational tasks and leveraged NOMA and Backscatter technologies to enhance network transmission efficiency and energy utilization efficiency. In our proposed scheme, the HAP provides power supply to users through WPT technology, assisting two MD2 at different distances (near-end and far-end) in completing their delay-sensitive tasks. We formalize the energy consumption minimization problem as a non-convex optimization mathematical model and, through in-depth analysis of the problem’s inherent structure, transform the original problem into a convex optimization problem with only a few variables by introducing auxiliary variables and performing variable substitution, which allows for rapid solution. Simulation results show that our proposed scheme outperforms existing baseline schemes.

The optimization of our method lies in the carefully designed variable substitution technique that converts the non-convex optimization problem into a convex one, resulting in high algorithmic solution efficiency, fast solution speed, and ease of deployment. The limitation of our scheme is that it only considers the channel state of a single time slot, without accounting for dynamic wireless channel state variations and imperfect channel state information. In future work, we plan to investigate energy consumption minimization in dynamically changing network environments based on deep reinforcement learning technology and expand our current model to scenarios with multiple MDs and multiple helper nodes, thereby increasing the practicality and flexibility of our algorithm.