Abstract
Non-intrusive load disaggregation is a technique that monitors the total electrical load of an entire building or household. It uses a single power metering device to measure the total load. Then, it employs algorithms to break it down into the individual usage of different electrical devices. To address issues in load disaggregation models such as long training times, feature interference caused by the activation of other loads, and accuracy deficiencies caused by behavioral interference from users’ electricity usage habits, this paper proposes a VMD–Nyströmformer–BiTCN network architecture. The variational mode decomposition (VMD) filters the raw power data, reducing errors caused by noise and enhancing the accuracy of decomposing the load. A deep learning network utilizes a modified attention model, Nyströmformer, to reduce feature entanglement and accuracy degradation caused by habitual behavior interference during load disaggregation, while ensuring precise accuracy and improving network operational speed. The training network uses a bidirectional temporal convolutional network (BiTCN) and incorporates a residual network to expand the receptive field, allowing it to receive longer load sequence data and acquire more effective load information, thereby improving the disaggregation effectiveness for target appliances.
1. Introduction
Monitoring household appliance electricity consumption in contemporary society holds significant practical importance. This practice not only helps users optimize their electricity usage and save energy but also supports the government in effectively managing power demand during peak periods, thus maintaining grid stability. The International Electrotechnical Commission (IEC) states that smart electrification is the best way to address energy issues [1,2]. According [3] to a research report by Vassieleva et al., 80% of consumers are interested in reports on electricity consumption based on individual appliances. Knowing the electricity usage of each appliance helps consumers identify the appliances with the highest energy consumption and encourages them to consciously optimize their energy usage. Understanding consumption trends and energy-intensive appliances can help reduce the power consumption of residential or commercial buildings by 12% [4]. Residents, as an important part of demand-side management of electricity, possess high load flexibility and significant demand response potential. However, the diversity in household electricity usage behaviors and the variety of decision-makers make it extremely challenging to fully tap into this demand response potential.
In 1982, Professor Hart [5] defined the concept of non-intrusive load monitoring (NILM) by analyzing the total energy consumption of a given segment to obtain the energy consumption and status of individual loads within that segment. With the advancement of computer technology, the technical approach to NILM has gradually been refined. Scholars have categorized NILM into load identification techniques and load disaggregation techniques based on whether they determine appliance on/off states or decompose appliance energy consumption [6,7]. Using regression methods to model NILM, individual appliance energy consumption is disaggregated from the total power, a method referred to as load disaggregation. By feeding data into the model for computation and mapping the results for output, the energy consumption values of appliances are obtained [8,9]. Compared to traditional load monitoring techniques, non-intrusive load disaggregation technology is low-cost, easy to implement, and convenient to operate, helping power grid companies establish a more comprehensive energy management system at a lower cost. Brazilian scholars, Lima et al., suggested that non-intrusive load disaggregation technology can help policymakers understand user behavior patterns, thereby facilitating electricity pricing reforms [10]. Zhao Ying from East China Jiaotong University [11] used load disaggregation technology to assist users in optimizing their electricity usage behavior under a time-of-use pricing policy, achieving energy savings and cost reduction. With the introduction of the smart-home-ecosystem concept, resident electricity usage behavior analysis, based on non-intrusive load disaggregation technology, has emerged as a novel field. By analyzing user electricity usage patterns, one can infer the user’s lifestyle. Chen Weiyu and colleagues, from Zhejiang University, proposed [12] that load disaggregation technology can be used for equipment fault monitoring. They developed an electrical safety monitoring scheme based on leakage current. Alcala and others [13] proposed using load disaggregation technology to monitor the health and safety of elderly individuals living alone. Additionally, by promoting rational electricity usage through peak shifting, energy savings can be achieved while reducing residents’ electricity expenses. In summary, the application of non-intrusive load disaggregation technology can benefit power users, grid companies, and society as a whole.
In the task of load disaggregation, the accuracy of disaggregation is undoubtedly the most important aspect. Recently, with the rapid development of deep learning technology, many innovative models and methods have been proposed by scholars to improve disaggregation accuracy. Kelly et al. [14] proposed a sequence-to-sequence (S2S) mapping method, where the output sequence aligns with the input sequence. Typical models corresponding to this method include the denoising autoencoder (DAE). The S2S model represents one of the early successful applications of deep learning in load disaggregation, marking a shift from traditional methods (such as hidden Markov models and cluster analysis) to deep learning approaches. By utilizing deep neural networks, S2S models can automatically learn and capture complex characteristics of load signals, which is a significant breakthrough in the NILM field. Zhang et al. [15] introduced a sequence-to-point (S2P) mapping method, where a sequence input corresponds to a single output point. Typical models corresponding to this method include S2P and bidirectional LSTM models. The S2P model’s more straightforward input–output mapping relationship allows it to better handle noise and anomalies in the data. Compared to the S2S model, the S2P model is more concise, facilitating training and deployment while reducing computational and storage requirements. Reference [16] proposes the enhancement of model performance through integrated methods. The combination of transfer learning and convolutional neural networks, along with the newly introduced WeCV voting mechanism, effectively improves the accuracy of appliance energy consumption disaggregation. Reference [17] introduced the WaveNet neural network, a typical one-to-one output model inspired by causal one-dimensional convolutional neural networks in the context of real-time applications. This approach builds causal connections between layers of deep neural networks, achieving faster convergence and higher cost efficiency. Reference [18] proposes an innovative time bar-chart method that effectively combines appliance operation modes with time features. It aims to improve the accuracy of appliance classification by the temporal modeling of power signals, particularly excelling in scenarios with multiple appliances. Reference [19] proposed a disaggregation algorithm based on deep recurrent neural networks, which selects electrical parameters most influential to the power consumption of each target appliance through information fusion methods. The selected parameters are then input into a multi-feature space for model computation, and the final results undergo post-processing to eliminate irrelevant sequences, enhancing real-time performance. References [20,21] introduced transfer learning methods, expanding the model’s generalization ability, reducing the time required for training models from scratch, and accelerating model deployment and application. This reference [22] reviews the non-intrusive load monitoring methods based on deep neural networks (DNN), focusing on appliance disaggregation from low-frequency data. It provides an overview of NILM methods, compares the performance of various models, studies the differences between different models, and suggests potential future directions and issues worth further researching for NILM. Reference [23] proposed a subtask network, integrating load disaggregation and load identification techniques to enhance overall model performance. Reference [24] introduced the attention mechanism into NILM, significantly enhancing feature extraction for appliance activation data and improving disaggregation accuracy. Reference [25] proposed a novel integration of the attention mechanism with disaggregation tasks by compressing two-dimensional convolutions into one-dimensional, and then converting them back to two-dimensional, achieving accurate disaggregation while reducing computational costs. Thanks to the in-depth research by numerous scholars, deep learning has shown outstanding performance in the field of load disaggregation. The introduction of the attention mechanism, in particular, has not only significantly improved disaggregation accuracy but also demonstrated its unique advantages in handling complex tasks. These academic research outcomes lay a solid theoretical foundation and provide strong support for the optimized model proposed in this paper.
2. Materials and Methods
2.1. Problem Definition
Non-intrusive load disaggregation refers to the process of extracting the power consumption data of individual appliances from the total household energy consumption. Suppose the user has electrical appliances, each with only two states (on and off), and the energy consumption of the appliances does not vary significantly while they are operating. Then, the total energy measured at time can be expressed as:
Here, represents the total number of electrical appliances in the user’s home. denotes the power consumption of the -th appliance at time , while represents the on/off state of the same appliance at time . stands for the noise present at the time . To obtain the power consumption of each appliance at a time , power-monitoring modules need to be installed between each appliance and the power supply, which undoubtedly increases the cost of the smart grid. Non-intrusive load monitoring avoids the need to install sensors at each individual load point, greatly reducing equipment installation costs. This allows for the estimation of based solely on the given total power consumption .
Load disaggregation, as an important component of non-intrusive load monitoring (NILM), aims to analyze the power consumption of specific appliances, whose consumption patterns often exhibit highly nonlinear characteristics, making traditional linear analysis methods ineffective for accurate parsing and disaggregation. Deep learning offers an efficient and accurate solution through its powerful data processing and pattern recognition capabilities, as well as its innate advantages in modeling nonlinear data. To formalize this problem, it can be described as finding an arbitrary function. This function can accurately map the observed aggregate energy consumption to the unique consumption profiles of individual appliances. The objective of load disaggregation is to infer the energy consumption patterns of individual appliances by analyzing the total energy consumption data . represents the entire framework of non-intrusive load disaggregation, requiring only the total power for research. In it, represents each appliance, for which a corresponding deep learning model must be established to perform disaggregation, and then these are aggregated to form a holistic NILM system. In NILM, the energy consumption data of appliances are typically time-series data, involving multiple time points. Using vectors can conveniently represent this data structure, where the power consumption at each unit of time (such as minutes or hours) can be a component of the vector. This process can be expressed as follows:
Therefore, the process of energy disaggregation involves establishing a mapping relationship between aggregate power consumption and the consumption of individual appliances. This implies the need to develop different models for various appliances since each mapping corresponds only to a specific appliance. Furthermore, the uniqueness of the load characteristics of each appliance further emphasizes the individuality of these models.
Ultimately, the modeling problem for load disaggregation is summarized as follows: For a set of appliances with known individual power consumption and total measured power consumption , the process of non-intrusive load monitoring can be conceptualized as an optimization problem. Specifically, for a given time point , the task is to find an dimensional vector that the error between the disaggregated power obtained through deep learning and the actual power is minimized, as shown in the following Equation (3):
2.2. VMD–Nyströmformer–BiTCN Model
This paper proposes the VMD–Nyströmformer–BiTCN load disaggregation model, which employs VMD filtering as the data processing component to preprocess raw data. By incorporating the Nyströmformer attention model as the feature extraction and variable-selection layer, the model performs weighted feature extraction of the power signals. Additionally, the BiTCN network is used as the deep learning network to train the power signals. Residual networks are introduced to enhance features and prevent overfitting, thereby improving the model’s disaggregation accuracy.
VMD generally outperforms EMD in load disaggregation, offering greater adaptability without the need for pre-selecting bases or determining decomposition levels like wavelet filtering. Instead, it automatically determines decomposition parameters through optimization. VMD can also adjust regularization parameters to balance accuracy and resistance to mode mixing, demonstrating flexibility and controllability when dealing with non-stationary appliance power signals. In contrast, the Nyströmformer enhances the operational speed and computational efficiency of attention mechanisms without compromising accuracy. Before the emergence of TCN, processing sequence data relied on RNNs such as GRU and LSTM, which are difficult to parallelize and limited by dependencies on time steps, restricting efficiency when handling large-scale data. TCN overcomes these limitations through convolution operations, enabling parallel computation and suitability for large-scale data processing, especially in performing load disaggregation tasks. The BiTCN further enhances processing efficiency by expanding the receptive field without increasing the number of convolution layers.
2.2.1. VMD Filtering
In 2014, Konstantin Dragomiretskiy et al. proposed [26] the VMD (variational mode decomposition) method, a novel, adaptive, completely non-recursive mode variance and signal processing technique. This method can use the alternating direction method of multipliers (ADMM) to optimize complex signals into several modal components (intrinsic mode functions, IMF) arranged from low to high frequencies. It has good time-frequency localization capabilities and better noise robustness.
The model initially chose VMD filtering because, when collecting appliance data at low frequencies, a signal outlier amplified due to the large time gap between consecutive samples adversely affects the training outcomes. For example, a spike in current may exist only momentarily. However, with a sampling frequency of 1/6 Hz, this point’s data might show a 12 s fluctuation. This fluctuation does not align with the normal operational power characteristics, therefore making filtering necessary.
Compared to other filtering methods, VMD filtering can better suppress mode mixing by introducing regularization terms and variational optimization than EMD (empirical mode decomposition) filtering, resulting in a cleaner power signal after denoising. VMD filtering identifies optimal modal functions through variational optimization, generally providing better decomposition accuracy than EMD. Compared to wavelet filtering, VMD’s adaptability is stronger. VMD does not require pre-selecting different wavelet bases or determining decomposition levels for different appliances. Instead, it automatically determines them through the optimization process. VMD filtering can balance decomposition accuracy and enhance anti-mode mixing ability by adjusting regularization parameters. Furthermore, it offers flexibility, controllability, and effective handling of non-stationary signals, such as the power signals of appliances.
In power signal filtering, the VMD signal filtering process is the process of obtaining the optimal solution to the variational problem. By shifting the modal functions’ spectra, we can obtain the respective computed center frequencies; then, using Gaussian smoothing to demodulate the data signal, we obtain the bandwidth of each IMF. Subsequently, by matching the optimal center frequencies and finite bandwidths of each IMF, we separate the IMFs, partition the signal’s frequency domain, extract the effective parts of the signal, and eventually obtain the optimal solution to the variational problem. The decomposition model is shown by the following equation:
In the formula, represents the different modal components of the target appliance obtained after VMD decomposition; represents the center frequencies of the modal components; is the gradient operator; represents the switching states of the appliance; is the sampling time of the appliance power; and is the original power signal. To find the optimal solution to the variational problem, the constrained variational problem needs to be converted into an unconstrained variational problem. This introduces the Lagrange multiplier and the quadratic penalty term . The augmented Lagrangian function expression is given by the following:
Then, after converting the parameters in the time domain to the frequency domain, and subsequently performing a secondary optimization within the non-negative frequency range, the various modal components can be obtained:
using the alternating direction method of multipliers (ADMM) to iteratively update the values of , , to obtain the optimal solution of Equation (5), thereby decomposing the original load power signal. In load disaggregation processing of power signals, VMD (variational mode decomposition) decomposes the power signals into a series of modal functions with different frequency characteristics. Based on the characteristics of the intrinsic mode functions (IMF), and through iterative training, the IMFs related to noise can be identified. By setting thresholds, selectively discarding certain IMFs, or weighting the IMFs, the identified noisy IMFs can be removed or suppressed. The remaining IMFs are then reconstructed to obtain the denoised power signal. This approach effectively removes noise while retaining the significant electrical power features in the data.
2.2.2. Nyströmformer
This attention mechanism is inspired by the human visual attention mechanism. When people observe objects, they focus on certain parts of the objects and ignore unimportant information. In load disaggregation tasks, attention can help the model focus on the most relevant and important power features in the input data. It allows the model to dynamically attend to different parts of the information during prediction, which helps capture long-distance dependencies in the input data, and thereby improves the model’s understanding of the data. Traditional attention mechanisms apply linear transformations of Query , Key , and Value to the input data to compute attention scores. These attention scores are then processed through a softmax function to obtain attention weights. These weights represent the importance of each value, indicating which parts the model should focus on. The standard scaled-dot attention in matrix form is written as follows:
In the above formula, the complexity of the model is . In non-intrusive load monitoring tasks, the data collected for each appliance is vast. The traditional attention model has a complexity of , which means that as N increases to maintain global feature input, this will lead to excessively long model training times. Therefore, this paper adopts a novel attention mechanism model that maintains the accuracy of traditional attention to reduce appliance training time and increase the feasibility of edge computing.
In the above formula, must be computed first before calculating the softmax, which prevents us from using the associative property of matrix multiplication. The matrix is an inner product of vectors, resulting in both time and space complexity of . To address this issue, Nyströmformer proposes [27] the following solution to reduce the computation complexity of attention while maintaining precision.
The softmax function of the matrix in the model cannot be directly computed. The best approach is to make it equivalent to a matrix that can be computed separately. The softmax matrix used in self-attention is as follows:
Here, , , , and . is a sample matrix obtained by selecting columns and rows (landmark) from . First, perform singular value decomposition (SVD) on the sample matrix . Let . The formula is as follows:
is the Moore–Penrose pseudoinverse of . is approximated by . Next, for a given query vector and key vector , let
where , . We can then construct this as follows:
with and available in hand, the matrix for standard Nyström proximation is calculated as follows:
The matrix represents selecting columns from an matrix, while the matrix represents selecting rows from the matrix. This representation is an application of (10) for softmax matrix approximation in self-attention. in (10) corresponds to the first matrix in (15) and in (10) corresponds to the last matrix in (15).
The model uses an iterative method to approximate the Moore–Penrose pseudoinverse through efficient matrix–matrix multiplications. Ultimately, its matrices will be equivalent to the following:
In the complexity analysis of the Nyström approximation, several key steps’ time complexity is primarily considered. First, landmark selection uses the segment means method, which has a time complexity of . This means that the efficiency of the algorithm for selecting landmarks is linearly related to the size of the input data, which can be accomplished through a simple linear scanning process. This is crucial for large-scale data processing, as it ensures that landmark selection does not become a performance bottleneck.
Next, the iterative approximation calculation of the pseudoinverse requires time in the worst case. Regarding matrix multiplication, the calculations involve first computing and , followed by the multiplication of these two results. The overall time complexity for this series of operations is . Overall, the analysis indicates that the Nyström approximation method is efficiently designed in terms of time complexity concerning the input size and the number of landmarks, maintaining good efficiency when handling large datasets. Thus, the total time complexity is . The principle can be referenced in the following flowchart (Figure 1):
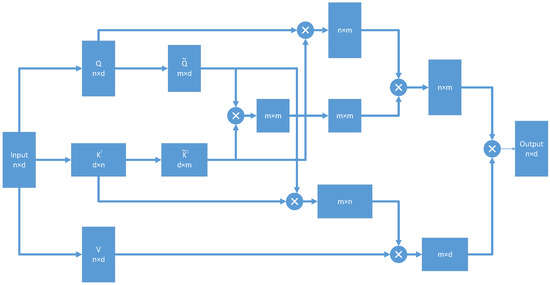
Figure 1.
Nyströmformer complexity flowchart.
In terms of memory, the cost of storing the landmark matrices and is , while the cost of storing the four Nyström approximation matrices is . Therefore, the total memory usage of the model proposed in this paper is .
This undoubtedly greatly reduces the training time of the load disaggregation part in NILM. Considering the current sample training time, using Nyströmformer to replace the traditional attention model can reduce computational maintenance costs as well as provide a feasible solution for lightweight models and rapid training of unknown devices in edge computing.
2.2.3. BiTCN Architecture
The main network trained in this paper adopts an extended network of the TCN, known as BiTCN (bidirectional temporal convolutional network). The BiTCN retains the dilated convolution and residual connections of the TCN but replaces the causal convolutions with a bidirectional temporal convolutional neural network structure. This bidirectional transmission of information allows the network to extract power feature information more effectively.
TCN stands for temporal convolutional network, a neural network architecture used for processing time-series data. It utilizes convolution operations to capture local patterns and long-term dependencies in time-series data. The advantage of TCN is its ability to map sequences of any length to output sequences of the same length. This feature makes it particularly suitable for tasks like load disaggregation that deal with large amounts of one-dimensional appliance power data. In a one-dimensional convolution, the receptive field of the later layers becomes increasingly larger, allowing more load features to be extracted. Such a network structure significantly enhances the ability to learn subtle fluctuations in load power, making the model more precise in learning load characteristics.
However, such a TCN structure limits the receptive field, requiring an unlimited number of network layers to expand the receptive field, which in turn brings a series of problems such as gradient explosion, overfitting, and inefficiency. To address this, the TCN network incorporates dilated convolutions, which expand the receptive field without increasing computational complexity. The receptive field of each layer increases exponentially with network depth through the progressive increase in the dilation factor. Dilated convolutions effectively extend the receptive field of the network model and improve its performance. As a result, the network can obtain more data information for analysis, thus better learning the global features of electrical appliances when processing power signals. A larger receptive field allows the model to capture more effective information, enhancing its capacity for data learning and analysis, and generating more accurate predictive results. The structure is illustrated in the following Figure 2:
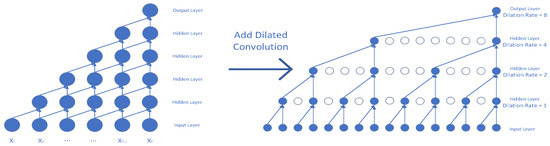
Figure 2.
Dilated convolution architecture diagram.
To tackle the issues of gradient vanishing and gradient explosion, we built deeper neural networks through residual connections. This allows information to be transmitted more directly, which in turn facilitates the training of deeper networks.
Before the emergence of TCN, sequence models were predominantly based on RNN models (such as GRU and LSTM). However, RNNs face computational challenges in parallelization because each time step depends on the output of the previous time step. This dependency restricts the efficiency of training and inference on large-scale data. When dealing with millions of power data points, the learning efficiency of RNNs limits their feasibility for edge computing. In contrast, TCNs can effectively manage large amounts of appliance data for load disaggregation tasks through convolutional operations, enabling efficient parallel computation that is ideal for processing large-scale data.
Besides using one-dimensional fully convolutional layers to ensure that the output length matches the input length, TCNs introduce a causal convolution structure in the temporal domain. Causal convolutions ensure that the network computes the current output value using only input data from past time steps. Building a network with causal convolution layers requires either a large convolution kernel or a very deep network to achieve a sufficiently large receptive field. To capture long-term dependencies more effectively and avoid the computational burden associated with large kernels or deep network structures, this paper introduces the bidirectional temporal convolutional network (BiTCN). BiTCN combines forward and backward causal convolutions, as illustrated in the following Figure 3:
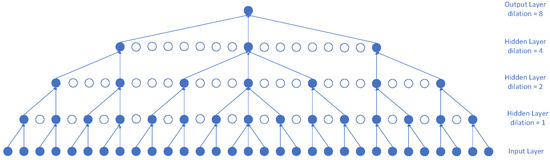
Figure 3.
BiTCN architecture diagram.
Its structure is capable of simultaneously processing the forward and backward information flow of time-series, thereby enhancing the ability to model complex temporal dependencies. Additionally, the results from the forward and backward convolutions are combined, usually through concatenation or weighted summation. This approach allows for the reduction in the number of network layers without altering the receptive field range when processing large amounts of power data, ensuring that the global characteristics of the power data from appliances are preserved.
2.2.4. Overall Network Model Structure
In the task of non-intrusive load disaggregation, the collected power signals are first processed through variational mode decomposition (VMD), decomposing the signals into multiple modes. Modes identified as noise are discarded, while modes highly correlated with the original signal are retained and summed to obtain the filtered signal. This method effectively filters out noise and singular points caused by external interference in the original signal, thus providing high-quality input data for subsequent deep learning models.
The deep learning network features a Nyströmformer-BiTCN structure. The initial Nyströmformer layer serves as a variable-selection layer to screen features from the appliance power signals. The goal is to select the variables that are most relevant to the response variable, reducing the impact of noise and irrelevant information. This process improves the model’s prediction accuracy and generalization capability in load disaggregation. This also reduces the computational burden during the training and prediction processes, enhancing the computational efficiency of load disaggregation. Identifying the most important features for model prediction allows the model to more effectively extract features related to the appliance’s power state, which enhances the model’s interpretability.
Subsequently, the structure combines bidirectional temporal convolution and dilated convolution within BiTCN layers, reducing the limitations of the receptive field to simultaneously incorporate past and future power data. This enables the load disaggregation model to learn global power characteristics more effectively. The point-wise weighted training approach allows the model to capture fine power fluctuations. Additionally, the inclusion of residual networks helps prevent overfitting, improving the model’s generalization, and making it applicable to different types of electrical appliances. Hence, BiTCN is used as the feature-learning layer to extract and train the power characteristics of appliances. Along with the variable-selection layer, the original data processed through a residual network with a low dropout rate is also input into the BiTCN network.
Implementing a residual network with a slightly lower dropout rate incorporates the original data as an additional feature input to the BiTCN network. Although minimal, the dropout rate acts as a regularization measure to help prevent overfitting. When training electrical equipment, residual connections may cause complex interactions between appliance features across layers. A slight dropout can mitigate these interactions, enhancing model robustness. It also prevents the variable-selection layer alone from overshadowing detail features, alleviating the gradient vanishing problem. Additionally, incorporating dropout further reduces inter-layer dependency, aiding better gradient propagation during training.
Finally, the output from BiTCN is used as the input for the weighted output layer of Nyströmformer. Nyströmformer, as the weighted output layer, introduces weight parameters, allowing flexible adjustment of the model’s emphasis on different features from various appliances. This helps the model adapt better to diverse appliance disaggregation tasks, thereby improving its performance and generalization across different types of electric appliances. The structure diagram is as follows Figure 4:
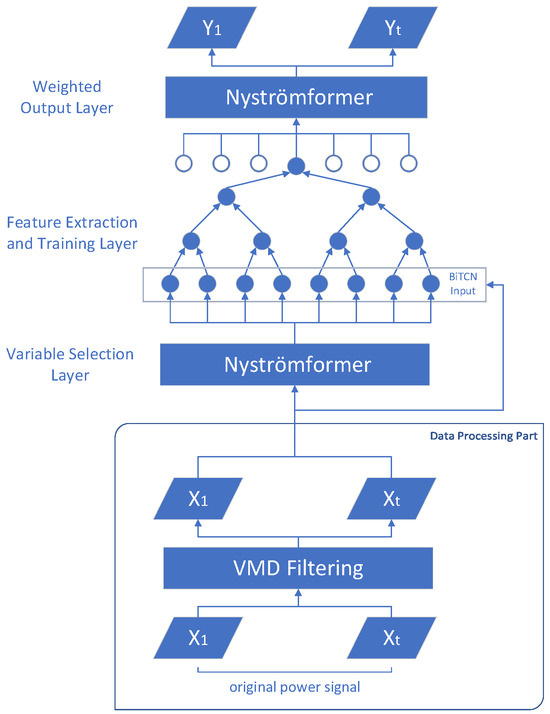
Figure 4.
The VMD-Nyströmformer-BiTCN model.
3. Results
3.1. Dataset Selection
The dataset selected for this study is the publicly available UK Domestic Appliance-Level Electricity (UK-DALE) dataset. The UK-DALE dataset collects power usage data from various households in the UK at a sampling frequency of 1/6 Hz. This dataset includes total power data from five households collected between November 2012 and January 2015. In this experiment, we use the appliance power data from House 2, which include 54 appliances. We selected five appliances with distinct and representative features as follows: kettle, dishwasher, microwave, washer–dryer, and refrigerator.
The kettle represents appliances with a simple on/off switch.
The dishwasher represents appliances with a regular multi-state process, exhibiting clear periodicity, including stages such as water intake, washing, rinsing, and draining, each with different power characteristics.
The microwave has an uncertain heating level but stable power usage during operation.
The washer–dryer represents appliances with complex and variable states, with an unpredictable number of operation modes.
The refrigerator demonstrates continuous operation, typically remaining on for extended periods under normal circumstances.
A one-year period was selected, totaling 5,300,000 readings. The input data consists of the total load power data features and the active power data of each appliance.
The experimental environment was based on the ASUS TUF Gaming A15 laptop from Asus Taiwan, featuring a 13th Gen Intel® Core™ i9-13900 H processor (2600 MHz), 32 GB of memory, and an NVIDIA GeForce RTX 4060 GPU. The software platform includes the Windows 11 operating system, Python 3.7 (64-bit), PyTorch 2.1.1 + cu121 deep learning framework, and the PyCharm Professional integrated development environment.
3.2. Normalization
Data normalization involves processing the data using a specific algorithm to constrain it within a given range, usually [0, 1] or [−1, 1]. This helps to avoid numerical instability, especially when using optimization algorithms like gradient descent. It also ensures that model parameters are updated more uniformly, accelerating the model’s convergence speed.
In disaggregation tasks, the power consumption of different appliances can vary significantly. Normalization helps prevent certain feature values from dominating the training process due to their magnitude, thus reducing the model’s dependency on a specific data range and enhancing its generalization ability across different datasets.
In this paper, Min–Max normalization is used.
Scale the data to the [0, 1] range. After obtaining the model’s output, denormalize the normalized output data to restore it to the original data scale. Normalization is used only to improve the stability and efficiency of model training, while the final prediction results need to be interpreted and applied on the original data scale.
The denormalization formula is as follows:
3.3. Evaluation Metrics
Mean Absolute Error (MAE)
The mean absolute error (MAE) is used to quantify the average absolute difference between the predicted signal and the actual values. The formula for MAE is as follows:
where variable represents the power prediction value at time index , and is the actual power measurement at the same moment.
Normalized Signal Aggregate Error (SAE)
SAE measures the relative error between the total actual energy consumption and the predicted energy consumption. It is defined as follows:
where represents the actual total energy consumption, and is the predicted value derived from the model.
3.4. Model Experimental Parameters
When the power signal is input into the model, it first undergoes VMD filtering. The parameter K represents the number of modes for VMD, i.e., how many modes the signal will be decomposed into. Considering the constraints of computational resources, we choose to set the range of the mode number (K) between 2 and 20. This setup ensures that, without exceeding the operational limits of the hardware, the frequency bandwidth covered is sufficient for effective signal decomposition. In the process of selecting the mode number, we iterate through values of K, conducting tests for each one to determine the optimal mode number. Specifically, we perform VMD decomposition for each mode count, then compare the noise-added signal with the original signal, selecting the mode count that results in the smallest reconstruction error as the most optimal choice. This process is tailored for each electrical appliance, ensuring specificity and accuracy in parameter selection. Moreover, theoretically, the penalty parameter alpha and other related parameters of VMD can be optimized through the adaptive and iterative characteristics of the algorithm. Therefore, in practical applications, we adopt the default values of these parameters to simplify the operational process of the model, relying on VMD’s internal optimization mechanism to adjust these values for efficient and effective signal decomposition. This approach fully utilizes the adaptive characteristics of VMD and combines experimental optimization of mode numbers, ensuring an optimal balance between computational costs and decomposition effects during signal processing. The parameter α controls the smoothness of the data in VMD, and τ is the temporal smoothness parameter in VMD. These two parameters iterate to their optimal values, with default settings α = 0.1 and τ = 1. Instead of setting a maximum iteration count maxItermaxIter, VMD convergence tolerance toltol is set at tol = 1 × 10−10.
After filtering, the model produces an output with the same length and dimensions as the input, which then enters the Nyströmformer model. Because the self-attention mechanism is generally more effective in high-dimensional spaces, providing more information for weighting and combination, the model first uses an embedding layer to increase its dimensionality to 128. Finally, during output, a fully connected layer reduces the dimensionality back to one dimension. The parameter num_landmark, denoted by ‘m’, which approximates the number of the original self-attention matrix, is set to 16, reflecting Nyströmformer’s role in enhancing model computation speed. Due to the computing mechanism of the Nyströmformer model, the ideal choice for the number of landmarks, m, typically favors powers of two, which helps optimize memory usage and computational efficiency. In our experiments, when m = 8, we observed a significant decrease in model accuracy, indicating that this number of landmarks was insufficient to capture enough sequence information, thereby impacting the performance. Increasing m to the model’s default value of 64 theoretically could enhance the model’s approximation and representation capabilities. However, such an increase closely approaches the next input size of the BiTCN, diluting the originally intended advantage of reducing computational costs. To find a balance between computational efficiency and model performance in the current hardware environment, we chose m = 16 as the final parameter. This not only avoids significant drops in accuracy but also maintains an advantage in computational cost, demonstrating adaptability and balance in maintaining model efficiency and effectiveness.
Simultaneously, the filtered data, through a residual connection layer, are input into the BiTCN network. Due to the non-negativity of power signals, the ReLU function is chosen as the activation function in the residual network, with dropout = 0.1. This paper employs a seven-layer deep BiTCN network, with a convolution kernel size of two, and the default dilated convolution size for each layer. In the end, the data is input into another Nyströmformer model with the same settings to obtain the load disaggregation results.
3.5. Experimental Results
3.5.1. Load Disaggregation Experiment
Load disaggregation involves processing total load power data through a model and recalculating it to obtain a new load power curve, thereby deriving the load power curve of individual electrical devices.
The results shown are disaggregation outcomes for different devices using various models. These models include the two classic models S2S and S2P from NILMTK, the traditional TCN model, a model combining convolutional networks and self-attention mechanisms (CNN + attention), and our proposed model. The visual representations of the various models are shown in Figure 5:
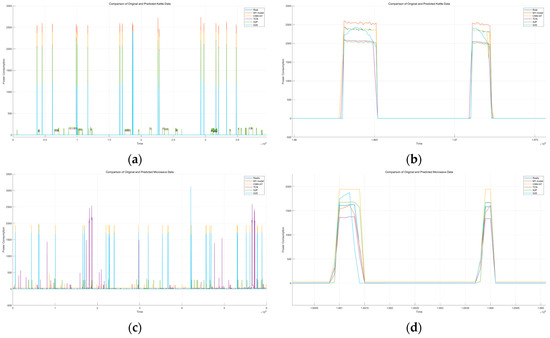
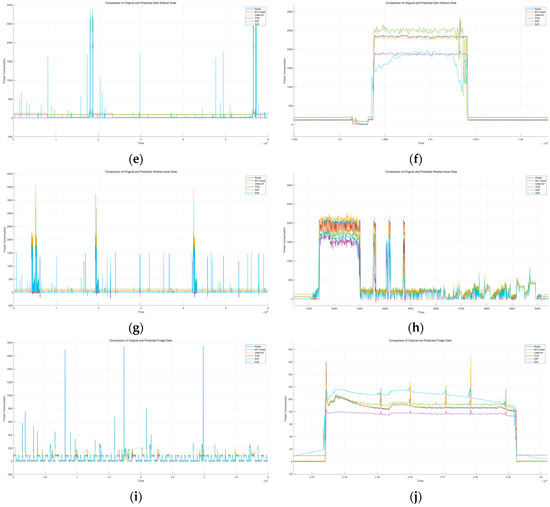
Figure 5.
Disaggregation diagram. (a) Overall output diagram of kettle. (b) Detailed section of output for kettle. (c) Overall output diagram of microwave. (d) Detailed section of output for microwave. (e) Overall output diagram of dishwasher. (f) Detailed section of output for dishwasher. (g) Overall output diagram of Washer–dryer. (h) Detailed section of output for washer–dryer. (i) Overall output diagram of fridge. (j) Detailed section of output for fridge.
The model loss values are shown in Table 1:

Table 1.
Comparative analysis of various models of appliances.
3.5.2. Model Performance Experiment
To demonstrate the performance of the model, we exported the iterative process of the kettle into a chart. By comparing the convergence speed among different models under the same number of iterations, we aim to prove the efficacy of our model. The comparative experiment is shown in Figure 6:
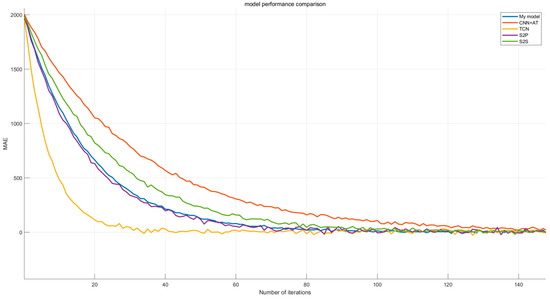
Figure 6.
Model performance comparison.
3.5.3. Computational Complexity Experiment
To emphasize how the Nyströmformer (N) attention mechanism improves efficiency compared to traditional attention (AT) mechanisms, we selected the duration of a batch during the training process as a reference. We evaluated both models on datasets of 10,000 and 50,000 data points, selecting different input dimensions (“input_dim” represents the size of the vector output by the embedding layer, indicating the shape of the data that the solution needs to receive and process) and batch sizes(batch_size refers to the number of data samples processed together in each training iteration. batch_size affects the training efficiency and final performance of the model). By comparing the traditional model with the Nyströmformer, we validated its value in enhancing efficiency. The experimental results are shown in Table 2 and Table 3:

Table 2.
1,000,000 num_samples comparative experiment.

Table 3.
5,000,000 num_samples comparative experiment.
3.5.4. Model Denoising Experiment
We conducted denoising experiments under the interference of transient impulse currents and noise to demonstrate the role of VMD filtering in our model. The experiments which compared our model with VMD included comparison against our model without VMD. The impulse current was added to the power value when a certain appliance was turned on, based on the power characteristics of the dataset. To mimic real-world conditions, noise was chosen to be 50 Hz white noise, and based on the dataset’s sampling frequency, noise values at 1/6 Hz were added to the original data when the appliance was turned on. The experimental results are shown in Figure 7 as follows.
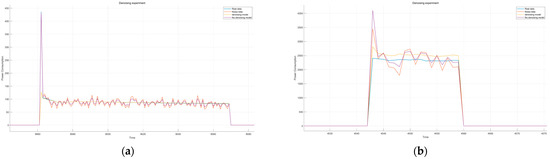
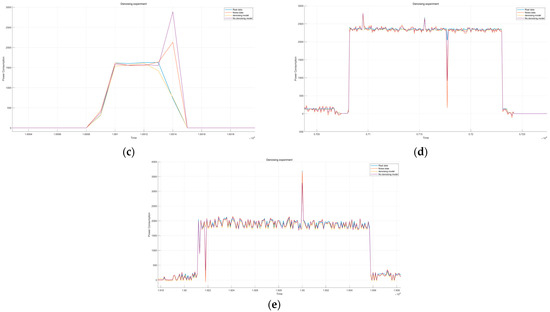
Figure 7.
Denoising experiment comparison diagram. (a) Fridge denoising experiment diagram. (b) Kettle denoising experiment diagram. (c) Microwave denoising experiment diagram. (d) Dishwasher denoising experiment diagram. (e) Washer–dryer denoising experiment diagram.
Next, data within the on/off cycle of each appliance are selected to calculate their mean absolute error (MAE), The results obtained are shown in Table 4:

Table 4.
Denoising contrast experiment MAE value.
4. Discussion
4.1. Load Disaggregation
Kettle: The waveform of the kettle is relatively simple yet distinct and does not have fixed operating times. The TCN model demonstrates detailed learning of the waveform but fails to accurately track its power values. This issue is prevalent in the subsequent four models as well. The model incorporating attention mechanisms shows significant improvement compared to the classic S2S and S2P models. The CNN+AT model, which includes a variable-selection layer, performs the best in this set of experiments. Our proposed model, which uses a lighter network, has a performance very close to it, making it a good model.
Dishwasher: The power waveform of a dishwasher is more complex and varies with different washing modes, making it difficult for convolutional networks to handle effectively. The MAE values for S2S, S2P, and TCN models are high. After incorporating attention mechanisms and applying weighted output to the features, the learning effect improved significantly. Our proposed model, which includes a variable-selection layer, performs the best in this set of experiments, with MAE and SAE values of 6.282 and 0.050, respectively.
Fridge: The fridge is typically always on, with complex waveform transformations, and interference occurs when other appliances are turned on or off. Consequently, the SAE and MAE values for all models are not as good as for other appliances. The S2P, S2S, and TCN models are significantly affected by the operation of other appliances, resulting in decreased accuracy. The models with incorporated attention mechanisms like CNN+AT and ours show improvements. Our proposed model demonstrates a higher precision in learning appliance characteristics, achieving the best MAE and SAE values of 15.951 and 0.081.
Microwave: The waveform of a microwave is the simplest compared to other appliances, making the key factor the model’s ability to accurately determine its activation. The S2P model has the best MAE at 6.791, but it misjudges activation states when the microwave is not in use, lowering its SAE score compared to our proposed model. In contrast, our model achieves the best SAE score of 0.081 in the comparative experiment, indicating higher precision in overall power value disaggregation.
Washer–dryer: In the UK-Dale dataset, the Washer–dryer is not frequently used and has relatively regular activation times. Its accuracy reflects the model’s anti-interference capabilities and its ability to learn characteristics. All models are sensitive to fixed activation times and features, but the S2S, S2P, and TCN models show interference from other appliance features when the Washer–dryer is not in use. Models incorporating attention mechanisms have relatively higher anti-interference abilities, improving accuracy. Our proposed model achieves the best MAE and SAE values of 5.847 and 0.011, respectively.
4.2. Analysis of Model Performance Experiment
In the same number of iterations, it can be observed that TCN exhibits the best convergence speed in testing. This is attributed to its relatively simple model structure. However, the fast convergence seen in the decomposition experiments does not yield good loss values, leading to insufficient model accuracy. Among them, CNN+AT has the slowest convergence speed, due to the increased computational cost caused by its traditional attention mechanism, whereas the model in this paper, which also incorporates an attention mechanism, can converge more rapidly. S2P is a classic model in NILM experiments and performs well when processing appliance data. The model in this paper achieves higher accuracy while maintaining similar performance, demonstrating the superiority of its structure.
4.3. Analysis of Computational Complexity Experiment
Experimental results can be seen in the table, where the traditional attention mechanism and Nyströmformer use the same input dimension, batch, and number of samples. Adjusting different values during training shows that the Nyströmformer significantly outperforms traditional attention, especially when the scale of data are increased. This demonstrates that using the Nyströmformer indeed effectively reduces the computational complexity of the model.
4.4. Analysis of Model Denoising Experiment
The graph shows that after the introduction of noise, the results from the non-filter model tend to reflect the noisy data more, while the introduction of VMD filtering significantly suppresses both impulse currents and white noise. From the table of MAE values, it is evident that the model with filtering also outperforms the non-filter model in terms of loss values.
5. Conclusions
The model proposed in this paper uses VMD filtering to maintain high decomposition accuracy while preventing poor filtering effects due to mode aliasing caused by filtering. This provides reliable noise suppression for deep learning disaggregation models, effectively removing noise and peak power signals, and improving the data’s smoothness and reliability. The Nyströmformer model, acting as the variable-selection layer, reduces the mingling of features in load disaggregation and, as the final weighted layer of the network, minimizes interference from user behavior habits, thereby improving the model’s prediction accuracy and significantly increasing computational speed. The integration of residual connection layers with the BiTCN network alleviates the vanishing gradient problem during model training and enables the model to better capture fine power signal features, enhancing the disaggregation accuracy. Due to computational costs, the Nyströmformer achieves the best results with M = 16 at this number of model layers. However, based on its principles, a deeper network might be more suitable for this attention mechanism. As computer hardware gradually upgrades, using deeper convolutional networks and larger receptive fields could potentially enhance the model’s learning performance. Overall, this model ensures effective disaggregation while also improving the training speed and reducing the computational training costs. It makes the training process for new types of appliances more convenient and introduces a new direction and approach for edge computing training of unknown appliances.
Author Contributions
Conceptualization, Z.L.; methodology, F.X. and H.W.; software, J.Q.; validation, Z.L., F.X., and H.W.; formal analysis, Z.L.; investigation, H.W. and Z.L.; resources, F.X.; data curation, J.Q.; writing—original draft preparation, H.W.; writing—review and editing, H.W.; visualization, Y.Z.; supervision, H.H.; project administration, F.X.; funding acquisition, F.X. and J.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Basic Scientific Research Business Expenses Research Project of Provincial Higher Education institutions in Heilongjiang Province under Grant 145309801.
Data Availability Statement
Data available on request due to restrictions, e.g., privacy or ethical.
Conflicts of Interest
Authors Jun Qiao, Yongqiang Zhang and Hu Heng were employed by the company State Grid Heilongjiang Electric Power Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Larcher, D.; Tarascon, J.M. Towards Greener and More Sustainable Batteries for Electrical Energy Storage. Nat. Chem. 2015, 7, 19–29. [Google Scholar] [CrossRef] [PubMed]
- International Electrotechnical Commission. Coping with the Energy Challenge: The IEC’s Role from 2010 to 2030; International Electrotechnical Commission: Geneva, Switzerland, 2010. [Google Scholar]
- Vassileva, I.; Dahlquist, E.; Wallin, F.; Campillo, J. Energy Consumption Feedback Devices’ Impact Evaluation on Domestic Energy Use. Appl. Energy 2013, 106, 314–320. [Google Scholar] [CrossRef]
- Laitner, J.A.; Ehrhardt-Martinez, K.; McKinney, V. Examining the Scale of the Behaviour Energy Efficiency Continuum. In People-Centred Initiatives for Increasing Energy Savings; American Council for an Energy-Efficient Economy: Washington, DC, USA, 2010; pp. 20–31. [Google Scholar]
- Hart, G.W. Nonintrusive Appliance Load Monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Shaw, S.R.; Abler, C.B.; Lepard, R.F.; Luo, D.; Leeb, S.B.; Norford, L.K. Instrumentation for High Performance Nonintrusive Electrical Load Monitoring. J. Sol. Energy Eng. 1998, 120, 224–229. [Google Scholar] [CrossRef]
- Yang, Y.; Zhong, J.; Li, W.; Aaron Gulliver, T.; Li, S. Semisupervised Multilabel Deep Learning Based Nonintrusive Load Monitoring in Smart Grids. IEEE Trans. Ind. Inform. 2020, 16, 6892–6902. [Google Scholar] [CrossRef]
- Du, L.; Restrepo, J.A.; Yang, Y.; Harley, R.G.; Habetler, T.G. Nonintrusive, Self-Organizing, and Probabilistic Classification and Identification of Plugged-In Electric Loads. IEEE Trans. Smart Grid 2013, 4, 1371–1380. [Google Scholar] [CrossRef]
- Lin, Y.-H.; Tsai, M.-S. Non-Intrusive Load Monitoring by Novel Neuro-Fuzzy Classification Considering Uncertainties. IEEE Trans. Smart Grid 2014, 5, 2376–2384. [Google Scholar] [CrossRef]
- Lima, D.A.; Oliveira, M.Z.C.; Zuluaga, E.O. Non-Intrusive Load Disaggregation Model for Residential Consumers with Fourier Series and Optimization Method Applied to White Tariff Modality in Brazil. Electr. Power Syst. Res. 2020, 184, 106277. [Google Scholar] [CrossRef]
- Zhao, Y. Research on Building Electrical Energy Management System Based on Non-Intrusive Load Monitoring. Master’s Thesis, East China Jiaotong University, Nanchang, China, 2021. [Google Scholar]
- Chen, W.; Gong, Q.; Geng, G.; Jiang, Q. Cloud-Based Non-Intrusive Leakage Current Detection for Residential Appliances. IEEE Trans. Power Deliv. 2020, 35, 1977–1986. [Google Scholar] [CrossRef]
- Alcala, J.M.; Urena, J.; Hernandez, A.; Gualda, D. Assessing Human Activity in Elderly People Using Non-Intrusive Load Monitoring. Sensors 2017, 17, 351. [Google Scholar] [CrossRef] [PubMed]
- Kelly, J.; Knottenbelt, W. The UK-DALE Dataset, Domestic Appliance-Level Electricity Demand and Whole-House Demand from Five UK Homes. Sci. Data 2015, 2, 150007. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhong, M.; Wang, Z.; Goddard, N.; Sutton, C. Sequence-to-Point Learning with Neural Networks for Non-Intrusive Load Monitoring. Available online: https://aaai.org/papers/11873-sequence-to-point-learning-with-neural-networks-for-non-intrusive-load-monitoring/ (accessed on 9 October 2024).
- Moreno, S.; Teran, H.; Villarreal, R.; Vega-Sampayo, Y.; Paez, J.; Ochoa, C.; Espejo, C.A.; Chamorro-Solano, S.; Montoya, C. An Ensemble Method for Non-Intrusive Load Monitoring (NILM) Applied to Deep Learning Approaches. Energies 2024, 17, 4548. [Google Scholar] [CrossRef]
- Harell, A.; Makonin, S.; Bajić, I.V. Wavenilm: A Causal Neural Network for Power Disaggregation from the Complex Power Signal. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8335–8339. [Google Scholar]
- Kim, H.; Lim, S. Temporal Patternization of Power Signatures for Appliance Classification in NILM. Energies 2021, 14, 2931. [Google Scholar] [CrossRef]
- Rafiq, H.; Shi, X.; Zhang, H.; Li, H.; Ochani, M.K. A Deep Recurrent Neural Network for Non-Intrusive Load Monitoring Based on Multi-Feature Input Space and Post-Processing. Energies 2020, 13, 2195. [Google Scholar] [CrossRef]
- Murray, D.; Stankovic, L.; Stankovic, V.; Lulic, S.; Sladojevic, S. Transferability of Neural Network Approaches for Low-Rate Energy Disaggregation. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 8330–8334. [Google Scholar]
- D’Incecco, M.; Squartini, S.; Zhong, M. Transfer Learning for Non-Intrusive Load Monitoring. IEEE Trans. Smart Grid 2020, 11, 1419–1429. [Google Scholar] [CrossRef]
- Review on Deep Neural Networks Applied to Low-Frequency NILM. Available online: https://www.mdpi.com/1996-1073/14/9/2390 (accessed on 13 November 2024).
- Shin, C.; Joo, S.; Yim, J.; Lee, H.; Moon, T.; Rhee, W. Subtask Gated Networks for Non-Intrusive Load Monitoring. Available online: https://arxiv.org/abs/1811.06692v1 (accessed on 9 October 2024).
- Piccialli, V.; Sudoso, A.M. Improving Non-Intrusive Load Disaggregation through an Attention-Based Deep Neural Network. Energies 2021, 14, 847. [Google Scholar] [CrossRef]
- Varanasi, L.N.S.; Karri, S.P.K. Enhancing Non-Intrusive Load Monitoring with Channel Attention Guided Bi-Directional Temporal Convolutional Network for Sequence-to-Point Learning. Electr. Power Syst. Res. 2024, 228, 110088. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Xiong, Y.; Zeng, Z.; Chakraborty, R.; Tan, M.; Fung, G.; Li, Y.; Singh, V. Nyströmformer: A Nyström-Based Algorithm for Approximating Self-Attention. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).