A GGCM-E Based Semantic Filter and Its Application in VSLAM Systems

Abstract

Image matching-based visual simultaneous localization and mapping (vSLAM) extracts low-level pixel features to reconstruct camera trajectories and maps through the epipolar geometry method. However, it fails to achieve correct trajectories and mapping when there are low-quality feature correspondences in several challenging environments. Although the RANSAC-based framework can enable better results, it is computationally inefficient and unstable in the presence of a large number of outliers. A Faster R-CNN learning-based semantic filter is proposed to explore the semantic information of inliers to remove low-quality correspondences, helping vSLAM localize accurately in our previous work. However, the semantic filter learning method generalizes low precision for low-level and dense texture-rich scenes, leading the semantic filter-based vSLAM to be unstable and have poor geometry estimation. In this paper, a GGCM-E-based semantic filter using YOLOv8 is proposed to address these problems. Firstly, the semantic patches of images are collected from the KITTI dataset, the TUM dataset provided by the Technical University of Munich, and real outdoor scenes. Secondly, the semantic patches are classified by our proposed GGCM-E descriptors to obtain the YOLOv8 neural network training dataset. Finally, several semantic filters for filtering low-level and dense texture-rich scenes are generated and combined into the ORB-SLAM3 system. Extensive experiments show that the semantic filter can detect and classify semantic levels of different scenes effectively, filtering low-level semantic scenes to improve the quality of correspondences, thus achieving accurate and robust trajectory reconstruction and mapping. For the challenging autonomous driving benchmark and real environments, the vSLAM system with respect to the GGCM-E-based semantic filter demonstrates its superiority regarding reducing the 3D position error, such that the absolute trajectory error is reduced by up to approximately 17.44%, showing its promise and good generalization.

1. Introduction

Visual simultaneous localization and mapping (vSLAM) is becoming a widely increasing research community, partly because of its affordable applications in autonomous navigation in complex and real environments [1] and partly because of leveraging vision for the semantic perception that results in computational affordability of mapping [2]. Traditional vSLAM methods refer to epipolar geometry for calculating camera motion, reconstructing 3D scenes, and then resolving camera/robot trajectories through huge filtering or optimization [3]. vSLAM shows promising performance in ideal scenarios while presenting many challenges for these conditions: (1) VSLAM algorithms proposed on the assumption of static scene usually reconstruct incorrect camera trajectories and 3D map points in dynamic targets presented scenarios [4]. (2) Traditional vSLAM algorithms reconstruct trajectories using pixels or low-level feature correspondences from keyframes, suffering from the accumulation of errors caused via a trajectory drift, especially due to uncertainty scale in monocular vSLAM [5]. (3) VSLAM algorithms relying on pixel features are not sufficiently robust in complex scenes such as brightness changes, object occlusion, low texture, and repeated texture in real environments, thus resulting in frame loss, wrong localization, and poor trajectory reconstruction. To overcome such challenges, Random Sampling Consistency (RANSAC)-based outlier detection has been developed in the past, which treats dynamic objects as outliers and removes them from the trajectory reconstructing and mapping. However, the typically epipolar constraints method generates feature correspondences using statistical or other matching criteria in feature space–image space, which is infeasible since identifying outliers in high-level semantic image space is difficult [6].

Compared to traditional image processing techniques and deep learning networks, ref. [7] reveals semantic patterns associated with different scenes to realize scene perception of complex environments. We can conclude that referring to semantic information can enhance the resilience of vSLAM in complex environments since semantic feature can be more stable than pixel features. In our previous study, a semantic filter based on Fast R-CNN learning was proposed to explore the semantic information of outliers [8]. However, the semantic information was defined by the proportion of inliers and outliers, ignoring the texture-rich environments, requiring further detailed semantic analysis. Experimental results show that removing regions containing complex textures (e.g., dense foliage) can effectively reduce the feature matching error and thus the VSLAM localization error to some extent. However, the Fast-RCNN filter is not effective in this case, and the prediction accuracy only approximates to 60%. Consequently, semantic levels of complex scenes for high-quality camera trajectories and map reconstructions in vSLAM systems are urgently required.

This paper, focusing on the texture-rich semantic scenes, presents a further detailed analysis of semantic levels, proposing a GGCM-E (Gray-Level Gradient Co-occurrence Matrix–Energy)-based semantic filter. With respect to YOLOv8 networks, the GGCM-E-based semantic filter can effectively improve the accuracy of camera trajectories and maps in vSLAM systems. The semantic filter at the vSLAM front end can effectively identify the semantic regions in the frames and classify them in terms of texture complexity by means of the GGCM-E descriptor, after which the semantic regions can be effectively targeted to filter out the low-level and dense texture-rich texture scenes to reduce low-quality feature correspondences, thus resulting in accurate camera motion and map points in many challenging scenes, such as dense texture-rich outdoor and indoor environments. To be precise, we propose the following contributions in this paper.

• A novel method to analyze the semantic level using GGCM-E features is proposed. This method calculates GGCM-E features of semantic patches according to visual complexity of texture images and then classifies the semantic patch in terms of its semantic level. These classified semantic patches are feasible for the semantic description of dense texture-rich scenes, helping generate semantic filter for low-level semantic scene filtering.
• A semantic filter trained using YOLOv8 networks is applied to the ORB-SLAM3 system, assisting ORB-SLAM3 to achieve accurate and robust trajectory reconstruction and mapping. Through filtering out low-level semantic scenes, the semantic filter effectively addresses outlier issues in the semantic image space, thereby improving the localization accuracy of the ORB-SLAM3 system.

Figure 1 shows the overview of the proposed semantic filter-based ORB-SLAM3 framework. The green part is the proposed semantic filter module, which pre-processes the frames by identifying semantic patches, extracting the GGCM-E descriptor, classifying the semantic level, and filtering out low-level semantic patches to produce high-quality frames for the visual odometry. The rest of this paper is organized as follows: Section 2 briefly summarizes the related works. The proposed semantic filtering is described in detail in Section 3. Section 4 presents the experimental results and analysis. Conclusions are drawn in Section 5.

2. Related Works

Traditional image matching-based vSLAM relies on feature descriptors to obtain matches and then estimates the fundamental matrix using epipolar geometry, reconstructing camera trajectories and maps in numerous environments. Epipolar geometry estimation can become computationally inefficient and inaccurate when there are low-quality correspondences. Although the RANSAC method shows superiority in eliminating low-quality correspondences [9], due to the computational complexity and noise-sensitivity, it can fail in many situations, such as dynamic model mismatch and texture-rich scenes outlier interference, and cumulative drift error. Therefore, improving the correspondences qualities to eliminate outliers is required in vSLAM systems, promoting the development of many semantic vSLAM methods. According to the various methodologies for implementing deep neural networks in vSLAM, these methods can be classified into the following two major categories.

2.1. Improved vSLAM Using Deep Neural Network-Based Specific Modules

Quach et al. propose SupSLAM using a new feature called SuperPoint to replace the ORB descriptor, releasing a pre-trained deep neural network to obtain accurate feature correspondences with a high computational efficiency [10]. Xiao Zhang et al. proposed the SL-SLAM method throughout the SLAM system with Lightglue, a SOTA (state-of-the-art) matching method that can generate local feature matches associated with a deep neural network [11]. The deep neural network-based improved vSLAM exhibits enhanced resilience in complex scenes, such as sparse textures and fluctuating light conditions. However, it is worth noting that a significant investment of learning time is required for the end-to-end approach, such as entailing camera motion estimation through a deep neural network to map from scenes to camera trajectories. The end-to-end improved vSLAM can be subdivided into supervised and unsupervised approaches [12,13,14], where the supervised approach relies on camera motion or ground-truth depth maps, and the unsupervised approach refers to the mutual constraints between camera motion and depth maps [15,16,17]. Note that depth maps are important in end-to-end work due to their benefits in network training and accurate camera trajectory estimation. However, this approach necessitates huge training data with considerable computational resources and storage space, rendering a challenge to real-time requirements of the tracking module. Consequently, it is necessary to perform research on hybrid approaches associated with deep learning-based vSLAM to enhance the functionality of vSLAM modules.

2.2. Improved vSLAM Using Deep Neural Networks + vSLAM Modules

In real environments, especially outdoors, dynamic targets are inevitably encountered, resulting in localization errors in vSLAM that are caused by low-quality feature correspondences. Zhong et al. proposed a Detect-SLAM method composed of single-shot multibox detector (SSD) network-based dynamic target detection [18], eliminating dynamic feature correspondences through a feature matcher and key-point-based probabilistic propagation of movement. However, due to failure to consider the state of the dynamic category target, whether it is in motion or at rest, this method also deals with static objects, i.e., parked cars, and excludes feature correspondences in highly dynamic scenes, thus reducing huge high-quality feature correspondences to result in accuracy degradation and a trajectory shift. Qiuyu Zang et al. employed a two-step process to detect potentially dynamic objects using YOLOv5 networks and exclude dynamic scenes through the Lucas–Kanade optical flow and RANSAC algorithms [19]. Berta proposed a DynaSLAM consisting of Mask-RCNN-based semantic segmentation for ORB-SLAM2 to filter out dynamic feature correspondences [20,21]. Currently, the DIG-SLAM applies YOLOv7-based instance segmentation to describe targets in terms of their movement consistency [22], estimating camera motion by the left static point and line features. These semantic segmentation and instance segmentation-based vSLAMs require significant computation and time–cost frame processing, making it difficult to realize real-time vSLAM.

Consequently, many point–line–plane features associated with approaches to save computation have been developed [23]. However, these approaches behave poorly in many challenging environments with respect to low-level feature correspondences, such as in low-texture and dense texture-rich scenes. Thanks to the deep neural network, acquiring semantic information can help vSLAM to perceive high-level scene context and yield feature correspondences dependence to enhance the resilience of vSLAM. Many semantic approaches regard semantic information of specific environmental landmarks [24], enabling accurate target measurements, resulting in precious localization. TextSLAM is proposed to cope with target textual objects, e.g., door numbers and billboards [25]. By extracting relevant semantic features, vSLAM localizes accurately and robustly on a map even under challenging scenes, i.e., image blurring, different viewpoints, and illumination changes. Qian developed the SmSLAM + LCD (Semantic SLAM + Loop Closure Detection) approach by integrating high-level 3D semantic information with low-level feature correspondences into a unified semantic vSLAM framework [26], enabling accurate closed-loop detection and effective drift reduction. In indoor environments , ref. [27] employed a semantic association method using parking lines to construct maps for self-driving vehicles and indoor parking. Kang et al. proposed a distinct semantic labeling to compare the semantic categories of map point–reprojection pairs between images by applying normalized information distance in information theory to improve the camera trajectory estimation in vSLAM [28]. Taking these into consideration, vSLAM associated with semantic information can improve its resilience to complex environments, realizing high-accuracy localization and reducing cumulative error.

According to human visual attention mechanisms, the semantic context of feature correspondences in the image space strongly influences the image matching-based vSLAM [29]. Not all feature correspondences have the same semantic labels in a vSLAM system. We have conducted extensive experiments to conclude that semantic labels, with respect to the outlier ratio, can reveal the semantic level of feature correspondences. Filtering out low-level semantic scenes can improve the quality of feature correspondences, thus helping vSLAM perform better in dynamic and static scenarios [8,30]. However, the outlier ratio-based semantic filter without texture information of semantic scenes has low accuracy, thus requiring further semantic analysis when dealing with complex environments. Considering the latest target detection algorithm-YOLOv8 networks, a novel semantic filter approach based on the GGCM-E feature is proposed, effectively improving semantic filter accuracy and the performance of vSLAM systems. Experiments demonstrate that, for dense texture-rich scenes, the semantic-based vSLAM approach can result high-quality feature correspondences, achieving accurate and robust trajectory reconstruction and mapping.

3. Methodology

3.1. Semantic Patches of Inliers

The goal of this paper is to filter out low-level semantic scenes and assist accurate vSLAM. In deep learning-based methods, data describing target objects can be pre-collected, labeled, and used to train a network. The model can predict objects with similar features in scenes. As illustrated in Figure 2, we initially focus on collecting semantic patches of inliers using challenging KITTI sequences, and we capture real environments [31]. Firstly, ORB brute force matching is performed on key frames calculated from these sequences, resulting high-ratio potential mismatches. Referring to the RANSAC algorithm, low-quality correspondences are filtered out using epipolar geometry. Then, semantic patches of $\mathit{n}\times \mathit{n}$ size centered on the inlier are extracted. The prior study indicates that the semantic filter with n = 33 shows the best performance in the vSLAM system. To extend the generalization on complex scenes, a YOLOv8-based network is pre-trained using semantic patches with the size of n = 33, since the YOLOv8 network provides high accuracy, low computation, and high flexibility in target detection. Finally, these semantic patches are classified into different classes according to GGCM-E features.

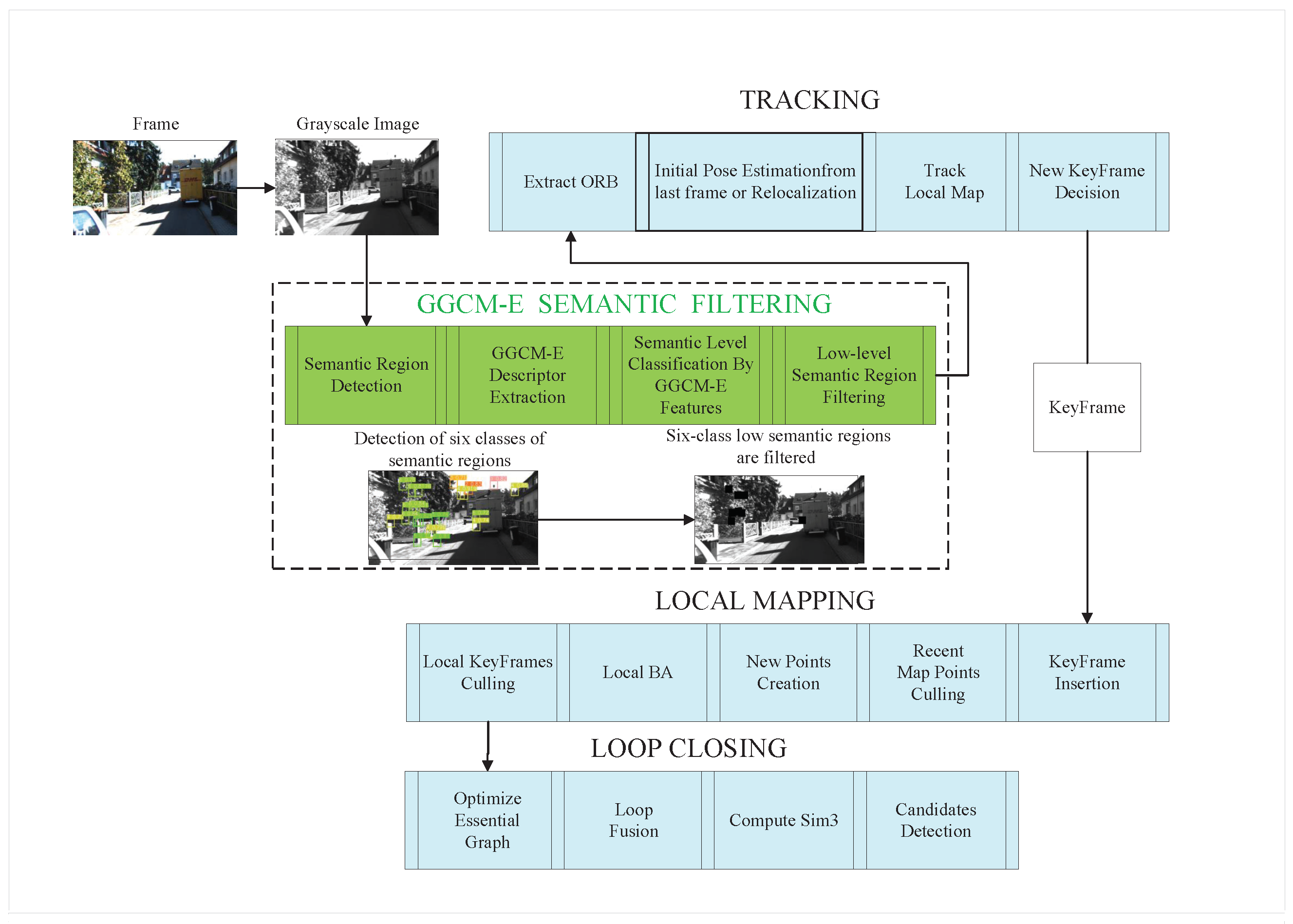
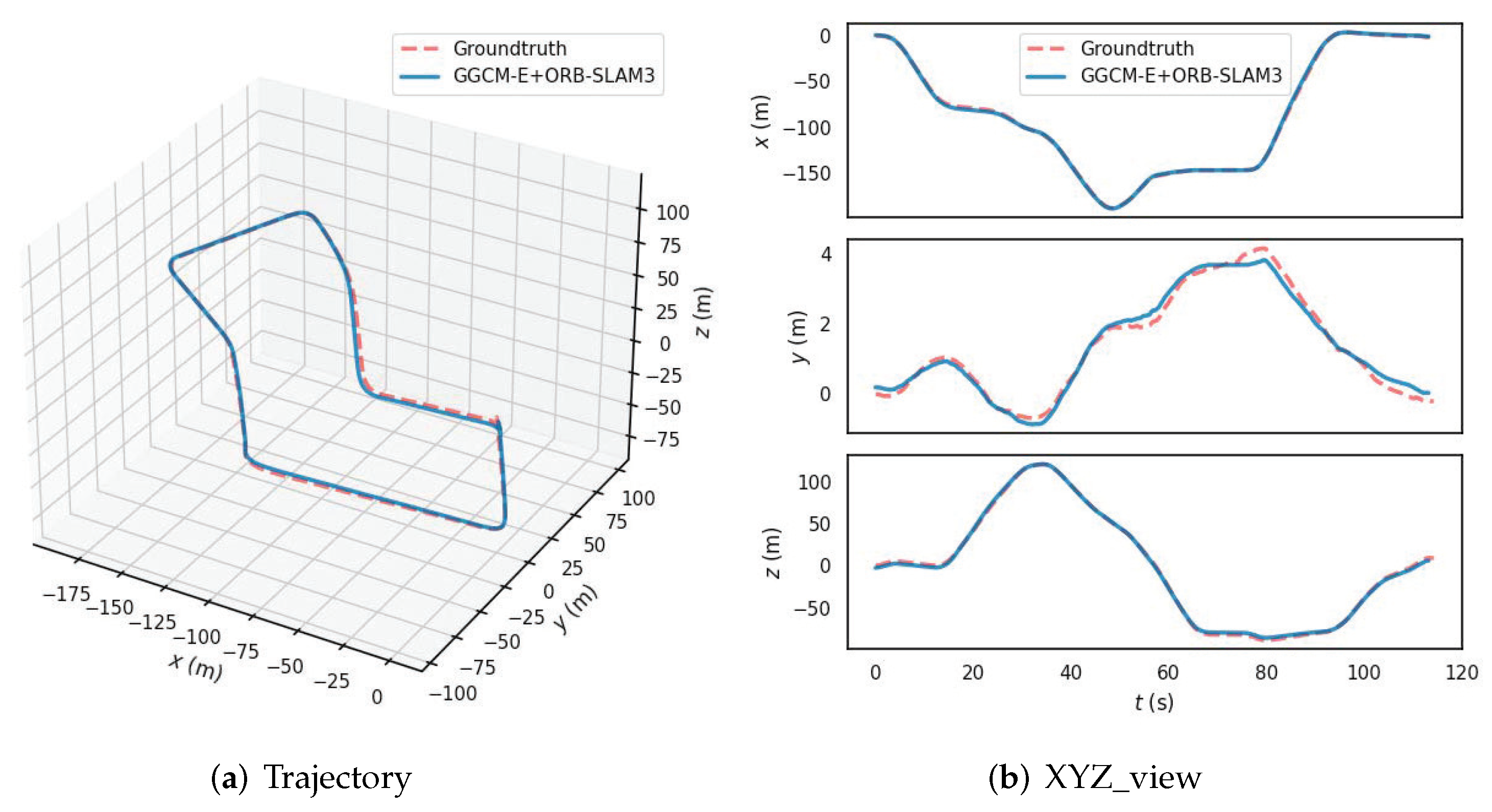
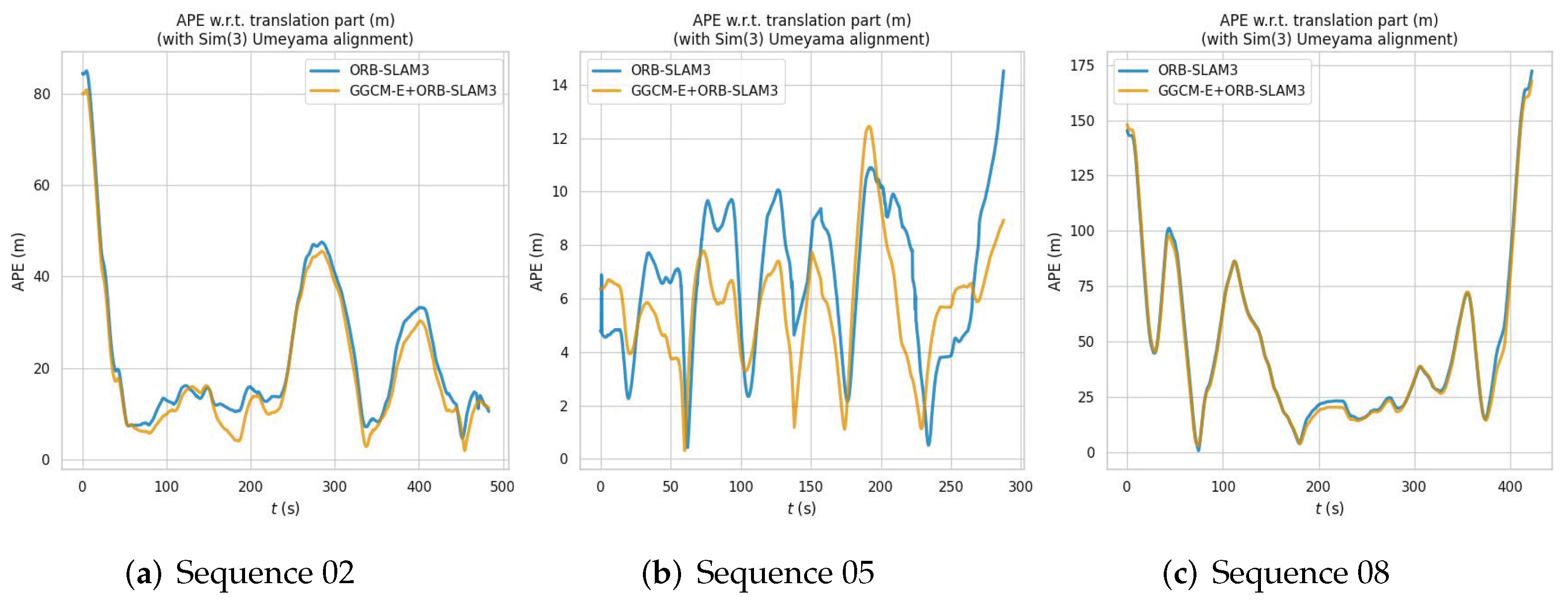
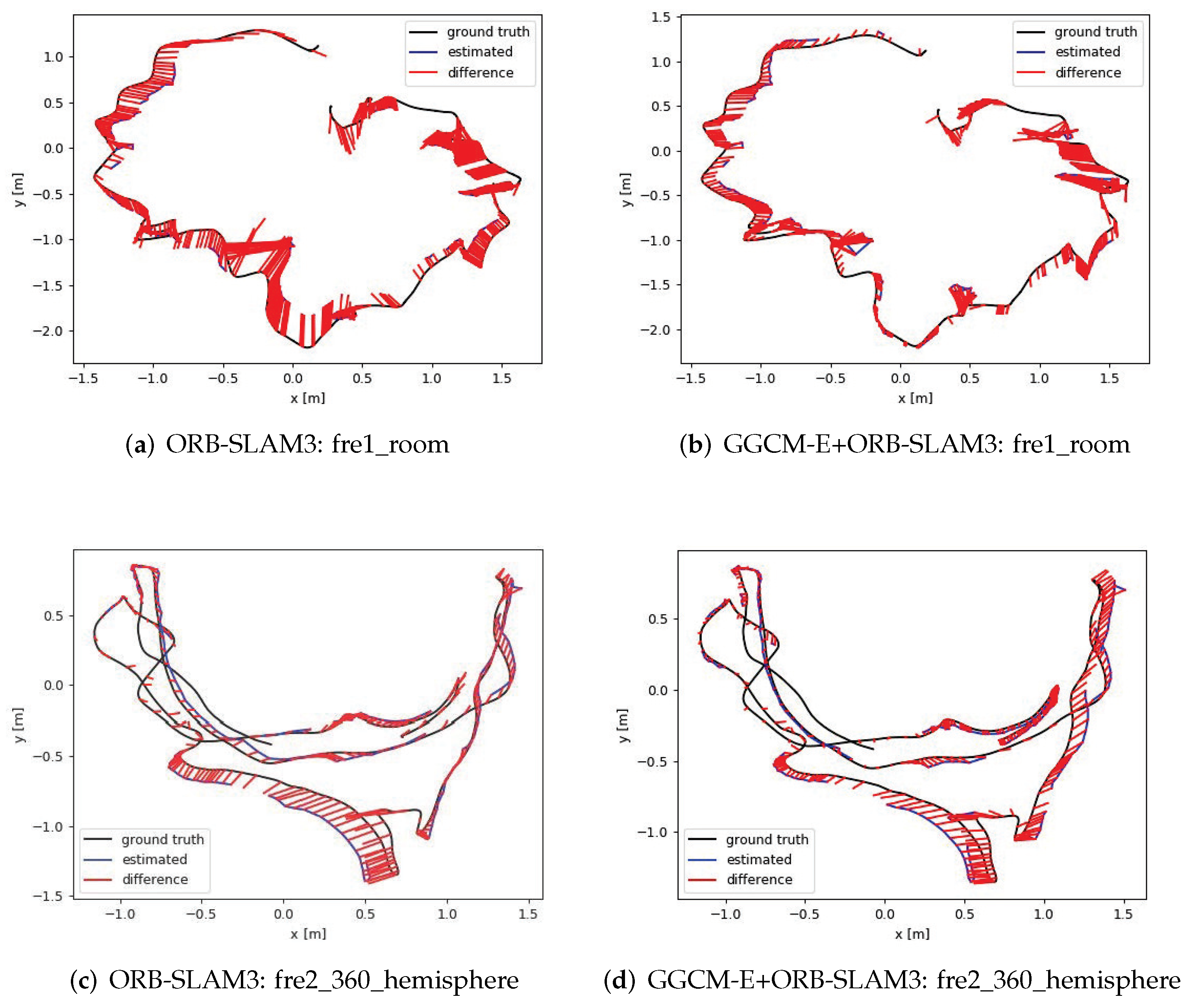
3.2. Semantic Patch Labeling Based on GGCM-E Features

In our previous study, semantic patches were labeled according to outlier ratios, assigning the centered inlier a semantic level, which is its quality with respect to feature correspondences. However, the outlier ratio-based semantic patches labeling cannot perceive high-level semantic information, such that the relevant semantic filter has low accuracy in segmenting within complex environments. Consequently, we conducted further research to analyze the semantic information in semantic patches. Our previous research demonstrates that the trajectory error in semantic filter-based vSLAM can be significantly reduced when filtering out dense texture-rich scenes, such as scenarios with trees. The reason we envisage is that in the region of dense, complex textures, the number of ORB feature points extracted is very high. However, because of the complex similarity of the texture, this will lead to a mismatch between the ORB feature points of consecutive frames, and this kind of mismatch cannot be entirely eliminated by just relying on the RANSAC algorithm. Then, it generates a localization error. In order to investigate how the feature correspondences in dense texture-rich scenes affect the accuracy in vSLAM systems, we propose a GGCM-E feature descriptor to classify semantic patches, which can be implemented to classify the texture complexity level of semantic image patches and then detect the regions of dense and complex textures, enabling us to predict low-level semantic scenes associated with deep learning networks.

The Gray-level Gradient Co-occurrence Matrix (GGCM) is a statistical method that focuses on the semantic information within images in terms of the grayscale and gradient. As we know, grayscale images can describe the semantic contexts for different visual tasks, and gradient images proved to be more discriminant and reliable when it comes to texture-less targets in complex scenes. Consequently, the GGCM feature can reveal the semantic information with respect to pixel levels, providing a comprehensive prediction in dense texture-rich scenes.

Firstly, semantic patches of inliers are divided into l equal-sized S-$regions$, $s(i,j)$, to process GGCM feature calculations. Then, the number of pixel pairs with coordinates $(x,y)=\left(F\right(i,j),G(i,j\left)\right)$ is accumulated to obtain $h(x,y)$ for the covariance matrix H. Note that the notion $h(x,y)$ is defined as the entire pixel-pair number in terms of the x-$value$ pixel in the normalized grayscale image $F(i,j)$ (Equation (1)) and the y-$value$ pixel in the normalized gradient image $G(i,j)$ (Equation (2)). Finally, the normalization of the GGCM is conducted to obtain $h^{\prime }(x,y)$. Equation (1) defines the normalized grayscale image of the S-$regions$:

$$F(i,j)={\displaystyle \frac{f(i,j)·(L_{gy}-1)}{f_{max}}}+1$$

(1)

where $f(i,j)$ denotes the gray value of pixel $(i,j)$ in the original image, $F(i,j)$ denotes the gray value of pixel $(i,j)$ in the normalized grayscale image, $f_{max}$ is the maximum gray value in the original image, and $L_{gy}$ is the maximum gray value after normalization, with $L_{gy}$ being set to l.

After that, the normalized gradient image is calculated as in Equation (2):

$$G(i,j)={\displaystyle \frac{g(i,j)·(L_{gt}-1)}{g_{max}}}+1$$

(2)

where $g(i,j)$ is the gradient value of pixel $(i,j)$ in the original image, $G(i,j)$ is the gradient value of pixel $(i,j)$ in the normalized grayscale image, $g_{max}$ is the maximum gradient value in the original image, and $L_{gt}$ is the maximum gradient value after normalization, with $L_{gt}$ being set to l. Note that, $g(i,j)$ is derived from the square sum of the Sobel’s operator in the horizontal and vertical directions, respectively, according to Equation (3):

$$g(i,j)=\sqrt{g_x^2+g_y^2}$$

(3)

Here,

$$g_x=f(i+1,j)-f(i,j)$$

(4)

$$g_y=f(i,j+1)-f(i,j)$$

(5)

Count the pixel pairs with respect to $\mathit{x}=\mathit{F}(\mathit{i},\mathit{j})$ and $\mathit{y}=\mathit{G}(\mathit{i},\mathit{j})$ in the normalized grayscale image $F(i,j)$ and the normalized gradient image $G(i,j)$.

$$x=F(i,j),x\in \left[\begin{array}{c}1,L_{gy}\end{array}\right]$$

(6)

$$y=G(i,j),y\in \left[\begin{array}{c}1,L_{gt}\end{array}\right]$$

(7)

Until now, the normalized GGCM $h^{\prime }$(x, y) can be derived, as follows:

$$h^{\prime }(x,y)={\displaystyle \frac{h(x,y)}{{\sum }_{x=0}^{L_{gy}}{\sum }_{y=0}^{L_{gt}}h(x,y)}}$$

(8)

$$E=\sum _x\sum _y{\left[h^{\prime }(x,y)\right]}^2$$

(9)

According to the normalized GGCM, we define the energy of the statistical property as Equation (9):

As demonstrated in Figure 3, when the energy is less than a threshold $Th$, the S-$region$ can be characterized by complex textures, such that a significant change within the gradient value and the gray value occurs, presenting the relevant GGCM-E feature with 1-$value$ result r. On the contrary, if the energy is larger than or equal to the preset threshold, the S-$region$ contains many backgrounds, indicating that the texture is sparse and that non-existed GGCM-E features change with respect to the gradient value and the gray value, thus presenting a 0-$value$ result r. We illustrated the $Th$ parameter in Figure 3. We set this value to 0.25. The reason for this is that when the proportion of flat and texture-free area reaches 50% of the S-$region$, the probability that its corresponding certain value in the gray-level gradient co-occurrence matrix is normalized is 0.5. Moreover, when calculating the energy characteristics of the whole matrix, the sum-of-squares operation will be performed, and the energy value corresponding to this region will be 0.25. So, when we calculate the energy value of the gray-level gradient covariance matrix to be less than 0.25, the flat untextured region is less than half of the area of this S-$region$. Alternatively, it means that the area of the textured region is more than half of the area of the S-$region$, and we default to the S-$region$ with a complex texture, GGCM -E feature number plus 1. Then, by calculating all S-$regions$, the sum of the number of GGCM-E features is derived, which is used as the basis for classifying the image complexity of different image semantic patches. When the sum of the number of GGCM-E features of a certain semantic patch is l, this indicates that all the S-$regions$ exhibit GGCM-E characteristics, i.e., each S-$region$ exhibits complex textures. Thus, the semantic patch is the one that has the most complex texture semantic patch, which is suitable to be divided into a individual class to study. After the $S-region{s}^{\prime }$ transformation and the energy calculation, GGCM-E features are obtained in terms of the r result. The GGCM-E feature calculation is summarized in Algorithm 1. Ultimately, these semantic patches will be classified in accordance with the number of GGCM-E features, which serves to ascertain the level of texture complexity.

To the end, a sequence of semantic patches labeled according to the GGCM-E features is obtained as the training data before they are input into the YOLOv8 network.

Algorithm 1 Compute GGCM_E feature values.

Input: Semantic patches of Inliers Output: GGCM_E feature values  1: $Lgy\leftarrow l,$ $Lgt\leftarrow l,$ $GGCM\_E\leftarrow 0$  2: for S in $patch$ do  3:       S←patch$[L:R,U:D]$// Extract S from the patch.  4:       $(g_x,g_y)\leftarrow$ Sobel gradients of S  5:       $g(i,j)$$\leftarrow \sqrt{g_x^2+g_y^2}$ // Compute Sobel gradient magnitude.  6:       $f\_max\leftarrow max\left(S\right)$  7:       $F(i,j)$$\leftarrow f(i,j)/f\_max\times (Lgy-1)+1$ // Normalize the gray level matrix.  8:       $g\_max\leftarrow max\left(g(i,j)\right)$  9:       $G(i,j)$$\leftarrow g(i,j)/g\_max\times (Lgt-1)+1$ // Normalize the gradient matrix. 10:       for pixel $(i,j)$ in S do 11:             $F_{xy}\leftarrow \mathrm{round}($$F(i,j)$) 12:             $G_{xy}\leftarrow \mathrm{round}($$G(i,j)$) 13:             $h(x,y)$$\leftarrow h(F_{xy},G_{xy})+1$ // Fill the gray-level gradient co-occurrence matrix. 14:       end for 15:       $h^{\prime }(x,y)$$\leftarrow h(x,y)/\sum h(x,y)$ 16:       $Energy$$\leftarrow \sum \left({h^{\prime }(x,y)}^2\right)$ // Compute energy of the normalized $h^{\prime }(x,y)$. 17:       if $Energy$ < $Th$ then 18:             $GGCM\_E\leftarrow GGCM\_E+1$ // Compute GGCM_E feature value. 19:       end if 20: end for

4. Analysis of Experiments and Results

4.1. Semantic Filter Model Training

After calculating the GGCM-E features of all the semantic patches, we classified them and utilized the YOLOv8 neural network for training. The initial approach was to categorize all semantic patches into one class. However, the experimental results indicated that this approach was not optimal. A superior classification method is devised based on the formulation of Equation (11). The formula’s interpretation is that the label with the greatest number of GGCM-E features is extracted as a standalone class. In contrast, the remaining classes are classified as a group comprising every c feature. The final total number of classes is, therefore, represented by the value of C. The value of l is set to 9, 16, and 25, respectively, and the model is trained according to one class within our own designed classes, as referenced in Equation (11), on this dataset in a separate training phase. The performance of the obtained model is demonstrated in

Table 1. Comparison of YOLOV8 semantic filters based on different parameters l and different classification methods.

l	Classes	Th	P	R	MAP@0.5
9	9	0.25	51.6%	37.8%	38.2%
	5	0.25	63.4%	72.0%	70.2%
16	16	0.25	57.5%	45.9%	49.1%
	6	0.20	72.8%	69.0%	75.6%
	6	0.25	77.6%	76.4%	82.4%
	6	0.30	73.9%	71.3%	78.2%
25	25	0.25	53.7%	46.9%	40.1%
	7	0.25	75.5%	72.9%	78.3%

.

$$c=\sqrt{l}-1$$

(10)

$$C={\displaystyle \frac{l-1}{\sqrt{l}-1}}+1$$

(11)

Table 1 demonstrates that the optimal results are achieved when l is set to 16, $Th$ is set to 0.25, and the semantic patches are classified into six classes. The experimental results serve to validate the scientific validity of the GGCM-E classification methodology. Semantic patches are obtained from three sources: the open source KITTI dataset, the TUM dataset provided by the Technical University of Munich, and our collection of TUM images of real scenes. The KITTI dataset comprises authentic images of urban, rural, and highway scenes, including intricate and dense texture scenes, such as leaves and houses, which are replete with scene images. It also furnishes the truth values for the subsequent comparison of the filter on ORB-SLAM3. The TUM dataset, provided by the Technical University of Munich, and our own TUM dataset, collected in the real world, contain a variety of complex and dense texture scenes, including wooden boards, tiles, messy desktops, and so on. Using datasets with different scenes is beneficial for improving the filter’s generalization ability. The total dataset contains approximately 11,500 image frames and 230,000 labeled file representations of semantic image patches. We divide the labeled semantic patches into six classes with training-to-validation ratios of 8:2, such as semantic patches with label1 to label3 are one-class filters, semantic patches with label4 to label6 are two-class filters, semantic patches with label7 to label9 are three-class filters, semantic patches with label10 to label12 are four-class filters, semantic patches with label13 to label15 are five-class filters, and semantic patches with label16 are six-class filters. As mentioned above, due to its highest accuracy, a YOLOv8 network-based semantic filter is then used to train for various challenging environments. We use the mechanism of transfer learning to train the network. For the backbone network, we adopt the pre-trained parameters, where the initial learning rate (lr0) is set to 0.01, the batch size is set to 8, and the pre-trained weights are set to YOLOv8l.pt. We train the network with 600 epochs in total to evaluate the loss convergence. We implement the training on a GPU server with four V100-PCIE-16GB and 320GB RAM in the programming environment Linux 20.04.6.

Table 2. YOLOv8-based detection results between different semantic filters.

GGCM-E Feature (Label)	Ratio	Class	P	R	MAP@0.5
1.2.3	1.4%	1	67.7%	83.6%	82.0%
4.5.6	8.9%	2	83.0%	82.2%	88.7%
7.8.9	7.3%	3	79.1%	78.1%	85.5%
10.11.12	16.4%	4	79.8%	76.7%	82.4%
13.14.15	36.9%	5	78.2%	69.7%	78.3%
16	28.8%	6	77.4%	67.9%	77.6%

summarizes the semantic filter accuracy using YOLOv8 networks and GGCM-E feature-based semantic patches’ information. Notably, the most common labels for the semantic filter are 13, 14, and 15 (five-class filter), respectively, such that the five-class semantic patch ratio is 36.9%. From the calculation in Algorithm 1, the 13–15 labeled semantic patches contain complex texture-rich scenes. We then compare the precision (P), recall (R), and mean average precision (MAP@0.5) on the six classes of semantic patches with respect to the relative semantic filter module. As presented in the results, the average precision, recall, and MAP@0.5 of the six classes based the semantic filter are 77.6%, 76.4%, and 82.4%, respectively.

We can conclude from the semantic filtering on the challenging KITTI dataset and real outdoor dataset that, as shown in Figure 4 and Figure 5, the GGCM-E-based semantic filter performs well with moderate detection confidence. Notably, the two-class, three-class, and four-class semantic patches predominantly depict scenes containing discernible edges and more regular textures, whereas five-class and six-class semantic patches are primarily blurred or dense texture-rich scenes, providing interesting results with regard to the research on the five-class- and six-class-based semantic filter.

4.2. Experiments on Semantic Filter-Based ORB-SLAM3

To verify the performance of the semantic filter-based vSLAM, we implement the proposed method on top of ORB-SLAM3 using monocular input data. KITTI07 and KITTI05 sequences are selected as the dataset for evaluation in the target domain because they contain dense texture-rich scenes. As discovered by Raul Muir Altar and Juan D. Tardos, accurate trajectory estimation can be obtained in terms of the average trajectory by running the ORB-SLAM3 system many times [21]. We implement the semantic filter-based ORB-SLAM3 11 times to evaluate the trajectory estimation. The comparison of the absolute attitude error (ATE) between ORB-SLAM3 and the proposed semantic filter-based ORB-SLAM3 is summarized in

Table 3. Comparison of ATEs of KITTI07 for ORB-SLAM3 and our proposed method.

KITTI07	RMSE/m	Std/m	Max/m	Min/m
ORB-SLAM3	2.58	1.11	5.42	0.46
One-class filter + ORB-SLAM3	2.59	1.19	6.13	0.64
Two-class filter + ORB-SLAM3	3.01	1.22	4.97	0.17
Three-class filter + ORB-SLAM3	2.89	1.34	4.88	0.69
Four-class filter + ORB-SLAM3	2.75	1.03	5.52	0.82
Five-class filter + ORB-SLAM3	2.25	0.82	4.30	0.15
Six-class filter + ORB-SLAM3	2.12	1.05	3.65	0.08
All-class filter + ORB-SLAM3	3.04	0.94	6.23	0.32

and

Table 4. Comparison of ATEs of KITTI05 for ORB-SLAM3 and our proposed method.

KITTI05	RMSE/m	Std/m	Max/m	Min/m
ORB-SLAM3	7.24	2.83	14.52	0.42
One-class filter + ORB-SLAM3	7.29	2.82	15.19	1.30
Two-class filter + ORB-SLAM3	7.99	3.20	15.96	0.45
Three-class filter + ORB-SLAM3	7.61	2.84	14.38	0.50
Four-class filter + ORB-SLAM3	7.14	2.48	13.18	0.75
Five-class filter + ORB-SLAM3	6.39	2.59	13.86	0.41
Six-class filter + ORB-SLAM3	6.25	2.79	14.23	0.15
All-class filter + ORB-SLAM3	6.66	2.89	15.47	0.27

.

As presented in Table 3 and Table 4, after filtering out the five-class and the six-class semantic scenes, the ATEs are effectively reduced. The six-class semantic filter-based vSLAM achieves the top performance, such that the root mean square error (RMSE) is reduced by about 17.4%, and the maximum and minimum localization errors are the lowest in the experiments with the KITTI07 sequence. The RMSE of the experiment with the KITTI05 sequence is diminished by approximately 13.7%, and the minimum localization error is the lowest. This indicates that vSLAM is more accurate when the low-level semantic scenes in patches labeled 13, 14, 15, and 16 are filtered out. As described previously, these labeled semantic patches contain blurry and dense texture-rich scenes, resulting in trajectory errors. We hence conclude that filtering out these semantic patches leads to the least loss in localization precision and trajectory estimation. Consequently, the six-class semantic patches are low-level semantic scenes, requiring further research on their performance on vSLAM systems. Accordingly, the six-class area was selected as the filtering region. Moreover, further comprehensive experiments were conducted in diverse scenarios through GGCM-E+ORB-SLAM3. As demonstrated in Figure 6, the trajectory provided by GGCM-E semantic filter-based vSLAM effectively completes loop closure with highly accurate ground-truth disparities.

4.3. Extensive Experiments on the Six-Class Semantic Filter-Based ORB-SLAM3

To further illustrate the performance obtained with the six-class semantic filter, we evaluate the six-class semantic filter-based ORB-SLAM3 on other KITTI sequences (sequences 00 to 09). We compare the estimated camera trajectories to their ground-truth trajectories while playing the sequences at the frame rate at which they are recorded.

In Figure 7, we compare the mapping results provided by the semantic filter-based ORB-SLAM3 with respect to the ground truth. As the figures show, we successfully detect most loop closures, i.e., sequences 00 and 09, and we have the most similar trajectory compared to the ground truth. Note that several accumulated trajectory drifts yield at sequence 00 because of the large camera rotation in the monocular vSLAM. Nevertheless, due to the large-scale loop closure that occurred in sequence 00, this drift was corrected after the loop was detected and closed. A qualitative comparison of the absolute position error (APE) is shown in Figure 8, from which the accuracy of our semantic filter can be qualitatively judged. In accordance with the results shown in the figures, our approach is capable of filtering out low-level semantic scenes, performing best on most of the sequences. For some parts of sequence 05, our approach yields several bad positions at 200 s and 250 s. This occurs due to the rapid increase in low-level semantic scenes generated by image rotation, e.g., the 2000th and 2500th frames (FPS = 10) are recorded using large rotations. Note that when the camera rotation is large in the semantic filter-based vSLAM, the high-level semantic decreases, leading to more high-quality feature correspondences being filtered out by the semantic filter, thus resulting in high position errors.

Table 5. Comparison of the RMSE with respect to the ATEs of different vSLAM methods—KITTI sequences (m).

	00	02	05	06	07	08	09
ORB-SLAM3	8.28	27.61	7.24	15.33	2.58	58.35	7.82
Inliers-Outliers+ORB-SLAM3	7.86	26.23	6.88	16.09	2.32	57.55	7.58
GGCM-E+ORB-SLAM3	8.15	25.13	6.25	13.67	2.13	57.12	7.79
Improvement *	1.57%	8.98%	13.7%	4.6%	17.44%	2.11%	0.38%

* Improvement in the ATEs of “GGCM-E+ORB-SLAM3” with the original ORB-SLAM3.

presents the comparison of RMSE metrics of the ATEs of various vSLAM methods. We compare the results obtained by ORB-SLAM3, GGCM-E+ORB-SLAM3, and our previously proposed Inliers-Outliers+ORB-SLAM3 semantic filter, where the semantic filter is generated using a Faster R-CNN learning-based method [8]. It can be concluded from these results that the semantic filter based on GGCM-E features is more effective than the inlier–outlier semantic filter. After filtering out low-level and dense texture-rich semantic scenes, the quality of feature correspondences was effectively improved, thus decreasing the RMSE of camera trajectories in vSLAM systems, such that the largest reduction was by about 17.44%.

4.4. Experiments on Dense Texture-Rich Sequences

To further explore the semantic filter-based vSLAM on dense texture-rich environments, we take seven sequences (named DTR sequences) consisting of large dense texture-rich scenes from the TUM dataset for evaluating our method. As illustrated in Figure 9, for the fre1_plant sequence, a flower pot near the wooden floor is recorded with a considerable duration to generate large dense texture-rich scenes. The fre1_room sequence contains many dense and complex scenes, such as the curtains, and wooden panels. The fre2_360_hemisphere sequence is recorded with the indoor environment, where the wall tiles, ceiling, and other surfaces exhibit dense texture-rich patterns. The same scene is recorded as the fre2_large_with_loop sequence, obtaining dense texture-rich scene-based loop closure for the camera motion trajectory. As shown by the experimental results summarized in

Table 6. Comparison of the RMSE with respect to the ATEs of different vSLAM methods—dense texture-rich sequences in TUM dataset (cm).

	ORB-SLAM3	PLP-SLAM	GGCM-E+ORB-SLAM3	Improvement *
fre1_desk	2.18	2.06	1.93	11.46%
fre1_plant	1.63	1.55	1.60	1.84%
fre1_room	8.03	7.68	7.26	9.58%
fre2_desk	0.86	0.90	0.85	1.16%
fre2_360_hemisphere	16.56	15.34	14.66	11.47%
fre2_large_with_loop	19.97	19.39	18.60	6.86%
fre3_long_office _household	0.93	1.01	0.89	4.30%

* Improvement in the ATEs of “GGCM-E+ORB-SLAM3” with the original ORB-SLAM3.

, the semantic filter-based vSLAM works well on full sequences, effectively decreasing the RMSE with respect to the absolute trajectory error, such that the top reduction on the fre2_360_hemisphere sequence is approximately 11.47%. In addition, we compare our method with PLP-SLAM because of its resilience to repetitive and dense texture environments [32], which is achieved by utilizing point and line features for tracking. We can conclude from the relevant results that our method performs best on most of the dense texture-rich scenes, yielding high-accuracy position estimation. Despite the fact that our method estimates the position well with vSLAM, its ability on scenes consisting of large rotation, i.e., a fre1_plant sequence, is slightly lower than that of PLP-SLAM.

A comparison of the camera trajectories in the DTR sequence between ORB-SLAM3 and our method is demonstrated in Figure 10, where our proposed method successfully reconstructed the landmarks around the camera path with a lower trajectory error. The above experiments demonstrate that our proposed semantic filter is stable for filtering out low-level semantic scenes, especially for dense texture-rich scenes, thus enabling vSLAM systems to operate well in various challenging environments.

4.5. Experiments on Other Semantic Filter-Based vSLAM Systems

To evaluate the generalization of the proposed semantic filter, we implement it in other vSLAM systems and conduct several experiments on KITTI sequences. Considering the case of dynamic target filtering, DynaSLAM is selected as the baseline algorithm for a comparison with [20]. The results presented in Figure 11 show that the GGCM-E semantic filter-based DynaSLAM works well concerning camera trajectory estimation, especially around the straight camera path, improving the camera trajectory with the help of a semantic filter, indicating the superiority of the semantic filter on low-level semantic scene filtering, even after dynamic target filtering.

In

Table 7. Comparison of the RMSE with respect to the ATEs of different vSLAM methods—KITTI sequences (m).

	00	02	05	06	07	08	09
Structure-SLAM	6.63	25.69	13.62	23.88.	2.99	109.38	13.40
GGCM-E+Structure-SLAM	6.36	24.75	11.84	20.57	2.75	103.91	12.06
LDSO	9.56	34.78	5.50	13.67	2.64	134.48	21.15
GGCM-E+LDSO	9.35	32.62	5.73	13.84	2.59	131.44	20.09
DynaSLAM	9.64	29.75	7.04	15.79	2.86	54.05	6.98
GGCM-E+DynaSLAM	8.50	25.91	6.66	14.48	2.46	52.83	6.62

, the GGCM-E filter was integrated with Structure-SLAM [33], LDSO [34], and DynaSLAM, and a comparative assessment was conducted on KIITTI sequences. The experimental outcomes indicated that the filter exhibited enhanced performance for Structure-SLAM and DynaSLAM, and the RMSE was diminished across all sequences, which substantiates the filter’s role in feature-based vSLAM. The impact of generality on the GGCM-E+LDSO on 05 and 06 sequences is contradictory. The RMSE increased somewhat, and the error increased compared to LDSO. We hypothesize that this may be due to the fact that LDSO is a direct-method SLAM and due to the localization accuracy being less correlated with the local complex texture region.

In Figure 12, the present study compares the error details of Structure-SLAM, LDSO, and DynaSLAM with the applied GGCM-E semantic filter in accordance with the KITTI07 experiment, respectively. The results demonstrate that the majority of SLAMs with the GGCM-E semantic filter have a notable reduction in the high error portion. The minimum errors obtained are effectively reduced, although the maximum errors are higher with GGCM-E+LDSO. It is notable that all SLAMs with GGCM-E semantic filters exhibit a reduction in APEs compared to those without such filters. The above experiments demonstrate that the proposed semantic filter is capable of filtering out low-level dense texture-rich scenes, being suitable for various vSLAM systems in challenging complex scenes. Consequently, filtering out low-level semantic information in dense texture-rich scenes using a GGCM-E-based semantic filter will generate high-quality feature correspondence, thus helping vSLAM achieve accurate and robust trajectory reconstruction and mapping.

5. Conclusions

In this paper, we propose a GGCM-E-based semantic filter with YOLOv8 networks. The proposed semantic filter can automatically filter out low-level semantic scenes. According to our previous research, different semantic patches centered on the inliers of various frames are labeled in terms of GGCM-E features, generating six classes of semantic filters. High-quality correspondences are obtained by applying these semantic filters to vSLAM systems, improving image matching-based camera trajectory estimation and mapping. The localization accuracy of the proposed semantic filter-based pipeline within different vSLAM frameworks is also evaluated. Extensive experiments on the KITTI dataset and the TUM dataset are performed. The results demonstrate that the position error can be significantly reduced when the semantic filter is used in feature-based vSLAM systems. For dynamic outdoor and indoor environments, the respective ATE can be reduced by up to approximately 17.44% and 11.47%, respectively. A comparison of the ATE results with respect to the semantic filter-based DynaSLAM, Structure-SLAM, and ORB-SLAM3 shows the promising generalization capabilities of the proposed method with regard to helping various vSLAM systems localize accurately and robustly on a map. In the future, we will include machine learning methods that can access semantic level-based information in different semantic scenes.