Quadratic Cascading in Quasi-Phase-Matching: An Alternative Route to Efficient Third-Harmonic Generation
Abstract
1. Introduction
2. Method
3. Model
4. Analytical Solution
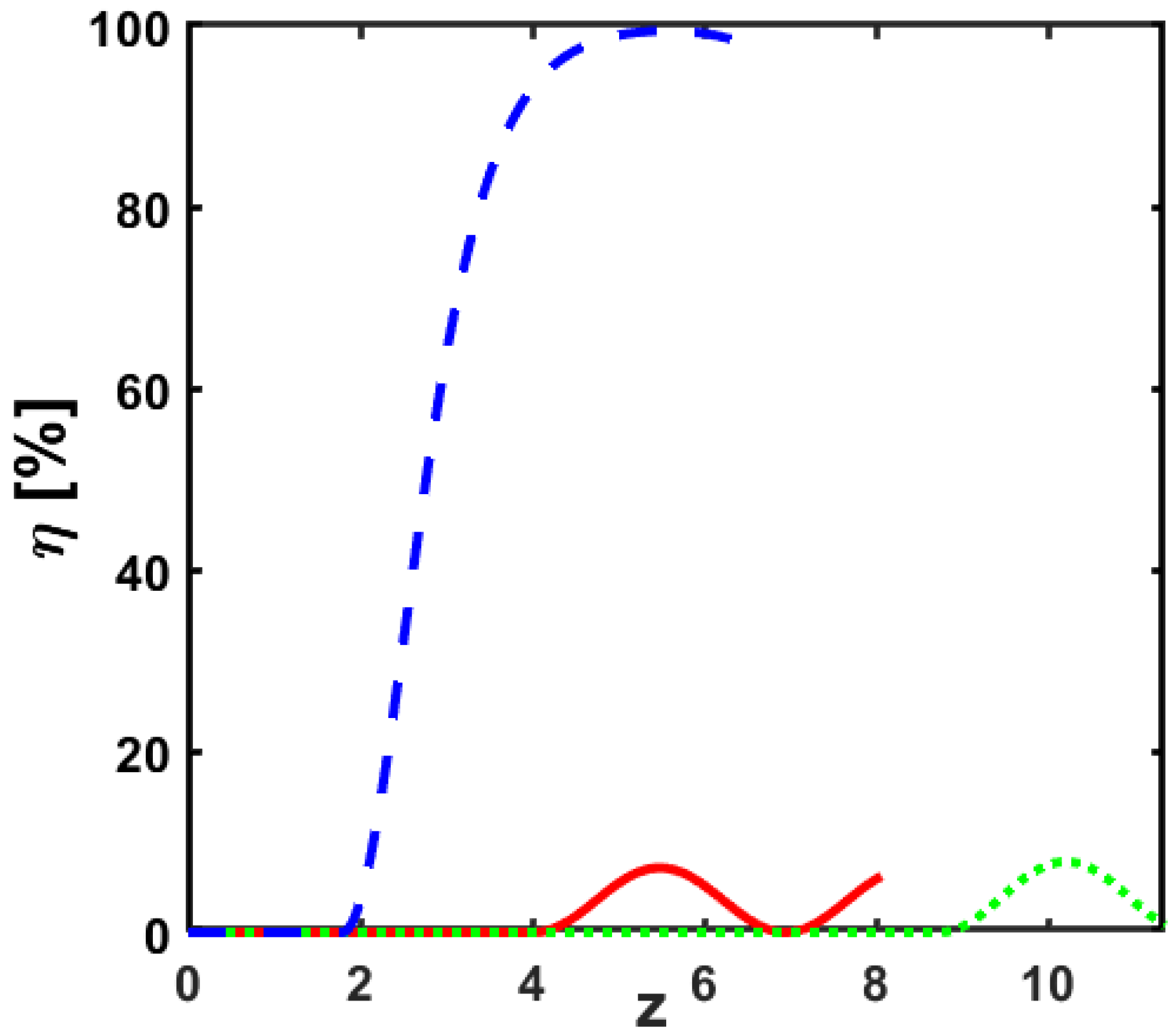
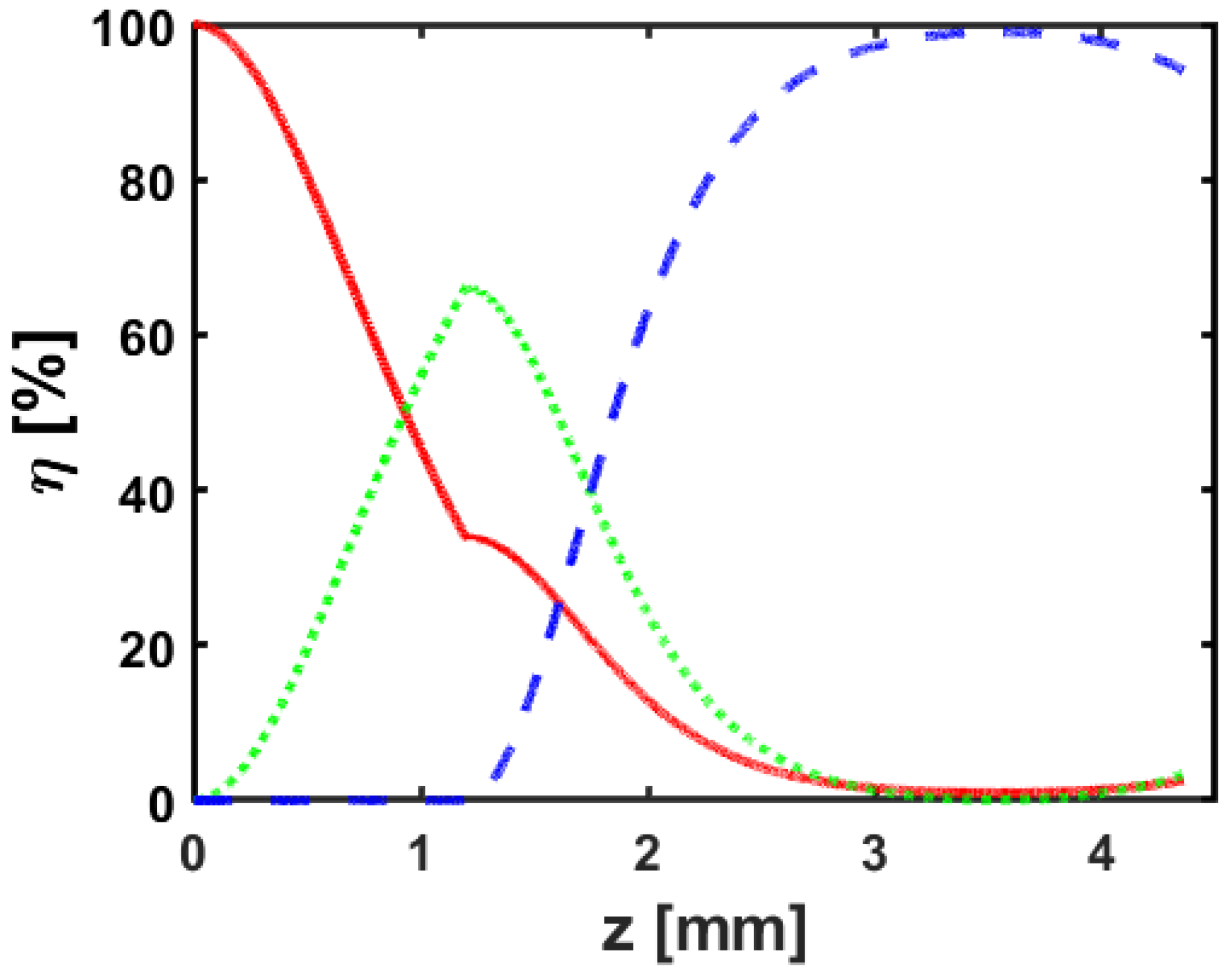
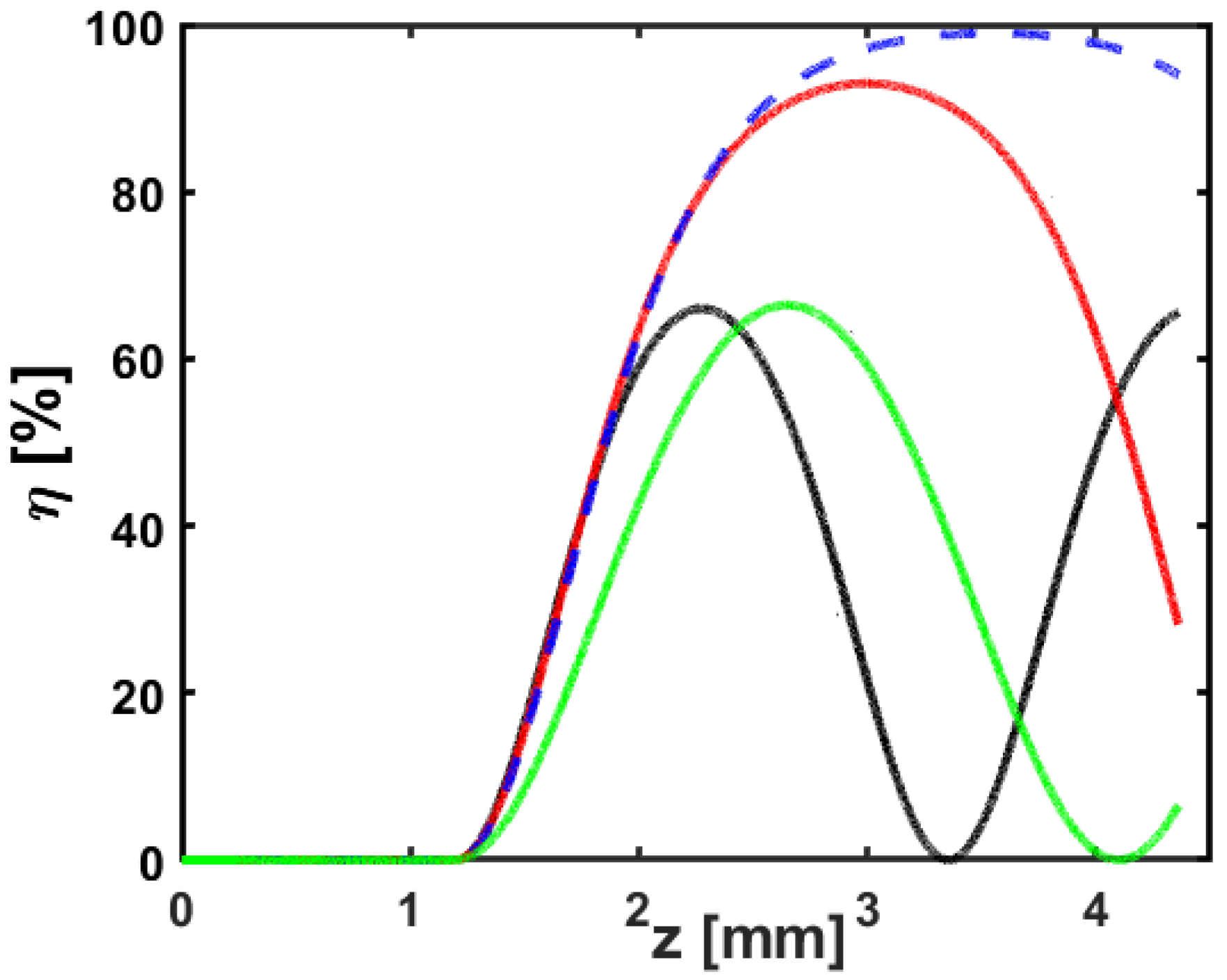
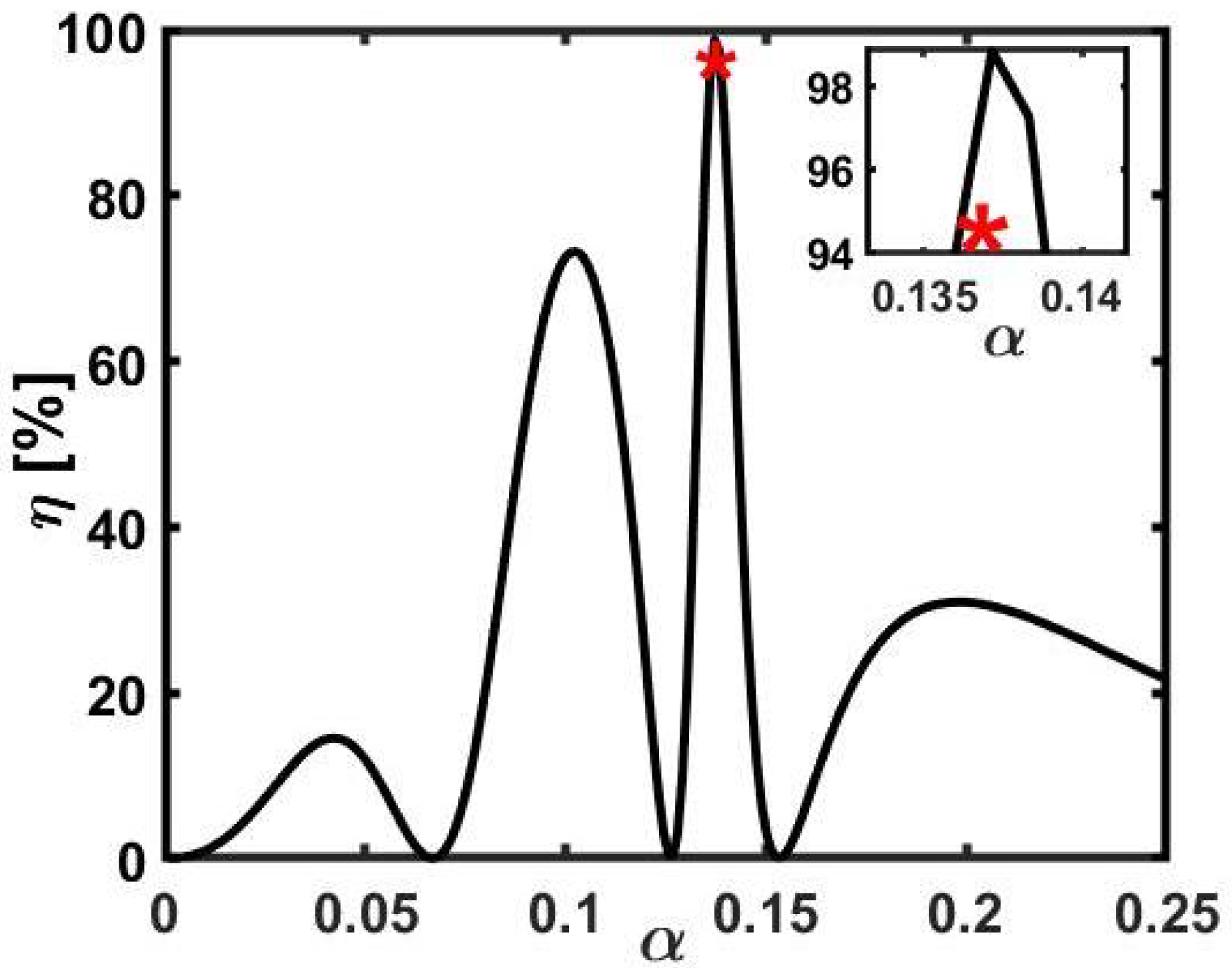
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Franken, P.A.; Hill, A.E.; Peters, C.W.; Weinreich, G. Generation of Optical Harmonics. Phys. Rev. Lett. 1961, 7, 118–120. [Google Scholar] [CrossRef]
- Armstrong, J.A.; Bloembergen, N.; Ducuing, J.; Pershan, P.S. Interactions between Light Waves in a Nonlinear Dielectric. Phys. Rev. Lett. 1962, 127, 1918–1939. [Google Scholar] [CrossRef]
- Boyd, R.W.; Gaeta, A.L.; Giese, E. Nonlinear optics. In Springer Handbook of Atomic, Molecular, and Optical Physics; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1097–1110. [Google Scholar]
- Stegeman, G.I.; Stegeman, R.A. Nonlinear Optics: Phenomena, Materials and Devices; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Li, C. Nonlinear Optics: Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Craxton, R.S. Theory of high efficiency third harmonic generation of high power Nd-glass laser radiation. Opt. Commun. 1980, 34, 474–478. [Google Scholar] [CrossRef]
- Fejer, M.M.; Magel, G.A.; Jundt, D.H.; Byer, R.L. Quasi-phase-matched second harmonic generation: Tuning and tolerances. IEEE J. Quantum Electron. 1992, 28, 2631–2654. [Google Scholar] [CrossRef]
- Hum, D.S.; Fejer, M.M. Quasi-phasematching. Comptes Rendus Phys. 2007, 8, 180–198. [Google Scholar] [CrossRef]
- Stegeman, G.I.; Sheik-Bahae, M.; Van Stryland, E.; Assanto, G. Large nonlinear phase shifts in second-order nonlinear-optical processes. Opt. Lett. 1993, 18, 13–15. [Google Scholar] [CrossRef]
- Assanto, G.; Stegeman, G.; Sheik-Bahae, M.; Van Stryland, E. All-optical switching devices based on large nonlinear phase shifts from second harmonic generation. Appl. Phys. Lett. 1993, 62, 1323–1325. [Google Scholar] [CrossRef]
- Hagan, D.J.; Wang, Z.; Stegeman, G.; Van Stryland, E.W.; Sheik-Bahae, M.; Assanto, G. Phase-controlled transistor action by cascading of second-order nonlinearities in KTP. Opt. Lett. 1994, 19, 1305–1307. [Google Scholar] [CrossRef]
- Assanto, G.; Stegeman, G.I.; Sheik-Bahae, M.; VanStryland, E. Coherent interactions for all-optical signal processing via quadratic nonlinearities. IEEE J. Quantum Electron. 1995, 31, 673–681. [Google Scholar] [CrossRef]
- Stegeman, G.I.; Hagan, D.J.; Torner, L. χ(2) cascading phenomena and their applications to all-optical signal processing, mode-locking, pulse compression and solitons. Opt. Quantum Electron. 1996, 28, 1691–1740. [Google Scholar] [CrossRef]
- Assanto, G. Transistor action through nonlinear cascading in Type II interactions. Opt. Lett. 1995, 20, 1595–1597. [Google Scholar] [CrossRef]
- Schiek, R.; Baek, Y.; Stegeman, G.; Sohler, W. One-dimensional quadratic walking solitons. Opt. Lett. 1999, 24, 83–85. [Google Scholar] [CrossRef]
- Picciau, M.; Leo, G.; Assanto, G. Versatile bistable gate based on quadratic cascading in a Bragg periodic structure. J. Opt. Soc. Am. B 1996, 13, 661–670. [Google Scholar] [CrossRef]
- Costantini, B.; De Angelis, C.; Barthelemy, A.; Laureti Palma, A.; Assanto, G. Polarization multiplexed χ(2) solitary waves interactions. Opt. Lett. 1997, 22, 1376–1378. [Google Scholar] [CrossRef]
- Leo, G.; Assanto, G.; Torruellas, W.E. Bidimensional spatial solitary waves in quadratically nonlinear bulk media. J. Opt. Soc. Am. B 1997, 14, 3134–3142. [Google Scholar] [CrossRef]
- Gallo, K.; Pasquazi, A.; Stivala, S.; Assanto, G. Parametric Solitons in Two-Dimensional Lattices of Purely Nonlinear Origin. Phys. Rev. Lett. 2008, 100, 053901. [Google Scholar] [CrossRef]
- Conti, C.; Trillo, S.; Assanto, G. Doubly Resonant Bragg Simultons via Second-Harmonic Generation. Phys. Rev. Lett. 1997, 78, 2341–2344. [Google Scholar] [CrossRef]
- Chen, B.Q.; Zhang, C.; Hu, C.Y.; Liu, R.J.; Li, Z.Y. High-efficiency broadband high-harmonic generation from a single quasi-phase-matching nonlinear crystal. Phys. Rev. Lett. 2015, 115, 083902. [Google Scholar] [CrossRef]
- Akhmanov, S.A.; Dmitriev, V.G.; Modenov, V.P. Towards the theory of frequency multiplication in nonlinear dispersive lines. Radiotech. Electron. 1964, 9, 13–20. [Google Scholar]
- Akhmanov, S.A.; Khokhlov, R.V. Problems of Nonlinear Optics: Electromagnetic Waves in Nonlinear Dispersive Media; Gordon and Breach: Moscow, Russia, 1972. [Google Scholar]
- Hareli, L.; Shoulga, G.; Bahabad, A. Phase matching and quasi-phase matching of high-order harmonic generation—A tutorial. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 233001. [Google Scholar] [CrossRef]
- Sapaev, U.K.; Kulagin, I.A.; Satlikov, N.K.; Usmanov, T. Optimization of third harmonic generation for two coupled three-frequency interactions of waves with multiple frequencies in periodic crystals. Opt. Spectr. 2006, 101, 983–985. [Google Scholar] [CrossRef]
- Aleksandrovski, A.L.; Chirkin, A.S.; Volkov, V.V. Realization of quasi-phase-matched parametric interactions of waves of multiple frequencies with simultaneous frequency doubling. J. Russ. Las. Res. 1997, 18, 101–106. [Google Scholar] [CrossRef]
- Pfister, O.; Wells, J.S.; Hollberg, L.; Zink, L.; Van Baak, D.A.; Levenson, M.D.; Bosenberg, W.R. Continuous-wave frequency tripling and quadrupling by simultaneous three-wave mixings in periodically poled crystals: Application to a two-step 1.19–10.71-µm frequency bridge. Opt. Lett. 1997, 22, 1211–1213. [Google Scholar] [CrossRef]
- Sabirov, O.I.; Assanto, G.; Sapaev, U.K. Efficient Third-Harmonic Generation by Inhomogeneous Quasi-Phase-Matching in Quadratic Crystals. Photonics 2023, 10, 76. [Google Scholar] [CrossRef]
- Norton, A.H.; de Sterke, C.M. Aperiodic 1-dimensional structures for quasi-phase matching. Opt. Express 2004, 12, 841–846. [Google Scholar] [CrossRef]
- Sapaev, U.K.; Assanto, G. Engineered quasi-phase matching for multiple parametric generation. Opt. Express 2009, 17, 3765–3770. [Google Scholar] [CrossRef]
- Yusupov, D.B.; Sapaev, U.K. Multistep third-harmonic generation of femtosecond laser pulses in periodically-poled and chirped-periodically-poled lithium niobate. J. Russ. Laser Res. 2009, 30, 321–326. [Google Scholar] [CrossRef]
- Tian, Y.; Li, Q.; Yan, L.; Cao, X.; Zhao, X. A Brief Review on Nonlinear Photonic Crystals Induced by Direct Femtosecond Laser Writing. Photonics 2023, 10, 833. [Google Scholar] [CrossRef]
- Zhu, S.; Zhu, Y.; Ming, N. Quasi-phase-matched third-harmonic generation in a quasi-periodic optical superlattice. Science 1997, 278, 843–846. [Google Scholar] [CrossRef]
- Longhi, S. Third-harmonic generation in quasi-phase-matched χ(2) media with missing second harmonic. Opt. Lett. 2007, 32, 1791–1793. [Google Scholar] [CrossRef] [PubMed]
- Chirkin, A.S.; Volkov, V.V.; Laptev, G.D.; Morozov, E.Y. Consecutive three-wave interactions in nonlinear optics of periodically inhomogeneous media. Quantum Electron. 2000, 30, 847. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, Y.; Yang, S.; Qin, Y.; Zhu, S.; Chen, Y.; Liu, H.; Ming, N. Crucial effects of coupling coefficients on quasi-phase-matched harmonic generation in an optical superlattice. Opt. Lett. 2000, 25, 436–438. [Google Scholar] [CrossRef]
- Sapaev, U.; Assanto, G. On the generation of optical third-harmonic through quasi-phase-matching in quadratic nonlinear crystals. Wave Motion 2024, 130, 103372. [Google Scholar] [CrossRef]
- Kintaka, K.; Fujimura, M.; Suhara, T.; Nishihara, H. Third harmonic generation of Nd:YAG laser light in periodically poled LiNbO3 waveguide. Electron. Lett. 1997, 33, 1459–1461. [Google Scholar] [CrossRef]
- Laurell, F.; Brown, J.B.; Bierlein, J.D. Sum-frequency generation in segmented KTP waveguides. Appl. Phys. Lett. 1992, 60, 1064–1066. [Google Scholar] [CrossRef]
- Dmitriev, V.G.; Gurzadyan, G.G.; Nikogosyan, D.N. Handbook of Nonlinear Optical Crystals; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapaev, U.; Assanto, G. Quadratic Cascading in Quasi-Phase-Matching: An Alternative Route to Efficient Third-Harmonic Generation. Electronics 2024, 13, 4348. https://doi.org/10.3390/electronics13224348
Sapaev U, Assanto G. Quadratic Cascading in Quasi-Phase-Matching: An Alternative Route to Efficient Third-Harmonic Generation. Electronics. 2024; 13(22):4348. https://doi.org/10.3390/electronics13224348
Chicago/Turabian StyleSapaev, Usman, and Gaetano Assanto. 2024. "Quadratic Cascading in Quasi-Phase-Matching: An Alternative Route to Efficient Third-Harmonic Generation" Electronics 13, no. 22: 4348. https://doi.org/10.3390/electronics13224348
APA StyleSapaev, U., & Assanto, G. (2024). Quadratic Cascading in Quasi-Phase-Matching: An Alternative Route to Efficient Third-Harmonic Generation. Electronics, 13(22), 4348. https://doi.org/10.3390/electronics13224348






