Geometry of Textual Data Augmentation: Insights from Large Language Models
Abstract
1. Introduction
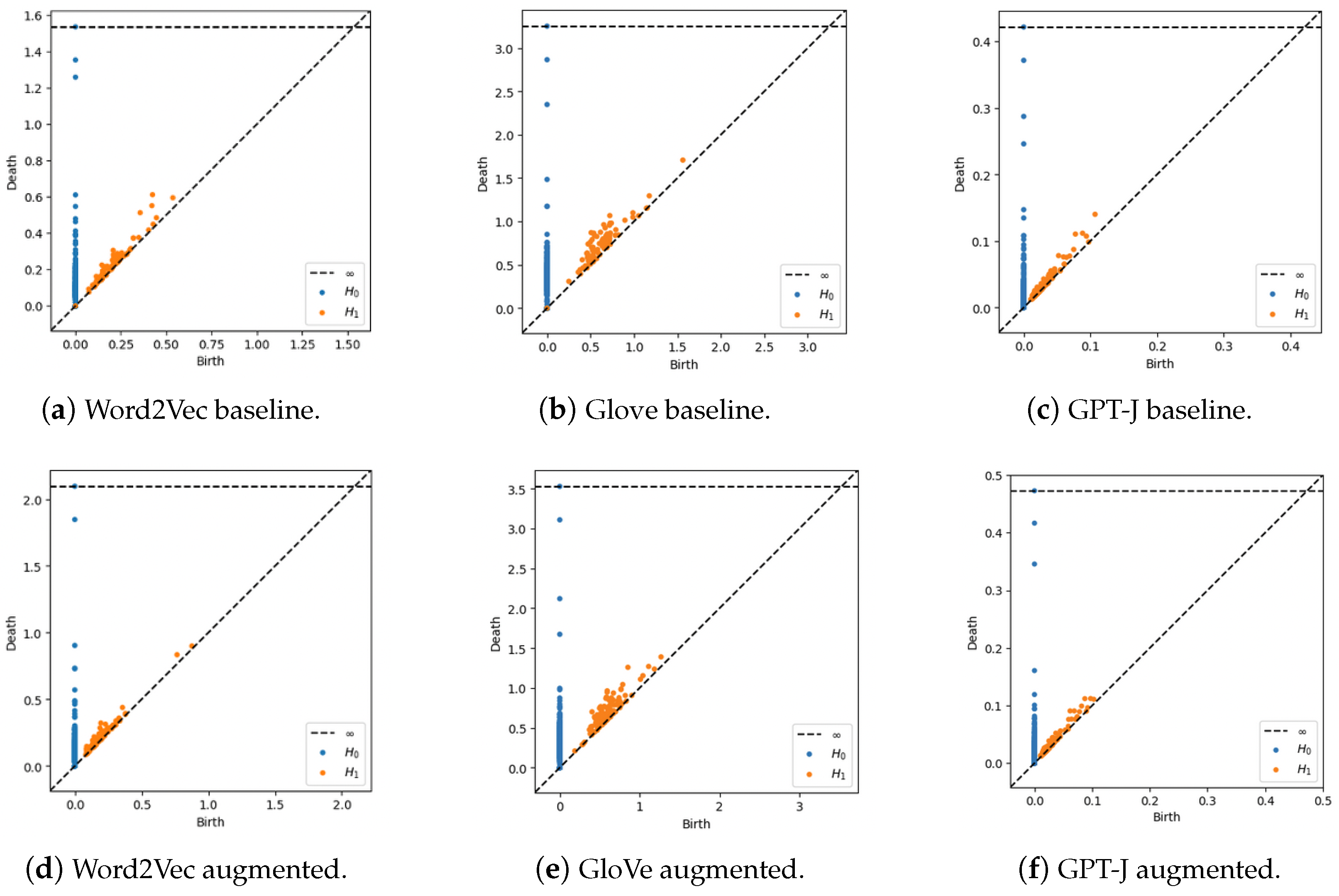
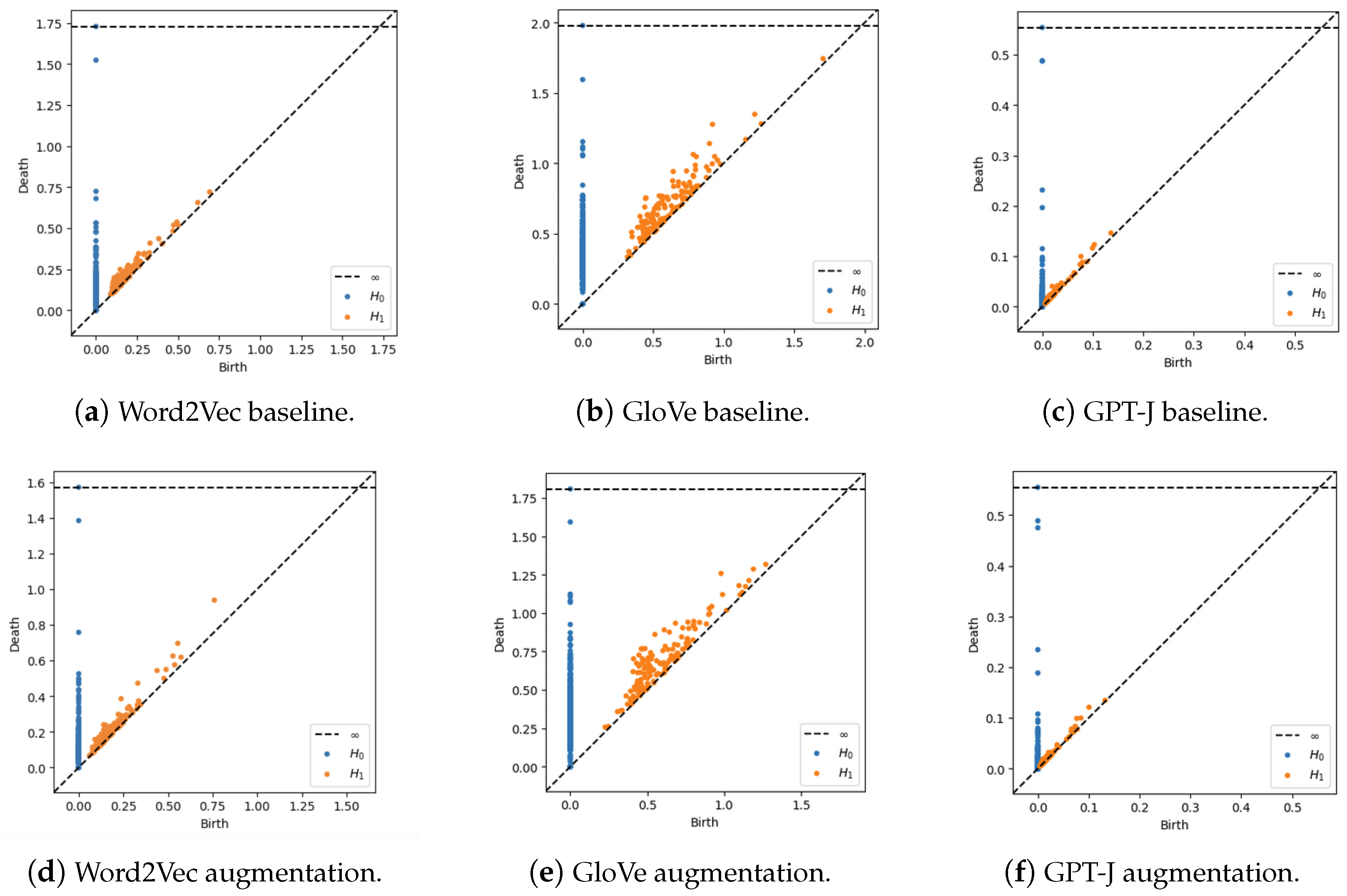
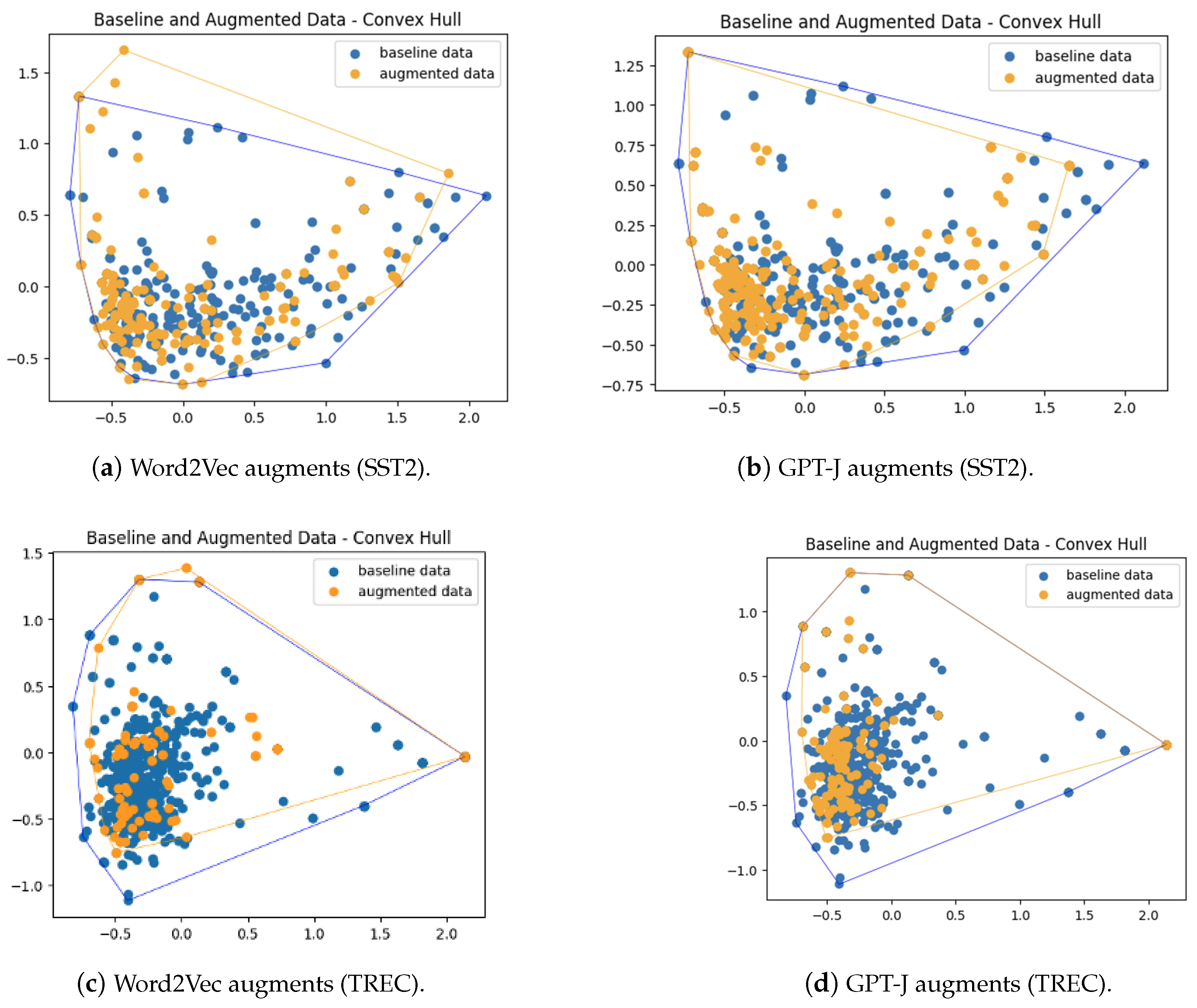
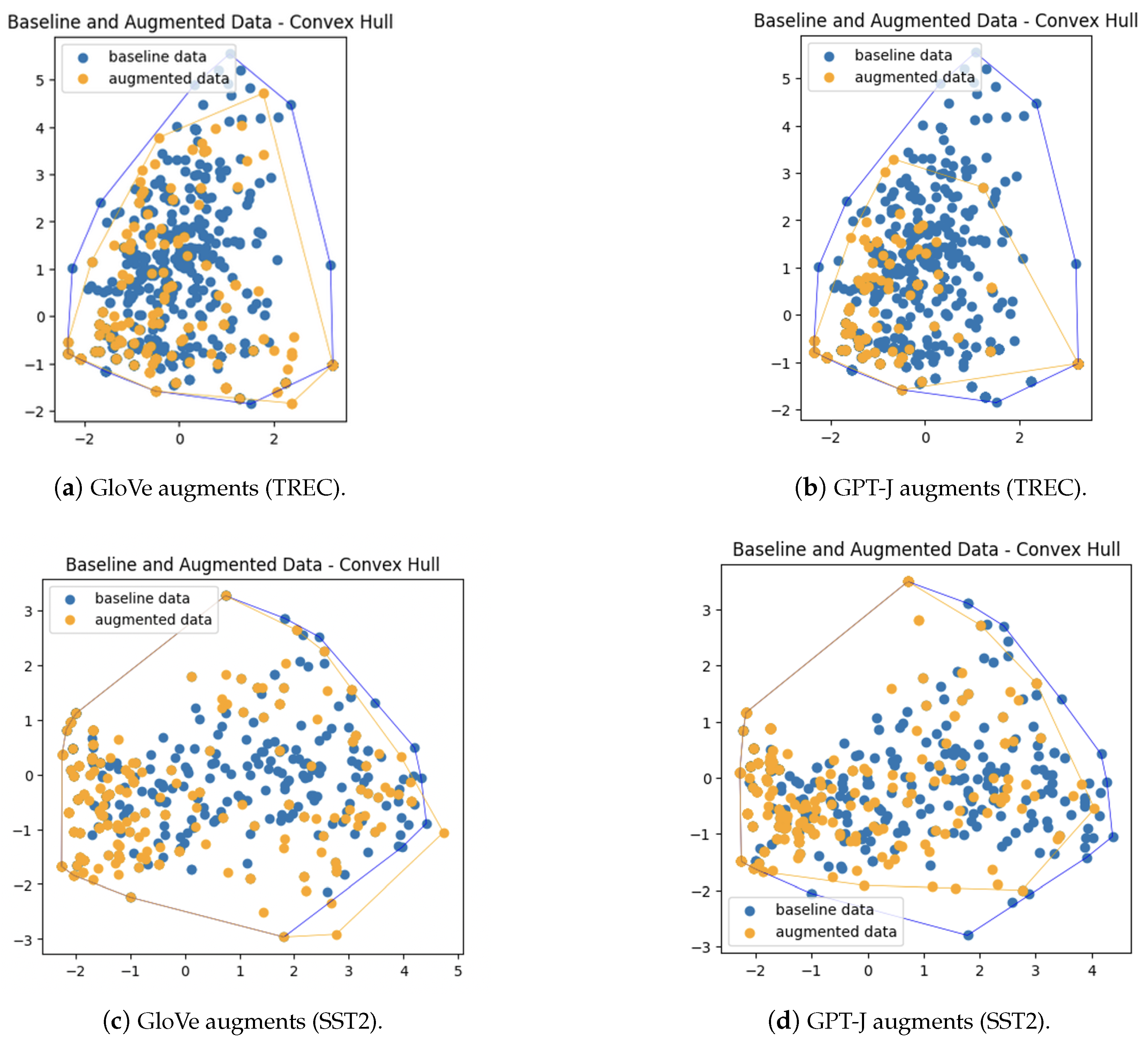
- Augmented data points generated by LLMs like GPT-J are closely aligned with the original training data in terms of spatial boundaries, maintaining semantic integrity and ensuring consistency of labels. This is in contrast to augmented data points generated by Word2Vec and GloVe embeddings, which often extend beyond the boundaries of the original training data.
- The addition of meaningful augmented data points within the convex hull of the original training data significantly enhances the efficacy of text classification systems by providing richer training datasets. Increasing the number of augmented data points within these defined boundaries correlates with improved classification accuracy.
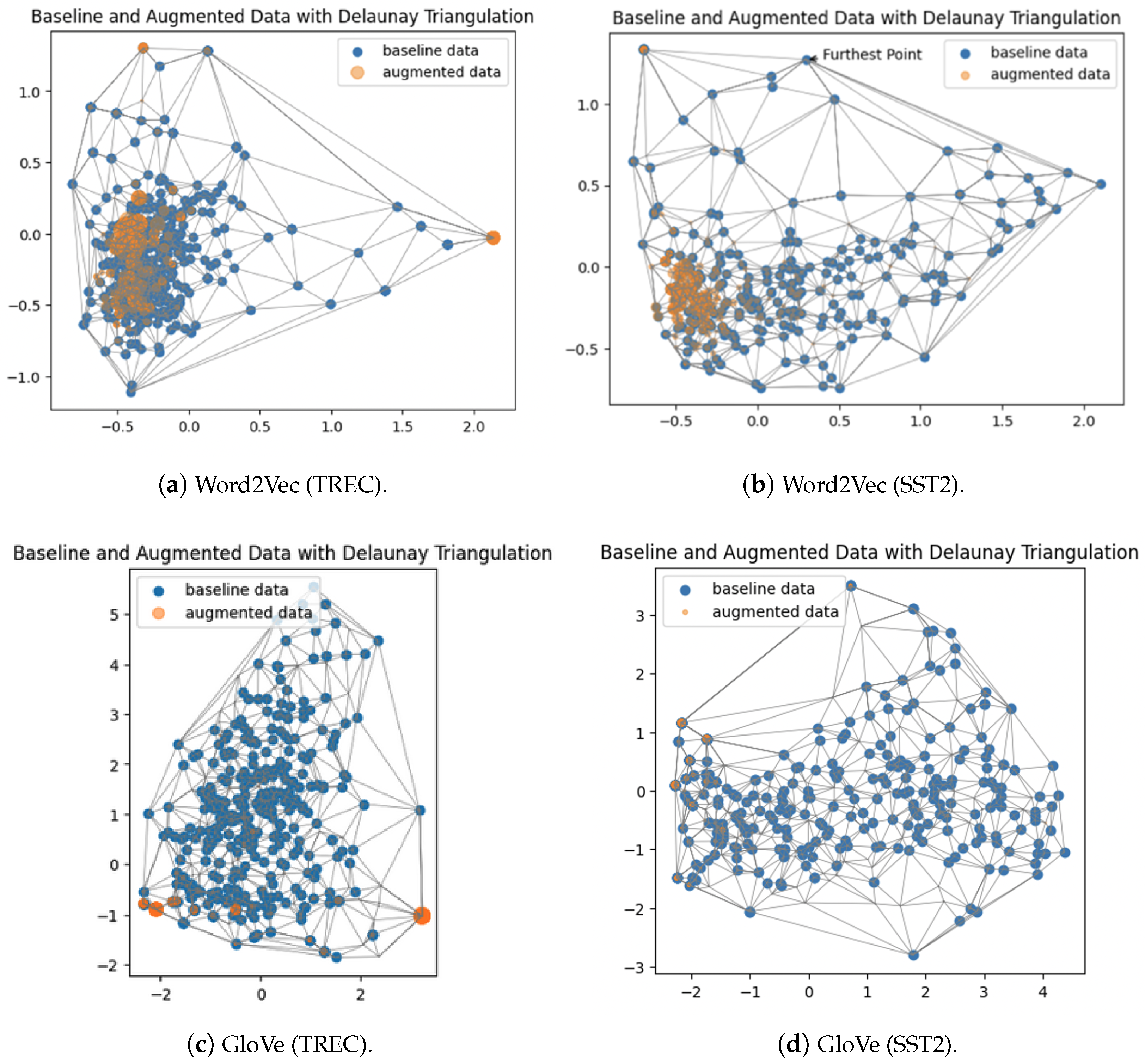
- Techniques such as topological data analysis, convex hull, and Delaunay triangulation prove effective in analyzing the spatial distribution and connectivity of NLP data points, offering a novel approach to understanding textual DA and explaining the superior performance of LLMs in this task.
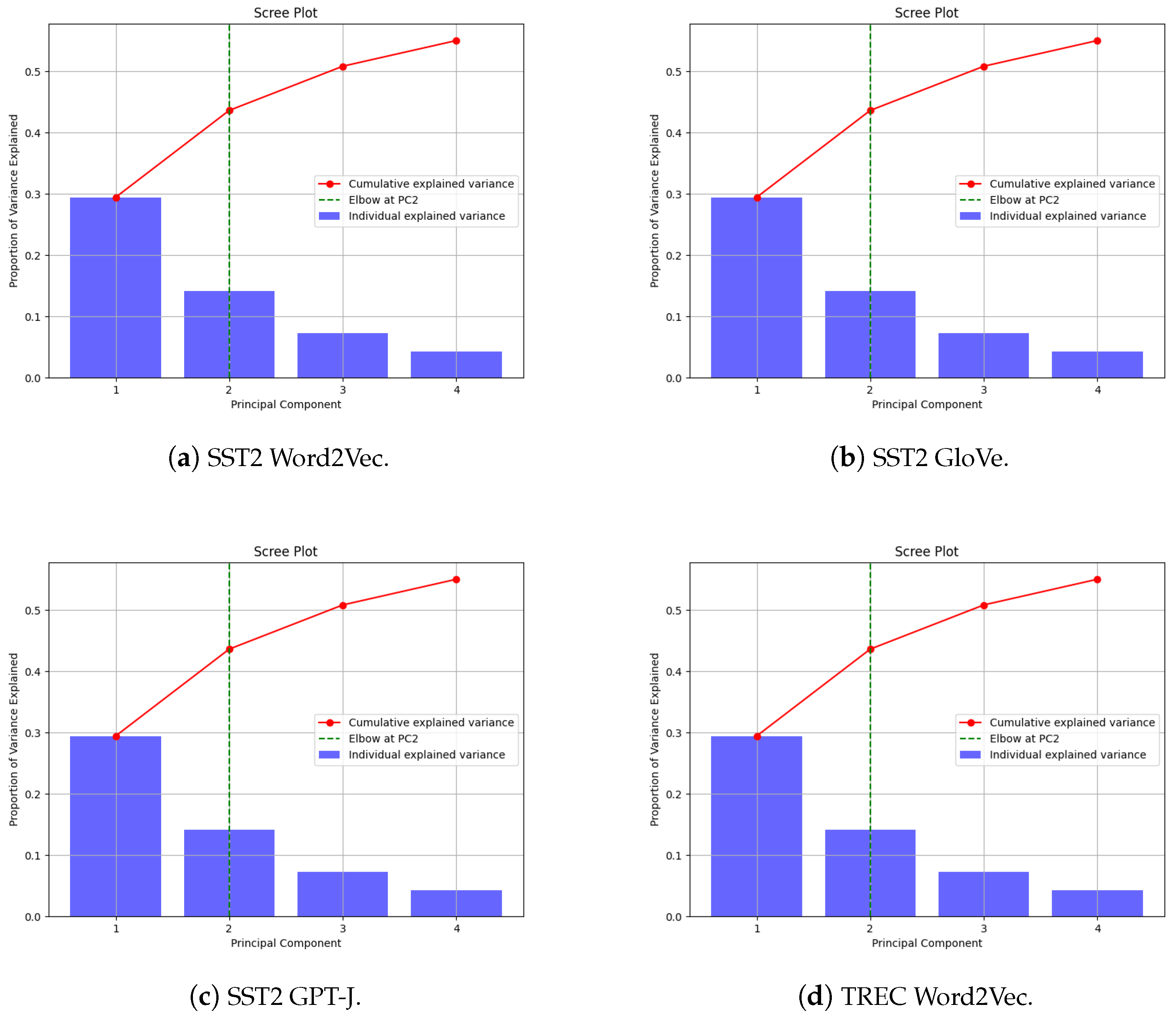
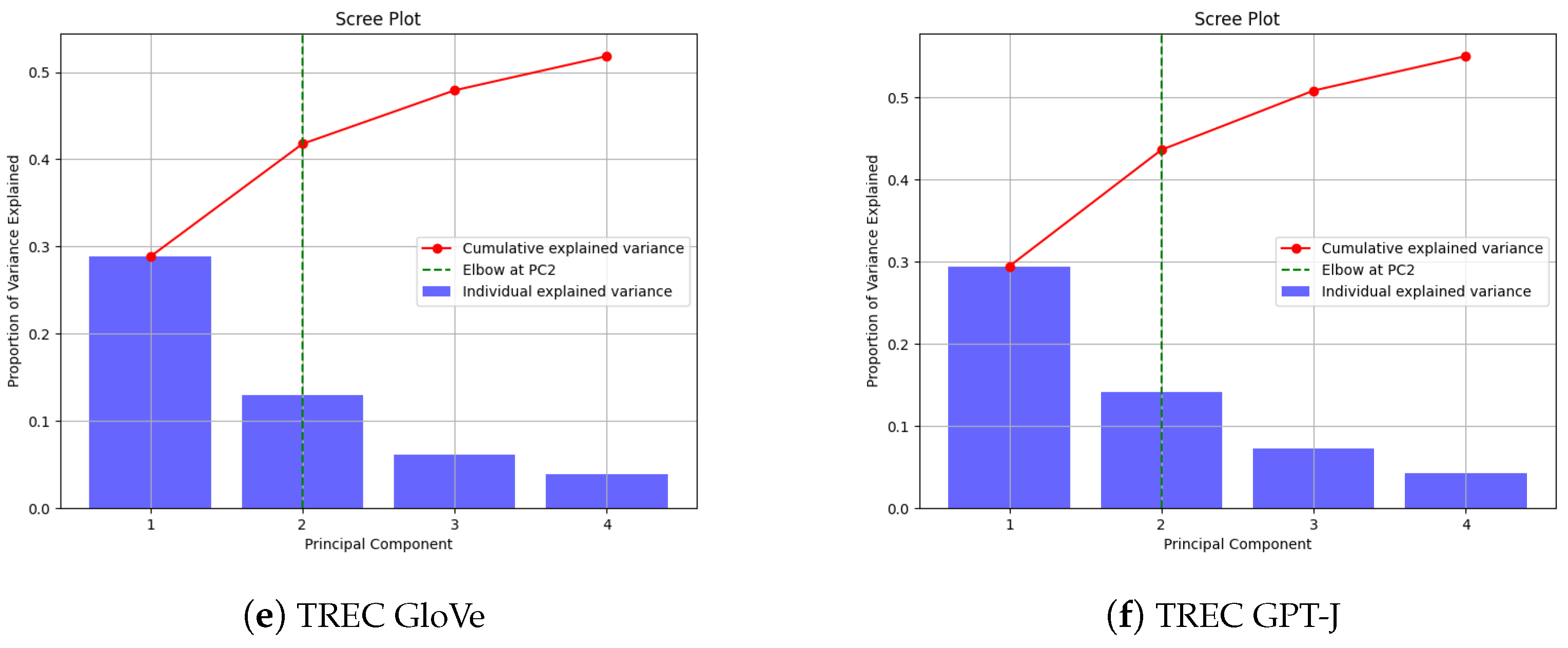
- In terms of dimensionality reduction, using principal component analysis with two components is optimal for capturing the majority of variance in augmented datasets. This approach balances information preservation with computational efficiency across various augmentation techniques, without significant loss of model performance compared to using three components.
1.1. Use of Topological and Geometric Techniques
1.2. Research Objectives
- Apply topological data analysis to examine the structural properties of the augmented data spaces.
- Utilize computational geometry techniques such as convex hull analysis and Delaunay triangulation to investigate the spatial distribution of augmented data points.
- Explore the relationship between these geometric and topological properties and the effectiveness of the augmentation methods in improving classification performance.
2. Review of Textual Data Augmentation Techniques
2.1. Word-Level Augmentation
2.2. Sentence-Level Augmentation
2.3. Document-Level Augmentation
2.4. Recent Advanced Techniques
3. Experimental Design
3.1. Data Augmentation Techniques
3.1.1. Word Replacement
| Algorithm 1 Word replacement algorithm |
| Require: , , |
| Ensure: |
| for all in do |
| for all in do |
| end for |
| end for |
| return |
3.1.2. GPT-J
- Model: a RAM-reduced GPT-J-6B model, which is publicly available through the Hugging Face model hub [41].
- Framework: the model is implemented using the transformer library (version 4.18.0) from Hugging Face, which provides a high-level API for working with pre-trained language models.
- Hardware: Single NVIDIA A100 GPU with 40 GB of VRAM.
3.2. Classification Model and Dataset
- With each of these two datasets, one of the class labels is randomly chosen.
- For this chosen label, five training samples are randomly selected.
- For each of the remaining labels, 20 training samples are randomly chosen.
4. Dimensionality Reduction
Principal Component Selection Analysis
5. Techniques in Analyzing Geometric Properties
5.1. Topological Data Analysis
5.2. Computational Geometry
6. Results and Analyses
6.1. Classification Results
6.2. TDA of Embedding Vectors
6.3. Bottleneck Distance Analysis
7. Geometric Analyses
7.1. Convex Hull Analysis
7.2. Delaunay Triangulation Analysis
7.3. Inspecting Generated Samples
7.3.1. GPT-J-Generated Text
7.3.2. Word2Vec-Generated Text
7.3.3. GloVe-Generated Text
8. Limitations and Future Research
- Dataset diversity: Our study focused on two datasets (SST2 and TREC). Future work should extend this analysis to a broader range of datasets across different domains and languages to validate the generalizability of our findings.
- Dimensionality reduction: Our analysis relied heavily on PCA for dimensionality reduction, with most datasets showing that two principal components captured the majority of the variance. However, the SNIPS dataset proved to be an exception, requiring higher-dimensional analysis. This limitation highlights the need for future research to cover the following:
- –
- Explore alternative dimensionality reduction techniques that might better capture the complexity of diverse datasets.
- –
- Develop methods to determine the optimal number of dimensions for analysis for different types of datasets.
- Linguistic structure analysis: Our current study looks at word-level analysis, examining the geometric and topological properties of individual word embeddings. While this approach has provided valuable insights, it does not fully capture the complexity of higher-level linguistic structures. Future research could extend our framework to analyze sentence-level properties, word order, and syntactic relationships.
- Multimodal data: As many real-world applications involve multimodal data, future research could extend our geometric framework to analyze augmentation techniques for combined text and image data.
- Optimization framework: Building on our findings, future research could develop an optimization framework that uses geometric and topological properties to automatically select or generate the most effective augmentation data for a given task and dataset.
- New augmentation strategies: Our geometric framework may prove useful in developing new augmentation strategies that explicitly consider the spatial distribution and connectivity of data points.
9. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, S.; Jafari, O.; Nagarkar, P. A survey on machine learning techniques for auto labeling of video, audio, and text data. arXiv 2021, arXiv:2109.03784. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M. A survey on image data augmentation for deep learning. J. Big Data 2019, 6, 1–48. [Google Scholar] [CrossRef]
- Bayer, M.; Kaufhold, M.A.; Reuter, C. A Survey on Data Augmentation for Text Classification. ACM Comput. Surv. 2022, 55, 146:1–146:39. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers); Burstein, J., Doran, C., Solorio, T., Eds.; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training; Technical Report; Open AI: San Francisco, CA, USA, 2018. [Google Scholar]
- Sahu, G.; Rodriguez, P.; Laradji, I.H.; Atighehchian, P.; Vazquez, D.; Bahdanau, D. Data augmentation for intent classification with off-the-shelf large language models. arXiv 2022, arXiv:2204.01959. [Google Scholar]
- Edwards, A.; Ushio, A.; Camacho-Collados, J.; de Ribaupierre, H.; Preece, A. Guiding generative language models for data augmentation in few-shot text classification. arXiv 2021, arXiv:2111.09064. [Google Scholar]
- Dai, H.; Liu, Z.; Liao, W.; Huang, X.; Cao, Y.; Wu, Z.; Zhao, L.; Xu, S.; Liu, W.; Liu, N.; et al. Auggpt: Leveraging chatgpt for text data augmentation. arXiv 2023, arXiv:2302.13007. [Google Scholar]
- Møller, A.G.; Aarup Dalsgaard, J.; Pera, A.; Aiello, L.M. Is a prompt and a few samples all you need? Using GPT-4 for data augmentation in low-resource classification tasks. arXiv 2023, arXiv:2304.13861. [Google Scholar] [CrossRef]
- Feng, S.Y.; Gangal, V.; Wei, J.; Chandar, S.; Vosoughi, S.; Mitamura, T.; Hovy, E. A survey of data augmentation approaches for NLP. arXiv 2021, arXiv:2105.03075. [Google Scholar]
- Shorten, C.; Khoshgoftaar, T.M.; Furht, B. Text data augmentation for deep learning. J. Big Data 2021, 8, 101. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; LeCun, Y. Character-level convolutional networks for text classification. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 7–12 December 2015; Volume 28. [Google Scholar]
- Wei, J.; Zou, K. EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification Tasks. In Proceedings of the 2019 Conference on Empirical Methods in Natural Language Processing and the 9th International Joint Conference on Natural Language Processing (EMNLP-IJCNLP); Inui, K., Jiang, J., Ng, V., Wan, X., Eds.; Association for Computational Linguistics: Minneapolis, MN, USA, 2019; pp. 6382–6388. [Google Scholar] [CrossRef]
- Miller, G.A. WordNet: A lexical database for English. Commun. ACM 1995, 38, 39–41. [Google Scholar] [CrossRef]
- Marivate, V.; Sefara, T. Improving short text classification through global augmentation methods. In Proceedings of the Machine Learning and Knowledge Extraction: 4th IFIP TC 5, TC 12, WG 8.4, WG 8.9, WG 12.9 International Cross-Domain Conference, CD-MAKE 2020, Dublin, Ireland, 25–28 August 2020; Springer: Berlin/Heidelberg, Germany, 2020; pp. 385–399. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. In Proceedings of the 2013 International Conference on Learning Representations, Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Pennington, J.; Socher, R.; Manning, C. Glove: Global Vectors for Word Representation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, 25–29 October 2014; pp. 1532–1543. [Google Scholar] [CrossRef]
- Kobayashi, S. Contextual Augmentation: Data Augmentation by Words with Paradigmatic Relations. In Proceedings of the 2018 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Volume 2 (Short Papers); Walker, M., Ji, H., Stent, A., Eds.; Association for Computational Linguistics: Minneapolis, MN, USA, 2018; pp. 452–457. [Google Scholar] [CrossRef]
- Sennrich, R.; Haddow, B.; Birch, A. Improving Neural Machine Translation Models with Monolingual Data. In Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers); Association for Computational Linguistics: Minneapolis, MN, USA, 2016. [Google Scholar]
- McKeown, K. Paraphrasing questions using given and new information. Am. J. Comput. Linguist. 1983, 9, 1–10. [Google Scholar]
- QUIRK, C. Monolingual machine translation for paraphrase generation. In Proceedings of the 2004 Conference on Empirical Methods in Natural Language Processing (EMNLP), Barcelona, Spain, 25–26 July 2004. [Google Scholar]
- Iyyer, M.; Wieting, J.; Gimpel, K.; Zettlemoyer, L. Adversarial example generation with syntactically controlled paraphrase networks. arXiv 2018, arXiv:1804.06059. [Google Scholar]
- Coulombe, C. Text data augmentation made simple by leveraging nlp cloud apis. arXiv 2018, arXiv:1812.04718. [Google Scholar]
- Fadaee, M.; Bisazza, A.; Monz, C. Data augmentation for low-resource neural machine translation. arXiv 2017, arXiv:1705.00440. [Google Scholar]
- Fu, Z.; Tan, X.; Peng, N.; Zhao, D.; Yan, R. Style transfer in text: Exploration and evaluation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018; Volume 32. [Google Scholar]
- Xie, Q.; Dai, Z.; Hovy, E.; Luong, T.; Le, Q. Unsupervised data augmentation for consistency training. Adv. Neural Inf. Process. Syst. 2020, 33, 6256–6268. [Google Scholar]
- Kumar, V.; Choudhary, A.; Cho, E. Data augmentation using pre-trained transformer models. arXiv 2020, arXiv:2003.02245. [Google Scholar]
- Maynez, J.; Narayan, S.; Bohnet, B.; McDonald, R. On Faithfulness and Factuality in Abstractive Summarization. In Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics, Online, 5–10 July 2020; pp. 1906–1919. [Google Scholar]
- Yang, S.; Wang, Y.; Chu, X. A survey of deep learning techniques for neural machine translation. arXiv 2020, arXiv:2002.07526. [Google Scholar]
- Brown, T.; Mann, B.; Ryder, N.; Subbiah, M.; Kaplan, J.D.; Dhariwal, P.; Neelakantan, A.; Shyam, P.; Sastry, G.; Askell, A.; et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst. 2020, 33, 1877–1901. [Google Scholar]
- Keskar, N.S.; McCann, B.; Varshney, L.R.; Xiong, C.; Socher, R. Ctrl: A conditional transformer language model for controllable generation. arXiv 2019, arXiv:1909.05858. [Google Scholar]
- Wang, B.; Komatsuzaki, A. GPT-J-6B: A 6 Billion Parameter Autoregressive Language Model. 2021. Available online: https://github.com/kingoflolz/mesh-transformer-jax (accessed on 17 September 2024).
- Zhu, C.; Cheng, Y.; Gan, Z.; Sun, S.; Goldstein, T.; Liu, J. Freelb: Enhanced adversarial training for natural language understanding. arXiv 2019, arXiv:1909.11764. [Google Scholar]
- Bender, E.M.; Gebru, T.; McMillan-Major, A.; Shmitchell, S. On the dangers of stochastic parrots: Can language models be too big? In Proceedings of the 2021 ACM Conference on Fairness, Accountability, and Transparency, Virtual, 3–10 March 2021; pp. 610–623. [Google Scholar]
- Howard, J.; Ruder, S. Universal language model fine-tuning for text classification. arXiv 2018, arXiv:1801.06146. [Google Scholar]
- Řehůřek, R.; Sojka, P. Gensim—Statistical Semantics in Python. Available online: https://radimrehurek.com/gensim/models/word2vec.html (accessed on 17 September 2024).
- Wang, W.Y.; Yang, D. That’s so annoying!!!: A lexical and frame-semantic embedding based data augmentation approach to automatic categorization of annoying behaviors using# petpeeve tweets. In Proceedings of the 2015 Conference on Empirical Methods in Natural Language Processing, Lisbon, Portugal, 17–21 September 2015; pp. 2557–2563. [Google Scholar]
- Wang, B. Mesh-Transformer-JAX: Model-Parallel Implementation of Transformer Language Model with JAX. 2021. Available online: https://github.com/kingoflolz/mesh-transformer-jax (accessed on 17 September 2024).
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2017; pp. 6000–6010. [Google Scholar]
- Wolf, T.; Debut, L.; Sanh, V.; Chaumond, J.; Delangue, C.; Moi, A.; Cistac, P.; Rault, T.; Louf, R.; Funtowicz, M.; et al. Transformers: State-of-the-art natural language processing. In Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations, Online, 16–20 November 2020; pp. 38–45. [Google Scholar]
- Yang, Y.; Malaviya, C.; Fernandez, J.; Swayamdipta, S.; Le Bras, R.; Wang, J.P.; Bhagavatula, C.; Choi, Y.; Downey, D. Generative Data Augmentation for Commonsense Reasoning. In Proceedings of the Findings of the Association for Computational Linguistics: EMNLP, Online, 16–20 November 2020; Association for Computational Linguistics: Minneapolis, MN, USA, 2020; pp. 1008–1025. [Google Scholar] [CrossRef]
- Anaby-Tavor, A.; Carmeli, B.; Goldbraich, E.; Kantor, A.; Kour, G.; Shlomov, S.; Tepper, N.; Zwerdling, N. Do not have enough data? Deep learning to the rescue! In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 7383–7390. [Google Scholar]
- Johnson, R.; Zhang, T. Effective use of word order for text categorization with convolutional neural networks. arXiv 2014, arXiv:1412.1058. [Google Scholar]
- Zhang, Y.; Wallace, B. A sensitivity analysis of (and practitioners’ guide to) convolutional neural networks for sentence classification. arXiv 2015, arXiv:1510.03820. [Google Scholar]
- Socher, R.; Perelygin, A.; Wu, J.; Chuang, J.; Manning, C.D.; Ng, A.; Potts, C. Recursive Deep Models for Semantic Compositionality Over a Sentiment Treebank. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013; pp. 1631–1642. [Google Scholar]
- Hovy, E.; Gerber, L.; Hermjakob, U.; Lin, C.Y.; Ravichandran, D. Toward Semantics-Based Answer Pinpointing. In Proceedings of the First International Conference on Human Language Technology Research, San Diego, CA, USA, 18–21 March 2001. [Google Scholar]
- Casadio, M.; Komendantskaya, E.; Rieser, V.; Daggitt, M.L.; Kienitz, D.; Arnaboldi, L.; Kokke, W. Why Robust Natural Language Understanding is a Challenge. arXiv 2022, arXiv:2206.14575. [Google Scholar]
- Ning-min, S.; Jing, L. A Literature Survey on High-Dimensional Sparse Principal Component Analysis. Int. J. Database Theory Appl. 2015, 8, 57–74. [Google Scholar] [CrossRef]
- Taloba, A.I.; Eisa, D.A.; Ismail, S.S.I. A Comparative Study on using Principle Component Analysis with Different Text Classifiers. Int. J. Comput. Appl. 2018, 180, 1–6. [Google Scholar] [CrossRef]
- Heimerl, F.; Gleicher, M. Interactive analysis of word vector embeddings. Comput. Graph. Forum 2018, 37, 253–265. [Google Scholar] [CrossRef]
- Raunak, V.; Gupta, V.; Metze, F. Effective Dimensionality Reduction for Word Embeddings. In Proceedings of the 4th Workshop on Representation Learning for NLP (RepL4NLP-2019), Florence, Italy, 2 August 2019; pp. 235–243. [Google Scholar] [CrossRef]
- Camastra, F.; Staiano, A. Intrinsic dimension estimation: Advances and open problems. Inf. Sci. 2016, 328, 26–41. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Cattell, R.B. The scree test for the number of factors. Multivar. Behav. Res. 1966, 1, 245–276. [Google Scholar] [CrossRef] [PubMed]
- Leykam, D.; Angelakis, D.G. Topological data analysis and machine learning. Adv. Phys. X 2023, 8, 2202331. [Google Scholar] [CrossRef]
- Rathore, A.; Zhou, Y.; Srikumar, V.; Wang, B. TopoBERT: Exploring the topology of fine-tuned word representations. Inf. Vis. 2023, 22, 186–208. [Google Scholar] [CrossRef]
- Jakubowski, A.; Gašić, M.; Zibrowius, M. Topology of word embeddings: Singularities reflect polysemy. arXiv 2020, arXiv:2011.09413. [Google Scholar]
- Niyogi, P.; Smale, S.; Weinberger, S. A topological view of unsupervised learning from noisy data. SIAM J. Comput. 2011, 40, 646–663. [Google Scholar] [CrossRef]
- Hensel, F.; Moor, M.; Rieck, B. A survey of topological machine learning methods. Front. Artif. Intell. 2021, 4, 681108. [Google Scholar] [CrossRef]
- Munch, E. A user’s guide to topological data analysis. J. Learn. Anal. 2017, 4, 47–61. [Google Scholar] [CrossRef]
- Maria, C. Persistent Cohomology. In GUDHI User and Reference Manual, 3.9.0 ed. Available online: https://gudhi.inria.fr/python/latest/persistent_cohomology_user.html (accessed on 17 September 2024).
- Wasserman, L. Topological data analysis. Annu. Rev. Stat. Its Appl. 2018, 5, 501–532. [Google Scholar] [CrossRef]
- de Berg, M.; Cheong, O.; van Kreveld, M.; Overmars, M. Convex Hulls. In Computational Geometry: Algorithms and Applications; Springer: Berlin/Heidelberg, Germany, 2008; pp. 243–258. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kobbelt, L.; Polthier, K.; Boissonnat, J.D.; Carlsson, G.; Chazelle, B.; Gao, X.S.; Gotsman, C.; Guibas, L.; Kim, M.S.; et al. Geometry and Computing; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Chazelle, B. An optimal convex hull algorithm in any fixed dimension. Discret. Comput. Geom. 1993, 10, 377–409. [Google Scholar] [CrossRef]
- Toussaint, G.T. Computational Geometry: Recent Developments. In New Advances in Computer Graphics: Proceedings of CG International’89; Springer: Berlin/Heidelberg, Germany, 1989; pp. 23–51. [Google Scholar]
- Yousefzadeh, R. Deep learning generalization and the convex hull of training sets. arXiv 2021, arXiv:2101.09849. [Google Scholar]
- Cohen-Steiner, D.; Edelsbrunner, H.; Harer, J. Stability of persistence diagrams. In Proceedings of the Twenty-First Annual Symposium on Computational Geometry, Pisa, Italy, 6–8 June 2005; pp. 263–271. [Google Scholar]
- Edelsbrunner, H.; Harer, J. Persistent homology—A survey. Contemp. Math. 2008, 453, 257–282. [Google Scholar]
- Carlsson, G. Topological pattern recognition for point cloud data. Acta Numer. 2014, 23, 289–368. [Google Scholar] [CrossRef]
- Barber, C.B.; Dobkin, D.P.; Huhdanpaa, H. The quickhull algorithm for convex hulls. ACM Trans. Math. Softw. 1996, 22, 469–483. [Google Scholar] [CrossRef]
- Musin, O.R. Properties of the Delaunay triangulation. In Proceedings of the Thirteenth Annual Symposium on Computational Geometry, Nice, France, 4–6 June 1997; pp. 424–426. [Google Scholar]



| Configuration | Values |
|---|---|
| Feature maps per region size | 2 |
| Univariate vectors per region size | 6 |
| Concatenated vectors per region size | Single feature vector |
| Sentence matrix size | 7 × 5 |
| Region sizes | (2, 3, 4) |
| Filters per region size | 2 |
| Total filters | 6 |
| Convolution | Yes |
| Activation function | ReLU |
| 1-Max pooling | Yes |
| Softmax function | Yes |
| Regularization | Yes |
| Dataset | Model | Baseline | Augmented | |
|---|---|---|---|---|
| Algorithm 1 | GPT-J | |||
| TREC | Word2Vec | 51.0% | −21.2% | +5.0% |
| GloVe | 32.8% | −18.4% | +3.2% | |
| GPT-J | 74.0% | – | +6.0% | |
| SST2 | Word2Vec | 51.2% | −0.8% | +11.4% |
| GloVe | 50.2% | −5.1% | +12.6% | |
| GPT-J | 62.0% | – | +13.2% | |
| Dataset (Label) | Technique | Generated Text |
|---|---|---|
| SST2 (0) | GPT-J | the only pleasure this film has to offer lies in the first twenty minutes when the protagonist is a normal guy |
| Word2Vec | it is a visual rorschach test and im should have failed | |
| GloVe | this a visual barcode test also think can still failed | |
| TREC (5) | GPT-J | What is the name of the river which carries the water from a large lake to the Atlantic Ocean? |
| Word2Vec | what river in scots is said to hold one or more zombies? | |
| GloVe | how lakes this scotland has adding could give another same more beast why |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, S.J.H.; Lai, E.M.-K.; Li, W. Geometry of Textual Data Augmentation: Insights from Large Language Models. Electronics 2024, 13, 3781. https://doi.org/10.3390/electronics13183781
Feng SJH, Lai EM-K, Li W. Geometry of Textual Data Augmentation: Insights from Large Language Models. Electronics. 2024; 13(18):3781. https://doi.org/10.3390/electronics13183781
Chicago/Turabian StyleFeng, Sherry J. H., Edmund M-K. Lai, and Weihua Li. 2024. "Geometry of Textual Data Augmentation: Insights from Large Language Models" Electronics 13, no. 18: 3781. https://doi.org/10.3390/electronics13183781
APA StyleFeng, S. J. H., Lai, E. M.-K., & Li, W. (2024). Geometry of Textual Data Augmentation: Insights from Large Language Models. Electronics, 13(18), 3781. https://doi.org/10.3390/electronics13183781








