Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network
Abstract
1. Introduction
2. Theoretical Foundation
2.1. Continuous Wavelet Transform
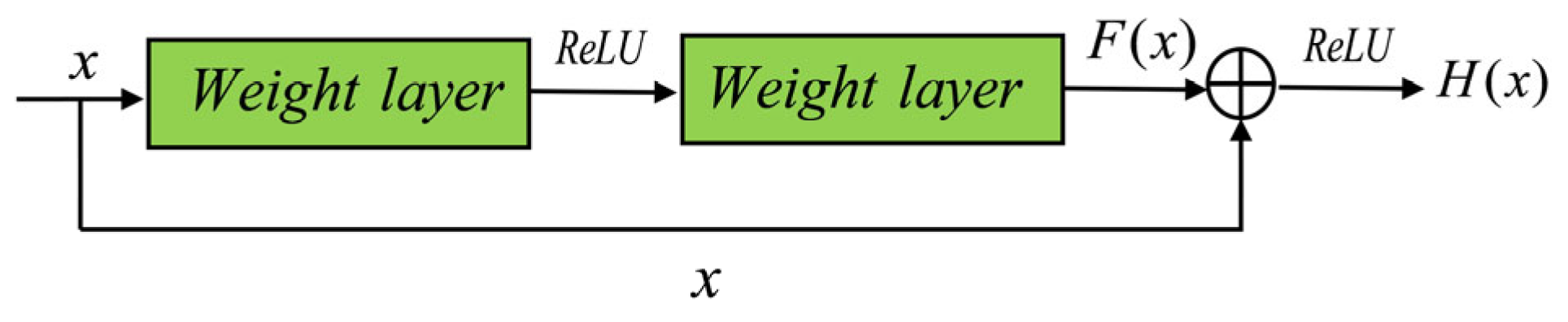
2.2. Residual Networks
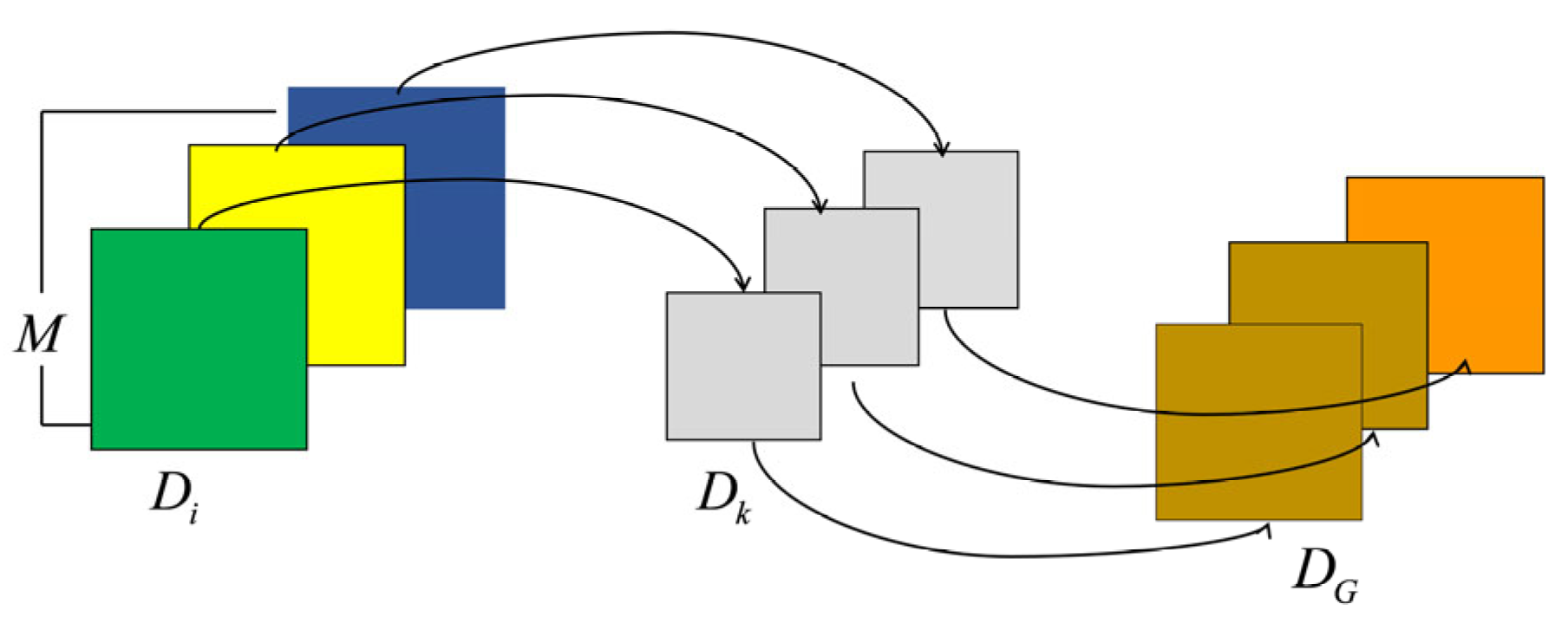
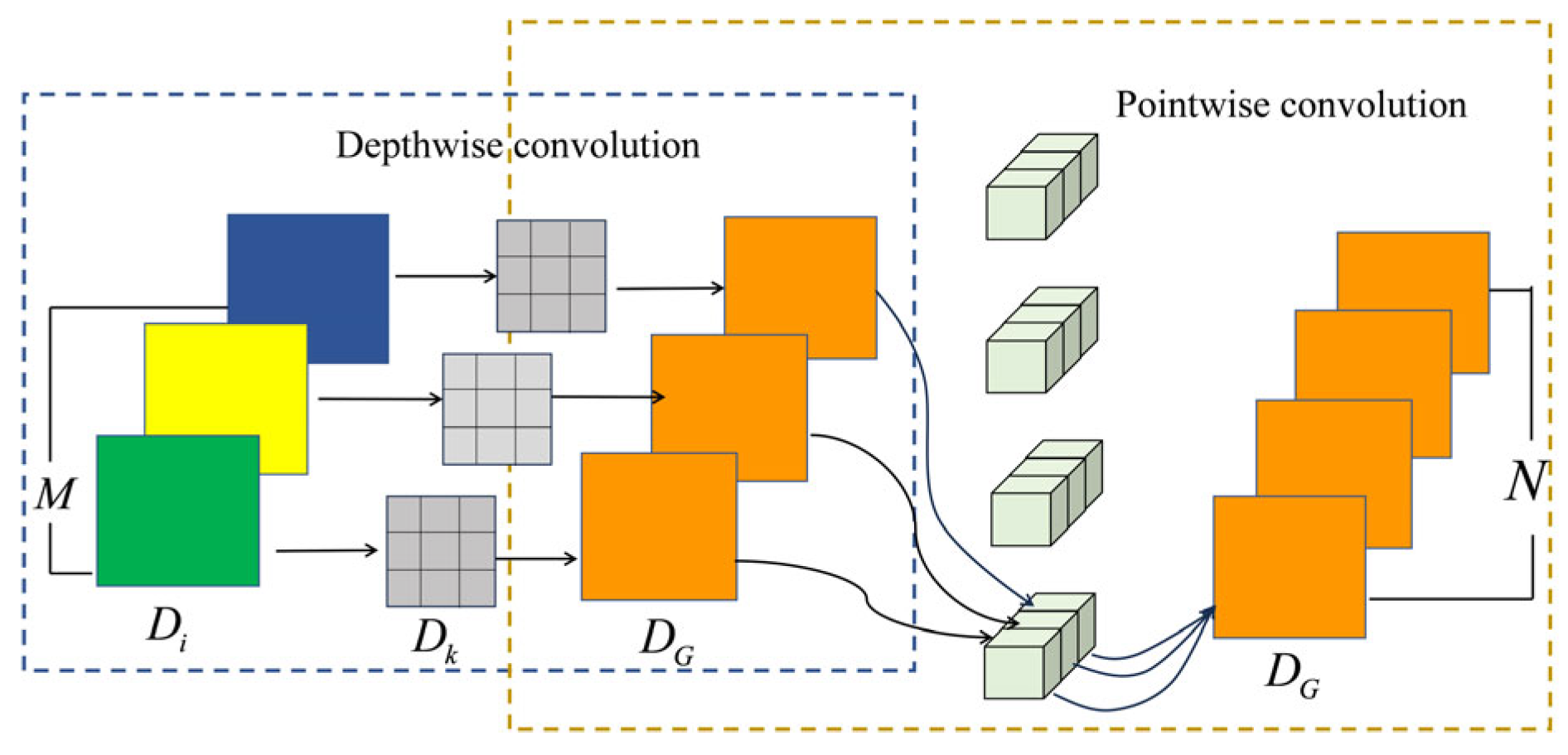
2.3. Depth-Separable Convolution
2.4. Criss-Cross Attention
2.5. Adaptive Activation Function Meta-Acon
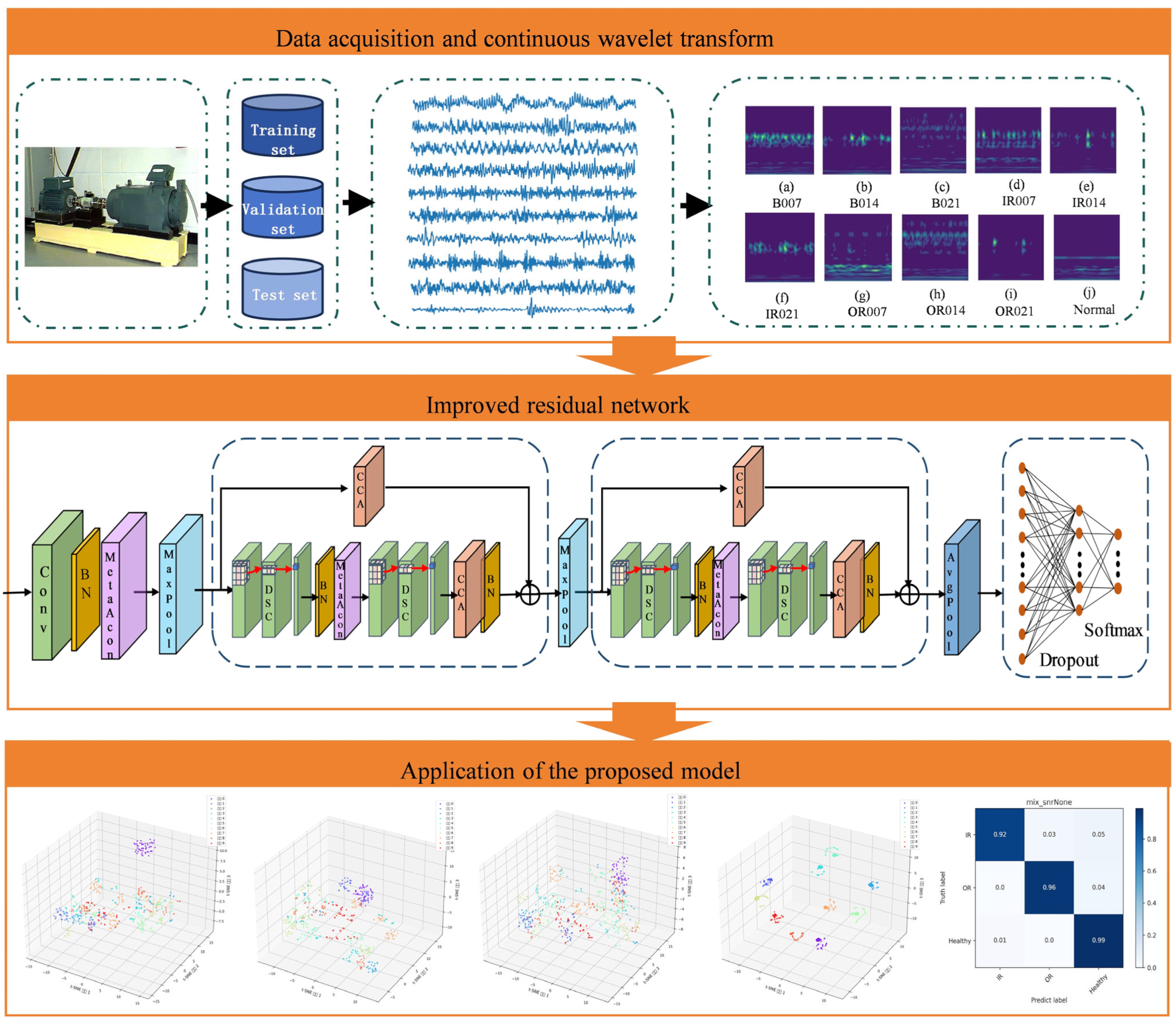
3. Improved Residual Network
3.1. Residual Block
3.2. Model Building
3.3. Fault Diagnosis Process
- Data processing: obtain the vibration signal, convert it to a time–frequency map after overlapping sampling to increase the number of samples using the continuous wavelet transform, and then convert the one-dimensional vibration signal to a two-dimensional time–frequency map.
- Model training: load the training set samples into the improved residual network for training and configure the network structure parameters, the maximum number of iterations of the loss function, and the number of training iterations.
- Model validation: Save the trained lightweight model, validate it using test set samples, and output the diagnosis findings. Use accuracy, precision, and recall as assessment metrics.
4. Experimental Validation
4.1. Data Description
4.1.1. CWRU Bearing Failure Dataset
4.1.2. PU Bearing Failure Dataset
4.2. Experimental Setup
4.3. Evaluation Indicators
4.4. Analysis of Experimental Results on the CWRU Dataset
4.4.1. Ablation Experiments
4.4.2. Model Complexity Experiments
4.4.3. Single-Load Scenario Experiments
4.4.4. Analysis of Model Performance in Noisy Environments
4.4.5. Fault Diagnosis Performance Analysis under Variable Load Conditions
4.4.6. Visualization Analysis
4.5. Analysis of Experimental Results on the PU Dataset
4.5.1. Analysis of Model Performance in Noisy Environments
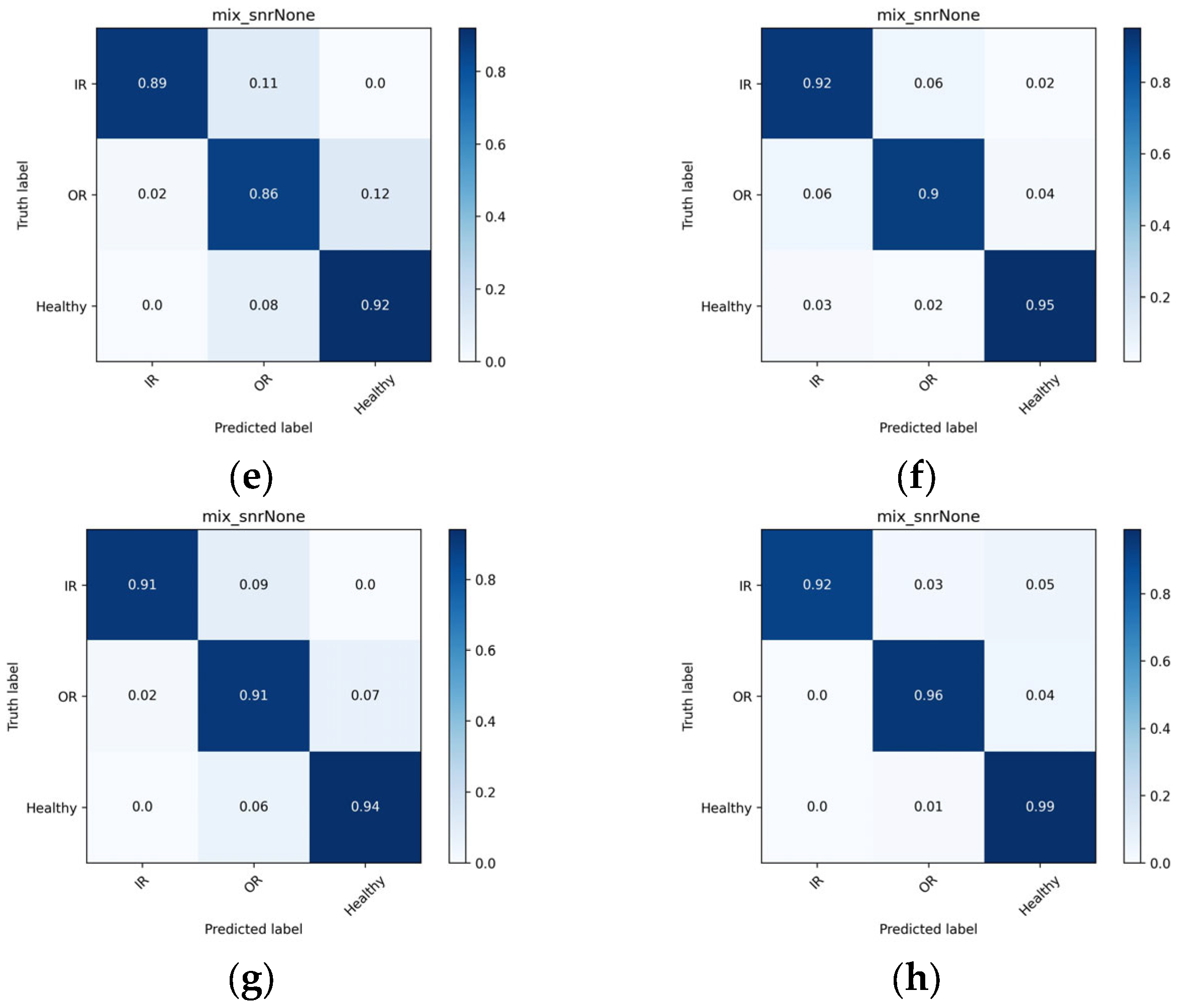
4.5.2. Confusion Matrix Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, J.; Hu, Y.; Wang, Y.; Wu, B.; Fan, J.; Hu, Z. An integrated multi-sensor fusion-based deep feature learning approach for rotating machinery diagnosis. Meas. Sci. Technol. 2018, 29, 055103. [Google Scholar] [CrossRef]
- Wu, G.; Yan, T.; Yang, G.; Chai, H.; Cao, C. A review on rolling bearing fault signal detection methods based on different sensors. Sensors 2022, 22, 8330. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, B.; Lin, Y. Machine learning based bearing fault diagnosis using the case western reserve university data: A review. IEEE Access 2021, 9, 155598–155608. [Google Scholar] [CrossRef]
- Zhu, Z.; Lei, Y.; Qi, G.; Chai, Y.; Mazur, N.; An, Y.; Huang, X. A review of the application of deep learning in intelligent fault diagnosis of rotating machinery. Measurement 2023, 206, 112346. [Google Scholar] [CrossRef]
- Hakim, M.; Omran, A.A.B.; Ahmed, A.N.; Al-Waily, M.; Abdellatif, A. A systematic review of rolling bearing fault diagnoses based on deep learning and transfer learning: Taxonomy, overview, application, open challenges, weaknesses and recommendations. Ain Shams Eng. J. 2023, 14, 101945. [Google Scholar] [CrossRef]
- Yang, H.; Li, X.; Zhang, W. Interpretability of deep convolutional neural networks on rolling bearing fault diagnosis. Meas. Sci. Technol. 2022, 33, 055005. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Fu, W.; Jiang, X.; Li, B.; Tan, C.; Chen, B.; Chen, X. Rolling bearing fault diagnosis based on 2D time-frequency images and data augmentation technique. Meas. Sci. Technol. 2023, 34, 045005. [Google Scholar] [CrossRef]
- Wang, H.; Du, W. Multi-source information deep fusion for rolling bearing fault diagnosis based on deep residual convolution neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 7576–7589. [Google Scholar] [CrossRef]
- Neupane, D.; Kim, Y.; Seok, J. Bearing fault detection using scalogram and switchable normalization-based CNN (SN-CNN). IEEE Access 2021, 9, 88151–88166. [Google Scholar] [CrossRef]
- Irfan, M.; Mushtaq, Z.; Khan, N.A.; Mursal, S.N.F.; Rahman, S.; Magzoub, M.A.; Latif, M.A.; Althobiani, F.; Khan, I.; Abbas, G. A Scalo gram-based CNN ensemble method with density-aware smote oversampling for improving bearing fault diagnosis. IEEE Access 2023, 11, 127783–127799. [Google Scholar] [CrossRef]
- Hao, X.; Zheng, Y.; Lu, L.; Pan, H. Research on intelligent fault diagnosis of rolling bearing based on improved deep residual network. Appl. Sci. 2021, 11, 10889. [Google Scholar] [CrossRef]
- Song, X.; Cong, Y.; Song, Y.; Chen, Y.; Liang, P. A bearing fault diagnosis model based on CNN with wide convolution kernels. J. Ambient Intell. Humaniz. Comput. 2022, 13, 4041–4056. [Google Scholar] [CrossRef]
- Plakias, S.; Boutalis, Y.S. Fault detection and identification of rolling element bearings with Attentive Dense CNN. Neurocomputing 2020, 405, 208–217. [Google Scholar] [CrossRef]
- Wang, P.; Chen, J. Fault diagnosis of spent fuel shearing machines based on improved residual network. Ann. Nucl. Energy 2024, 196, 110228. [Google Scholar]
- Chen, Y.; Zhan, W.; Jiang, Y.; Zhu, D.; Guo, R.; Xu, X. DDGAN: Dense Residual Module and Dual-stream Attention-Guided Generative Adversarial Network for colorizing near-infrared images. Infrared Phys. Technol. 2023, 133, 104822. [Google Scholar] [CrossRef]
- Wang, Y.; Zou, Y.; Hu, W.; Chen, J.; Xiao, Z. Intelligent fault diagnosis of hydroelectric units based on radar maps and improved GoogleNet by depthwise separate convolution. Meas. Sci. Technol. 2023, 35, 025103. [Google Scholar] [CrossRef]
- Saghi, T.; Bustan, D.; Aphale, S.S. Bearing fault diagnosis based on multi-scale CNN and bidirectional GRU. Vibration 2022, 6, 11–28. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Y.; Liang, Z.; Shao, H.; Yu, K.; Yu, W. An adaptive domain adaptation method for rolling bearings’ fault diagnosis fusing deep convolution and self-attention networks. IEEE Trans. Instrum. Meas. 2023, 72, 1–14. [Google Scholar] [CrossRef]
- Karnavas, Y.L.; Plakias, S.; Chasiotis, I.D. Extracting spatially global and local attentive features for rolling bearing fault diagnosis in electrical machines using attention stream networks. IET Electr. Power Appl. 2021, 15, 903–915. [Google Scholar] [CrossRef]
- Ren, H.; Liu, S.; Wei, F.; Qiu, B.; Zhao, D. A novel two-stream multi-head self-attention convolutional neural network for bearing fault diagnosis. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2024, 238, 5393–5405. [Google Scholar] [CrossRef]
- Gou, L.; Li, H.; Zheng, H.; Li, H.; Pei, X. Aeroengine control system sensor fault diagnosis based on CWT and CNN. Math. Probl. Eng. 2020, 2020, 5357146. [Google Scholar] [CrossRef]
- Yan, R.; Shang, Z.; Xu, H.; Wen, J.; Zhao, Z.; Chen, X.; Gao, R.X. Wavelet transform for rotary machine fault diagnosis: 10 years revisited. Mech. Syst. Signal Process. 2023, 200, 110545. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Zhou, Y.; Kang, X.; Ren, F.; Lu, H.; Nakagawa, S.; Shan, X. A multi-attention and depthwise separable convolution network for medical image segmentation. Neurocomputing 2024, 564, 126970. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. CCNet: Criss-Cross Attention for Semantic Segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV 2019), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 603–612. [Google Scholar]
- Ma, N.; Zhang, X.; Liu, M.; Sun, J. Activate or not: Learning customized activation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Wei, X.; Zhang, X.; Li, Y. SARN: A lightweight stacked attention residual network for low-light image enhancement. In Proceedings of the 2021 6th International Conference on Robotics and Automation Engineering (ICRAE), Guangzhou, China, 19–22 November 2021. [Google Scholar]
- Case Western Reserve University Bearing Data Center Website. Available online: https://eecs.cwru.edu (accessed on 20 June 2024).
- Lessmeier, C.; Kimotho, J.K.; Zimmer, D.; Sextro, W. Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification. In Proceedings of the PHM Society European Conference, Bilbao, Spain, 5–8 July 2016. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Yang, X.; Sun, S.; Wang, G.; Shi, N.; Xie, Y. Bearing fault diagnosis method based on ECA_ResNet. Bearing 2023. (published online in Chinese). Available online: http://kns.cnki.net/kcms/detail/41.1148.th.20230414.1947.004.html (accessed on 20 June 2024).
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]










| Layer | Convolution Kernel | Input and Output Dimensions | |
|---|---|---|---|
| Input | - | 3 × 64 × 64 | |
| Conv | 16 × 16 | 128 × 55 × 55 | |
| BN Meta-Acon | - | 128 × 55 × 55 | |
| Maxpool | 2 × 2 | 128 × 28 × 28 | |
| Residual block 1 | Criss-cross attention | - | 128 × 28 × 28 |
| DSCconv | 3 × 3 | 128 × 28 × 28 | |
| BN Meta-Acon | - | 128 × 28 × 28 | |
| DSCconv | 3 × 3 | 128 × 28 × 28 | |
| BN | - | 128 × 28 × 28 | |
| Meta-Acon | - | 128 × 28 × 28 | |
| Maxpool | 2 × 2 | 128 × 15 × 15 | |
| Residual block 2 | Criss-cross attention | - | 128 × 15 × 15 |
| DSCconv | 3 × 3 | 128 × 15 × 15 | |
| BN Meta-Acon | - | 128 × 15 × 15 | |
| DSCconv | 3 × 3 | 128 × 15 × 15 | |
| BN | - | 128 × 15 × 15 | |
| Avgpool | - | 128 × 1 × 1 | |
| Fc | - | 256 | |
| Softmax | - | 10 | |
| Load | Fault Type | Fault Diameter/mm | Training/Validation/Test Set | Tags |
|---|---|---|---|---|
| 0/1/2/3 HP | Normal | 0 | 800/100/100 | 0 |
| Inner-ring fault | 0.178 | 800/100/100 | 1 | |
| 0.356 | 800/100/100 | 2 | ||
| 0.533 | 800/100/100 | 3 | ||
| Outer-ring failure | 0.178 | 800/100/100 | 4 | |
| 0.356 | 800/100/100 | 5 | ||
| 0.533 | 800/100/100 | 6 | ||
| Rolling body failure | 0.178 | 800/100/100 | 7 | |
| 0.356 | 800/100/100 | 8 | ||
| 0.533 | 800/100/100 | 9 |
| Fault Type | Tags | Bearing Number | Training/Validation/Test Set |
|---|---|---|---|
| Inner-ring failure | 0 | KI01, KI05, KI07, KI14, KI16, KI17 | 1920/240/240 |
| Outer-ring failure | 1 | KA01, KA05, KA07, KA04, KA15, KA16 | 1920/240/240 |
| Healthy | 2 | K001, K002, K003, K004, K005, K006 | 1920/240/240 |
| Network Model | Mixed-Load Datasets | |||
|---|---|---|---|---|
| Accuracy/% | Precision/% | Recall/% | AUC/% | |
| Basic model | 93.52 | 94.2 | 93.41 | 99.42 |
| Basic model + DSC | 93.7 | 94.51 | 93.6 | 99.42 |
| Basic model + CCA | 95.94 | 95.78 | 95.84 | 99.63 |
| Basic model + DSC + CCA | 99.82 | 96.62 | 96.49 | 96.88 |
| Improved residual network | 99.95 | 96.64 | 96.53 | 99.74 |
| Number of Residual Blocks | Params/M | FLOPs/GF | Accuracy/% |
|---|---|---|---|
| One | 0.38 | 0.45 | 95.32 |
| Two | 0.53 | 0.49 | 99.95 |
| Three | 0.73 | 0.52 | 99.96 |
| Network Method | Params/MB | FLOPs/GF | Accuracy/% |
|---|---|---|---|
| ShuffleNetV2 | 1.26 | 0.23 | 99.26 |
| MobileNetV2 | 2.3 | 0.39 | 99.43 |
| VGG16 | 264 | 4.87 | 98.70 |
| ResNet18 | 22 | 0.69 | 99.78 |
| ResNet50 | 47 | 1.26 | 99.9 |
| Swin-T | 275 | 0.79 | 99.75 |
| ECA_ResNet | 0.78 | 0.62 | 99.75 |
| Our method | 0.53 | 0.49 | 99.95 |
| Network Model | SNR (dB) | |||||
|---|---|---|---|---|---|---|
| −4 | −2 | −0 | 2 | 4 | 8 | |
| ShuffleNetV2 | 55.05 | 79.05 | 94.15 | 97.15 | 98.3 | 98.75 |
| MobileNetV2 | 64.9 | 84 | 96.8 | 98.2 | 98.7 | 99.1 |
| VGG16 | 66.56 | 86 | 95.36 | 96.32 | 97.24 | 97.94 |
| ResNet18 | 64.3 | 86 | 97.7 | 98.5 | 99.2 | 99.36 |
| ResNet50 | 62.3 | 84.5 | 97.4 | 98.4 | 99.5 | 99.65 |
| Swin-T | 74.45 | 85.42 | 97.53 | 98.46 | 99.54 | 99.67 |
| ECA_ResNet | 64.6 | 86.8 | 93.1 | 97.5 | 99.3 | 99.72 |
| Our method | 82.56 | 87.02 | 97.9 | 99.3 | 99.65 | 99.75 |
| Network Model | SNR (dB)% | ||||||
|---|---|---|---|---|---|---|---|
| −4 | −2 | 0 | 2 | 4 | 8 | None | |
| ShuffleNetV2 | 72.4 | 76.2 | 83.7 | 87.5 | 83.3 | 87.5 | 90.6 |
| MobileNet V2 | 66.8 | 70 | 77.9 | 70.1 | 80.7 | 83.7 | 93.6 |
| VGG16 | 71.6 | 69.4 | 78.1 | 84 | 79.8 | 86.1 | 91.6 |
| ResNet18 | 70.5 | 73.3 | 82.2 | 74.8 | 69.6 | 75.3 | 89.1 |
| ResNet50 | 73.5 | 71.8 | 78.5 | 73.3 | 76.1 | 73.7 | 89.4 |
| Swin-T | 71.7 | 72.6 | 75.2 | 79.4 | 81.8 | 83.6 | 92.3 |
| ECA_ResNet | 73 | 76.4 | 80.6 | 82.9 | 79.7 | 87.5 | 92.2 |
| Our method | 73.8 | 78.8 | 83.7 | 88 | 87.2 | 93.5 | 95.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, L.; Pang, C.; Wang, G.; Shi, N. Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network. Electronics 2024, 13, 3749. https://doi.org/10.3390/electronics13183749
Gong L, Pang C, Wang G, Shi N. Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network. Electronics. 2024; 13(18):3749. https://doi.org/10.3390/electronics13183749
Chicago/Turabian StyleGong, Lei, Chongwen Pang, Guoqiang Wang, and Nianfeng Shi. 2024. "Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network" Electronics 13, no. 18: 3749. https://doi.org/10.3390/electronics13183749
APA StyleGong, L., Pang, C., Wang, G., & Shi, N. (2024). Lightweight Bearing Fault Diagnosis Method Based on Improved Residual Network. Electronics, 13(18), 3749. https://doi.org/10.3390/electronics13183749







