Forecasting Flower Prices by Long Short-Term Memory Model with Optuna
Abstract
1. Introduction
2. Long Short-Term Memory and the Optuna Framework
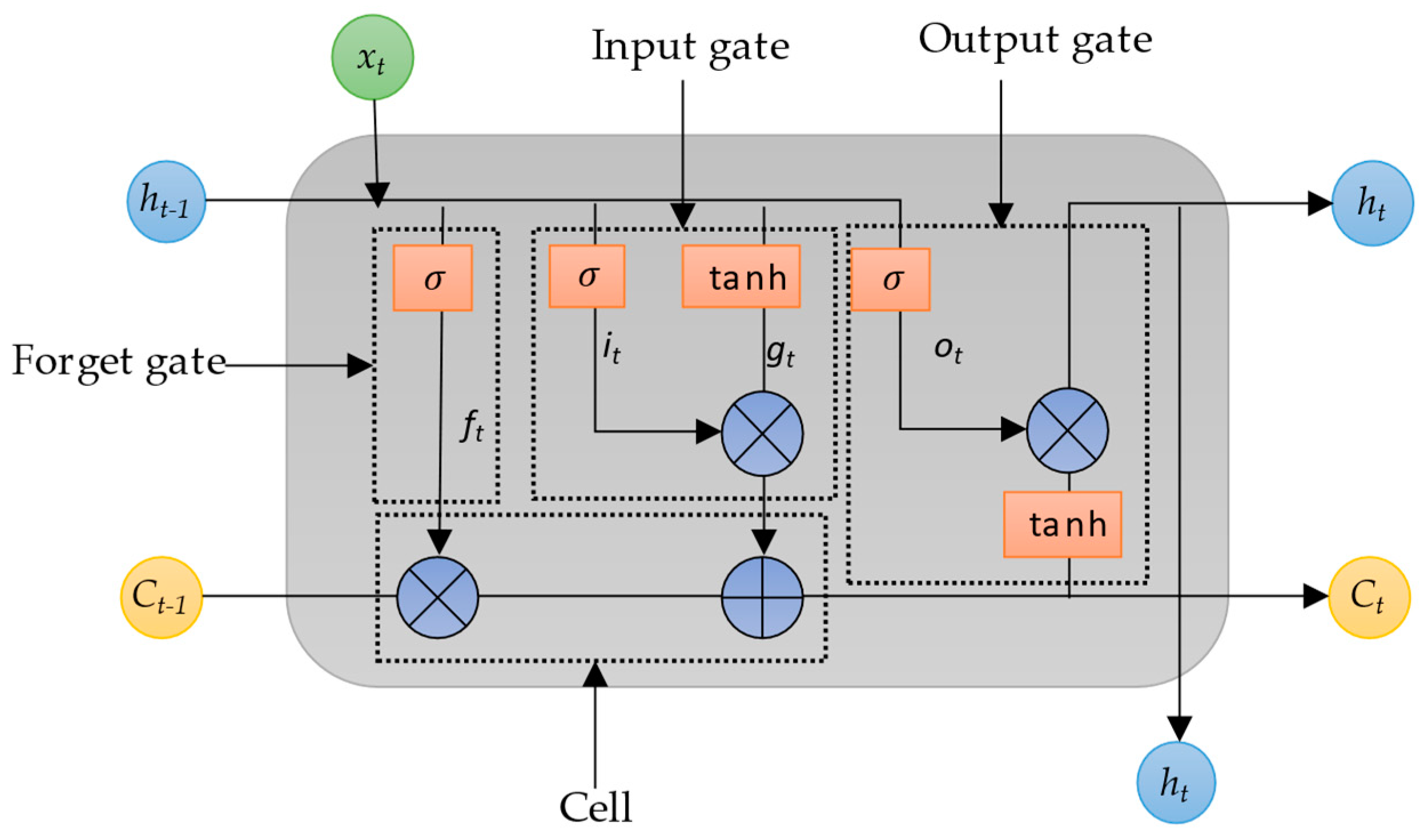
2.1. Long Short-Term Memory
2.2. The Optuna Framework
3. The Proposed MMLSTMOPT Model for Forecasting Daily Oriental Lily Prices
3.1. Data Collection and Preprocessing
3.2. The Many-to-Many LSTM Model
3.3. The Determination of Hyperparameters by Optuna for MMLSTMOPT Models
4. Numerical Results and Discussion
4.1. Numerical Results
4.2. A Hypothetical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Days | MMLSTMOPT Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasting | 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | Average | |
| Modeling | |||||||||
| 7 days | 265.22 | 386.76 | 603.58 | 666.99 | 834.12 | 930.54 | 1119.13 | 686.62 | |
| 14 days | 271.65 | 482.66 | 569.20 | 822.44 | 759.93 | 825.22 | 1110.45 | 691.65 | |
| 21 days | 273.87 | 374.01 | 534.72 | 721.81 | 747.38 | 731.37 | 1056.37 | 634.22 | |
| 28 days | 268.82 | 464.83 | 558.35 | 601.81 | 958.67 | 851.45 | 1176.40 | 697.19 | |
| Days | MMLSTMOPT Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasting | 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | Average | |
| Modeling | |||||||||
| 7 days | 11.87 | 14.33 | 17.72 | 18.78 | 20.96 | 23.49 | 24.32 | 18.78 | |
| 14 days | 11.97 | 16.20 | 17.65 | 21.10 | 20.31 | 22.89 | 24.31 | 19.21 | |
| 21 days | 12.03 | 13.91 | 16.91 | 19.54 | 19.69 | 19.72 | 23.40 | 17.89 | |
| 28 days | 12.00 | 16.08 | 17.28 | 18.33 | 22.86 | 20.99 | 24.10 | 18.81 | |
| Days | MMLSTMOPT Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasting | 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | Average | |
| Modeling | |||||||||
| 7 days | 16.29 | 19.67 | 24.57 | 25.83 | 28.88 | 30.50 | 33.45 | 25.60 | |
| 14 days | 16.48 | 21.97 | 23.86 | 28.68 | 27.57 | 28.73 | 33.32 | 25.80 | |
| 21 days | 16.55 | 19.34 | 23.12 | 26.87 | 27.34 | 27.04 | 32.50 | 24.68 | |
| 28 days | 16.40 | 21.56 | 23.63 | 24.53 | 30.96 | 29.18 | 34.30 | 25.79 | |
| Days | MMLSTMOPT Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasting | 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | Average | |
| Modeling | |||||||||
| 7 days | 0.84 | 0.77 | 0.65 | 0.61 | 0.51 | 0.45 | 0.35 | 0.60 | |
| 14 days | 0.84 | 0.72 | 0.67 | 0.52 | 0.56 | 0.52 | 0.36 | 0.60 | |
| 21 days | 0.84 | 0.78 | 0.69 | 0.58 | 0.56 | 0.58 | 0.39 | 0.63 | |
| 28 days | 0.84 | 0.72 | 0.67 | 0.64 | 0.44 | 0.50 | 0.31 | 0.59 | |
References
- Sun, F.; Meng, X.; Zhang, Y.; Wang, Y.; Jiang, H.; Liu, P. Agricultural product price forecasting methods: A review. Agriculture 2023, 13, 1671. [Google Scholar] [CrossRef]
- Wang, L.; Feng, J.; Sui, X.; Chu, X.; Mu, W. Agricultural product price forecasting methods: Research advances and trend. Br. Food J. 2020, 122, 2121–2138. [Google Scholar] [CrossRef]
- Pinheiro, C.A.O.; Senna, V.d. Multivariate analysis and neural networks application to price forecasting in the Brazilian agricultural market. Ciência Rural 2017, 47, e20160077. [Google Scholar] [CrossRef]
- Zhang, D.; Zang, G.; Li, J.; Ma, K.; Liu, H. Prediction of soybean price in China using qr-rbf neural network model. Comput. Electron. Agric. 2018, 154, 10–17. [Google Scholar] [CrossRef]
- Fan, J.; Liu, H.; Hu, Y. Soybean future prices forecasting based on lstm deep learning. Prices Mon 2021, 2. [Google Scholar] [CrossRef]
- Li, J.; Li, G.; Liu, M.; Zhu, X.; Wei, L. A novel text-based framework for forecasting agricultural futures using massive online news headlines. Int. J. Forecast. 2022, 38, 35–50. [Google Scholar] [CrossRef]
- An, W.; Wang, L.; Zeng, Y.R. Text-based soybean futures price forecasting: A two-stage deep learning approach. J. Forecast. 2023, 42, 312–330. [Google Scholar] [CrossRef]
- Cheung, L.; Wang, Y.; Lau, A.S.; Chan, R.M. Using a novel clustered 3d-cnn model for improving crop future price prediction. Knowl.-Based Syst. 2023, 260, 110133. [Google Scholar] [CrossRef]
- Cao, S.; He, Y. Wavelet decomposition-based svm-arima price forecasting model for agricultural products. Stat. Decis. 2015, 92–95. [Google Scholar] [CrossRef]
- Xu, K. Short-Term Price Forecast Model for Fresh Agricultrual Products Based on Price Decomposition. Ph.D. Thesis, Chinese Academy of Agricultural Sciences, Beijing, China, 2016. [Google Scholar]
- Ye, L.; Qin, X.; Li, Y.; Liu, Y.; Liang, W. Vegetables price forecasting in hainan province based on linear and nonlinear combination model. In Proceedings of the 13th International Conference on Service Systems and Service Management (ICSSSM), Kunming, China, 24–26 June 2016; IEEE: Piscatawa, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Xiong, T.; Li, C.; Bao, Y. Seasonal forecasting of agricultural commodity price using a hybrid stl and elm method: Evidence from the vegetable market in China. Neurocomputing 2018, 275, 2831–2844. [Google Scholar] [CrossRef]
- Yin, H.; Jin, D.; Gu, Y.H.; Park, C.J.; Han, S.K.; Yoo, S.J. Stl-attlstm: Vegetable price forecasting using stl and attention mechanism-based lstm. Agriculture 2020, 10, 612. [Google Scholar] [CrossRef]
- Li, Z.; Xu, S.; Cui, L.; Zhang, J. Prediction study based on dynamic chaotic neural network—Taking potato time-series prices as an example. Syst. Eng.-Theory Pract. 2015, 35, 2083–2091. [Google Scholar]
- Li, Z.M.; Xu, S.W.; Cui, L.G.; Li, G.Q.; Dong, X.X.; Wu, J.Z. The short-term forecast model of pork price based on cnn-ga. Adv. Mater. Res. 2013, 628, 350–358. [Google Scholar] [CrossRef]
- Niu, C. Integration Prediction Method Research of Agricultural Products Market Price. Master’s Thesis, Central China Normal University, Wuhan, China, 2016. [Google Scholar]
- Li, Z.-M.; Cui, L.-G.; Xu, S.-W.; Weng, L.-y.; Dong, X.-x.; Li, G.-Q.; Yu, H.-P. Prediction model of weekly retail price for eggs based on chaotic neural network. J. Integr. Agric. 2013, 12, 2292–2299. [Google Scholar] [CrossRef]
- Gao, Y.; An, S. Comparative study on the predictive effect of the price of eggs in China—Comparative analysis based on bp neural network model and egg futures predictive model. Price Theory Pr. 2021, 4, 441. [Google Scholar]
- Wang, B.; Liu, P.; Chao, Z.; Junmei, W.; Chen, W.; Cao, N.; O’Hare, G.M.; Wen, F. Research on hybrid model of garlic short-term price forecasting based on big data. Comput. Mater. Contin. 2018, 57, 283–296. [Google Scholar] [CrossRef]
- Guo, Y.; Tang, D.; Tang, W.; Yang, S.; Tang, Q.; Feng, Y.; Zhang, F. Agricultural price prediction based on combined forecasting model under spatial-temporal influencing factors. Sustainability 2022, 14, 10483. [Google Scholar] [CrossRef]
- Xu, Y.; Wei, Y.; Li, X. Establishment of agricultural products, price prediction. Stat. Decis. 2017, 12, 75–77. [Google Scholar]
- Yu, X.H. Acquisition Price Forecast of Yantai Apple Based on bp Neural Network. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Xie, J.Q. Research on Price Forecasting of Gannan Navel Based on bp Neural Network. Master’s Thesis, Huazhong Agricultural University, Wuhan, China, 2017. [Google Scholar]
- Polyiam, K.; Boonrawd, P. A hybrid forecasting model of cassava price based on artificial neural network with support vector machine technique. In Proceedings of the 3rd International Conference on Information Management (ICIM), Chengdu, China, 21–23 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 123–127. [Google Scholar]
- Zhang, M.; Huang, X.; Yang, C. A sales forecasting model for the consumer goods with holiday effects. J. Risk Anal. Crisis Response 2020, 10, 69–76. [Google Scholar] [CrossRef]
- Laibuni, N.; Waiyaki, N.; Ndirangu, L.; Omiti, J. Kenyan cut-flower and foliage exports: A cross country analysis. J. Dev. Agric. Econ. 2012, 4, 37–44. [Google Scholar]
- Zhao, S.; Yue, C.; Meyer, M.H.; Hall, C.R. Factors affecting us consumer expenditures of fresh flowers and potted plants. HortTechnology 2016, 26, 484–492. [Google Scholar] [CrossRef]
- Kathayat, B.; Dixit, A.K. Paddy price forecasting in india using arima model. J. Crop Weed 2021, 17, 48–55. [Google Scholar] [CrossRef]
- Mahmoud Sayed Agbo, H. Forecasting agricultural price volatility of some export crops in egypt using arima/garch model. Rev. Econ. Political Sci. 2023, 8, 123–133. [Google Scholar] [CrossRef]
- Zhao, H. Futures price prediction of agricultural products based on machine learning. Neural Comput. Appl. 2021, 33, 837–850. [Google Scholar] [CrossRef]
- Yuan, C.Z.; Ling, S.K. Long short-Term Memory Model Based Agriculture Commodity Price Prediction Application. In Proceedings of the 2nd International Conference on Information Technology and Computer Communications, Online, 12–14 August 2020; pp. 43–49. [Google Scholar]
- Purohit, S.K.; Panigrahi, S.; Sethy, P.K.; Behera, S.K. Time series forecasting of price of agricultural products using hybrid methods. Appl. Artif. Intell. 2021, 35, 1388–1406. [Google Scholar] [CrossRef]
- Nassar, L.; Okwuchi, I.E.; Saad, M.; Karray, F.; Ponnambalam, K. Deep Learning Based Approach for Fresh Produce Market Price Prediction. In Proceedings of the International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Harshith, N.; Kumari, P. Memory based neural network for cumin price forecasting in Gujarat, India. J. Agric. Food Res. 2024, 15, 101020. [Google Scholar] [CrossRef]
- Zhang, T.; Tang, Z. Agricultural commodity futures prices prediction based on a new hybrid forecasting model combining quadratic decomposition technology and lstm model. Front. Sustain. Food Syst. 2024, 8, 1334098. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, W.; Zhao, A.; Wang, X.; Wang, Z.; Zhang, L. Short-term forecasting of vegetable prices based on lstm model—Evidence from Beijing’s vegetable data. PLoS ONE 2024, 19, e0304881. [Google Scholar] [CrossRef]
- Kang, J.; Xu, N.; Li, X. Banana price prediction based on chaotic particle swarm lstm. In Proceedings of the 2024 International Conference on Computer and Multimedia Technology, Sanming, China, 24–26 May 2024; pp. 540–546. [Google Scholar]
- Rana, H.; Farooq, M.U.; Kazi, A.K.; Baig, M.A.; Akhtar, M.A. Prediction of agricultural commodity prices using big data framework. Eng. Technol. Appl. Sci. Res. 2024, 14, 12652–12658. [Google Scholar] [CrossRef]
- Jaiswal, R.; Jha, G.K.; Kumar, R.R.; Choudhary, K. Deep long short-term memory based model for agricultural price forecasting. Neural Comput. Appl. 2022, 34, 4661–4676. [Google Scholar] [CrossRef]
- Chen, C.-H. Using lstm Model with Optuna for Predicting Flower Wholesale Prices. Ph.D. Thesis, National Chi Nan University, Puli Township, Taiwan, 2024, (unpublished doctoral dissertation). [Google Scholar]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference On Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Fang, W.; Chen, Y.; Xue, Q. Survey on research of rnn-based spatio-temporal sequence prediction algorithms. J. Big Data 2021, 3, 97. [Google Scholar] [CrossRef]
- Alom, M.Z.; Taha, T.M.; Yakopcic, C.; Westberg, S.; Sidike, P.; Nasrin, M.S.; Hasan, M.; Van Essen, B.C.; Awwal, A.A.; Asari, V.K. A state-of-the-art survey on deep learning theory and architectures. Electronics 2019, 8, 292. [Google Scholar] [CrossRef]
- Lindemann, B.; Müller, T.; Vietz, H.; Jazdi, N.; Weyrich, M. A survey on long short-term memory networks for time series prediction. Procedia CIRP 2021, 99, 650–655. [Google Scholar] [CrossRef]
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for hyper-parameter optimization. In Proceedings of the Advances in Neural Information Processing Systems 24 (NIPS 2011), Granada, Spain, 12–14 December 2011. [Google Scholar]
- Niu, Q.; Wang, Z.; Li, H.; Zhao, J. A parameters optimization framework for pose estimation algorithm based on point cloud. J. Phys. Conf. Ser. 2024, 2746, 012039. [Google Scholar] [CrossRef]
- Jeba, J.A. Case Study of Hyperparameter Optimization Framework Optuna on a Multi-Column Convolutional Neural Network. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2021. [Google Scholar]
- Chen, C.-H.; Lai, J.-P.; Chang, Y.-M.; Lai, C.-J.; Pai, P.-F. A study of optimization in deep neural networks for regression. Electronics 2023, 12, 3071. [Google Scholar] [CrossRef]
- Shin, D.-H.; Chung, K.; Park, R.C. Prediction of traffic congestion based on lstm through correction of missing temporal and spatial data. IEEE Access 2020, 8, 150784–150796. [Google Scholar] [CrossRef]
- Lu, X.; Yuan, L.; Li, R.; Xing, Z.; Yao, N.; Yu, Y. An improved bi-lstm-based missing value imputation approach for pregnancy examination data. Algorithms 2022, 16, 12. [Google Scholar] [CrossRef]
- Yan, J.; Gao, Y.; Yu, Y.; Xu, H.; Xu, Z. A prediction model based on deep belief network and least squares svr applied to cross-section water quality. Water 2020, 12, 1929. [Google Scholar] [CrossRef]
- Shao, B.; Song, D.; Bian, G.; Zhao, Y. Wind speed forecast based on the lstm neural network optimized by the firework algorithm. Adv. Mater. Sci. Eng. 2021, 2021, 4874757. [Google Scholar] [CrossRef]
- Shao, B.; Song, D.; Bian, G.; Zhao, Y. A hybrid approach by ceemdan-improved pso-lstm model for network traffic prediction. Secur. Commun. Netw. 2022, 2022, 4975288. [Google Scholar] [CrossRef]
- Liguori, A.; Markovic, R.; Ferrando, M.; Frisch, J.; Causone, F.; van Treeck, C. Augmenting energy time-series for data-efficient imputation of missing values. Appl. Energy 2023, 334, 120701. [Google Scholar] [CrossRef]
- Yin, X.; Liu, Q.; Huang, X.; Pan, Y. Real-time prediction of rockburst intensity using an integrated cnn-adam-bo algorithm based on microseismic data and its engineering application. Tunn. Undergr. Space Technol. 2021, 117, 104133. [Google Scholar] [CrossRef]
- Zhang, Y. Short-term power load forecasting based on sapso-cnn-lstm model considering autocorrelated errors. Math. Probl. Eng. 2022, 2022, 2871889. [Google Scholar] [CrossRef]
- Zhao, A.; Mi, L.; Xue, X.; Xi, J.; Jiao, Y. Heating load prediction of residential district using hybrid model based on cnn. Energy Build. 2022, 266, 112122. [Google Scholar] [CrossRef]
- Rao, A.R.; Reimherr, M. Modern non-linear function-on-function regression. Stat. Comput. 2023, 33, 130. [Google Scholar] [CrossRef]
- Karijadi, I.; Chou, S.-Y.; Dewabharata, A. Wind power forecasting based on hybrid ceemdan-ewt deep learning method. Renew. Energy 2023, 218, 119357. [Google Scholar] [CrossRef]
- He, Q.-Q.; Wu, C.; Si, Y.-W. Lstm with particle swam optimization for sales forecasting. Electron. Commer. Res. Appl. 2022, 51, 101118. [Google Scholar] [CrossRef]
- Gupta, M.; Kumar, P. Robust neural language translation model formulation using seq2seq approach. Fusion Pract. Appl. 2021, 5, 61–67. [Google Scholar] [CrossRef]
- Bhandari, H.N.; Rimal, B.; Pokhrel, N.R.; Rimal, R.; Dahal, K.R.; Khatri, R.K. Predicting stock market index using lstm. Mach. Learn. Appl. 2022, 9, 100320. [Google Scholar] [CrossRef]
- Gong, G.; An, X.; Mahato, N.K.; Sun, S.; Chen, S.; Wen, Y. Research on short-term load prediction based on seq2seq model. Energies 2019, 12, 3199. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination r-squared is more informative than smape, mae, mape, mse and rmse in regression analysis evaluation. Peerj Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef] [PubMed]
- Namoun, A.; Hussein, B.R.; Tufail, A.; Alrehaili, A.; Syed, T.A.; BenRhouma, O. An ensemble learning based classification approach for the prediction of household solid waste generation. Sensors 2022, 22, 3506. [Google Scholar] [CrossRef] [PubMed]
- Govindarajan, P.; Venkatanathan, N. Towards real-time earthquake forecasting in Chile: Integrating intelligent technologies and machine learning. Comput. Electr. Eng. 2024, 117, 109285. [Google Scholar]
- Dong, S.; Wang, P.; Abbas, K. A survey on deep learning and its applications. Comput. Sci. Rev. 2021, 40, 100379. [Google Scholar] [CrossRef]
- Anh, D.T.; Thanh, D.V.; Le, H.M.; Sy, B.T.; Tanim, A.H.; Pham, Q.B.; Dang, T.D.; Mai, S.T.; Dang, N.M. Effect of gradient descent optimizers and dropout technique on deep learning lstm performance in rainfall-runoff modeling. Water Resour. Manag. 2023, 37, 639–657. [Google Scholar] [CrossRef]
- Kothona, D.; Panapakidis, I.P.; Christoforidis, G.C. A novel hybrid ensemble lstm-ffnn forecasting model for very short-term and short-term pv generation forecasting. IET Renew. Power Gener. 2022, 16, 3–18. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control; John Wiley & Sons: New York, NY, USA, 2015. [Google Scholar]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Cheng, J.; Tiwari, S.; Khaled, D.; Mahendru, M.; Shahzad, U. Forecasting bitcoin prices using artificial intelligence: Combination of ml, sarima, and facebook prophet models. Technol. Forecast. Soc. Chang. 2024, 198, 122938. [Google Scholar] [CrossRef]
- Sunki, A.; SatyaKumar, C.; Narayana, G.S.; Koppera, V.; Hakeem, M. Time series forecasting of stock market using arima, lstm and fb prophet. In Proceedings of the MATEC Web of Conferences, Kuala Lumpur, Malaysia, 6–8 November 2024; EDP Sciences: Les Ulis, France, 2024; p. 01163. [Google Scholar]






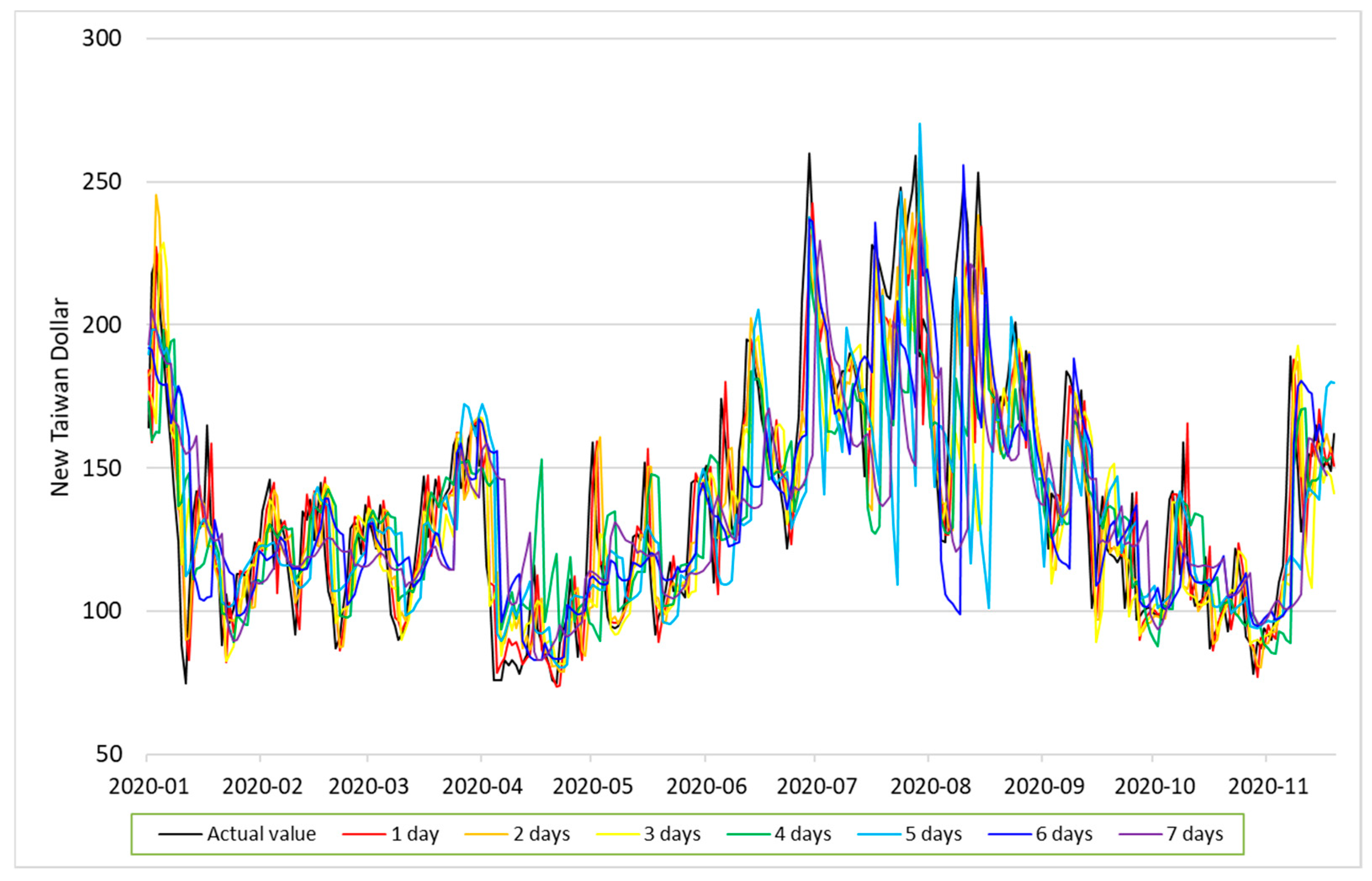

| Models | MSE | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|
| MMLSTMOPT_21 days_AVG | 634.22 | 17.89 | 24.68 | 12.70% | 0.63 |
| MMLSTM_21 days_AVG | 700.07 | 18.56 | 25.94 | 13.21% | 0.59 |
| ARIMA (3, 1, 1) | 1742.61 | 34.24 | 41.74 | 26.97% | −0.02 |
| Prophet | 2618.27 | 42.41 | 51.17 | 35.99% | −0.54 |
| (a) | ||
| Hyperparameters | Types | Hyperparameters Ranges of the MMLSTM Model |
| Optimizer | Categorical data | [Adam, Adagrad, RMSprop] |
| The number of the first-layer MMLSTM neurons | Integer | [20, 40, …, 1180, 1200] |
| The number of the second-layer MMLSTM neurons | Integer | [20, 40, …, 1180, 1200] |
| The number of the fully connected-layer neurons | Integer | [20, 40, …, 1180, 1200] |
| The loss function | Categorical data | [MSE, MAE] |
| The number of epochs | Integer | [100, 150, …, 950, 1000] |
| The batch size | Integer | [16, 32, 64, 128, 256, 512] |
| The learning rate | Real number | [1 × 10−5, 8 × 10−1] |
| (b) | ||
| Hyperparameters | Hyperparameters Set for the MMLSTM Model | |
| Optimizer | Adam | |
| The number of the first-layer MMLSTM neurons | 100 | |
| The number of the second-layer MMLSTM neurons | 100 | |
| The number of the fully connected-layer neurons | 60 | |
| The loss function | MAE | |
| The number of epochs | 300 | |
| The batch size | 64 | |
| The learning rate | 0.001 | |
| Models | Hyperparameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Modeling Days | Forecasting Days | Optimizer | * 1st-Layer Neurons | * 2nd-Layer Neurons | * F-Layer Neurons | Loss Function | Epoch | Batch Size | Learning Rate |
| 7 | 1 | Adagrad | 340 | 720 | 1120 | MAE | 500 | 128 | 0.5093 |
| 7 | 2 | Adagrad | 920 | 260 | 160 | MAE | 900 | 512 | 0.4453 |
| 7 | 3 | Adagrad | 20 | 1140 | 360 | MAE | 950 | 32 | 0.4616 |
| 7 | 4 | Adagrad | 20 | 140 | 520 | MAE | 1000 | 64 | 0.4910 |
| 7 | 5 | Adagrad | 20 | 20 | 40 | MAE | 1000 | 512 | 0.1977 |
| 7 | 6 | Adagrad | 840 | 760 | 20 | MAE | 950 | 512 | 0.2097 |
| 7 | 7 | Adagrad | 440 | 440 | 220 | MAE | 650 | 32 | 0.3802 |
| 14 | 1 | Adagrad | 20 | 860 | 140 | MSE | 700 | 512 | 0.0997 |
| 14 | 2 | Adagrad | 960 | 440 | 920 | MAE | 700 | 64 | 0.2849 |
| 14 | 3 | Adagrad | 820 | 20 | 180 | MAE | 800 | 128 | 0.4768 |
| 14 | 4 | Adagrad | 1040 | 920 | 640 | MAE | 950 | 32 | 0.3546 |
| 14 | 5 | Adagrad | 20 | 20 | 100 | MAE | 1000 | 64 | 0.4707 |
| 14 | 6 | Adagrad | 200 | 780 | 20 | MSE | 900 | 128 | 0.2532 |
| 14 | 7 | Adagrad | 20 | 620 | 680 | MSE | 900 | 64 | 0.1168 |
| 21 | 1 | Adagrad | 20 | 540 | 60 | MSE | 1000 | 128 | 0.4091 |
| 21 | 2 | Adagrad | 20 | 660 | 20 | MAE | 850 | 512 | 0.2345 |
| 21 | 3 | Adagrad | 20 | 180 | 1200 | MAE | 850 | 32 | 0.4991 |
| 21 | 4 | Adagrad | 520 | 880 | 20 | MAE | 1000 | 256 | 0.2879 |
| 21 | 5 | Adagrad | 280 | 120 | 60 | MAE | 1000 | 512 | 0.4004 |
| 21 | 6 | Adagrad | 80 | 20 | 300 | MAE | 950 | 32 | 0.4886 |
| 21 | 7 | Adagrad | 40 | 220 | 80 | MAE | 850 | 128 | 0.2753 |
| 28 | 1 | Adagrad | 60 | 340 | 80 | MAE | 1000 | 128 | 0.5358 |
| 28 | 2 | Adagrad | 420 | 720 | 160 | MAE | 1000 | 128 | 0.1456 |
| 28 | 3 | Adagrad | 640 | 380 | 120 | MAE | 950 | 32 | 0.4887 |
| 28 | 4 | Adagrad | 660 | 120 | 40 | MAE | 900 | 256 | 0.3457 |
| 28 | 5 | Adagrad | 20 | 340 | 840 | MAE | 600 | 16 | 0.3480 |
| 28 | 6 | Adagrad | 20 | 960 | 320 | MAE | 1000 | 256 | 0.4906 |
| 28 | 7 | Adagrad | 620 | 60 | 240 | MAE | 400 | 512 | 0.3801 |
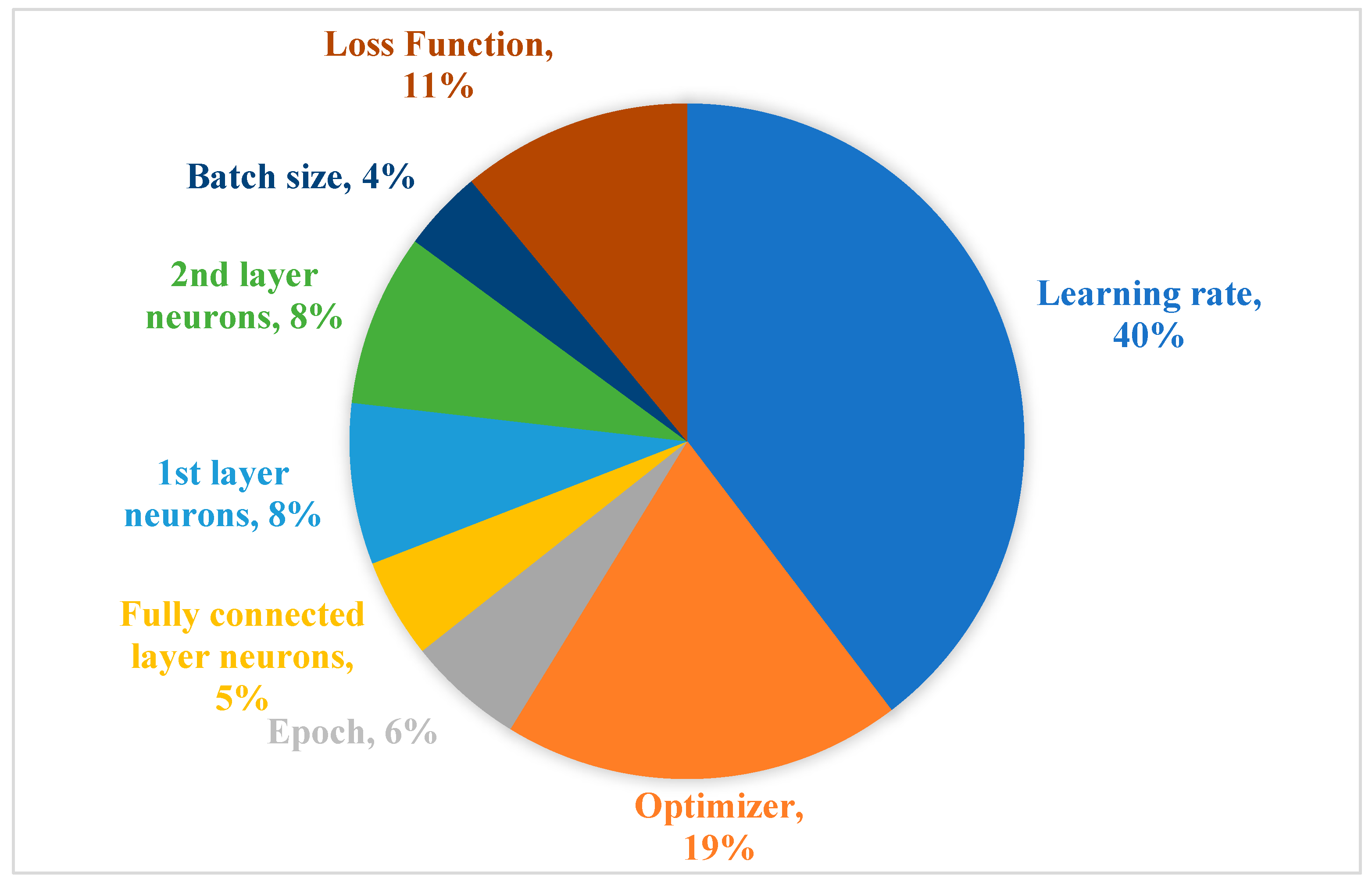
| Models | The Importance of Hyperparameters | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Modeling Days | Forecasting Days | Learning Rate | Optimizer | Epoch | F-Layer Neurons | 1st-Layer Neurons | 2nd-Layer Neurons | Batch Size | Loss Function |
| 7 | 1 | 0.2179 | 0.7126 | 0.0050 | 0.0071 | 0.0041 | 0.0133 | 0.0065 | 0.0334 |
| 7 | 2 | 0.3282 | 0.2519 | 0.0073 | 0.0048 | 0.0167 | 0.1906 | 0.0233 | 0.1772 |
| 7 | 3 | 0.1453 | 0.1687 | 0.0478 | 0.2252 | 0.0181 | 0.0727 | 0.0721 | 0.2500 |
| 7 | 4 | 0.1299 | 0.0273 | 0.0039 | 0.0679 | 0.0074 | 0.0098 | 0.2395 | 0.5143 |
| 7 | 5 | 0.6443 | 0.2756 | 0.0075 | 0.0262 | 0.0192 | 0.0070 | 0.0037 | 0.0165 |
| 7 | 6 | 0.3718 | 0.0472 | 0.0390 | 0.0602 | 0.4340 | 0.0055 | 0.0074 | 0.0350 |
| 7 | 7 | 0.3582 | 0.1082 | 0.0083 | 0.0272 | 0.0184 | 0.0260 | 0.0577 | 0.3960 |
| 14 | 1 | 0.5735 | 0.3408 | 0.0334 | 0.0067 | 0.0025 | 0.0179 | 0.0072 | 0.0178 |
| 14 | 2 | 0.6158 | 0.3368 | 0.0140 | 0.0163 | 0.0027 | 0.0074 | 0.0030 | 0.0041 |
| 14 | 3 | 0.8039 | 0.0817 | 0.0005 | 0.0412 | 0.0019 | 0.0167 | 0.0004 | 0.0538 |
| 14 | 4 | 0.1011 | 0.0307 | 0.0405 | 0.0127 | 0.0753 | 0.4158 | 0.0752 | 0.2486 |
| 14 | 5 | 0.4214 | 0.0725 | 0.0607 | 0.0308 | 0.1431 | 0.0181 | 0.0245 | 0.2289 |
| 14 | 6 | 0.8875 | 0.0556 | 0.0029 | 0.0006 | 0.0034 | 0.0013 | 0.0013 | 0.0475 |
| 14 | 7 | 0.6273 | 0.0997 | 0.0948 | 0.0521 | 0.0219 | 0.0083 | 0.0178 | 0.0782 |
| 21 | 1 | 0.0854 | 0.5558 | 0.0224 | 0.0242 | 0.1644 | 0.0788 | 0.0689 | 0.0001 |
| 21 | 2 | 0.5826 | 0.2142 | 0.0129 | 0.0765 | 0.0512 | 0.0469 | 0.0053 | 0.0104 |
| 21 | 3 | 0.1389 | 0.0417 | 0.0251 | 0.0715 | 0.3400 | 0.0969 | 0.0620 | 0.2240 |
| 21 | 4 | 0.4684 | 0.2145 | 0.1287 | 0.0050 | 0.0157 | 0.1079 | 0.0117 | 0.0479 |
| 21 | 5 | 0.1612 | 0.2534 | 0.3262 | 0.1636 | 0.0328 | 0.0124 | 0.0171 | 0.0333 |
| 21 | 6 | 0.1936 | 0.0381 | 0.1178 | 0.0323 | 0.0120 | 0.4974 | 0.0097 | 0.0990 |
| 21 | 7 | 0.4947 | 0.0496 | 0.0309 | 0.0028 | 0.0087 | 0.3620 | 0.0393 | 0.0119 |
| 28 | 1 | 0.2147 | 0.3889 | 0.0494 | 0.1336 | 0.0392 | 0.0293 | 0.1443 | 0.0006 |
| 28 | 2 | 0.5198 | 0.2372 | 0.0622 | 0.0060 | 0.1013 | 0.0059 | 0.0054 | 0.0622 |
| 28 | 3 | 0.5490 | 0.0444 | 0.0892 | 0.1137 | 0.0289 | 0.0586 | 0.0656 | 0.0507 |
| 28 | 4 | 0.2548 | 0.2517 | 0.0185 | 0.0233 | 0.2451 | 0.0078 | 0.0186 | 0.1801 |
| 28 | 5 | 0.4404 | 0.1163 | 0.1687 | 0.0492 | 0.0805 | 0.1098 | 0.0055 | 0.0296 |
| 28 | 6 | 0.3412 | 0.1094 | 0.0883 | 0.0210 | 0.1542 | 0.0852 | 0.0836 | 0.1172 |
| 28 | 7 | 0.4303 | 0.2320 | 0.0546 | 0.0319 | 0.1170 | 0.0061 | 0.0127 | 0.1155 |
| Days | MMLSTMOPT Models | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Forecasting | 1 Day | 2 Days | 3 Days | 4 Days | 5 Days | 6 Days | 7 Days | Average | |
| Modeling | |||||||||
| 7 days | 8.55 | 10.38 | 12.70 | 13.29 | 14.83 | 16.56 | 16.58 | 13.27 | |
| 14 days | 8.56 | 11.39 | 12.82 | 14.74 | 14.51 | 16.68 | 16.77 | 13.64 | |
| 21 days | 8.64 | 10.13 | 11.83 | 13.88 | 13.57 | 14.71 | 16.11 | 12.70 | |
| 28 days | 8.69 | 11.53 | 12.49 | 13.69 | 16.19 | 14.94 | 16.75 | 13.47 | |
| Model | MSE | MAE | RMSE | MAPE | R2 |
|---|---|---|---|---|---|
| ARIMA (3, 1, 1) | 1742.61 | 34.24 | 41.74 | 26.97% | −0.02 |
| Prophet | 2618.27 | 42.41 | 51.17 | 35.99% | −0.54 |
| No | Date | Actual Market Prices (NTD) | Strategy A | Strategy B | ||||
|---|---|---|---|---|---|---|---|---|
| Harvests (Pieces) | Sales A (NTD) | Average Predicted Prices of 1–7 Days (NTD) | Cumulative Quantity (Pieces) | Selling Quantity (Pieces) | Sales B (NTD) | |||
| 1 | 2020/1/22 | 164 | 1000 | 164,000 | 181 | 1000 | 0 | 0 |
| 2 | 2020/1/23 | 218 | 1000 | 218,000 | 182 | 2000 | 0 | 0 |
| 3 | 2020/1/24 | 223 | 1000 | 223,000 | 185 | 3000 | 0 | 0 |
| 4 | 2020/1/25 | 207 | 1000 | 207,000 | 189 | 4000 | 4000 | 828,000 |
| 5 | 2020/1/26 | 190 | 1000 | 190,000 | 188 | 1000 | 1000 | 190,000 |
| 6 | 2020/1/27 | 174 | 1000 | 174,000 | 185 | 1000 | 1000 | 174,000 |
| 7 | 2020/1/28 | 157 | 1000 | 157,000 | 170 | 1000 | 1000 | 157,000 |
| 8 | 2020/1/29 | 141 | 1000 | 141,000 | 169 | 1000 | 1000 | 141,000 |
| 9 | 2020/1/30 | 124 | 1000 | 124,000 | 153 | 1000 | 1000 | 124,000 |
| … | ||||||||
| 93 | 2020/4/23 | 116 | 1000 | 116,000 | 154 | 1000 | 1000 | 116,000 |
| 94 | 2020/4/24 | 108 | 1000 | 108,000 | 143 | 1000 | 1000 | 108,000 |
| 95 | 2020/4/25 | 76 | 1000 | 76,000 | 136 | 1000 | 1000 | 76,000 |
| 96 | 2020/4/26 | 76 | 1000 | 76,000 | 127 | 1000 | 1000 | 76,000 |
| 97 | 2020/4/27 | 76 | 1000 | 76,000 | 100 | 1000 | 1000 | 76,000 |
| 98 | 2020/4/28 | 83 | 1000 | 83,000 | 98 | 1000 | 1000 | 83,000 |
| 99 | 2020/4/29 | 81 | 1000 | 81,000 | 93 | 1000 | 0 | 0 |
| 100 | 2020/4/30 | 83 | 1000 | 83,000 | 94 | 2000 | 2000 | 166,000 |
| Total 100 days | NTD 12,566,000 | NTD 12,926,000 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.-H.; Lin, Y.-L.; Pai, P.-F. Forecasting Flower Prices by Long Short-Term Memory Model with Optuna. Electronics 2024, 13, 3646. https://doi.org/10.3390/electronics13183646
Chen C-H, Lin Y-L, Pai P-F. Forecasting Flower Prices by Long Short-Term Memory Model with Optuna. Electronics. 2024; 13(18):3646. https://doi.org/10.3390/electronics13183646
Chicago/Turabian StyleChen, Chieh-Huang, Ying-Lei Lin, and Ping-Feng Pai. 2024. "Forecasting Flower Prices by Long Short-Term Memory Model with Optuna" Electronics 13, no. 18: 3646. https://doi.org/10.3390/electronics13183646
APA StyleChen, C.-H., Lin, Y.-L., & Pai, P.-F. (2024). Forecasting Flower Prices by Long Short-Term Memory Model with Optuna. Electronics, 13(18), 3646. https://doi.org/10.3390/electronics13183646








