Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine
Abstract
1. Introduction
- (1)
- This paper summarizes the background and research status of wind turbine fault diagnosis and points out the value of support vector machine algorithms in fault diagnosis. The common fault forms of wind turbine are introduced.
- (2)
- Halton sequence initialization, subtraction average optimization strategy, and smooth development variation were added to improve the DBO algorithm—which solved the problems of uneven population distribution and easily fall into the local optimal solution—and proposed an IDBO-SVM fault diagnosis model.
- (3)
- The convergence and performance of IDBO algorithm on 12 standard test functions are evaluated and compared with the DBO algorithm, FTTA, ZOA, SO algorithm, and ARO algorithm.
- (4)
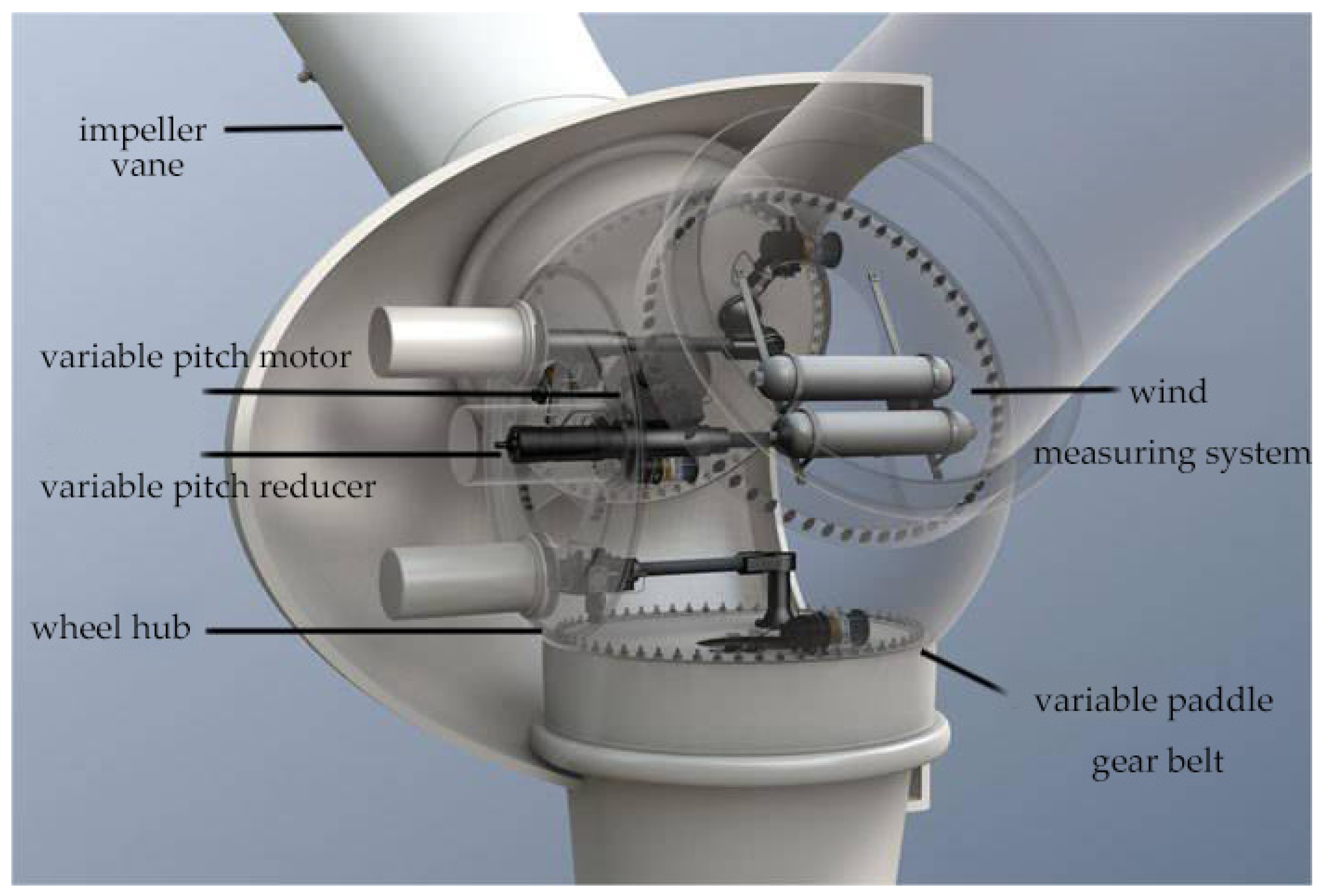
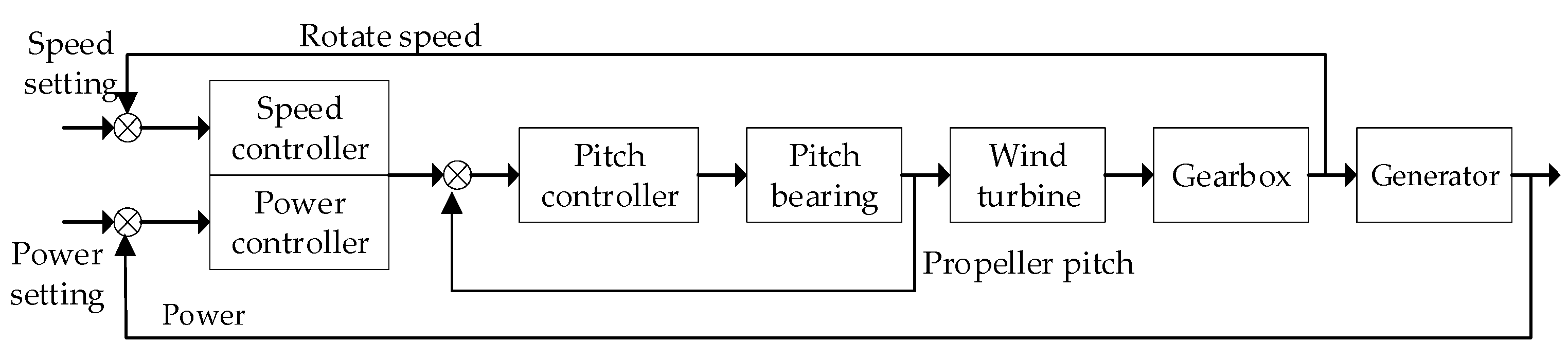
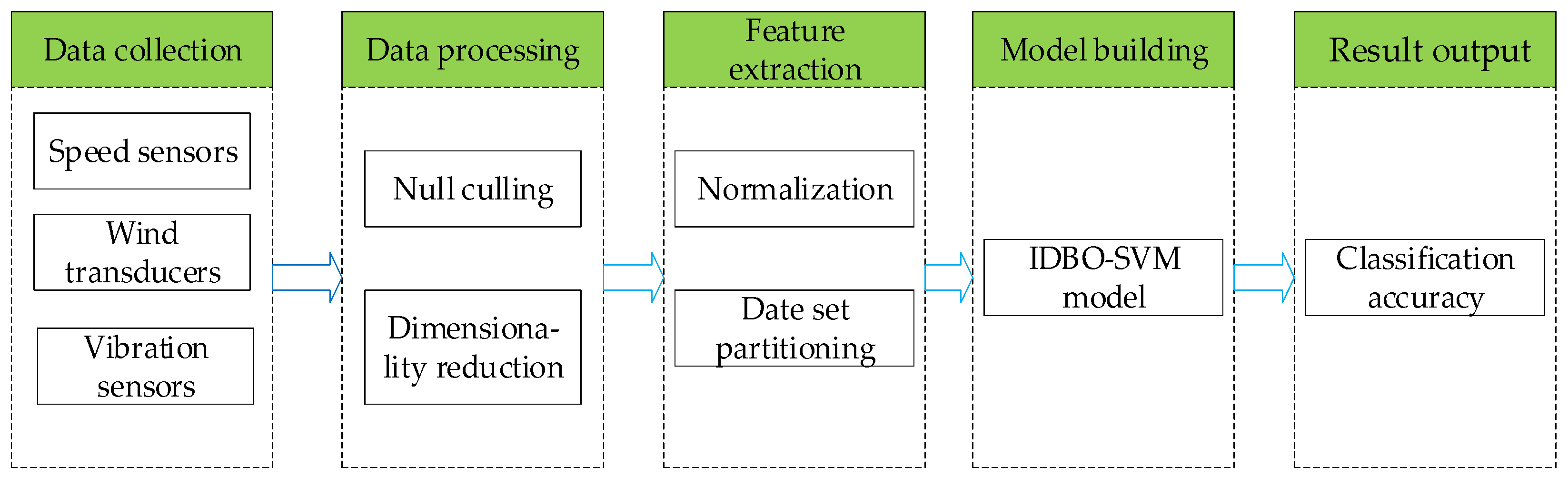
- Two sets of data of wind turbine under normal environment and severe environment are collected by using speed sensors, wind transducers, and vibration sensors. Each set of data includes six parameters: wind speed, wind direction, rotor speed, rotor position, power and pitch angle. The experimental results show that the average fault diagnosis rate reaches about 96% under the two conditions, which improves the reliability and stability of the wind power system.
2. Basic Principle
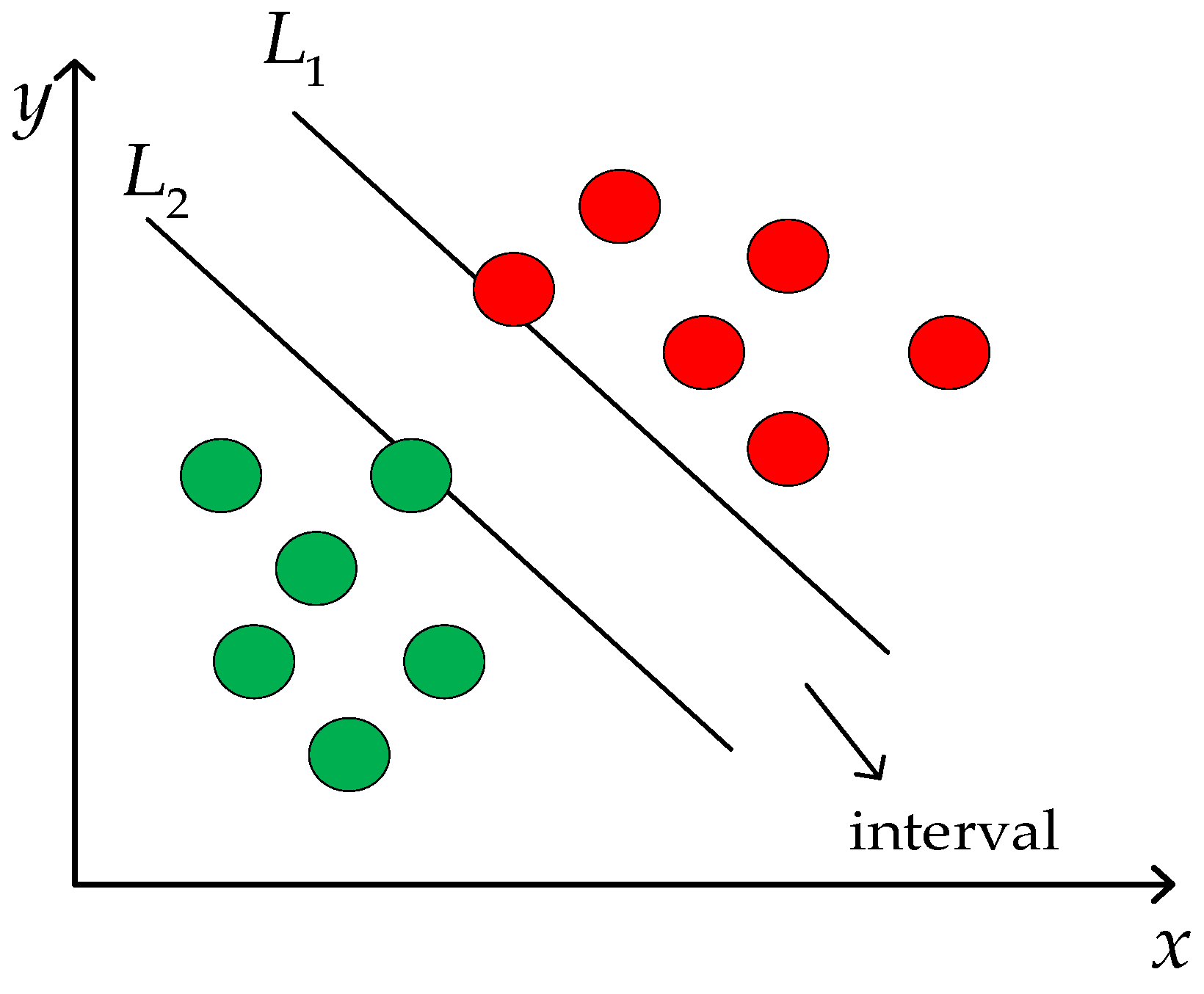
2.1. Support Vector Machines
2.2. Dung Beetle Optimization Algorithm
2.2.1. Ball Rolling Dung Beetles
2.2.2. Breeding Dung Beetles
2.2.3. Small Dung Beetles
2.2.4. Stealing Dung Beetles
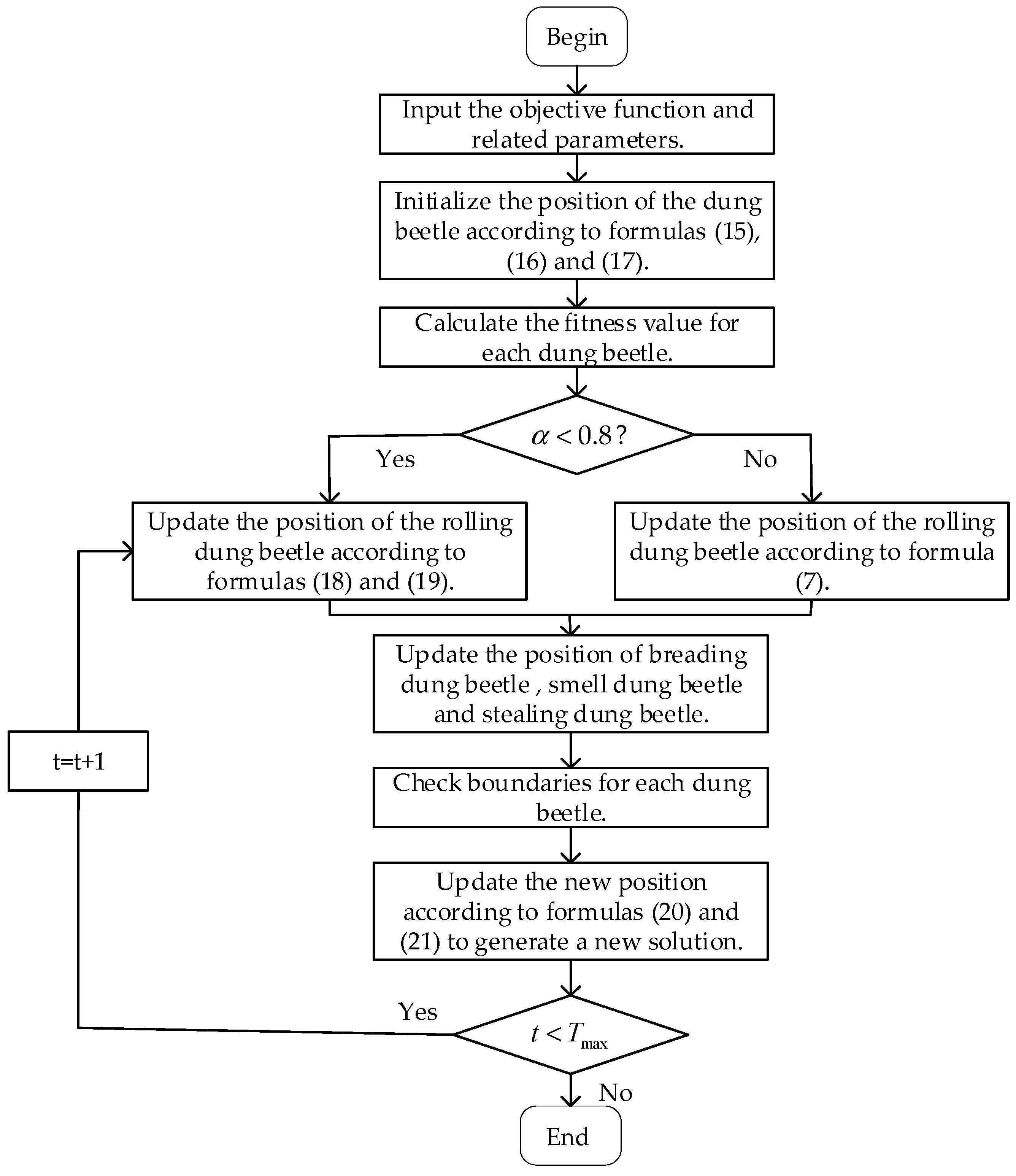
3. Improved Dung Beetle Optimization Algorithm
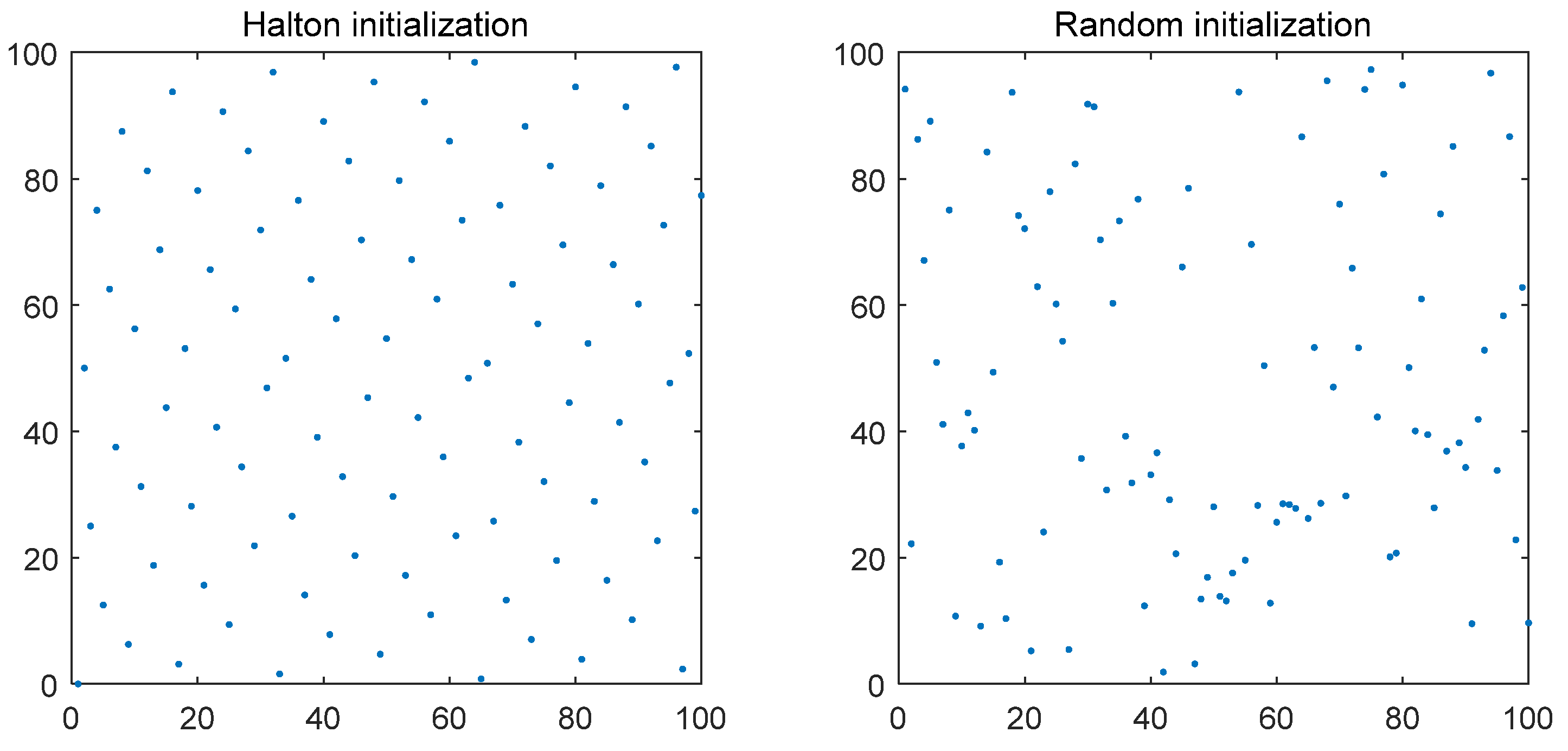
3.1. Halton Sequence Initializes the Population
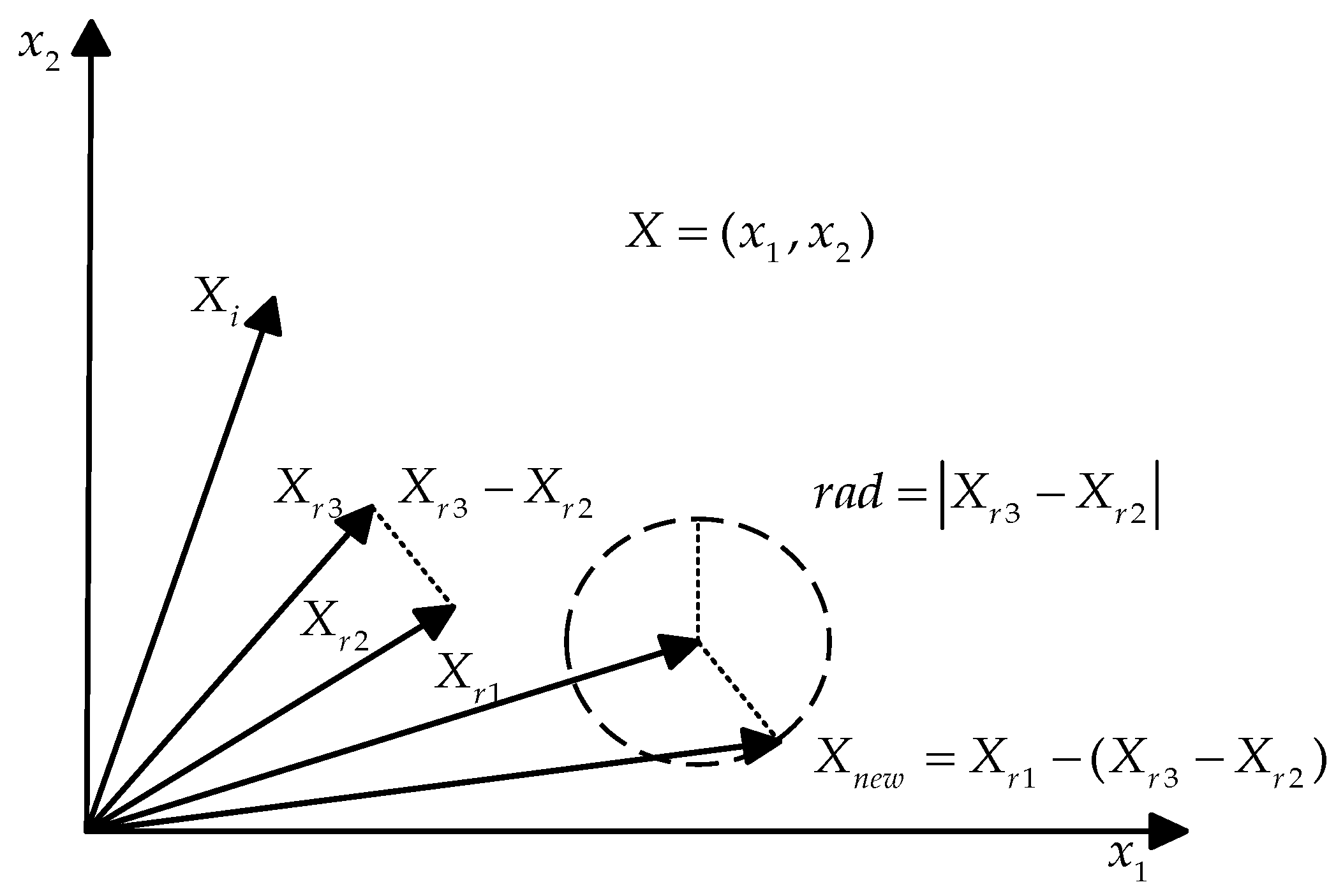
3.2. Subtraction Average Optimization Strategy
3.3. Smooth Development Variation
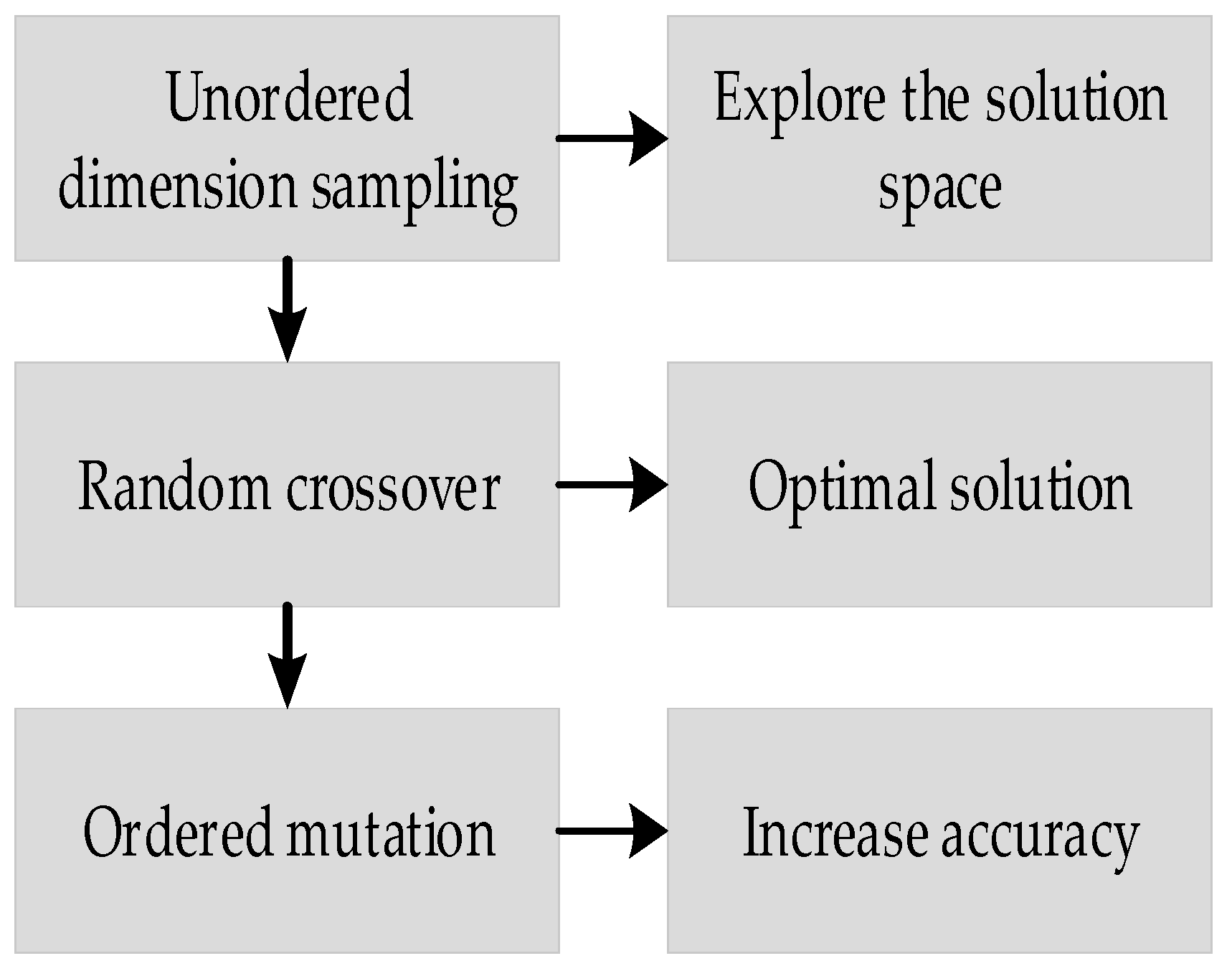
3.3.1. Unordered Dimension Sampling
3.3.2. Random Crossover
3.3.3. Ordered Mutation
3.3.4. IDBO-SVM Fault Diagnosis Model
4. Discussion
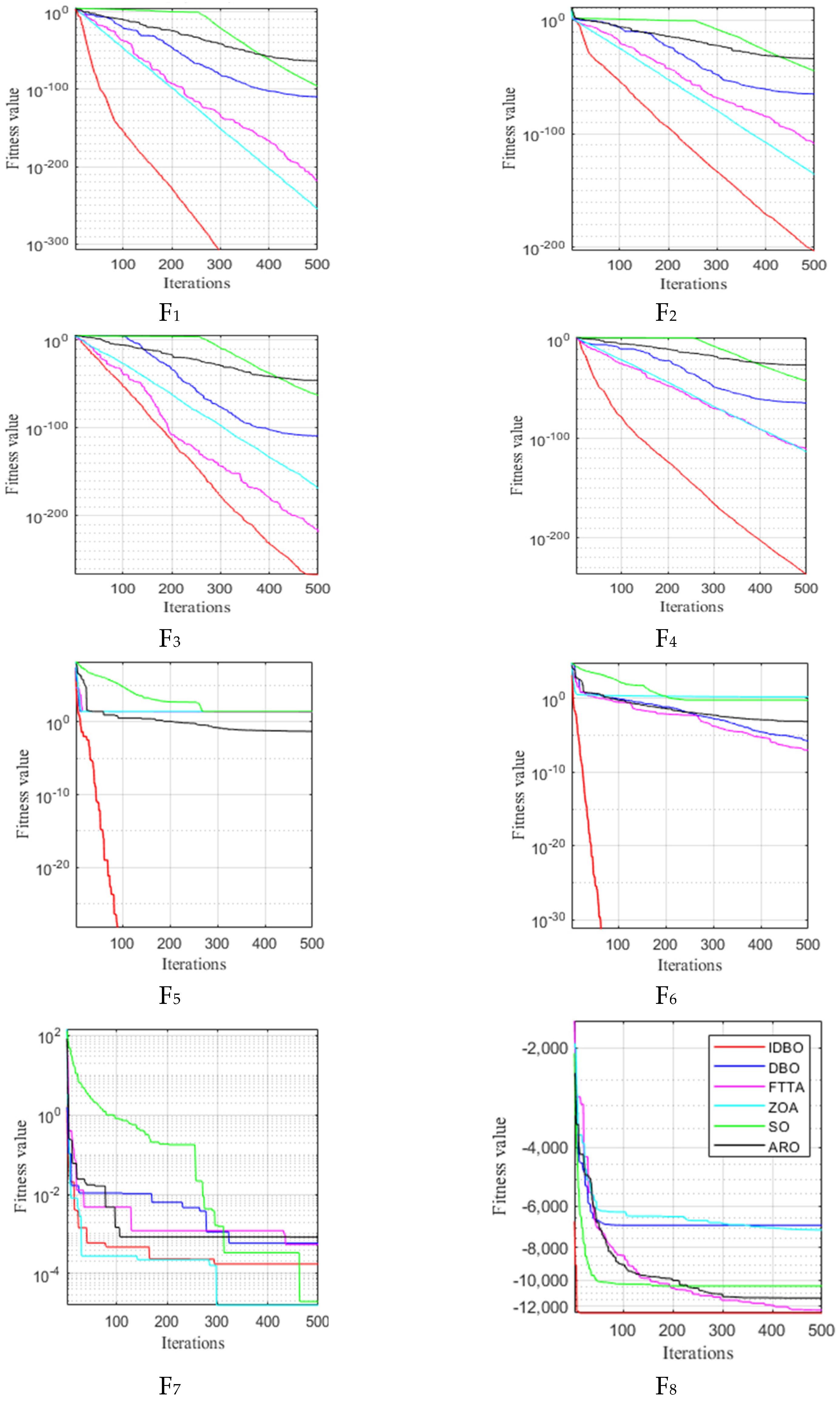
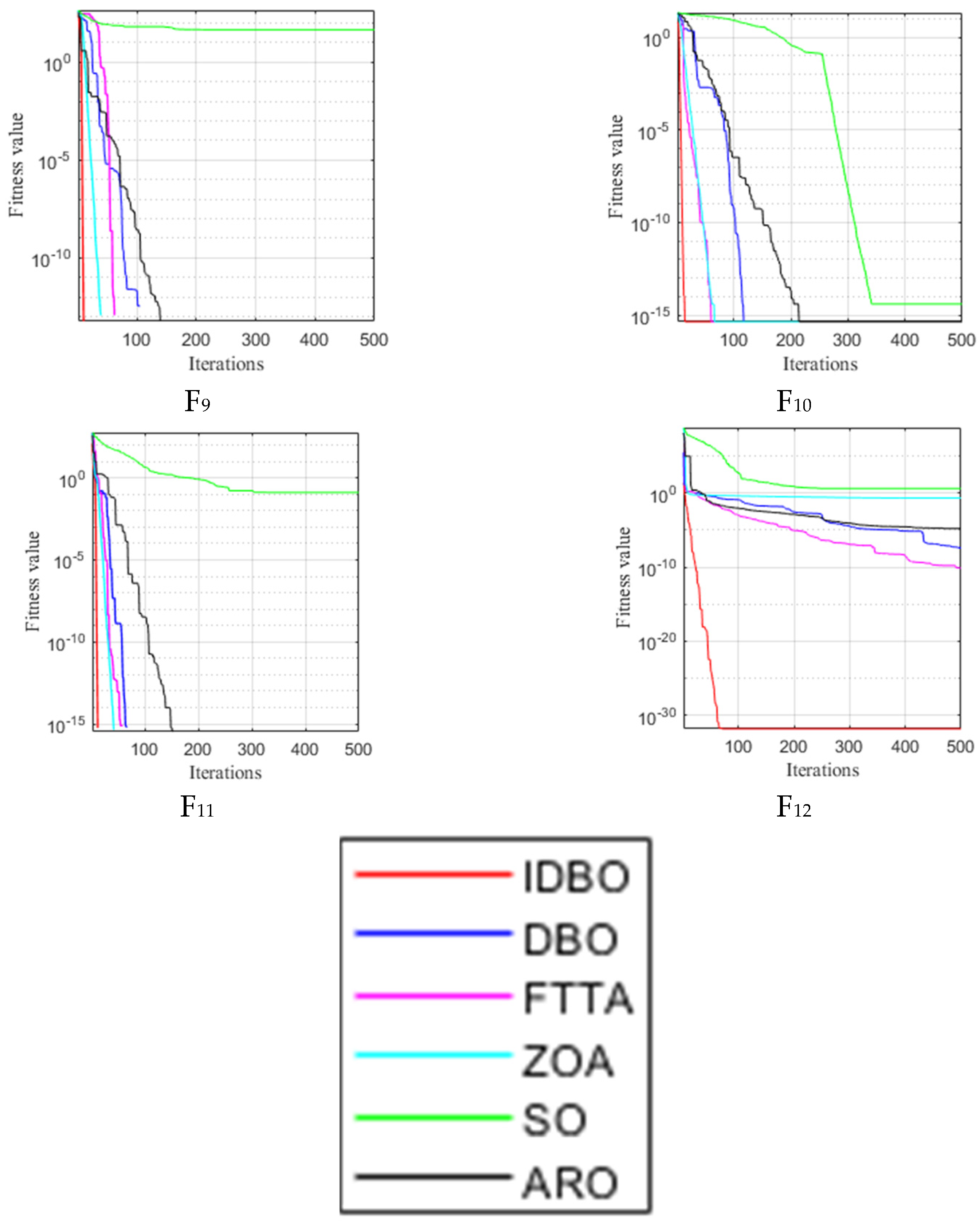
4.1. Comparison of Convergence and Performance between IDBO and Other Algorithms
4.1.1. Introduction of Test Functions
4.1.2. Convergence Analysis of IDBO and Other Algorithms
4.1.3. Performance Comparison between IDBO and Other Algorithms
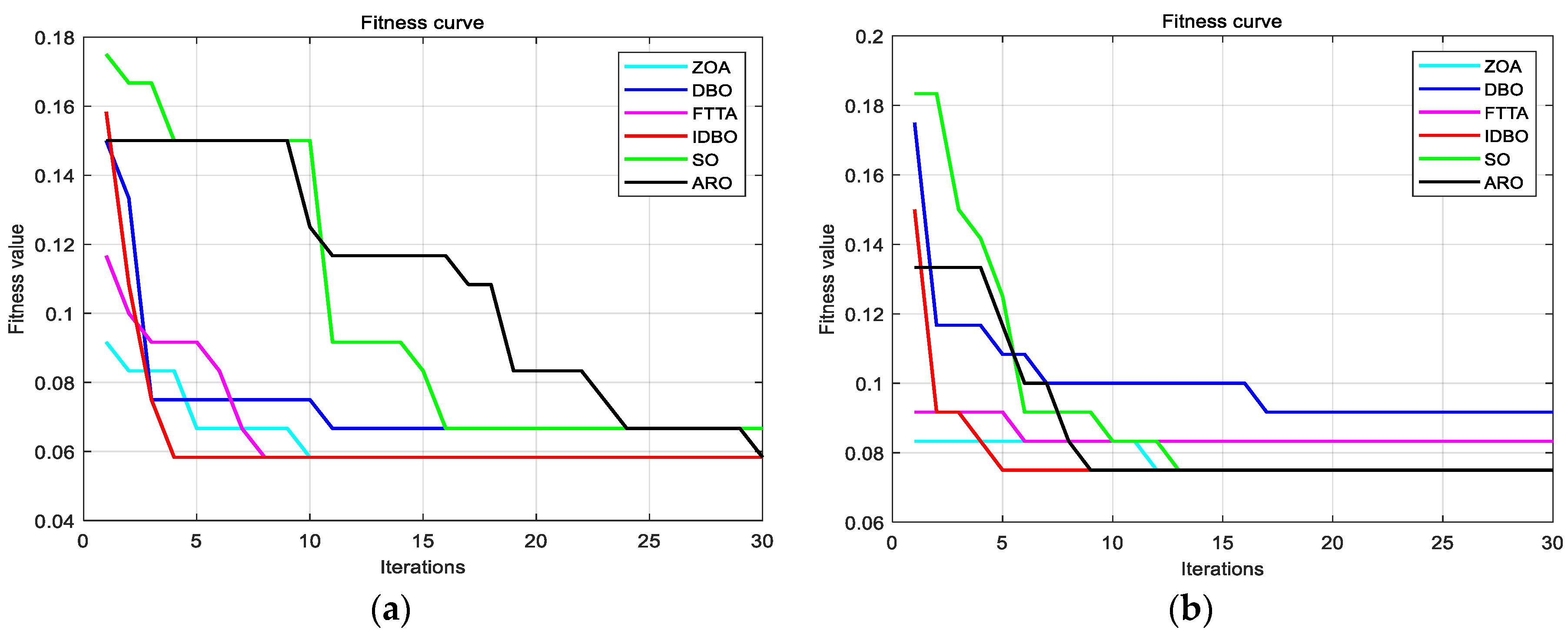
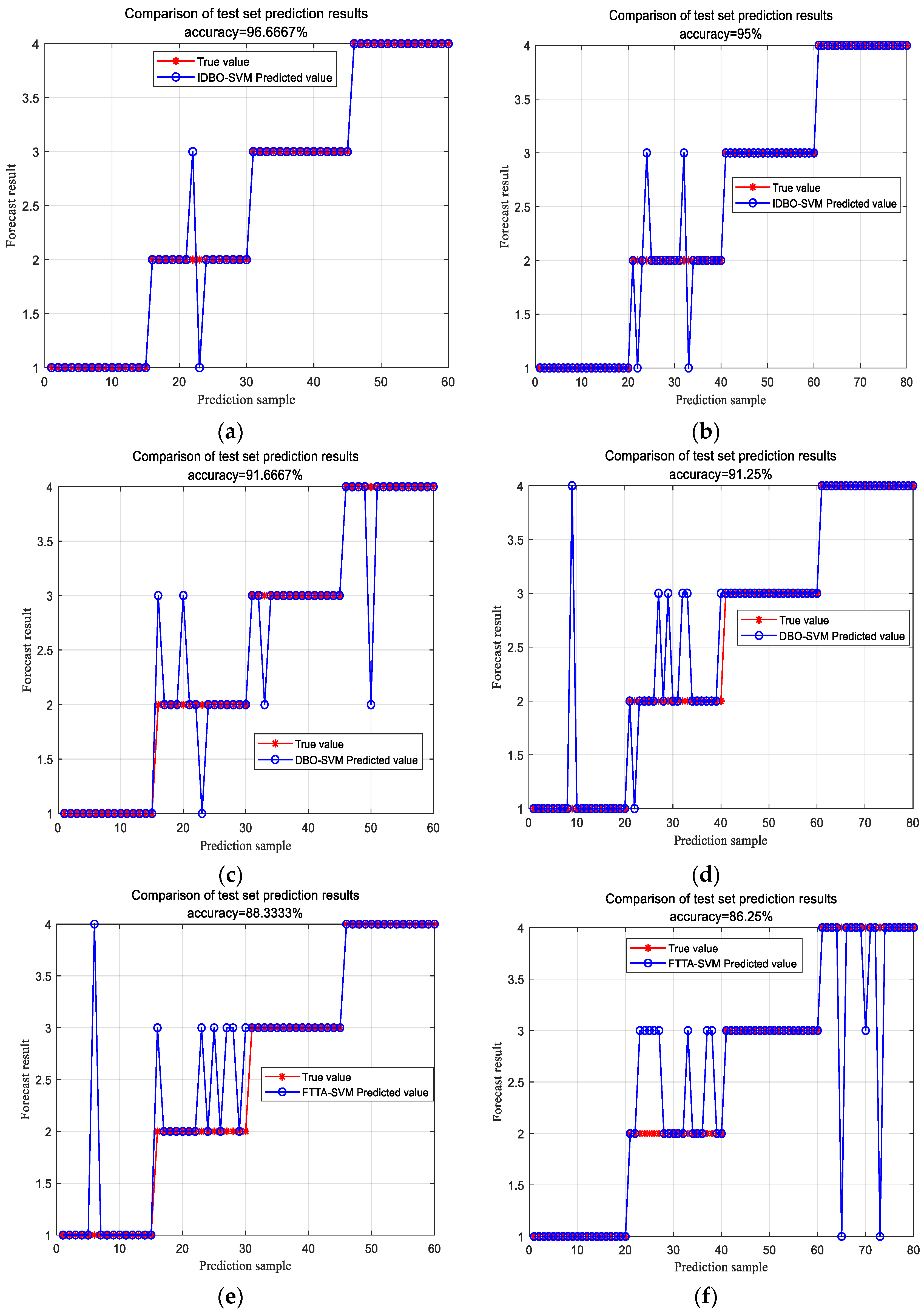
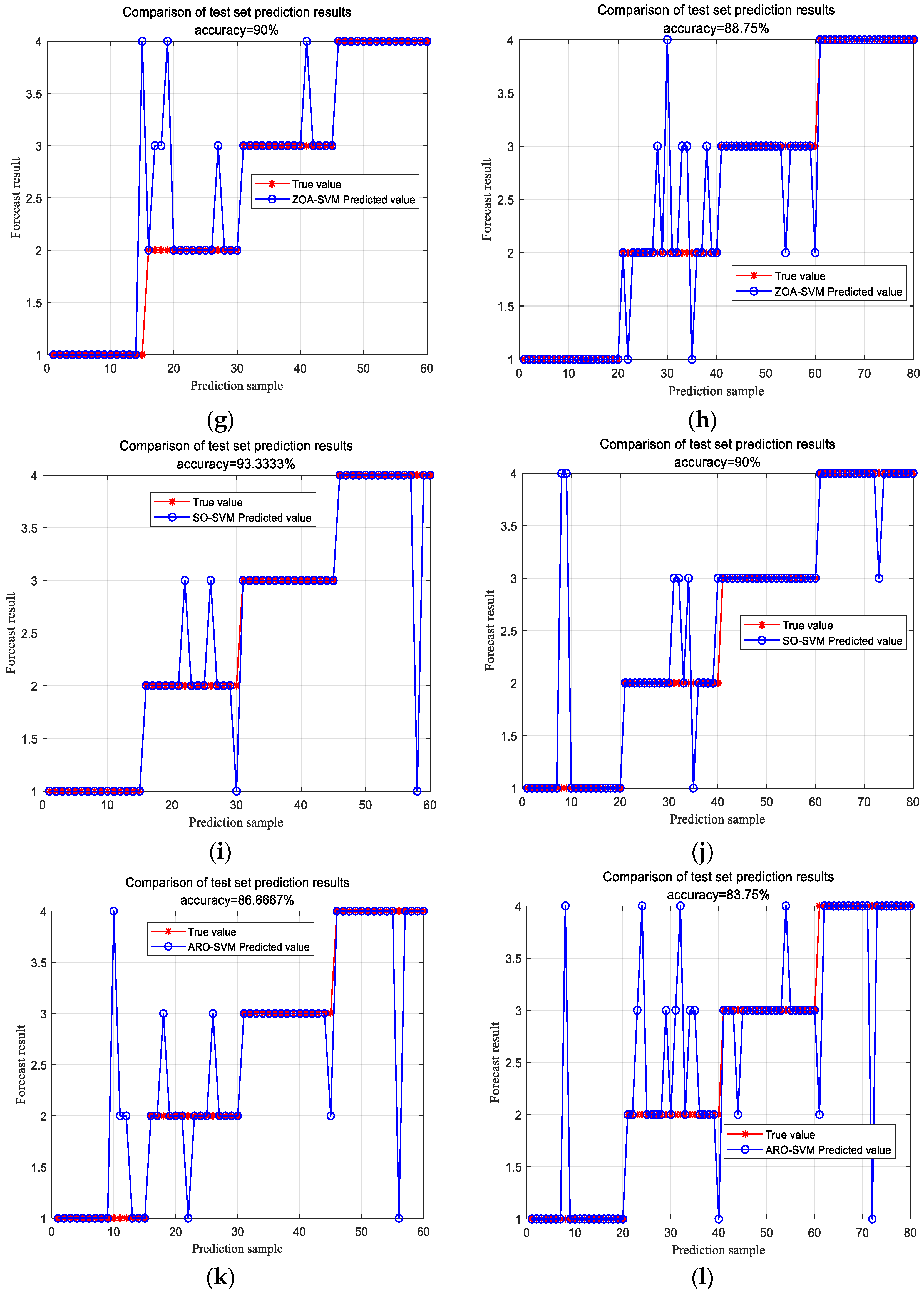
4.2. Case Study Analysis
5. Conclusions
- (1)
- Twelve standard test functions were used to test the performance of IDBO. The experimental results showed that the IDBO algorithm has a faster convergence rate than the other five optimization algorithms.
- (2)
- Apply the six optimization algorithms to the identical wind farm and unit model. Compared to the other five algorithms, the IDBO algorithm has higher diagnostic accuracy, improving the diagnosis accuracy rate to 96.67%. The limitations of this study are the data collection is on a small number of specific wind farms, so the model performance may differ under different climate conditions, wind speed variations and load conditions. Therefore, future research will consider combining IDBO algorithm with deep learning methods to make full use of the feature extraction capability of deep neural networks, so that the model can better capture complex nonlinear relationships.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| DBO | Dung beetle optimization |
| SVM | Support vector machine |
| IDBO | Improved dung beetle optimization |
| FTTA | Football team training algorithm |
| ZOA | Zebra optimization algorithm |
| SO | Snake optimization |
| ARO | Artificial rabbit optimization |
| GWO | Gray wolf optimization |
| Penalty factor | |
| Kernel parameter | |
| The number of iterations of the population | |
| The maximum number of iterations in a population | |
| The maximum dimension of a vector |
References
- Liu, D.; Zhang, F.; Dai, J.; Xiao, X.; Wen, Z. Study of the Pitch Behaviour of Large-Scale Wind Turbines Based on Statistic Evaluation. IET Renew. Power Gener. 2021, 15, 2315–2324. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, Q.; Hao, Y. Research on Temperature Distribution of Large Permanent Magnet Synchronous Direct Drive Wind Turbine. Electronics 2023, 12, 2251. [Google Scholar] [CrossRef]
- Lan, J.; Chen, N.; Li, H.; Wang, X. A review of fault diagnosis and prediction methods for wind turbine pitch systems. Int. J. Green Energy 2024, 21, 1613–1640. [Google Scholar] [CrossRef]
- Ding, G.; Liu, Y.; Guo, Y. Design of variable pitch system for large wind turbine unit. Wind Energy 2021, 7, 104–107. [Google Scholar]
- Song, R. Research on Fault Diagnosis Method of Variable Pitch System of Wind Turbine. Equip. Manag. Maint. 2024, 4, 25–28. [Google Scholar]
- Shigang, Q.; Jie, T.; Zhilei, Z. Fault diagnosis of wind turbine pitch system based on LSTM with multi-channel attention mechanism. Energy Rep. 2023, 10, 104087–104096. [Google Scholar]
- Elorza, I.; Arrizabalaga, I.; Zubizarreta, A.; Martín-Aguilar, H.; Pujana-Arrese, A.; Calleja, C. A Sensor Data Processing Algorithm for Wind Turbine Hydraulic Pitch System Diagnosis. Energies 2021, 15, 33. [Google Scholar] [CrossRef]
- Kandukuri, S.T.; Klausen, A.; Robbersmyr, K.G. Fault diagnostics of wind turbine electric pitch systems using sensor fusion approach. J. Phys. Conf. Ser. 2018, 1037, 032036. [Google Scholar] [CrossRef]
- Li, H.C.; Wang, X.D.; Wang, D.M.; Cao, C.Y.; Chen, N.C.; Pan, W.G. Research on fault diagnosis of wind turbine variable pitch system based on fault tree. Equip. Manag. Maint. 2022, 168–169. [Google Scholar]
- Yin, Z.K.; Lin, Z.W.; Lv, G.H.; Li, D.Z. Research on fault diagnosis and health status prediction of wind turbine variable pitch system based on data-driven. J. Northeast Electr. Power Univ. 2023, 43, 1–11+17. [Google Scholar]
- Jamadar, I.M.; Nithin, R.; Nagashree, S.; Prasad, V.P.; Preetham, M.; Samal, P.K.; Singh, S. Spur Gear Fault Detection Using Design of Experiments and Support Vector Machine (SVM) Algorithm. J. Fail. Anal. Prev. 2023, 23, 2014–2028. [Google Scholar] [CrossRef]
- Lu, L.; Zhang, X.; Ma, H.; Pu, Q.; Lu, Y.; Xu, H. Transformer fault acoustic identification model based on acoustic denoising and DBO-SVM. J. Electr. Eng. Technol. 2024, 19, 3621–3633. [Google Scholar] [CrossRef]
- Hou, J.; Cui, Y.; Rong, M. An Improved Football Team Training Algorithm for Global Optimization. Biomimetics 2024, 9, 419. [Google Scholar] [CrossRef] [PubMed]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization problems. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Lan, P.; Xia, K.; Pan, Y.; Fan, S. An improved GWO algorithm optimized RVFL model for oil layer prediction. Electronics 2021, 10, 3178. [Google Scholar] [CrossRef]
- Hashim, F.A.; Hussien, A.G. Snake Optimizer: A novel meta-heuristic optimization algorithm. Knowl. Based Syst. 2022, 242, 108320. [Google Scholar] [CrossRef]
- Wang, R.; Zhang, S.; Jin, B. Improved multi-strategy artificial rabbits optimization for solving global optimization problems. Sci. Rep. 2024, 14, 18295. [Google Scholar] [CrossRef]
- Li, L.; Meng, W.; Liu, X.; Fei, J. Research on rolling bearing fault diagnosis based on variational modal decomposition parameter optimization and an improved support vector machine. Electronics 2023, 12, 1290. [Google Scholar] [CrossRef]
- Amaya-Tejera, N.; Gamarra, M.; Vélez, J.I.; Zurek, E. A distance-based kernel for classification via Support Vector Machines. Front. Artif. Intell. 2024, 7, 1287875. [Google Scholar] [CrossRef]
- Pan, J.; Li, S.; Zhou, P.; Yang, G.L.; Lv, D.C. An improved dung beetle colony optimization algorithm guided by sine algorithm. Comput. Eng. Appl. 2023, 59, 92–110. [Google Scholar]
- Zhang, D.; Zhang, C.; Han, X.; Wang, C. Improved DBO-VMD and optimized DBN-ELM based fault diagnosis for control valve. Meas. Sci. Technol. 2024, 35, 075103. [Google Scholar] [CrossRef]
- He, J.; Guo, W.; Wang, S.; Chen, H.; Guo, X.; Li, S. Application of Multi-Strategy Based Improved DBO Algorithm in Optimal Scheduling of Reservoir Groups. Water Resour. Manag. 2024, 38, 1883–1901. [Google Scholar] [CrossRef]
- Sun, L.; Xin, Y.; Chen, T.; Feng, B. Rolling Bearing Fault Feature Selection Method Based on a Clustering Hybrid Binary Cuckoo Search. Electronics 2023, 12, 459. [Google Scholar] [CrossRef]
- Zhang, G.F. Research on optimization of construction project management based on genetic algorithm. J. Xinyang Agric. For. Coll. 2020, 30, 126–129+133. [Google Scholar]
- Jiang, Y.; Ding, Y. A Target Localization Algorithm for a Single-Frequency Doppler Radar Based on an Improved Subtractive Average Optimizer. Remote Sens. 2024, 16, 2123. [Google Scholar] [CrossRef]
- Moustafa, G.; Tolba, M.A.; El-Rifaie, A.M.; Ginidi, A.; Shaheen, A.M.; Abid, S. A subtraction-average-based optimizer for solving engineering problems with applications on TCSC allocation in power systems. Biomimetics 2023, 8, 332. [Google Scholar] [CrossRef]
| Serial Number | Function | Dim | Range | Min |
|---|---|---|---|---|
| 1 | 30 | [–100, 100] | 0 | |
| 2 | 30 | [–10, 10] | 0 | |
| 3 | 30 | [–100, 100] | 0 | |
| 4 | 30 | [–100, 100] | 0 | |
| 5 | 30 | [–30, 30] | 0 | |
| 6 | 30 | [–100, 100] | 0 | |
| 7 | 30 | [−1.28, 1.28] | 0 | |
| 8 | 30 | [–500, 500] | −418.98 | |
| 9 | 30 | [−5.12, 5.12] | 0 | |
| 10 | 30 | [–32, 32] | 0 | |
| 11 | 30 | [–600, 600] | 0 | |
| 12 | 30 | [–50, 50] | 0 |
| Fun | IDBO vs. DBO | IDBO vs. FTTA | IDBO vs. ZOA | IDBO vs. SO | IDBO vs. ARO |
|---|---|---|---|---|---|
| F1 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| F2 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| F3 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| F4 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| F5 | 0.007937 | 0.015873 | 0.007937 | 0.015873 | 0.015873 |
| F6 | 0.007937 | 0.015873 | 0.007937 | 0.015873 | 0.015873 |
| F7 | 0.111111 | 0.007937 | 0.015873 | 0.015873 | 0.111111 |
| F8 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| F9 | 0.007937 | 0.007937 | 0.015873 | 0.007937 | 0.015873 |
| F10 | 0.007937 | 0.111111 | 0.007937 | 0.445485 | 0.007937 |
| F11 | 0.007937 | 0.015873 | 0.007937 | 0.007937 | 0.007937 |
| F12 | 0.007937 | 0.007937 | 0.007937 | 0.007937 | 0.007937 |
| Instrument Parameter | Model | Accuracy | Brand |
|---|---|---|---|
| Speed sensors | SS495A1 | Honeywell | |
| Wind transducers | WMT52 | Vaisala | |
| Vibration sensors | 352C33 | PCB | |
| Remark | Collection every 30 min | ||
| Data Type | Wind Speed | Wind Direction | Rotor Speed | Rotor Position | Power | Pitch Angle |
|---|---|---|---|---|---|---|
| Scope of date | 7.8–19.7 | 115.3–211.2 | 8.6–16.9 | 159.1–306.2 | 1411–1546 | 6.7–88.9 |
| Data unit | m/s | degree | rpm | degree | kw | degree |
| Algorithms | IDBO | DBO | FTTA | ZOA | SO | ARO |
|---|---|---|---|---|---|---|
| Normal environment | 96.67% | 91.67% | 88.34% | 90% | 93.33% | 86.67% |
| Severe environment | 95% | 91.25% | 86.25% | 88.75% | 90% | 83.75% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Q.; Li, M.; Fu, C.; Wang, J. Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine. Electronics 2024, 13, 3621. https://doi.org/10.3390/electronics13183621
Li Q, Li M, Fu C, Wang J. Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine. Electronics. 2024; 13(18):3621. https://doi.org/10.3390/electronics13183621
Chicago/Turabian StyleLi, Qiang, Ming Li, Chao Fu, and Jin Wang. 2024. "Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine" Electronics 13, no. 18: 3621. https://doi.org/10.3390/electronics13183621
APA StyleLi, Q., Li, M., Fu, C., & Wang, J. (2024). Fault Diagnosis of Wind Turbine Component Based on an Improved Dung Beetle Optimization Algorithm to Optimize Support Vector Machine. Electronics, 13(18), 3621. https://doi.org/10.3390/electronics13183621





