An Improved Deep Deterministic Policy Gradient Pantograph Active Control Strategy for High-Speed Railways
Abstract
1. Introduction
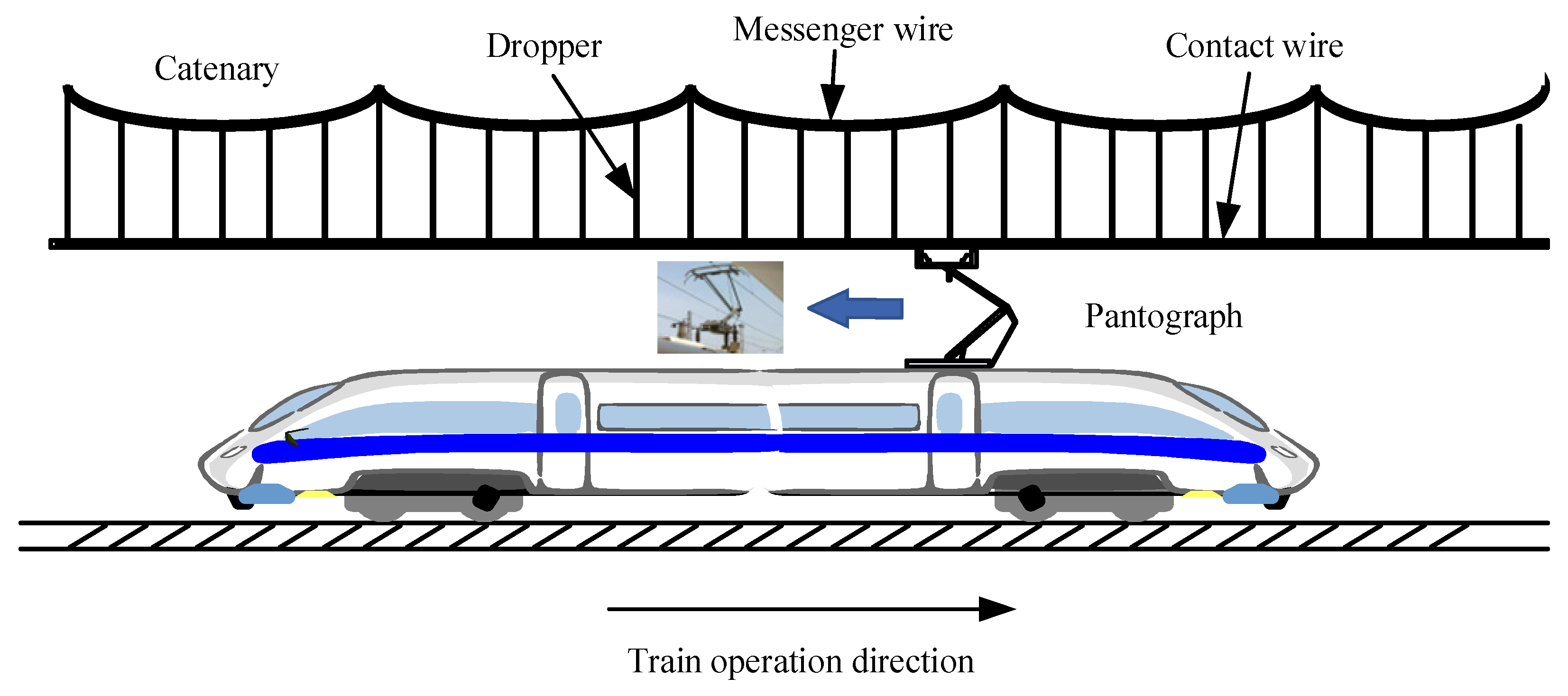
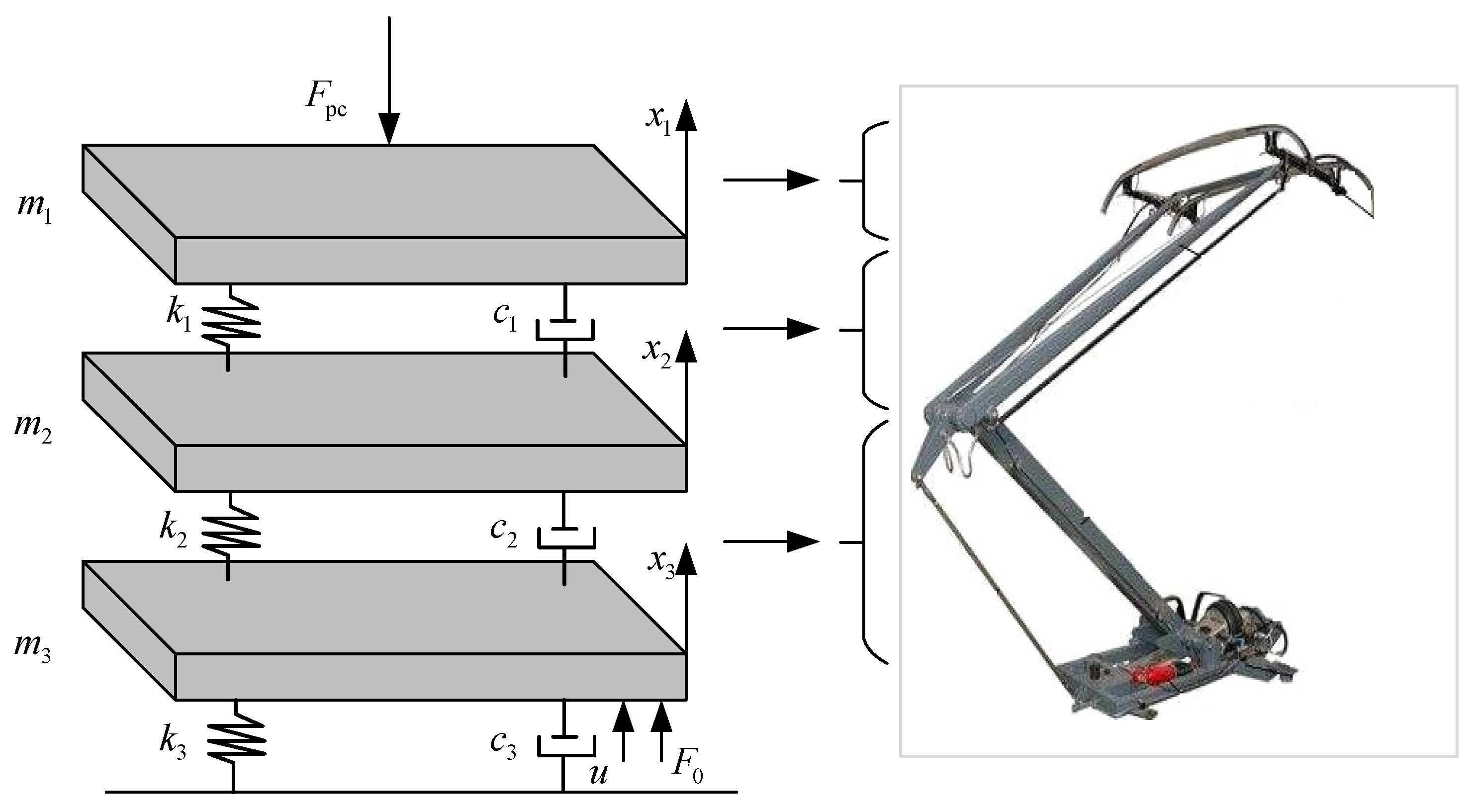
2. Modeling the Pantograph–Catenary Coupling System
2.1. Pantograph Modeling
2.2. Catenary Modeling
2.3. Pantograph–Catenary Coupling System Modeling
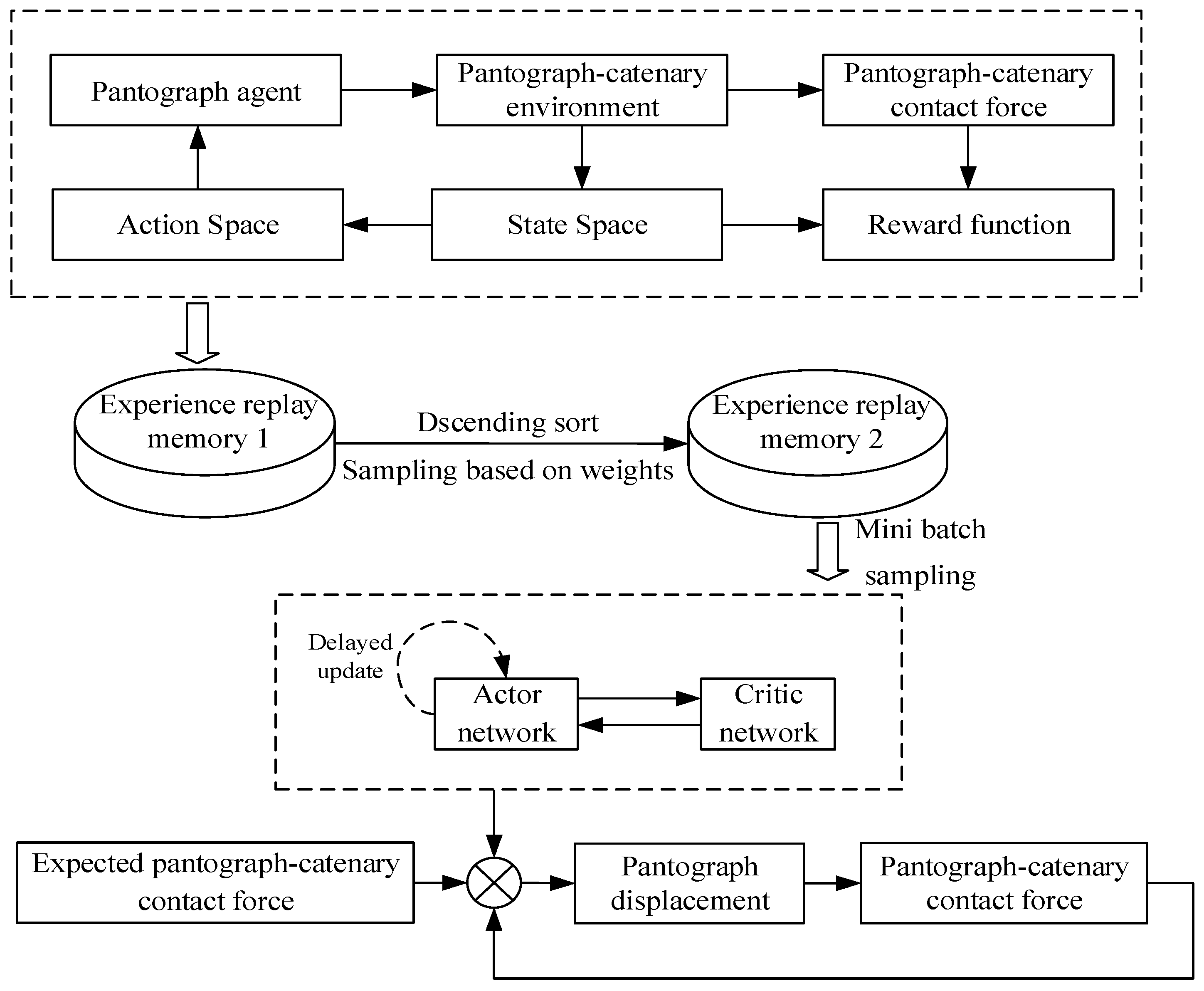
3. Improved Deep Reinforcement Learning for Controller Design
3.1. Basic Deep Reinforcement Learning
3.2. DDPG Strategy
- (1)
- The Actor network generates a set of actions and adds Ornstein–Uhlenbeck (OU) noise;
- (2)
- Based on the current action, the agent inputs the next state st+1 into the reward function and stores (st, at, rt, st+1) in the experience replay buffer;
- (3)
- n samples from the experience replay buffer are extracted, st and st+1 are input to the Actor network, and (st, at, rt, st+1) are input to the Critic network for iterative updating, respectively;
- (4)
- The Target–Actor network receives the states st and st+1, inputs the action at and random noise into the interaction between the agent and the environment, outputs the next action at+1 to the Target–Critic network, then receives the action Q-value and updates the network;
- (5)
- The Target–Critic network receives st+1, at+1, calculates the Q-value, and then combines Q with the reward r for iterative network updating.
3.3. Improved DDPG Solution
| Algorithm 1: IDDPG |
| 1: Initialize empty experience replay buffer D1, D2, and the environment E. |
| 2: Initialize the current total number of experiences for the replay buffer N1. |
| 3: Randomly initialize the Critic network and Actor network with weights and . |
| 4: Initialize the target network Q′ and with weights . |
| 5: For episode = 1, M perform the following: |
| 6: Initialize the random process N for exploration. |
| 7: Initialize observation state s1. |
| 8: For step = 1, T perform the following: |
| 9: Select action based on the Actor network. |
| 10: Execute action at, observe reward rt and next state st+1. |
| 11: Store (st, at, rt, st+1) in the experience replay buffer D1. |
| 12: D2 is obtained by sorting D1 in the descending order of reward values and then removing the data with small reward values at the end. |
| 13: Set the weight w according to priority sampling and uniform sampling in the experience divided by proportional batch_size*w and batch_size*(1 − w) in D2, respectively. |
| 14: Update Critic network parameters and the loss. |
| 15: According to the formula , determine whether the Actor network needs to be updated. |
| 16: If it is a multiple of N, conduct the following: |
| 17: Update the Actor policy using the sampling policy gradient: |
| 18: Update the target networks: . |
| 19: End. |
| 20: End. |
3.4. Deep Reinforcement Learning Module Design for Controller
- (1)
- State space design: In an actual environment, measuring the velocity and displacement of a pantograph is challenging. Nonetheless, non-contact measurement techniques make it simple to measure pantograph head displacement.
- (2)
- Action space design: Agents adjust the lift force in order to control the PCCF. The primary concept for pantograph control is to keep the lift force within a safe and appropriate range while guarding against unintentional forces that could harm or wear down mechanical parts. A variation range of −50 N to 50 N was adopted for pantograph control. The action space can be represented as follows.
- (3)
- Design of the reward function: The controller’s main objective is to reduce the PCCF’s fluctuations and make the PCCF smoother. The objective is to achieve optimal control performance and minimize the control force, taking into account the actuator’s energy problem [26]. Negative reward signals are given for excessively high or low PCCF, and positive reward signals are obtained if the PCCF is within the normal range. Training ends when the PCCF stabilizes within a specific range, concluding the current episode. The reward function is set as follows:
4. Test Verification of Pantograph IDDPG Network Active Control
4.1. Training Results
4.2. Controller Validity Verification
4.3. Controller Robustness Validation at Different Train Speeds
4.4. Controller Robustness Validation under Various Railway Lines
4.5. Controller Robustness Verification under Different Pantograph Parameter Perturbations
- (1)
- Modifying the mass of each component;
- (2)
- Modifying the damping of each component;
- (3)
- Modifying the stiffness of each component;
- (4)
- Modifying all parameters concurrently.
5. Conclusions
- (1)
- Reinforcement learning selects the optimal action in the current state through its powerful trial-and-error ability, and there is no negative impact, such as reduced control performance, due to the inability of traditional controller parameters to optimize adaptively.
- (2)
- Through multiple experiments, DRL has the ability to estimate the relationship between local conditions and actions and maximize the cumulative reward. By anticipating and promptly modifying the strategy in response to the local state’s consequences, the DRL-based control strategy may effectively adjust to modifications in the external environment.
- (3)
- The IDDPG strategy efficiently decreases the training process error, improves learning efficiency, dramatically increases the training speed, and increases algorithm exploration to enable faster convergence in order to address problems with a large cumulative error and the slow training speed of the DDPG strategy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| DDPG | IDDPG | |
|---|---|---|
| 280 km/h | 50 | 27 |
| 320 km/h | 51 | 26 |
| 360 km/h | 49 | 25 |
| Control Method | Without Control | LQR | VFFPID | DDPG | IDDPG | |
|---|---|---|---|---|---|---|
| Speed | Contact Force | |||||
| 280 km/h | Max | 279.5453 | 237.8598 | 226.8654 | 218.5034 | 176.6796 |
| Min | 9.9796 | 9.1249 | 11.5429 | 12.3172 | 13.4633 | |
| Mean | 126.0376 | 136.4832 | 124.3352 | 107.0818 | 95.7824 | |
| STD | 70.6821 | 52.2767 | 49.6091 | 39.1876 | 38.7872 | |
| 320 km/h | Max | 304.2178 | 234.7181 | 230.0273 | 184.2673 | 178.6796 |
| Min | 12.3821 | 11.6223 | 10.2254 | 11.3626 | 13.2936 | |
| Mean | 127.8825 | 132.7975 | 129.6325 | 106.8854 | 105.7506 | |
| STD | 77.2735 | 52.2991 | 51.8612 | 43.5479 | 42.9887 | |
| 360 km/h | Max | 314.1288 | 232.7940 | 250.2295 | 227.4663 | 179.6263 |
| Min | 13.0708 | 12.4390 | 13.4014 | 10.8986 | 12.7248 | |
| Mean | 132.1117 | 134.2196 | 123.2099 | 106.7462 | 106.8854 | |
| STD | 81.1289 | 51.9724 | 52.2504 | 45.2220 | 43.9998 | |
References
- Chen, J.; Hu, H.; Wang, M.; Ge, Y.; Wang, K.; Huang, Y.; Yang, K.; He, Z.; Xu, Z.; Li, Y.R. Power Flow Control-Based Regenerative Braking Energy Utilization in AC Electrified Railways: Review and Future Trends. IEEE Trans. Intell. Transp. Syst. 2024, 25, 6345–6365. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, Y.; Wang, M.; Wang, K.; Huang, Y.; Xu, Z. Power Sharing and Storage-Based Regenerative Braking Energy Utilization for Sectioning Post in Electrified Railways. IEEE Trans. Transp. Electrif. 2024, 10, 2677–2688. [Google Scholar] [CrossRef]
- Chen, X.; Xi, Z.; Wang, Y.; Wang, X. Improved study on the fluctuation velocity of high-speed railway catenary considering the influence of accessory parts. IEEE Access 2020, 8, 138710–138718. [Google Scholar] [CrossRef]
- Jiang, X.; Gu, X.; Deng, H.; Zhang, Q.; Mo, J. Research on Damage Mechanism and Optimization of Integral Dropper String Based on Fretting Theory. Tiedao Xuebao/J. China Railw. Soc. 2019, 41, 40–45. [Google Scholar]
- Shi, G.; Chen, Z.; Guo, F.; Hui, L.; Dang, W. Research on Characteristic of the Contact Resistance of Pantograph-Catenary under Load Fluctuation Condition. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2019, 34, 2287–2295. [Google Scholar]
- Wang, Y.; Liu, Z.-G.; Huang, K.; Gao, S.-B. Pantograph-catenary surface heat flow analysis and calculations based on mechanical and electrical characteristics. Tiedao Xuebao/J. China Railw. Soc. 2014, 36, 36–43. [Google Scholar]
- Song, Y.; Li, L. Robust Adaptive Contact Force Control of Pantograph-Catenary System: An Accelerated Output Feedback Approach. IEEE Trans. Ind. Electron. 2021, 68, 7391–7399. [Google Scholar] [CrossRef]
- Zdziebko, P.; Martowicz, A.; Uhl, T. An investigation on the active control strategy for a high-speed pantograph using co-simulations. Proc. Inst. Mech. Engineers. Part I J. Syst. Control Eng. 2019, 233, 370–383. [Google Scholar] [CrossRef]
- Wang, Y.; Jiao, Y.; Chen, X. Active Control of Pantograph with Fluctuating Wind Excitation of Contact Wire Considered. Mech. Sci. Technol. Aerosp. Eng. 2021, 40, 1149–1157. [Google Scholar]
- Zheng, Y.; Ran, B.; Qu, X.; Zhang, J.; Lin, Y. Cooperative Lane Changing Strategies to Improve Traffic Operation and Safety Nearby Freeway Off-Ramps in a Connected and Automated Vehicles Environment. IEEE Trans. Intell. Transp. Syst. 2019, 21, 4605–4614. [Google Scholar] [CrossRef]
- Xie, S.; Zhang, J.; Song, B.; Liu, Z.; Gao, S. Optimal Control of Pantograph for High-Speed Railway Considering Actuator Time Delay. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2022, 37, 505–514. [Google Scholar]
- Song, Y.; Liu, Z.; Ouyang, H.; Wang, H.; Lu, X. Sliding mode control with PD sliding surface for high-speed railway pantograph-catenary contact force under strong stochastic wind field. Shock Vib. 2017, 2017 Pt 1, 4895321. [Google Scholar] [CrossRef]
- Schirrer, A.; Aschauer, G.; Talic, E.; Kozek, M.; Jakubek, S. Catenary emulation for hardware-in-the-loop pantograph testing with a model predictive energy-conserving control algorithm. Mechatronics 2017, 41, 17–28. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Song, B.; Xie, S.; Liu, Z. A New Active Control Strategy for Pantograph in High-Speed Electrified Railways Based on Multi-Objective Robust Control. IEEE Access 2019, 7, 173719–173730. [Google Scholar] [CrossRef]
- Chater, E.; Ghani, D.; Giri, F.; Haloua, M. Output feedback control of pantograph-catenary system with adaptive estimation of catenary parameters. J. Med. Biol. Eng. 2015, 35, 252–261. [Google Scholar] [CrossRef]
- Duguleana, M.; Mogan, G. Neural networks based reinforcement learning for mobile robots obstacle avoidance. Expert Syst. Appl. 2016, 62, 104–115. [Google Scholar] [CrossRef]
- Cully, A.; Clune, J.; Tarapore, D.; Mouret, J. Robots that can adapt like animals. Nature 2015, 521, 503. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, H.; Wu, Y.; Peng, J. Hybrid Electric Vehicle Energy Management with Computer Vision and Deep Reinforcement Learning. IEEE Trans. Ind. Inform. 2021, 17, 3857–3868. [Google Scholar] [CrossRef]
- Zhao, R.; Chen, Z.; Fan, Y.; Li, Y.; Gao, F. Towards Robust Decision-Making for Autonomous Highway Driving Based on Safe Reinforcement Learning. Sensors 2024, 24, 4140. [Google Scholar] [CrossRef]
- Liu, C.H.; Ma, X.; Gao, X.; Tang, J. Distributed Energy-Efficient Multi-UAV Navigation for Long-Term Communication Coverage by Deep Reinforcement Learning. IEEE Trans. Mob. Comput. 2020, 19, 1274–1285. [Google Scholar] [CrossRef]
- Chen, X.; Shen, Y.; Wang, Y.; Zhang, X.; Cao, L.; Mu, X. Irregularity Detection of Contact Wire Based on Spectral Kurtosis and TimeℋFrequency Analysis. Zhendong Ceshi Yu Zhenduan/J. Vib. Meas. Diagn. 2021, 41, 695–700. [Google Scholar]
- WUY Research on Dynamic Performance and Active Control Strategy of High-Speed Pantograph-Catenary System; Beijing Jiaotong University: Beijing, China, 2011.
- Chen, Z.; Tang, B.; Shi, G. Design of the pantograph optimal tracking controller based on linear quadratic. J. Electron. Meas. Instrum. 2015, 29, 1647–1654. [Google Scholar]
- Mu, R.; Zeng, X. A review of deep learning research. KSII Trans. Internet Inf. Syst. 2019, 13, 1738–1764. [Google Scholar]
- Fan, Q.-Y.; Cai, M.; Xu, B. An Improved Prioritized DDPG Based on Fractional-Order Learning Scheme. IEEE Trans. Neural Netw. Learn. Syst. 2024, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Han, Z.; Wang, H. Active Pantograph Control of Deep Reinforcement Learning Based on Double Delay Depth Deterministic Strategy Gradient. Diangong Jishu Xuebao/Trans. China Electrotech. Soc. 2024, 39, 4547–4556. [Google Scholar]









| Parameters | Nominal Values | Perturbation Values |
|---|---|---|
| m1 (kg) | 6.1 | 7.5 |
| m2 (kg) | 10.2 | 12.2 |
| m3 (kg) | 10.3 | 13.3 |
| c1 (Ns · m−1) | 10 | 13.8 |
| c2 (Ns · m−1) | 0 | 2 |
| c3 (Ns · m−1) | 120 | 115.4 |
| k1 (N · m−1) | 10,400 | 10,300 |
| k2 (N · m−1) | 10,600 | 10,700 |
| k3 (N · m−1) | 0 | 0 |
| Target contact force (N) | F0 = 70 + 0.00097v2 [22] | |
| Parameters | Value |
|---|---|
| Actor learning rate | 0.0001 |
| Critic learning rate | 0.001 |
| Discount factor | 0.99 |
| Experience relay buffer | 1,000,000 |
| Batch_size | 64 |
| Weight w | 0.5 |
| Soft update rate | 0.005 |
| Maximum steps per episode T | 20,000 |
| Maximum number of episodes M | 100 |
| Railway Line Parameter | China Beijing-Tianjin Line | China Beijing-Shanghai Line |
|---|---|---|
| Contact wire tension (kN) | 27 | 33 |
| Messenger wire tension (kN) | 21 | 20 |
| Encumbrance (m) | 1.6 | 1.6 |
| Contact Wire linear density (kg · m−1) | 1.082 | 1.35 |
| Messenger wire linear density (kg · m−1) | 1.068 | 1.065 |
| Span (m) | 48 | 50 |
| Dropper intervals (m) | 5/9.5/9.5/9.5/9.5/5 | 5/8/8/8/8/5 |
| Perturbation Case | Change Mass | Change Damping | Change Stiffness | Change Simultaneously |
|---|---|---|---|---|
| Without control | 81.67 | 86.22 | 84.08 | 82.87 |
| VFFPID | 50.59 | 52.25 | 52.06 | 50.70 |
| Decline (%) | 38.06 | 39.40 | 38.08 | 38.82 |
| DDPG | 47.29 | 45.55 | 45.64 | 45.89 |
| Decline (%) | 42.10 | 47.17 | 45.72 | 44.62 |
| Improved DDPG | 44.01 | 44.67 | 43.04 | 40.47 |
| Decline (%) | 46.11 | 48.19 | 48.81 | 51.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, Y.; Chen, X.; Wang, Y.; Chang, Z. An Improved Deep Deterministic Policy Gradient Pantograph Active Control Strategy for High-Speed Railways. Electronics 2024, 13, 3545. https://doi.org/10.3390/electronics13173545
Wang Y, Wang Y, Chen X, Wang Y, Chang Z. An Improved Deep Deterministic Policy Gradient Pantograph Active Control Strategy for High-Speed Railways. Electronics. 2024; 13(17):3545. https://doi.org/10.3390/electronics13173545
Chicago/Turabian StyleWang, Ying, Yuting Wang, Xiaoqiang Chen, Yixuan Wang, and Zhanning Chang. 2024. "An Improved Deep Deterministic Policy Gradient Pantograph Active Control Strategy for High-Speed Railways" Electronics 13, no. 17: 3545. https://doi.org/10.3390/electronics13173545
APA StyleWang, Y., Wang, Y., Chen, X., Wang, Y., & Chang, Z. (2024). An Improved Deep Deterministic Policy Gradient Pantograph Active Control Strategy for High-Speed Railways. Electronics, 13(17), 3545. https://doi.org/10.3390/electronics13173545





