Abstract
To improve the performance of the sparrow search algorithm in solving complex optimization problems, this study proposes a novel variant called the Improved Beetle Antennae Search-Based Sparrow Search Algorithm (IBSSA). A new elite dynamic opposite learning strategy is proposed in the population initialization stage to enhance population diversity. In the update stage of the discoverer, a staged inertia weight guidance mechanism is used to improve the update formula of the discoverer, promote the information exchange between individuals, and improve the algorithm’s ability to optimize on a global level. After the follower’s position is updated, the logarithmic spiral opposition-based learning strategy is introduced to disturb the initial position of the individual in the beetle antennae search algorithm to obtain a more purposeful solution. To address the issue of decreased diversity and susceptibility to local optima in the sparrow population during later stages, the improved beetle antennae search algorithm and sparrow search algorithm are combined using a greedy strategy. This integration aims to improve convergence accuracy. On 20 benchmark test functions and the CEC2017 Test suite, IBSSA performed better than other advanced algorithms. Moreover, six engineering optimization problems were used to demonstrate the improved algorithm’s effectiveness and feasibility.
1. Introduction
In recent years, driven by the rapid advancements in information technology and the continuous enhancements in computing power, heuristic algorithms have gradually become an important tool and method for solving various complex problems [1]. As one of the research hotspots in the field of artificial intelligence, heuristic algorithms can discover laws, optimize decisions, and provide innovative solutions in various fields by simulating human intelligent thinking and learning processes, as well as analyzing and processing large amounts of data. The research scope of heuristic algorithms is wide, including but not limited to genetic algorithms [2], ant colony algorithms [3], particle swarm algorithms [4], artificial neural networks [5], fuzzy logic [6], and simulated annealing algorithms [7]. These algorithms have the characteristics of adaptability, learning ability, and parallel processing ability, and they can effectively solve complex problems that traditional algorithms find difficult to deal with, such as optimization problems [8,9], data mining [10], pattern recognition [11], image processing [12], and machine learning [13].
The research and application of heuristic algorithms have not only attracted widespread attention in academia but have also had a huge impact on the industrial and commercial fields. In the industrial field, intelligent algorithms are applied to production scheduling, supply chain management, equipment failure prediction, etc., significantly improving production efficiency and resource utilization. In the commercial field, meta-heuristic algorithms are applied in market analysis, consumer behavior prediction, recommendation systems, etc., providing enterprises with more accurate and personalized services. However, although heuristic algorithms have achieved remarkable achievements in various fields, they still face many challenges and problems. For example, the performance and stability of the algorithm need to be further improved, the explainability and interpretability of the algorithm also need to be strengthened, and the consideration of data privacy and security in the algorithm has become particularly important. Therefore, it is an urgent need to conduct in-depth research on and make improvements in intelligent algorithms.
Zhu D et al. [14] introduced an enhanced version of bare-bones particle swarm optimization for addressing the DNA sequence design challenge, initialized the population through dynamic lens learning to obtain a better-quality initial solution, updated it through a proposed signal-to-noise ratio distance particle position, and finally proposed to eliminate the poor-quality solutions of the weed optimization algorithm to improve the search’s efficiency. Experiments show that the designed DNA sequence has a higher-quality solution. Zhang E et al. [15] proposed a stochastic elitist learning strategy to optimize the upper-level particles and lower-level particles of PSO to solve large-scale optimization problems. Sui FL et al. [16] created a multi-objective collision-free underwater robot path optimization scheme by establishing the upper-level path planning model of PSO-ACO and the lower-level path planning model composed of the A* algorithm. Experiments show that an optimal conflict-free path with shorter length and higher security can be generated. Wang Y et al. [17] effectively reduced the probability of premature convergence by optimizing the pheromone recording rules and parameters of the traditional ant colony algorithm. The application of the TSP problem shows significant improvement compared to the conventional ant colony algorithm, and the improved algorithm achieves solutions that are close to the theoretical optimum.
Not only these classic heuristic algorithms but also intelligent optimization algorithms, such as the bald eagle search optimization algorithm [18], the arithmetic optimization algorithm [19], the grasshopper optimization algorithm [20], etc., are widely used by scholars all over the world and improved to handle a growing number of optimization problems. TM et al. [21] introduced a local search algorithm called LSAM, which incorporates a mutation operator to enhance the diversity of solutions in the butterfly optimization algorithm. Experimental results demonstrate that the improved algorithm outperforms other algorithms in terms of feature selection and classification accuracy. Pan J. et al. [22] improved the search capability of the Golden Eagle optimization algorithm by introducing a dual learning mechanism. They further applied this enhanced algorithm to UAV path planning and demonstrated its excellent performance.
The sparrow search algorithm (SSA) introduced in this paper is a novel intelligent optimization algorithm developed by Xue J. et al. [23] in 2020 that has attracted extensive attention and research in recent years. It is based on the observed group behavior of sparrows and aims to simulate the intelligent behavior of sparrows in predation and anti-predation and apply it to solve practical problems. It is superior to many swarm intelligence algorithms in performance, but SSA also has the disadvantage of being easily trapped in the local optimum. Several researchers have proposed enhanced versions of the sparrow search algorithm for addressing this problem. Wang Z. et al. [24] presented an improved version of the sparrow search algorithm that incorporates the particle swarm optimization (PSO) algorithm. The objective was to enhance the optimization performance specifically in the context of UAV path planning. Zheng F. et al. [25] made several enhancements to the sparrow search algorithm. They improved the quality of the initial population using cubic chaotic mapping, incorporated a sinusoidal disturbance strategy into the discoverer’s position update formula to enhance global search performance, and introduced an adaptive Cauchy mutation strategy to improve the algorithm’s ability to escape local optima. The improved sparrow search algorithm was then utilized to optimize the parameters of the Long Short-Term Memory (LSTM) network. The effectiveness and feasibility of the enhanced algorithm were verified through experimental evaluation. Huang, Z et al. [26] improved the diversity of the initial population by introducing Tent mapping and generalized oppositional learning. Then, they introduced adaptive inertia weight to dynamically adjust the position of the discoverer to improve the search efficiency, and they used the non-uniform mutation strategy and somersault strategy, respectively. The update formula for followers and vigilantes improves the convergence accuracy of the algorithm, and the improved algorithm is applied to K-means image segmentation to verify the effectiveness of the improved algorithm. Sun H. et al. [27] improved the initialization process of the sparrow population by incorporating CAT chaotic mapping. This enhancement increased the randomness and ergodicity of the initial population. Additionally, they introduced Cauchy mutation and Tent chaotic perturbation techniques to enhance the local search capability of the algorithm. The improved algorithm was applied to network security situation prediction, resulting in improved prediction accuracy. Xue, Z. et al. [28] utilized the Circle map to initialize the sparrow population, thereby enhancing both the quality and diversity of the solutions. They further incorporated the information exchange enhancement mechanism from the gray wolf algorithm to update the discoverer’s position. Moreover, they introduced a chaotic sine–cosine mechanism in the follower’s position update formula, thereby improving the algorithm’s ability to escape local optima. The effectiveness of the improved algorithm was verified by applying it to solve the optimal load problem of a chiller parallel system. Liu R et al. [29] introduced the Latin hypercube sampling technique to obtain the initial population during the sparrow initialization process. Then, in order to enhance the convergence efficiency of the algorithm, an adaptively adjusted sine–cosine algorithm was proposed, incorporating the Levy flight strategy, and they finally introduced a mutation interference mechanism to optimize the population. The improved algorithm’s performance is validated through its application to the wireless sensor network coverage problem. Zhang G et al. [30] introduced an enhanced sparrow search algorithm by incorporating improved adversarial learning and adaptive inertial weights. This improved algorithm was then applied to path planning to validate its effectiveness. Wu H et al. [31] initialized the population with the sine chaotic map and introduced adaptive adjustment of hyperparameters and mutation strategies to improve the optimization ability of the sparrow search algorithm. They applied it to flame image recognition, thus improving the accuracy of fire recognition. Liu J et al. [32] proposed to introduce the Circle chaotic map into the population initialization process and, at the same time, introduce T distribution variation to improve the position update law of sparrows. Finally, they constructed a sparrow population dispersion similarity function and verified the effectiveness of the improved algorithm through engineering examples. Gao B et al. [33] initialized the population with Tent chaotic map and introduced the Levy flight and differential mutation strategy into the update formula of the sparrow population to improve the performance of the sparrow search algorithm. They applied it to improve the dynamic and steady-state performance of the servo system. Liu G Y et al. [34] obtained a high-quality solution by introducing the Cubic chaotic map initialization population and adopted the adaptive inertia weight to balance the convergence speed and exploration ability of the algorithm. The application of the improved algorithm in UAV path planning effectively addresses the challenges associated with UAV track planning. Wang, Z et al. [35] initialized the sparrow population through the improved ICMIC chaotic map and used lens imaging opposite learning to update the discoverer position with a high fitting degree in the discoverer update stage. Finally, they used generalized opposite learning to update the current global worst solution. The practicality of the improved algorithm is demonstrated through real-world engineering examples.
As stated by the NFL theorem [36], no optimization algorithm can outperform all other algorithms on all possible problems. Although various methods proposed by many experts and scholars can indeed improve the optimization effect of SSA, they still fall into the local optimum and face insufficient convergence accuracy when encountering more complex optimization problems. Most of the above studies have introduced traditional chaotic maps to solve the problem of population initialization distribution, but there are still uncertainties. Similarly, traditional opposite learning can only solve in a certain opposite space, and the effect of obtaining high-quality solutions is not obvious. In the above literature, there is no lack of introduction of adaptive inertia weight to dynamically adjust the position update of the discoverer. Although the global search capability of the algorithm can be enhanced in the initial update, the inertia weight is not considered in the case of the reduction of population diversity in the middle and late stages. In the pursuit of improving the algorithm’s performance, integrating other optimization algorithms can help mitigate convergence problems and enhance the ability to identify the global optimal solution, but only part of the update strategy is simply integrated into the position update of the sparrow algorithm, which is not used in dealing with different types of optimization problems. Considering that the performance of jumping out of the local optimum of the original sparrow algorithm is also superior, this affects the performance of the traditional sparrow search algorithm.
Considering the aforementioned issues, this paper introduces a novel approach, named IBSSA (’Improved Beetle Antennae Search-Based Sparrow Search Algorithm), which combines the strengths of both the learning hybrid beetle antennae search algorithm and the sparrow search algorithm. In the population initialization stage, an elite dynamic opposite learning strategy is proposed to obtain high-quality sparrow initial solutions and avoid solution uncertainty. Then, a stage-by-stage adaptive inertial weight guidance mechanism is proposed to improve the global optimization performance of the sparrow search algorithm. To mitigate the risk of the sparrow search algorithm converging to local optima, a combination of strategies is proposed in this study. The improved algorithm integrates the greedy strategy with the enhanced beetle antennae search algorithm and logarithmic spiral opposition-based learning. Additionally, updates are made to the formula used by the sparrow vigilante. These modifications aim to enhance the algorithm’s overall stability, the balance between exploration and exploitation, and search flexibility. The performance of the improved algorithm is evaluated using 20 commonly employed benchmark functions, and the results are compared against those obtained from nine advanced algorithms. Furthermore, to reduce reliance on the optimal value at 0, the algorithm is also benchmarked against the CEC2017 test suite using the same set of algorithms. The findings reveal that the Improved Beetle Antennae Search-Based Sparrow Search Algorithm (IBSSA) exhibits favorable optimization performance and versatility. To analyze the individual impact of each strategy, ablation experiments are conducted. Finally, the effectiveness of the improved algorithm is demonstrated through six classic engineering application examples.
The global optimization task of the algorithm proposed in this article is to prove the optimization performance of the algorithm on public datasets, such as benchmark test functions and CEC2017. The theoretical optimal value of the dataset is the global optimal value that the algorithm seeks, and the practicality test of the algorithm is selected under six classic constrained engineering optimization problems. The same optimization objective is to minimize the consumption of the engineering optimization objective model, and the proposed algorithm aims to find the minimum consumption. Therefore, the optimization objective of this article is to find or approach the theoretical minimum value of the test set to demonstrate the effectiveness of the improved algorithm, find the global minimum value, and avoid the risk of falling into local optima.
The work and innovations of IBSSA are as follows:
- (1)
- An elite dynamic opposite learning strategy is proposed to select elite individuals in the initial population and individuals after dynamic opposite learning to form a new population and select high-quality individuals as new populations, which improves the problem of uncertain quality of the initial population solution.
- (2)
- To enhance the global optimization capability of the algorithm, a staged inertial weight guidance mechanism is proposed, which improves the position update method for the discoverer.
- (3)
- To address the vulnerability of the sparrow search algorithm to local optima, the proposed approach introduces the improved beetle antennae search algorithm and the logarithmic spiral opposition-based learning using a greedy strategy. These enhancements are incorporated into the position update mechanism of the sparrow vigilante, effectively improving the algorithm’s local optimization performance.
- (4)
- The IBSSA algorithm is applied to engineering optimization problems in order to evaluate its practicality and effectiveness. Through this application, the improved algorithm’s performance and efficacy can be verified in real-world scenarios.
This paper is structured as follows: the first part introduces the meaning and application of the heuristic algorithm and the development status of the sparrow search algorithm; the second part introduces the traditional sparrow search algorithm; the third part describes the improved sparrow search algorithm and the corresponding process; the fourth part verifies the superiority of IBSSA through 20 benchmark functions and CEC2017 experiments; and the fifth part verifies the practicability of IBSSA through six engineering examples and, finally, summarizes the improvement work of this paper and analyzes the advantages and disadvantages of IBSSA and prospects for future work.
2. Sparrow Search Algorithm
The sparrow search algorithm is a novel optimization technique inspired by the predation and anti-predation behavior observed in sparrows within their natural habitat. Within the sparrow population, there are three distinct types of sparrows. One is the discoverer, which is the part of the sparrow population that is looking for food, accounting for 20% of the sparrow population. The update formula of the discoverer is as follows:
Among them, represents the position of the sparrow in dimension , is the current number of iterations, , are random numbers in the range of and obey the normal distribution, and , are the warning value and safety value, respectively. When , the population is in a safe period, no predators appear, and the discoverer can forage extensively. When , a predator appears near the population, and the followers and vigilantes will escape to a farther place for food as the discoverer is far away from the range of the predator. One type is the follower, who will follow the discoverer to forage. During the foraging process, if the fitness value of the discoverer is smaller than that of the follower, then the follower will turn into a discoverer at this time, but for the discoverer and the follower, the ratio is constant. The follower update formula is as follows:
represents the optimal position of the discoverer in the global search process of the generation, represents the worst position of the sparrow in the global search process of the generation, represents the number of sparrows in the population, and represents the -dimensional matrix, , in the formula. The other type is vigilantes, who account for about 10–20% of the population, and its position update formula is as follows:
Among them, is an optimal position of the global iteration at this time, in the formula is a random number and obeys the normal distribution, represents the fitness value of the population at this time, and represents the global optimal position. The optimal fitness value, , represents the global worst fitness value, represents a random number, for which the range is , and represents a very small constant, preventing the denominator from being zero. This paper takes . When , sparrows are at the fringes of the population and vulnerable to predators; when , sparrows in danger will stay close to other sparrows to prevent predation.
3. Improved Sparrow Search Algorithm
3.1. Justification for These Improvement Strategies
The adaptability of heuristic algorithms enables them to handle various types of optimization problems. These algorithms do not rely on specific properties of the objective function, such as differentiability or convexity, and can therefore be applied to black box functions, discrete optimization problems, and combinatorial optimization problems [37].
In the initialization stage of SSA, because a certain number of sparrows are randomly generated, the positions and fitness values are both random, so there must be sparrow individuals with poor fitness values. With the continuous loss of population diversity in the iterative process, the flexibility of the sparrow population to find the optimal value is reduced. On the other hand, the update of the discovers’ position in the sparrow population only considers the influence of the position of the previous generation of sparrows, and sparrow individuals tend to jump directly to the vicinity of the current extremum at the end of the iteration, resulting in insufficient search range and being trapped in the local optimum. Finally, the position update of the vigilante in the update formula of the sparrow comprises a process of performing a local search on the entire algorithm, while the sparrow search algorithm does not have a good balance between the discoverer and the follower. The global search process is transferred to the local search process and the optimal sparrow position is not explored more extensively, resulting in a local optimum.
Based on the analysis presented above, this paper proposes an elite dynamic opposite learning strategy to enhance the quality of the initial sparrow solution. Additionally, a staged inertia weight guidance strategy is designed to facilitate stable global search during different stages of sparrow transition while considering the influence of the current optimal individual on the position update. This enhances the algorithm’s ability to optimize global optimization. Furthermore, by incorporating the improved beetle antennae search algorithm and the sparrow search algorithm vigilante through logarithmic spiral opposition-based learning, the sparrow is transformed into a beetle individual. This facilitates local mining near the optimal value and prevents falling into local optima. It ensures that the original algorithm’s optimization performance is maintained, and the overall algorithm’s optimization stability is improved through the application of a greedy strategy. Ultimately, a high-quality solution is obtained.
3.2. Elite Dynamic Opposite Learning
The initial population of a meta-heuristic optimization algorithm is typically generated randomly, which ensures the distribution of individuals in the search space but not necessarily their solution quality. The quality of the initialization directly impacts the convergence speed and accuracy of the algorithm. To improve the initialization process in meta-heuristic algorithms, various strategies are employed, such as chaotic mapping and reverse learning, to control the distribution of initial positions. In line with this, the literature [38] introduces a dynamic opposite learning (DOL) strategy to enhance the quality of the initial population’s solutions and address the issue of low population diversity resulting from uneven initial distribution.
DOL can be expressed as . represents the population position after dynamic learning, represents the position of the randomly initialized population, and a new population is obtained by merging two populations. Select individuals with the highest fitness, where represents the number of populations. To enhance the precision of individual distribution within the population and improve the quality of population solutions, this paper proposes an elite dynamic opposite learning method based on the DOL strategy. DOL deals with the entire population of individuals, but there are also differences among population individuals, and the quality of the distribution and the quality of the solution cannot be guaranteed. Therefore, on the basis of DOL, this paper first performs the elite opposite learning operation on the individual positions generated through random initialization. The elite individuals in the population contain more effective information than other individuals. By constructing the reverse solution of elite individuals, the population’s diversity can be augmented. This contributes to enhancing the variety within the population. Compared with DOL, which can have a greater advantage in solving the random initialization position, the following is the improved DOL method:
represents the position of the individual after the opposite reverse learning, and is the position of the individual after the elite’s reverse learning. is the elite opposite coefficient between , among which , represent the maximum and minimum values in and is the boundary range. Similarly, by selecting individuals with the highest fitness among as a new population, compared with treatment of the random initial population, the population of after elite opposite learning will obtain a more stable distribution than the original random population and improve the quality of the solution, thus increasing the probability that the search space expands to a position closer to the optimal solution.
3.3. Improved Discoverer Update Formula
Among many methods of balancing global optimization and local optimization, the introduction of inertial weight is widely recognized as one of the most impactful methods to improve the performance of meta-heuristic algorithms. This method is the most common in improving the performance of PSO. Large inertial weight is beneficial to search, but it will make the particles search in the space for too long, and the small inertia weight will speed up the convergence speed, but sometimes it will lead to a local optimum. To balance the global search and local optimization capabilities of the algorithm, a staged inertial weight reduction strategy is devised. This strategy is built upon the aforementioned principle. In the literature [39], a two-stage linear decreasing inertia weight method is proposed. The set stage inertia weight is the real value in the first stage of the extensive search, although a large step size can improve the global optimal performance of the discoverer. However, as the iteration progresses, to ensure a stable transition between exploration and exploitation and promote steady convergence, the algorithm is designed to avoid rapid convergence. Therefore, this paper proposes a new staged inertia weight reduction strategy to balance development and exploration. The designed linear reduction strategy is as follows:
is an extremely small number to prevent the denominator from being zero, as shown in Figure 1 for comparison with the strategy presented in study [39].
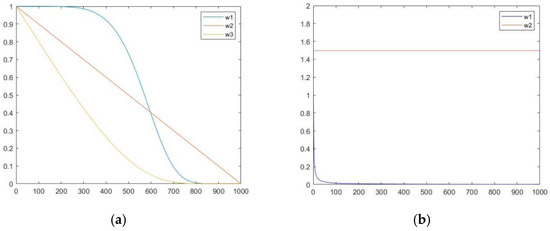
Figure 1.
The stage-by-stage inertia weight curves in this paper and study [39]. The staged control proposed in this paper (a). The staged control (b) that appeared in literature [39].
The control strategy discussed in study [39] primarily focuses on the wide-area search during the initial stage. While a larger search space may expedite the algorithm’s convergence speed, it also poses a risk of overlooking the optimal solution during the later stages if convergence happens too quickly. The three-stage decrement strategy ensures a comprehensive search in the early stage while effectively controlling the convergence speed of the algorithm, and the transformation process from the discoverer to the follower is stable. Even in the mid-term and the later small-scale development process, the discoverer will quickly explore but will not easily miss the global optimal position. In the traditional sparrow search algorithm, the position update of the discoverer solely relies on the position of the previous generation, overlooking the influence of the current optimal solution and the global optimal solution on the overall exploration of the discoverer. When , based on the aforementioned staged control strategy diagram, it is observed that the staged linear decreasing strategy enhances the relationship between global search and local search. However, in the later stages of the iteration, the inertia coefficient tends to approach zero, resulting in a predominant focus on local search. As a consequence, the global search aspect of the algorithm is disregarded. To tackle this limitation, this paper proposes a new discoverer update formula:
where , . is the impact factor of balancing global search and local search in the EO algorithm [40]. Considering that the position update formula of the discoverer in the sparrow search algorithm solely relies on the positions of the previous generation of sparrows, it overlooks any disparity between the global optimal position and the individual positions of the previous generation. Through the above improved formula, it can be concluded that when the global optimal and the position are the same as those of the previous iteration, the sparrow position of the next generation is updated according to the staged inertia weight. If the sparrow position of the previous generation is not optimal, the shadow persistently updates the individual positions of the next generation through the equilibrium of the EO algorithm. Throughout the entire position update process of the sparrow discoverer, the global optimal position plays a guiding role. As the algorithm advances to the later stages, a balance factor is introduced to mitigate the problem of easily falling into local optima caused by the inertia weight nearing zero. This facilitates a more refined balance between exploration and exploitation capabilities.
3.4. Fusion of Greedy Strategy to Improve Search Algorithm of Beetle Antennae Search Algorithm and Sparrow
3.4.1. Logarithmic Spiral Opposition-Based Learning
Logarithmic spiral opposition-based learning (LsOBL) is an innovative methodology introduced by Izci D et al. [41] as a further development of OBL. It has shown excellent performance in the application of the magnetic ball levitation system by combining it with the Hunger Games search algorithm. The traditional OBL involves performing reverse operations on all positions with a boundary range between to obtain new positions; it can be expressed as . represents all individual positions within the boundary, represents the position after reverse learning, and the modified LsOBL can be defined as:
Among them, , represents a random number between (0, 1), represents the best position in the iterative process, and is the position after spiral opposition learning. is a random number that controls the entire logarithmic spiral space between .
The key distinction between LsOBL and OBL lies in their treatment of positions. While OBL considers the reverse position of all individuals within the boundary, LsOBL specifically focuses on the reverse solution of the optimal individual within the boundary. Throughout the iterative process, the position of the optimal individual undergoes constant changes, leading to a reduced search space for spiral oppositional learning within OBL. In contrast, LsOBL aims to target individuals undergoing changes within a smaller space, particularly those in proximity to the optimal solution. This approach proves valuable during the later iterations, when population diversity decreases. It prevents premature convergence of the algorithm and ensures the search for the global optimal value is not missed. The schematic diagram of logarithmic spiral opposition-based learning is depicted in Figure 2 below.
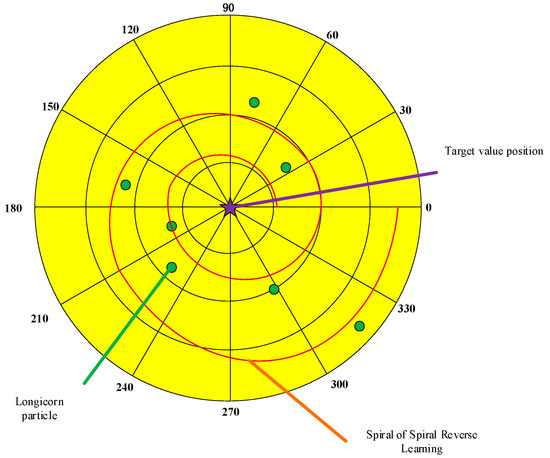
Figure 2.
Schematic diagram of logarithmic spiral opposition-based learning.
3.4.2. Hybrid Search Algorithm of Beetle Antennae Search and Sparrow
The beetle antennae search algorithm (BAS) is a simple and efficient optimization algorithm proposed by Jiang et al. [42] in 2017. Inspired by the foraging behavior of longhorn beetles, the algorithm simulates the process of beetles searching for food. BAS is particularly effective for low-dimensional optimization problems due to its straightforward principle, minimal parameters, and low computational requirements.
During foraging, beetles are attracted to food by its smell. They perceive food odors through their two antennae, which results in different odor concentrations at each antenna due to the varying distance between the food and the antennae. By detecting the concentration difference, beetles randomly move towards the side with the stronger odor. Through repeated iterations, the beetle eventually locates the food source. Figure 3 provides a schematic representation of the bionic algorithm based on beetle antennae.
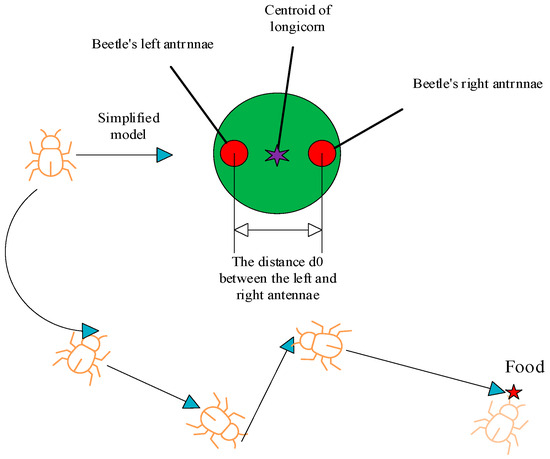
Figure 3.
Schematic diagram of the bionic algorithm of the beetle antennae.
After applying elite dynamic opposite learning to obtain a better initial population, the improved finder formula allows sparrow individuals to escape local optima more effectively. However, maintaining a balanced and stable process for finding the optimal solution is crucial. The sparrow search algorithm relies on random selection and probability distribution to update the sparrow’s position during the local search stage. However, as the algorithm progresses, the decrease in population diversity reduces randomness and increases the risk of falling into local optima. To address this, the global optimization ability of the beetle antennae algorithm is leveraged. By introducing logarithmic spiral opposition-based learning, the position of the original beetle individual is slightly adjusted, enabling exploration in the best area and obtaining a more stable optimal solution. The beetle antennae algorithm is integrated into the local update stage of the sparrow search algorithm. After updating the position of the sparrow follower, it is treated as a beetle individual and iteratively updated. Through a greedy strategy, the fitness value obtained by the beetle antennae algorithm and the sparrow algorithm’s vigilant update are compared. If the fitness value improves, the beetle antennae algorithm’s update process is executed; otherwise, it is not executed. By employing the greedy selection strategy, the loss of population diversity in the later iterations of the sparrow search algorithm is mitigated. This approach continuously incorporates better solutions into the iterative calculation process, enhancing the algorithm’s ability to escape local optima. The improved local beetle antennae algorithm update can be summarized as follows.
First, the logarithmic spiral opposition-based learning operation is performed on the initial beetle position obtained from the sparrow follower so that it can be processed in the area that is more likely to be explored:
Then, use the beetle antennae algorithm update formula to update the position:
Among them, represents a random unit vector, and represents the value after normalizing the random unit vector.
How to update the left antennae of the beetle:
How to update the right antennae of the beetle:
Among them, , represent the length between the particle and the beetle, represents the maximum step size initially set, generally set to 5, and represents the ratio between the step and .
When the beetle obtains the objective function values of two positions, it needs to choose the best of the two positions:
represents the step size of the last iteration, represents the current step size, and represents the step size attenuation coefficient, generally 0.95. represents the position after the beetle antennae algorithm is updated. Then, a greedy strategy is introduced to compare the fitness values of and , and the one with better fitness is taken as the new position.
4. Time Complexity Analysis
The time complexity of an intelligent algorithm is a crucial factor for assessing its performance and execution time. Assume that the dimension of the data in the original algorithm is , the maximum number of iterations is , and the number of populations is , and then the time complexity of SSA is . To analyze the time complexity of IBSSA, first use the improved elite dynamic opposite learning to initialize the sparrow population; the time complexity is . Then, improve the update formula of the discoverer; its time complexity is . The time complexity when using the improved BAS update alone is . The total time complexity of the improved greedy strategy is .
Through the above analysis of the time complexity of the increased improvement strategy, the time complexity of the IBSSA algorithm is . It is consistent with the original algorithm and does not increase the time complexity, so as to prove that the improved algorithm has no additional consumption.
5. Pseudocode of IBSSA
Based on the analysis of the mathematical model mentioned above, the pseudocode of IBSSA (Algorithm 1) can be obtained as follows:
| Algorithm 1. IBSSA |
| Import: |
| : Initial step size of beetle antennae algorithm. |
| Output: |
| : the fitness value associated with the optimal position. |
| 1: Initialize the population using Formula (4) |
| 3: Sort the population based on fitness values to identify the best and worst individuals. |
| 5: Update the discoverer’s position according to Formula (6) |
| 6: end for |
| 8: Update follower position according to Formula (2) |
| 9: end for |
| 11: According to the Formulas (8)–(13) and Formula (3), update the beetle’s step length, the position of the tentacles, and the position of the sparrow vigilante, and calculate the fitness of the two. |
| 12: Greedy selection of optimal fitness through Formula (14) |
| 13: end for |
| 14: Obtain a new population. |
| 15: Update the position if the new position is superior to the current position. |
| 17: end while |
| 18: Return the objective function value. |
The overall algorithm flowchart is shown in Figure 4.
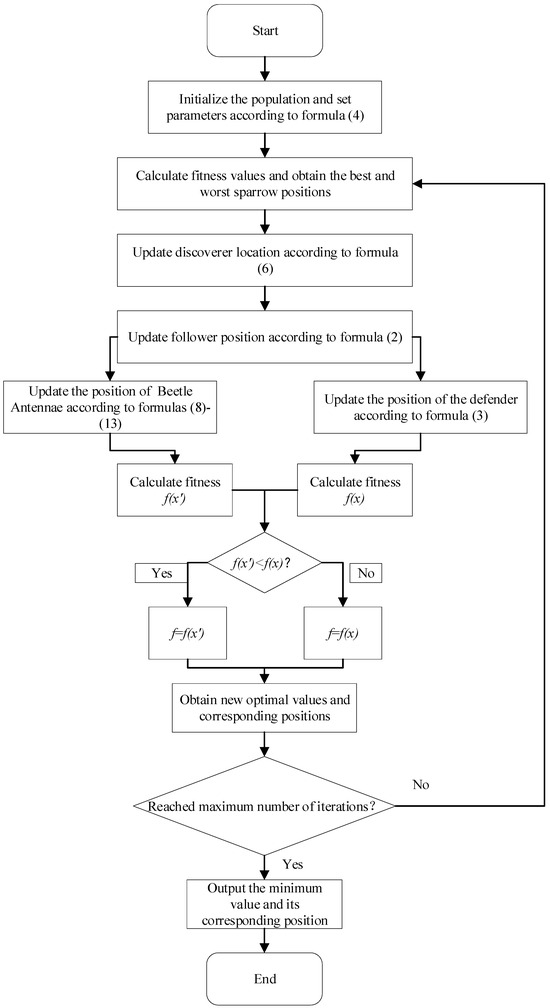
Figure 4.
IBSSA flowchart.
6. Analysis of Experimental Results
Intelligent optimization algorithms require a large amount of experimental table data and iterative graphs to prove their performance because these algorithms are usually applied to solve complex and variable optimization problems, which involve multiple variables, nonlinear relationships, and the possibility of multiple local optimal solutions. When facing these problems, relying solely on theoretical analysis often fails to provide sufficient insight and verification of practical effects. Therefore, a large amount of experimental data and charts are needed to visually demonstrate the performance of the algorithm, so we used multiple sets of test functions for experiments.
6.1. Benchmark Function Experiments
To evaluate the performance of IBSSA, the algorithm was tested on the first 20 benchmark functions to assess its accuracy and stability. Among the selected test functions, f1–f7 is the single modal benchmark function, f8–f13 is the multimodal benchmark function, and f14–f20 is the composite benchmark test function. The original SSA, the two SSA variants, LSSA and TSSA, proposed in the literature [43,44], the adaptive gbest-guided gravitational search algorithm (GGSA) [45], the improved gray wolf optimizer (IGWO) [46], the dung beetle optimizer (DBO) [47], the Whale Optimization Algorithm (WOA) [48], the sine–cosine Algorithm (SCA) [49], the beetle antennae search algorithm (BAS), and the improved algorithm were subjected to a comprehensive evaluation to verify their effectiveness. Table 1 presents the parameter settings for each algorithm. To ensure fairness in the comparison, the initial population size for each algorithm was set to 30, the maximum number of iterations was set to 1000, and three performance indicators (optimal value, average value, and standard deviation) were obtained from the benchmark test function. The optimal value is indicated in bold, and the effectiveness of the algorithm was assessed through the Wilcoxon rank sum test and the Friedman test with a significance level of 5%. Among them, P represents the value after the Wilcoxon test between IBSSA and each algorithm, NaN represents the algorithm with higher similarity, and Rank represents the comprehensive ranking of each algorithm after the Friedman test. The 20 benchmark functions are shown in Table 2. The experimental environment of this article is 12th-Gen-IntelR)-CoreTM)i5-12500H@3.10GHz, and the experimental software used is Matlab2021a.

Table 1.
Parameter settings of each algorithm.

Table 2.
Twenty benchmark functions.
From the experimental test data of IBSSA and each algorithm in Table 3, it can be seen that for the unimodal functions F1–F4, IBSSA has obvious advantages, and the optimal value can be found stably in 30 experiments. For the unimodal function F5, the optimal value sought by IBSSA is several orders of magnitude lower than that of other algorithms. IBSSA demonstrates robust optimization performance, surpassing other algorithms in many cases. Its stability is comparable to that of LSSA, with differences within an order of magnitude. For the unimodal function F6, IBSSA is superior to other comparative algorithms not only in stability but also in optimization performance. Similarly, the optimal value sought on function F7 and the average value of 30 experiments are also higher than other algorithms. The gap between stability and LSSA is also within an order of magnitude. It can be seen that IBSSA exhibits strong optimization performance on the unimodal test function. For the multimodal function F8, in the classical function, only the DBO algorithm is able to find the optimal value. However, in the improved variants of the function, both LSSA and IBSSA algorithms are capable of finding the optimal value. For the multimodal functions F9–F12, IBSSA is the same as other variants of SSA, as both can find the optimal value, which shows the advantage of the overall SSA in the multimodal function. IBSSA continues to take advantage of its optimization performance on multimodal functions F12–F13, ranking first among all algorithms. For the complex fixed-dimensional function F14, IBSSA demonstrates a strong advantage over other algorithms due to its stable performance. While other algorithms can find the optimal value in various scenarios, IBSSA outperforms them in terms of accuracy and optimization stability. Thus, it can be concluded that IBSSA exhibits the best overall performance. The Wilcoxon statistical test reveals significant differences between IBSSA and other algorithms, particularly when compared to the other two algorithms of SSA. Only some similarities are observed among the other algorithms. This further validates the uniqueness of the IBSSA algorithm. Moreover, the comprehensive ranking of the Friedman test confirms that IBSSA ranks first with an average of 2.175 across the 20 benchmark functions. This reaffirms the superior performance of IBSSA.

Table 3.
Experimental test data of IBSSA and each algorithm.
In order to verify the role of the improved strategies in the IBSSA in the optimization process, this paper uses the original sparrow search algorithm (SSA), the improved SSA (SSA1) of elite dynamic opposite learning, the improved SSA of staged inertia weight (SSA2), SSA (SSA3) improved by the beetle antennae algorithm, SSA (SSA4) combined with SSA1 and SSA2, SSA (SSA5) combined with SSA1 and SSA3, SSA (SSA6) combined with SSA2 and SSA3, and IBSSA combined with all strategies for comparison. The statistical results are in Table 4, and the optimal value is bolded.

Table 4.
IBSSA benchmark function ablation experiments.
It can be clearly seen from Table 4 that IBSSA performs the best on these 20 test functions, and it even leads in all three indicators on 14 test functions. IBSSA exhibits superior performance after fusion, surpassing its performance on F5. The mean and variance of SSA1 and SSA2 are not as favorable as those of IBSSA. This indicates that the integration of dynamic elite opposite learning leads to a more evenly distributed initialization population, enabling the algorithm to achieve more accurate optimal value discovery in unimodal test functions. Furthermore, the stage-guided inertia weight enhances the algorithm’s developmental capabilities. The gap between IBSSA and SSA1 and SSA2 under these two indicators is within an order of magnitude, but the optimal value it finds is better than the optimal value under other strategies. The value is multiple orders of magnitude, and the optimal value sought on F7 is slightly lower than that of SSA3. The integration of the beetle antennae algorithm has resulted in an improved developmental ability of the algorithm. Both SSA6 and SSA6 can find the theoretical optimal value. It can be seen that the SSA integrated with the beetle antennae algorithm has a significant advantage in the case where the optimal value is not near 0, and it can be seen from the data of F12, F13, and F19 that the robustness of the SSA after incorporating the beetle’s antennae algorithm has been improved. The exploration performance has also been improved. The improved SSA of each strategy can only be consistent with the performance of the original algorithm on the four test functions. Only on F15 can the optimal value sought by SSA be the same as that of IBSSA, and it is slightly higher than the SSA of other improved strategies. The performance of the original SSA can be enhanced to a certain degree through the individual actions and mutual integration of the strategies. Especially for the IBSSA with all strategies integrated, the robustness and exploration performance are significantly improved.
6.2. CEC2017 Function Test
In order to further test the characteristics of IBSSA to get rid of the dependence on the benchmark function with the optimal value at 0, 10 algorithms were tested on CEC2017 to verify the practicability of IBSSA, namely LSSA, QMESSA [50], TSSA, LMHHO [51], AOA, POA [52], BAS, DBO, SSA, and IBSSA. CEC2017 has a total of 30 single objective test functions, including unimodal function (F1–F3), simple multimodal function (F4-F10), mixed function (F11–F20), and combination function (F21–F30). Due to the instability of the F2 function, no testing was conducted. Set the number of evaluations to 10,000 × dim, and conduct experiments under three different complexities with dimensions of 10, 30, and 50. It is worth noting that among several advanced algorithms, such as LMHHO, QMESSA, TSSA, and LSSA proposed in recent years, QMESSA and LSSA have passed the verification of CEC2017, and the specific parameter settings of each algorithm can be found in the literature. Each algorithm was independently run 30 times, and their performance, as reflected in Table 5, Table 6 and Table 7, was evaluated based on the mean and variance. The Wilcoxon rank sum test was employed to determine if there were significant differences between the algorithms, with a significance level of 5%. In Table 5, Table 6 and Table 7, the symbols “+” and “-” indicate whether the optimization performance of IBSSA is worse or better, respectively, compared to other algorithms. The symbol “NaN” denotes that the performance of IBSSA is equivalent to that of other algorithms. All of the results are compiled and presented in Table 5, Table 6 and Table 7, and a 30-dimensional CEC2017 convergence graph is included to observe the convergence differences between IBSSA and other algorithms.

Table 5.
CEC2017 test data (dim = 10).

Table 6.
CEC2017 test data (dim = 30).

Table 7.
CEC2017 test data (dim = 50).
6.2.1. CEC2017 Function Comparison under 10 Dimensions
Based on the experimental data provided in Table 5, IBSSA performs optimally on the following 19 functions from the CEC2017 test suite with a dimension of 10: F01, F04, F05, F07, F09, F10, F11, F12, F15, F16, F18, F19, F20, F22, F23, F26, F27, F28, and F30. One of the seven functions F03, F08, F13, F17, F21, F25, and F29 is in the optimal state, and IBSSA shows better performance on unimodal functions, multimodal functions, hybrid functions, and combined functions. The test results of IBSSA in multimodal functions F06 and F08, mixing function F14, and combination function F24 are slightly worse than those of QMESSA, POA, DBO, and SSA. According to the Wilcoxon rank sum test (dim = 10) data, it can be seen that IBSSA is similar to other algorithms only in individual functions, and more than half of the test results compared with QMESSA are better than QMESSA. In the Friedman test results, IBSSA ranked first among the ten algorithms, with an average ranking of 1.72 on 29 functions. In summary, IBSSA has the best performance on the CEC2017 test suite (dim = 10).
6.2.2. CEC2017 Function Comparison under 30 Dimensions
Based on the experimental data provided in Table 6, IBSSA performs optimally on the following 15 functions: F01, F03, F04, F05, F08, F17, F18, F20, F22, F24, F25, F26, F27, F29, and F30. The two performance indicators for these functions are at their best. One of the four functions of F10, F21, F23, and F27 has an index in the optimal state. As the dimension increases, the complexity of the calculation is also increasing, but IBSSA is in the single-modal function, multimodal function, and mixed function. It also shows good performance in terms of combination functions. Although the experimental data of F06, F07, F09, F19, and F28 are slightly less effective than LMHHO, QMESA, and DBO, the results of the Wilcoxon rank sum test and Friedman rank sum test indicate that IBSSA shows no strong similarity with other algorithms on the CEC2017 test suite when the dimension is 30. This suggests that IBSSA has unique characteristics when applied to problems of this dimensionality. Additionally, based on the average ranking, IBSSA achieves the top position with a ranking of 1.21. From the convergence curve (Figure 5), it can be observed that IBSSA exhibits strong capabilities in both early global search and later local search. The algorithm maintains stability throughout the entire search process.
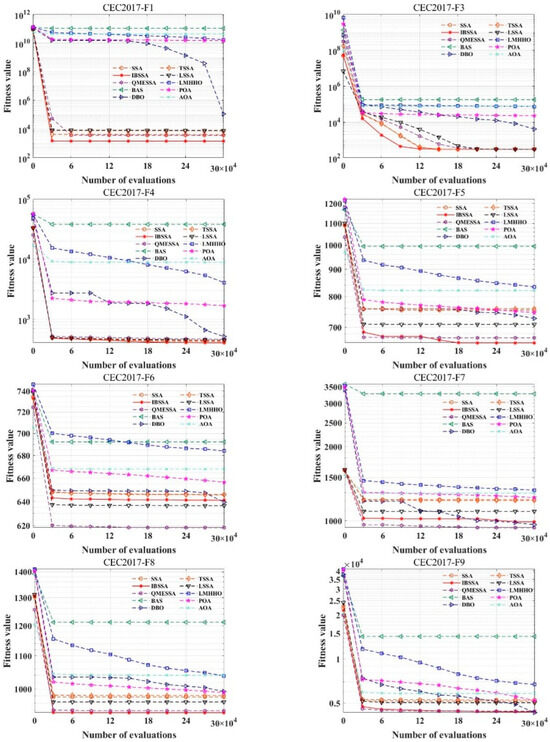
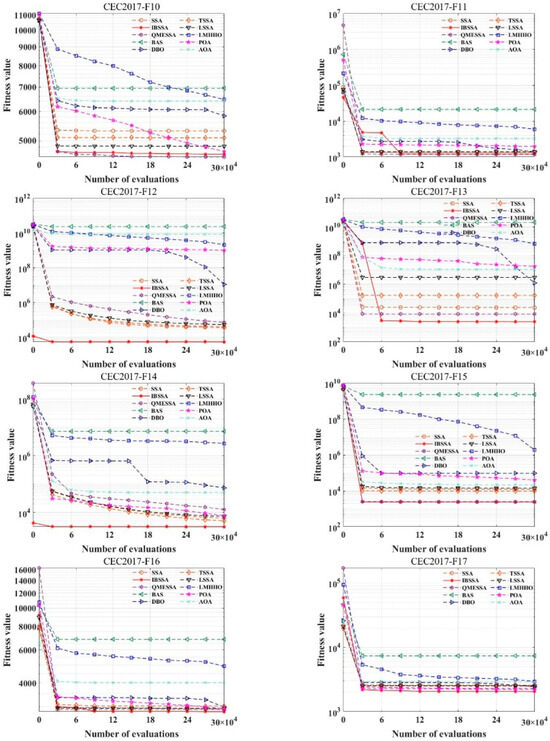
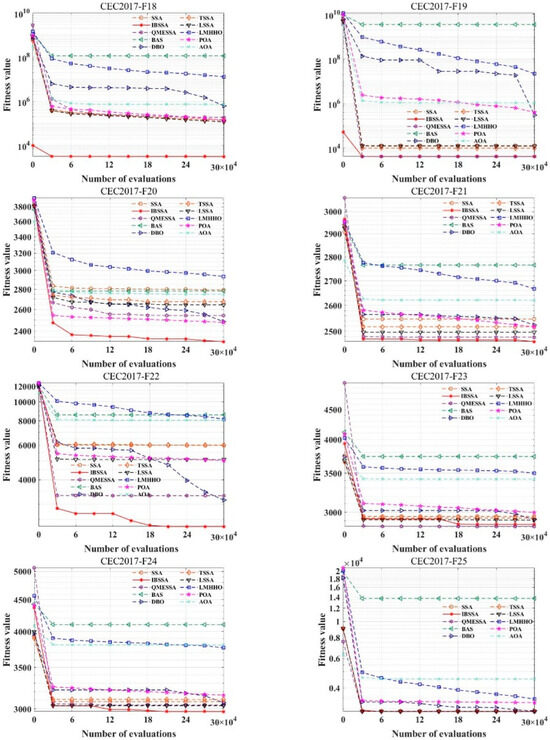
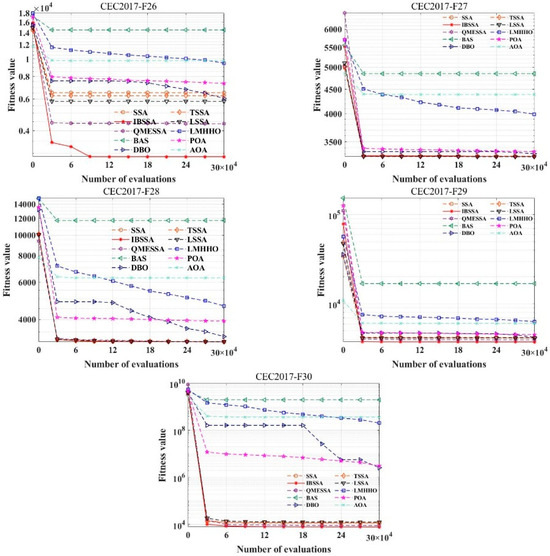
Figure 5.
Convergence graph of IBSSA and the other 9 algorithms on the CEC2017 (dim = 30) test suite.
It is difficult to observe the various data and the relationship between them from Table 6. In order to verify the stability and convergence of IBSSA, this paper also conducts a box plot analysis. Box plots summarize six types of data: maximum, upper quartile, median, lower quartile, minimum, and outlier. Figure 6 shows the box plot (dim = 30) of each algorithm in CEC2017 on 29 functions. In the figure, “+” in each box subplot indicates an outlier, “−” indicates the median, the two ends of the rectangular box are the upper and lower quartiles, and “-” indicates the largest value or minimum value. From Figure 6 below, it can be clearly seen that the length of the box plot of IBSSA is mostly shorter than those of other algorithms, and the stability is only worse in the comparison with SSA and SSA variants, but they are all in a small range. The gap indicates that IBSSA has good optimization performance and stability.
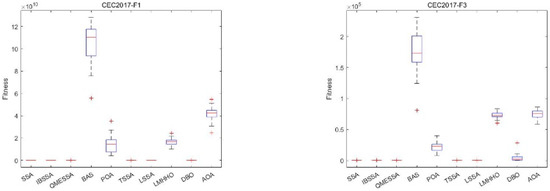
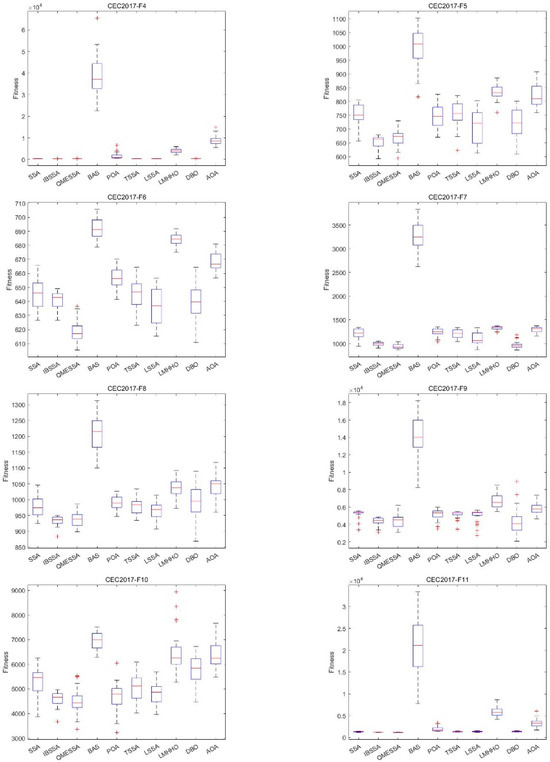
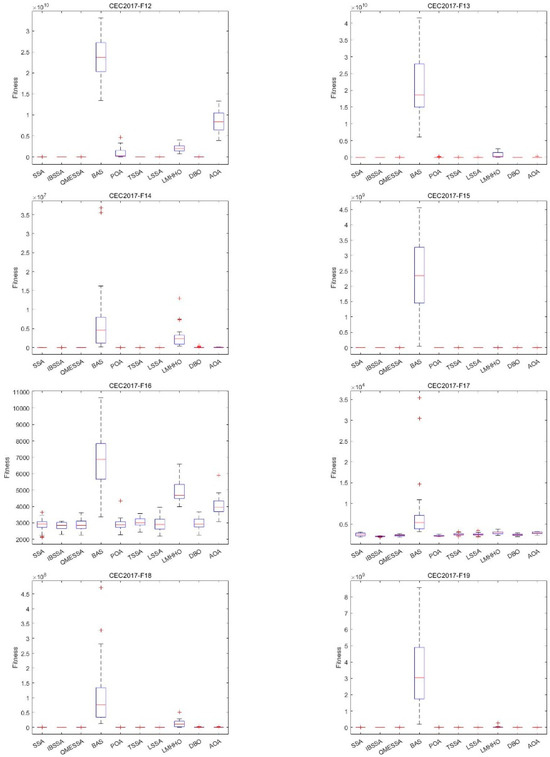
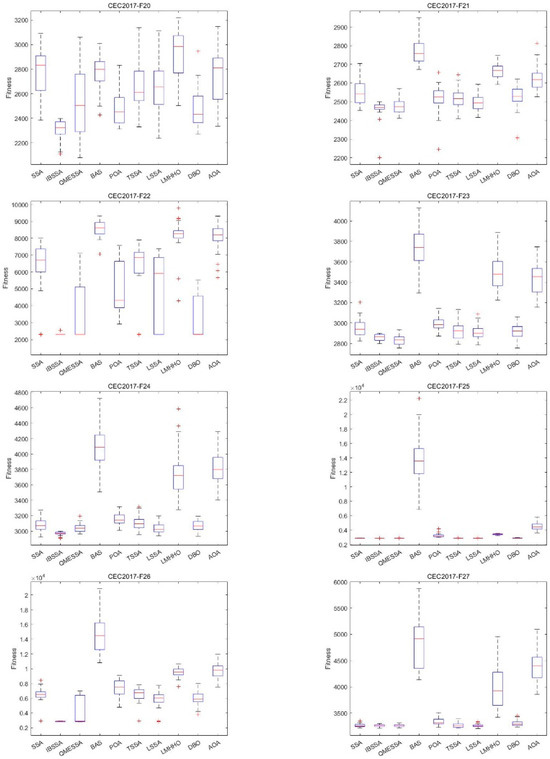
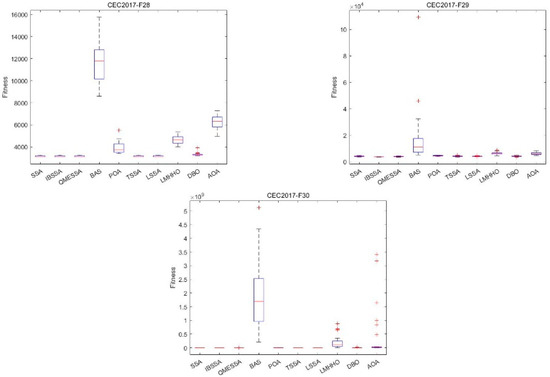
Figure 6.
Box plot of IBSSA and the other 9 algorithms on the CEC2017 (dim = 30) test suite.
The results indicate that IBSSA surpasses the SSA algorithm, its variants, and other algorithms in terms of optimization performance. IBSSA achieves this by enhancing the quality of the initial solution through the integration of elite individuals and employing elite dynamic opposite learning in the early stage. This improvement in the initialization process contributes to the overall effectiveness of IBSSA, and in the update formula of the original sparrow discoverer, the sparrow individual directly jumps to the current optimal solution instead of a slow process. The improved stage-by-stage guidance mechanism makes the update formula of the sparrow discoverer divided into three stages, slowly approaching the optimal solution to avoid falling into a local optimum and missing high-quality solutions and using a greedy strategy to fuse improvements The beetle’s antennae algorithm is used to further explore the particles near the optimal solution in a small range. IBSSA successfully combines the strengths of the sparrow search algorithm and the beetle’s antennae algorithm. It maintains the performance of the sparrow search algorithm while harnessing the global optimization capabilities of the beetle’s antennae algorithm. This integration prevents the sparrow search algorithm from getting trapped in local optima, ensuring better overall optimization performance. There is excellent maintenance of the optimization stability of the improved algorithm. It can be seen from the box plot (dim = 30) that IBSSA has good universality and robustness in terms of optimization stability.
6.2.3. CEC2017 Function Comparison under 50 Dimensions
According to the experimental data in Table 7, the two performance indicators of IBSSA on the following benchmark functions are at their best: F01, F12, F13, F14, F15, F16, F17, F18, F19, F21, F22, F23, and F25. These functions demonstrate the superior optimization performance of IBSSA. Additionally, on the CEC2017 test suite (dim = 50), the F30 function also shows optimal performance with IBSSA. One index of the 10 functions F05, F08, F09, F10, F17, F22, F26, F27, F28, and F29 is in the optimal state. IBSSA has shown better performance in single-mode function, multimode function, mixed function, and combination function. The test results of multimodal functions F03, F04, F06, and F07, mixed functions F11 and F20, and combined functions F23 and F24 are slightly worse than those of TSSA, LSSA, QMESSA, and SSA. According to Wilcoxon rank sum test (dim = 50) data, IBSSA is not similar to other algorithms, and more than half of the test results compared with QMESSA are better than QMESSA. With the rise of the problem dimension, although the performance of IBSSA decreases when compared with lower dimensions, in Friedman’s test results, IBSSA ranks first among the ten algorithms with an average ranking of 2.03 on 29 functions, which is still strong compared to other algorithms. In conclusion, IBSSA has the best performance on the CEC2017 test suite (dim = 50).
6.2.4. CEC2017 Ablation Experiment
Similarly, in order to better verify the role of the proposed strategies in the optimization process and the ability of each strategy to get rid of the optimal value that is not at the zero point, IBSSA was again ablated on the CEC2017 (dim = 30) test suite. The meanings of the tables represented by SSA1, SSA2, SSA3, SSA4, SSA5, and SSA6 are the same as those of the 20 benchmark test functions, the evaluation times are also 10000 * dim, and the parameter settings are the same as those of the comparison test. We ran the tests independently 30 times and recorded the average and standard deviation in Table 8.

Table 8.
IBSSA ablation test on CEC2017 test suite (dim = 30).
As shown in Table 8, IBSSA has the most bold font to indicate the optimal value, and it ranks first with 1.34 in the Friedman test ranking. It exhibits excellent performance in unimodal functions, simple multimodal functions, mixed functions, and combination functions. From the test values of SSA1-SSA6, we can see that they have significant improvements in some functions compared to SSA. Therefore, it can be verified that the proposed strategy has a good effect on the CEC 2017 test suite (dimension = 30). At the same time, the number of bold values with the fusion of the beetle antennae algorithm ranks second, and the number of bold values with dynamic reverse learning ranks third. This shows that the integration of the beetle antennae algorithm greatly improves the stability and optimization accuracy of the overall algorithm. F28 is the only function for which IBSSA and other strategies are not as good as SSA, while for other functions they are better than SSA. IBSSA considers the balance between development and exploration, maintaining individual progress to improve the algorithm’s local optimization ability.
7. Application of Engineering Optimization Problems
Through the performance analysis of the above algorithms, it can be concluded that the optimization performance of IBSSA is theoretically superior to other latest intelligent optimization algorithms. However, unlike the test function, there are many constraints in actual engineering problems, which is undoubtedly a challenge. Therefore, the practicality of IBSSA can be further verified through six optimization constraint problems in engineering, The compression spring design problem is tested for practicality. Each design problem is independently run 30 times, and the optimal value from the 30 results is taken for analysis [53]. The obtained data are shown in Table 9, Table 10, Table 11, Table 12, Table 13 and Table 14.

Table 9.
Experimental results of three truss problems.

Table 10.
WBD problem experimental results.

Table 11.
Experimental results of CSD problems.

Table 12.
Experimental results of PVD problems.

Table 13.
Experimental results of I-beam design problem.

Table 14.
Experimental results of gear train design problem.
7.1. Three Truss Problems
The three-bar truss design problem is a structural optimization problem in the field of civil engineering. As shown in Figure 7, its main purpose is to minimize the weight of the stress, disturbance, and buckling constraint between two bars and to minimize the volume of the three-bar truss by adjusting the cross-sectional area. The constraints for adjustment are as follows.
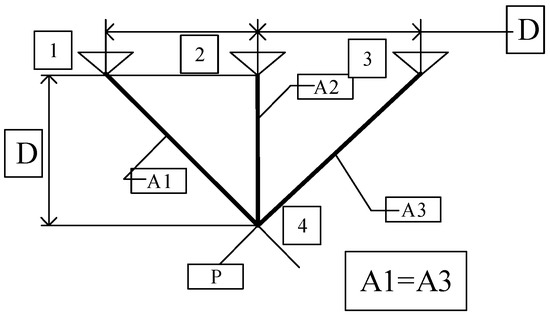
Figure 7.
Schematic diagram of three truss problems.
Consider:
Reduce to a minimum:
The following conditions must be met:
Variable range of parameters:
where
7.2. WBD
The purpose of the welding beam design problem is to estimate the best value of the thickness of the bar (b), the length of the attached part of the bar (l), the height of the bar (t), and the thickness of the weld (h). As shown in Figure 8, this is performed so as to minimize the consumables and reduce the construction cost. The model expression is as follows:
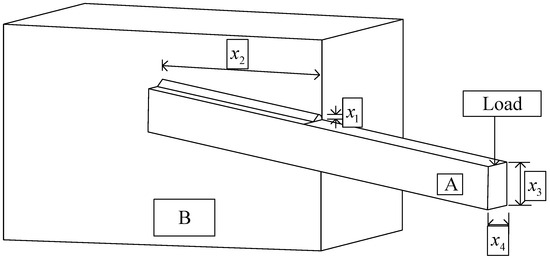
Figure 8.
Schematic diagram of WBD problem.
Variable:
The following conditions need to be met:
Domain of variables:
where
7.3. CSD
The tension/compression spring design problem is intended to obtain the minimum tension/compression spring weight, and it should meet the minimum disturbance, vibration frequency, and shear stress constraints. As shown in Figure 9, the model for this case is expressed as follows:
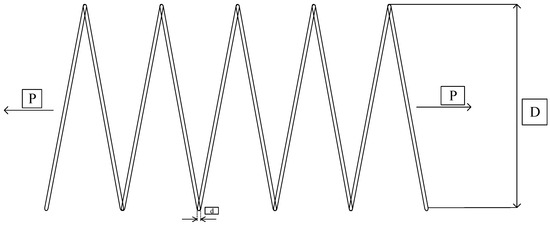
Figure 9.
Schematic diagram of CSD problems.
Variable:
Need to reach the minimum:
The following conditions need to be met:
Domain of variables:
7.4. PVD
The objective of the pressure vessel design is to minimize the manufacturing cost associated with the production of the pressure vessel. The design of the pressure vessel is illustrated in Figure 10. Both ends of the pressure vessel are enclosed by covers, with the cover at one end of the head being hemispherical. The four design variables that must be taken into account are the thickness of the shell (Ts), the thickness of the head (Th), the inner radius of the shell (R), and the length of the container (L). The mathematical model is as follows:
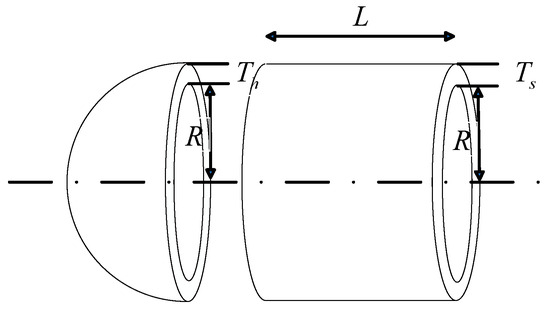
Figure 10.
Schematic diagram of PVD problems.
7.5. Vertical Deflection of an I-Beam
The goal of this problem is to optimize four parameters, I1, I2, I3, and I4, namely the flange width, beam height, web thickness, and flange thickness, using the given objective function. The goal is to find the optimal variable that minimizes the vertical deflection of the I-beam while satisfying the preset cross-sectional area and stress constraints under the load, as shown in Figure 11. The objective function considers a length beam of 5200 cm, a design load of 600 KN, and an elastic modulus of 523,104 KN/cm2 [54].
where
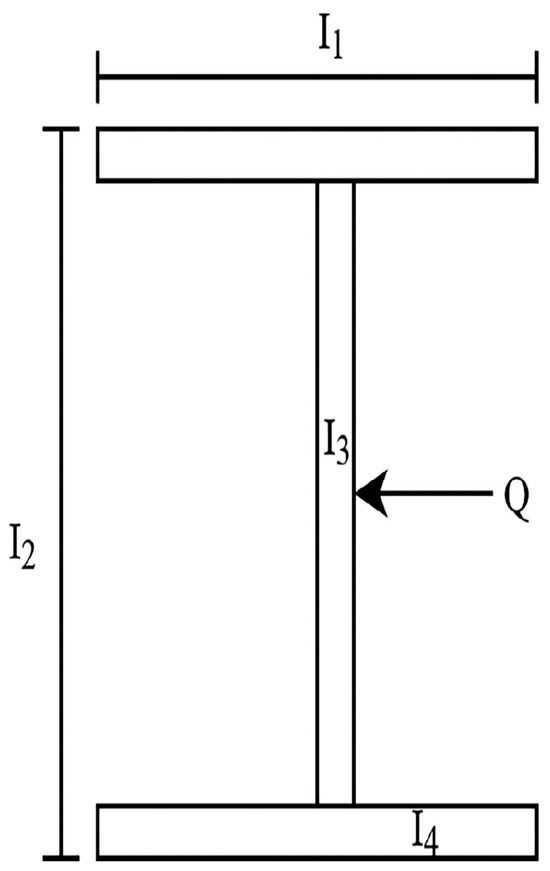
Figure 11.
Schematic diagram of I-beam design problem.
7.6. Gear Train Design
The gear system design problem is a discrete unconstrained optimization problem with the goal of minimizing the cost of the gear transmission ratio. To solve this problem, it is necessary to optimize four integer design variables, g1, g2, g3, and g4, each representing the number of teeth of four different gears. The structural schematic diagram of the wheel system design problem is shown in Figure 12.
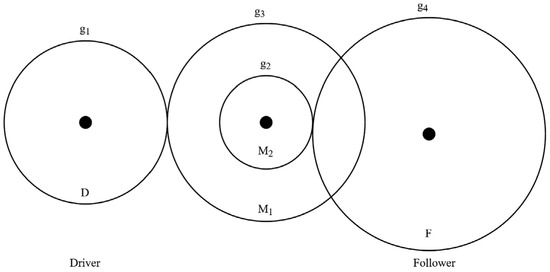
Figure 12.
Schematic diagram of gear train design problem.
The objective function is:
where
Through the calculation results of six typical engineering optimization problems, it can be seen that QMESSA has advantages in engineering optimization problems, and IBSSA has significant advantages in handling engineering optimization problems, which can reduce design costs.
8. Summary
In this study, a new algorithm (IBSSA) was proposed that combines the improved learning-based beetle antennae algorithm with the sparrow search algorithm. Due to the simple population initialization process of the basic sparrow search algorithm and its randomness in obtaining high-quality initial solutions, an elite dynamic opposite learning mechanism was proposed to obtain elite solutions from randomly generated initial solutions, thus improving the quality of initial solutions. It is beneficial for the discoverers of sparrow algorithms to develop. At the same time, the development process of the sparrow search algorithm was further strengthened through a phased guidance mechanism. Finally, the improved beetle antennae algorithm was integrated with the sparrow’s vigilante update through logarithmic spiral opposition-based learning. Through a greedy strategy, combined with the improved global optimization performance of the beetle antennae algorithm, the development and exploration performance of the sparrow search algorithm are ensured. When the sparrow search algorithm falls into a local optimum, it can be improved by using the beetle antennae algorithm to jump out of the local optimum, which is conducive to achieving a balance between development and exploration through local optimization. This algorithm optimizes the basic sparrow search algorithm from both global search and local collaborative search. These three strategies can simultaneously improve the global and local optimization performance of the sparrow search algorithm. Considering that original dynamic opposite learning is a dynamic process for the entire population of particles, there will also be poorly randomized particles. Through the operation of elite opposite learning, not only can the elite particles in the original initialization process solution be obtained, but also the randomness of these elite particles can be further improved through the dynamic process, thus obtaining a wider range of solutions and improving the development performance of the algorithm. The proposal of a phased guidance mechanism takes into account the need for a stable transition in the development process of the discoverer in the sparrow search algorithm. In the early stage, due to the existence of local solutions, it is manifested as a larger parameter value to obtain better global solutions. In the mid-term, it should ensure a stable transition from development to local parts of the algorithm, achieving a balance between development and exploration. Therefore, the parameter value shows a linear decreasing trend. In the later stages of algorithm iteration, more emphasis should be placed on local development of the algorithm and improving the search speed. The logarithmic spiral opposition-based learning strategy obtains the position of particles near the optimal value and combines it with the beetle antennae algorithm to purposefully search for the optimal value in a smaller range, thus preventing the algorithm from falling into local optima. And, it greedily integrates with the vigilance update method of the sparrow population, further improving the overall algorithm optimization accuracy without affecting the performance of the sparrow search algorithm itself. In order to verify the overall performance of IBSSA, it was benchmark-tested with nine advanced algorithms, and we further discussed its performance characteristics using the Wilcoxon rank sum test. In order to break away from the algorithm’s dependence on zero points, IBSSA was tested with nine advanced algorithms in CEC2017, and its performance was further verified through the Wilcoxon rank sum test. Two sets of experiments have shown that IBSSA outperforms other comparative algorithms in terms of convergence accuracy, stability, and other aspects. Finally, the robustness and applicability of IBSSA were verified through six basic engineering applications, further demonstrating its good performance and reducing design costs in practical engineering applications.
However, for multi-dimensional optimization problems, the optimization performance of IBSSA may slightly decrease. IBSSA cannot maintain good performance like it does with low-dimensional problems, so it cannot guarantee good optimization performance when facing multi-objective optimization problems and high-dimensional problems. This is also a problem that needs to be considered in the future. With the continuous development of the field of artificial intelligence, multi-dimensional and multi-objective optimization problems will be the mainstream problems in the field of evolutionary algorithms, so the future work will be to further modify and improve the existing single-objective optimization IBSSA, which can give it good multi-objective optimization performance, and apply it to more application scenarios to deal with complex optimization problems. And, by conducting more detailed analysis on higher-dimensional test functions (such as 100 or 1000 dimensions), the results of the 10-, 30-, and 50-dimensional test functions represent a part of the performance of the improved algorithm. Considering the special needs of high-dimensional optimization problems, we plan to expand the experimental scope in future research to cover higher-dimensional test problems and further verify the performance of the algorithm in these high-dimensional problems.
Author Contributions
Conceptualization, C.Y. and D.Z.; methodology, X.Z. and D.Z.; software, C.Y. and D.Z.; validation, X.Z.; formal analysis, Y.L.; investigation, C.Y. and X.Z.; resources, X.Z.; data curation, X.Z.; writing—original draft preparation, C.Y.; writing—review and editing, C.Y. and X.Z.; visualization, C.Y. and D.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the University–Industry Collaborative Education Program: Design and Practice of “Data Visualization” Course Based on Blended Teaching Mode (Project Number: 230710174707184).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Pepelyshev, A.; Zhigljavsky, A.; Žilinskas, A. Performance of global random search algorithms for large dimensions. J. Glob. Optim. 2018, 71, 57–71. [Google Scholar] [CrossRef]
- Bullock, G.N.; Denham, M.J.; Parmee, I.C.; Wade, J.G. Developments in the use of the genetic algorithm in engineering design. Des. Stud. 1995, 16, 507–524. [Google Scholar] [CrossRef]
- Gajpal, Y.; Rajendran, C. An ant-colony optimization algorithm for minimizing the completion-time variance of jobs in flowshops. Int. J. Prod. Econ. 2006, 101, 259–272. [Google Scholar] [CrossRef]
- Fang, H.; Chen, L.; Shen, Z. Application of an improved PSO algorithm to optimal tuning of PID gains for water turbine governor. Energy Convers. Manag. 2011, 52, 1763–1770. [Google Scholar] [CrossRef]
- Niculescu, S.P. Artificial neural networks and genetic algorithms in QSAR. J. Mol. Struct. THEOCHEM 2003, 622, 71–83. [Google Scholar] [CrossRef]
- Kumru, M. Assessing the visual quality of sanitary ware by fuzzy logic. Appl. Soft Comput. 2013, 13, 3646–3656. [Google Scholar] [CrossRef]
- Peng, F.; Cui, G. Efficient simultaneous synthesis for heat exchanger network with simulated annealing algorithm. Appl. Therm. Eng. 2015, 78, 136–149. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Huang, Z.; Zhou, C.; Zhang, L. A JAYA algorithm based on normal clouds for DNA sequence optimization. Clust. Comput. 2023, 27, 2133–2149. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, S.; Zhou, C.; Yan, S. Manta ray foraging optimization based on mechanics game and progressive learning for multiple optimization problems. Appl. Soft Comput. 2023, 145, 110561. [Google Scholar] [CrossRef]
- Rambabu, D.; Govardhan, A. Optimization assisted frequent pattern mining for data replication in cloud: Combining sealion and grey wolf algorithm. Adv. Eng. Softw. 2023, 176, 103401. [Google Scholar]
- Zhang, Y.; Hou, X. Application of video image processing in sports action recognition based on particle swarm optimization algorithm. Prev. Med. 2023, 173, 107592. [Google Scholar] [CrossRef]
- Fahmy, H.; El-Gendy, E.M.; Mohamed, M.A.; Saafan, M.M. ECH3OA: An Enhanced Chimp-Harris Hawks Optimization Algorithm for copyright protection in Color Images using watermarking techniques. Knowl. Based Syst. 2023, 269, 110494. [Google Scholar] [CrossRef]
- Zhang, F.; Deng, S.; Zhao, H.; Liu, X. A new hybrid method based on sparrow search algorithm optimized extreme learning machine for brittleness evaluation. J. Appl. Geophys. 2022, 207, 104845. [Google Scholar] [CrossRef]
- Zhu, D.; Huang, Z.; Liao, S.; Zhou, C.; Yan, S.; Chen, G. Improved Bare Bones Particle Swarm Optimization for DNA Sequence Design. IEEE Trans. NanoBiosci. 2023, 22, 603–613. [Google Scholar] [CrossRef] [PubMed]
- Zhang, E.; Nie, Z.; Yang, Q.; Wang, Y.; Liu, D.; Jeon, S.; Zhang, J. Heterogeneous cognitive learning particle swarm optimization for large-scale optimization problems. Inf. Sci. 2023, 633, 321–342. [Google Scholar] [CrossRef]
- Sui, F.; Tang, X.; Dong, H.; Gen, X.; Luo, P.; Sun, J. ACO+PSO+A*: A bi-layer hybrid algorithm for multi-task path planning of an AUV. Comput. Ind. Eng. 2023, 175, 108905. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, D.; Wang, X. Shortest Path Planning Based on Improved Ant Colony Algorithm. ASP Trans. Comput. 2021, 1, 6–11. [Google Scholar]
- Alsattar, H.A.; Zaidan, A.A.; Zaidan, B.B. Novel meta-heuristic bald eagle search optimisation algorithm. Artif. Intell. Rev. 2020, 53, 2237–2264. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.; Gondomi, A. The Arithmetic Optimization Algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Tubishat, M.; Alswaitti, M.; Mirjalili, S.; Al-Garadi, M.; Alrashdan, M.T.; Rana, T.A. Dynamic Butterfly Optimization Algorithm for Feature Selection. IEEE Access 2020, 8, 194303–194314. [Google Scholar] [CrossRef]
- Pan, J.; Lv, J.; Yan, L.; Weng, S.; Chu, S.; Xue, J. Golden eagle optimizer with double learning strategies for 3D path planning of UAV in power inspection. Math. Comput. Simul. 2022, 193, 509–532. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G.; Zhou, K.; Zhu, L. A parallel particle swarm optimization and enhanced sparrow search algorithm for unmanned aerial vehicle path planning. Heliyon 2023, 9, 14784. [Google Scholar] [CrossRef]
- Zheng, F.; Liu, G. An Adaptive Sinusoidal-Disturbance-Strategy Sparrow Search Algorithm and Its Application. Sensors 2022, 22, 8787. [Google Scholar] [CrossRef]
- Huang, Z.; Zhu, D.; Liu, Y.; Wang, X. Multi-strategy sparrow search algorithm with non-uniform mutation. Syst. Sci. Control Eng. 2022, 10, 936–954. [Google Scholar] [CrossRef]
- Sun, H.; Wang, J.; Chen, C.; Li, Z.; Li, J. ISSA-ELM: A Network Security Situation Prediction Model. Electronics 2023, 12, 25. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, J.; Zhao, A.; Zhong, Y.; Yang, S.; Wang, M. Optimal chiller loading by improved sparrow search algorithm for saving energy consumption. J. Build. Eng. 2023, 67, 105980. [Google Scholar] [CrossRef]
- Liu, R.; Mo, Y. Performance of a Novel Enhanced Sparrow Search Algorithm for Engineering Design Process: Coverage Optimization in Wireless Sensor Network. Processes 2022, 10, 1691. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, E. An improved sparrow search based intelligent navigational algorithm for local path planning of mobile robot. J. Ambient. Intell. Humaniz. Comput. 2022, 14, 14111–14123. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, A.; Han, Y.; Nan, J.; Li, K. Fast stochastic configuration network based on an improved sparrow search algorithm for fire flame recognition. Knowl. Based Syst. 2022, 245, 108626. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z. A Hybrid Sparrow Search Algorithm Based on Constructing Similarity. IEEE Access 2021, 9, 117581–117595. [Google Scholar]
- Gao, B.; Shen, W.; Guan, H.; Zheng, L.; Zhang, W. Research on Multistrategy Improved Evolutionary Sparrow Search Algorithm and its Application. IEEE Access 2022, 10, 62520–62534. [Google Scholar] [CrossRef]
- Liu, G.; Shu, C.; Liang, Z.; Liang, Z.; Peng, B.; Cheng, L. A Modified Sparrow Search Algorithm with Application in 3d Route Planning for UAV. Sensors 2021, 21, 1224. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Huang, X.; Zhu, D. A Multistrategy-Integrated Learning Sparrow Search Algorithm and Optimization of Engineering Problems. Comput. Intell. Neurosci. 2022, 2022, 2475460. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997, 1, 67–82. [Google Scholar] [CrossRef]
- Žilinskas, A.; Calvin, J. Bi-objective decision making in global optimization based on statistical models. J. Glob. Optim. 2019, 74, 599–609. [Google Scholar] [CrossRef]
- Xu, Y.; Yang, Z.; Li, X.; Kang, H.; Yang, X. Dynamic opposite learning enhanced teaching–learning-based optimization. Knowl. Based Syst. 2020, 188, 104966. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, K.; Li, P. An Improved Chaos Sparrow Search Optimization Algorithm Using Adaptive Weight Modification and Hybrid Strategies. IEEE Access 2020, 10, 96159–96179. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Izci, D.; Ekinci, S.; Eker, E.; Kayri, M. Augmented hunger games search algorithm using logarithmic spiral opposition-based learning for function optimization and controller design. J. King Saud Univ. Eng. Sci. 2022, in press, corrected proof. [Google Scholar] [CrossRef]
- Jiang, X.; Li, S. BAS: Beetle Antennae Search Algorithm for Optimization Problems. arXiv 2017, arXiv:1710.10724. [Google Scholar] [CrossRef]
- Ouyang, C.; Zhu, D.; Wang, F. A Learning Sparrow Search Algorithm. Comput. Intell. Neurosci. 2021, 2021, 23. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Huang, Y. Short term photovoltaic power prediction based on BP neural network optimized by improved sparrow search algorithm. In Proceedings of the 2022 4th International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 9–11 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 314–317. [Google Scholar]
- Mirjalili, S.; Lewis, A. Adaptive gbest-guided gravitational search algorithm. Neural Comput. Appl. 2014, 25, 1569–1584. [Google Scholar] [CrossRef]
- Mohammad, H.; Nadimi, S.; Shokooh, T. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar]
- Xue, J.; Shen, B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization. J. Supercomput. 2023, 79, 7305–7336. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2014, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Wu, R.; Huang, H.; Wei, J. An improved sparrow search algorithm based on quantum computations and multi-strategy enhancement. Expert Syst. Appl. 2023, 215, 119421. [Google Scholar] [CrossRef]
- Naik, M.K.; Panda, R.; Wunnava, A. A leader Harris hawks optimization for 2-D Masi entropy-based multilevel image thresholding. Multimed. Tools Appl. 2021, 80, 35543–35583. [Google Scholar] [CrossRef]
- Trojovský, P.; Dehghani, M. Pelican Optimization Algorithm: A Novel Nature-Inspired Algorithm for Engineering Applications. Sensors 2022, 22, 855. [Google Scholar] [CrossRef] [PubMed]
- Oszust, M. Enhanced Marine Predators Algorithm with Local Escaping Operator for Global Optimization. Knowl. Based Syst. 2021, 232, 107467. [Google Scholar] [CrossRef]
- Minocha, S.; Singh, B. A novel equilibrium optimizer based on levy flight and iterative cosine operator for engineering optimization problems. Expert Syst. 2022, 39, e12843. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).