Multisite Long-Term Photovoltaic Forecasting Model Based on VACI

Abstract

In the field of photovoltaic (PV) power prediction, long-term forecasting, which is more challenging than short-term forecasting, can provide more comprehensive and forward-looking guidance. Currently, significant achievements have been made in the field of short-term forecasting for PV power, but inadequate attention has been paid to long-term forecasting. Additionally, multivariate global forecasting across multiple sites and the limited historical time series data available further increase the difficulty of prediction. To address these challenges, we propose a variable–adaptive channel-independent architecture (VACI) and design a deep tree-structured multi-scale gated component named DTM block for this architecture. Subsequently, we construct a specific forecasting model called DTMGNet. Unlike channel-independent modeling and channel-dependent modeling, the VACI integrates the advantages of both and emphasizes the diversity of training data and the model’s adaptability to different variables across channels. Finally, the effectiveness of the DTM block is empirically validated using the real-world solar energy benchmark dataset. And on this dataset, the multivariate long-term forecasting performance of DTMGNet achieved state-of-the-art (SOTA) levels, particularly making significant breakthroughs in the 720-step ultra-long forecasting window, where it reduced the MSE metric below 0.2 for the first time (from 0.215 to 0.199), representing a reduction of 7.44%.

1. Introduction

In recent years, the severe issue of global non-renewable energy scarcity [1,2], coupled with long-term plans for carbon neutrality and peak carbon dioxide emissions [3], has made the demand for clean energy generation more urgent than ever [4]. The significant advantages of photovoltaic power generation have garnered special attention and promotion from countries worldwide [5]. Accurate prediction of PV power generation not only provides a basis for grid-connected operation and energy management of PV plants but also serves as a reference for timely detection of equipment anomalies and troubleshooting [6].

However, the key factor influencing PV power, solar irradiance, is affected by a combination of climate, geographical location, and time, exhibiting significant non-stationarity [7]. This is manifested in the continuously changing statistical properties and joint distributions, making accurate prediction extremely challenging. Traditional methods such as autoregressive integrated moving average (ARIMA) [8], exponential smoothing (ES) [9], and Kalman filtering [10] are based on the assumption of time series stationarity or statistical properties to predict future values, and thus are no longer applicable in the current non-stationary environment [11].

Additionally, due to the unique characteristics of electricity and the stringent requirements of power grid management, there is a more urgent need for long-term forecasting of PV power generation compared to short-term forecasting. The long-term forecasting is crucial for better planning of energy storage and grid-connected power generation [12,13]. And this necessitates higher predictive capabilities from the models, requiring accurate and effective capture of long-term dependencies between inputs and outputs over extended periods [14]. Simultaneously, the challenge of prediction is further compounded by the need for multivariate global forecasting across multiple sites and the limited availability of historical time series data [15]. In this context, multivariate time series forecasting models must capture the dependencies among various variables or channels to better predict multivariate outputs [16].

To address the aforementioned issues, this paper first proposes an approach from the perspective of improving channel architecture to solve the problem of data scarcity when training highly expressive, large-scale forecasting models and the issue of inter-variable dependencies in multivariate forecasting. Secondly, a deep tree-structured multi-scale gated guidance model framework is constructed. The deep residual connection stacking significantly ensures the model’s representational capacity, allowing for better modeling of both global and local detail dependencies in long-term time series, as well as the mapping information to the predictive outcomes.

In summary, the contributions of this paper are as follows:

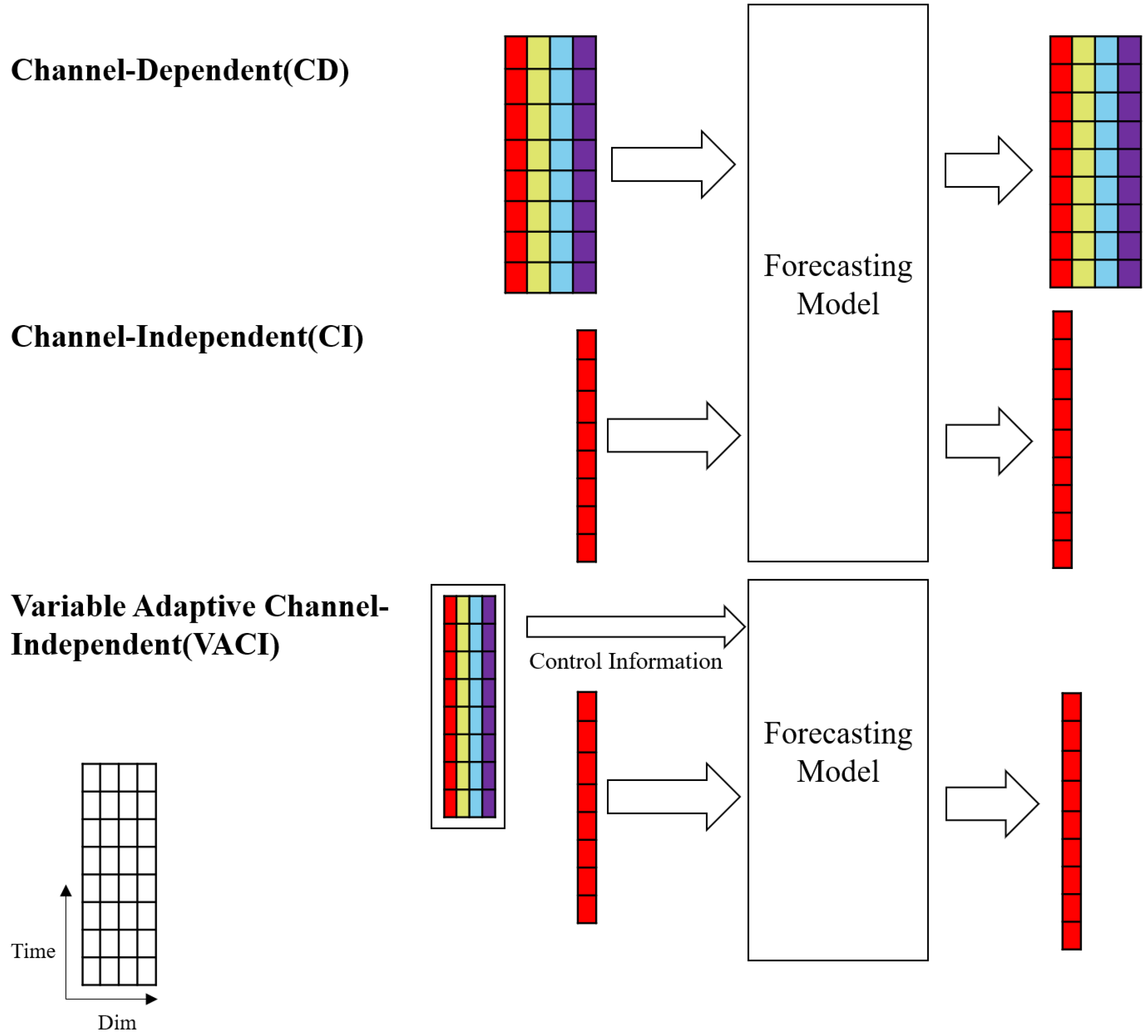
• Proposing an improved model architecture—variable–adaptive channel-independent architecture, which combines the advantages of increased training data volume and high robustness brought by channel independence and the benefits of enhanced representation performance from channel dependence;
• Presenting a specific scheme for the variable–adaptive channel-independent architecture by introducing a deep tree-structured multi-scale gated component into the backbone of the forecasting model, and subsequently demonstrating its effectiveness through ablation experiments;
• Developing a forecasting model called DTMGNet based on the deep tree-structured multi-scale gated component, which outperforms existing advanced methods on the solar energy benchmark dataset, achieving SOTA performance.

2. Related Work

2.1. PV Power Forecasting Task

Currently, research on PV power forecasting primarily concentrates on short-term forecasting, with forecast cycles generally ranging from seconds to one hour ahead [17]. These short-term forecasting approaches can be broadly categorized into three main types: physical methods, statistical methods, and deep learning methods [18]. Physical methods typically utilize measurement data and detailed geographical information of the power station to calculate PV power [19,20,21]. However, relying solely on physical modeling to compute PV power exhibits moderate interference resistance and lacks robustness [22]. Traditional statistical methods, such as ETS [23] and ARIMA [8], often demonstrate inadequate performance in capturing complex temporal dynamics [14]. Deep learning-based methods usually employ convolutional neural networks (CNN) [24], long short-term memory networks (LSTM) [25], or hybrid models combining both, along with some signal processing techniques for short-term forecasting [26].

For PV power forecasting tasks, diverse data are typically required for modeling, and correlation analysis needs to be conducted [18]. However, in the current field of multivariate long-term prediction, researchers often use the publicly available “solar energy” dataset [27]. This dataset only contains power generation records from 137 PV facilities, which requires researchers to build models for 137 variables or channels and make 137 sets of predictions. And the prediction work is based on exploring historical patterns from historical data to make overall predictions. It does not need to involve more detailed and underlying information about different PV grid-connected systems. Therefore, this multivariate prediction method demands the ability to comprehensively capture both the local and global characteristics of each channel from the perspective of data mining, thereby enhancing the overall accuracy and reliability of predictions [15]. This is of great significance for optimizing energy scheduling, improving grid stability, and promoting large-scale integration of renewable energy [18].

2.2. Long-Term Series Forecasting (LTSF)

In recent years, the emergence of transformers has significantly advanced the field of LTSF. Initially, the transformer architecture gained widespread attention in the LTSF domain due to its powerful capability to model long-term dependencies. Models such as Informer [14], Autoformer [28], and FEDformer [29] have modified the native transformer structure to better accommodate time series forecasting tasks.

Recently, models like PatchTST [30] and PETformer [31] have demonstrated that the original transformer architecture can achieve better results through appropriate patching strategies, a technique commonly applied in the computer vision field. Additionally, iTransformer [32] has further advanced the field by treating independent time series as tokens and capturing multivariate correlations through self-attention mechanisms, achieving top-tier performance. Moreover, CNNs, recurrent neural networks (RNNs), and graph neural networks (GNNs) [33] have also shown promising results in LTSF tasks. Notable works include SCINet [34], TimesNet [35], SegRNN [36], and CrossGNN [37].

Of particular interest is the resurgence of methods, based on multi-layer perceptron (MLP), which provide a straightforward and highly effective approach for learning the nonlinear temporal dependencies in time series [38]. Recent work, LTSF-Linear [39], suggests that transformer-based methods may not be as effective as previously thought in other domains. It was found that their impressive forecasting results might primarily rely on single-step forecasting rather than iterative forecasting. Surprisingly, LTSF-Linear, which uses only a single linear layer, outperforms many existing complex architectures. Additionally, MLP-based architectures such as FreTS [40], TiDE [41], TSMixer [42], FITS [43], and TimeMixer [44] have also achieved state-of-the-art results.

In this paper, the aforementioned methods were comprehensively considered, with a particular focus on their experimental performance in long-term forecasting. We have chosen a more direct and efficient MLP architecture as the backbone for our forecasting model. Innovatively, a deep tree-structured multi-scale gated component is introduced to control the flow, effectively integrating it with the backbone to achieve the variable–adaptive channel-independent architecture.

2.3. Multivariate Time Series Forecasting (MTSF)

There are two primary approaches for addressing the task of MTSF: channel-dependent methods and channel-independent methods. The channel-dependent architecture considers all channels simultaneously as input, with the predicted future values depending on the historical values of all channels. In contrast, the channel-independent architecture treats the multivariate sequence as multiple univariate sequences, training a unified model on these sequences where each channel is predicted independently, ignoring the relationships between different channels [45].

Channel-dependent methods exhibit stronger learning capabilities but often lack robustness in accurately predicting time series with distribution shifts. Conversely, channel-independent methods trade off model performance for increased robustness in predictions [15]. Thus, resolving the trade-off between model performance and prediction robustness is crucial in the design of multivariate forecasting models. In this work, we propose a variable–adaptive channel-independent architecture that combines the high robustness advantage of channel-independent methods with the representational performance enhancement brought by channel-dependent methods. This approach emphasizes training robustness and the model’s adaptive capability to different variables across channels.

3. Preliminaries

Multisite long-term forecasting can essentially be defined as multivariate long-term time series forecasting (MLTSF). In this context, multivariate time series forecasting refers to predicting future values $\mathrm{Y}=\left\{{\mathrm{y}}_{\mathrm{L}+1},\dots ,{\mathrm{y}}_{\mathrm{L}+\mathrm{H}}\right\} \in {\mathrm{R}}^{\mathrm{H}\times \mathrm{C}}$, given historical observations $\mathrm{X}=\left\{{\mathrm{x}}_1,\dots ,{\mathrm{x}}_{\mathrm{L}}\right\} \in {\mathrm{R}}^{\mathrm{L}\times \mathrm{C}}$, where $\mathrm{L}$ denotes the length of the historical observation window, $\mathrm{C}$ is the number of different features or channels, typically far more than 1, and $\mathrm{H}$ is the length of the forecasting horizon. Long-term time series forecasting involves using previously observed time series data to predict the sequence values over a longer future period. The primary objective of LTSF is to extend the forecasting horizon $\mathrm{H}$, as it provides richer and more forward-looking guidance in practical applications, often referring to predictions for more than 100 future time points, with the forecast cycle generally ranging from a day to one month ahead [14]. However, the extended forecasting horizon $\mathrm{H}$ also increases the challenge and complexity of the prediction model.

4. Proposed Method

4.1. Variable–Adaptive Channel-Independent Architecture (VACI)

The core improvement concept of the proposed variable–adaptive channel-independent architecture is to integrate the advantages of both channel independence and channel dependence. This approach aims to simultaneously harness the high robustness brought by channel independence and the enhanced representational performance provided by channel dependence [15].

As illustrated in Figure 1, the VACI emphasizes adaptive perception of input time sequences in the channel dimension and generates control information to guide the model. And this is built upon the foundation that channel independence focuses solely on the time dimension, yielding richer training data and a more robust model. The adaptive perception is particularly important when there are significant statistical differences between variables.

In terms of handling channel dependence, unlike current channel-dependent methods that directly fuse all features for modeling and rely on complex internal mechanisms of the model to select, suppress, or amplify features, the channel dependence in VACI is manifested in a more direct and explicit perception of common patterns and unique patterns among different variables. The perceived feature control information then guides the model, and with the increased training data volume brought by channel independence, the trained model exhibits higher robustness in predicting different variables.

To implement the VACI concept, this work proposes a specific solution: the deep tree-structured multi-scale gated component (DTM block) guides the channel-independent backbone model to address channel dependence issues. This will be elaborated in detail when describing the DTMGNet model in the following sections.

4.2. DTMGNet

As illustrated in Figure 2, DTMGNet comprises two primary data flows. One is the input stream that performs subtraction decomposition operations through residual connections, and the other is the deep multi-scale control stream that adaptively perceives different variables and input features via the DTM block. The foundational framework is based on residual connections, which facilitate the stacking of multiple layers [46]. Throughout this process, the input data pass through several neural blocks capable of extracting and transforming signals. Subsequently, the intricate details of each component within the architecture will be delved into.

4.2.1. Instance Normalization

Time series data often exhibit distributional changes between training and testing datasets. Recent studies have shown that employing a simple instance normalization strategy between the model’s input and output can help mitigate this issue [47]. In our work, a normalization strategy is also utilized. Specifically, we perform normalization and denormalization directly when the sequences are processed through the model. This process can be expressed as

$${\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}={\displaystyle \frac{{\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}-{\mathrm{E}}_{\mathrm{t}}\left({\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}\right)}{\mathrm{\sigma }\left({\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}\right)}}$$

(1)

$${\mathrm{x}}_{\mathrm{t}+1:\mathrm{t}+\mathrm{H}}=\left[{\mathrm{x}}_{\mathrm{t}+1:\mathrm{t}+\mathrm{H}}+{\mathrm{E}}_{\mathrm{t}}\left({\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}\right)\right]\ast \mathrm{\sigma }\left({\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}\right)$$

(2)

where ${\mathrm{x}}_{\mathrm{t}-\mathrm{L}+1:\mathrm{t}}$ is the input sequence from time t − L + 1 to t, ${\mathrm{x}}_{\mathrm{t}+1:\mathrm{t}+\mathrm{H}}$ is the predicted sequence from time t + 1 to t + H, ${\mathrm{E}}_{\mathrm{t}}\left(·\right)$ denotes the expected value or mean of the sequence, and $\mathrm{\sigma }\left(·\right)$ denotes the standard deviation of the sequence.

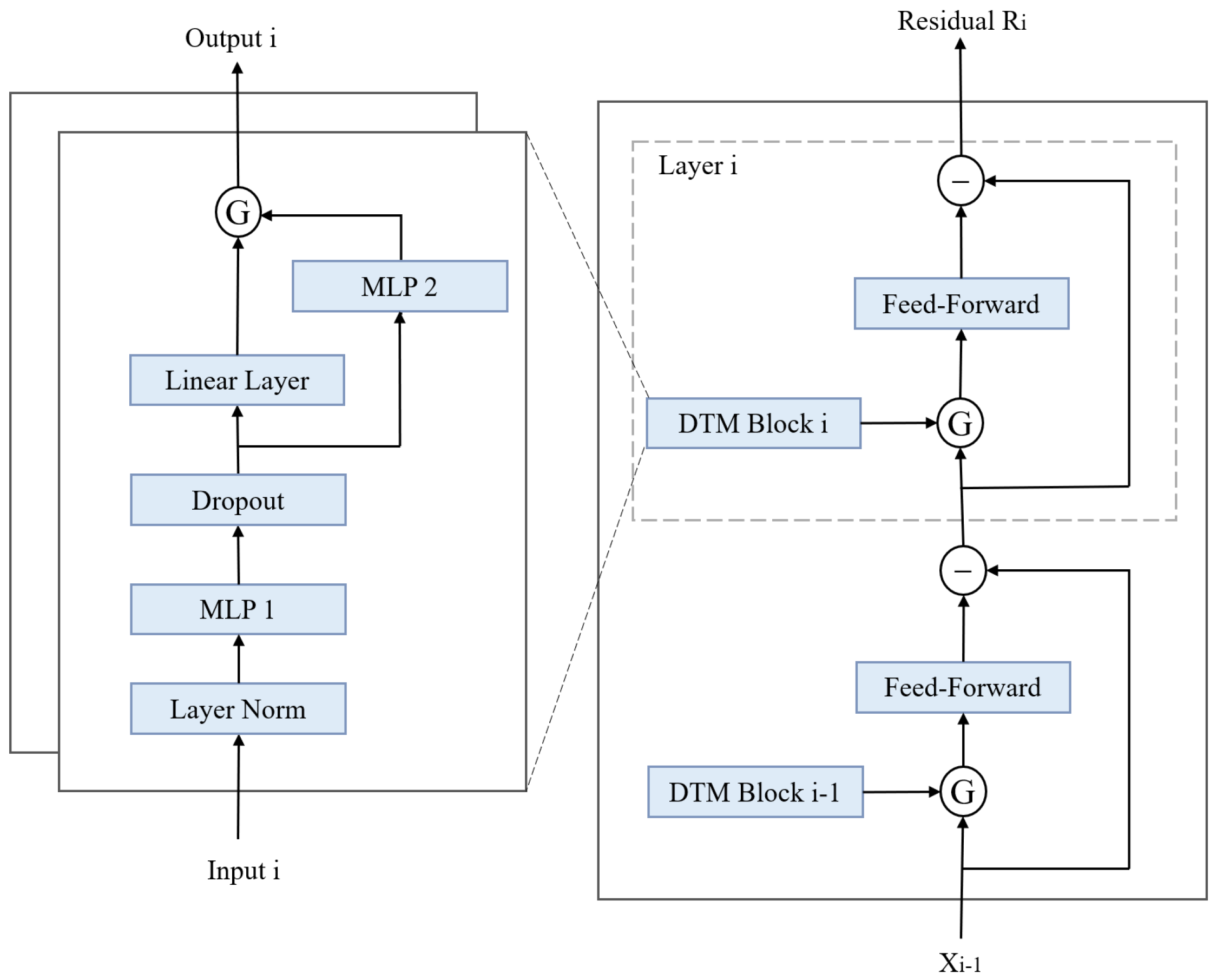
4.2.2. Backbone

As illustrated on the right side of Figure 2, the initial input ${\mathrm{X}}_{\left(\mathrm{i}-1\right)} \in {\mathrm{R}}^{\mathrm{L}\times \mathrm{C}}$ is historical data of length $\mathrm{L}$. This input undergoes gating with the output of the DTM block before passing through the first feed-forward layer, and then residual processing with the previous inputs after passing through the feed-forward layer. The residual connections in the model essentially facilitate progressive learning. With each deeper layer, the model subtracts the previously learned results. This layer-by-layer subtraction process enables the model to gradually comprehend the overall envelope and complementary components of the time series, progressing from macro-level concepts to micro-level specifics [11].

4.2.3. DTM Block

The DTM block, a crucial component in the DTMGNet architecture characterized by variable–adaptive channel independence, incorporates two specialized processing configurations: input information handling and a dual-module modeling approach.

Firstly, as illustrated in Figure 3, the input information stream undergoes a hierarchical multi-scale processing before being fed into the module. The patching process segments the sequence along the time dimension, with varying scales applied in a tree-like manner to control different depths of DTMGNet. It is noteworthy that in time series forecasting, the positional characteristic information diminishes with increasing network depth. Enhancing positional feature information in deeper networks can significantly improve model performance [48]. Therefore, DTM blocks are applied at various depths to control the main input information stream and reinforce positional feature information. Additionally, the multi-scale processing method applied at different depths extends the control information from fine local details to broad global information, facilitating the model’s progressive learning.

Secondly, to enhance the representational capacity of the DTM block and its variable–adaptive control ability, we employed a unique lateral processing approach alongside the vertical four-level modeling. Specifically, two sets of DTM blocks model the data with shared parameters. As depicted on the left side of Figure 2, after tree-structured multi-scale processing, the DTM block performs layer normalization on the time series, followed by MLP processing and dropout. Finally, the gated processing of the linearly transformed raw information and the MLP-processed block control information generates the final control information output, which serves as the input stream for the main control information. The overall process of DTM block is illustrated in Algorithm 1.

Algorithm 1: DTM block
Require: input lookback time series X ∈ RL×C; input length L; the number of channels C; embedding dimension E; the number of the block N.
01:	Xi = StandardScaler(XT) {Xi ∈ RL×C}
02:	▷ Tree-structured multi-scale processing for i in {1,···, N}:
03:	XRi = Reshape(Xi) {Xi ∈ RC×j×L/j, j = 2i}
	X1,i = XRi[:, 1::2, :] {X1,i ∈ RC×j×L/2j, j = 2i}
	X2,i = XRi[:, ::2, :] {X2,i ∈ RC×j×L/2j, j = 2i}
04:	▷ 2 sets of blocks are adopted:
05:	for XBi in {X1,i, X2,i}:
06:		▷ LayerNorm is adopted to reduce attribute discrepancies.
07:		XNi = LayerNorm(XBi) {XNi ∈ RC×j×L/2j}
08:		▷ The MLP performs nonlinear transformations on the temporal aspect.
09:		XFi = MLP(XNi) {XFi ∈ RC×j×E}
10:		▷ Add dropout to output stream.
11:		XDi = Dropout(XFi) {XDi∈RC×j×E}
12:		▷ Add internalgate mechanism
13:		XGi = G(Linear(XDi), MLP(XDi)) {XGi ∈ RC×j×L/2j}
14:	End for
15:	Output: O = Reshape(Connect(XG1,i, XG2,i)) {O ∈ RC×L}

4.2.4. Gating Mechanism

The gating mechanism is another distinctive feature of DTMGNet. In this model, a specialized gating process is applied to the input of each layer, particularly to the deeper layers that were previously overlooked. This approach ensures that the injected control information does not diminish with increasing network depth. Instead, it enhances the control information within the deeper layers, guiding the model to focus more on data diversity and adaptability to different variables within a single-channel shared yet channel-independent architecture. The gating mechanism can be described as:

$$\mathrm{G}\left(\mathrm{C}, \mathrm{X}\right)=\mathrm{normal}\left(\mathrm{C}\right)\odot \mathrm{X},$$

(3)

where $\mathrm{normal}\left(\mathrm{C}\right)$ represents layer normalization [49].

4.2.5. Feed-Forward Layer

As illustrated in Figure 4, the feed-forward layer consists of three linear layers arranged in an encoder–decoder diamond structure. The layers perform complex transformations on the signals that have been enhanced through gating processes. This is particularly crucial for the model to share channels while simultaneously adapting to different temporal dependency patterns and various variables. Additionally, for the final prediction output, a linear layer is connected to the feed-forward layer as the prediction head to achieve the ultimate temporal transformation. It is worth noting that the choice of a linear layer is justified by its proven representational capacity in the LTSF-Linear series and its superior adaptability to time series compared to other base models [39].

Additionally, to facilitate a comprehensive understanding of DTMGNet’s working principles, we provide detailed pseudocode outlining its implementation, as shown in Algorithm 2.

Algorithm 2: DTMGNet Architecture
Require: input lookback time series X ∈ RL×C; input length L; the number of channels C; predicted length O; embedding dimension E; the number of the block N.
01:	Xi = StandardScaler(XT) {Xi ∈ RC×L}
02:	for i in {1,···, N}: {Run through the backbone.}
03:		Ci = DTM block(X) {Ci ∈ RC×L}
04:		▷ Add gate mechanism to input stream.
05:		XGi = G(Xi, Ci){Ci ∈ RC×L} {XGi ∈ RC×L}
06:		▷ The feedforward layer performs nonlinear transformations.
07:		XFi = FeedForward(XGi) {XFi ∈ RC×L}
08:		▷ Subtract the previously learned output.
09:		Xi+1 = XFi − Xi {Xi+1 ∈ RC×L}
10:	End for
11:	▷ Linear layer is adopted as prediction head.
12:	Oi = Linear(Xi+1) {Oi ∈ RC×O}
13:	Output: O = InvertedScaler(OiT) {Output the final prediction results O ∈ RO×C}

5. Experimental Validation and Analysis

We first validate the performance of DTMGNet on the real-world solar energy benchmark dataset across four prediction windows. The results are then compared with 12 mainstream baseline models. Subsequently, we verify the effectiveness of the DTM block and conduct detailed tests on DTMGNet’s performance with varying depths of stacking.

5.1. Experimental Setup

Dataset: We performed experiments on the well-established benchmark dataset, solar energy [27], which recorded solar power generation from 137 PV facilities in Alabama in 2006, with data collected every 10 min. Detailed descriptions of the dataset are provided in

Table 1. Dataset detailed descriptions.

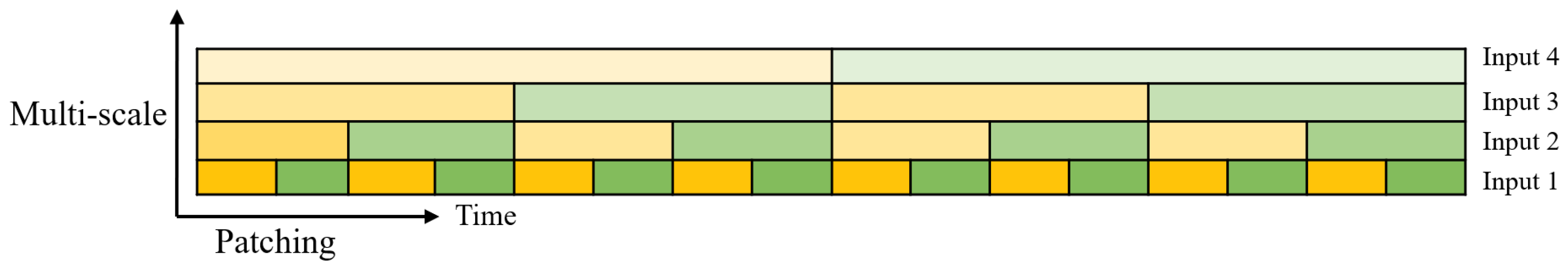
Dataset	Dim	Dataset Size	Frequency	Forecastability
Solar Energy	137	(36601, 5161, 10417)	10 min	0.33

, where the forecastability values are calculated as 1 minus the entropy of the time series’ Fourier decomposition [50]. Higher values indicate better predictability. It can be observed that the forecastability values presented in the Table 1 are relatively low, indicating that making predictions based on this benchmark dataset poses significant challenges.

Implementation details: Our experiments were performed using the PyTorch framework (v2.2.2) [51] and conducted on a single NVIDIA A100 40 GB GPU. The ADAM optimizer [52] was used to train the model, with the initial learning rate set to 0.0005. An early stopping strategy was employed to minimize the Mean Squared Error (MSE) loss function. The batch size was fixed at 32. The training, validation, and test sets were split following the same scheme as previous works, with a ratio of 7:1:2. The specific sizes are detailed in Table 1 under “Dataset Size”.

Metrics: Consistent with prior work, mean squared error (MSE) and mean absolute error (MAE) were used as evaluation metrics for long-term forecasting [14].

(1) MSE: The most commonly used metric for regression tasks. It calculates the average squared difference between the predicted values and the true values. The formula is as follows:

$$\mathrm{MSE}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}^2$$

(4)

(2) MAE: Another widely used metric for regression tasks, MAE calculates the average absolute difference between the predicted values and the true values. The formula is as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{\mathrm{n}}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right|$$

(5)

where n denotes the number of samples, ${\mathrm{y}}_{\mathrm{i}}$ denotes the true value of the ith sample, and $\widehat{{\mathrm{y}}_{\mathrm{i}}}$ denotes the predicted value of the ith sample.

Baselines: We compared DTMGNet against 12 baseline models, including state-of-the-art long-term forecasting models such as Timemixer (ICLR 2024) [44], iTransformer (ICLR 2024) [32], and PatchTST (ICLR 2023) [30]. Other competitive models included TimesNet [35], Crossformer [53], MICN [54], FiLM [55], DLinear [39], FEDformer [29], Stationary [56], Autoformer [28], and Informer [14].

Among these, Crossformer, PatchTST and iTransformer are recent representative works based on the transformer architecture. Crossformer utilizes channel-dependent methods, while PatchTST and iTransformer employ channel-independent methods. Crossformer utilizes cross-dimensional dependencies for multivariate time series prediction, embedding the input into a two-dimensional vector array through a novel dimensional segment embedding, and then employing a two-stage attention layer to effectively capture dependencies across time and dimensions. PatchTST adopts a channel-independent approach, sharing the same embedding across all sequences, and employs a subsequence-level patch design to enhance its performance in long-term time series prediction tasks. iTransformer treats independent time series as tokens, capturing multivariate correlations through self-attention mechanisms, and utilizes layer normalization and feed-forward network modules to learn better global sequence representations.

Timenet and MICN are representative works based on CNN architectures, and they both utilize channel-dependent methods. Timenet innovatively transforms time series into two-dimensional representations through periods extracted by discrete Fourier transform, then processes these 2D representations using convolutional networks for prediction. MICN adopts a multi-scale branch structure to model different latent patterns separately. Each pattern uses downsampling convolution and dilated convolution to extract local features and global correlations, capturing an overall view of the time series.

Additionally, DLinear and Timemixer are representative works based on MLP architectures, and they both utilize channel-independent methods. DLinear models trend and periodic sequences through two groups of single-layer linear layers, ultimately adding the two sequences to form the final prediction. Despite its simple design, it outperforms ordinary transformer-based models. Timemixer mixes decomposed seasonal and trend components in both fine-to-coarse and coarse-to-fine directions, thereby aggregating microscopic seasonal and macroscopic trend information sequentially. It further introduces multiple predictors to leverage the complementary predictive capabilities of multi-scale sequences.

We tested performance at four prediction lengths $\mathrm{T}\in \left\{96,192,336,720\right\}$. For the look-back window size L, we ran three different sizes $\mathrm{L}\in \left\{96,192,336\right\}$ for DTMGNet and iTransformer models, always selecting the best result to address the issue that not all models are suited for the same look-back window size. The remaining baseline models used the parameter search results from the Timemixer work. This makes the comparative results of DTMGNet more convincing, because DTMGNet demonstrated strong performance without relying on extensive parameter search.

5.2. Experimental Results

Table 2. Experiment results.

	Metric	96		192		336		720		Avg		1st Count
Model		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
DTMGNet		0.1673	0.215	0.194	0.241	0.197	0.247	0.199	0.2500	0.189	0.238	8
TimeMixer		0.167	0.220	0.187	0.249	0.200	0.258	0.215	0.250	0.192	0.244	3
iTransformer		0.193	0.243	0.217	0.269	0.227	0.280	0.239	0.298	0.219	0.272	0
PatchTST		0.224	0.278	0.253	0.298	0.273	0.306	0.272	0.308	0.256	0.298	0
TimesNet		0.219	0.314	0.231	0.322	0.246	0.337	0.280	0.363	0.244	0.334	0
Crossformer		0.181	0.240	0.196	0.252	0.216	0.243	0.220	0.256	0.204	0.248	1
MICN		0.188	0.252	0.215	0.280	0.222	0.267	0.226	0.264	0.213	0.266	0
FiLM		0.320	0.339	0.360	0.362	0.398	0.375	0.399	0.368	0.369	0.361	0
DLinear		0.289	0.377	0.319	0.397	0.352	0.415	0.356	0.412	0.329	0.400	0
FEDformer		0.201	0.304	0.237	0.337	0.254	0.362	0.280	0.397	0.243	0.350	0
Stationary		0.321	0.380	0.346	0.369	0.357	0.387	0.335	0.384	0.340	0.380	0
Autoformer		0.456	0.446	0.588	0.561	0.595	0.588	0.733	0.633	0.593	0.557	0
Informer		0.200	0.247	0.220	0.251	0.260	0.287	0.244	0.301	0.231	0.272	0

The “1st Count” represents the number of times a model achieved the best result among all metrics. Lower values of MSE and MAE indicate better performance.

presents a performance comparison between DTMGNet and other baseline models. And when the look-back window size L is 192 and 336, DTMGNet and iTransformer achieve their best results, respectively. It can be observed that DTMGNet achieves SOTA performance in overall metrics (Avg indicator), obtaining the best performance in 8 out of the total 10 evaluation metrics.

In specific prediction length configurations, DTMGNet outperforms or matches the performance of the current leading model, TimeMixer, as shown in Figure 5a. Notably, for the extended prediction lengths of 336 and 720, DTMGNet is the first to reduce the MSE metric below 0.2. In the ultra-long prediction of 720 points, there is a significant breakthrough (from 0.215 to 0.199), with a reduction of 7.44%. Compared to representative transformer-based models like PatchTST and iTransformer, which exhibit excellent overall performance, DTMGNet consistently demonstrates superior performance across various prediction length configurations, as shown in Figure 5c. Additionally, compared to convolutional models with representative works such as TimesNet and MICN, DTMGNet also achieves consistently leading performance across all metrics, as illustrated in Figure 5b.

In summary, the experimental results confirm that the proposed DTMGNet exhibits outstanding predictive performance for different long-term prediction lengths on the solar energy dataset, highlighting its effectiveness in handling multivariate time series forecasting tasks. Simultaneously, the experiments also demonstrate the superiority of our proposed variable–adaptive channel-independent architecture.

Additionally, as illustrated in Figure 6, prediction examples from four different prediction windows of three cases show that the predicted values (orange line) align consistently with the actual values (blue line) across multivariate different scenarios. Although the model’s sensitivity to peak values is not extremely precise, DTMGNet exhibits excellent handling of various patterns, particularly trends. This is evident in how the orange prediction line closely follows the overall shape and direction of the blue ground truth line. It effectively captures long-term dependencies in the temporal dimension and the mapping relationships between past and future even in the longer forecast windows, providing highly valuable foresight for long-term forecasting scenarios.

5.3. Ablation Study and Analysis

To validate the effectiveness of the DTM block as a specific implementation of variable–adaptive channel-independent architecture, we conducted a comprehensive ablation study on the core component of DTMGNet, the DTM block. This study included component replacement and removal experiments. The “normal block” is a variant where the tree-structured multi-scale processing and grouped modeling of input information are removed, and the raw time series is directly used as the input for a single group DTM block. The “Without Adaption” variant is one where all DTM blocks are removed. The final experimental results are shown in

Table 3. Results of ablation experiment.

	Metric	96		192		336		720		Avg
Model		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
DTMGNet		0.167	0.215	0.194	0.241	0.197	0.247	0.199	0.250	0.189	0.238
Normal Gate		0.181	0.227	0.197	0.245	0.203	0.252	0.202	0.252	0.196	0.244
Without Adaption		0.180	0.231	0.193	0.246	0.200	0.252	0.200	0.253	0.193	0.245

.

Obviously, as shown in Figure 7, both component replacement and removal result in a performance degradation of the model. Notably, when the component is replaced with a conventional gating input, the performance is even worse than the model without using the DTM block. This indicates the significant challenge in adaptive channel processing and, conversely, demonstrates the success and effectiveness of the deep tree-structured multi-scale gated component design.

5.4. Deep Stacking Experiments and Analysis

To evaluate the influence of different deep stacking configurations on DTMGNet, we conducted a series of experiments with varying numbers of stacked layers in the DTMGNet backbone. The experimental results are presented in

Table 4. Results of Deep Stacking.

	Metric	96		192		336		720		Avg
Depth		MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE	MSE	MAE
1		0.184	0.233	0.196	0.245	0.203	0.251	0.206	0.254	0.197	0.246
2		0.175	0.223	0.195	0.243	0.201	0.250	0.201	0.251	0.193	0.242
3		0.173	0.218	0.195	0.242	0.199	0.248	0.199	0.250	0.191	0.240
4		0.167	0.215	0.194	0.241	0.197	0.247	0.199	0.250	0.189	0.238

.

Compared to the representative work of transformer-based models, iTransformer, which tend to suffer from overfitting when the model depth increases [3], DTMGNet effectively mitigates this risk. This is due to its integration of the high robustness advantages of single channel-independent architectures and the enhanced representational capacity benefits brought by channel dependency. As shown in Figure 8, when the depth of the model increases, the evaluation metrics show consistent improvement. This demonstrates that deep stacking in DTMGNet effectively enhances the model’s representational capacity and allows for deeper designs that result in better performance.

6. Conclusions

In this paper, we propose a variable–adaptive channel-independent architecture that integrates the advantages of channel independence and channel dependence. This architecture addresses the common issues of insufficient training data and multi-channel dependency in long-term multivariate prediction models for solar power plants. And a deep tree-structured multi-scale gated component DTM block and a prediction model DTMGNet were designed based on this architecture. DTMGNet includes two data streams: one is the input stream through residual stacking layers, and the other is the deep multi-scale control stream provided by the DTM block, which adaptively perceives different variables and input features. And ablation experiments demonstrate that the deep stacking in DTMGNet effectively enhances model performance, while also validating the effectiveness of the DTM block’s design and the success of variable–adaptive channel-independent architecture.

Furthermore, in comparison with other models on the real-world benchmark dataset, solar energy, DTMGNet achieved SOTA performance. Specifically, when compared to TimeMixer, the current best-performing prediction model, DTMGNet demonstrated average reductions of 1.56% in MSE and 2.46% in MAE across four different prediction window scales. Notably, for the extended 720-step prediction horizon, we observed a substantial 7.44% decrease in MSE. This also demonstrates the superiority of our proposed variable–adaptive channel-independent architecture.

Based on the results, we believe that in the field of multivariate long-term prediction, besides innovations at the module level and in data processing, the success of the variable–adaptive channel-independent architecture demonstrates the importance of innovation at the architectural level. Moreover, we consider that exploring multivariate long-term prediction based on optimizing modules and data processing on top of an innovative architecture is a valuable approach worth emulating.

7. Limitations and Future Directions

Although this study proposes a novel architecture and develops a prediction model based on this architecture achieving superior performance, our research has primarily focused on improving prediction accuracy. It is noteworthy that in the field of multivariate long-term forecasting, due to the large-scale input and output data, when stacking multiple layers of DTMGNet, the training time and inference computational time resulting from the parameter scale may not show advantages compared to models such as TimeMixer and iTransformer. Furthermore, constrained by the limitations of existing public datasets, we were unable to conduct more in-depth explorations in data augmentation and online learning.

Therefore, the following three aspects will be essential research priorities for our future continuous optimization of this research, as well as extremely important avenues for further exploration of multivariate long-term forecasting models:

• Optimizing the model processing architecture to enhance computational efficiency;
• Exploring the application of data augmentation techniques in multivariate and long-term prediction by mining time series data characteristics;
• Integrating online learning mechanisms by collecting the latest time series data to continuously optimize the model in real-time.