Inherently Decoupled Dc-Link Capacitor Voltage Control of Multilevel Neutral-Point-Clamped Converters

Abstract

This letter derives and discusses the superiority of a simple dc-link capacitor voltage control configuration for multilevel neutral-point-clamped converters with any number of levels. The control involves n − 2 control loops regulating the difference between the voltage of neighbor capacitors. These control loops are inherently decoupled, i.e., they are independent and the control action of one loop does not affect the others. This method is proven to be equivalent to previously published approaches, with the added advantages of increased simplicity and scalability to a higher number of levels, all while imposing a lower computational burden. The good performance of such control is confirmed through simulations and experiments.

1. Introduction

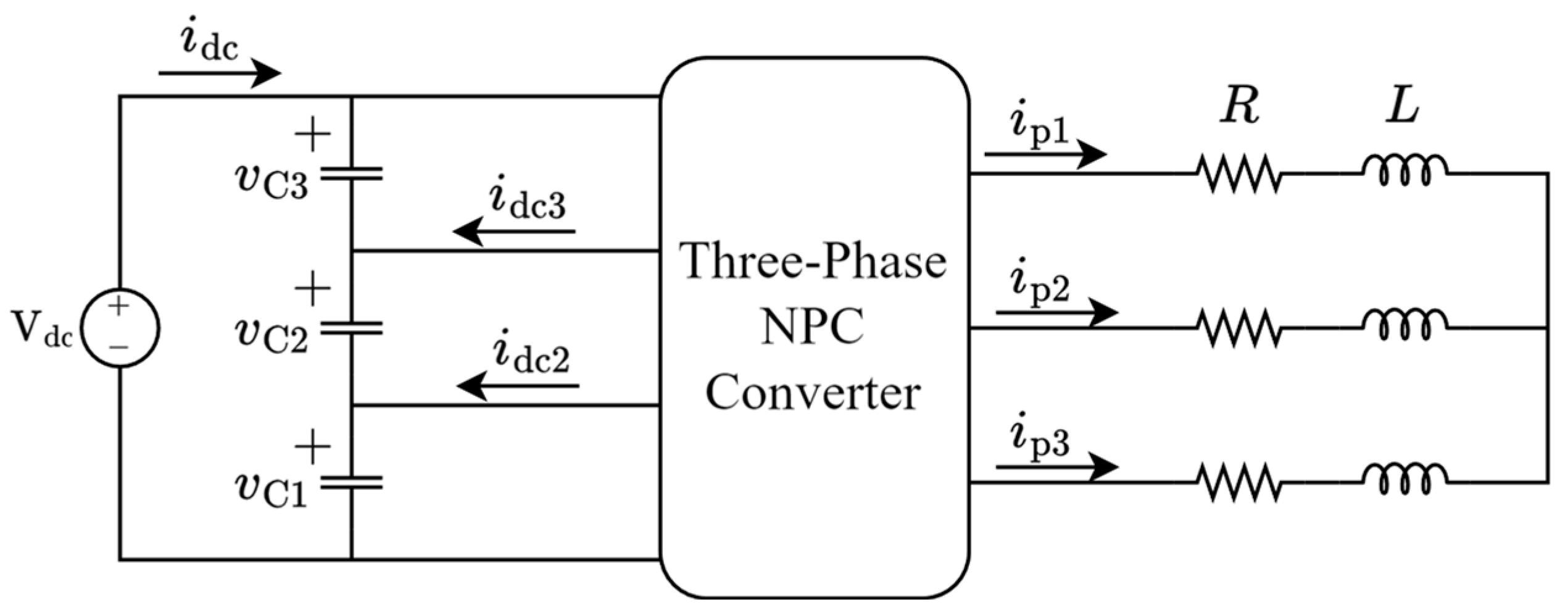
Multilevel conversion techniques are nowadays widely applied in power electronics systems, in a number of different applications and at low-, medium-, and high-power levels [1,2,3]. Among the multilevel topologies, the neutral-point-clamped (NPC) family stands as one of the most analyzed and applied, particularly at three levels. NPC conversion stages are configured by a set of converter legs connected to a common dc link, which is typically formed by a number of capacitors connected in series. Each converter leg, as depicted in Figure 1, behaves as a single-pole multiple-throw switch, connecting, at each point in time, the pole terminal p to one of the dc-link points: dc₁ to dc_n. These legs can be implemented through different circuit configurations [4]. Figure 2 shows some of them for the particular case of four levels. As can be observed, these legs only require a suitable combination of semiconductor devices with no capacitors or inductors, thus potentially featuring a very high power density.

Each NPC converter leg receives as inputs the dc-link capacitor voltages v_C1, v_C2, …, v_Cn−1, forced by the capacitors, and the pole terminal current i_p, forced by the external system connected to p. The NPC leg then imposes as outputs the pole terminal voltage v_p and the dc-link currents i_dc1 to i_dcn. The inner dc-link or neutral-point currents, i_dc2 to i_dcn−1, are the ones responsible for the control of the dc-link capacitor voltage balance, a challenging and widely studied issue of NPC topologies [4]. Each average neutral-point current, as a result of the combined contribution of all converter legs, must be equal to zero (<i_dc2> = <i_dc3> = … = <i_dcn−1> = 0) to maintain a given capacitor voltage balance. Although challenging, suitable pulsewidth modulations have already been defined to meet this constraint for any number of levels, as explained in [4], which is a recent survey paper providing a comprehensive review of the literature in this field. However, converter nonidealities, such as mismatches in gate driving circuits, transistors or capacitors, and leakage currents, can still generate capacitor voltage imbalances that will need to be corrected through a proper closed-loop control, determining the suitable value of the neutral-point currents at each point in time. This letter derives and discusses the most beneficial approach to set up this control, i.e., the best option in the selection of the variables to be regulated, from the point of view of performance and simplicity. This method is proven to be equivalent to other possible variable selections if properly decoupled [5], with the added advantages of increased simplicity and scalability to a higher number of levels, all while imposing a lower computational burden.

The letter is organized as follows. In Section 2, the proposed control configuration is presented. In Section 3, its good performance is confirmed through simulations and experiments. Finally, the letter is concluded in Section 4.

2. Inherently Decoupled Capacitor Voltage Balancing Control

Applying Kirchhoff’s current law and the characteristic equation of a capacitor, the neutral point currents can be expressed as:

$$\begin{gathered} i_{\mathrm{d}\mathrm{c}k}=i_{\mathrm{C}k-1}-i_{\mathrm{C}k}=C·\frac{{\mathrm{d}v}_{\mathrm{C}k-1}}{\mathrm{d}t}-C·\frac{{\mathrm{d}v}_{\mathrm{C}k}}{\mathrm{d}t} \\ {i}_{\mathrm{d}\mathrm{c}k}=C·\frac{{\mathrm{d}(v}_{\mathrm{C}k-1}-v_{\mathrm{C}k}) }{\mathrm{d}t}, \end{gathered}$$

(1)

with k ∈ {2, 3, n − 1}. From (1), it is clear that the voltage difference between neighbor capacitors can be controlled through the corresponding neutral point current. This leads to the control structure of Figure 3, with n − 2 control loops. These control loops, together with an additional converter control loop or external control of the total dc-link voltage v_dc, enable the full control of all capacitor voltages to the commanded values.

It is interesting to note that in this simple control structure, all control loops are inherently decoupled. Indeed, the value of i_dck only affects the value of v_Ck−1 − v_Ck. Current i_dck does not cause variations in the voltage difference between any other pair of neighbor capacitors. For instance, with reference to Figure 1, i_dc2 can be decomposed into two components: i_dc2u, which flows through the upper capacitors, C₂, C₃, …, and C_n−1, and i_dc2l, which flows through the lower capacitor C₁. Assuming that all capacitors have equal capacitance, i_dc2u decreases v_C2, …, v_Ck by the same amount, and i_dc2l increases v_C1. Thus, overall, the injection of i_dc2 only affects the voltage difference v_C1 − v_C2 and does not vary the value of v_Ck−1 − v_Ck for k ≥ 3. 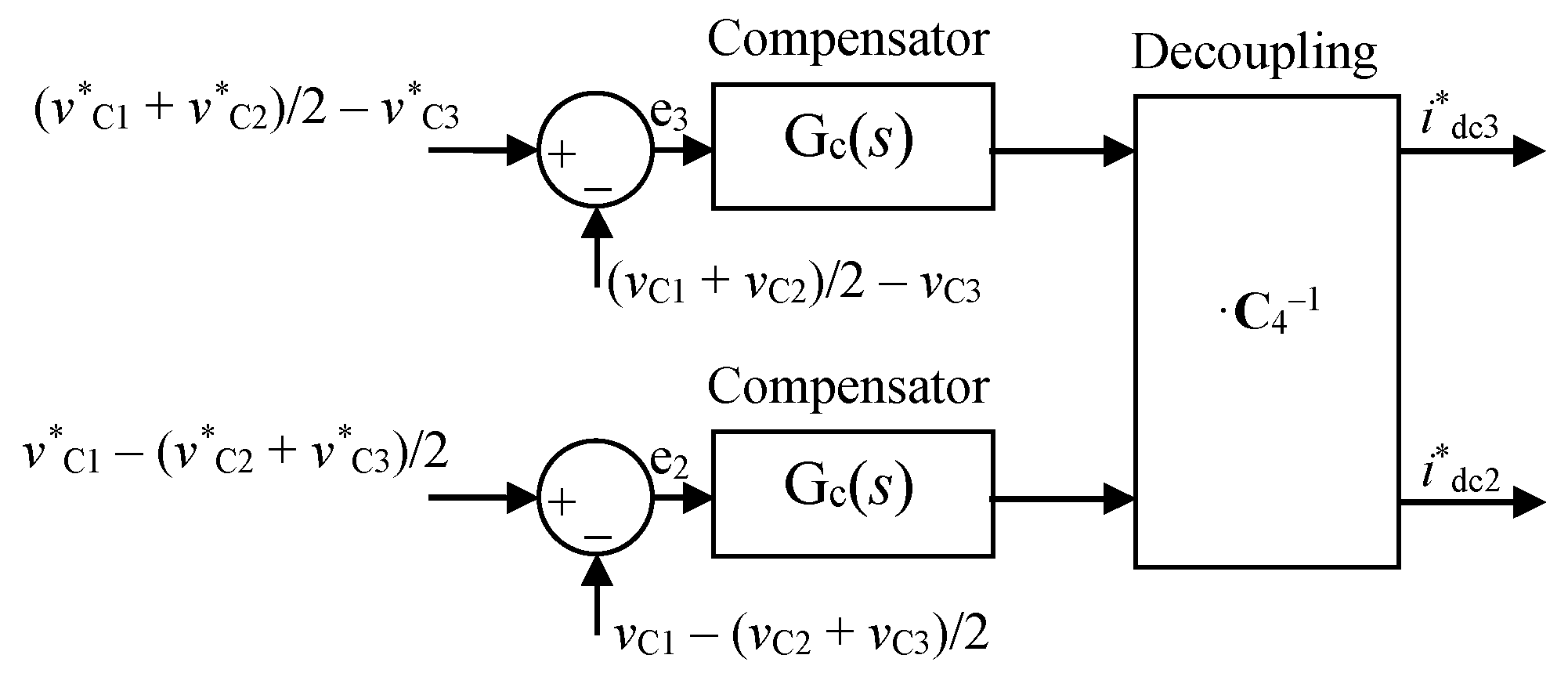In fact, the proposed control approach is completely equivalent to the control presented in [5] and illustrated in Figure 4 for four levels. In this control, the two loops are a priori coupled since

$$\left[\begin{array}{c}{v}_{\mathrm{C}1}-\frac{v_{\mathrm{C}2}+v_{\mathrm{C}3}}{2}\\ \frac{v_{\mathrm{C}1}+v_{\mathrm{C}2}}{2}-v_{\mathrm{C}3}\end{array}\right]=\frac{1}{Cs}·{\mathbf{C}}_4·\left[\begin{array}{c}{i}_{\mathrm{d}\mathrm{c}2}\\ i_{\mathrm{d}\mathrm{c}3}\end{array}\right]$$

(2)

where

$${\mathbf{C}}_4=\left[\begin{array}{cc}1& 1/2\\ 1/2& 1\end{array}\right]$$

(3)

is the matrix of coupling coefficients. However, multiplying by the inverse of C₄, as shown in Figure 4, the control becomes decoupled. Interestingly, if the decoupling matrix is directly applied to the regulated variables (the difference, at each neutral point, between the average bottom capacitor voltages and the average top capacitor voltages),

$$\left[\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\right]={\mathbf{C}}_4^{-1}\left[\begin{array}{c}{v}_{\mathrm{C}1}-\frac{v_{\mathrm{C}2}+v_{\mathrm{C}3}}{2}\\ \frac{v_{\mathrm{C}1}+v_{\mathrm{C}2}}{2}-v_{\mathrm{C}3}\end{array}\right],$$

(4)

the new regulated variables of Figure 3 appear (the voltage difference between neighbor capacitors at each neutral point), which essentially proves that both control configurations lead to exactly the same behavior, while the control in Figure 3 is simpler. In fact, any alternative choice of the variables to be regulated in the control loops (individual capacitor voltages, neutral-point voltages, etc. [6,7,8,9,10]) leads to a coupled control system, where a decoupling would need to be applied for the best performance. Thus, the control configuration in Figure 3 is the most optimal, as it is the only one not requiring this decoupling.

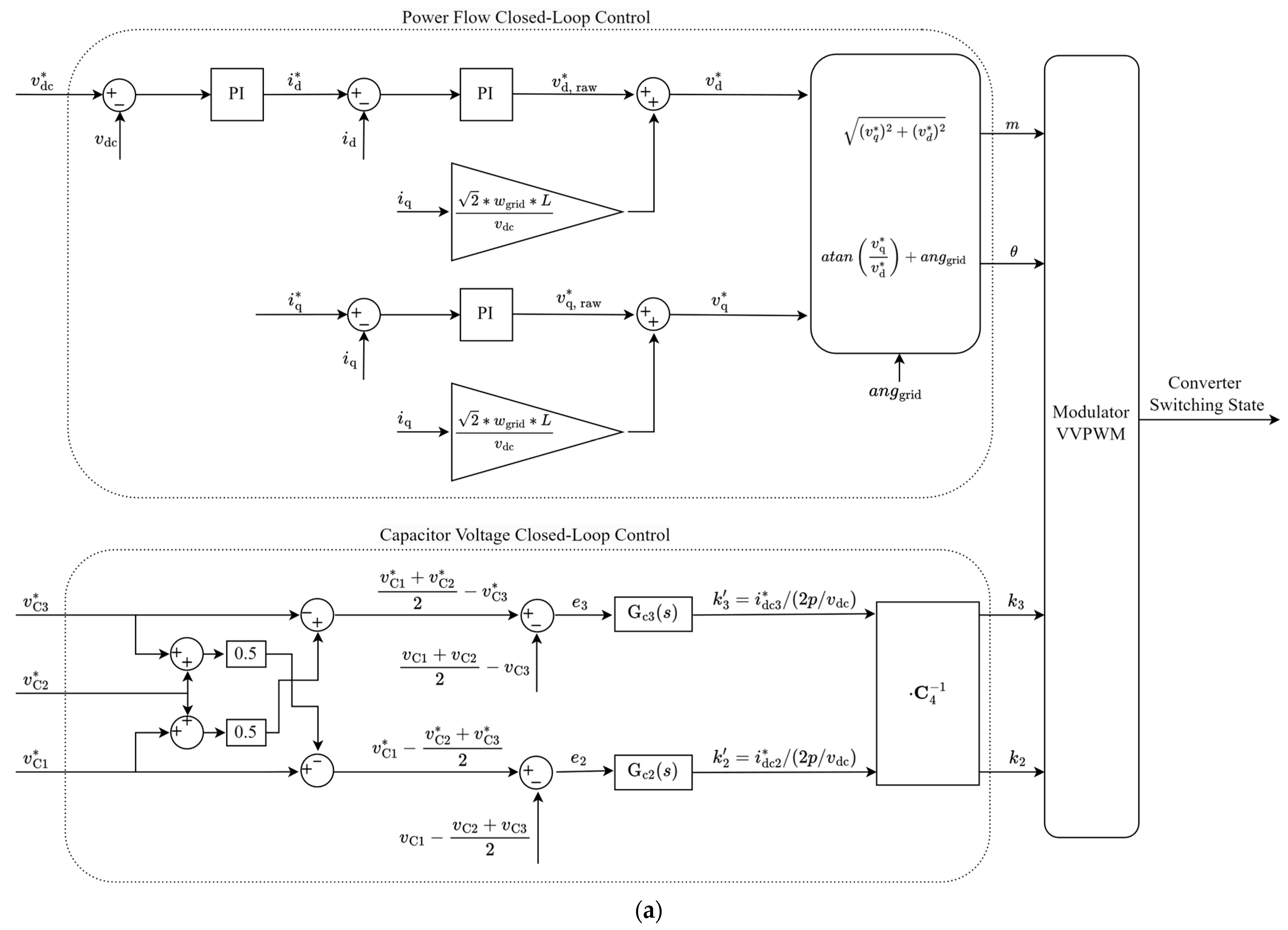
To better illustrate the proposed voltage balancing control in the context of a full system, a typical application is considered and depicted in Figure 5. A current source, representing a generic power source, is connected to the grid through a four-level, three-phase NPC inverter. A suitable control strategy to operate the system is presented in Figure 6. Two types of closed-loop controls are introduced. First, the closed-loop control is in charge of ensuring that all the energy supplied by the dc power source is transferred to the grid. This is achieved by regulating the dc-link voltage v_dc = v_C1 + v_C2 + v_C3. The error in the v_dc is processed by a first PI compensator to produce the direct component of the grid current command, proportional to the active power to be transferred. An additional command of the in-quadrature component of the grid current is established, proportional to the desired reactive power. Two PI compensators then process the error in the direct and quadrature components of the current to finally generate the reference three-phase inverter output voltage vector in dq coordinates, v_d^* and v_q^*, which are finally converted into its polar coordinates: the modulation index, m, and the line-cycle angle, θ, both required by the modulator. A virtual vector pulsewidth modulation (VVPWM) with neutral-point current control, following [11], determines the converter switching state, establishing the connection of each NPC leg output ac terminal to a given dc-link point at each point in time. Second, the closed-loop control is in charge of regulating the dc-link capacitor voltages v_C1, v_C2, and v_C3. The two loops in this control determine the values of the modulation parameters k₂ and k₃, which represent the normalized command value of the neutral point currents i_dc2 and i_dc3, respectively (p is the instantaneous power being transferred from the converter dc side to the converter ac side). In the case of the control loop presented in [5], corresponding to Figure 6a, more arithmetical operations are performed compared to the proposed simplified version shown in Figure 6b. In particular, the control loop in Figure 6a requires multiplying by the decoupling matrix C₄⁻¹.

When the decoupled dc-link capacitor voltage control from [5] and the proposed control are implemented in Matlab, the proposed capacitor voltage control results in a reduction of the computation time of 45% for four levels and 65% for five levels. This performance improvement is due to the simplified definition of the control variables, which previously required multiple additions and products but now involves only a subtraction of two terms, as well as the elimination of the n − 2 by n − 2 decoupling matrix multiplication. Therefore, systems with a higher number of levels should benefit more from this optimization. At four levels, the new control strategy reduces the number of arithmetical operations of the decoupled control loop in [5] from 12 sums and 10 products to 4 sums and 2 products. At five levels, the arithmetical operations are further reduced from 27 sums and 20 products to 6 sums and 3 products.

While a few works in the literature have already proposed a control strategy involving the regulation of the difference of neighbor capacitor voltages (e.g., the work in [12]), the intended contribution of this paper is to reveal its inherent decoupling among control loops, its equivalence to the control proposed in [5], and to emphasize its superiority compared to other alternative options often applied in the literature.

Table 1. Different definitions of control variables used in the literature.

Number of Levels	Control Variables (U)	Coupling Matrix (C)	Decoupling Matrix (C−1)	C−1 · U	Reference
4	$\left[\begin{array}{c}{v}_{\mathrm{C}1}-\frac{1}{2}\left(v_{\mathrm{C}2}+v_{\mathrm{C}3}\right)\\ \frac{1}{2}\left(v_{\mathrm{C}1}+v_{\mathrm{C}2}\right)-v_{\mathrm{C}3}\end{array}\right]$	$\left[\begin{array}{cc}1& 0.5\\ 0.5& 1\end{array}\right]$	$\left[\begin{array}{cc}4/3& -2/3\\ -2/3& 4/3\end{array}\right]$	$\left[\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\right]$	[5]
4	$\left[\begin{array}{c}{∆v}_{dc2}\\ {∆v}_{dc3}\end{array}\right]$	$\left[\begin{array}{cc}2/3& 1/3\\ 1/3& 2/3\end{array}\right]$	$\left[\begin{array}{cc}2& -1\\ -1& 2\end{array}\right]$	$\left[\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\right]$	[6]
4	$\left[\begin{array}{c}{v}_{C2}\\ v_{\mathrm{C}3}-v_{\mathrm{C}1}\end{array}\right]$	$\left[\begin{array}{cc}-1/3& 1/3\\ -1& -1\end{array}\right]$	$\left[\begin{array}{cc}-3/2& -1/2\\ 3/2& -1/2\end{array}\right]$	$\left[\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\right]$	[9]
5	$\left[\begin{array}{c}{v}_{C1}-\frac{1}{3}\left(v_{\mathrm{C}2}+v_{\mathrm{C}3}+v_{\mathrm{C}4}\right)\\ \frac{1}{2}\left(v_{\mathrm{C}1}+v_{\mathrm{C}2}\right)-\frac{1}{2}\left(v_{\mathrm{C}3}+v_{\mathrm{C}4}\right)\\ \frac{1}{3}\left(v_{\mathrm{C}1}+v_{\mathrm{C}2}+v_{\mathrm{C}3}\right)-v_{\mathrm{C}4}\end{array}\right]$	$\left[\begin{array}{ccc}1& 2/3& 1/3\\ 1/2& 1& 1/2\\ 1/3& 2/3& 1\end{array}\right]$	$\left[\begin{array}{ccc}3/2& -1& 0\\ -3/4& 2& -3/4\\ 0& -1& 3/2\end{array}\right]$	$\left[\begin{array}{c}\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\\ v_{\mathrm{C}3}-v_{\mathrm{C}4}\end{array}\right]$	[5]
5	$\left[\begin{array}{c}{v}_{C4}-v_{C1}\\ v_{C2}-v_{C3}\\ {(v}_{C2}+v_{C3})-{(v}_{C1}+v_{C4})\end{array}\right]$	$\left[\begin{array}{ccc}-1& -1& -1\\ 0& 1& 0\\ -1& 0& 1\end{array}\right]$	$\left[\begin{array}{ccc}-1/2& -1/2& -1/2\\ 0& 1& 0\\ -1/2& -1/2& 1/2\end{array}\right]$	$\left[\begin{array}{c}\begin{array}{c}{v}_{\mathrm{C}1}-v_{\mathrm{C}2}\\ v_{\mathrm{C}2}-v_{\mathrm{C}3}\end{array}\\ v_{\mathrm{C}3}-v_{\mathrm{C}4}\end{array}\right]$	[10]

presents a review of the most commonly used control variables, showing a significant diversity. The work presented in [6] defines the neutral-point voltages as the control objectives, leading to a rule-based control strategy where the larger absolute deviation takes priority. As a result, the selected redundant state minimizes only one neutral-point voltage error. Compared to the proposed approach, this control is strongly coupled and leads to poorer performance. These problems will increase as the number of levels increases. A different definition is used in reference [9], where the balance of the two outer capacitors of a four-level, three-phase converter is controlled by a zero-sequence voltage injection method, while the voltage of the inner capacitor is controlled by modifying the parameters of a redundant-level modulation. Two primary limitations restrict the feasibility of this solution. First, the control variables are coupled, leading to poorer voltage control. Second, the presented four-level, closed-loop control is not symmetric and scalable to systems with a higher number of levels. The approach in [10] is similar, where the balance of the two outer capacitors of a five-level converter is controlled by a zero-sequence voltage injection through a first control loop, while the other two control loops affect other modulation parameters. Similar to other solutions, in this approach, the control loops are coupled, multiple mathematical operations are required and it lacks scalability for higher number of levels. The different control variables used in these references are indicated in the second column of Table 1. All of the control variables present inherent coupling among control loops, defined by the corresponding coupling matrix. By multiplying the inverse of the coupling matrix by the control variables, the proposed variables in this letter arise.

In the case that the dc link is formed with battery modules in parallel with each dc-link capacitor, the regulated variable in each control loop (v_Ck−1 − v_Ck) should be replaced by the difference in the current of neighbor battery modules (i_Bk−1 − i_Bk) or their difference in state of charge (sc_k−1 − sc_k).

3. Simulation and Experimental Results

This section presents simulations and experiments that verify the good performance of the proposed inherently decoupled dc-link capacitor voltage control, in combination with a VVPWM [11] as in [5].

Simulations have been performed in Matlab-Simulink under different numbers of levels and phases. Figure 7 shows the schematic of the simulated system in the four-level, three-phase case. The dc link is fed by a constant voltage source, and a wye-connected multiphase series resistive-inductive load is assumed at the converter ac side with per-phase characteristic parameters R and L.

The first simulation, depicted in Figure 8, shows the system’s behavior under an initial voltage unbalance among the capacitor voltages in a four-level, three-phase system. When the control is not enabled, the initial voltages are maintained as the VVPWM modulation ensures zero average neutral point currents. Both the control from [5] without decoupling and the proposed inherently decoupled control are able to correct this initial deviation. It can be observed that the proposed decoupled control improves the transient response, especially in voltages v_C3 and v_C2. When the system is not decoupled (Figure 8b), v_C3 shows an overshoot in the initial phase of the voltage correction, and the transient response of v_C2 is considerably slower.

Figure 9 depicts the performance under ramp variations of v^*_C2 and v^*_C3 commands in a four-level, three-phase system. As it can be observed, under control in [5] without decoupling, undesired variations of v_C1 occur, while these variations are fully suppressed with the proposed control.

Figure 10 shows the performance under a five-level, five-phase system to prove the applicability of the proposed control to systems with a higher number of levels and legs. Similar to Figure 9, two ramps are generated in v^*_C1 and v^*_C4 commands. With the use of the proposed control, v_C2 and v_C3 remain constant over the transients, as desired. In a similar manner, Figure 11 further proves the good performance under a seven-level, five-phase system.

The simulation in Figure 12 is performed in the same conditions as in Figure 9 and demonstrates the control robustness against variations in the dc-link capacitor values. In this case, the capacitance of C₂ is increased by 20%, while the capacitance of C₃ is decreased by the same amount. Even with this large variation, the proposed decoupled system response shown in Figure 12c remains mostly unchanged and is superior to the non-decoupled control from Figure 9b and Figure 12b.

Figure 13 and Figure 14 verify the good system performance against unbalances in the dc-link capacitor leakage currents, emulated through a resistor in parallel with each capacitor. At the beginning of the simulations, the resistance value is the same for all of the capacitors with a value of 100 kΩ. At t = 20 ms, the resistance in parallel with capacitor C₃ is reduced to 2 kΩ. When the control is not active, as in Figure 13a and Figure 14a, the capacitor voltages divert rapidly. However, in the cases where the control is active, as in Figure 13b,c and Figure 14b,c, the capacitor voltages remain stable. Figure 13b,c shows that with both controls, a small steady-state error remains in the capacitor voltages, as only a proportional compensator with moderate gain is being employed. In Figure 14b,c, a proportional–integral compensator is employed, which completely eliminates this steady-state error for both the decoupled and non-decoupled control cases.

Experiments have also been carried out with a four-level, three-phase active-clamped dc–ac converter prototype built upon 100 V metal-oxide-semiconductor field-effect transistors and controlled with a dSPACE control platform, as shown in Figure 15. These experiments were performed under the same conditions as in Figure 9. The experimental results depicted in Figure 16 corroborate the corresponding simulation results from Figure 9.

4. Conclusions

The most effective and simple dc-link capacitor voltage balance control in NPC topologies is the one establishing n − 2 control loops regulating the voltage difference between neighbor capacitors. This control can be easily applied to any number of levels and features inherent decoupling among all control loops.

Reducing the complexity of the capacitor voltage control yields substantial benefits, directly influencing the system performance and enhancing its dynamic response, all while reducing the computational burden. The benefits in terms of computational cost increase with the number of levels. At the same time, the resulting reduced complexity decreases the required expertise for the implementation of multilevel converters, thereby facilitating their market adoption. The robustness of the proposed decoupling method is verified against different nonidealities. The precise regulation of the capacitor voltages of the proposed balancing control, in combination with a virtual vector pulsewidth modulation, enables the possibility to operate with multiple different capacitor voltage values along the converter dc-link without introducing low-frequency harmonic distortion in the converter ac voltages and currents.

The main limitation of this balancing method is that the maximum value of the neutral-point current i_dck that the converter can inject depends on the value of the converter leg output current i_p and on the value of the converter modulation index. The lower the output leg current and the higher the modulation index, the lower the regulation margin. Thus, the regulation margin has some limits. This regulation margin also depends on the number of balancing control loops enabled and the sign and value of their commands [12]. One possible future research topic is to study how to optimally distribute this regulation margin among the different balancing control loops.