Integrated Neural Network Approach for Enhanced Vital Signal Analysis Using CW Radar
Abstract
1. Introduction
2. Proposed Method for CW Radar Signal Processing
2.1. Characteristics of CW Radar Signal
2.2. Signal Preprocessing for CW Radar
2.3. Signal Preprocessing for ECG
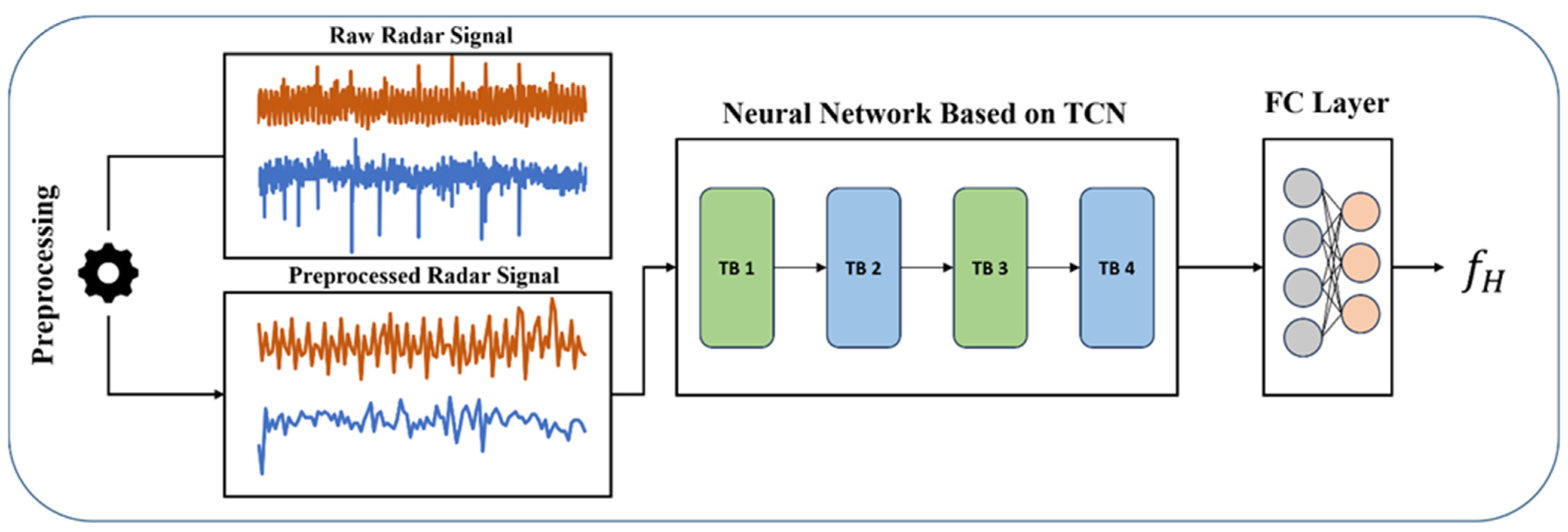
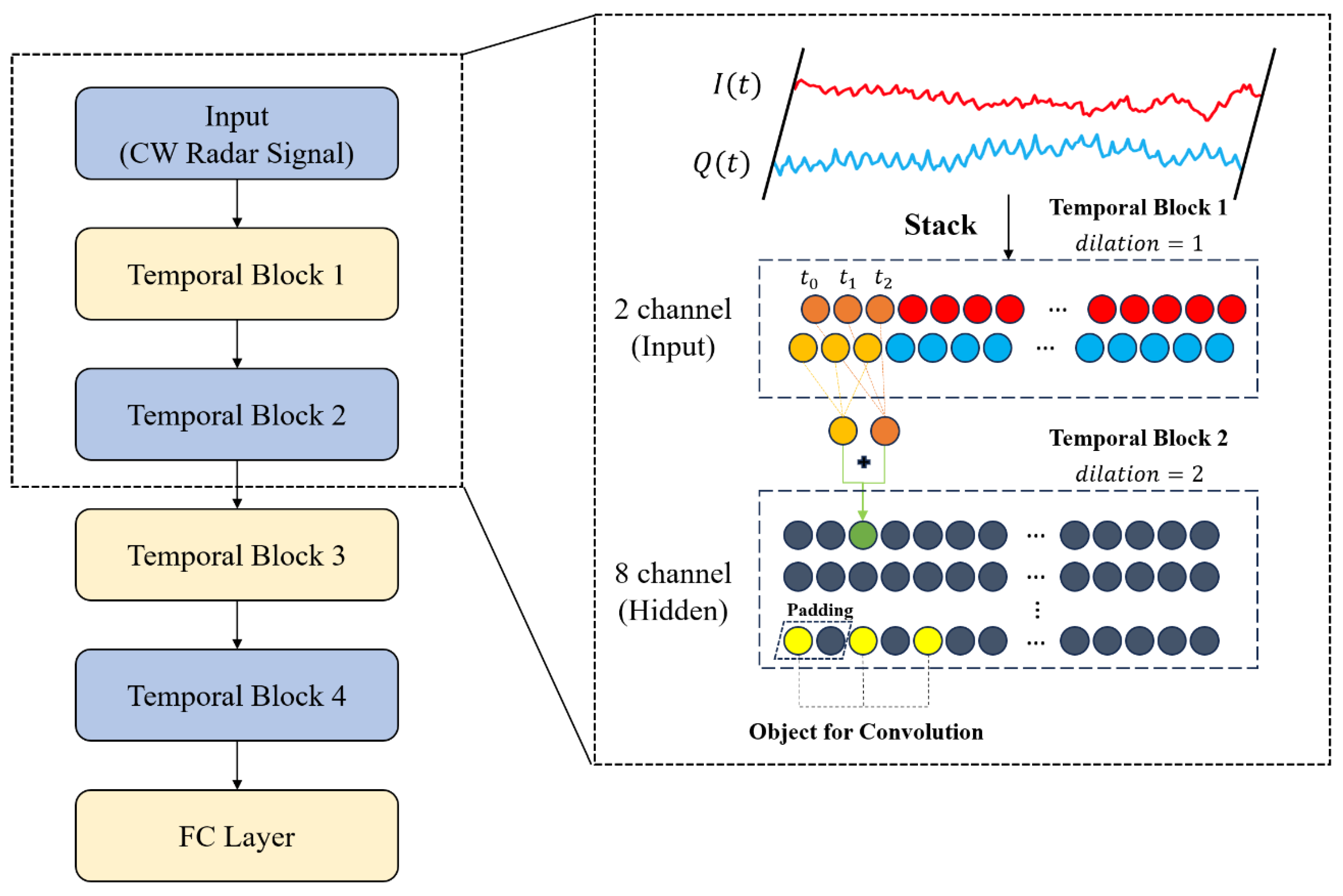
2.4. The Proposed CW Signal Processing Procedure
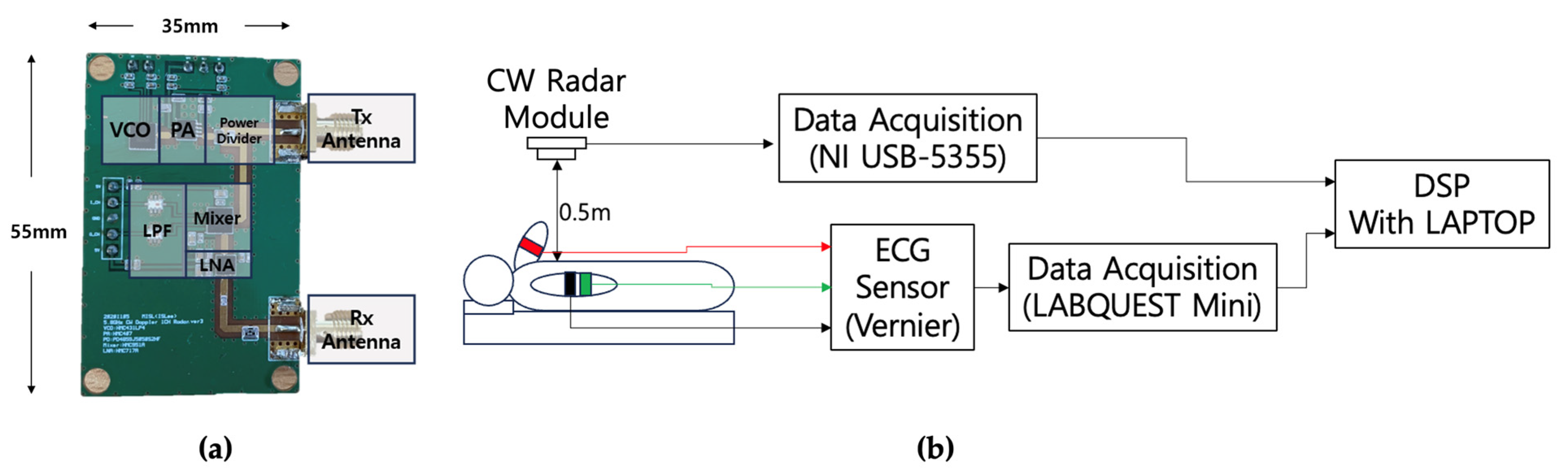
3. Experiment
3.1. Dataset Configurations
3.2. Experimental Procedure
3.3. Experimental Result
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Murphy, S.L.; Kochanek, K.D.; Arias, E. Deaths: Final data for 2019. Natl. Vital Stat. Rep. 2021, 70, 8. [Google Scholar]
- Bernstein, R.A.; Kamel, H.; Granger, C.B.; Piccini, J.P.; Sethi, P.P.; Katz, J.M.; Vives, C.A.; Ziegler, P.D.; Franco, N.C.; Schwamm, L.H.; et al. Effect of Long-term Continuous Cardiac Monitoring vs Usual Care on Detection of Atrial Fibrillation in Patients With Stroke Attributed to Large- or Small-Vessel Disease: The STROKE-AF Randomized Clinical Trial. JAMA 2021, 325, 2169–2177. [Google Scholar] [CrossRef] [PubMed]
- Tsao, C.W.; Aday, A.W.; Almarzooq, Z.I.; Alonso, A.; Beaton, A.Z.; Bittencourt, M.S.; Boehme, A.K.; Buxton, A.E.; Carson, A.P.; Commodore-Mensah, Y. Heart disease and stroke statistics—2022 update: A report from the American Heart Association. Circulation 2022, 145, e153–e639. [Google Scholar] [PubMed]
- Serhani, M.A.; T. El Kassabi, H.; Ismail, H.; Nujum Navaz, A. ECG monitoring systems: Review, architecture, processes, and key challenges. Sensors 2020, 20, 1796. [Google Scholar] [CrossRef] [PubMed]
- Heo, S.; Kwon, S.; Lee, J. Stress detection with single PPG sensor by orchestrating multiple denoising and peak-detecting methods. IEEE Access 2021, 9, 47777–47785. [Google Scholar] [CrossRef]
- Slapničar, G.; Luštrek, M.; Marinko, M. Continuous blood pressure estimation from PPG signal. Informatica 2018, 42, 33–42. [Google Scholar]
- Li, P.; Laleg-Kirati, T.-M. Central blood pressure estimation from distal PPG measurement using semiclassical signal analysis features. IEEE Access 2021, 9, 44963–44973. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, Z. A SVM method for continuous blood pressure estimation from a PPG signal. In Proceedings of the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; pp. 128–132. [Google Scholar]
- Cowie, M.R.; Lam, C.S. Remote monitoring and digital health tools in CVD management. Nat. Rev. Cardiol. 2021, 18, 457–458. [Google Scholar] [CrossRef]
- Alizadeh, M.; Shaker, G.; De Almeida, J.C.M.; Morita, P.P.; Safavi-Naeini, S. Remote monitoring of human vital signs using mm-wave FMCW radar. IEEE Access 2019, 7, 54958–54968. [Google Scholar] [CrossRef]
- Wang, Y.; Shui, Y.; Yang, X.; Li, Z.; Wang, W. Multi-target vital signs detection using frequency-modulated continuous wave radar. EURASIP J. Adv. Signal Process. 2021, 2021, 103. [Google Scholar] [CrossRef]
- Botina-Monsalve, D.; Benezeth, Y.; Miteran, J. RTrPPG: An ultra light 3DCNN for real-time remote photoplethysmography. In Proceedings of the Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 2146–2154. [Google Scholar]
- Karthick, R.; Dawood, M.S.; Meenalochini, P. Analysis of vital signs using remote photoplethysmography (RPPG). J. Ambient. Intell. Humaniz. Comput. 2023, 14, 16729–16736. [Google Scholar] [CrossRef]
- Lokendra, B.; Puneet, G. AND-rPPG: A novel denoising-rPPG network for improving remote heart rate estimation. Comput. Biol. Med. 2022, 141, 105146. [Google Scholar] [CrossRef]
- Kim, D.-Y.; Lee, K.; Sohn, C.-B. Assessment of roi selection for facial video-based rppg. Sensors 2021, 21, 7923. [Google Scholar] [CrossRef] [PubMed]
- Casado, C.A.; López, M.B. Face2PPG: An unsupervised pipeline for blood volume pulse extraction from faces. IEEE J. Biomed. Health Inform. 2023, 27, 5530–5541. [Google Scholar] [CrossRef] [PubMed]
- Paterniani, G.; Sgreccia, D.; Davoli, A.; Guerzoni, G.; Di Viesti, P.; Valenti, A.C.; Vitolo, M.; Vitetta, G.M.; Boriani, G. Radar-based monitoring of vital signs: A tutorial overview. Proc. IEEE 2023, 111, 277–317. [Google Scholar] [CrossRef]
- Hoang, T.Y. CW Radar-based Non-contact Vital Sign Monitoring. Ph.D. Thesis, The University of Electro-Communications, Tokyo, Japan, 2023. [Google Scholar]
- Ebrahim, M.P.; Tom, N.; Redoute, J.-M.; Yuce, M.R. A low-frequency portable continuous wave radar system for vital signs monitoring. IEEE Sens. J. 2023, 23, 8876–8886. [Google Scholar] [CrossRef]
- Fan, S.; Deng, Z. Chest Wall Motion Model of Cardiac Activity for Radar-Based Vital-Sign-Detection System. Sensors 2024, 24, 2058. [Google Scholar] [CrossRef] [PubMed]
- Liang, Z.; Xiong, M.; Jin, Y.; Chen, J.; Zhao, D.; Yang, D.; Liang, B.; Mo, J. Non-contact human vital signs extraction algorithms using IR-UWB radar: A review. Electronics 2023, 12, 1301. [Google Scholar] [CrossRef]
- Kyrarini, M.; Lygerakis, F.; Rajavenkatanarayanan, A.; Sevastopoulos, C.; Nambiappan, H.R.; Chaitanya, K.K.; Babu, A.R.; Mathew, J.; Makedon, F. A survey of robots in healthcare. Technologies 2021, 9, 8. [Google Scholar] [CrossRef]
- Soares, B.; Gouveia, C.; Albuquerque, D.; Pinho, P. Impact and Classification of Body Stature and Physiological Variability in the Acquisition of Vital Signs Using Continuous Wave Radar. Appl. Sci. 2024, 14, 921. [Google Scholar] [CrossRef]
- Holland, J.; Kingston, L.; McCarthy, C.; Armstrong, E.; O’Dwyer, P.; Merz, F.; McConnell, M. Service robots in the healthcare sector. Robotics 2021, 10, 47. [Google Scholar] [CrossRef]
- Ahn, H.S.; Lee, M.H.; MacDonald, B.A. Healthcare robot systems for a hospital environment: CareBot and ReceptionBot. In Proceedings of the 2015 24th IEEE International Symposium on Robot and Human Interactive Communication (RO-MAN), Kobe, Japan, 31 August–4 September 2015; pp. 571–576. [Google Scholar]
- Broadbent, E.; Kuo, I.H.; Lee, Y.I.; Rabindran, J.; Kerse, N.; Stafford, R.; MacDonald, B.A. Attitudes and reactions to a healthcare robot. Telemed. E-Health 2010, 16, 608–613. [Google Scholar] [CrossRef]
- Ragno, L.; Borboni, A.; Vannetti, F.; Amici, C.; Cusano, N. Application of social robots in healthcare: Review on characteristics, requirements, technical solutions. Sensors 2023, 23, 6820. [Google Scholar] [CrossRef]
- Barrick, D.E. FM/CW Radar Signals and Digital Processing; National Oceanic and Atmospheric Administration Boulder Co Wave Propagation Lab: Tokyo, Japan, 1973. [Google Scholar]
- Kumawat, H.C.; Raj, A.B. Approaching/receding target detection using cw radar. In Proceedings of the 2020 5th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 10–12 June 2020; pp. 136–141. [Google Scholar]
- Lee, I.-S.; Park, J.-H.; Yang, J.-R. Detrending technique for denoising in CW radar. Sensors 2021, 21, 6376. [Google Scholar] [CrossRef]
- Salmi, J.; Luukkonen, O.; Koivunen, V. Continuous wave radar based vital sign estimation: Modeling and experiments. In Proceedings of the 2012 IEEE Radar Conference, Atlanta, GA, USA, 7–11 May 2012; pp. 0564–0569. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Boric-Lubecke, O.; Lubecke, V.M.; Droitcour, A.D.; Park, B.-K.; Singh, A. Doppler Radar Physiological Sensing; John Wiley & Sons: New York, NJ, USA, 2015. [Google Scholar]
- Christov, I.I. Real time electrocardiogram QRS detection using combined adaptive threshold. Biomed. Eng. Online 2004, 3, 28. [Google Scholar] [CrossRef] [PubMed]
- Ostchega, Y.; Porter, K.S.; Hughes, J.; Dillon, C.F.; Nwankwo, T. Resting pulse rate reference data for children, adolescents, and adults; United States, 1999–2008. Natl. Health Stat. Rep. 2011, 24, 1–6. [Google Scholar]
- Hewage, P.; Behera, A.; Trovati, M.; Pereira, E.; Ghahremani, M.; Palmieri, F.; Liu, Y. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, J.; Chen, X.; Zeng, X.; Kong, Y.; Sun, S.; Guo, Y.; Liu, Y. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans. Power Syst. 2020, 36, 1984–1997. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, F.; Song, Z.; Wang, X.; Du, Y.; Dong, S. Short-term traffic flow forecasting model based on GA-TCN. J. Adv. Transp. 2021, 2021, 1338607. [Google Scholar] [CrossRef]
- Hao, H.; Wang, Y.; Xue, S.; Xia, Y.; Zhao, J.; Shen, F. Temporal convolutional attention-based network for sequence modeling. arXiv 2020, arXiv:2002.12530. [Google Scholar]
- Gopali, S.; Abri, F.; Siami-Namini, S.; Namin, A.S. A comparison of tcn and lstm models in detecting anomalies in time series data. In Proceedings of the 2021 IEEE International Conference on Big Data (Big Data), Orlando, FL, USA, 15–18 December 2021; pp. 2415–2420. [Google Scholar]





| Dataset Used to Train the Network | Correlated | |
|---|---|---|
| Number of Train Set | 2000 | 2000 |
| Number of Validation Set | 838 | 838 |
| Correlation with Validation and Train | Correlated | Unrelated |
| Dataset Used to Train the Network | Correlated | Unrelated |
|---|---|---|
| L1 Loss | 0.095 | 0.129 |
| Accuracy (%) | 83.65 | 71.46 |
| Difference between the converted BPMs | 5.7 | 7.74 |
| Window Size | 10 (30 s) | 20 (60 s) |
|---|---|---|
| Average Loss | 0.128 | 0.130 |
| Accuracy (%) | 75.37 | 75.71 |
| Difference between the converted BPM | 7.68 | 7.80 |
| Window Size | 10 (30 s) | 20 (60 s) |
|---|---|---|
| Average Loss | 0.093 | 0.091 |
| Accuracy (%) | 95.23 | 96.36 |
| Difference between the converted BPM | 5.58 | 5.46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoon, W.Y.; Kwon, N.K. Integrated Neural Network Approach for Enhanced Vital Signal Analysis Using CW Radar. Electronics 2024, 13, 2666. https://doi.org/10.3390/electronics13132666
Yoon WY, Kwon NK. Integrated Neural Network Approach for Enhanced Vital Signal Analysis Using CW Radar. Electronics. 2024; 13(13):2666. https://doi.org/10.3390/electronics13132666
Chicago/Turabian StyleYoon, Won Yeol, and Nam Kyu Kwon. 2024. "Integrated Neural Network Approach for Enhanced Vital Signal Analysis Using CW Radar" Electronics 13, no. 13: 2666. https://doi.org/10.3390/electronics13132666
APA StyleYoon, W. Y., & Kwon, N. K. (2024). Integrated Neural Network Approach for Enhanced Vital Signal Analysis Using CW Radar. Electronics, 13(13), 2666. https://doi.org/10.3390/electronics13132666





