N-Dimensional Non-Degenerate Chaos Based on Two-Parameter Gain with Application to Hash Function
Abstract
:1. Introduction
2. Construction Algorithm
| Algorithm 1 Construction Algorithm of Non-degenerate Chaotic System | |
| Input: | , …, , M, ; |
| where A serves as the Jacobi matrix, is the initial value of chaotic system, | |
| and are using to obtain desired LEs, M is the modulus of modulo function. | |
| Step 1: | ; |
| where is the function to obtain the eigvalues of matrix A. | |
| Step 2: | ; |
| where the is the minimum of . | |
| Step 3: | ; |
| where the E is an identity matrix. | |
| Output: | the chaotic system . |
3. Characteristic Testing of Chaotic System
3.1. The Relationship between LEs and Control Parameters
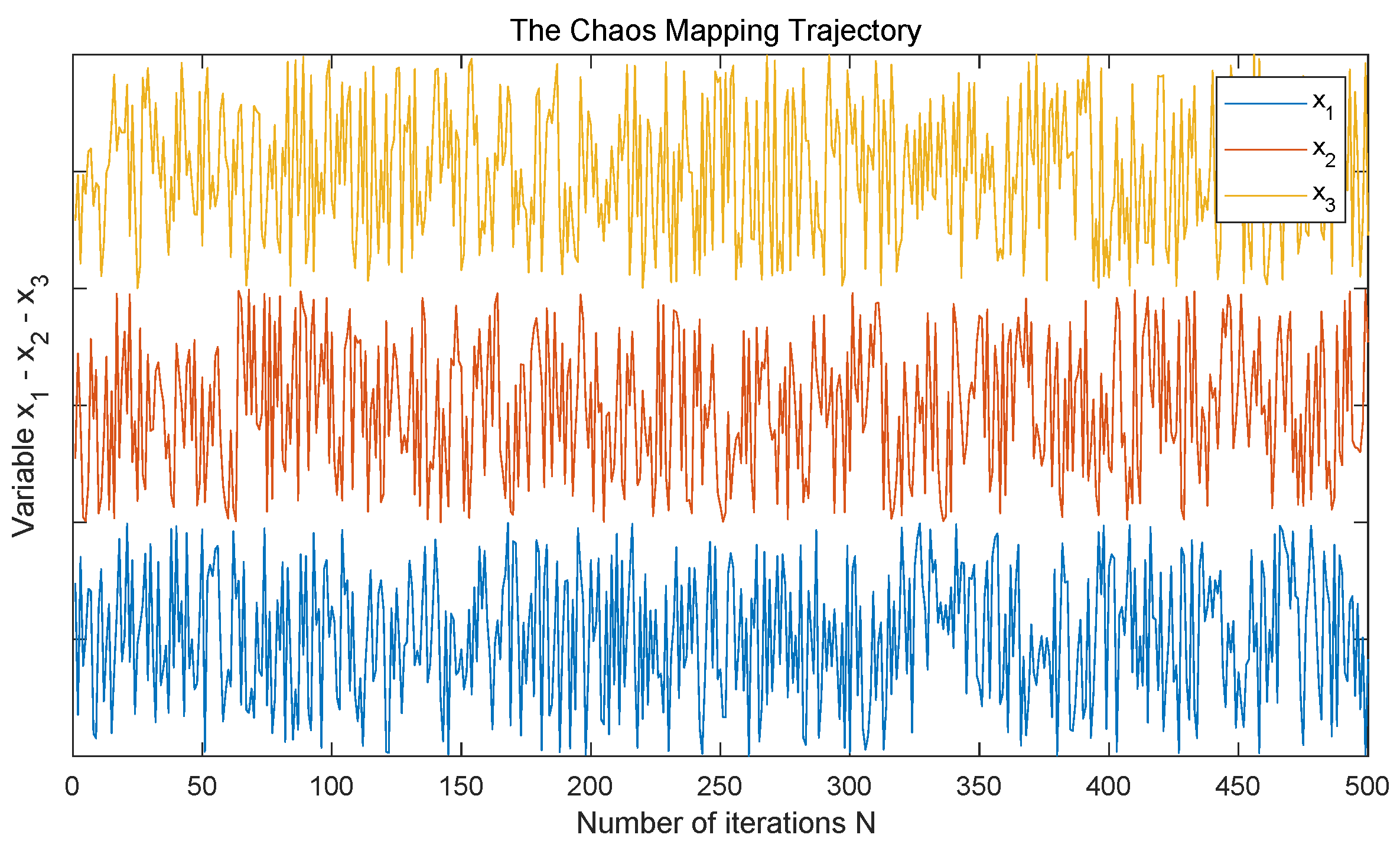
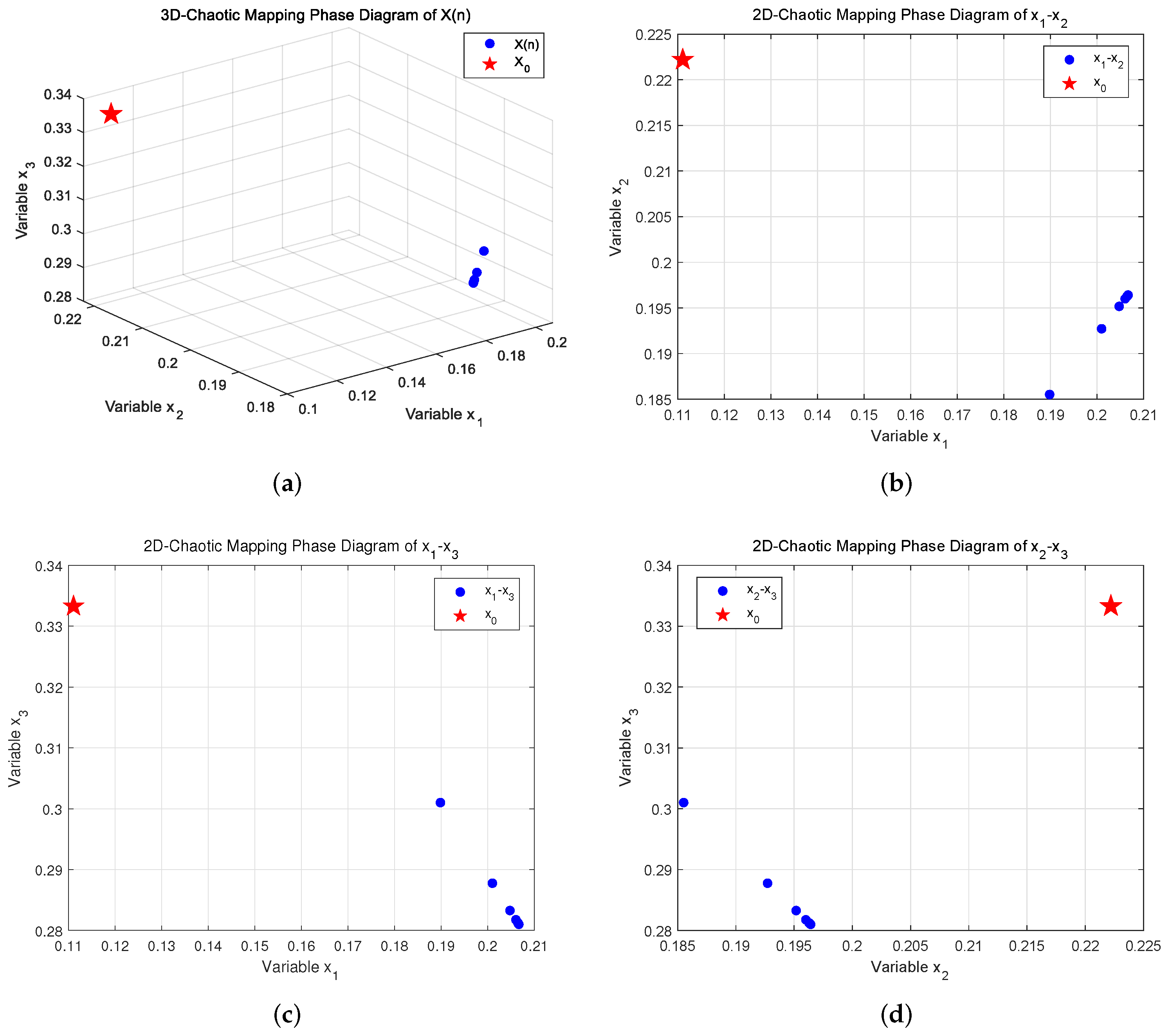
3.2. Chaotic Phase Diagrams and Bifurcation Diagrams
3.3. Periodization of Chaotic Systems
3.4. Periodic Testing of Digital Chaotic System
3.5. Joint Entropy
3.6. Standard Uniform Distribution Test
3.7. Sequence Sample Entropy
3.8. Correlation Dimension
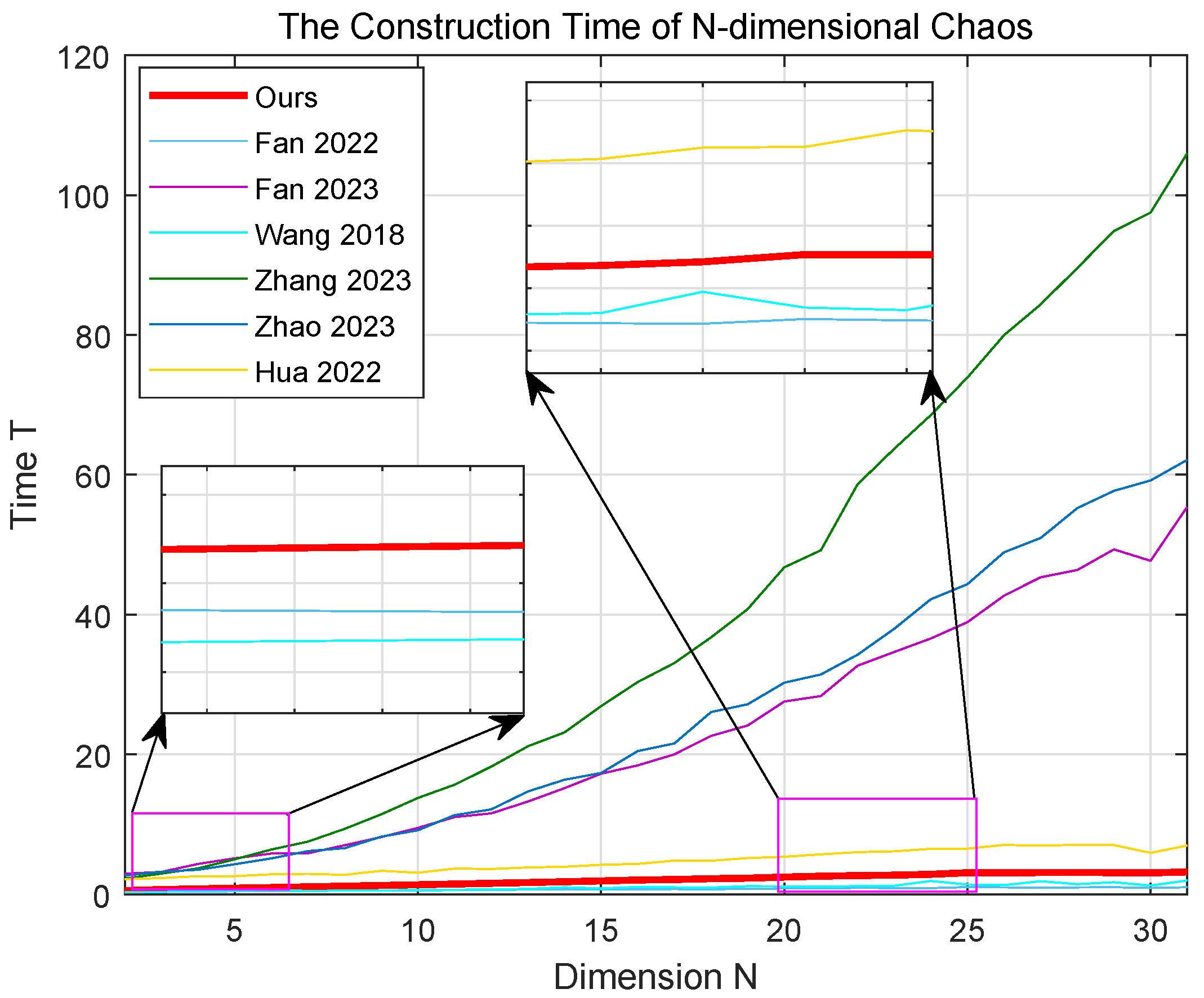
3.9. Time Complexity of Algorithms
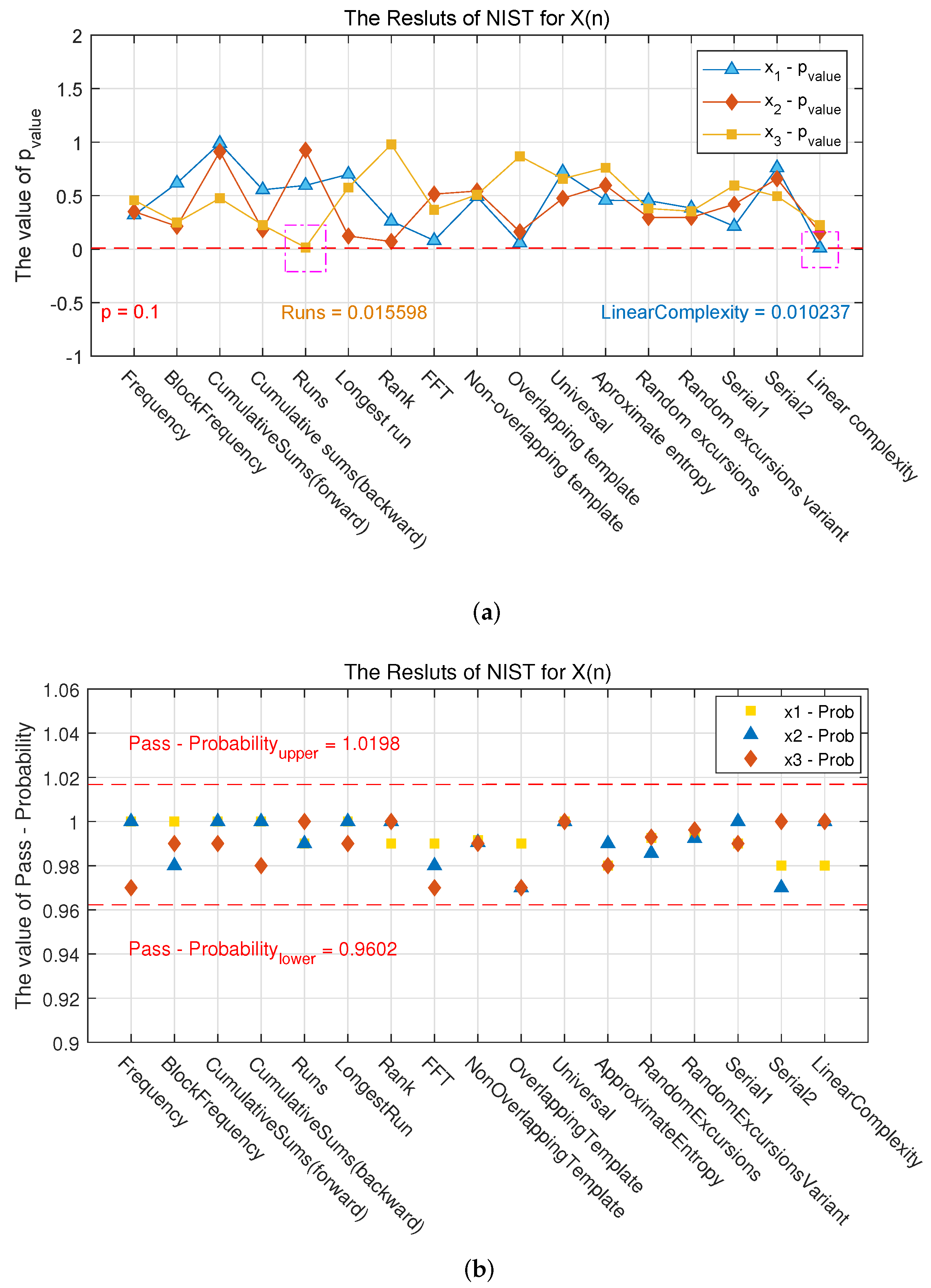
3.10. NIST SP800-22 Testing
4. Hash Functions Based on Non-Degenerate Chaotic System
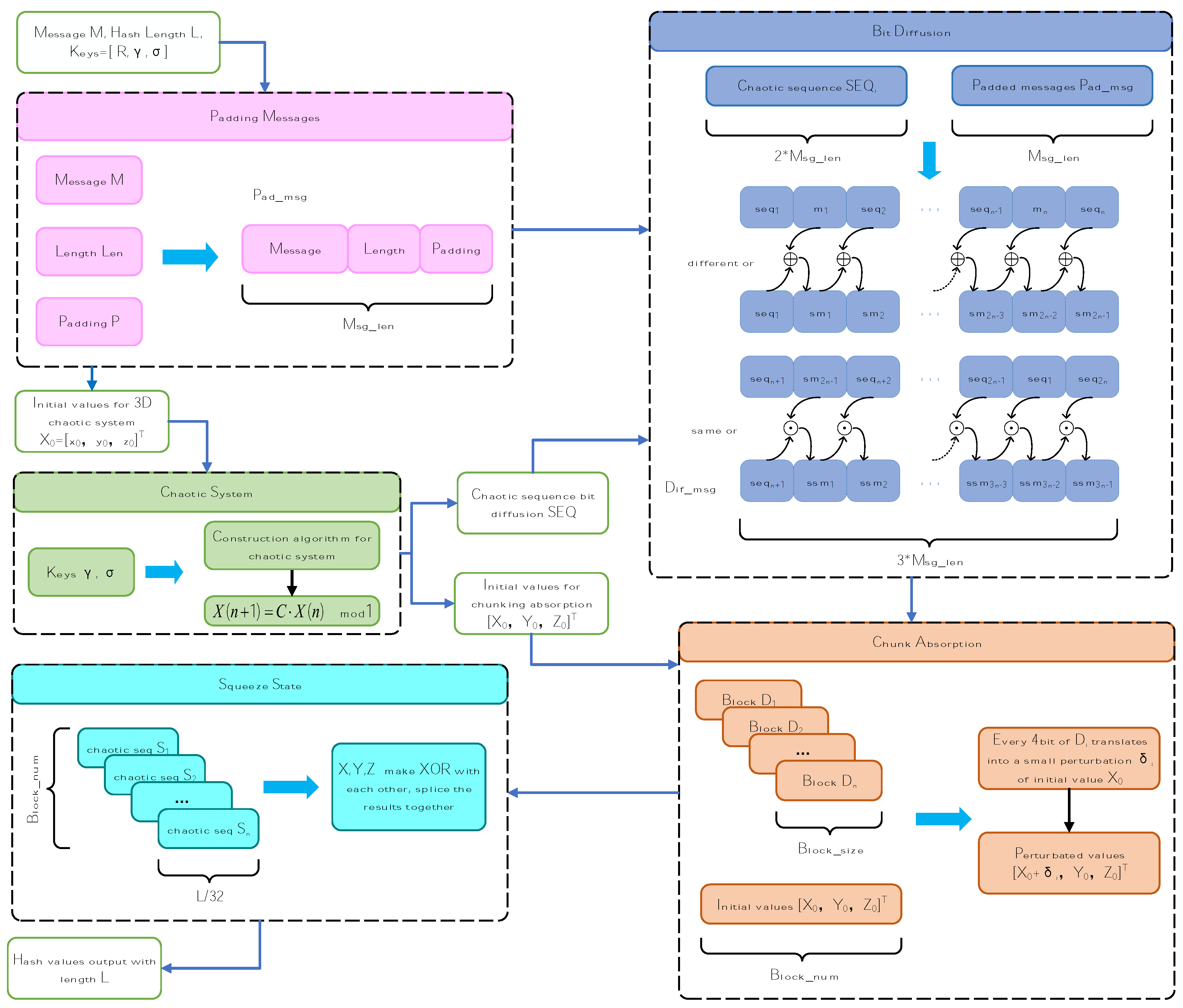
4.1. Hash Function Construction Algorithm
- Include the length of messages in the padding to resist length extension attacks;
- Significantly increase the number of iterations of the compression function to increase the difficulty of cryptanalysis;
- Adopt mature structures in the design of the compression function to avoid security risks;
- Ensure rapid diffusion of input differentials in algorithm design to resist arithmetic differential analysis methods.
4.2. The Key Space of Algorithm
4.3. Hash Sensitivity Analysis
4.4. Statistical Analysis of Scrambling and Diffusion
- The minimum number of changed bits as Equation (15);
- The maximum number of changed bits as Equation (16);
- The average number of changed bits as Equation (17);
- The average rate of changed bits as Equation (18);
- The standard deviation of changed bits as Equation (19);
- The average rate of change in standard deviation as Equation (20).
4.5. Uniform Distribution Analysis of Hash Values
4.6. Collision Analysis of the Hash Function
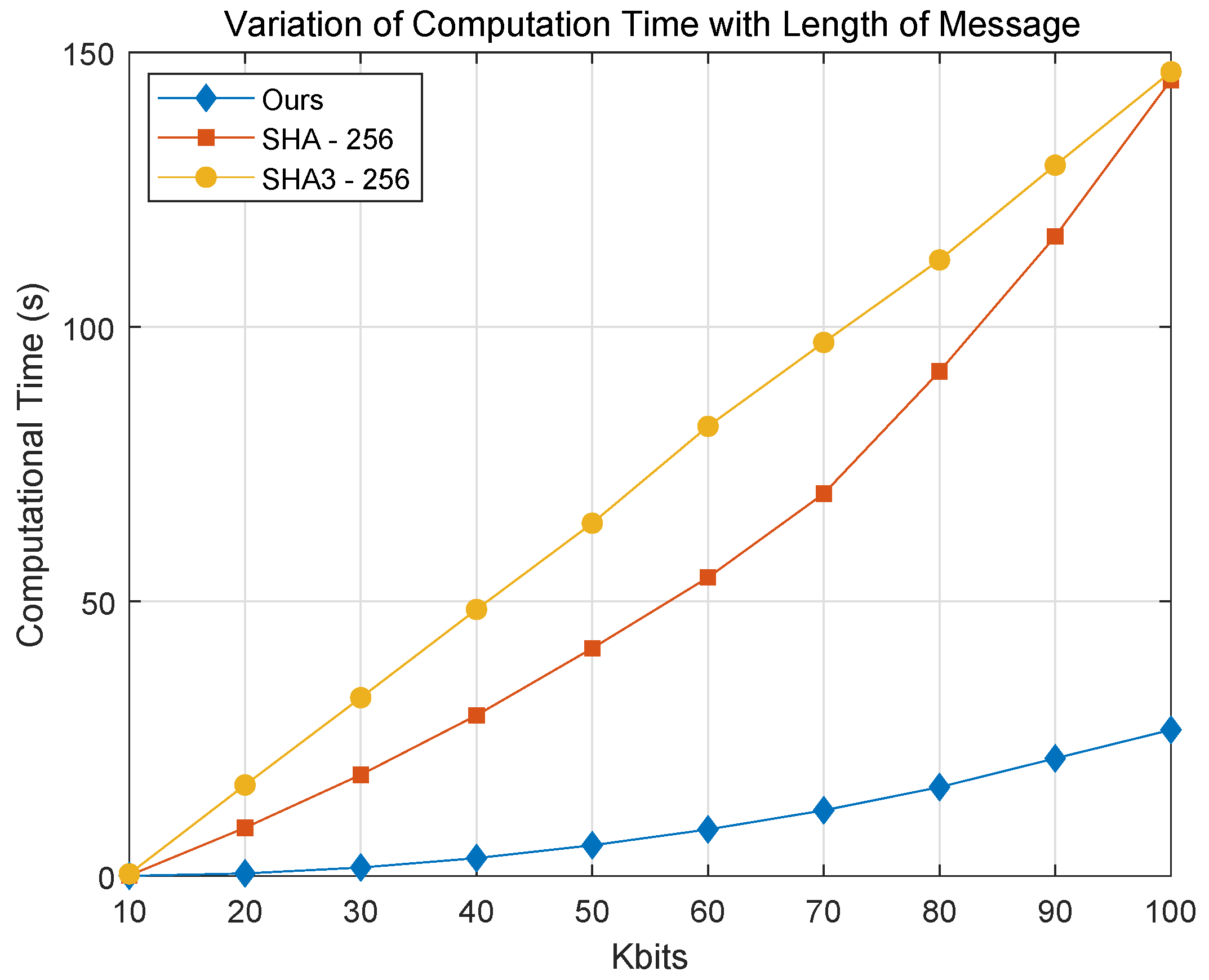
4.7. Comparative Analysis of Hash Performance and Speed
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Din, Q.; Naseem, R.; Shabbi, M. Predator-Prey Interaction with Fear Effects: Stability, Bifurcation and Two-Parameter Analysis Incorporating Complex and Fractal Behavior. Fractal Fract. 2024, 8, 221. [Google Scholar] [CrossRef]
- Pacheco, P.; Mera, E.; Navarro, G.; Parodi, C. Urban Meteorology, Pollutants, Geomorphology, Fractality, and Anomalous Diffusion. Fractal Fract. 2024, 8, 204. [Google Scholar] [CrossRef]
- Han, H.; Xu, J.; Cheng, X.; Jia, Z.; Zhang, J.; Shore, K. Simulation of Gb/s free space optical secure communication using interband cascade laser chaos. Opt. Commun. 2024, 559, 130424. [Google Scholar] [CrossRef]
- Cui, Z.; Zhou, Y.; Li, R. Complex Dynamics Analysis and Chaos Control of a Fractional-Order Three-Population Food Chain Model. Fractal Fract. 2023, 7, 548. [Google Scholar] [CrossRef]
- Chen, Z. Nonlinear dynamics of thin plates excited by a high-power ultrasonic transducer. Nonlinear Dyn. 2016, 84, 355–370. [Google Scholar] [CrossRef]
- Chang, H.; Wang, E.; Liu, J. Research on Image Encryption Based on Fractional Seed Chaos Generator and Fractal Theory. Fractal Fract. 2023, 7, 221. [Google Scholar] [CrossRef]
- Qi, F.; Qu, J.; Chai, Y.; Chen, L.; Lopes, A. Synchronization of Incommensurate Fractional-Order Chaotic Systems Based on Linear Feedback Control. Fractal Fract. 2023, 6, 221. [Google Scholar] [CrossRef]
- Pancóatl-Bortolotti, P.; Costa, A.H.; Enríquez-Caldera, R.A.; Guerrero-Castellanos, J.F.; Tello-Bello, M. Time-frequency high-resolution for weak signal detection using chaotic intermittenceImage 1. Digit. Signal Process. 2023, 141, 1051–2004. [Google Scholar]
- Tan, Y.; Xu, W.; Huang, T.; Wang, L. A Multilevel Code Shifted Differential Chaos Shift Keying Scheme With Code Index Modulation. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1743–1747. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. A novel algorithm to analyze the dynamics of digital chaotic maps in finite-precision domain. Chin. Phys. B 2023, 32, 010501. [Google Scholar] [CrossRef]
- Addabbo, T.; Alioto, M.; Fort, A.; Pasini, A.; Rocchi, S.; Vignoli, V. A Class of Maximum-Period Nonlinear Congruential Generators Derived From the Rényi Chaotic Map. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 816–828. [Google Scholar] [CrossRef]
- Bhatnagar, G.; Wu, Q. Chaos-Based Security Solution for Fingerprint Data During Communication and Transmission. IEEE Trans. Instrum. Meas. 2021, 61, 876–887. [Google Scholar] [CrossRef]
- Solak, E. Partial identification of Lorenz system and its application to key space reduction of chaotic cryptosystems. IEEE Trans. Circuits Syst. II Express Briefs 2004, 51, 557–560. [Google Scholar] [CrossRef]
- Xie, E.; Li, C.; Yu, S.; Lu, J. On the cryptanalysis of Fridrich’s chaotic image encryption scheme. Signal Process. 2017, 132, 150–154. [Google Scholar] [CrossRef]
- Feng, S.; Han, M.; Zhang, J.; Qiu, T.; Ren, W. Learning Both Dynamic-Shared and Dynamic-Specific Patterns for Chaotic Time-Series Prediction. IEEE Trans. Cybern. 2022, 52, 4115–4125. [Google Scholar] [CrossRef] [PubMed]
- You, R.; Huang, X. Phase space reconstruction of chaotic dynamical system based on wavelet decomposition. Chin. Phys. B 2011, 20, 020505. [Google Scholar] [CrossRef]
- Li, Y. Parameters identification of nonlinear Lorenz chaotic system for high-precision model reference synchronization. Nonlinear Dyn. 2022, 108, 1733–1754. [Google Scholar]
- Moastsum, A.; Azman, S.; Je, S. Enhanced digital chaotic maps based on bit reversal with applications in random bit generators. Inf. Sci. 2020, 512, 1155–1169. [Google Scholar]
- Zheng, J.; Hu, H. Bit cyclic shift method to reinforce digital chaotic maps and its application in pseudorandom number generator. Appl. Math. Comput. 2022, 420, 126788. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. Counteracting the dynamic degradation of high-dimensional digital chaotic systems via a stochastic jump mechanism. Digit. Signal Process. 2022, 129, 103651. [Google Scholar] [CrossRef]
- Zhu, M.; Wang, C. A novel parallel chaotic system with greatly improved Lyapunov exponent and chaotic range. Int. J. Mod. Phys. B 2020, 34, 2050048. [Google Scholar] [CrossRef]
- Chen, G.; Lai, D. Making a dynamical system chaotic: Feedback control of Lyapunov exponents for discrete-time dynamical systems. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 1997, 44, 250–253. [Google Scholar] [CrossRef]
- Chen, G.; Lai, D. Feedback Control of Lyapunov Exponents For Discrete-Time Dynamical Systems. Int. J. Bifurc. Chaos 1996, 6, 1341–1349. [Google Scholar] [CrossRef]
- Peng, H.; Ji’e, M.; Du, X.; Duan, S.; Wang, L. Design of pseudorandom number generator based on a controllable multi-double-scroll chaotic system. Chaos Solitons Fractals 2023, 174, 113803. [Google Scholar] [CrossRef]
- Zhang, Y.; Hua, Z.; Bao, H.; Huang, H.; Zhou, Y. Generation of n-Dimensional Hyperchaotic Maps Using Gershgorin-Type Theorem and its Application. IEEE Trans. Syst. Man, Cybern. Syst. 2023, 53, 6516–6529. [Google Scholar] [CrossRef]
- Wang, C.; Fan, C.; Ding, Q. Constructing Discrete Chaotic Systems with Positive Lyapunov Exponents. Int. J. Bifurc. Chaos 2018, 28, 1850084. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. A universal method for constructing non-degenerate hyperchaotic systems with any desired number of positive Lyapunov exponents. Chaos Solitons Fractals 2022, 161, 112323. [Google Scholar] [CrossRef]
- Huang, L.; Liu, J.; Xiang, J.; Zhang, Z.; Du, X. A construction method of N-dimensional non-degenerate discrete memristive hyperchaotic map. Chaos Solitons Fractals 2022, 160, 112248. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. Constructing n-dimensional discrete non-degenerate hyperchaotic maps using QR decomposition. Chaos Solitons Fractals 2023, 174, 113915. [Google Scholar] [CrossRef]
- Fan, C.; Ding, Q. Design and geometric control of polynomial chaotic maps with any desired positive Lyapunov exponents. Chaos Solitons Fractals 2023, 169, 113258. [Google Scholar] [CrossRef]
- Ding, D.; Wang, W.; Yang, Z.; Hu, Y.; Wang, J.; Wang, M.; Niu, Y.; Zhu, H. An n-dimensional modulo chaotic system with expected Lyapunov exponents and its application in image encryption. Chaos Solitons Fractals 2023, 174, 113841. [Google Scholar] [CrossRef]
- He, J.; Yu, S.; Lü, J. Constructing Higher-Dimensional Nondegenerate Hyperchaotic Systems with Multiple Controllers. Int. J. Bifurc. Chaos 2023, 27, 1750146. [Google Scholar] [CrossRef]
- Zhang, Y.; Hua, Z.; Bao, H.; Huang, H.; Zhou, Y. An n-Dimensional Chaotic System Generation Method Using Parametric Pascal Matrix. IEEE Trans. Ind. Inform. 2022, 18, 8434–8444. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, W.; Guo, W.; Zhang, J. Secure chaotic system with application to chaotic ciphers. Inf. Sci. 2013, 221, 555–570. [Google Scholar] [CrossRef]
- Hua, Z.; Zhang, Y.; Bao, H.; Huang, H.; Zhou, Y. n-Dimensional Polynomial Chaotic System with Applications. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 784–797. [Google Scholar] [CrossRef]
- Sotirov, A.; Stevens, M.; Appelbaum, J.; Lenstra, A.; Molnar, D.; Osvik, D.; Weger, B. MD5 considered harmful today: Creating a rogue CA certificate. In Proceedings of the 25th Chaos Communications Congress, Berlin, Germany, 28–30 December 2008. EPFL-CONF-164547. [Google Scholar]
- Wang, X.; Yu, H. Finding Collisions in the Full SHA-1; Springer: Berlin/Heidelberg, Germany, 2005; Volume 3621, pp. 17–36. [Google Scholar]
- Ayubi, P.; Saeed, S.; Amir, M. Chaotic Complex Hashing: A simple chaotic keyed hash function based on complex quadratic map. Chaos Solitons Fractals 2023, 173, 113647. [Google Scholar] [CrossRef]
- Masrat, R.; Samir, B. From Collatz Conjecture to chaos and hash function. Chaos Solitons Fractals 2023, 176, 114103. [Google Scholar]
- Teh, J.; Alawida, M.; Ho, J. Unkeyed hash function based on chaotic sponge construction and fixed-point arithmetic. Nonlinear Dyn. 2020, 100, 713–729. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Liu, X. A fast and efficient hash function based on generalized chaotic mapping with variable parameters. Neural Comput. Appl. 2017, 28, 1405–1415. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Kadir, A. Constructing chaos-based hash function via parallel impulse perturbation. Soft Comput. 2021, 25, 11077–11086. [Google Scholar] [CrossRef]
- Strang, G. The Properties of Eigenvalues and Eigenvectors. In Linear Algebra and Its Applications; Brooks Cole: Boston, MA, USA, 2016; pp. 290–295. [Google Scholar]
- Ablay, G. Lyapunov Exponent Enhancement in Chaotic Maps with Uniform Distribution Modulo One Transformation. Chaos Theory Appl. 2022, 4, 45–58. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, H. A Nondegenerate n-Dimensional Hyperchaotic Map Model with Application in a Keyed Parallel Hash Function. Int. J. Bifurc. Chaos 2023, 33, 2350070. [Google Scholar] [CrossRef]
- Natiq, H.; Santo, B.; Shaobo, H.; M, R.; Adem, K. Designing an M-dimensional nonlinear model for producing hyperchaos. Chaos Solitons Fractals 2018, 114, 506–515. [Google Scholar] [CrossRef]
- Addabbo, T.; Fort, A.; Rocchi, S.; Vignoli, V. Digitized Chaos for Pseudo-Random Number Generation in Cryptography; Springer: Berlin/Heidelberg, Germany, 2011; Volume 354, pp. 67–97. [Google Scholar]
- Guo, W. Cryptoanalysis and Construction of Chaotic Hash Functions; Southwest Jiaotong University: Chengdu, China, 2012. [Google Scholar]
- Lin, C.; Yeh, Y.; Lee, C. Keyed/Unkeyed SHA-2. J. Discret. Math. Sci. Cryptogr. 2003, 6, 45–58. [Google Scholar] [CrossRef]
- Morris, D. SHA-3 Standard: Permutation-Based Hash and Extendable-Output Functions; Federal Inf. Process. Stds. (NIST FIPS); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2015. [Google Scholar]
- Alawida, M.; Teh, J.; Oyinloye, D.; Alshoura, W.; Ahmad, M.; Alkhawaldeh, R. A New Hash Function Based on Chaotic Maps and Deterministic Finite State Automata. IEEE Access 2020, 8, 113163–113174. [Google Scholar] [CrossRef]
- Chenaghlu, M.; Jamali, S.; Khasmakhi, N. A novel keyed parallel hashing scheme based on a new chaotic system. Chaos Solitons Fractals 2016, 87, 216–225. [Google Scholar] [CrossRef]
- Dong, C. Constructing a discrete memristor chaotic map and application to hash function with dynamic S-Box. Eur. Phys. J. Spec. Top. 2022, 231, 3239–3247. [Google Scholar] [CrossRef]










| ND Discrete Chaotic System | Function Relationship | Remark |
|---|---|---|
| Zhang [25] | , is the sum of the non-primary diagonal elements of the kth row or column, respectively, is the control parameter, is a constant greater than 1 | |
| Wang [26] | is the eigenvalue of the constructed coefficient matrix | |
| Fan [27] | is the singular value of the constructed coefficient matrix | |
| Fan [30] | is the control parameter | |
| Wang [34] | is control eigenvalue for construction of matrix | |
| Hua [35] | is the control parameter for diagonal elements of matrix | |
| Ablay [44] | is the LEs of the original system and is the control gain | |
| Zhao [45] | , r are control parameters and is chaotic mapping function | |
| Natiq [46] | is the upper triangular matrix of the controlled matrix undergoing QR decomposition | |
| Ours | both and are control parameters and is the eigenvalue of the original matrix, where |
| Q | |||||
|---|---|---|---|---|---|
| Logistic | 0 | 5.32 | 3.16 | 17.31 | 139.54 |
| Zhang [25] | 2.63 | 117.2 | 5404.19 | 30,982.07 | 157,539.81 |
| Wang [26] | 22.72 | 2327.03 | 34,303.80 | 93,032.75 | 264,198.62 |
| Fan [27] | 18.81 | 530.89 | 9949.62 | 154,844.12 | U |
| Fan [30] | 4.58 | 884.12 | 15,725.72 | 274,758.68 | U |
| Wang [34] | 5.85 | 114.68 | 440.60 | 1808.92 | 14,137.88 |
| Hua [35] | 2.04 | 917.55 | 1038.36 | 73,567.63 | 171,460.61 |
| Zhao [45] | 0.50 | 21.88 | 79.92 | 313.4 | 16,008.89 |
| Ours | 159.68 | 3077.48 | 19,565.24 | 131,474.3 | U |
| I | 3 | 5 | 7 | 9 | 11 |
|---|---|---|---|---|---|
| Zhang [25] | 4.7225 | 6.9465 | 8.4101 | 9.5020 | 10.3729 |
| Wang [26] | 4.7179 | 6.9393 | 8.4011 | 8.4844 | 10.3499 |
| Fan [27] | 4.7347 | 6.9588 | 8.4165 | 9.5046 | 10.3732 |
| Fan [30] | 2.5153 | 2.4711 | 2.8456 | 3.1830 | 3.4649 |
| Wang [34] | 2.1695 | 0.3772 | 0.09749 | 0.03385 | 0.01409 |
| Hua [35] | 3.1584 | 4.6419 | 5.6141 | 6.3397 | 6.9188 |
| Zhao [45] | 4.5856 | 6.6305 | 7.9812 | 8.9964 | 9.8108 |
| Ours | 4.7486 | 6.9623 | 8.4213 | 9.5094 | 10.3782 |
| Ideal Value | 4.7549 | 6.9658 | 8.4221 | 9.5098 | 10.3783 |
| I | 4 | 6 | 8 | 10 | 12 |
|---|---|---|---|---|---|
| Zhang [25] | 6.1746 | 9.2702 | 12.4259 | 15.5899 | 18.7601 |
| Wang [26] | 6.3082 | 9.5052 | 12.6791 | 15.8495 | 19.0195 |
| Fan [27] | 6.3178 | 9.5059 | 12.6791 | 15.8495 | 19.0195 |
| Fan [30] | 2.1934 | 8.0402 | 7.9972 | 14.2671 | 19.0192 |
| Wang [34] | 2.8302 | 9.5063 | 12.6790 | 15.8495 | 19.0195 |
| Hua [35] | 5.3993 | 5.1094 | 11.1042 | 15.8495 | 19.0195 |
| Zhao [45] | 6.1271 | 9.2193 | 12.2802 | 15.3700 | 18.4455 |
| Ours | 6.3167 | 9.5057 | 12.6791 | 15.8495 | 19.0195 |
| Ideal Value | 6.3399 | 9.5098 | 12.6797 | 15.8496 | 19.0196 |
| Items | Mean | Median | Variance | Skewness | Kurtosis | Range |
|---|---|---|---|---|---|---|
| Ideal Value | 0.5 | 0.5 | 0.0833 | 0 | 1.8 | * |
| Sinh Map | 0.0023796 | 0.0050234 | 4.5068 | 0.008751 | 1.6078 | [−4, 3] |
| LE-Sinh Map [44] | 0.49967 | 0.49920 | 0.083528 | 0.0026249 | 1.7977 | [0, 1] |
| Zhang [25] | 0.50001 | 0.50059 | 0.082348 | −0.0097979 | 1.807 | [0, 1] |
| 0.49987 | 0.49348 | 0.083916 | 0.018366 | 1.7872 | [0, 1] | |
| 0.50445 | 0.50704 | 0.083995 | −0.016506 | 1.7863 | [0, 1] | |
| Wang [26] | 0.50247 | 0.49967 | 0.083871 | 0.0044182 | 1.7855 | [0, 1] |
| 0.50095 | 0.505 | 0.083448 | −0.010964 | 1.7928 | [0, 1] | |
| 0.50322 | 0.50453 | 0.083691 | 0.00088488 | 1.7908 | [0, 1] | |
| Fan [27] | 0.49992 | 0.49553 | 0.08519 | 0.003484 | 1.7747 | [0, 1] |
| 0.49561 | 0.49127 | 0.083511 | 0.034834 | 1.7853 | [0, 1] | |
| 0.50385 | 0.50263 | 0.083448 | −0.003464 | 1.7995 | [0, 1] | |
| Fan [30] | 10.5040 | 10.5060 | 0.083473 | −0.016895 | 1.8046 | [, ] |
| 5.0029 | 5 | 0.0019533 | 16.416 | 286.9 | [, ] | |
| 10.003 | 10 | 0.0018545 | 17.906 | 340.62 | [, ] | |
| Wang [34] | −0.0075109 | −0.013969 | 0.33091 | 0.01284 | 1.8076 | [−1, 1] |
| −0.0074616 | −0.013969 | 0.33097 | 0.012932 | 1.8075 | [−1, 1] | |
| −0.0073961 | −0.013969 | 0.33103 | 0.012793 | 1.8072 | [−1, 1] | |
| Hua [35] | 0.50065 | 0.49824 | 0.083753 | −0.0007237 | 1.7914 | [0, 1] |
| 0.50218 | 0.50295 | 0.084684 | −0.013139 | 1.7906 | [0, 1] | |
| 0.49654 | 0.49173 | 0.082741 | 0.022562 | 1.8088 | [0, 1] | |
| Zhao [45] | −0.0013744 | 0.0057337 | 0.50272 | −0.0028507 | 1.4966 | [−1, 1] |
| 0.0028256 | −0.001282 | 0.49867 | −0.0043736 | 1.5004 | [−1, 1] | |
| 0.0083704 | 0.021124 | 0.50525 | −0.013516 | 1.4899 | [−1, 1] | |
| Ours | 0.49996 | 0.49985 | 0.083288 | 0.0010726 | 1.8010 | [0, 1] |
| 0.50035 | 0.50056 | 0.083396 | −0.0019546 | 1.8005 | [0, 1] | |
| 0.49998 | 0.50015 | 0.083362 | −0.0004369 | 1.8012 | [0, 1] |
| Reference | |||
|---|---|---|---|
| Zhang [25] | 1.9782 | 1.8676 | 1.9149 |
| Wang [26] | 1.9748 | 1.9752 | 1.9746 |
| Fan [27] | 1.9674 | 1.9796 | 1.9709 |
| Fan [30] | 1.9930 | 1.9893 | 1.0486 |
| Wang [34] | 0.9971 | 0.9972 | 0.9972 |
| Hua [35] | 1.9829 | 1.4212 | 1.9776 |
| Zhao [45] | 1.7656 | 1.3631 | 1.7059 |
| Ours | 1.9841 | 1.9897 | 1.9800 |
| Chaotic Maps | Matrix Entity Addition | Matrix Entity Multiplication | Matrix Multiplication | Time Complexity |
|---|---|---|---|---|
| Zhang [25] | ||||
| Wang [26] | 0 | 0 | ||
| Fan [27] | 0 | 0 | ||
| Fan [30] | 0 | |||
| Wang [34] | ||||
| Hua [35] | ||||
| Zhao [45] | 0 | |||
| Ours |
| Texts | Hash Length | Hash Values |
|---|---|---|
| ‘This is my hash function based on non-degeneracy chaotic system.’ | 32 | #460253AB |
| 64 | #2D67BF5A677C80EA | |
| 128 | #22F1A4BC39FA9C6F52D8771E06DB06DD | |
| 160 | #74D5B1150B3964970B7784492C1D5914F74374BB | |
| 256 | #CEE721F92A4B2AF8A170E8B521BBE17CCA5EC4A2B9FF279EC81B91C184660A08 | |
| 512 | #E0FF8DB02955A8FA2E3A9B62E2A6B57E0FEDE5F472C80E49C844E4319ED06CB9B48CC338194 5993D1D78A6D5A49D53D8B0CCBA2990EC4D2ED395DBBCFF857E12 | |
| 1024 | #FE2298023B45A7E3ABAF87FB841625934A0D20FF5B451233FEDF07257058EEF9B207B0AE91EB 7A7678B879070F6B1DECB0DB02F49DFE1316EE4F909883474E7858376284F61CE3C1B53C3AB2C 10779B66186025BCC0CF656E20EBAF385DE06B699F89047E26885F9240B63CF29AF8314C1C5253 A69F9C9B012416DDCF01712E5 | |
| ‘this is my hash function based on non-degeneracy chaotic system.’ | 32 | #F5711BF1 |
| 64 | #E02355ED92C11821 | |
| 128 | #B089C84953E6864C478320AFF3B07259 | |
| 160 | #60EA997D08E51DAB644DA647998D146F73103821 | |
| 256 | #4D78F7C78E59B31DC78B69207E570CDE880462ADCB6B985E24473E7B0803ABF7 | |
| 512 | #0D56911B38EB5CDA7FBF049D5D81C31014AF5AD9ECF0360D0FC65F4DD7D2A405FB6C16EB 0EC6A6BFC7A4653D09E12ABC4F77B2BBD7A9ECDBE152A2382316CD95 | |
| ‘this is my hash function based on non-degeneracy cheotic system.’ | 32 | #3F804107 |
| 64 | #B6B1678BBA624937 | |
| 128 | #621750DD7573FAF57847BED8B7134FA6 | |
| 160 | #33F68A1ED5D305D2A041D9CB86E72FA668CCB4A3 | |
| 256 | #70A9CD20D962AEC304ED813E0F71161884EBC76AE3C8BD69F22548A7E9DCB673 | |
| 512 | #2EB4817E0C5375877BFA0BDFDB1C1E23EC784EA73088F6FBFD6CF57B20BDF3AF320101F5225 5DF92A703F640F7FC33926C80A113183AC8E79BBE41106626160D | |
| ‘This is my hash function based on non-degeneracy chaotic system,’ | 32 | #5B431614 |
| 64 | #6A75EDC0043DC8C6 | |
| 128 | #59F43060DE8737E25B8F7D71E2FC5707 | |
| 160 | #4B6468110DE4DA6CABBA854172D030C212F402C9 | |
| 256 | #E51CC9CF028B1000B72F8CB526A9981127093514A23D083A94F3DCF7C562C1F0 | |
| 512 | #6710CD43557C6FC7EC74B4D604CD1ADC4CA15BC5FA0CC0C6B88ADBEEDD4DB8E15B063E 2E935EFE0ADE1A27FFEEF703717D240643ACD820BDCDB7ED01C2B433A6 | |
| ‘This is my hash function based on non-degeneracy chaotic system. ’ | 32 | #6B9EA22D |
| 64 | #B3E9F9C9AE093428 | |
| 128 | #7D88D061ECB3ADC9C759FED83652000C | |
| 160 | #F439813134751F87FADB50307291081F89DDCF2B | |
| 256 | #486E86F73DC7825DB375496D2B1B9E720101839D071A26EB093059820ED786C7 | |
| 512 | #AB6C198CDCEF3E348778B5060B0FD2557EF571DED5EFBFE3249C56ABB75CCD081E72717B47 94B4024DB44C96F0B4399C7486F79828DC69A98FC9B892F020CE96 | |
| ‘This is my hash function based on non-degeneracy chaotic system.’ | 32 | #2D913059 |
| 64 | #1CF30D69EB50DE64 | |
| 128 | #55319D52E7038DCC04CBFCD76BE2FC51 | |
| 160 | #D026A6C438F1022BA278DF3DF6C6E2E7BF9DD551 | |
| 256 | #EDD1E9BB6EA2B4E8AEEBA803FD1A7CDFE2D02229BEE98BB2524177BD8C436B49 | |
| 512 | #778F7BC923E28FEFA1973D457B5BD95780196376236CAB17C9AEDBA4F1F546BDD8523B456E8 E96873042D3A6F5E1771BF500690DE5CEF3695C4A2ABC0E426681 | |
| ‘This is my hash function based on non-degeneracy chaotic system.’ | 32 | #58BFC20A |
| 64 | #E95C6C0997BA8CFA | |
| 128 | #B0DDC0E8BEB632105366797E05FFDF15 | |
| 160 | #536559C9609BE57039D77DAF1DDC82DA8675C15E | |
| 256 | #42FDEB8E43E6C1A883C7F31DF392F59A1A6794711AC4A16E1985B997E54CEB2C | |
| 512 | #B55A6C422F83693BA3FA318A9C43D6DF7CF162D1DD5735479256A8A40E18ADBF97A4237EC C4689287E1CBE49AB15CF1076FEF55A5B0659C917AE67FC6ED3171C |
| Hash Size | Statistic | N | ||||
|---|---|---|---|---|---|---|
| 256 | 512 | 1024 | 2048 | 10,000 | ||
| 9 | 8 | 8 | 6 | 6 | ||
| 24 | 24 | 24 | 24 | 27 | ||
| 25.9570 | 16.1172 | 16.0186 | 15.9688 | 15.9811 | ||
| 49.8657% | 50.3662% | 50.0580% | 49.9023% | 49.9409% | ||
| 2.8186 | 2.8288 | 2.8642 | 2.8816 | 2.8320 | ||
| 8.8082% | 8.8401% | 8.9505% | 9.0049% | 8.8444% | ||
| 22 | 21 | 21 | 16 | 16 | ||
| 42 | 48 | 48 | 48 | 48 | ||
| 31.8984 | 32.1055 | 31.9854 | 31.8984 | 32.0450 | ||
| 49.8413% | 50.1647% | 49.9771% | 49.8413% | 50.0703% | ||
| 4.0360 | 4.0529 | 4.0420 | 3.9618 | 3.9801 | ||
| 6.3063% | 6.3326% | 6.3157% | 6.1903% | 6.2190% | ||
| 51 | 47 | 47 | 45 | 43 | ||
| 82 | 82 | 82 | 83 | 84 | ||
| 64.0586 | 63.8320 | 63.9863 | 63.9785 | 64.0005 | ||
| 50.0458% | 49.8688% | 49.9893% | 49.9832% | 50.0004% | ||
| 5.5521 | 5.6387 | 5.8364 | 5.7691 | 5.6550 | ||
| 4.3376% | 4.4052% | 4.5597% | 4.5071% | 4.4180% | ||
| 60 | 60 | 60 | 57 | 56 | ||
| 96 | 99 | 99 | 99 | 103 | ||
| 79.6680 | 79.7988 | 79.7822 | 79.8706 | 79.9557 | ||
| 4.9792% | 4.9874% | 4.9864% | 4.9929% | 4.9971% | ||
| 6.5379 | 6.4420 | 6.3458 | 6.3012 | 6.2929 | ||
| 4.0862% | 4.0263% | 3.9661% | 3.9382% | 3.9330% | ||
| 105 | 105 | 100 | 100 | 100 | ||
| 145 | 153 | 153 | 153 | 161 | ||
| 126.7383 | 127.5742 | 127.9424 | 127.850 | 127.8563 | ||
| 49.5071% | 49.8337% | 49.9775% | 49.9416% | 49.9439% | ||
| 8.1165 | 8.1045 | 7.8636 | 7.8134 | 8.0326 | ||
| 3.1705% | 3.1658% | 3.0717% | 3.0521% | 3.1378% | ||
| 227 | 221 | 221 | 221 | 204 | ||
| 286 | 288 | 293 | 293 | 300 | ||
| 255.2891 | 255.2090 | 255.6074 | 255.4736 | 255.8933 | ||
| 49.8611% | 49.8455% | 49.9233% | 49.8972% | 49.9792% | ||
| 10.4371 | 10.8034 | 11.1439 | 11.1294 | 11.2280 | ||
| 2.0385% | 2.1100% | 2.1765% | 2.1737% | 2.1930% | ||
| 474 | 461 | 461 | 459 | 449 | ||
| 558 | 574 | 574 | 574 | 580 | ||
| 510.2578 | 510.5312 | 510.8643 | 511.7490 | 511.8808 | ||
| 49.8297% | 49.8566% | 49.8891% | 49.9755% | 49.9884% | ||
| 16.3566 | 15.9703 | 16.2582 | 15.9548 | 16.0323 | ||
| 1.5973% | 1.5596% | 1.5877% | 1.5581% | 1.5657% | ||
| N | Hash Length | The Change in Each Bit | |||
|---|---|---|---|---|---|
| 32 | 987 | 1067 | 1022.0000 | 23.4369 | |
| 64 | 965 | 1090 | 1020.7500 | 24.1477 | |
| 128 | 961 | 1094 | 1023.6563 | 23.1641 | |
| 160 | 950 | 1085 | 1022.3438 | 25.1146 | |
| 256 | 964 | 1083 | 1022.8047 | 23.4334 | |
| 512 | 955 | 1079 | 1021.8947 | 22.5991 | |
| 1024 | 948 | 1103 | 1023.4980 | 23.0450 | |
| 2048 | 945 | 1110 | 1023.5415 | 22.9031 | |
| N = 10,000 | 32 | 4863 | 5051 | 4994.0938 | 39.8945 |
| 64 | 4874 | 5113 | 5007.0313 | 49.6812 | |
| 128 | 4884 | 5128 | 5000.0391 | 46.6701 | |
| 160 | 4885 | 5135 | 4997.2313 | 48.1530 | |
| 256 | 4823 | 5148 | 4994.3867 | 54.3185 | |
| 512 | 4857 | 5156 | 4997.9160 | 49.7407 | |
| 1024 | 4865 | 5176 | 4998.8359 | 50.8643 | |
| 2048 | 4851 | 5189 | 5000.6880 | 50.2703 | |
| N | Hash Length | The Absolute Difference d in Hash Value | |||
|---|---|---|---|---|---|
| 32 | 50 | 697 | 36.7730 | 91.9326 | |
| 64 | 189 | 1140 | 631.8417 | 78.9802 | |
| 128 | 681 | 2178 | 1352.7851 | 84.5491 | |
| 160 | 832 | 2686 | 1612.6947 | 80.6347 | |
| 256 | 1679 | 3834 | 2738.6194 | 85.5819 | |
| 512 | 3769 | 7187 | 5577.7469 | 87.1523 | |
| 1024 | 9163 | 13,644 | 11,223.8559 | 87.6864 | |
| 2048 | 18,429 | 24,254 | 21,555.1690 | 84.1999 | |
| N = 10,000 | 32 | 29 | 773 | 36.7685 | 91.6921 |
| 64 | 179 | 1173 | 635.3298 | 79.4162 | |
| 128 | 642 | 2178 | 1353.1496 | 84.5719 | |
| 160 | 828 | 2686 | 1621.8514 | 81.0926 | |
| 256 | 1408 | 3940 | 2732.9695 | 85.4053 | |
| 512 | 3769 | 7733 | 5569.5015 | 87.0235 | |
| 1024 | 8706 | 13,644 | 11,200.4177 | 87.5033 | |
| 2048 | 18,336 | 25,251 | 21,558.5556 | 84.2131 | |
| N | Hash Length | The Number of Hash Collisions | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The Statistics Values | The Ideal Values | ||||||||||||||
| 32 | 2009 | 38 | 0 | 0 | 0 | 0 | 0 | 2016 | 32 | 0 | 0 | 0 | 0 | 0 | |
| 64 | 1976 | 70 | 1 | 0 | 0 | 0 | 0 | 1985 | 62 | 1 | 0 | 0 | 0 | 0 | |
| 128 | 1916 | 126 | 5 | 0 | 0 | 0 | 0 | 1924 | 120 | 4 | 0 | 0 | 0 | 0 | |
| 160 | 1899 | 146 | 2 | 0 | 0 | 0 | 0 | 1894 | 148 | 6 | 0 | 0 | 0 | 0 | |
| 256 | 1775 | 254 | 18 | 0 | 0 | 0 | 0 | 1807 | 226 | 14 | 1 | 0 | 0 | 0 | |
| 512 | 1610 | 386 | 44 | 5 | 2 | 0 | 0 | 1594 | 400 | 50 | 4 | 0 | 0 | 0 | |
| 1024 | 1268 | 588 | 162 | 22 | 7 | 0 | 0 | 1241 | 632 | 155 | 26 | 3 | 0 | 0 | |
| 2048 | 770 | 736 | 368 | 128 | 39 | 5 | 1 | 752 | 755 | 378 | 125 | 31 | 6 | 1 | |
| N = 10,000 | 32 | 9839 | 160 | 0 | 0 | 0 | 0 | 0 | 9845 | 154 | 1 | 0 | 0 | 0 | 0 |
| 64 | 9682 | 315 | 2 | 0 | 0 | 0 | 0 | 9692 | 304 | 4 | 0 | 0 | 0 | 0 | |
| 128 | 9371 | 605 | 22 | 1 | 0 | 0 | 0 | 9393 | 589 | 17 | 0 | 0 | 0 | 0 | |
| 160 | 9248 | 730 | 20 | 1 | 0 | 0 | 0 | 9247 | 725 | 27 | 1 | 0 | 0 | 0 | |
| 256 | 8766 | 1162 | 71 | 0 | 0 | 0 | 0 | 8823 | 1107 | 67 | 3 | 0 | 0 | 0 | |
| 512 | 7803 | 1942 | 233 | 19 | 2 | 0 | 0 | 6059 | 3042 | 757 | 125 | 15 | 2 | 0 | |
| 1024 | 6115 | 2937 | 798 | 130 | 19 | 0 | 0 | 6059 | 3042 | 757 | 125 | 15 | 2 | 0 | |
| 2048 | 3716 | 3653 | 1832 | 597 | 165 | 33 | 2 | 3672 | 3686 | 1843 | 612 | 152 | 30 | 5 | |
| Hash Length | N | Method | Statistical Analysis | |||||
|---|---|---|---|---|---|---|---|---|
| Ideal | - | - | 128 | 50.00% | - | - | ||
| Ayubi [38] | 107 | 146 | 127.17 | 49.68% | 7.79 | 3.05 | ||
| Masrat [39] | 123 | 131 | 128 | 50.00% | 8.132 | 3.00 | ||
| Liu [42] | 102 | 156 | 128.34 | 50.13% | 8.26 | 3.23 | ||
| Sha2 [49] | 104 | 153 | 128.05 | 50.02% | 7.94 | 3.10 | ||
| Sha3 [50] | 101 | 153 | 128.05 | 50.02% | 8.01 | 3.13 | ||
| Alawida [51] | 101 | 155 | 128.1 | 50.04% | 7.96 | 3.11 | ||
| Chenaghlu [52] | 101 | 153 | 126.75 | 49.51% | 7.98 | 3.12 | ||
| Dong [53] | 108 | 147 | 128.78 | 50.31% | 8.19 | 3.10 | ||
| Ours | 100 | 153 | 127.85 | 49.94% | 7.81 | 3.05 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, X.; Wang, X.; Han, H.; Wang, E. N-Dimensional Non-Degenerate Chaos Based on Two-Parameter Gain with Application to Hash Function. Electronics 2024, 13, 2627. https://doi.org/10.3390/electronics13132627
Dai X, Wang X, Han H, Wang E. N-Dimensional Non-Degenerate Chaos Based on Two-Parameter Gain with Application to Hash Function. Electronics. 2024; 13(13):2627. https://doi.org/10.3390/electronics13132627
Chicago/Turabian StyleDai, Xu, Xiaotong Wang, Haotong Han, and Erfu Wang. 2024. "N-Dimensional Non-Degenerate Chaos Based on Two-Parameter Gain with Application to Hash Function" Electronics 13, no. 13: 2627. https://doi.org/10.3390/electronics13132627
APA StyleDai, X., Wang, X., Han, H., & Wang, E. (2024). N-Dimensional Non-Degenerate Chaos Based on Two-Parameter Gain with Application to Hash Function. Electronics, 13(13), 2627. https://doi.org/10.3390/electronics13132627









