Sliding Mode Speed Control for PMSM Based on Model Predictive Current
Abstract
1. Introduction
- (1)
- A disturbance observer is designed based on MPCC to improve the parameter robustness of MPCC. Additionally, a novel sliding mode reaching law is designed in the speed loop to reduce system chattering while achieving fast system convergence to the sliding mode surface. The sign function sgn(s) in the reaching law is replaced with a piecewise square root switching function f(x) to further reduce chattering. Simultaneously, a fractional-order integral sliding mode surface is introduced to reduce steady-state errors in the system.
- (2)
- To enhance the system’s resistance to load disturbances, a sliding mode load torque observer is designed to rapidly and accurately estimate the load torque value, enabling compensation of the output of the novel sliding mode controller. This approach aims to mitigate the effects of sudden changes in velocity on the control system.
2. PMSM Model Predictive Current Control
2.1. Mathematical Model of PMSM
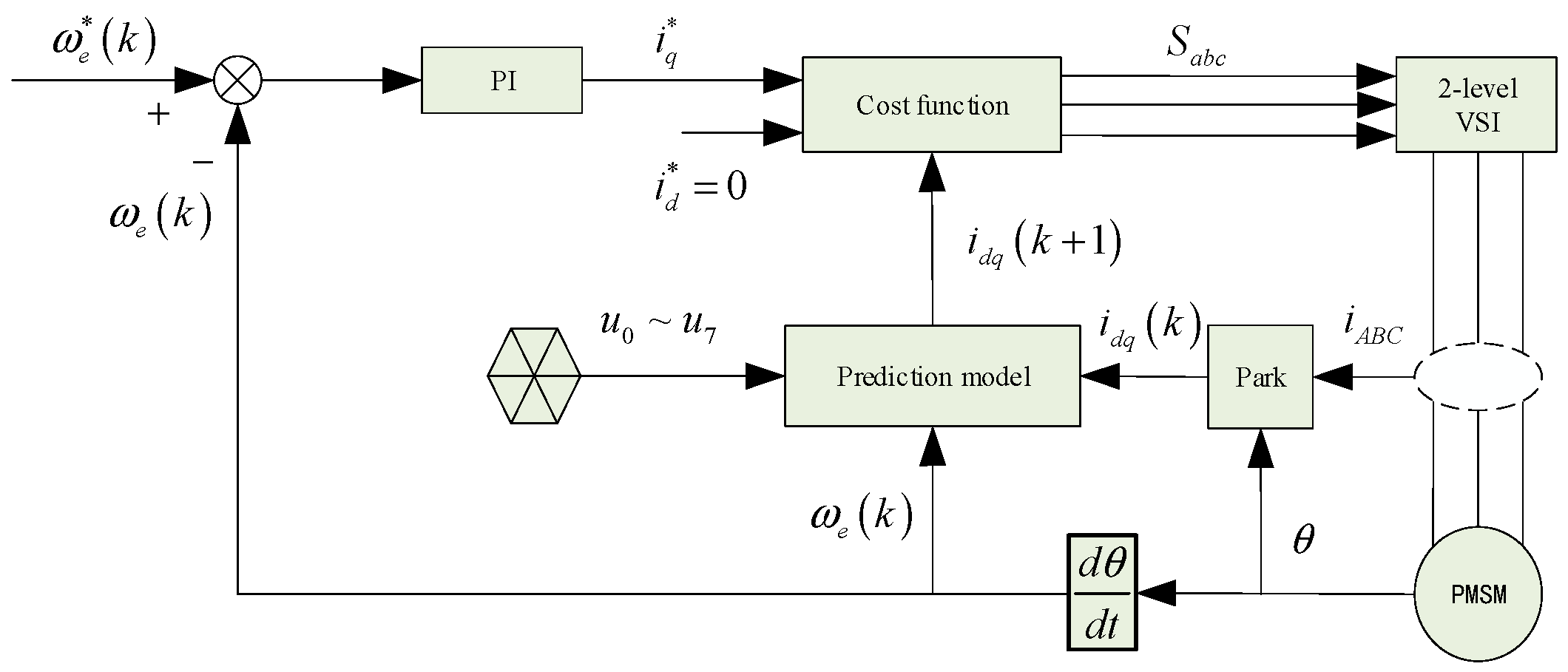
2.2. Model Predictive Current Control
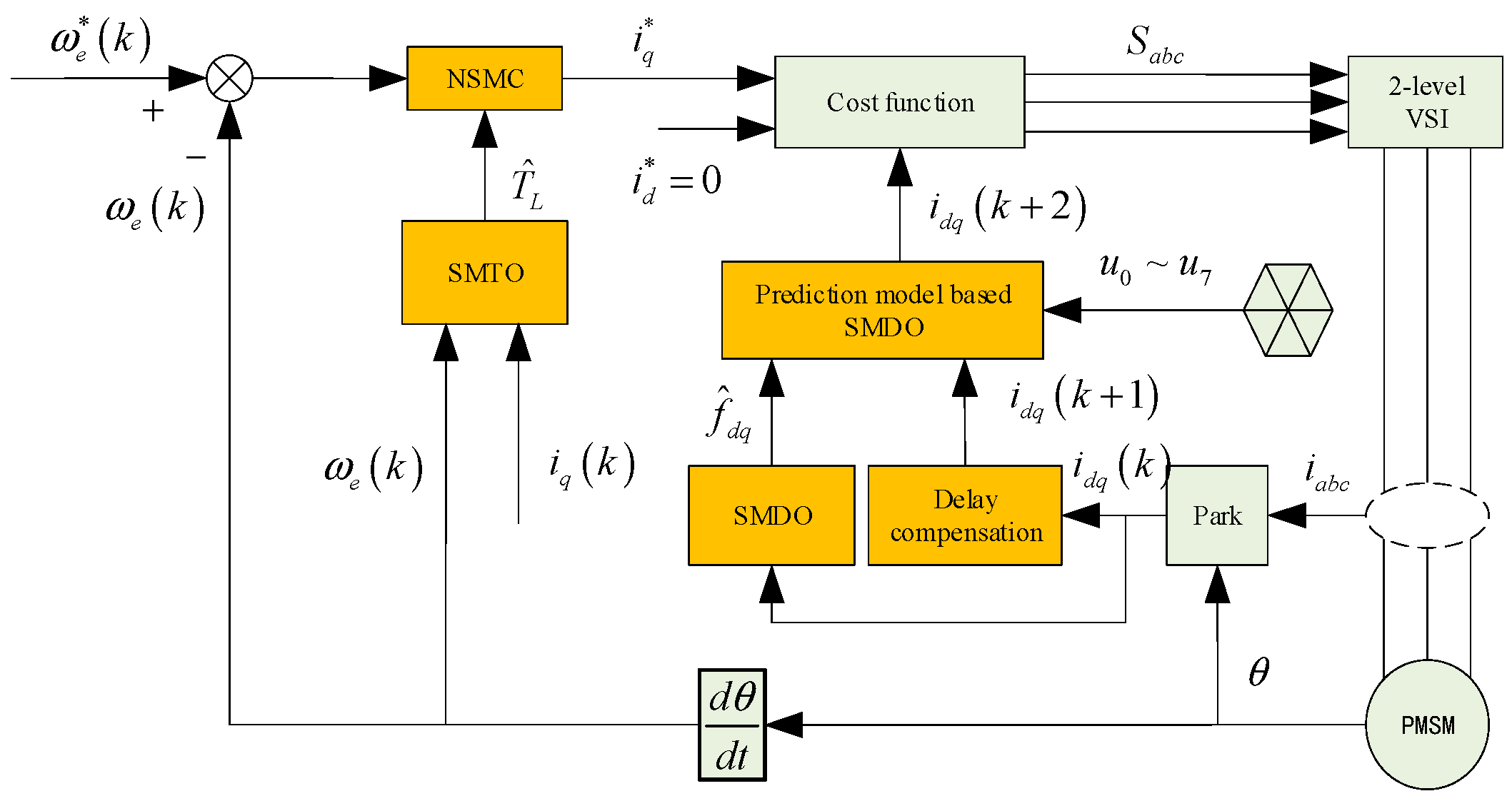
3. MPCC with Sliding Mode Disturbance Observer
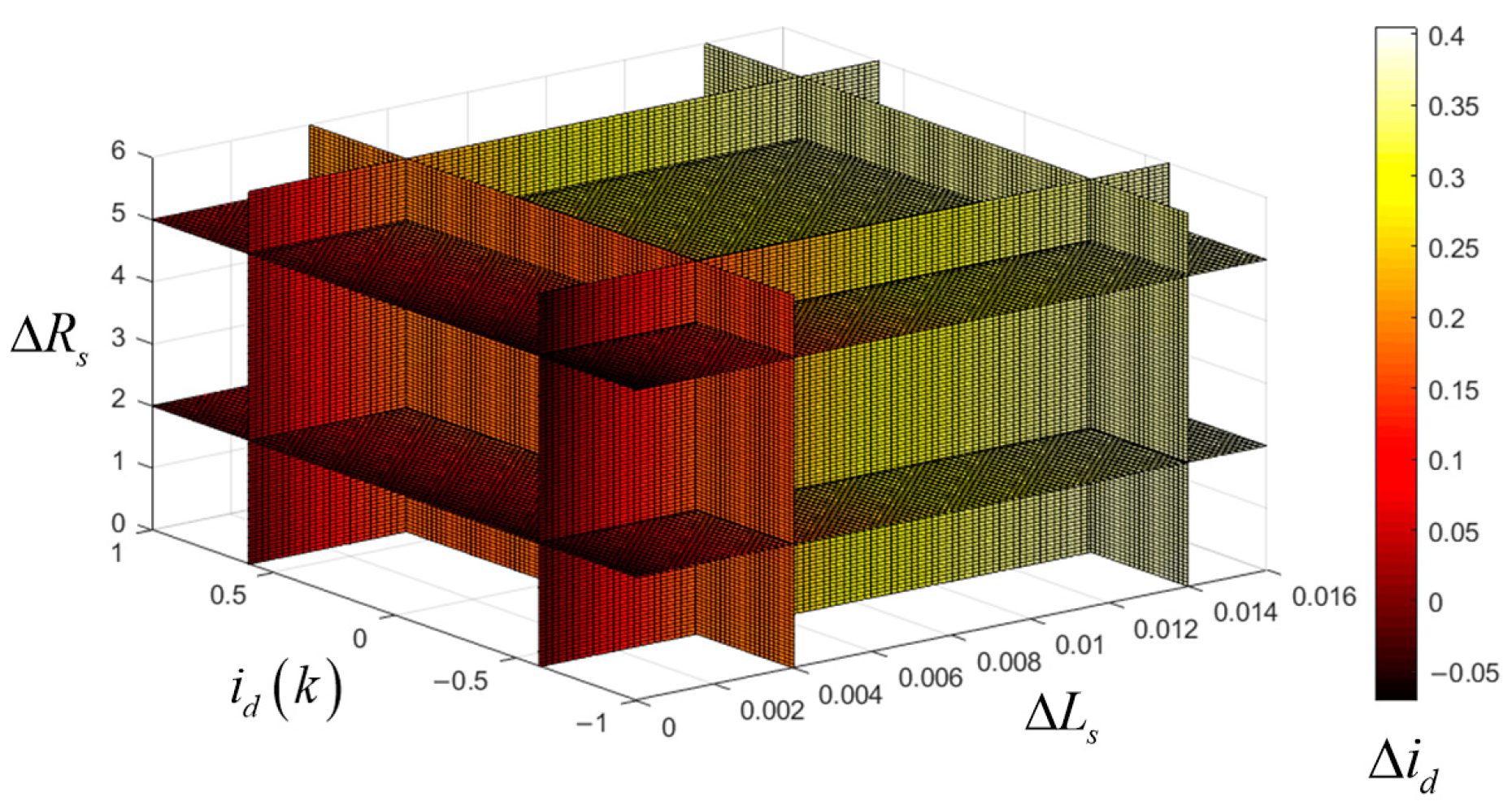
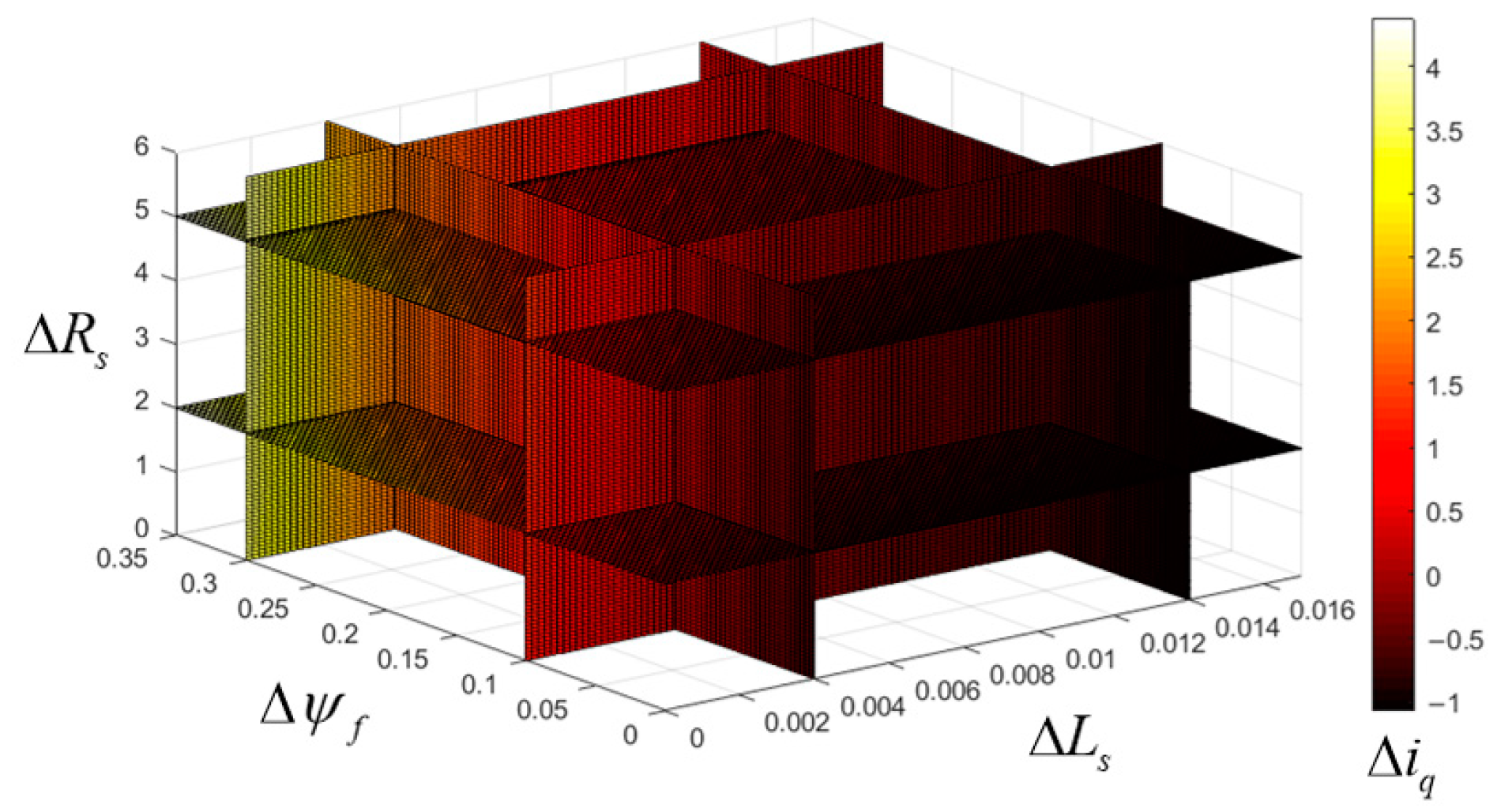
3.1. Parameter Sensitivity of MPCC
3.2. The Design of SMDO
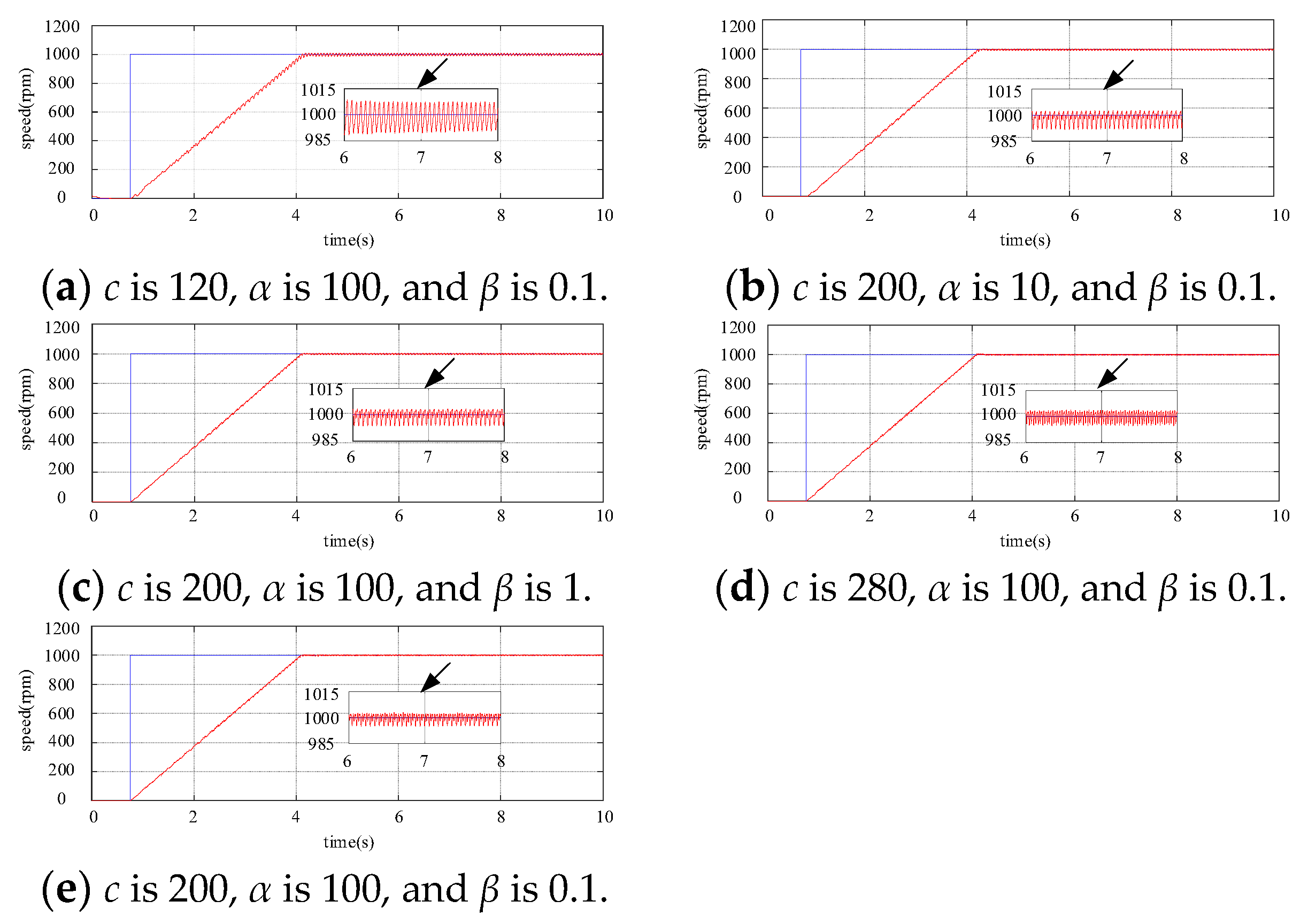
4. The Novel Sliding Mode Speed Controller
4.1. The Design of the NSMC Controller
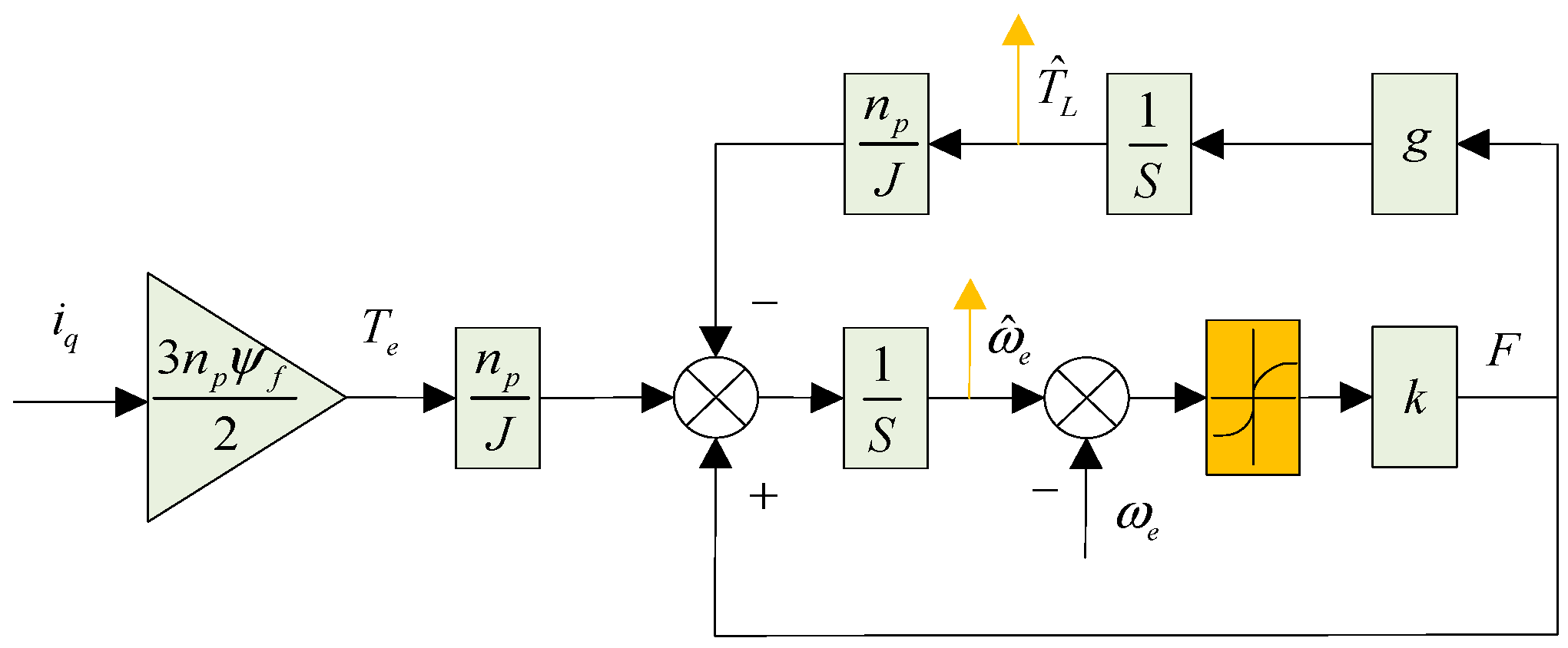
4.2. Design of the Sliding Mode Torque Observer
4.3. The Principle of Load Disturbance Compensation in PMSM
5. Experimental Research
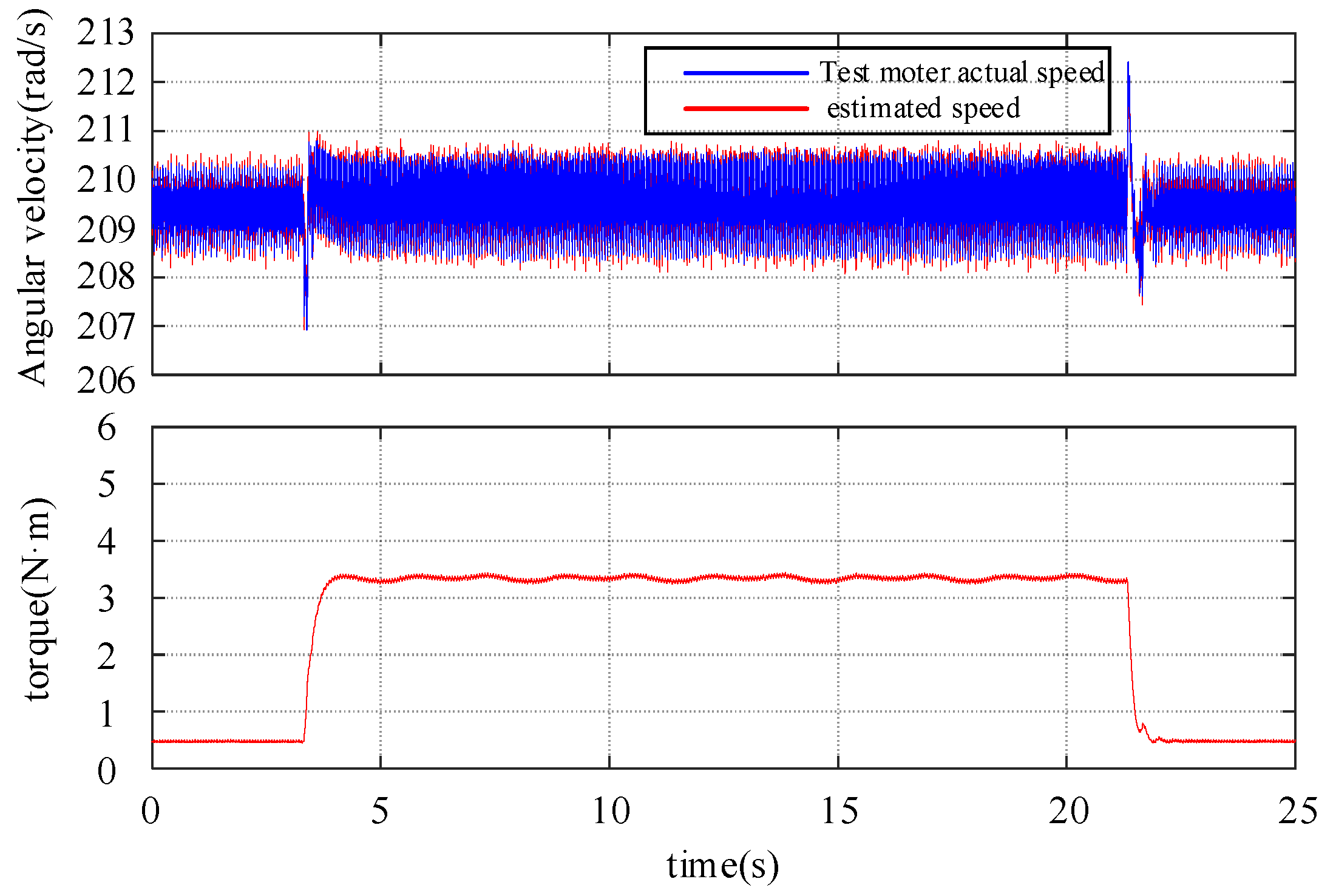
5.1. The Performance of the SMTO
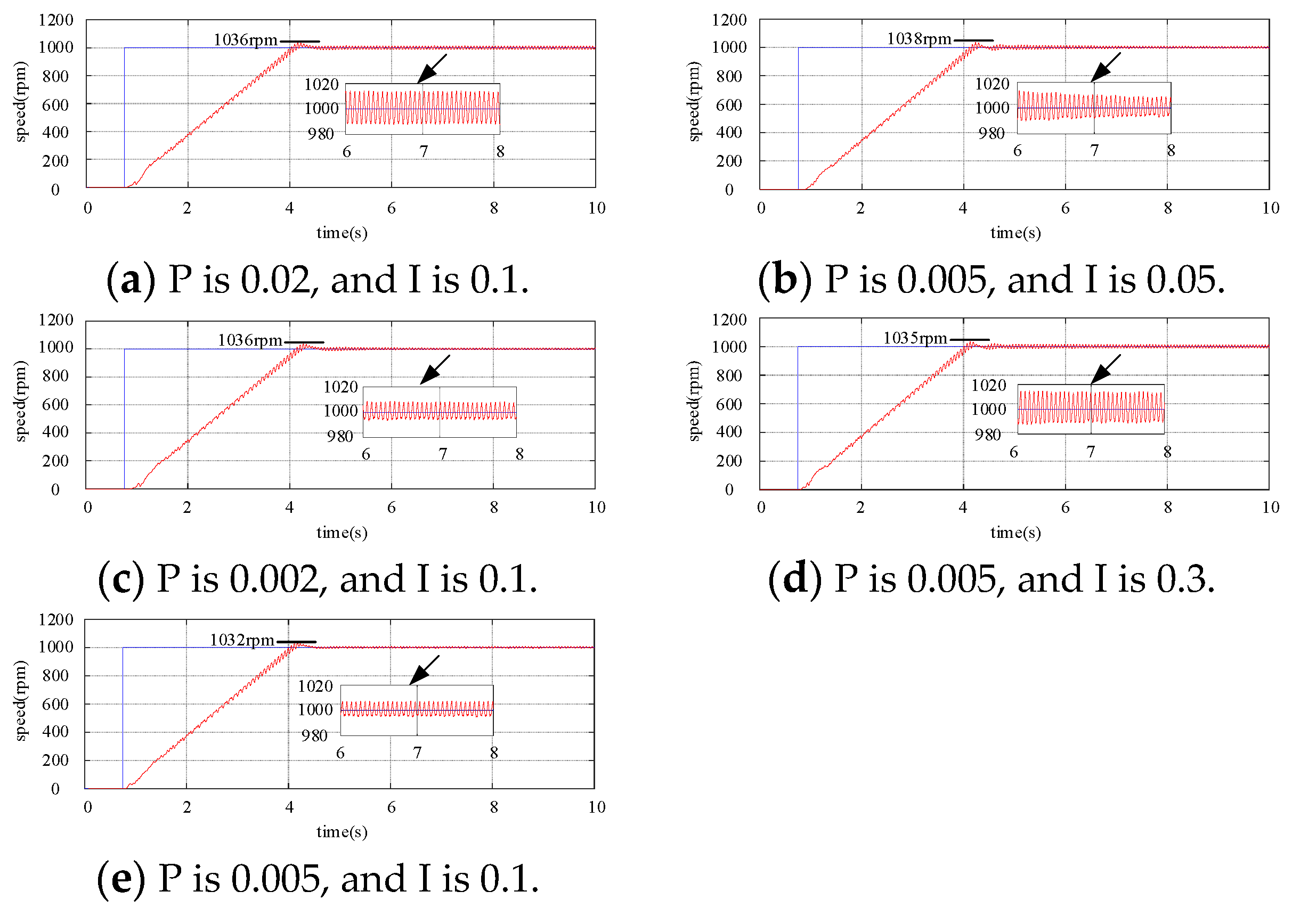
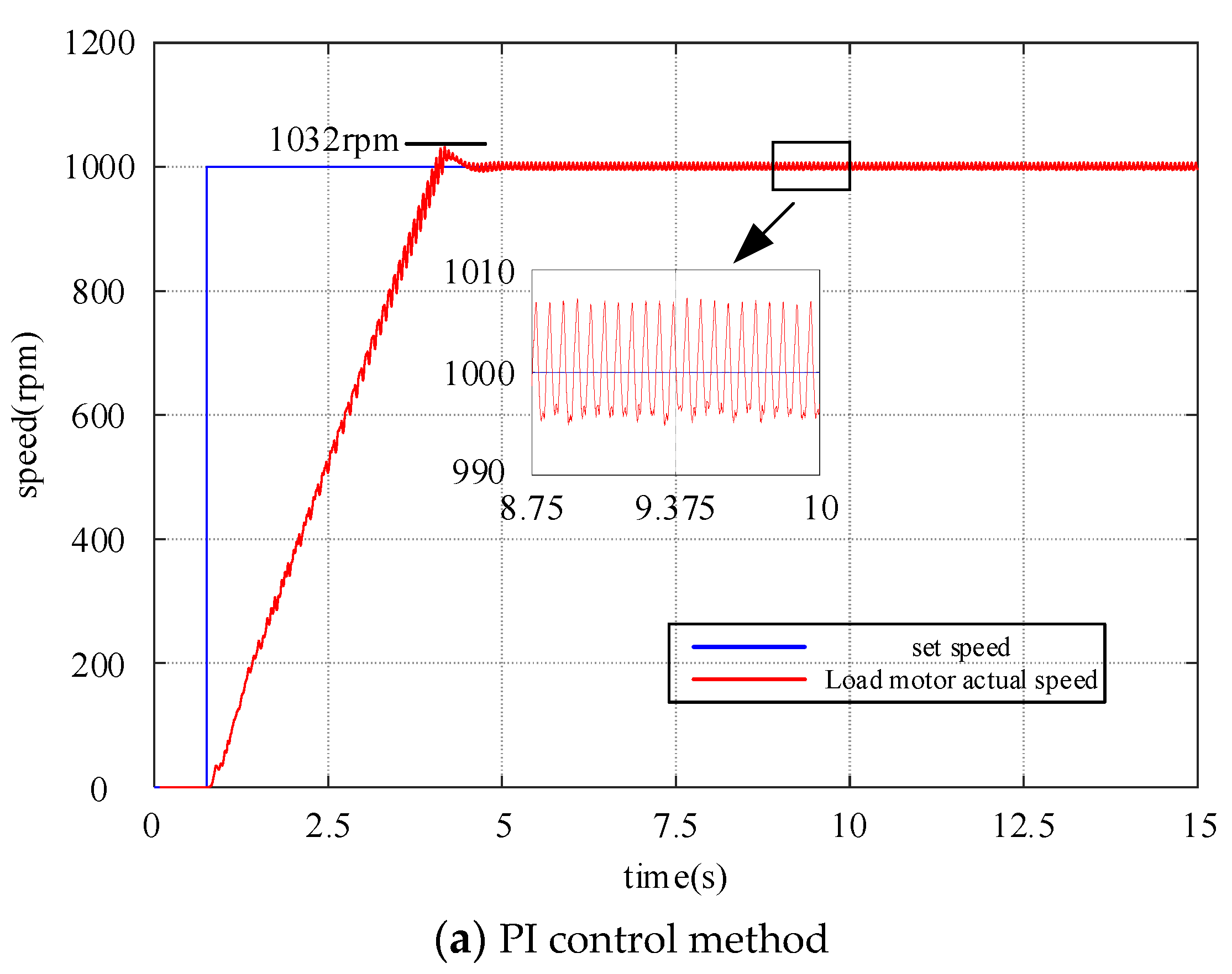
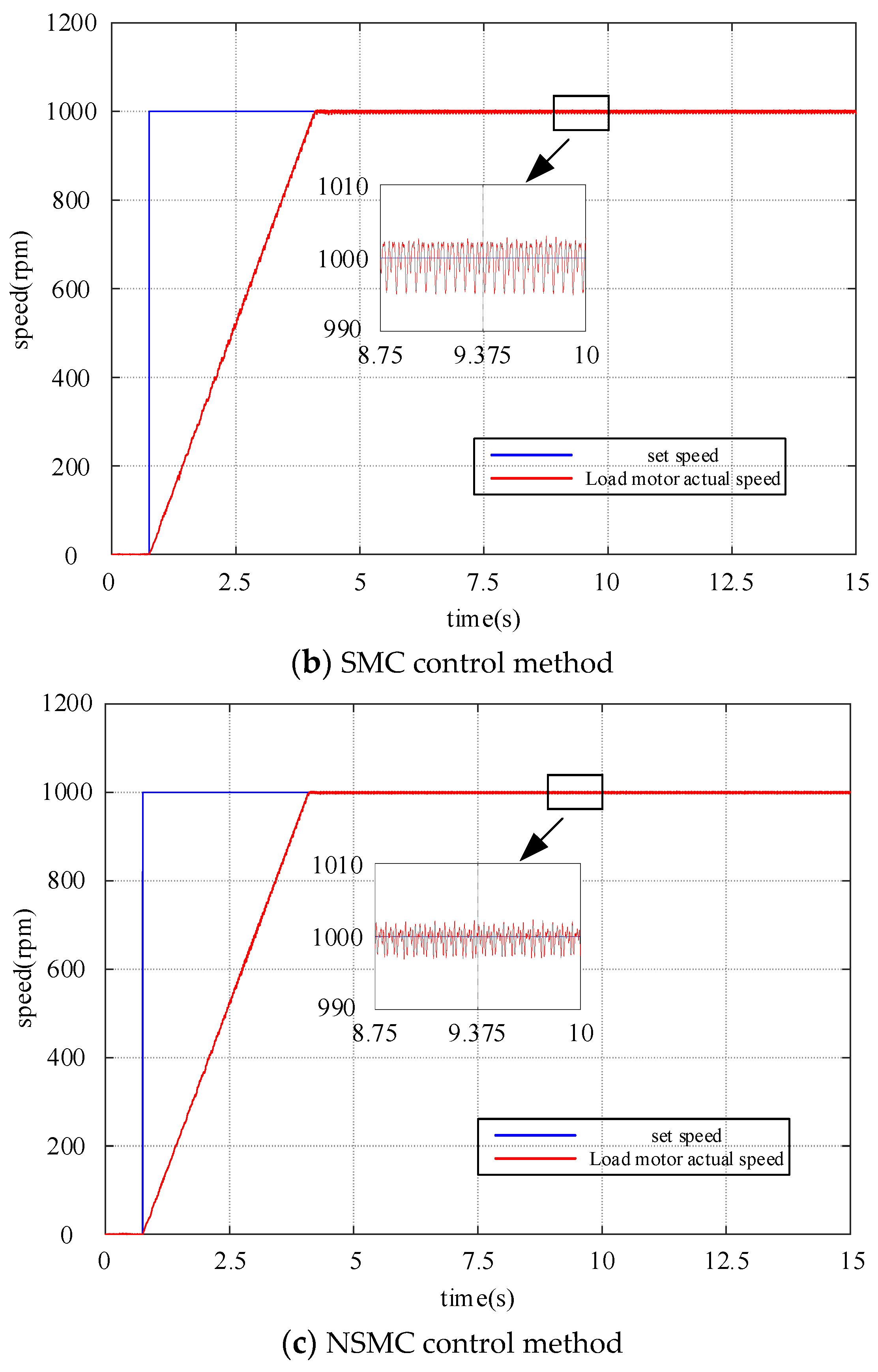
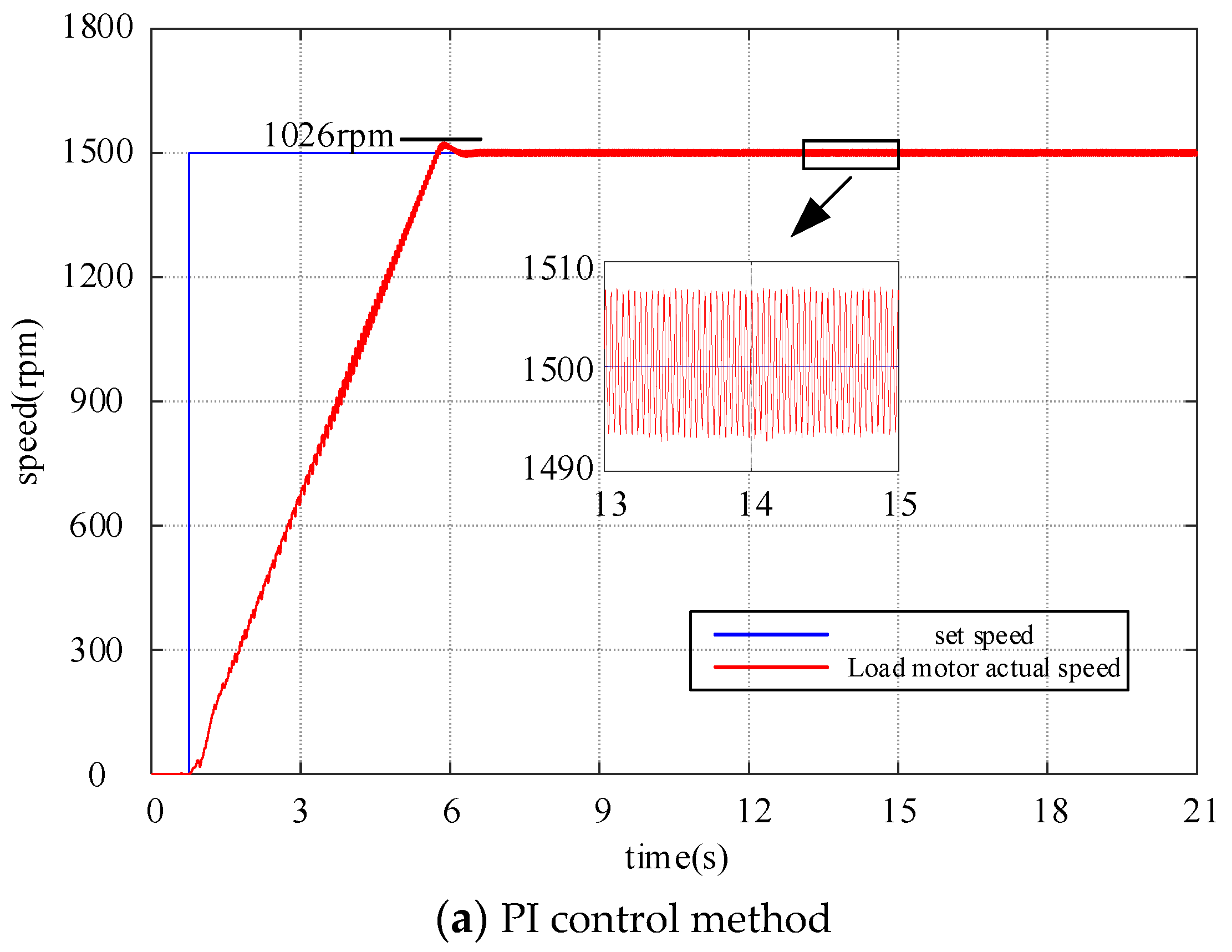
5.2. The Startup Performance of PMSM
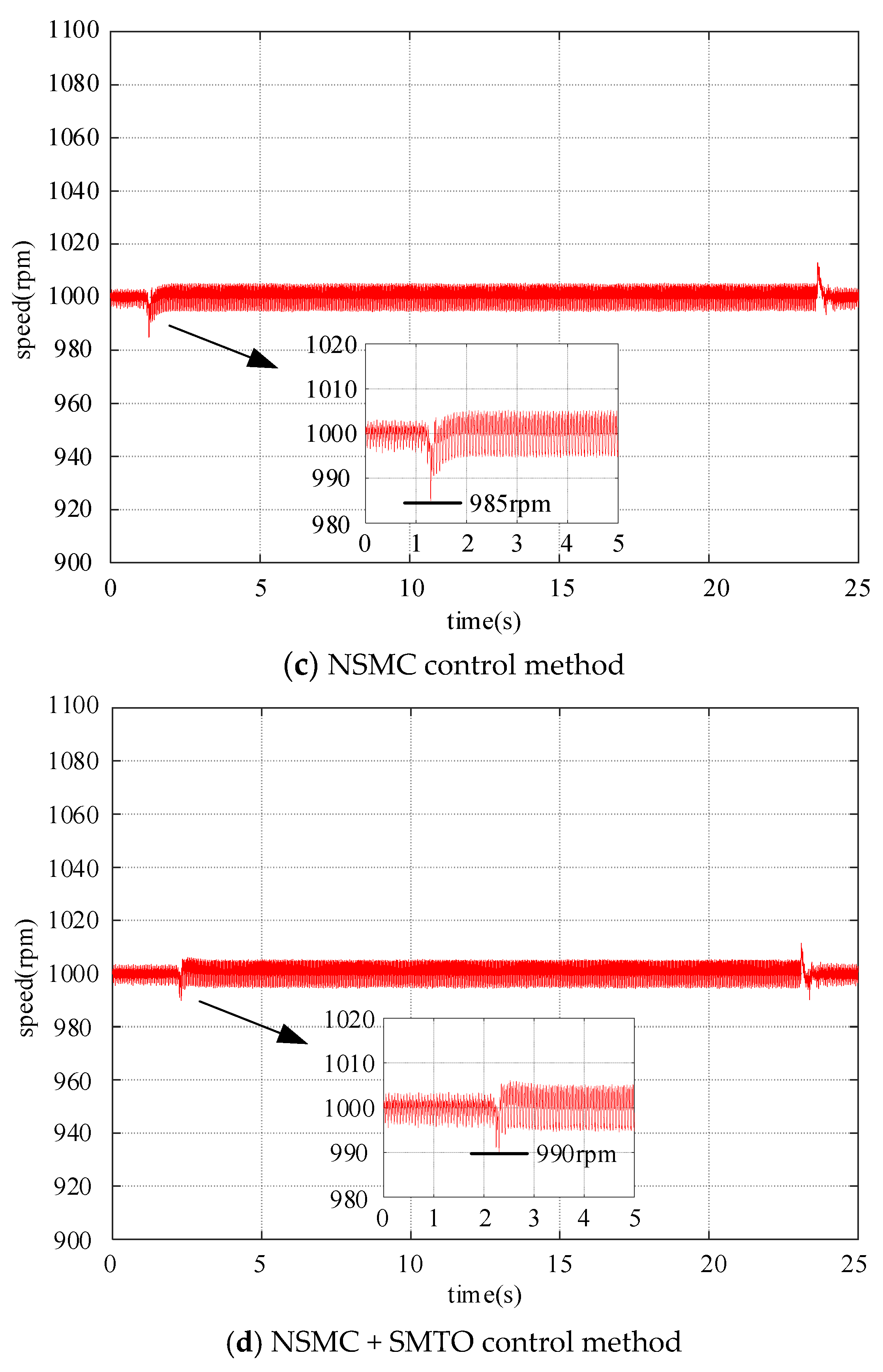
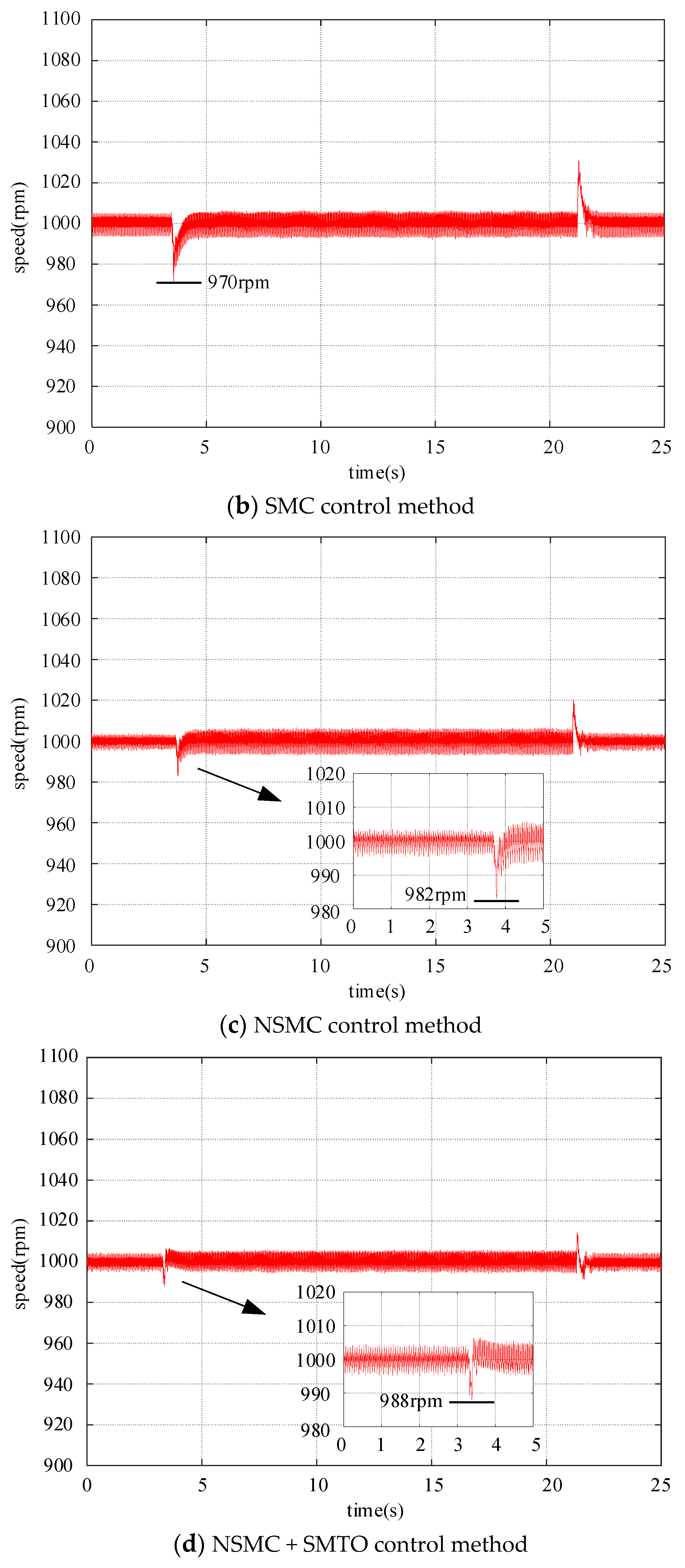
5.3. The Tracking Performance of PMSM
5.4. PMSM Load Disturbance Rejection Performance
6. Conclusions
- (1)
- Firstly, to enhance the parameter robustness of MPCC, a disturbance observer-based MPCC is designed. Subsequently, a NSMC is proposed in the velocity loop, effectively suppressing vibration phenomena and ensuring fast convergence and steady-state characteristics.
- (2)
- The NSMC controller exhibits superior tracking performance. Experimental results show that, compared to PI and SMC, the NSMC controller achieves the smallest tracking error, effectively enhancing the control performance of the system.
- (3)
- Designing a sliding mode load torque observer to provide real-time feedback on the load torque value to the control system enables speed compensation control, thereby enhancing the system’s disturbance rejection capability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Guo, S.; Guo, H.; Tian, X. Fault-Tolerant Current Control of Six-Phase Permanent Magnet Motor With Multifrequency Quasi-Proportional-Resonant Control and Feedforward Compensation for Aerospace Drives. IEEE Trans. Power Electron. 2023, 38, 283–293. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, Z.; Wen, L.; Jiang, W.; Gu, X.; Li, Y. Multigain Online Autotuning Technique-Based Discrete-Time Current Regulator for Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2024, 39, 260–269. [Google Scholar] [CrossRef]
- Jing, H.; Chen, Z.; Wang, X.; Wang, X.; Ge, L.; Fang, G.; Xiao, D. Gradient Boosting Decision Tree for Rotor Temperature Estimation in Permanent Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 10617–10622. [Google Scholar] [CrossRef]
- Brosch, A.; Tinazzi, F.; Wallscheid, O.; Zigliotto, M.; Böcker, J. Finite Set Sensorless Control With Minimum a Priori Knowledge and Tuning Effort for Interior Permanent-Magnet Synchronous Motors. IEEE Trans. Power Electron. 2023, 38, 12508–12519. [Google Scholar] [CrossRef]
- Schenke, M.; Haucke-Korber, B.; Wallscheid, O. Finite-Set Direct Torque Control via Edge-Computing-Assisted Safe Reinforcement Learning for a Permanent-Magnet Synchronous Motor. IEEE Trans. Power Electron. 2023, 38, 13741–13756. [Google Scholar] [CrossRef]
- Gao, J.; Gong, C.; Li, W.; Liu, J. Novel Compensation Strategy for Calculation Delay of Finite Control Set Model Predictive Current Control in PMSM. IEEE Trans. Ind Electron. 2020, 67, 5816–5819. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives With Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Sun, Z.; Deng, Y.; Wang, J.; Yang, T.; Wei, Z.; Cao, H. Finite Control Set Model-Free Predictive Current Control of PMSM With Two Voltage Vectors Based on Ultralocal Model. IEEE Trans. Power Electron. 2023, 38, 776–788. [Google Scholar] [CrossRef]
- Wei, Y.; Young, H.; Ke, D.; Huang, D.; Wang, F.; Rodríguez, J. Adaptive Ultralocalized Time-Series for Improved Model-Free Predictive Current Control on PMSM Drives. IEEE Trans. Power Electron. 2024, 39, 5155–5165. [Google Scholar] [CrossRef]
- Liu, X.; Yang, H.; Lin, H.; Yu, F.; Yang, Y. A Novel Finite-Set Sliding-Mode Model-Free Predictive Current Control for PMSM Drives Without DC-Link Voltage Sensor. IEEE Trans. Power Electron. 2024, 39, 320–331. [Google Scholar] [CrossRef]
- Liu, H.; Lin, W.; Liu, Z.; Buccella, C.; Cecati, C. Model Predictive Current Control With Model-Aid Extended State Observer Compensation for PMSM Drive. IEEE Trans. Power Electron. 2023, 38, 3152–3162. [Google Scholar] [CrossRef]
- Li, X.; Tian, W.; Gao, X.; Yang, Q.; Kennel, R. A Generalized Observer-Based Robust Predictive Current Control Strategy for PMSM Drive System. IEEE Trans. Ind. Electron. 2020, 69, 1322–1332. [Google Scholar] [CrossRef]
- Yin, Z.; Han, X.; Du, C.; Liu, J.; Zhong, Y. Research on Model Predictive Current Control for Induction Machine Based on Immune-Optimized Disturbance Observer. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1699–1710. [Google Scholar] [CrossRef]
- Tao, T.; Zhao, W.; Du, Y.; Cheng, Y.; Zhu, J. Simplified Fault-Tolerant Model Predictive Control for a Five-Phase Permanent-Magnet Motor With Reduced Computation Burden. IEEE Trans. Power Electron. 2020, 35, 3850–3858. [Google Scholar] [CrossRef]
- Sun, X.; Tang, Y.; Xiao, X.; Xie, Y. Predictive Trajectory Control Strategy for Permanent Magnet Synchronous Motor Drives Based on Deadbeat Predictive Flux Linkage Control Method. IEEE Trans. Power Electron. 2023, 38, 2327–2338. [Google Scholar] [CrossRef]
- Ismail, M.M.; Xu, W.; Ge, J.; Tang, Y.; Junejo, A.K.; Hussien, M.G. Adaptive Linear Predictive Model of an Improved Predictive Control of Permanent Magnet Synchronous Motor Over Different Speed Regions. IEEE Trans. Power Electron. 2022, 37, 15338–15355. [Google Scholar] [CrossRef]
- Brosch, A.; Wallscheid, O.; Böcker, J. Time-Optimal Model Predictive Control of Permanent Magnet Synchronous Motors Considering Current and Torque Constraints. IEEE Trans. Power Electron. 2023, 38, 7945–7957. [Google Scholar] [CrossRef]
- Chaoui, H.; Khayamy, M.; Okoye, O.; Gualous, H. Simplified Speed Control of Permanent Magnet Synchronous Motors Using Genetic Algorithms. IEEE Trans. Power Electron. 2019, 34, 3563–3574. [Google Scholar] [CrossRef]
- Huang, K.; Peng, W.; Lai, C.; Feng, G. Efficient Maximum Torque Per Ampere (MTPA) Control of Interior PMSM Using Sparse Bayesian Based Offline Data-Driven Model With Online Magnet Temperature Compensation. IEEE Trans. Power Electron. 2023, 38, 5192–5203. [Google Scholar] [CrossRef]
- Lin, F.J.; Wang, P.L.; Hsu, I.M. Intelligent Nonsingular Terminal Sliding Mode Controlled Nonlinear Time-Varying System Using RPPFNN-AMF. IEEE Trans. Fuzzy Syst. 2024, 32, 1036–1049. [Google Scholar] [CrossRef]
- Wu, T.; Feng, Z.; Wu, C.; Lei, G.; Guo, Y.; Zhu, J.; Wang, X. Multiobjective Optimization of a Tubular Coreless LPMSM Based on Adaptive Multiobjective Black Hole Algorithm. IEEE Trans. Ind Electron. 2020, 67, 3901–3910. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, C.; Gao, W.; Zhou, L. Reinforcement Learning and Optimal Control of PMSM Speed Servo System. IEEE Trans. Ind. Electron. 2023, 70, 8305–8313. [Google Scholar] [CrossRef]
- Zheng, B.; Zou, J.; Li, B.; Tang, M.; Xu, Y.; Zanchetta, P. Analysis and Fault-Tolerant Control for Dual-Three-Phase PMSM Based on Virtual Healthy Model. IEEE Trans. Power Electron. 2022, 37, 15411–15424. [Google Scholar] [CrossRef]
- Fu, D.; Zhao, X.; Zhu, J. A Novel Robust Super-Twisting Nonsingular Terminal Sliding Mode Controller for Permanent Magnet Linear Synchronous Motors. IEEE Trans. Power Electron. 2022, 37, 2936–2945. [Google Scholar] [CrossRef]
- Wu, G.; Huang, S.; Wu, Q.; Rong, F.; Zhang, C.; Liao, W. Robust Predictive Torque Control of N*3-Phase PMSM for High-Power Traction Application. IEEE Trans. Power Electron. 2020, 35, 10799–10809. [Google Scholar] [CrossRef]
- Li, Z.; Wang, F.; Ke, D.; Li, J.; Zhang, W. Robust Continuous Model Predictive Speed and Current Control for PMSM With Adaptive Integral Sliding-Mode Approach. IEEE Trans. Power Electron. 2021, 36, 14398–14408. [Google Scholar] [CrossRef]
- Song, X.; Wang, H.; Ma, X.; Yuan, X.; Wu, X. Robust Model Predictive Current Control for a Nine-Phase Open-End Winding PMSM With High Computational Efficiency. IEEE Trans. Power Electron. 2023, 38, 13933–13943. [Google Scholar] [CrossRef]
- Li, H.; Wang, S.; Xie, Y.; Zheng, S.; Shi, P. Virtual Reference-Based Fuzzy Noncascade Speed Control for PMSM Systems With Unmatched Disturbances and Current Constraints. IEEE Trans. Fuzzy Syst. 2023, 31, 4249–4261. [Google Scholar] [CrossRef]
- Zhao, K.; Chen, X.; Liu, J.; Yu, J. Discrete-Time Adaptive Fuzzy Event-Triggered Control for PMSMs With Voltage Faults via Command Filter Approximator. IEEE Trans. Power Electron. 2024, 39, 7343–7350. [Google Scholar] [CrossRef]
- Yeam, T.I.; Lee, D.C. Design of Sliding-Mode Speed Controller With Active Damping Control for Single-Inverter Dual-PMSM Drive Systems. IEEE Trans. Power Electron. 2021, 36, 5794–5801. [Google Scholar] [CrossRef]
- Xu, W.; Junejo, A.K.; Liu, Y.; Hussien, M.G.; Zhu, J. An Efficient Antidisturbance Sliding-Mode Speed Control Method for PMSM Drive Systems. IEEE Trans. Power Electron. 2021, 36, 6879–6891. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, Y.; Zhang, X.; Liang, J. A New Reaching Law for Antidisturbance Sliding-Mode Control of PMSM Speed Regulation System. IEEE Trans. Power Electron. 2020, 35, 4117–4126. [Google Scholar] [CrossRef]
- Lian, C.; Xiao, F.; Gao, S.; Liu, J. Load Torque and Moment of Inertia Identification for Permanent Magnet Synchronous Motor Drives Based on Sliding Mode Observer. IEEE Trans. Power Electron. 2019, 34, 5675–5683. [Google Scholar] [CrossRef]
- Tang, S.; Shi, T.; Cao, Y.; Lin, Z.; Wang, Z.; Yan, Y. Simultaneous Identification of Load Torque and Moment of Inertia of PMSM Based on Variable Structure Extended Sliding Mode Observer. IEEE Trans. Power Electron. 2024, 39, 8585–8596. [Google Scholar] [CrossRef]
- Gu, M.; Wang, Z.; Wang, B. Optimization of Torque Ripple for Low-Carrier-Ratio Dual Three-Phase PMSM With Pulse Pattern Control. IEEE Trans. Power Electron. 2023, 38, 15091–15096. [Google Scholar] [CrossRef]
- Yu, K.; Wang, Z. An Online Compensation Method of VSI Nonlinearity for Dual Three-Phase PMSM Drives Using Current Injection. IEEE Trans. Power Electron. 2022, 37, 3769–3774. [Google Scholar] [CrossRef]
- Ge, Y.; Song, W.; Yang, Y.; Wheeler, P. A Polar-Coordinate-Multisignal-Flux-Observer-Based PMSM Non-PLL Sensorless Control. IEEE Trans. Power Electron. 2023, 38, 10579–10583. [Google Scholar] [CrossRef]
- Zhang, X.; He, Y. Direct Voltage-Selection Based Model Predictive Direct Speed Control for PMSM Drives Without Weighting Factor. IEEE Trans. Power Electron. 2019, 34, 7838–7851. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, G.; Rong, F.; Feng, J.; Jia, L.; He, J.; Huang, S. Robust Fault-Tolerant Predictive Current Control for Permanent Magnet Synchronous Motors Considering Demagnetization Fault. IEEE Trans. Ind. Electron. 2018, 65, 5324–5334. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, Y.; Zhao, Z.; He, Y. Robust Model Predictive Direct Speed Control for SPMSM Drives Based on Full Parameter Disturbances and Load Observer. IEEE Trans. Power Electron. 2020, 35, 8361–8373. [Google Scholar] [CrossRef]
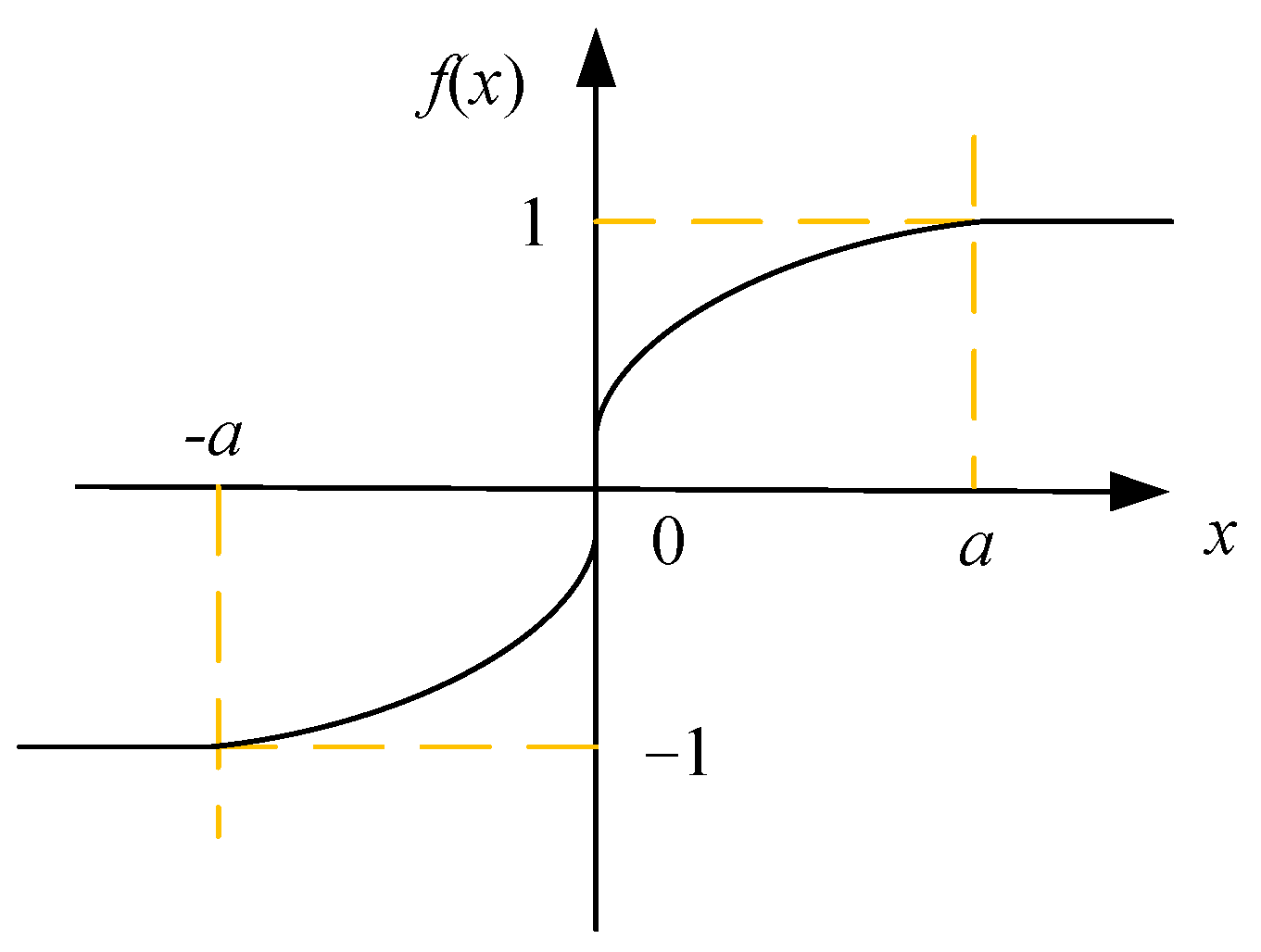





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power | 3.0 kW | Parameters magnet flus linkage ψf | 0.2811 Wb |
| Rated speed | 3000 rpm | Stator inductance Ld | 6.3 mH |
| Rated current | 5.0 A | Stator inductance Lq | 16 mH |
| Number of pole-pairs | 2 | Stator resistance R | 1.386 Ω |
| PI | SMC | NSMC | SMTO | ||||
|---|---|---|---|---|---|---|---|
| P | 0.005 | c | 200 | c | 200 | k | −20,000 |
| a | 100 | a | 100 | ||||
| I | 0.1 | β | 0.1 | β | 0.1 | g | −0.01 |
| γ | 0.5 | ||||||
| Control Method | Recovery Time (s) at Speeds of 1000 r/min and 1500 r/min | Steady-State Error (±rpm) at Speeds of 1000 r/min and 1500 r/min | ||
|---|---|---|---|---|
| PI | 3.748 | 5.362 | 6.5 | 7.7 |
| SMC | 3.373 | 5.029 | 4 | 5.9 |
| NSMC | 3.369 | 5.012 | 2.9 | 4.5 |
| Control Technique | Speed Decrease (rpm) and Recovery Time (s) with 2 Nm Load | Speed Decrease (rpm) and Recovery Time (s) with 3 Nm Load | ||
|---|---|---|---|---|
| PI | 50 | 0.797 | 60 | 1.093 |
| SMC | 24 | 0.31 | 30 | 0.487 |
| NSMC | 15 | 0.205 | 18 | 0.223 |
| NSMC + SMTO | 10 | 0.115 | 12 | 0.122 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; Song, Z.; Xiao, X.; Guo, Y.; Mo, Y. Sliding Mode Speed Control for PMSM Based on Model Predictive Current. Electronics 2024, 13, 2561. https://doi.org/10.3390/electronics13132561
Zhou W, Song Z, Xiao X, Guo Y, Mo Y. Sliding Mode Speed Control for PMSM Based on Model Predictive Current. Electronics. 2024; 13(13):2561. https://doi.org/10.3390/electronics13132561
Chicago/Turabian StyleZhou, Weihong, Zhe Song, Xi Xiao, Yougui Guo, and Yu Mo. 2024. "Sliding Mode Speed Control for PMSM Based on Model Predictive Current" Electronics 13, no. 13: 2561. https://doi.org/10.3390/electronics13132561
APA StyleZhou, W., Song, Z., Xiao, X., Guo, Y., & Mo, Y. (2024). Sliding Mode Speed Control for PMSM Based on Model Predictive Current. Electronics, 13(13), 2561. https://doi.org/10.3390/electronics13132561






