Advanced Method for Improving Marine Target Tracking Based on Multiple-Plot Processing of Radar Images
Abstract
1. Introduction
- -
- Using high-precision filters;
- -
- Increasing the quality of the input parameters.
- -
- Low accuracy in estimating the target center of coordinates (error greater than the resolution of the radar);
- -
- Provision of only the target center of the coordinates;
- -
- Confusion regarding trajectories when tracking multiple targets.
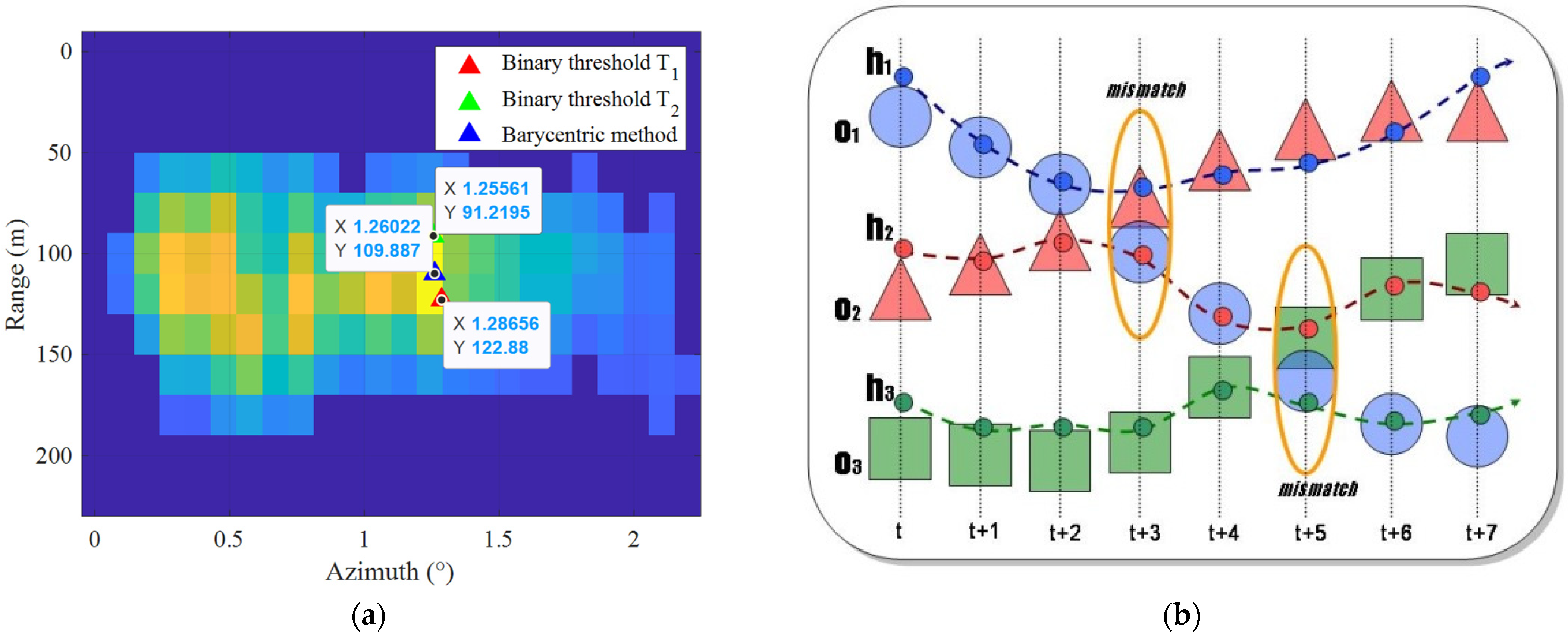
2. Materials
3. Proposed Method
3.1. Estimating Basic Parameters of Targets
| Algorithm 1 Basic parameter estimation. | |
| Input data: Dataset Output data: Centroids , reflected energies , and areas , | |
| Step 1: Determine the number of layers L based on an image histogram [17]; Step 2: Set upper and lower limits Step 3: Calculate intensity step and intensity value of the kth layer using (1) [18]. | |
| (1) | |
| Step 4: Encode dataset using (2). | |
| (2) | |
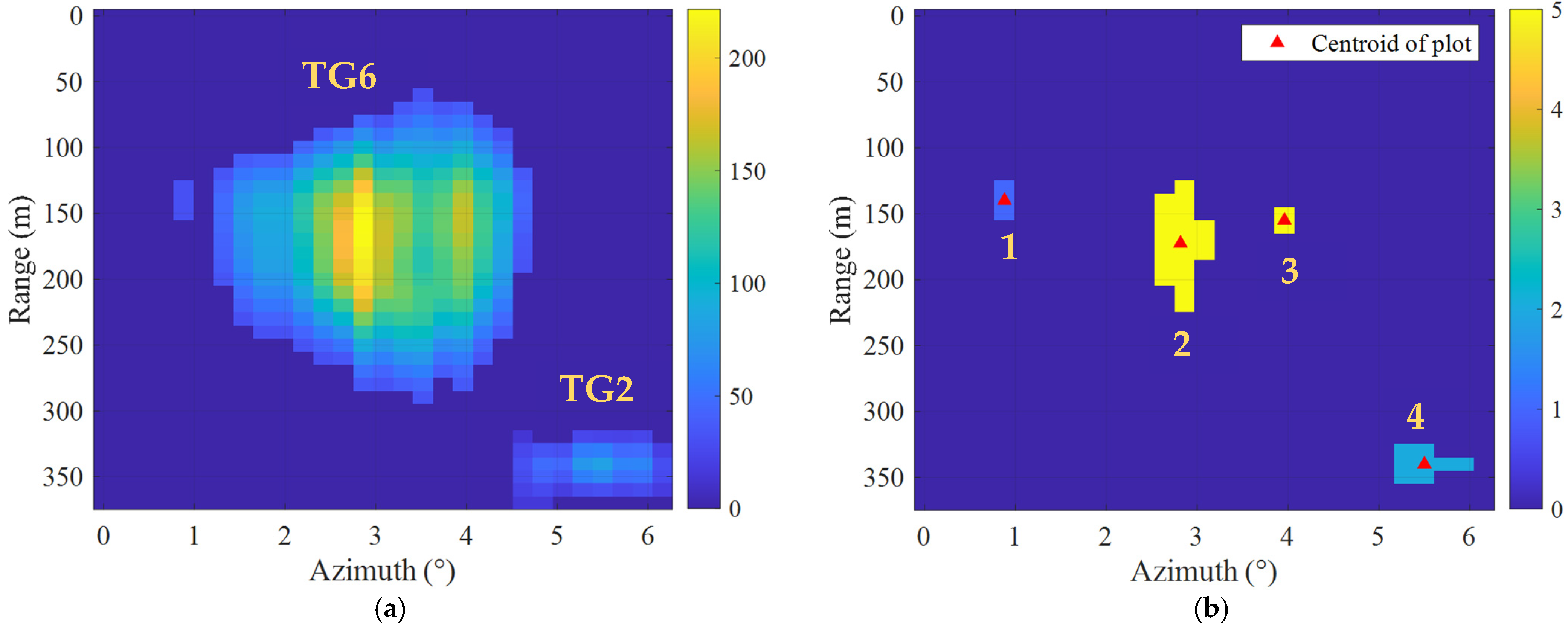
| Step 5: Determine local maximum region , for i = 1,.., N, with N as the total local maximum regions [17]. Step 6: Determine centroid of using (3), energies , and areas of the plots [18]. | |
| (3) | |
| Where is the total number of cells i region D, is the total number of cells in the ith column, and is the total number in the jth row [18]. | |
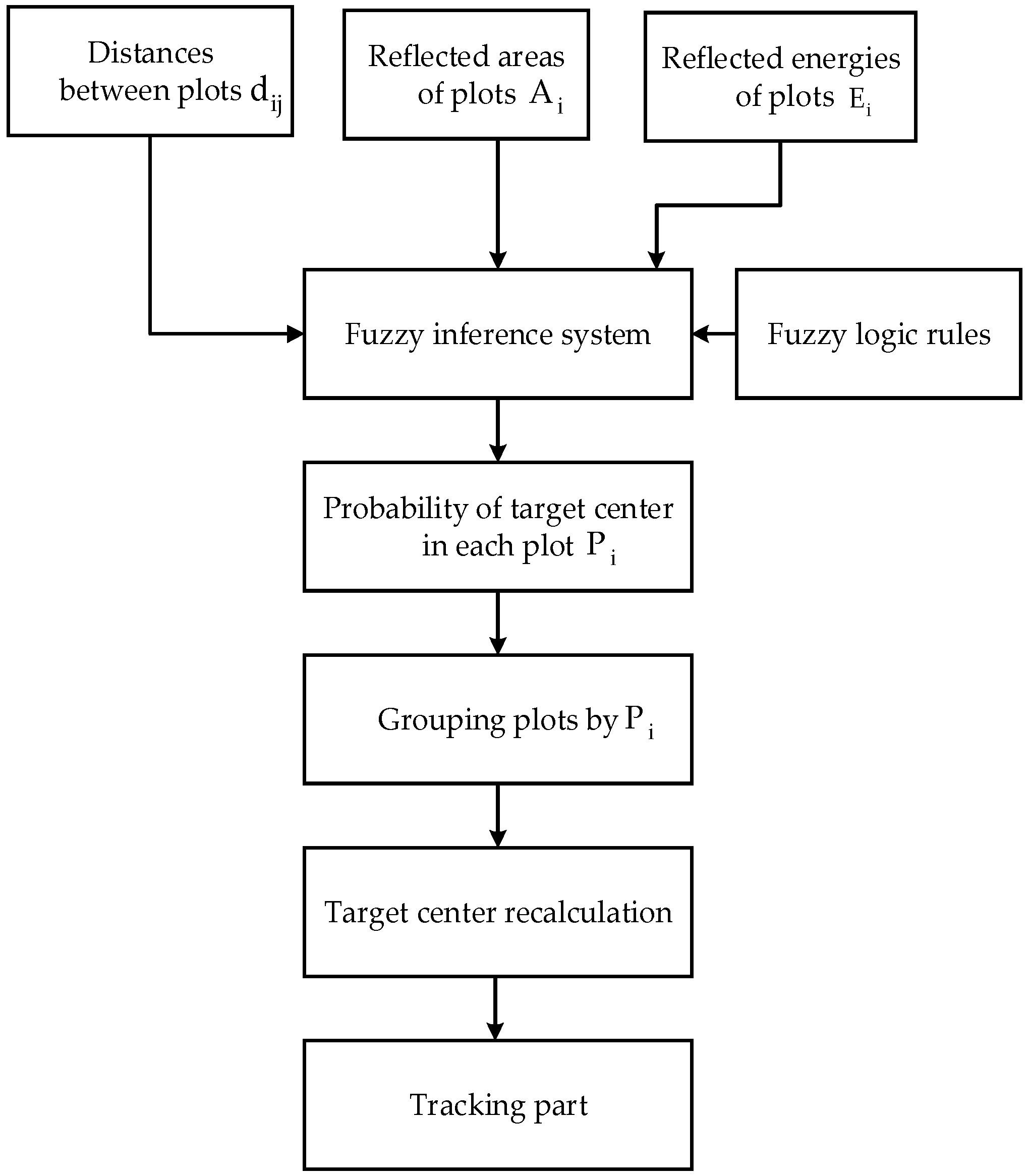
3.2. Clustering Plots and Direction Estimation
| Algorithm 2 FCM-M for clustering plots. | |
| Input data: Centroids , reflected energy , and area , of the plot and threshold value . Output data: Target center coordinates and number of targets N. | |
| Step 1: Design fuzzy logic rules. Step 2: Find the appropriate membership function for the input data. Step 3: Select a plot with the highest reflected energy as the cluster header. Step 4: Calculate distance between plots and using (4) | |
| (4) | |
| Step 5: Calculate the probability of a target center in each plot using (5): | |
| (5) | |
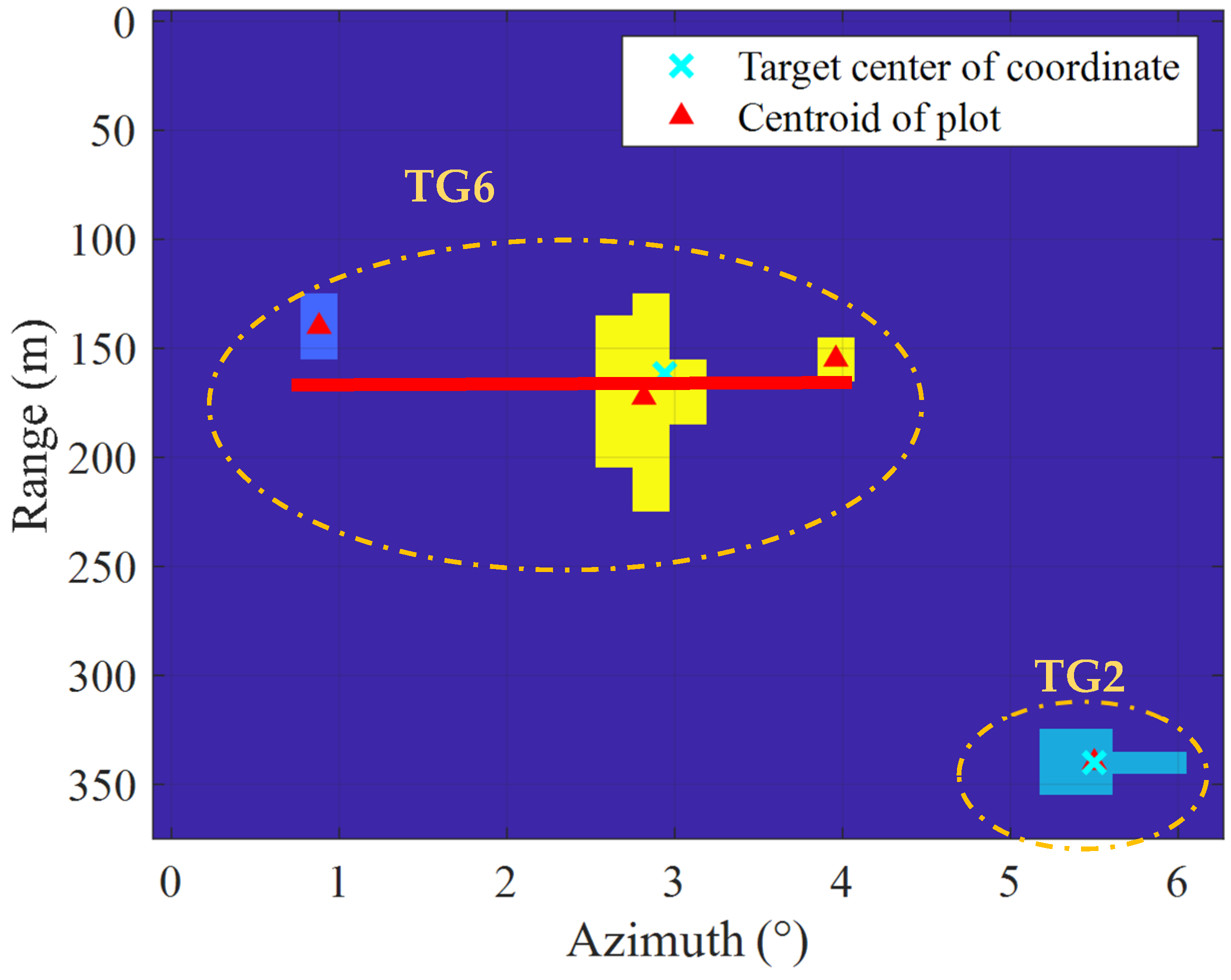
| Step 6: Group plots into clusters, CL, using (6). | |
| (6) | |
| Step 7: Recalculate the target center coordinates using (7): | |
| (7) | |
| where K is the total number of plots in cluster CL, and the total number of clusters N is known for several detected targets. | |
Fuzzy Logic Rules
- -
- If a plot has a higher reflected energy E and a larger reflected area A, the center of gravity is inside the region of interest. Then, the plot and any close targets can be clustered into one group.
- -
- If a plot has a lower reflected energy E and a smaller reflected area A, the probability of the target center of gravity being present in the region of interest is low. Thus, the controller can ignore such plots.
- -
- When two plots have higher reflected energy E and larger reflected area S, a controller can use the probability that a target center is present to decide which plots to track.
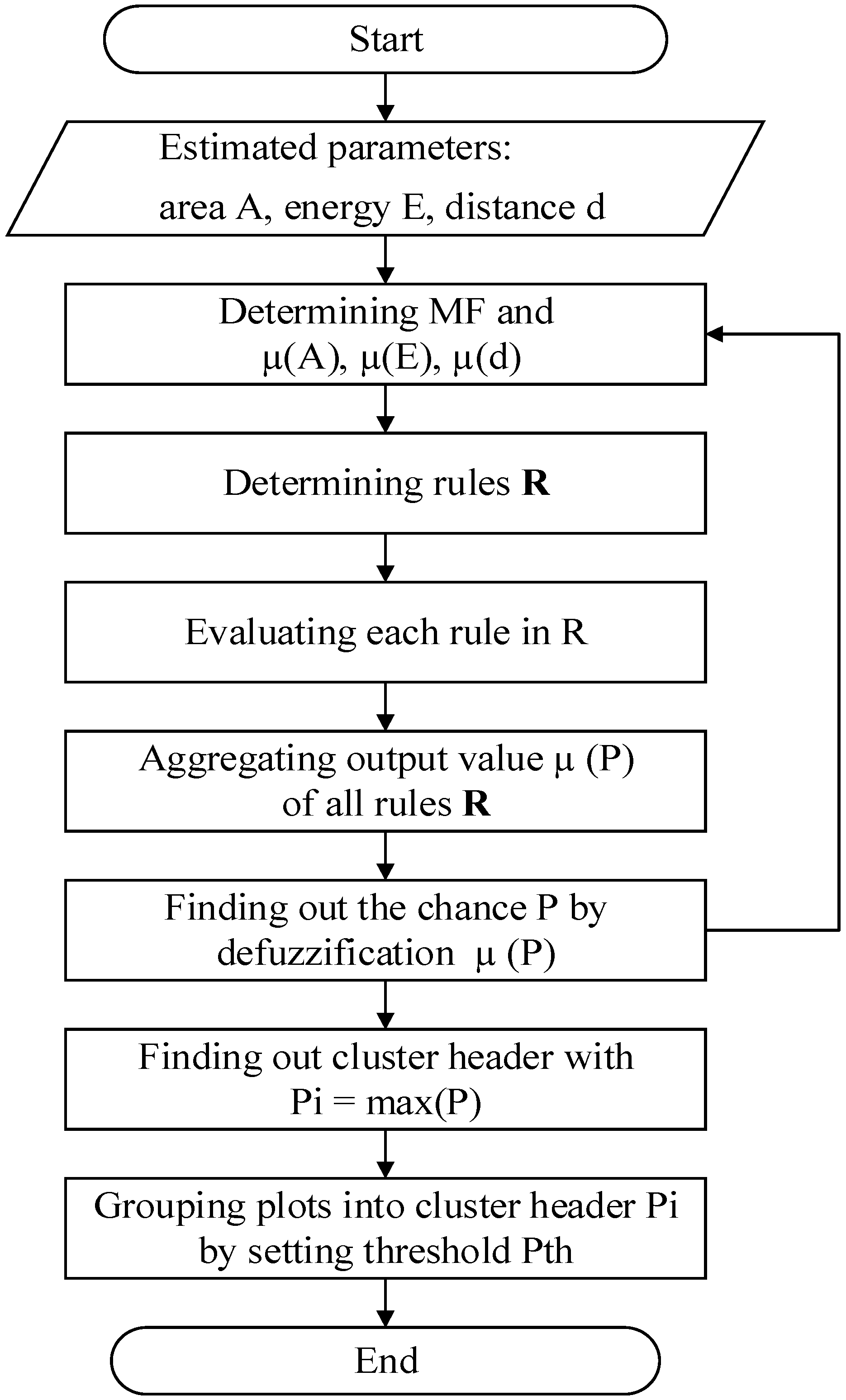
3.3. Fuzzy Logic Membership Functions
| Algorithm 3 Detailed steps for clustering plots. |
| Input data: Estimated area A, energy E of the plots, and distance d between plots. Output data: Chance of each plot being in the region of interest P. |
| Step 1: Determine the membership function and the probability of each input value , . Step 2: Determine the fuzzy logic rules R corresponding to each input and output parameter. Step 3: Evaluate every rule in R using the fuzzy definition of AND. |
| Step 4: Aggregate the output value. Step 5: Find the chance of a plot being in the region of interest using defuzzification (5). |
| Step 6: Select plots with the highest chance of becoming the cluster header and group plots into a cluster header using Pth threshold value. |
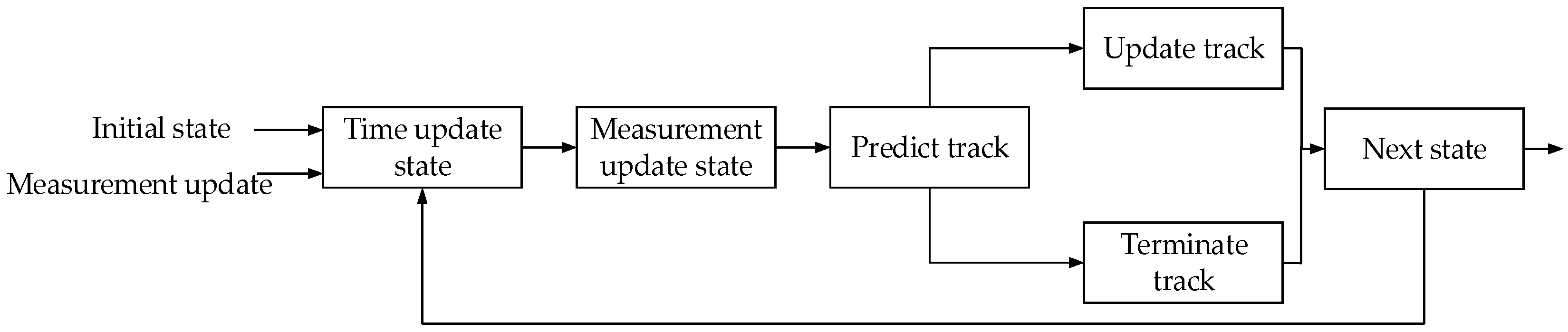
3.4. Target Tracking
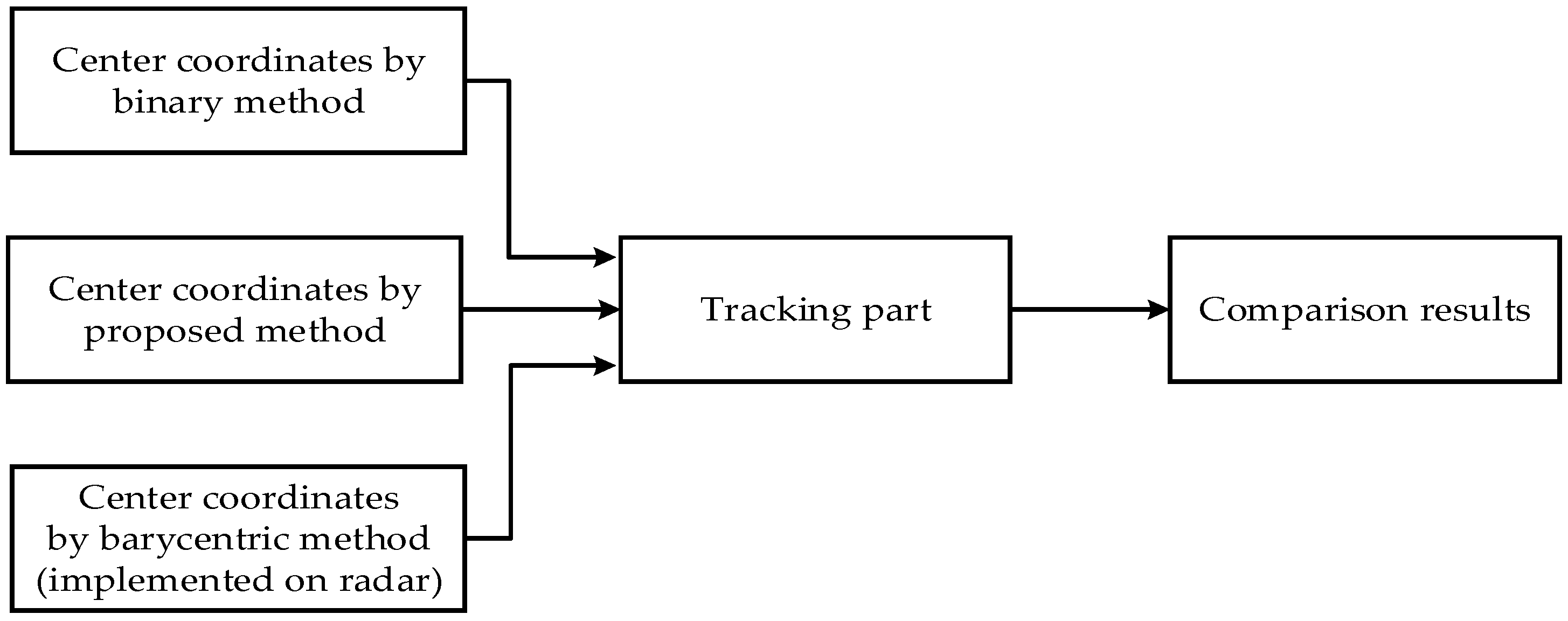
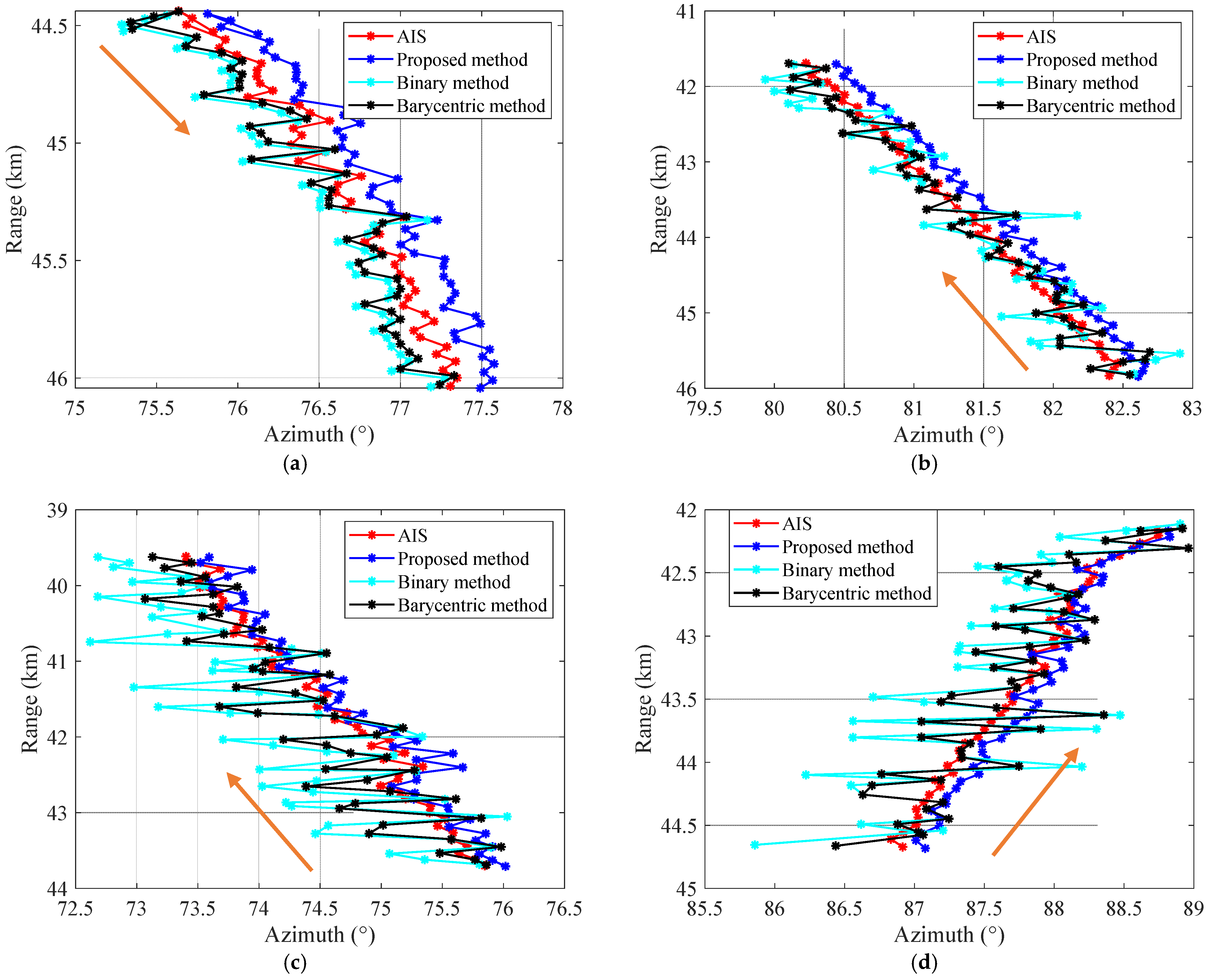
4. Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Wang, Y. Review of Multi-target Tracking Technology for Marine Radar. J. Radar 2021, 10, 100–115. [Google Scholar] [CrossRef]
- Beard, M.; Vo, B.T.; Vo, B.N. Bayesian Multi-Target Tracking with Merged Measurement using Labelled Random Finite Sets. IEEE Trans. Signal Process. 2015, 63, 1433–1447. [Google Scholar] [CrossRef]
- Wang, X.; Gang, L.; You, H. Ship detection in SAR images via local contrast of fisher vector. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6467–6479. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Daum, F.; Huang, J. The probabilistic data association filter. IEEE Control Syst. Mag. 2009, 29, 82–100. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Rong, L.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004; pp. 421–490. ISBN 9780471221272. [Google Scholar] [CrossRef]
- Mansour, H.; Voicu, G.; Emil, P. The Use of Kalman Filter Techniques for Ship Track Estimation. WSEAS Trans. Syst. 2020, 19, 7–13. [Google Scholar] [CrossRef]
- Sun, B.; Yan, B.; Jiang, R.; Zhang, J. A progressive update extended Kalman filter for ship tracking with static electric field. J. Natl. Univ. Def. Technol. 2018, 40, 134–140. [Google Scholar] [CrossRef]
- Wanjin, X.; Liying, L.; Junjie, B.; Yingying, Z. Ship Tracking based on the fusion of Kalman filter and particle filter. In Proceedings of the 2021 the 4th International Conference on Mechatronics and Computer Technology Engineering (MCTE 2021), Xi’an, China, 15–17 October 2021. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, S.; Lou, Y.; Cheng, L. Integrated Sensing and Communication with Massive MIMO: A Unified Tensor Approach for Channel and Target Parameter Estimation. IEEE Trans. Wirel. Commun. 2024, 99, 1–16. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Cheng, D.; Chen, W.; Chen, C. Marine Extended Target Tracking for Scanning Radar Data Using Correlation Filter and Bayes Filter Jointly. Remote Sens. 2022, 14, 5937. [Google Scholar] [CrossRef]
- Fowdur, J.S.; Baum, M.; Heymann, F. Real-World Marine Radar Datasets for Evaluating Target Tracking Methods. Sensors 2021, 21, 4641. [Google Scholar] [CrossRef] [PubMed]
- Dang, C.; Li, Z.; Hao, C.; Xiao, Q. Infrared Small Marine Target Detection Based on Spatiotemporal Dynamics Analysis. Remote Sens. 2023, 15, 1258. [Google Scholar] [CrossRef]
- Fan, E.; Xie, W.; Pei, J.; Hu, K.; Li, X.; Podpečan, V. Improved Joint Probabilistic Data Association (JPDA) Filter Using Motion Feature for Multiple Maneuvering Targets in Uncertain Tracking Situations. Information 2018, 9, 322. [Google Scholar] [CrossRef]
- Duan, G.; Wang, Y.; Zhang, Y.; Wu, L. A Network Model for Detecting Marine Floating Weak Targets Based on Multimodal Data Fusion of Radar Echoes. Sensors 2022, 22, 9163. [Google Scholar] [CrossRef] [PubMed]
- Score Coastal Radar. Available online: https://www.radartutorial.eu/19.kartei/07.naval/karte075.en.html (accessed on 1 June 1999).
- Above Water Warfare. Available online: https://www.thalesgroup.com/en/global/activities/defence/naval-forces/above-water-warfare (accessed on 1 June 1999).
- Vo, X.H.; Nguyen, T.K.; Nguyen, P.B. Calculating the Optimal Number of Layers for Separating Radar Images of Marine Objects by level. J. Eurasian Union Sci. 2023, 13, 10–20. [Google Scholar] [CrossRef]
- Vo, X.H.; Nguyen, T.K.; Nguyen, P.B.; Duong, V.M. A Real-time Processing Algorithm for Multi-plot Marine Targets based on Radar Image Decomposition. In Proceedings of the 2023 12th International Conference on Control, Automation and Information Sciences (ICCAIS), Hanoi, Vietnam, 29 November 2023; pp. 781–876. [Google Scholar] [CrossRef]
- Park, J.; Choi, M. A K-Means Clustering Algorithm to Determine Representative Operational Profiles of a Ship Using AIS Data. J. Mar. Sci. Eng. 2022, 10, 1245. [Google Scholar] [CrossRef]
- Mendel, J.M. Fuzzy logic systems for engineering: A tutorial. Proc. IEEE 1995, 83, 345–377. [Google Scholar] [CrossRef]

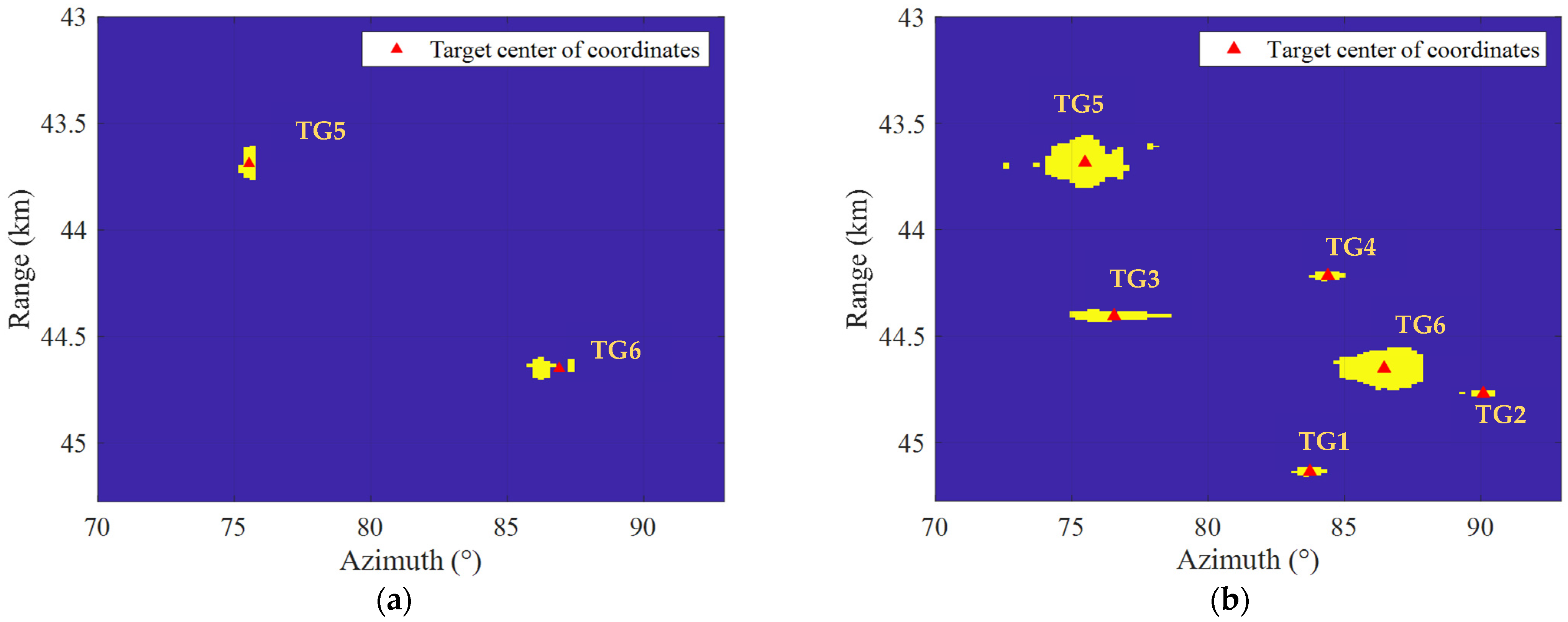


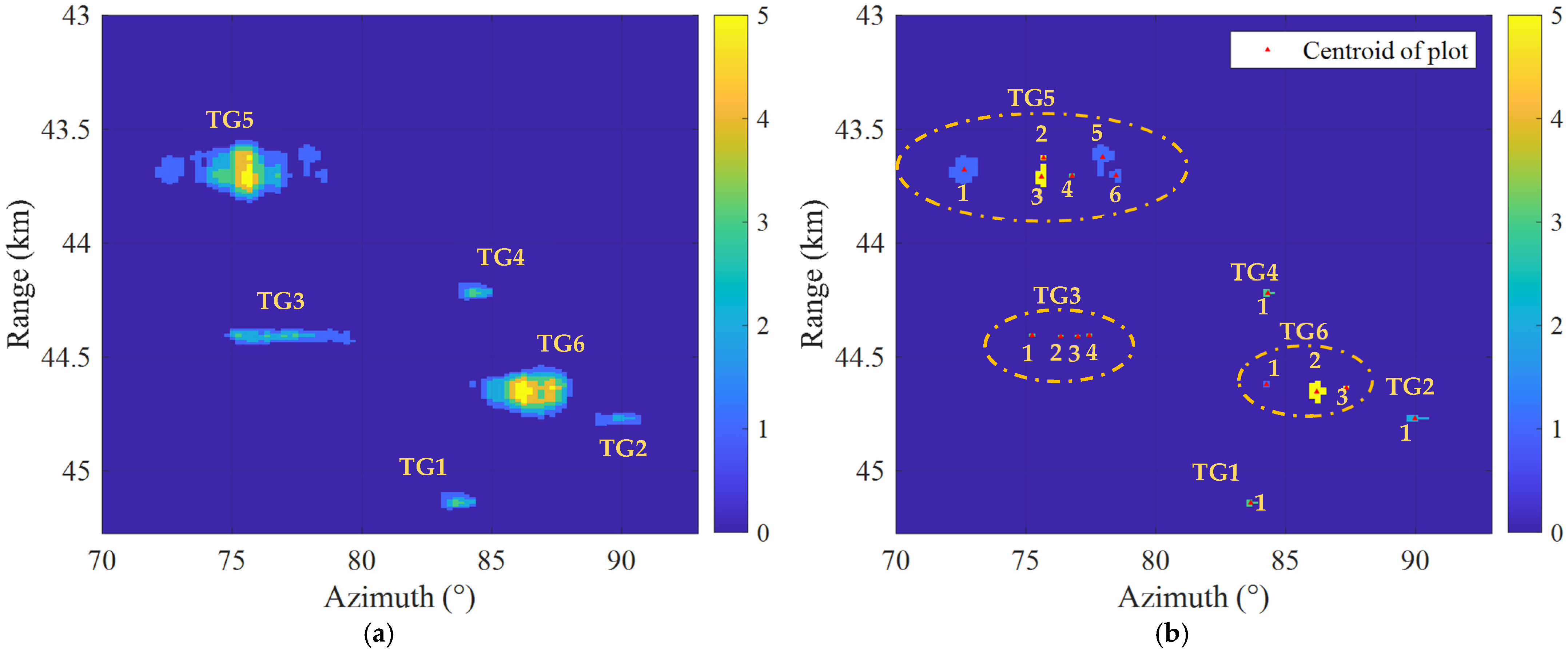

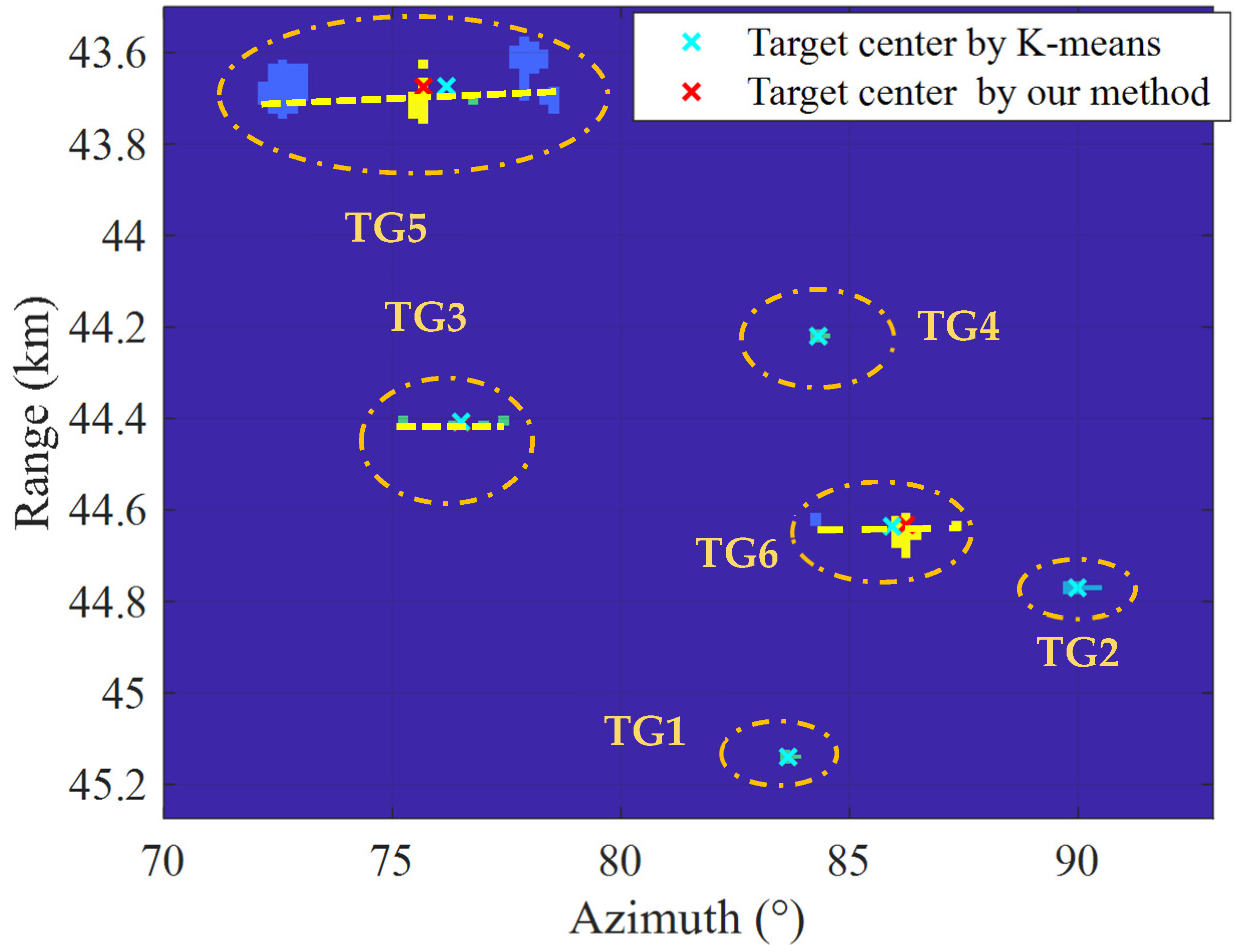

| Target Type | Target Symbol | Initial Range (km) | Initial Azimuth (°) | Velocity (km/h) | Target Size (m) | Average No. of Cells |
|---|---|---|---|---|---|---|
| Fishing ship | TG1 | 44.37 | 267.52 | 1.68 | 20–70 | 40 |
| TG2 | 45.58 | 145.64 | 2.10 | 20–70 | 40 | |
| Cargo ship | TG3 | 44.55 | 347.38 | 29.66 | 150–250 | 220 |
| TG4 | 44.35 | 80.74 | 24.55 | 150–250 | 220 | |
| Container ship | TG5 | 44.45 | 72.38 | 19.72 | 300–700 | 600 |
| TG6 | 43.57 | 348.48 | 30.88 | 300–700 | 600 |
| Target | Plot | Proposed Method | Binary Method | ||||
|---|---|---|---|---|---|---|---|
| Range r (km) | (°) | Area A (Cell) | Energy E (Layer) | Range r (km) | (°) | ||
| TG1 | 1 | 45.14 | 83.66 | 4 | 3 | 45.136 | 83.73 |
| TG2 | 1 | 44.77 | 89.98 | 8 | 2 | 44.77 | 90.10 |
| TG3 | 1 | 44.41 | 75.24 | 2 | 3 | 44.40 | 76.55 |
| 2 | 44.41 | 76.34 | 1 | 3 | |||
| 3 | 44.41 | 77.00 | 1 | 3 | |||
| 4 | 44.41 | 77.44 | 2 | 3 | |||
| TG4 | 1 | 44.22 | 84.32 | 4 | 3 | 44.21 | 84.39 |
| TG5 | 1 | 43.68 | 72.63 | 48 | 1 | 44.65 | 86.46 |
| 2 | 43.71 | 75.60 | 16 | 5 | |||
| 3 | 43.63 | 75.68 | 2 | 5 | |||
| 4 | 43.71 | 76.78 | 2 | 3 | |||
| 5 | 43.62 | 77.95 | 30 | 1 | |||
| 6 | 43.70 | 78.47 | 9 | 1 | |||
| TG6 | 1 | 44.62 | 84.26 | 3 | 1 | 43.68 | 75.48 |
| 2 | 44.65 | 86.20 | 20 | 5 | |||
| 3 | 44.64 | 87.34 | 2 | 5 | |||
| Time (s) | 0.21 | 0.17 | |||||
| No. | Energy E | Distance D | Area A | Probability P |
|---|---|---|---|---|
| 1 | High | Close | Big | Very High |
| 2 | High | Close | Medium | Very High |
| 3 | High | Close | Small | High |
| 4 | High | Medium | Big | High |
| 5 | High | Medium | Medium | Medium |
| 6 | High | Medium | Small | Medium |
| 7 | High | Far | Big | Medium |
| 8 | High | Far | Medium | Medium |
| 9 | High | Far | Small | Medium |
| 10 | Medium | Close | Big | Low |
| 11 | Medium | Close | Medium | Very Low |
| 12 | Medium | Close | Small | Low |
| 13 | Medium | Medium | Big | Medium |
| 14 | Medium | Medium | Medium | Medium |
| 15 | Medium | Medium | Small | Medium |
| 16 | Medium | Far | Big | Medium |
| 17 | Medium | Far | Medium | Medium |
| 18 | Medium | Far | Small | Medium |
| 19 | Low | Close | Big | Medium |
| 20 | Low | Close | Medium | Medium |
| 21 | Low | Close | Small | Low |
| 22 | Low | Medium | Big | Low |
| 23 | Low | Medium | Medium | Very Low |
| 24 | Low | Medium | Small | Very Low |
| 25 | Low | Far | Big | Low |
| 26 | Low | Far | Medium | Very Low |
| 27 | Low | Far | Small | Very Low |
| Plot ID | Range r (m) | Azimuth α (°) | Area A (cell) | Energy E (layer) |
|---|---|---|---|---|
| 1 | 150.0 | 0.88 | 3 | 1 |
| 2 | 195.5 | 2.82 | 20 | 5 |
| 3 | 165.0 | 3.96 | 2 | 5 |
| 4 | 345.0 | 5.55 | 8 | 2 |
| Plot ID | 1st Plot | 2nd Plot | 3rd Plot | 4th Plot |
|---|---|---|---|---|
| 1st Plot | 77.34 | 50 | 20.80 | |
| 2nd Plot | 77.34 | 77.74 | 41.59 | |
| 3rd Plot | 50 | 77.74 | 50 | |
| 4th Plot | 20.80 | 41.59 | 50 |
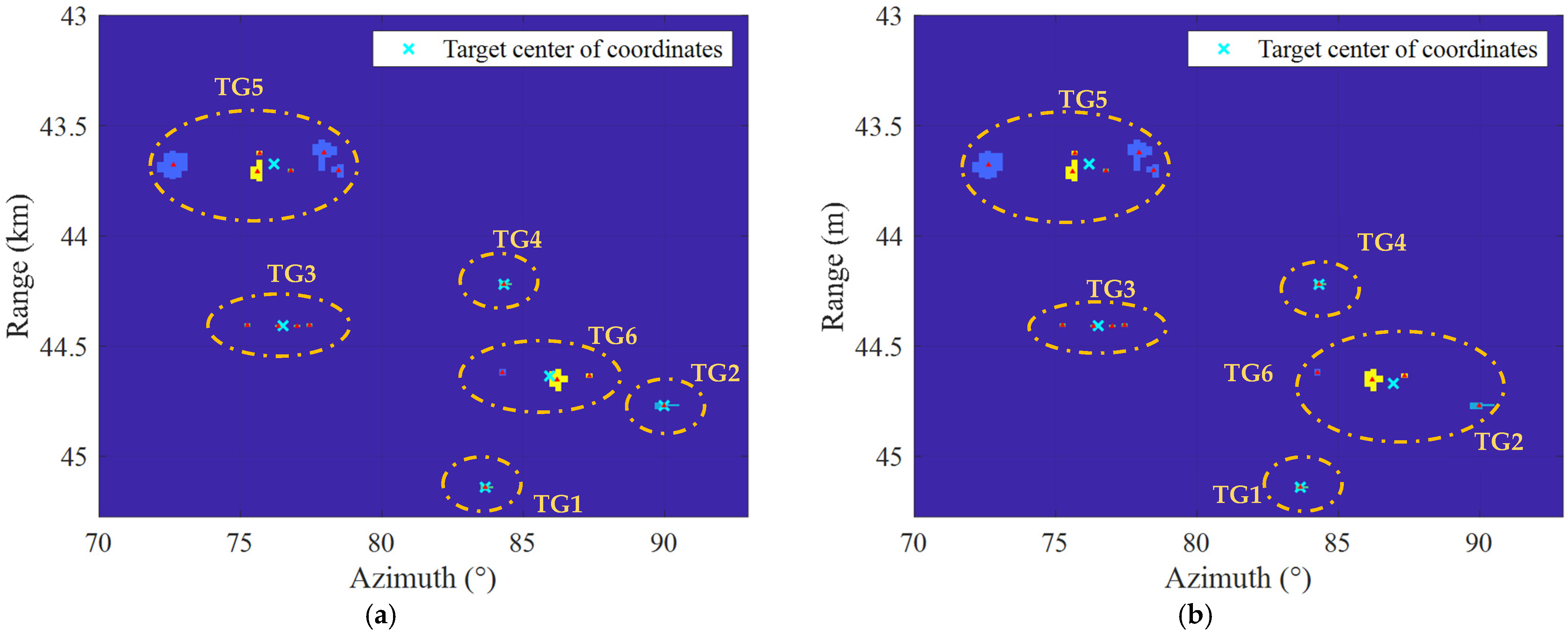
| Barycentric Method (Radar) | Binary Method | Proposed Method | ||||
|---|---|---|---|---|---|---|
| Range r (km) | Azimuth α (°) | Range r (km) | Azimuth α (°) | Range r (km) | Azimuth α (°) | |
| TG1 | 45.14 | 83.66 | 45.136 | 83.73 | 45.14 | 83.66 |
| TG2 | 44.77 | 89.98 | 44.77 | 90.10 | 44.77 | 89.98 |
| TG3 | 44.41 | 76.51 | 44.40 | 76.55 | 44.41 | 76.51 |
| TG4 | 44.22 | 84.32 | 44.21 | 84.39 | 44.22 | 84.32 |
| TG5 | 44.64 | 85.93 | 44.65 | 86.46 | 44.64 | 86.54 |
| TG6 | 43.68 | 76.18 | 43.68 | 75.48 | 43.68 | 75.99 |
| Proposed Method | Binary Method | Barycentric Method | ||||
|---|---|---|---|---|---|---|
| Range (m) | Azimuth (°) | Range (m) | Azimuth (°) | Range (m) | Azimuth (°) | |
| TG3 | 11.05 | 0.16 | 38.51 | 0.20 | 18.55 | 0.21 |
| TG4 | 10.65 | 0.20 | 14.46 | 0.41 | 13.92 | 0.32 |
| TG5 | 7.49 | 0.12 | 11.60 | 0.42 | 10.39 | 0.27 |
| TG6 | 9.89 | 0.13 | 21.86 | 0.58 | 21.87 | 0.31 |
| Average | 8.59 | 0.14 | 21.61 | 0.41 | 16.15 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vo, X.H.; Nguyen, T.K.; Nguyen, P.B.; Duong, V.M. Advanced Method for Improving Marine Target Tracking Based on Multiple-Plot Processing of Radar Images. Electronics 2024, 13, 2548. https://doi.org/10.3390/electronics13132548
Vo XH, Nguyen TK, Nguyen PB, Duong VM. Advanced Method for Improving Marine Target Tracking Based on Multiple-Plot Processing of Radar Images. Electronics. 2024; 13(13):2548. https://doi.org/10.3390/electronics13132548
Chicago/Turabian StyleVo, Xung Ha, Trung Kien Nguyen, Phung Bao Nguyen, and Van Minh Duong. 2024. "Advanced Method for Improving Marine Target Tracking Based on Multiple-Plot Processing of Radar Images" Electronics 13, no. 13: 2548. https://doi.org/10.3390/electronics13132548
APA StyleVo, X. H., Nguyen, T. K., Nguyen, P. B., & Duong, V. M. (2024). Advanced Method for Improving Marine Target Tracking Based on Multiple-Plot Processing of Radar Images. Electronics, 13(13), 2548. https://doi.org/10.3390/electronics13132548






