Design of Ultrasonic Guided Wave Pipeline Non-Destructive Testing System Based on Adaptive Wavelet Threshold Denoising
Abstract
1. Introduction
2. Overall Program Design
3. Hardware Design
3.1. Main Controller Module
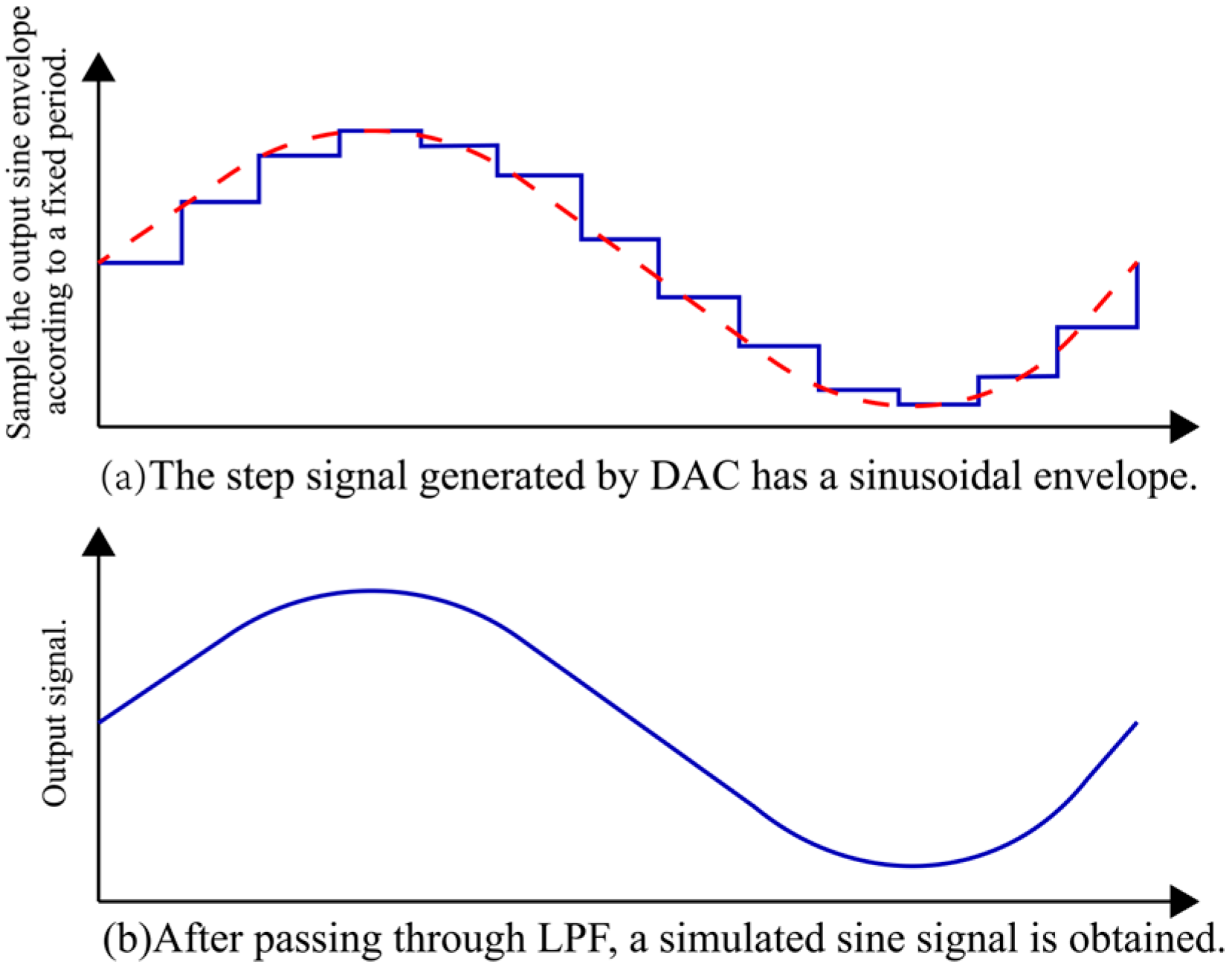
3.2. Signal Generation Circuit
3.3. Power Amplifier Circuit
3.4. Impedance Matching Circuit
3.5. Signal Acquisition Module
4. Software Design
4.1. Host Computer Design
4.2. Adaptive Wavelet Thresholding Denoising
4.3. Butterfly Optimization Algorithm
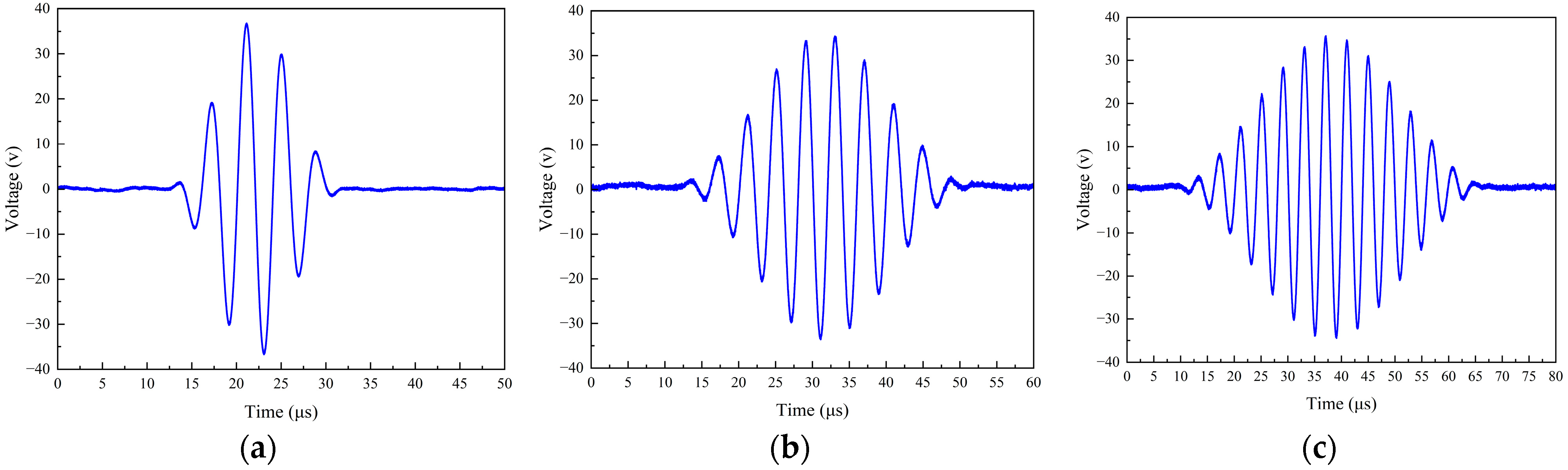
4.4. Waveform Synthesis Design
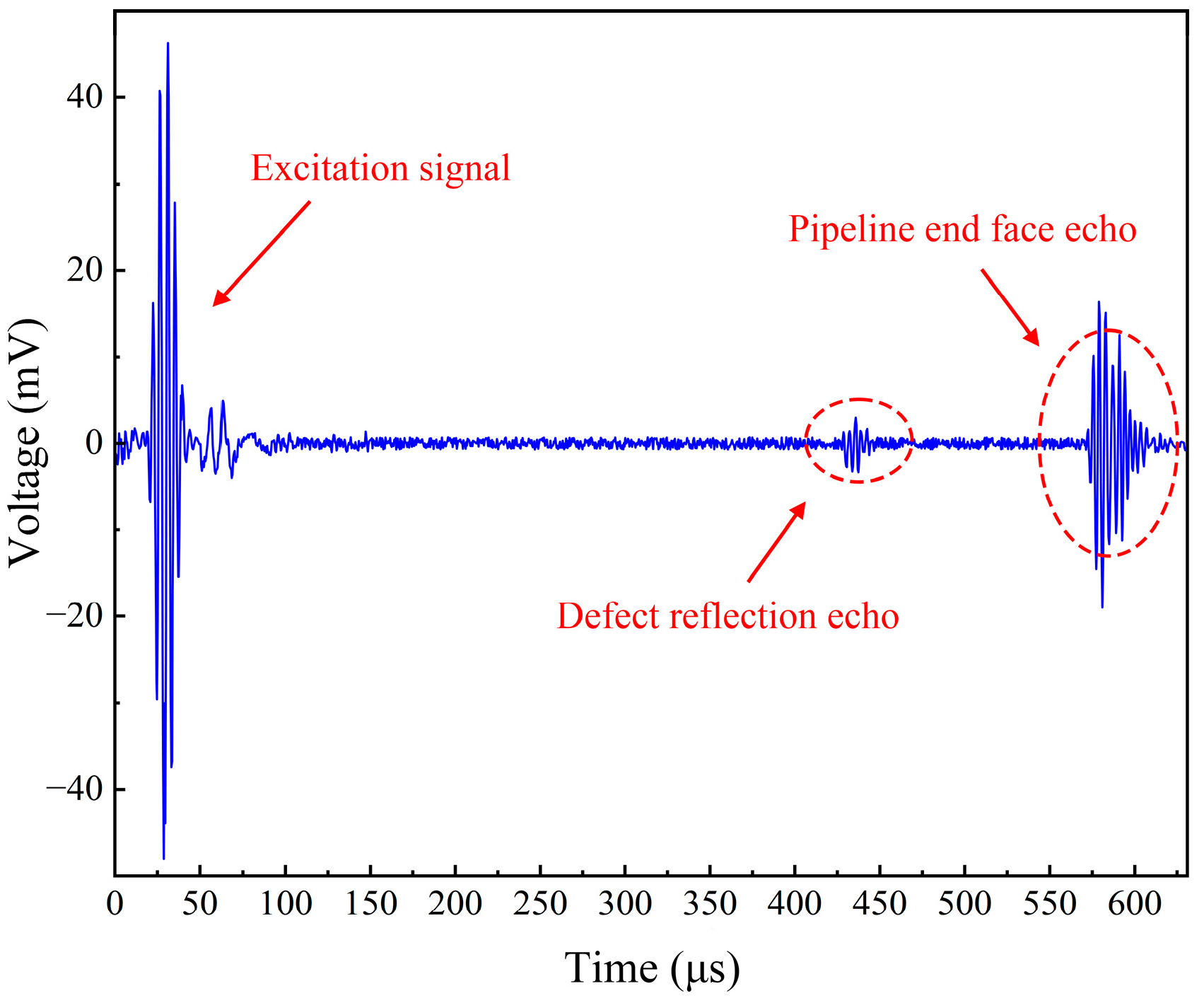
5. Experimental Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Waqar, M.; Memon, A.M.; Sabih, M.; Alhems, L.M. Composite Pipelines: Analyzing Defects and Advancements in Non-Destructive Testing Techniques. Eng. Fail. Anal. 2024, 157, 107914. [Google Scholar] [CrossRef]
- Xia, X.; Wu, D.; Yang, F.; Hu, M.; Ma, L.; Li, M.; Dong, X.; Duan, Z. Early Underground Pipeline Collapse Detection and Optimization Based on Water Hammer Vibration Signal. Int. J. Press. Vessel. Pip. 2023, 206, 105045. [Google Scholar] [CrossRef]
- Liu, B.; Tian, R.; Yu, H.; He, L.; Yang, L.; Wang, F.; Geng, H.; Tian, Y. Research on the Characteristics of Weak Magnetic Internal Detection Signals for Critical Damage in Pipeline Stress Based on Density Functional Theory. Eng. Fail. Anal. 2024, 159, 108145. [Google Scholar] [CrossRef]
- Banjara, N.K.; Sasmal, S.; Kapuria, S. Fatigue and Leakage-Type Damage Detection in Metallic Plates and Pipelines Using Piezoelectric Patch Acoustic Sensors. Int. J. Press. Vessel. Pip. 2024, 209, 105162. [Google Scholar] [CrossRef]
- Gusev, B.V.; Fedotov, M.Y.; Leshchenko, V.V.; Lepikhin, A.M.; Makhutov, N.A.; Budadin, O.N. Nondestructive Testing of Offshore Subsea Pipelines and Calculation Substantiation of Their Safety According to Risk Criteria. Chem. Pet. Eng. 2023, 58, 776–787. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, S.; Zhang, R.; Tian, J.; Li, X. State of Charge Estimation of Lithium-Ion Batteries Based on Ultrasonic Guided Waves by Chirped Signal Excitation. J. Energy Storage 2024, 84, 110897. [Google Scholar] [CrossRef]
- Yue, J.; Hong, X.; Zhang, B. A Damage Imaging Method Based on Particle Swarm Optimization for Composites Nondestructive Testing Using Ultrasonic Guided Waves. Appl. Acoust. 2024, 218, 109878. [Google Scholar] [CrossRef]
- Tang, B.; Wang, Y.; Chen, A.; Zhao, Y.; Xu, J. Split-Spectrum Processing with Raised Cosine Filters of Constant Frequency-to-Bandwidth Ratio for L(0,2) Ultrasonic Guided Wave Testing in a Pipeline. Appl. Sci. 2022, 12, 7611. [Google Scholar] [CrossRef]
- Hong, X.; Zhang, B.; Liu, Y.; Qi, H.; Li, W. Deep-Learning-Based Guided Wave Detection for Liquid-Level State in Porcelain Bushing Type Terminal. Struct. Control Health Monit. 2021, 28, e2651. [Google Scholar] [CrossRef]
- Zang, X.; Xu, Z.-D.; Lu, H.; Zhu, C.; Zhang, Z. Ultrasonic Guided Wave Techniques and Applications in Pipeline Defect Detection: A Review. Int. J. Press. Vessel. Pip. 2023, 206, 105033. [Google Scholar] [CrossRef]
- Du, C.; Li, X.; Liu, C.; Song, C.; Yuan, J.; Xin, Y. Combining Ultrasonic Guided Wave and Low-Frequency Electromagnetic Technology for Defect Detection in High-Temperature Cr–Ni Alloy Furnace Tubes. Sci. Rep. 2023, 13, 18592. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Virupakshappa, K.; Oruklu, E. FPGA Implementation of an Ultrasonic Flaw Detection Algorithm Based on Convolutional Neural Networks. J. Signal Process. Syst. 2022, 94, 1447–1457. [Google Scholar] [CrossRef]
- Lyu, Y.; Hong, H.; Song, G.; He, C. A Simplified Integration of Multi-Channel Ultrasonic Guided Wave System for Phased Array Detection and Total Focusing Imaging. Int. J. Acoust. Vib. 2021, 26, 104–109. [Google Scholar] [CrossRef]
- He, J.; Zhou, C.; Yang, L.; Sun, X. Research on Pipeline Damage Imaging Technology Based on Ultrasonic Guided Waves. Shock Vib. 2019, 2019, 1470761. [Google Scholar] [CrossRef]
- Song, Z.; Qi, X.; Liu, Z.; Ma, H. Experimental Study of Guided Wave Propagation and Damage Detection in Large Diameter Pipe Filled by Different Fluids. NDT E Int. 2018, 93, 78–85. [Google Scholar] [CrossRef]
- Zhang, H.; Teng, F.; Wei, J.; Lv, S.; Zhang, L.; Zhang, F.; Jiang, M. Damage Location Method of Pipeline Structure by Ultrasonic Guided Wave Based on Probability Fusion. IEEE Trans. Instrum. Meas. 2024, 73, 9504914. [Google Scholar] [CrossRef]
- Abbassi, A.; Römgens, N.; Tritschel, F.F.; Penner, N.; Rolfes, R. Evaluation of Machine Learning Techniques for Structural Health Monitoring Using Ultrasonic Guided Waves under Varying Temperature Conditions. Struct. Health Monit. 2023, 22, 1308–1325. [Google Scholar] [CrossRef]
- Tiwari, K.A.; Raisutis, R.; Tumsys, O.; Ostreika, A.; Jankauskas, K.; Jakutavicius, J. Defect Estimation in Non-Destructive Testing of Composites by Ultrasonic Guided Waves and Image Processing. Electronics 2019, 8, 315. [Google Scholar] [CrossRef]
- Xu, Z.-D.; Zhu, C.; Shao, L.-W. Damage Identification of Pipeline Based on Ultrasonic Guided Wave and Wavelet Denoising. J. Pipeline Syst. Eng. Pract. 2021, 12, 04021051. [Google Scholar] [CrossRef]
- Chang, Y.; Zi, Y.; Zhao, J.; Yang, Z.; He, W.; Sun, H. An Adaptive Sparse Deconvolution Method for Distinguishing the Overlapping Echoes of Ultrasonic Guided Waves for Pipeline Crack Inspection. Meas. Sci. Technol. 2017, 28, 035002. [Google Scholar] [CrossRef]
- Ling, E.H.; Abdul Rahim, R.H. A Review on Ultrasonic Guided Wave Technology. Aust. J. Mech. Eng. 2020, 18, 32–44. [Google Scholar] [CrossRef]
- Da, Y.; Dong, G.; Shang, Y.; Wang, B.; Liu, D.; Qian, Z. Circumferential Defect Detection Using Ultrasonic Guided Waves: An Efficient Quantitative Technique for Pipeline Inspection. Eng. Comput. 2020, 37, 1923–1943. [Google Scholar] [CrossRef]
- Rathod, V.T. A Review of Electric Impedance Matching Techniques for Piezoelectric Sensors, Actuators and Transducers. Electronics 2019, 8, 169. [Google Scholar] [CrossRef]
- Wang, H.; Wu, B.; Gao, X.; Liu, Y.; Li, X.; Liu, X. Ultrasonic Guided Wave Defect Detection Method for Tank Bottom Plate Based on SH0 Mode Multichannel Magnetostrictive Sensor. Measurement 2023, 223, 113790. [Google Scholar] [CrossRef]
- Pikuleva, N.I.; Khafizova, A.S.; Gornaev, A.D. System for Updating the Program Code of STM32 Microcontrollers Based on a Composite USB Device. In Proceedings of the 2022 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), Sochi, Russia, 16 May 2022; pp. 813–818. [Google Scholar]
- Du, Y.H.; Ouyang, Q.R. Fast Frequency Hopping Signal Generator Based on DDS. Adv. Mater. Res. 2011, 142, 162–165. [Google Scholar] [CrossRef]
- Li, J.; Tan, Q.L.; Yu, H.Y.; Zhou, Z.; Li, J.M.; Cui, Y.J. Design of the Circuit for FSK Modulation Based on AD9910. Appl. Mech. Mater. 2011, 58–60, 2664–2669. [Google Scholar] [CrossRef]
- Minase, J.; Lu, T.-F.; Cazzolato, B.; Grainger, S. A Review, Supported by Experimental Results, of Voltage, Charge and Capacitor Insertion Method for Driving Piezoelectric Actuators. Precis. Eng. 2010, 34, 692–700. [Google Scholar] [CrossRef]
- Andany, S.H.; Nievergelt, A.P.; Kangül, M.; Ziegler, D.; Fantner, G.E. A High-Bandwidth Voltage Amplifier for Driving Piezoelectric Actuators in High-Speed Atomic Force Microscopy. Rev. Sci. Instrum. 2023, 94, 093703. [Google Scholar] [CrossRef]
- Rathod, V.T. A Review of Acoustic Impedance Matching Techniques for Piezoelectric Sensors and Transducers. Sensors 2020, 20, 4051. [Google Scholar] [CrossRef]
- Halidou, A.; Mohamadou, Y.; Ari, A.A.A.; Zacko, E.J.G. Review of Wavelet Denoising Algorithms. Multimed. Tools Appl. 2023, 82, 41539–41569. [Google Scholar] [CrossRef]
- Donoho, D.L. De-Noising by Soft-Thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Optimization Algorithm: A Novel Approach for Global Optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Zhou, Z.; La Rue, G.S. A 12-Bit Nonlinear DAC for Direct Digital Frequency Synthesis. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 2459–2468. [Google Scholar] [CrossRef]
- Langlois, J.M.P.; Al-Khalili, D. Novel Approach to the Design of Direct Digital Frequency Synthesizers Based on Linear Interpolation. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 2003, 50, 567–578. [Google Scholar] [CrossRef]
- Lévesque, L. Nyquist Sampling Theorem: Understanding the Illusion of a Spinning Wheel Captured with a Video Camera. Phys. Educ. 2014, 49, 697. [Google Scholar] [CrossRef]














| Testing Methods | Advantages | Shortcomings |
|---|---|---|
| magnetic particle | Easy to operate, low cost | Limited ability to detect deep defects |
| infiltration | Suitable for all shapes and materials | Easily corrodes piping |
| rays | Very effective against internal defects | High cost and radiation risk to operators |
| ultrasonic guided wave | Long detection distance, no damage to pipes | High cost and susceptibility to interference |
| Design Schemes | Component | Maximum Output Frequency | Power Consumption | Cost |
|---|---|---|---|---|
| 1 | EP4CE10F17C8N | 800 MHz | 5.93 W | 386¥ |
| 2 | AD9914 + HMC830 | 3.30 GHz | 4.76 W | 278¥ |
| 3 | STM32F103 + AD9910 | 420 MHz | 1.36 W | 102¥ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, S.-Y.; Guo, Y.-Q.; Zang, X.-L.; Xu, Z.-D. Design of Ultrasonic Guided Wave Pipeline Non-Destructive Testing System Based on Adaptive Wavelet Threshold Denoising. Electronics 2024, 13, 2536. https://doi.org/10.3390/electronics13132536
Huang S-Y, Guo Y-Q, Zang X-L, Xu Z-D. Design of Ultrasonic Guided Wave Pipeline Non-Destructive Testing System Based on Adaptive Wavelet Threshold Denoising. Electronics. 2024; 13(13):2536. https://doi.org/10.3390/electronics13132536
Chicago/Turabian StyleHuang, Si-Yu, Ying-Qing Guo, Xu-Lei Zang, and Zhao-Dong Xu. 2024. "Design of Ultrasonic Guided Wave Pipeline Non-Destructive Testing System Based on Adaptive Wavelet Threshold Denoising" Electronics 13, no. 13: 2536. https://doi.org/10.3390/electronics13132536
APA StyleHuang, S.-Y., Guo, Y.-Q., Zang, X.-L., & Xu, Z.-D. (2024). Design of Ultrasonic Guided Wave Pipeline Non-Destructive Testing System Based on Adaptive Wavelet Threshold Denoising. Electronics, 13(13), 2536. https://doi.org/10.3390/electronics13132536








