Reversible Cellular Automata Based Cryptosystem
Abstract
1. Introduction
2. Cellular Automata and Cryptography
2.1. Cellular Automata Overview
2.2. Cellular Automata for Cryptographic Applications
3. Proposed Encryption Algorithm: Materials and Methods
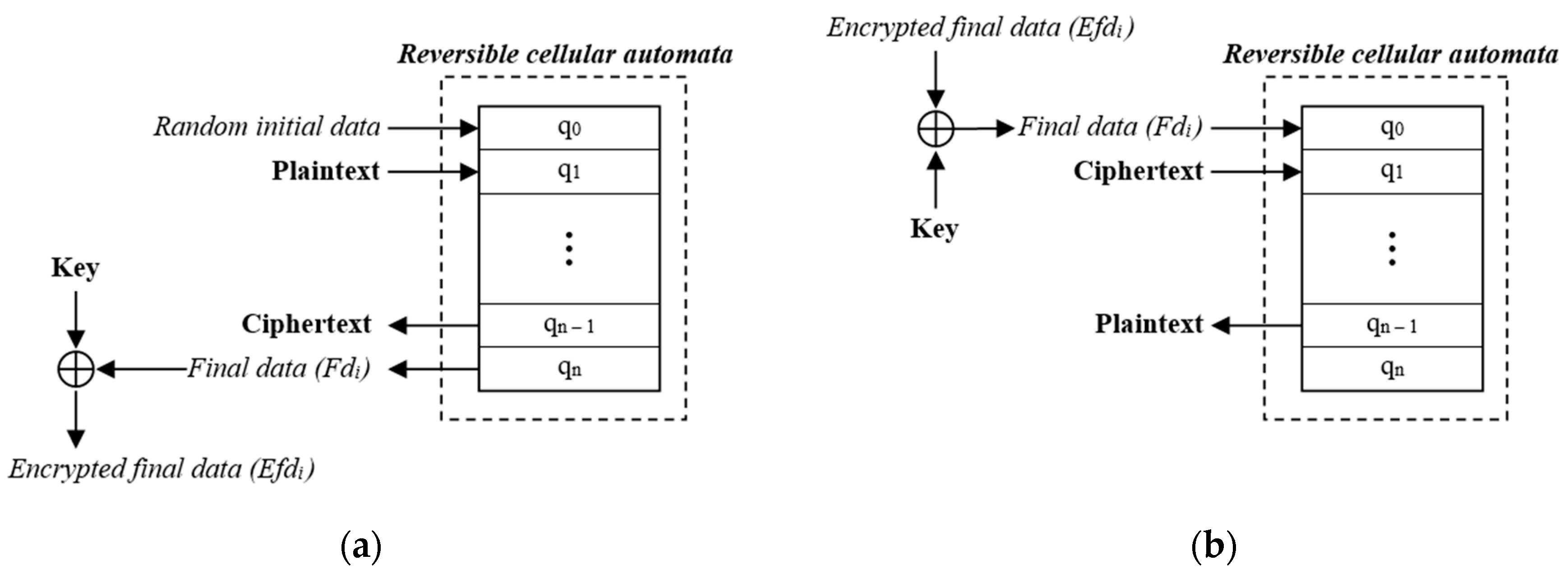
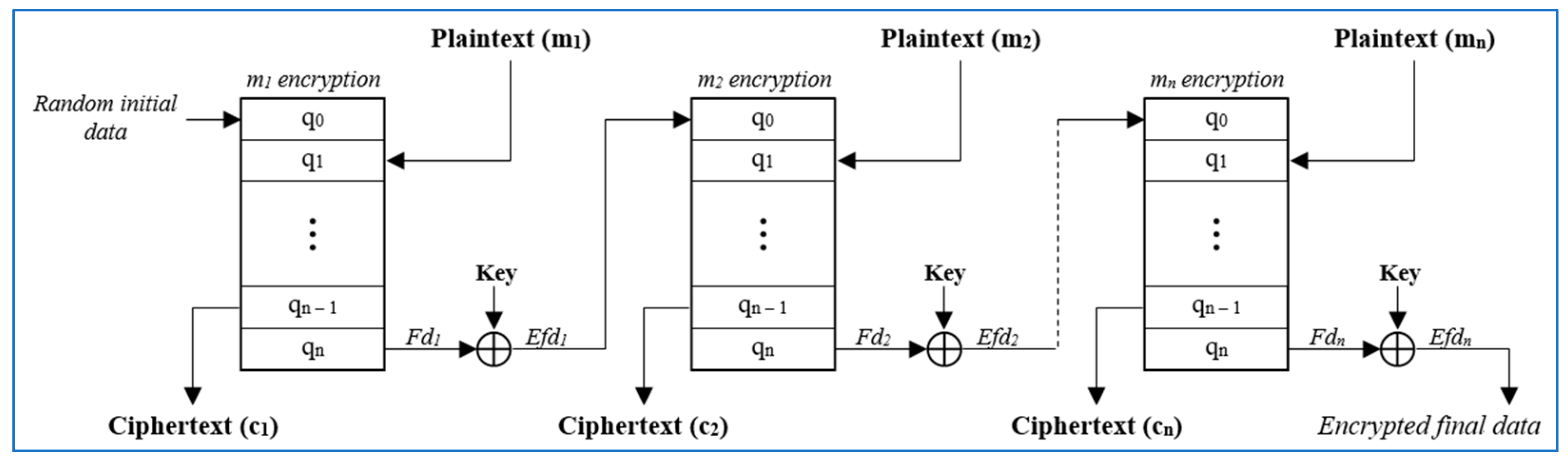
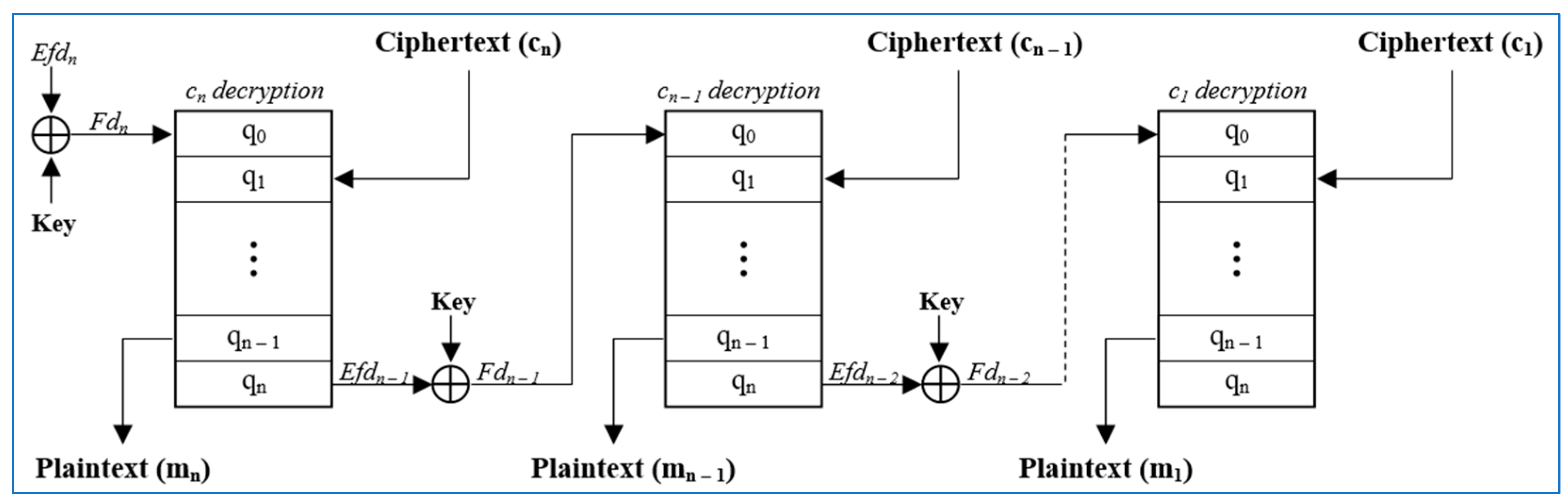
3.1. Fundamentals of the Proposed Algorithm
- Generate random initial data (first state of the RCA);
- Set the second state of the RCA to plaintext to be encrypted
- Evolve the RCA state for a predetermined number of generations (n steps)
- Save the state n − 1 as encrypted data
- Perform the XOR operation between state n (final data) and the key to obtain encrypted final data for the next block.
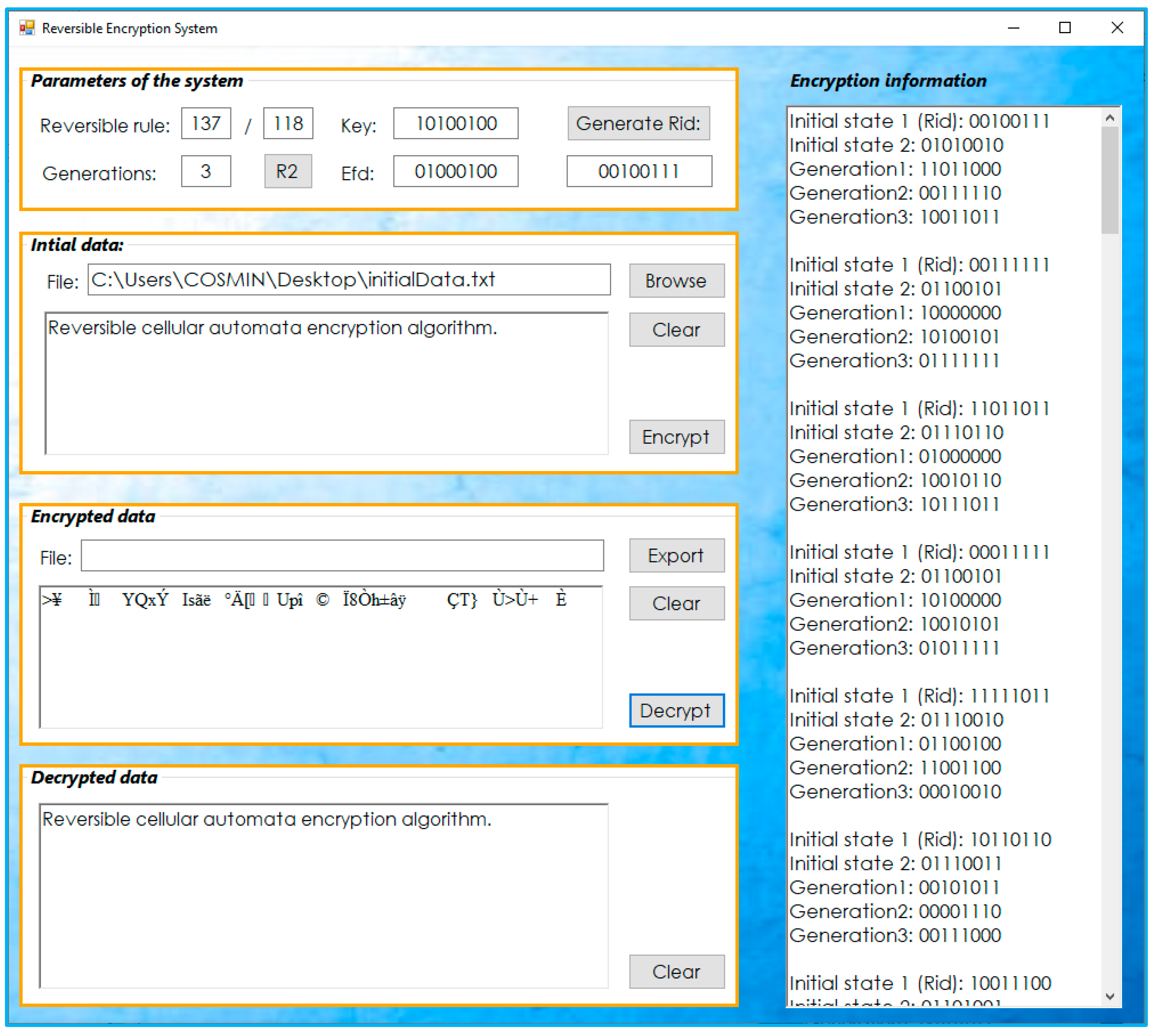
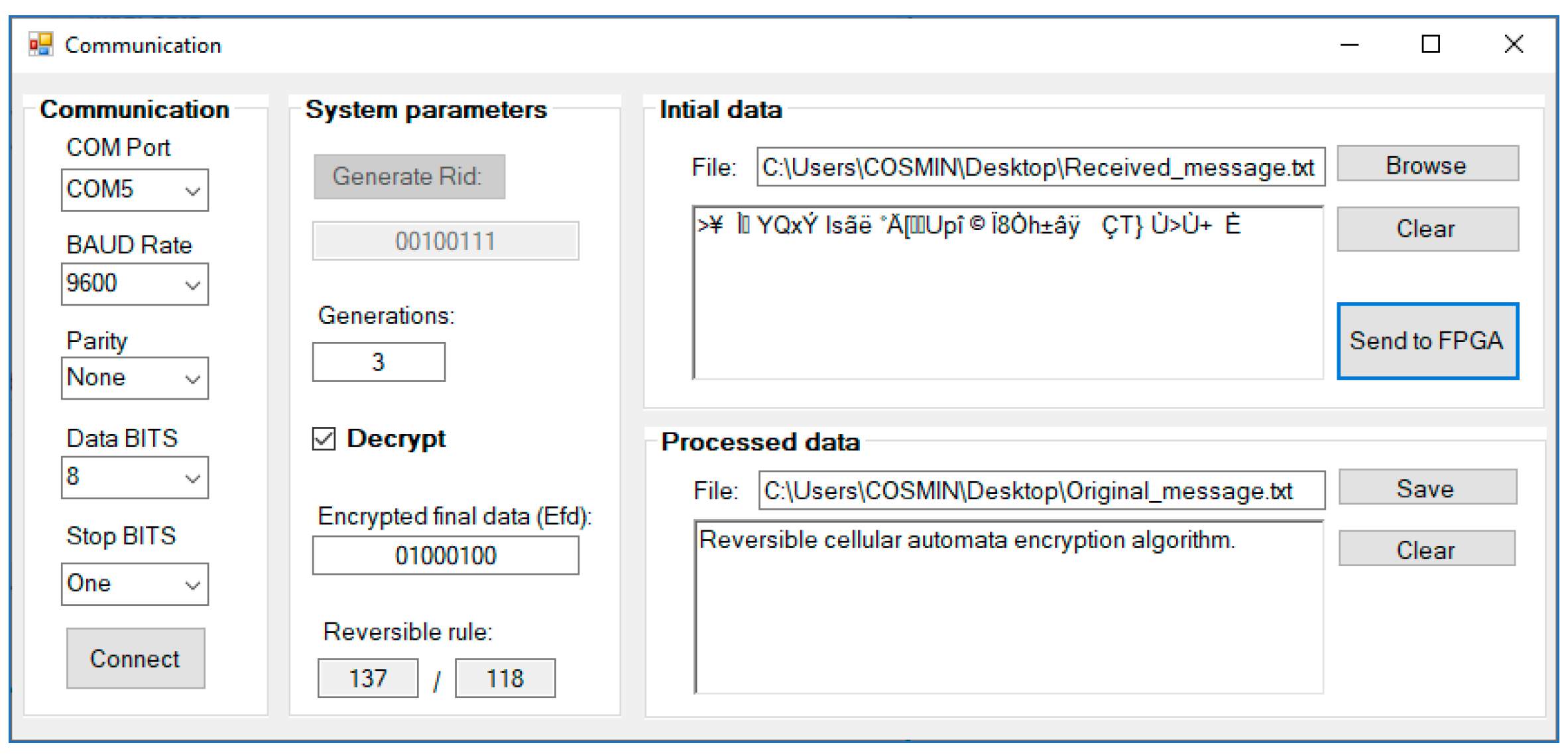
3.2. Software Implementation
- Step 1:
- Select a reversible rule (predefined or custom)
- Step 2:
- Specify the number of RCA generations
- Step 3:
- Complete random initial generated data (for encryption) or input encrypted final data (for decryption)
- Step 4:
- Input the encryption/decryption key
- Step 5:
- Upload data (plain or ciphertext) then choose the appropriate process.
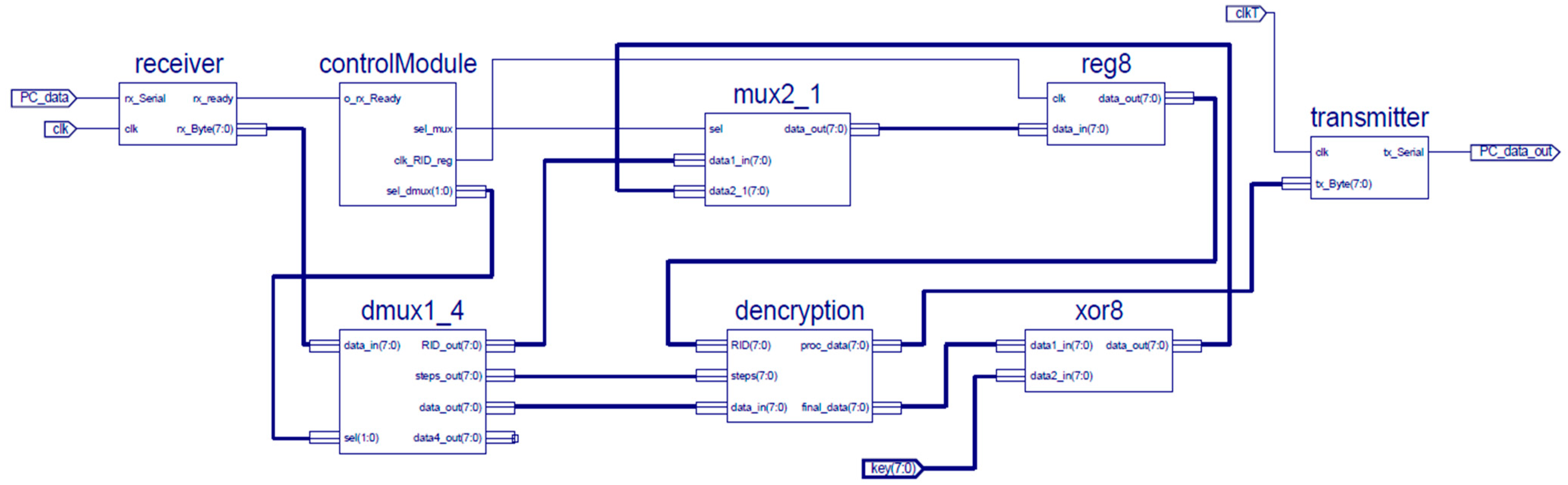
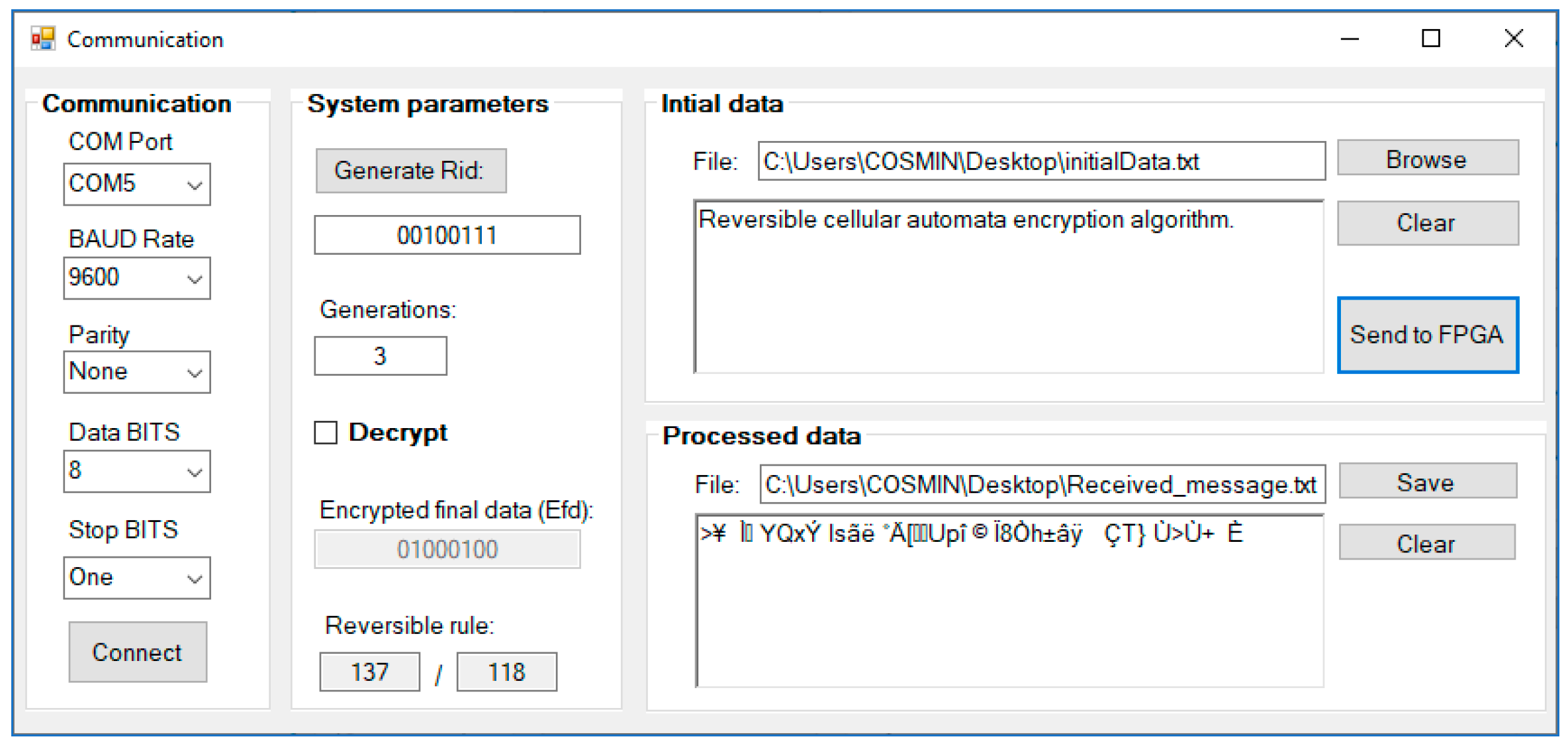
3.3. Hardware Implementation
- Minimum period: 4.640 ns (maximum frequency: 215.529 MHz)
- Minimum input arrival time before clock: 2.044 ns
- Maximum output required time after clock: 6.854 ns.
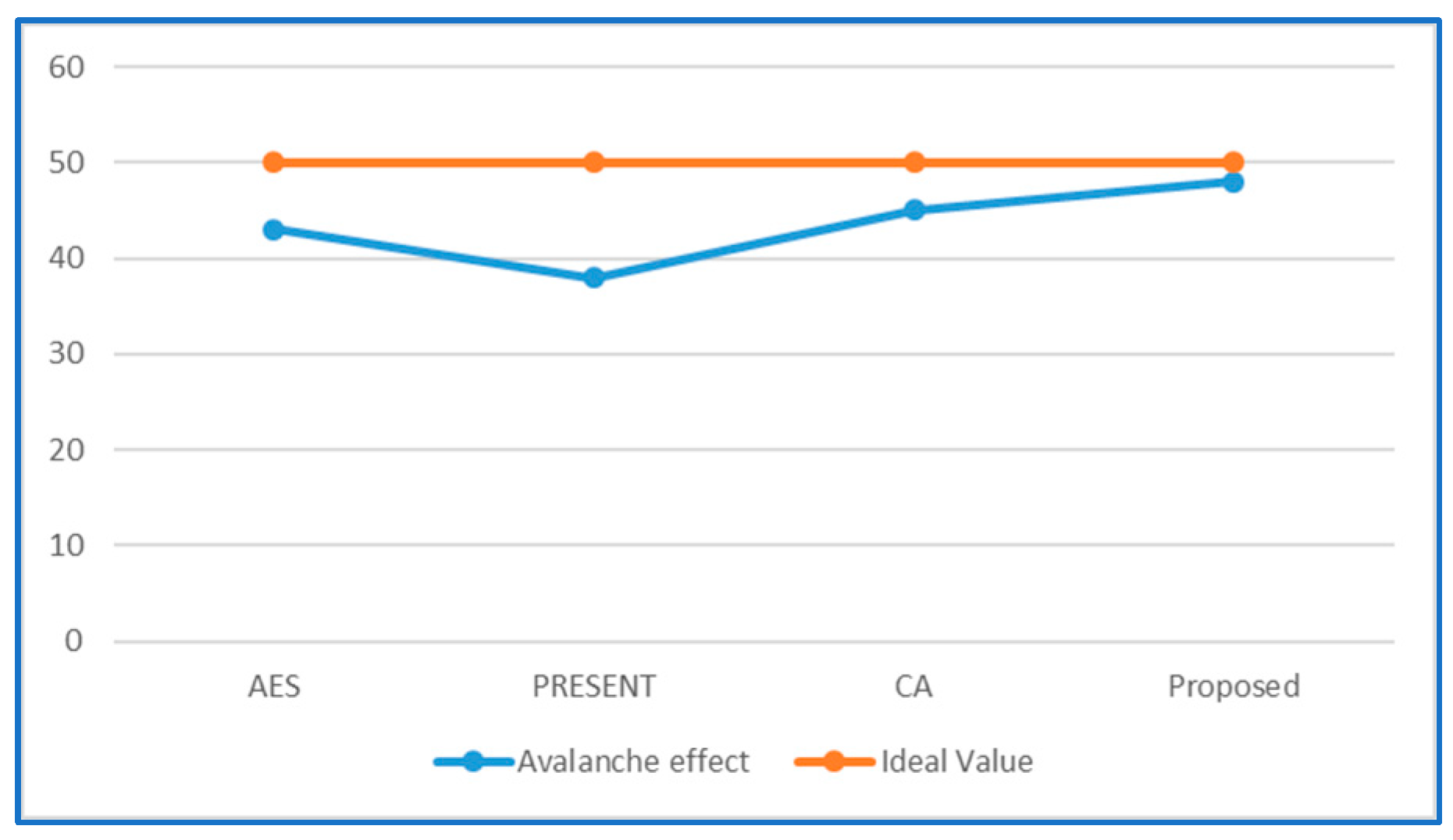
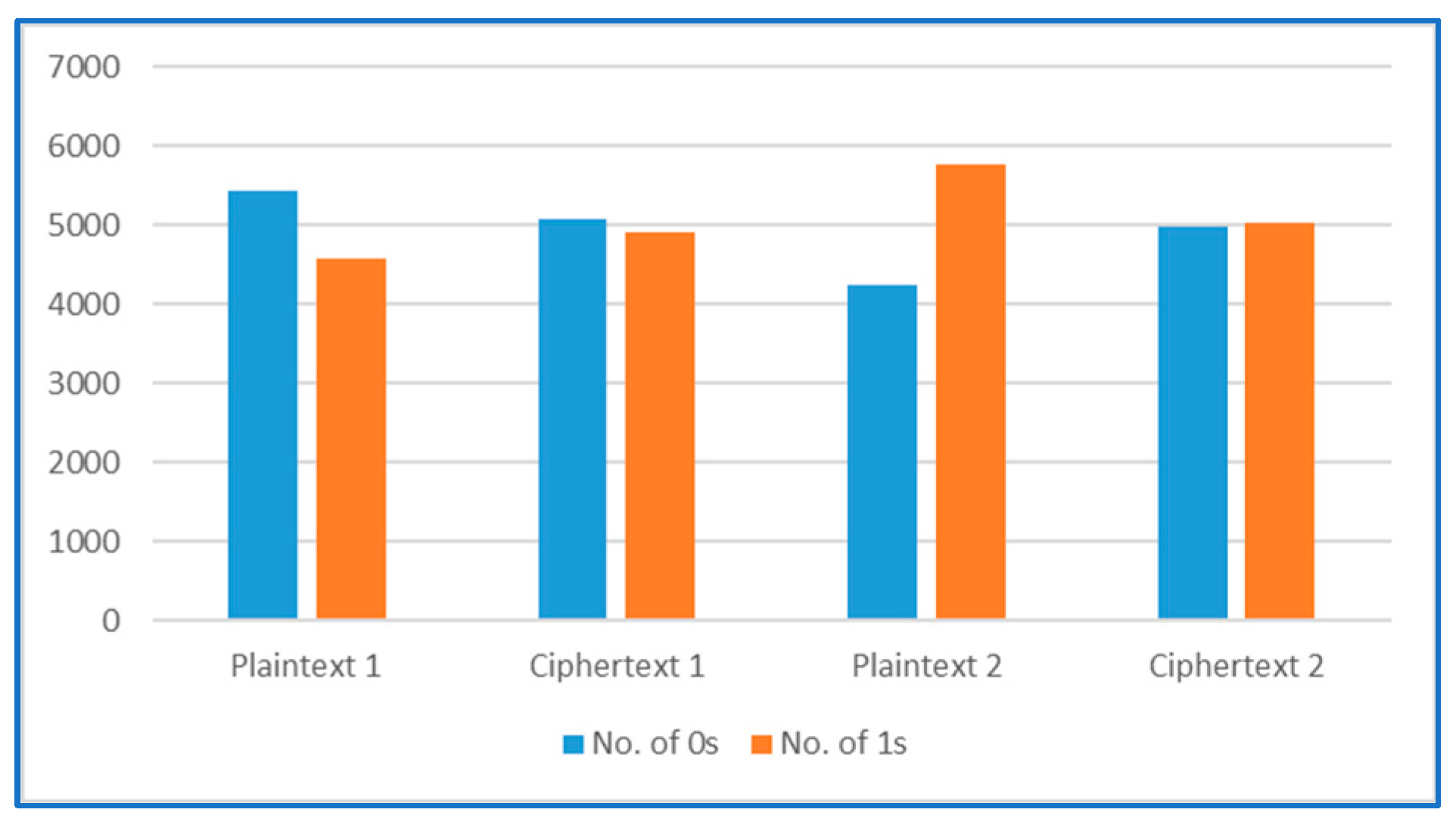
4. Testing and Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Romania Insider. Available online: https://www.romania-insider.com/hackers-confidential-information-cyber-attack-parliament-romania-2024 (accessed on 17 April 2024).
- Krause, T.; Ernst, R.; Klaer, B.; Hacker, I.; Henze, M. Cybersecurity in Power Grids: Challenges and Opportunities. Sensors 2021, 21, 6225. [Google Scholar] [CrossRef]
- Almalawi, A.; Khan, A.I.; Alsolami, F.; Abushark, Y.B.; Alfakeeh, A.S. Managing Security of Healthcare Data for a Modern Healthcare System. Sensors 2023, 23, 3612. [Google Scholar] [CrossRef]
- Pritika; Shanmugam, B.; Azam, S. Risk Assessment of Heterogeneous IoMT Devices: A Review. Technologies 2023, 11, 31. [Google Scholar] [CrossRef]
- Valahia News. Available online: https://valahia.news/ransomware-cyber-attack-romanian-hospitals (accessed on 17 April 2024).
- Arachchige, K.G.; Branch, P.; But, J. An Analysis of Blockchain-Based IoT Sensor Network Distributed Denial of Service Attacks. Sensors 2024, 24, 3083. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Abdulkader, H.; Elatif, S.S.A.; Oliva, D.; Sosa-Gómez, G.; Snášel, V. On the Cryptanalysis of a Simplified AES Using a Hybrid Binary Grey Wolf Optimization. Mathematics 2023, 11, 3982. [Google Scholar] [CrossRef]
- Shafique, A.; Khan, K.H.; Hazzazi, M.M.; Bahkali, I.; Bassfar, Z.; Rehman, M.U. Chaos and Cellular Automata-Based Substitution Box and Its Application in Cryptography. Mathematics 2023, 11, 2322. [Google Scholar] [CrossRef]
- Zhang, C.; Liang, Y.; Tavares, A.; Wang, L.; Gomes, T.; Pinto, S. An Improved Public Key Cryptographic Algorithm Based on Chebyshev Polynomials and RSA. Symmetry 2024, 16, 263. [Google Scholar] [CrossRef]
- Nyangaresi, V.O.; Jasim, H.M.; Mutlaq, K.A.-A.; Abduljabbar, Z.A.; Ma, J.; Abduljaleel, I.Q.; Honi, D.G. A Symmetric Key and Elliptic Curve Cryptography-Based Protocol for Message Encryption in Unmanned Aerial Vehicles. Electronics 2023, 12, 3688. [Google Scholar] [CrossRef]
- Sadeghi-Nasab, A.; Rafe, V. A comprehensive review of the security flaws of hashing algorithms. J. Comput. Virol. Hack. Tech. 2023, 19, 287–302. [Google Scholar] [CrossRef]
- Anghelescu, P. Parallel Optimization of Program Instructions Using Genetic Algorithms. Comput. Mater. Contin. 2021, 67, 3293–3310. [Google Scholar] [CrossRef]
- John, A.; Lakra, R.; Jose, J. On the design of stream ciphers with Cellular Automata having radius = 2. Cryptol. Eprint Arch. 2020, 2020, 327. [Google Scholar]
- Abbassi, N.; Gafsi, M.; Hajjaji, M.A.; Mtibaa, A. Hardware design and implementation of a lightweight stream-cipher cryptosystem: A Chaotic/Reversible Cellular Automata Approach. In Proceedings of the International Conference on Sciences and Techniques of Automatic Control and Computer Engineering (STA), Sousse, Tunisia, 19–21 December 2022; pp. 255–260. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Stănică, G.C.; Anghelescu, P. Software implementation of a two-dimensional cellular automaton. In Proceedings of the 12th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Bucharest, Romania, 25–27 June 2020. [Google Scholar] [CrossRef]
- Anghelescu, P. Evolution of Hybrid Cellular Automata for Density Classification Problem. Symmetry 2024, 16, 599. [Google Scholar] [CrossRef]
- Wolfram, S. Cryptography with Cellular Automata. In Proceedings of the Advances in Cryptology: Crypto ’85, Linz, Austria, 9–11 April 1985. [Google Scholar] [CrossRef]
- Corona-Bermúdez, E.; Chimal-Eguía, J.C.; Téllez-Castillo, G. Cryptographic Services Based on Elementary and Chaotic Cellular Automata. Electronics 2022, 11, 613. [Google Scholar] [CrossRef]
- Degala, D.P.; Athithan, S.; Chinnasamy, P. A Survey on Data Security using Reversible Cellular Automata. In Proceedings of the International Conference on Computer Communication and Informatics (ICCCI), Coimbatore, India, 23–25 January 2023; pp. 1–6. [Google Scholar]
- Martín del Rey, A.; Casado Vara, R.; Hernández Serrano, D. Reversibility of Symmetric Linear Cellular Automata with Radius r = 3. Mathematics 2019, 7, 816. [Google Scholar] [CrossRef]
- Yingri, S.; Yan, W.; Guoqiang, H. Reversible cellular automata image encryption for similarity search. Signal Process. Image Commun. 2019, 72, 134–147. [Google Scholar]
- Xiuli, C.; Yinjing, W.; Zhihua, G.; Xiuhui, C.; Yushu, Y. Preserving privacy while revealing thumbnail for content-based encrypted image retrieval in the cloud. Inf. Sci. 2022, 604, 115–141. [Google Scholar]
- Nanda, S.K.; Mohanty, S.; Pattnaik, P.K.; Sain, M. Throughput Optimized Reversible Cellular Automata Based Security Algorithm. Electronics 2022, 11, 3190. [Google Scholar] [CrossRef]
- Kim, S.; Kim, D. Data-Tracking in Blockchain Utilizing Hash Chain: A Study of Structured and Adaptive Process. Symmetry 2024, 16, 62. [Google Scholar] [CrossRef]
- Jeon, J.-C. Multi-Layer QCA Shift Registers and Wiring Structure for LFSR in Stream Cipher with Low Energy Dissipation in Quantum Nanotechnology. Electronics 2023, 12, 4093. [Google Scholar] [CrossRef]
- Kim, H.-I.; Jeon, J.-C. Quantum LFSR Structure for Random Number Generation Using QCA Multilayered Shift Register for Cryptographic Purposes. Sensors 2022, 22, 3541. [Google Scholar] [CrossRef]
- Das, S.; Sarkar, A.; Sikdar, B.K. Synthesis of reversible asynchronous cellular automata for pattern generation with specific hamming distance. In Proceedings of the International Conference on Cellular Automata for Research and Industry (ACRI), Springer, Greece, 24–27 September 2012. [Google Scholar]
- Hatkar, S.S.; Pawar, B.K. Symmetric key algorithm using Vernam cipher: VSA. In Proceedings of the International Conference on Inventive Computation Technologies (ICICT), Coimbatore, India, 26–27 August 2016. [Google Scholar]
- Stănică, G.C.; Anghelescu, P. Encryption Algorithm using Linear Hybrid Cellular Automaton. In Proceedings of the International Semiconductor Conference (CAS), Poiana Brasov, Romania, 12–14 October 2022; pp. 257–260. [Google Scholar] [CrossRef]
- Dascălu, M. Cellular Automata Hardware Implementations—An Overview. Sci. Technol. 2016, 19, 360–368. [Google Scholar]
- Rukhin, A.; Soto, J.; Nechvatal, J.; Smid, M.; Barker, E.; Leigh, S.; Levenson, M.; Vangel, M.; Banks, D.; Heckert, N.; et al. A Statistical Test Suite for Random and Pseudorandom Number Generators for Cryptographic Applications. Natl. Inst. Stand. Technol. Spec. Publ. 2010, 800-22 Rev. 1a. [Google Scholar] [CrossRef]
- Nanda, S.K.; Mohanty, S.; Pattnaik, P.K. A performance optimized reversible cellular automata based security algorithm for secure data communication and storage in healthcare. J. Thoretical Appl. Inf. Technol. 2022, 100, 17. [Google Scholar]
- Shanmuganathan, H.; Mahendran, A. Encryption Based on Cellular Automata for Wireless Devices in IoT Environment. Int. Arab. J. Inf. Technol. 2021, 18, 3. [Google Scholar] [CrossRef]
- Stănică, G.C.; Anghelescu, P. Cryptographic Algorithm Based on Hybrid One-Dimensional Cellular Automata. Mathematics 2023, 11, 1481. [Google Scholar] [CrossRef]
- Alharbi, M.; Edwards, G.; Stocker, R. Reversible Quantum-Dot Cellular Automata-Based Arithmetic Logic Unit. Nanomaterials 2023, 13, 2445. [Google Scholar] [CrossRef]
- Levina, A.; Mukhamedjanov, D.; Bogaevskiy, D.; Lyakhov, P.; Valueva, M.; Kaplun, D. High Performance Parallel Pseudorandom Number Generator on Cellular Automata. Symmetry 2022, 14, 1869. [Google Scholar] [CrossRef]
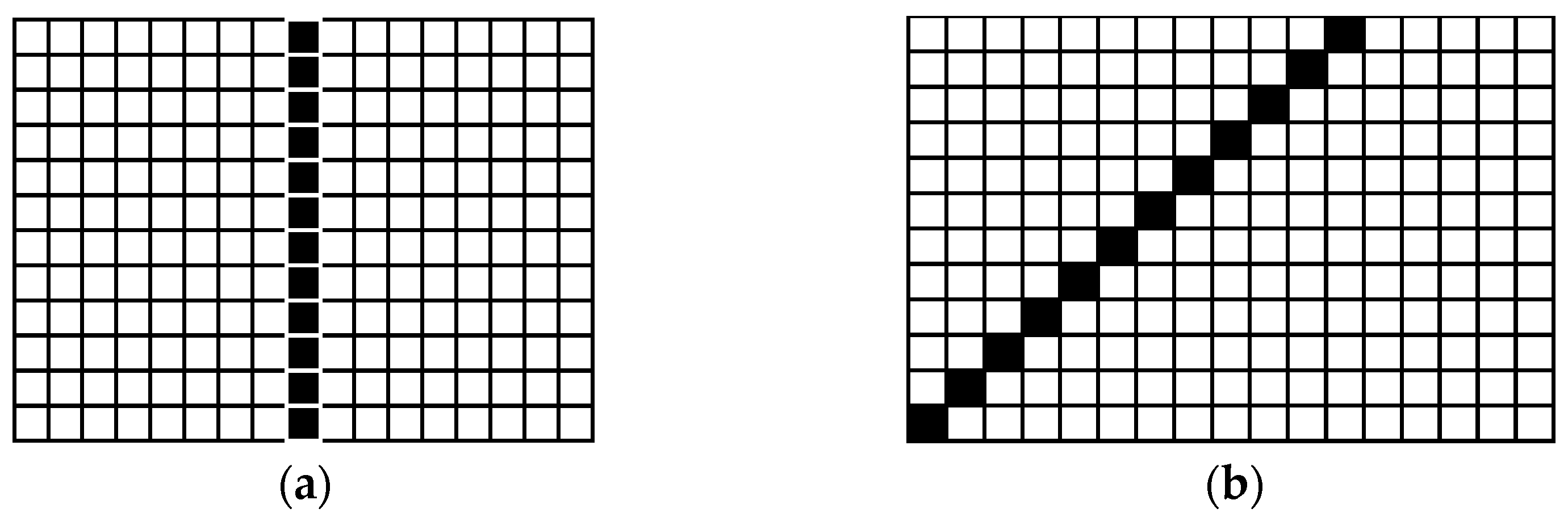




| Resource | Used | Available | Area (%) |
|---|---|---|---|
| Number of slices | 195 | 4656 | 4 |
| Number of slice flip flops | 118 | 9312 | 2 |
| Number of 4 input LUTs | 384 | 9312 | 4 |
| Number of bonded IOBs | 24 | 232 | 10 |
| Number of GCLKs | 1 | 8 | 12 |
| NIST Statistical Test | p-Value | Proportion (Pass Rate) |
|---|---|---|
| Frequency (monobits) | 0.739918 | 10/10 |
| Block frequency | 0.122325 | 10/10 |
| Runs | 0.739918 | 9/10 |
| Longest run | 0.739918 | 10/10 |
| Rank | 0.122325 | 9/10 |
| FFT | 0.122325 | 10/10 |
| Non-overlapping template | 0.000439 | 9/10 |
| Overlapping template | 0.739918 | 10/10 |
| Linear complexity | 0.911413 | 10/10 |
| Serial 1 | 0.350485 | 10/10 |
| Serial 2 | 0.213309 | 10/10 |
| Universal | undefined | undefined |
| Approximate Entropy | 0.000199 | 9/10 |
| Cumulative Sum (forward) | 0.534146 | 10/10 |
| Cumulative Sum (reverse) | 0.534146 | 10/10 |
| Plaintext = 01001101 Key = 10010111 Rid = 01011101 | Plaintext = 01001101 Key = 10010111 Rid = 01011100 | Plaintext = 01001101 Key = 10010111 Rid = 01011001 |
|---|---|---|
| Initial state 1 (Rid): 01011101 | Initial state 1 (Rid): 01011100 | Initial state 1 (Rid): 01011001 |
| Initial state 2: 01001101 | Initial state 2: 01001101 | Initial state 2: 01001101 |
| Generation1: 10101010 | Generation1: 10101011 | Generation1: 10101110 |
| Generation2: 10110010 | Generation2: 10110000 | Generation2: 10111110 |
| Generation3: 01110101 | Generation3: 01110011 | Generation3: 01101101 |
| Generation4: 00101101 | Generation4: 00101101 | Generation4: 00001001 |
| Generation5: 00000010 | Generation5: 00000100 | Generation5: 01110010 |
| Generation6: 00101010 | Generation6: 00100011 | Generation6: 10010110 |
| Generation7: 01111101 | Generation7: 01110001 | Generation7: 10001001 |
| Generation8: 10101101 | Generation8: 10111000 | Generation8: 01001001 |
| Generation9: 10001010 | Generation9: 10111101 | Generation9: 01110110 |
| Generation10: 01110010 | Generation10: 01111111 | Generation10: 11010010 |
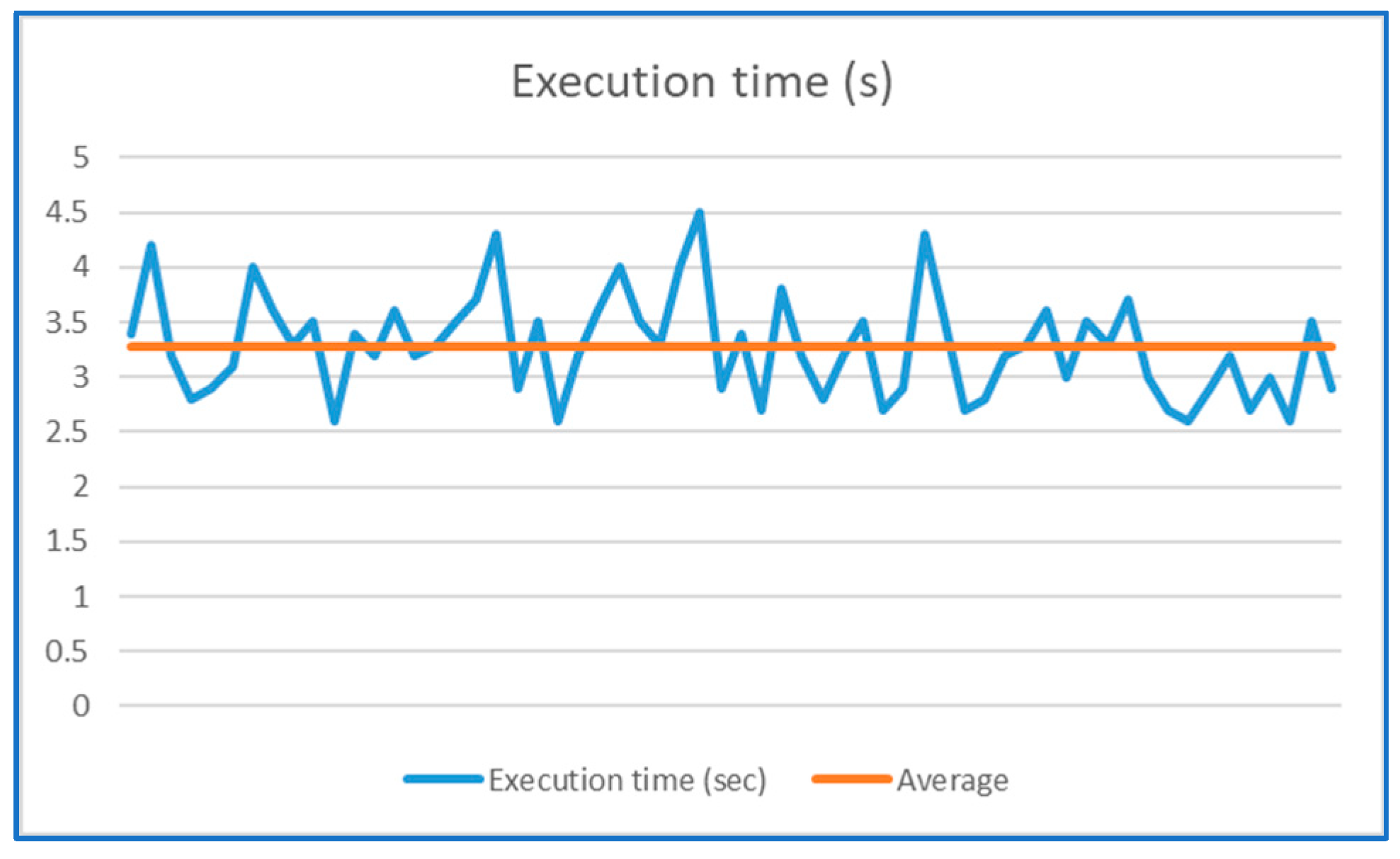
| Algorithm | Execution Time (Avg) | Execution Time (Min) | Execution Time (Max) |
|---|---|---|---|
| Proposed algorithm | 3.283 | 2.6 | 4.5 |
| [33] | 3.533 | 2.7 | 4.7 |
| [24] | 4.238 | 3.4 | 5.2 |
| Data Size (Bits) | Power Consumption (mW) |
|---|---|
| 10,000 | 75.28 |
| 15,000 | 89.54 |
| 50,000 | 193.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stănică, G.C.; Anghelescu, P. Reversible Cellular Automata Based Cryptosystem. Electronics 2024, 13, 2515. https://doi.org/10.3390/electronics13132515
Stănică GC, Anghelescu P. Reversible Cellular Automata Based Cryptosystem. Electronics. 2024; 13(13):2515. https://doi.org/10.3390/electronics13132515
Chicago/Turabian StyleStănică, George Cosmin, and Petre Anghelescu. 2024. "Reversible Cellular Automata Based Cryptosystem" Electronics 13, no. 13: 2515. https://doi.org/10.3390/electronics13132515
APA StyleStănică, G. C., & Anghelescu, P. (2024). Reversible Cellular Automata Based Cryptosystem. Electronics, 13(13), 2515. https://doi.org/10.3390/electronics13132515