Analysis of Factors Influencing the Generation of a Higher-Order Hermite–Gaussian Mode Based on Cascaded Spatial Light Modulators

Abstract

Due to its complex spatial distribution, the higher-order Hermite–Gaussian mode possesses significant application in fields such as precision measurement and optical communication. The spatial light modulator, with its capability to modulate the complex amplitude distribution of the incident light field, finds extensive applications in optical information processing and adaptive optics, thus making it an indispensable tool in these fields. Using cascaded spatial light modulators can efficiently and superbly generate a higher-order Hermite–Gaussian mode; however, the experimental system is challenging, and there are many influencing factors, such as the misalignment between the optical field on the plane of the second spatial light modulator and the hologram loaded onto it, as well as the spot size of the optical field on the plane of the second spatial light modulator. In this paper, we analyzed the influence of the above factors on the quality of generating a higher-order Hermite–Gaussian mode, providing a reference for the efficient and high-quality generation of the higher-order Hermite–Gaussian mode.

1. Introduction

The higher-order Hermite–Gaussian (HG) mode is the eigenmode of a square mirror optical resonator. It is denoted as HGnm, where the subscripts n and m represent the number of nodes in the x and y directions of the spot of light, respectively. The higher-order HG modes constitute a structurally stable family of laser modes characterized by their rectangular symmetry along the axis of propagation. The spatial distribution of the higher-order HG mode is more complex than that of the fundamental mode, endowing the higher-order HG mode with richer spatial degrees of freedom, and thus receiving increasing attention in fields such as precision measurement and optical communication. For example, it enables biological measurement beyond the quantum limit [1], measurement of the momentum and position of atoms in the microcavity [2], small displacement measurement [3], and enhancement of the cooling process in the ensemble of atoms [4]. In gravitational wave detection, the use of the higher-order HG mode can eliminate mode-matching losses [5]. Therefore, the efficient and high-quality generation of the higher-order HG mode holds great significance. A higher quality of a higher-order HG mode, which means it contains fewer components of other spatial modes, can obtain sub-Rayleigh precision in optical imaging [6], greater precision in cutting or welding effects in laser processing [7], and it can effectively minimize noise to enhance the signal-to-noise ratio, thereby optimizing optical communication performance [8].

Currently, there are two methods for generating higher-order HG modes, which are direct generation inside the cavity and external cavity beam shaping generation. For the former method, the experimental setup is simple and convenient, but it requires the addition of special optical elements inside the optical resonator, which complicates the resonator structure and results in poorer stability [9,10,11,12]. Shu-Chun Chu et al. inserted metal wires into the resonator cavity of the laser to select the laser mode that meets the gain competition criteria. Due to the diffraction caused by the metal wires, all other competing gain modes suffer significant energy losses during their round trip within the cavity, ultimately resulting in the desired higher-order HG mode output. However, achieving high-power higher-order HG mode output remains challenging due to the relatively low conversion efficiency [9]. Mach Lam et al. generated higher-order HG modes as well as arbitrary spatial modes by inserting a holographic phase mask into the laser cavity. The holographic phase mask, with its excellent flexibility, allows for encoding arbitrary spatial phase distributions into laser modes [10]. By adjusting the mirror curvature of an intra-cavity deformable mirror under specific pumping voltage and current conditions, Dong Wang et al. generated a variety of higher-order HG modes within the Z-shaped resonant cavity of a Yb:CALGO laser [11]. Tradonsky Chene et al. proposed a fast and effective method to generate laser beams with arbitrary intensity and phase distribution. It is based on a digital degenerate cavity laser, which combines a phase-only spatial light modulator (SLM) and spatial filter. Through this method, they generated higher-order HG modes and arbitrary spatial distribution modes, and the laser output power changed slightly [12].

External cavity beam shaping is the process of shaping the fundamental mode into a higher-order HG mode through a mode converter cavity or optical diffraction elements [13,14,15,16,17,18,19,20,21,22,23]. Lassen Mikael et al. used a mode conversion cavity to mismatch the incident fundamental mode, thereby exciting the generation of higher-order HG modes. By locking the cavity length of the mode conversion cavity, different orders of HG modes can be output. As the order of the higher-order HG mode increases, the signal-to-noise ratio of the error signal becomes smaller, making it difficult to lock the mode conversion cavity length. Therefore, this scheme is suitable for generating low-order HG modes [13]. Delaubert V et al. used specially structured phase plates to reshape the phase distribution of the incident fundamental mode into the phase distribution of the target higher-order HG mode. Then, by utilizing mode-filtering devices, they obtained a standard higher-order HG mode. It should be noted that each phase plate can only generate a specific order of the HG mode, and the phase distribution of a higher-order HG mode is more complex, which demands better processing technology for the phase plates [14]. Morizur Jean-Francois et al. used the deformable mirror to reflect the fundamental mode three times and interfered with the standard higher-order HG mode, combined with the simulated annealing algorithm, to generate the first third-order HG modes. However, due to the size limitation of the deformable mirror, it is challenging to generate a HG mode higher than the third order [15]. The SLM is one of the commonly used optical diffraction elements for generating higher-order spatial modes. Beam shaping using SLM can be achieved by simply changing the loaded hologram to generate different higher-order HG modes, providing excellent flexibility. The SLM consists of liquid crystal molecules, which are typically a few to tens of micrometers in size. This allows the SLM to have millions of pixels, enabling precise wavefront control of the incident beam.

There have been reports of using a single SLM [16,17,18] or cascaded SLMs [19,20,21,22,23,24] to modulate both the amplitude and phase distributions of the incident light field simultaneously, resulting in the generation of higher-order HG modes. The principle of complex amplitude modulation using a single SLM involves superimposing a function onto the grating function, ultimately obtaining the target light field at the first diffraction order of the emitted light field. The purity of the target light field produced by this complex amplitude modulation with a single SLM can theoretically reach 99%, but the system has significant optical losses, resulting in low efficiency. Stefan Ast et al. used a single SLM to shape the incident fundamental mode into fifth- HG mode, tenth- HG mode, and fifteenth-order HG mode, achieving conversion efficiencies of 6.6%, 3.7%, and 1.7%, respectively. They also proved that the higher-order HG modes are structurally compatible with gravitational wave detectors and can effectively reduce mirror thermal noise [17]. Kui Liu et al. theoretically analyzed the conversion efficiency of a higher-order HG mode when the incident light field was a fundamental Gaussian beam and an elliptical Gaussian beam, respectively. Through experiments, they verified that using an elliptical Gaussian beam as the incident light field has a higher conversion efficiency compared to using a fundamental Gaussian beam. In the experiment, the conversion efficiency of the generated HG60 mode was 17.5% [18]. Using cascaded SLMs for complex amplitude modulation to generate higher-order HG modes offers high conversion efficiency and allows for the simultaneous modulation of both the phase and amplitude distributions of the incident light field. Long Zhu et al. proposed a method to modulate the intensity and phase of the incident light field by controlling its polarization through cascaded SLMs and generated light fields with arbitrary intensity distributions in experiments. Nevertheless, controlling the polarization of the light field inevitably leads to optical losses, which reduces the conversion efficiency of the system [19]. Alexander Jesacher et al. proposed modulating the complex amplitude of the incident light field with cascaded SLMs, theoretically achieving a conversion efficiency of up to 100% [22]. Long Ma et al. efficiently generated the first five orders of HG modes using cascaded SLMs, achieving a conversion efficiency of over 66% [23].

An efficient generation of higher-order HG modes can be accomplished by using cascaded SLMs. However, the experimental system poses significant challenges due to various influencing factors, and the quality of the generated higher-order HG modes will be affected, for instance, the misalignment between the optical field on the plane of the second SLM and the hologram loaded onto it and the spot size of the optical field on the plane of the second SLM. In this paper, combined with the experimental parameters, the effect of these two influencing factors on the quality of higher-order HG mode generation is discussed in detail, which provides references for further efficient and high-quality higher-order HG mode generation.

2. Theoretical Model

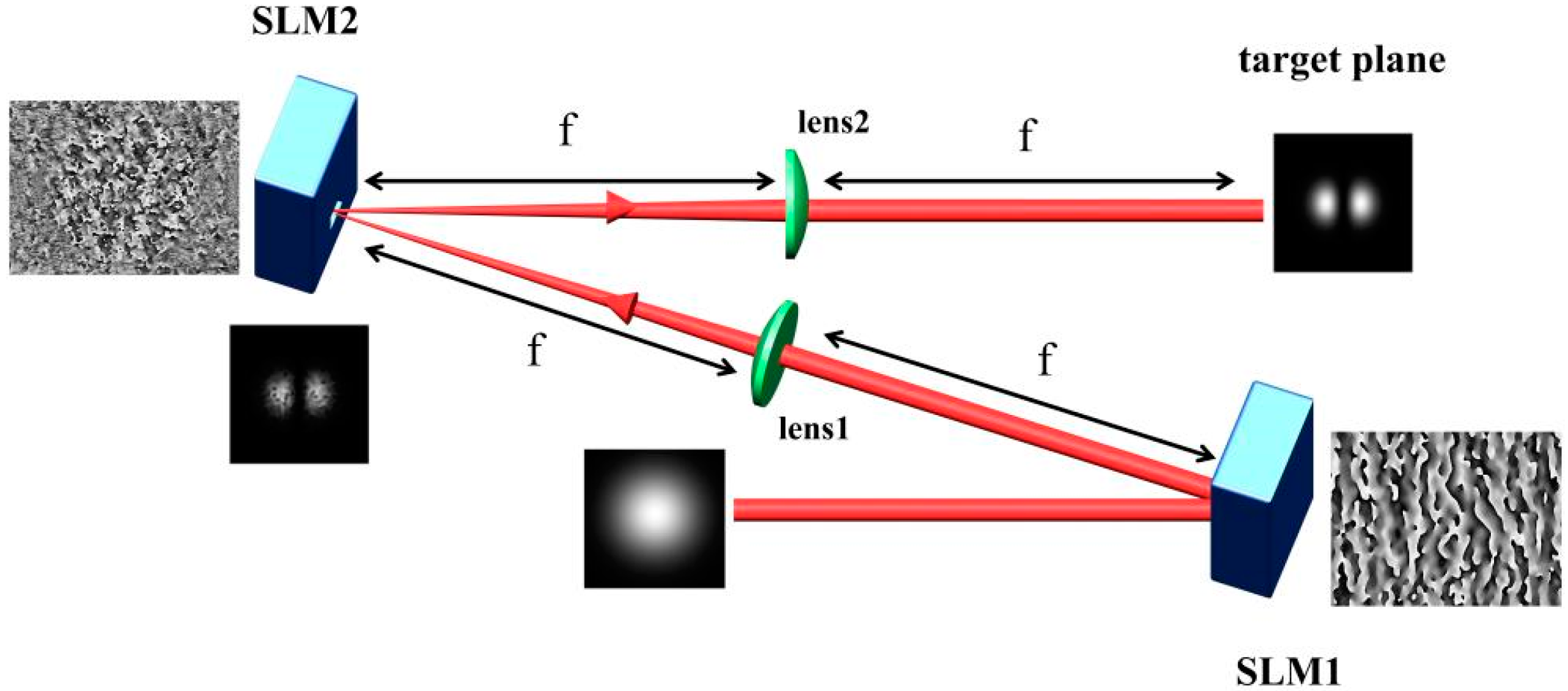
The principle of cascaded SLMs that generated a higher-order HG mode is shown in Figure 1, consisting of two SLMs and two Fourier transform lenses. The Fourier transform lens 1 features two focal planes, with the front focal plane housing the SLM1 and the back focal plane accommodating the SLM2. To generate a higher-order HG mode $t(x,y)=\left|t(x,y)\right|\exp \left[i\varphi (x,y)\right]$ at the target plane, lens 2 is utilized to perform an inverse Fourier transform. This process necessitates the acquisition of a complex amplitude distribution $A(u,v)=\left|A(u,v)\right|\exp \left[i\Phi (u,v)\right]$ on the SLM2 plane. The expression is as follows [25]:

$$A(u,v)=\frac{1}{\lambda f}{\displaystyle {\int }_x{\displaystyle {\int }_{y}t(x,y)\exp \left[-i\frac{2\pi }{\lambda f}(ux+vy)\right]}}dxdy$$

(1)

In this equation, $\lambda$ represents the laser wavelength, while $f$ denotes the focal length of the Fourier transform lens. The phase distribution of the optical field $A(u,v)$ can be directly modulated by SLM2; however, generating the amplitude distribution requires a more complex approach. Specifically, SLM1 must be used in conjunction with a phase retrieval algorithm to accurately produce the desired amplitude distribution of the optical field. The Gerchberg–Saxton (GS) algorithm stands as a widely utilized method for phase retrieval [26]. Through iterative optimization employing the GS algorithm, the phase distribution function, often referred to as the hologram, can be determined at SLM1. Upon completing n iterations of the GS algorithm, the resulting optical field $A_n(u,v)$ emerges in the plane of SLM2, described as follows:

$$A_n(u,v)=\frac{1}{\lambda f}{\displaystyle {\int }_{\epsilon }{\displaystyle {\int }_{r}I(\epsilon ,r)\exp \left[i{H}_1(\epsilon ,r)\right]\exp \left[i\frac{2\pi }{\lambda f}(u\epsilon +vr)\right]}}d\epsilon dr$$

(2)

where $I(\epsilon ,r)$ represents the fundamental mode incident on the SLM1 plane and $A_n(u,v)=\left|A_n(u,v)\right|\exp \left[i\phi (u,v)\right]$ represents the optical field distribution at the SLM2 plane, which has the same amplitude distribution as $A(u,v)$. Since SLM1 only shapes the intensity distribution of the incident optical field, the distribution of phase within the optical field $A_n(u,v)$ located at the SLM2 plane is random, but theoretically we know it. To manipulate the phase distribution of the light field emitted by SLM2 as $\Phi (u,v)$, the phase distribution function (i.e., hologram) $H_2(u,v)$ that needs to be loaded on SLM2 is given by

$$H_2(u,v)=\mathrm{mod}2\pi \left\{\Phi (u,v)-\phi (u,v)\right\}$$

(3)

where mod2$\pi${…} stands for the modulo operation, which ensures that the phase modulation function $H_2(u,v)$ ranges from 0 to 2$\pi$. Altogether, a fundamental mode can be shaped into a higher-order HG mode through cascaded SLMs, and we can theoretically obtain an arbitrary complex amplitude distribution at the target plane. Additionally, the conversion efficiency is 100% since the system solely utilizes non-absorbing phase elements.

3. Results and Discussion

Because of the constraints imposed by the limited resolution of the SLM, it is impractical to experimentally produce precise standard intensity and phase distributions, and therefore, obtaining a standard higher-order HG mode in the target plane is unfeasible. To assess the quality of the generated mode, we utilize a quantitative measure known as mode purity. This metric provides a reliable indication of how closely the generated HG mode aligns with the ideal HG mode, enabling us to evaluate the accuracy and effectiveness of our mode generation process. Mode purity refers to the degree of interference between the generated mode and the theoretical standard mode. Specifically, it is quantified as the inner product between these two modes, expressed in the following form [23]:

$$\mathrm{P}={\left|{\displaystyle \iint t(x,y)b^{\ast }(x,y)dxdy}\right|}^2/\left({\displaystyle \iint {\left|t(x,y)\right|}^{2}dxdy{\displaystyle \iint {\left|b(x,y)\right|}^{2}dxdy}}\right)$$

(4)

where $t(x,y)$ and $b(x,y)$ denote the higher-order HG mode generated by cascaded SLMs and the corresponding theoretical standard mode, respectively.

From the theoretical model, it is evident that the experimental requirements for the cascaded SLMs are stringent. To ensure accurate mode generation, it is essential to achieve precise point-to-point alignment between the optical field present at the plane of the SLM2 and the hologram that is loaded onto it. This alignment is crucial for obtaining the desired higher-order Hermite–Gaussian (HG) mode with high mode purity. Specifically, alignment perpendicular to the propagation direction is essential to achieve stray phase correction of the optical field. The current commercially available SLM has pixel sizes on the micrometer scale, making perfect alignment experimentally challenging.

Here, we have chosen HG30 and HG50 modes as our target optical fields. To illustrate the generation process, Figure 2 presents the holograms loaded onto the cascaded SLMs for generating these two modes. The holograms displayed on SLM1 were derived through 500 iterations of the GS algorithm. Within these holograms, various gray values correspond to distinct phases. Evidently, from Figure 2, it is clear that as the order of the target optical field escalates, the spatial distribution becomes more complex, and the holograms loaded on the cascaded SLMs become more intricate, with more dramatic phase changes. The numerical simulation was implemented using Python 3.6.5. The experimental system parameters used in the simulation were as follows: both lenses used in the cascaded SLMs possessed a focal length of 75 cm, the SLM we used had a resolution of 792 × 600, with individual pixels sized at 20 μm, and the spot size at the plane of the SLM2 was 0.8 mm.

From Figure 2, it is evident that the intensity distribution of HG30 mode and HG50 mode accounts for a larger proportion in the horizontal direction, and the misalignment of the hologram in the horizontal direction has a greater impact on the quality of the generated mode. Therefore, we conducted an analysis focusing on the horizontal offset of the hologram loaded onto the SLM2. This analysis involved shifting the position of the hologram on the SLM2 to assess its impact on the generated mode. Through this process, we aimed to gain a deeper understanding of how precise hologram alignment affects the quality and accuracy of the resulting HG modes. To accomplish this, we adjusted the hologram’s position on SLM2, introducing offsets of zero pixels (perfectly aligned), two pixels, four pixels, and six pixels in the horizontal directions. The purity of the theoretically simulated HG30 mode and HG50 mode is shown in Figure 3. The left four columns show the generated HG30 mode and the corresponding standard HG30 mode when the hologram is offset by zero pixels (perfectly aligned), two pixels, four pixels, and six pixels, respectively. The right four columns display the generated HG50 mode and the corresponding standard HG50 mode under the same pixel misalignment conditions. The mode purity in Figure 3 is calculated by taking the inner product of the generated HG mode and the corresponding standard HG mode using Equation 4. Therefore, for the standard HG30 mode and HG50 mode, their mode purity is 100%. With an increase in the number of horizontally offset pixels of the hologram, there is a sharp decline in the purity of the resulting higher-order HG mode. Additionally, as the mode order generated increases, the magnitude of decrease in mode purity becomes even greater. This is because the HG50 mode has a more complex spatial distribution, more drastic phase changes, and higher requirements for phase accuracy compared to the HG30 mode. This can be observed from the holograms that generate the HG30 mode and HG50 mode in Figure 2.

To generate a high-quality higher-order HG mode, it is necessary to achieve point-to-point alignment, that is, micrometer-level alignment, between the optical field at the SLM2 plane and the hologram loaded onto it. During the experimental process, this alignment can be accomplished by adjusting the position of the hologram on the SLM2 while monitoring the mode purity of the generated mode. The mode purity is determined through interference measurements between the generated mode and the corresponding standard mode. This approach ensures optimal alignment for achieving the desired HG mode quality.

Next, we analyzed the spot size of the optical field on the plane of the SLM2. The liquid crystal molecules of the SLM are discrete, and the spot size of the incident beam affects the accuracy of phase modulation and energy utilization. Therefore, to achieve optimal phase modulation, it is necessary to consider the spot size of the optical field on the plane of the SLM2. When the beam waist radius on the plane of the SLM2 was selected as 0.4 mm, 0.6 mm, 0.8 mm, 1.0 mm, and 1.2 mm, we theoretically calculated the mode purity of the generated HG50 mode as 96.5%, 97.2%, 97.6%, 97.1%, 96.3%, respectively. The results show that the generated HG50 mode has the highest mode purity when the beam waist radius on the SLM2 plane is set to 0.8 mm. If a smaller beam waist radius is chosen, the diffraction effect of light is relatively weakened, making the light field more concentrated and uniform. Additionally, a small spot size of the optical field helps retain more high-frequency information. In optical systems, high-frequency information corresponds to the fine structure and details of the light field. When the spot size of the optical field is small, the filtering effect of optical elements such as lenses on high-frequency information is reduced. This results in the intensity distribution generated by SLM1 to be at a higher resolution, have detailed expressive power, and be closer to the standard intensity distribution. However, due to the limited resolution of the SLM, SLM2 cannot perform phase correction effectively.

On the other hand, if a larger beam waist radius is chosen, although phase correction can be better performed by SLM2, the intensity distribution generated by SLM1 is poorer, resulting in a notable deterioration of the final generated mode’s quality. This phenomenon can be explained from the following perspectives. First, in optical systems, light passing through optical components can experience diffraction effects due to factors like edge influence, causing light rays to bend and scatter. When the target spot is larger, diffraction effects may become more pronounced, resulting in an uneven light field distribution and energy dispersion, thereby reducing the quality of the optical field. Next, diffraction through optical elements like lenses can lead to the loss of high-frequency information, acting as a low-pass filter. An increase in the target spot size may indicate that more high-frequency details are smoothed out, reducing fine structures in the optical field and consequently decreasing its quality. Finally, the GS algorithm recovers phase information from two known intensity distributions. As the target spot grows, the accuracy of phase recovery may be affected. A larger spot might introduce more noise and interference, compromising the precision of phase recovery and subsequently degrading the optical field quality.

Figure 4 shows the intensity distribution and mode purity of the generated HG30 mode and HG50 mode at the target plane under different beam waist radius at the plane of the SLM2. As can be seen from Figure 4, when the waist radius at the plane of the SLM2 is 0.8 mm, the generated HG30 mode and HG50 mode have the highest mode purity, which is consistent with the theoretical simulation results. The experimental system parameters used in Figure 4 are as follows: the incident fundamental mode is a nearly collimated beam of 2.5 mm with a wavelength of 1080 nm, the beam size of the generated HG30 mode is approximately 1.2 mm, the beam size of the generated HG50 mode is approximately 1.6 mm, and the diffraction efficiency of the SLM is 95%.

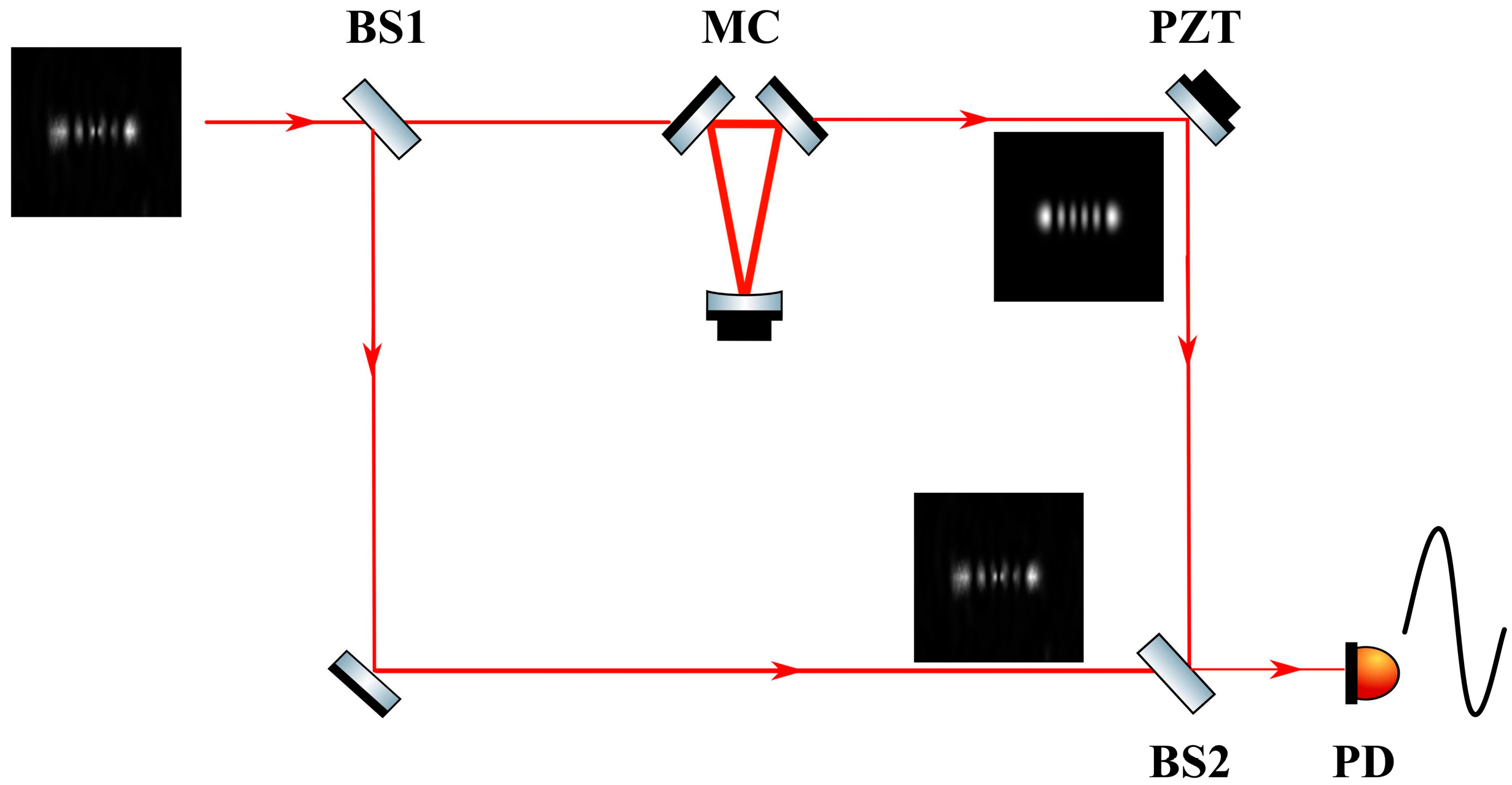
Experimentally, the mode purity of the generated higher-order HG mode is obtained by measuring the degree of interference between the generated mode and the standard mode. Figure 5 shows the mode purity measurement device. The generated higher-order HG mode is incident on the mode purity measurement device and split into two paths by a beam splitter (BS1). One of the paths passes through a high-finesse mode cleaner (MC) to generate a standard higher-order HG mode; then, it interferes with the other path at BS2. By scanning the phase between the standard HG mode and the generated HG mode using the piezoelectric transducer (PZT) and measuring the degree of interference with a photoelectric detector (PD), the mode purity of the generated higher-order HG mode is obtained. The MC adopts a three-mirror ring cavity structure consisting of two flat mirrors and one concave mirror (radius of curvature is 100 cm). The cavity length of the MC is 50 cm, with a free spectral range of 600 MHz. The measured cavity finesse is about 1000, and the cavity bandwidth is approximately 600 kHz.

In addition, there is a deviation between the mode purity of the generated higher-order HG mode and the simulation results, and the deviation increases with the increase in the order of the generated mode. The main reasons for this are as follows: (1) There is a crosstalk effect between pixels on the SLM [27,28]. When the phase difference between adjacent pixels that are loaded is large, the corresponding driving voltages will affect each other, resulting in a deviation between the actual loaded hologram and the theoretically loaded hologram. As evident from Figure 2, the hologram for the HG50 mode exhibits greater complexity compared to that of the HG30 mode, with more dramatic phase changes between adjacent pixels and a more pronounced pixel crosstalk effect. (2) Losses in the high-frequency optical field lead to phase deviations. With the increment in mode order, there is a corresponding rise in the percentage of high-frequency elements present within the beam, and the limited optical aperture in the optical path reduces the generation efficiency of the mode, causing phase distortion during beam propagation and reducing the purity of the generated mode. (3) The SLM used in the experiment is not a perfect device, and its diffraction efficiency is not 100%, resulting in a small portion of the unmodulated optical field entering the final measurement system and reducing the purity of the generated mode [29]. In the future, the quality of the generated HG mode can be further improved by optimizing the aforementioned factors.

4. Conclusions

We have analyzed the effects of misalignment of the hologram loaded on the SLM2 and the spot size of incident light on the SLM2 plane on the generated higher-order HG mode. The results indicate that the optical field at the SLM2 plane and the hologram loaded onto it need to achieve micrometer-level alignment. Based on experimental parameters, the optimal spot size of the incident light at the SLM2 plane is selected, thereby significantly improving the quality of the generated higher-order HG mode.

By integrating cascaded spatial light modulators with quantum states, we can generate higher-order HG mode quantum states, conferring remarkable spatial dimensional advantages to quantum states. This integration plays a significant role in quantum precision measurement and high-dimensional quantum communication. For instance, utilizing a higher-order HG mode squeezed state enables spatial displacement and tilt measurements beyond the standard quantum limit [3]. Additionally, the higher-order HG mode quantum state can increase the channel capacity and enhance the transmission efficiency in quantum communication [30]. Furthermore, the utilization of higher-order HG modes can effectively reduce the losses introduced by mode mismatches in gravitational wave detection [31].