Cost-Effective Planning of Hybrid Energy Systems Using Improved Horse Herd Optimizer and Cloud Theory under Uncertainty
Abstract
1. Introduction
2. Research Methodology
2.1. Overview of the Research Approach
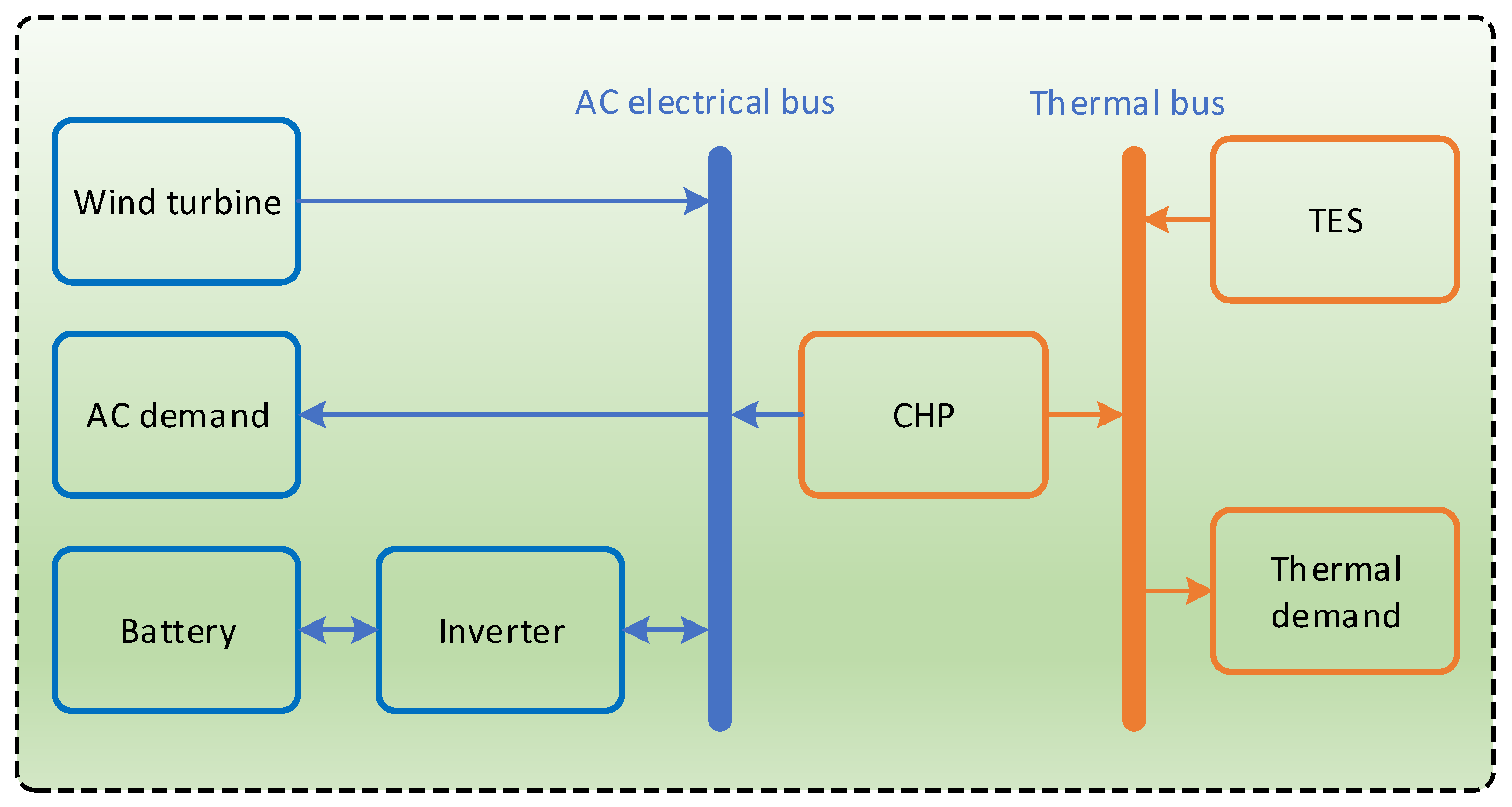
2.2. System Description
- WT: Provides renewable electricity.
- CHP: Generates both electricity and thermal energy, prioritizing thermal load due to cost-effectiveness and low emissions.
- Electric battery storage: Balances electricity supply and demand.
- TES: Manages surplus and deficit in thermal energy from CHP.
- Inverter: Utilized with the battery system to facilitate the connection of batteries to the AC bus, enabling efficient energy storage and discharge.
2.3. Component Models
2.3.1. WT Model
2.3.2. CHP Model
2.3.3. TES Model
2.3.4. Battery Model
2.3.5. Inverter Model
2.4. Problem Formulation
Objective Function
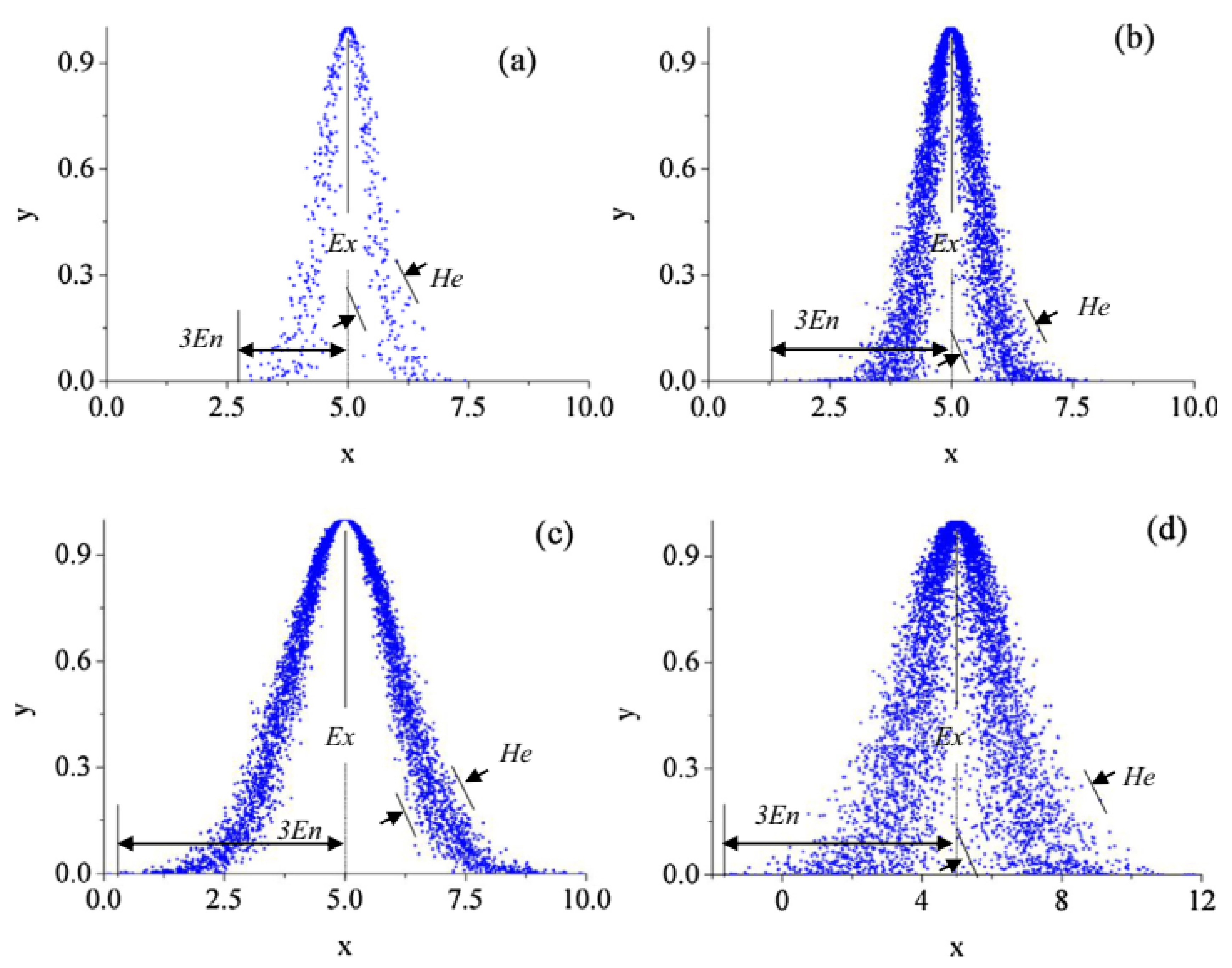
2.5. Stochastic Modeling with Cloud Theory
2.5.1. Production of the Normal CM
- Phase (1): Data input: The Ex value is obtained from forecast data and signifies the mean, while En represents the standard deviation value. The He entropy indicates the rate of spread, and N refers to the droplet count.
- Phase (2): Generate a random En value that follows a normal distribution, utilizing En and He.
- Phase (3): Produce a random xi within a distribution normally based on Ex and En.
- Phase (4): Determine the membership degree using the following equation:
- Phase (5): Calculate xi and ui for all instances in N. To convert a small quantity into a qualitative evaluation, the regression cloud model suitable for normal distribution is utilized in the following stages.
- Stage (1): Establish the mean and variance of xi as described below:
- Stage (2):
- Stage (3):
- Stage (4):
2.5.2. Weibull Distribution-Based CM
- Input data
- Produce Weibull-distributed values
- Certainty level calculation
3. Proposed Meta-Heuristic Optimizer
3.1. Overview of the HHO
| Algorithm 1: Horse Herd Optimization |
| (a) Fundamental framework: Setting up the algorithm’s parameters and variables. (b) Initial placement: Randomly dispersing horses across the search space. (c) Evaluating fitness: Assessing the fitness level of each horse based on its location. (d) Age determination: Calculating the age of each horse (α, β, γ, δ). (e) Velocity adjustment: Adjusting the velocity of each horse relative to its age. (f) Updating positions: Modifying the search space to accommodate the new positions of each horse. (g) Convergence check: Returning to step c until the algorithm terminates and the convergence criterion is met. |
3.2. Overview of the IHHO
3.3. The IHHO Implementation
- (1)
- Initialization: The algorithm starts by generating an initial population of horses within the search space in a random manner. Every horse symbolizes a potential solution to the optimization problem.
- (2)
- Fitness Evaluation: Each horse’s fitness is assessed by utilizing the objective function of the optimization problem. The candidate solutions’ quality is evident in this.
- (3)
- Herd Movement: The horses in the herd exhibit movements that mimic the natural behavior of horses. This involves horses taking the lead in guiding the herd, other horses following and aligning themselves with the herd’s direction, and some horses lagging behind to explore new regions of the search space.
- (4)
- The IHHO incorporates a technique called RDR local search to address the problem of premature convergence. This process entails rotating the coordinate axes in the direction of the initial search direction and subsequently transitioning to a new starting point to generate effective search actions.
- (5)
- Orthonormal Basis Update: Utilizing the equations provided in the overview, the orthonormal basis is updated following the RDR local search. This allows for the ongoing enhancement and optimization of the search directions.
- (6)
- Convergence check: The algorithm assesses if the termination criteria, such as a maximum number of iterations or a target fitness value, have been met. Otherwise, the process goes back to Step 3 for the next iteration.
- (7)
- Output: Upon convergence, the IHHO outputs the most optimal solution discovered, which represents the best or second-best solution to the deterministic optimization problem.
4. Results and Discussion
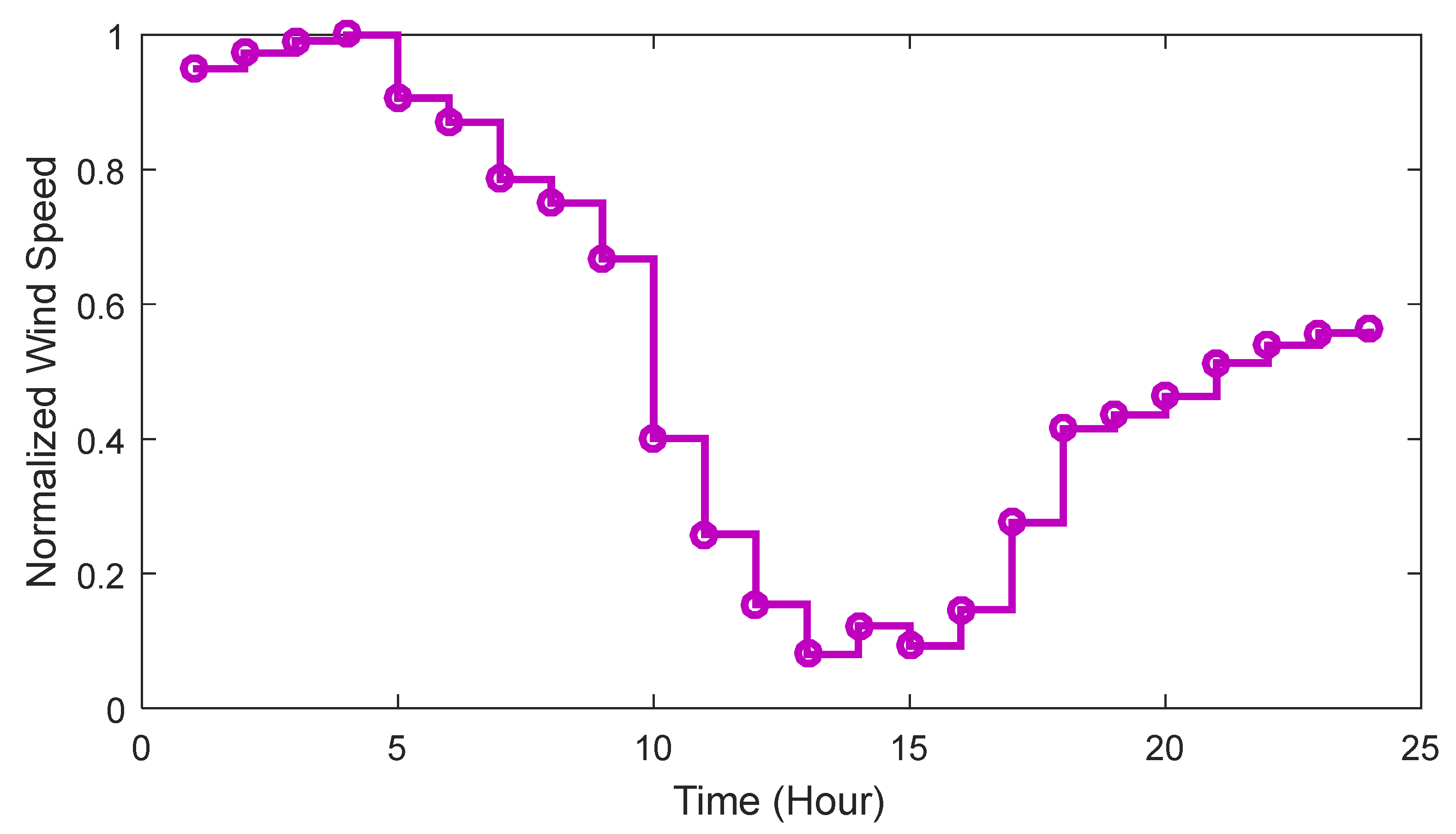
4.1. Application and Simulation Scenarios
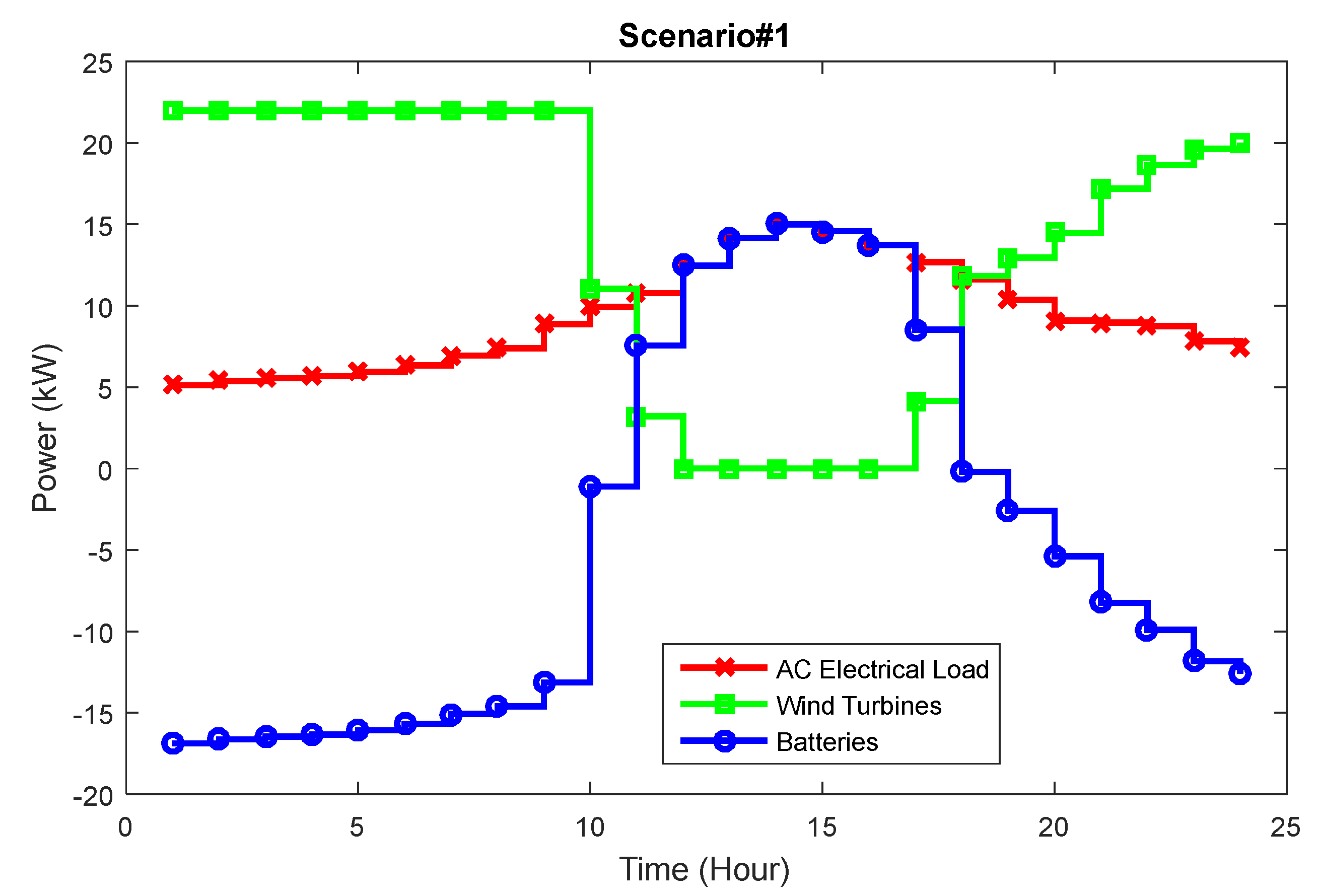
- Scenario 1: Optimization of the hybrid Wind/Battery system;
- Scenario 2: Optimization of the hybrid Wind/CHP/Battery system;
- Scenario 3: Optimization of the hybrid Wind/CHP/Battery/TES system.
4.2. Deterministic Results of Scenario 1
4.3. Deterministic Results of Scenario 2
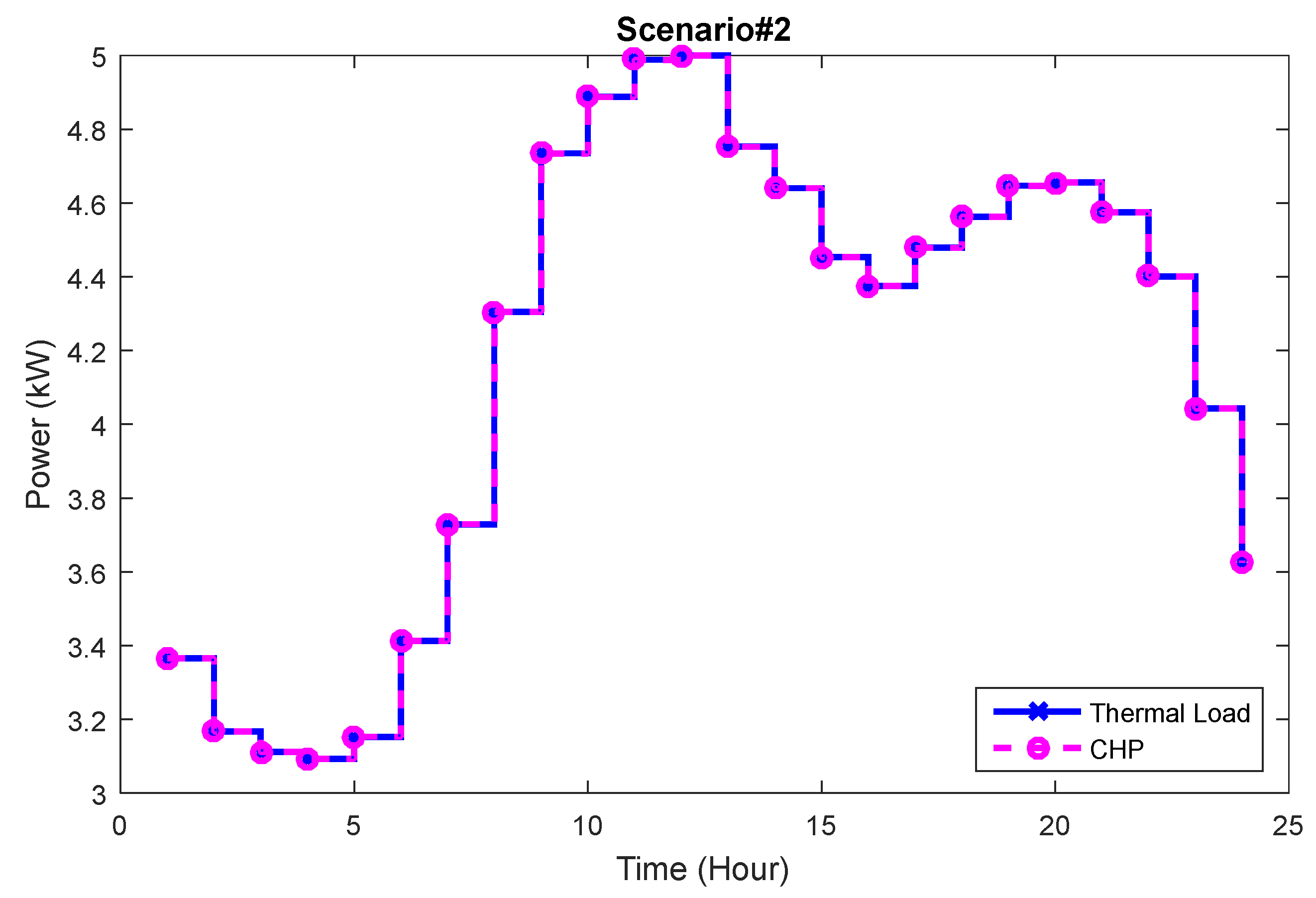
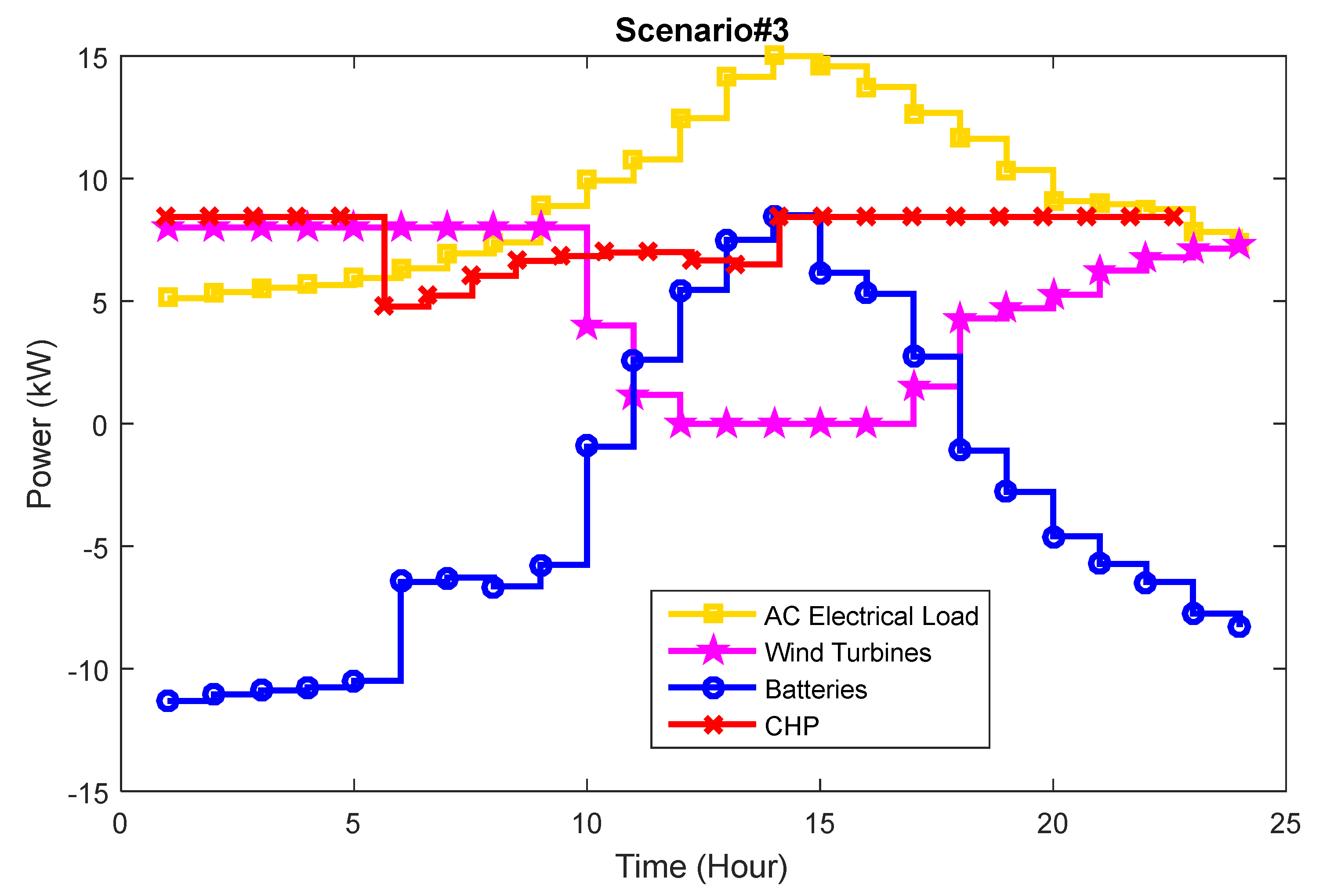
4.4. Deterministic Results of Scenario 3
4.5. Comparison of the Deterministic Results
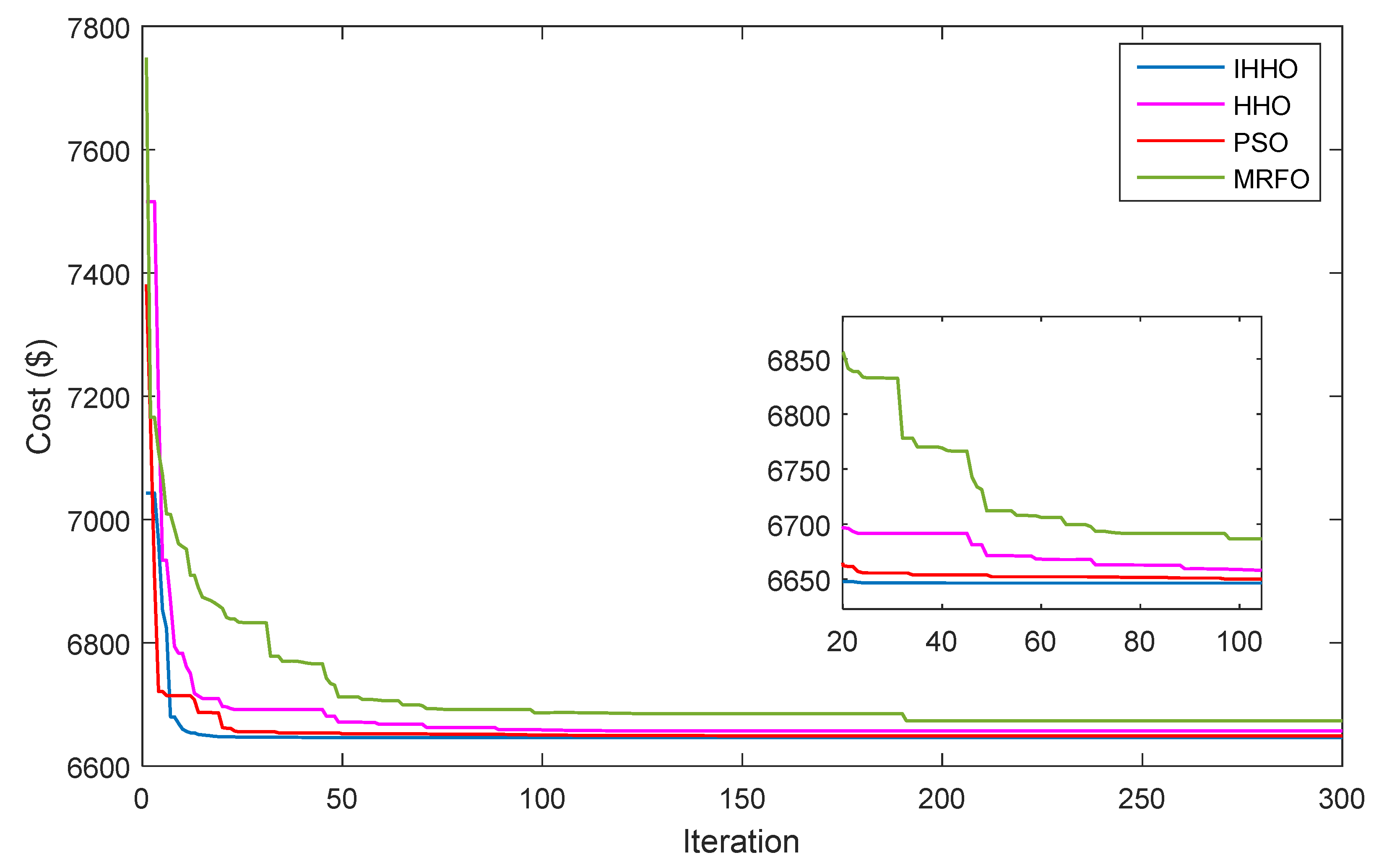
4.6. Proposed Optimizer Superiority
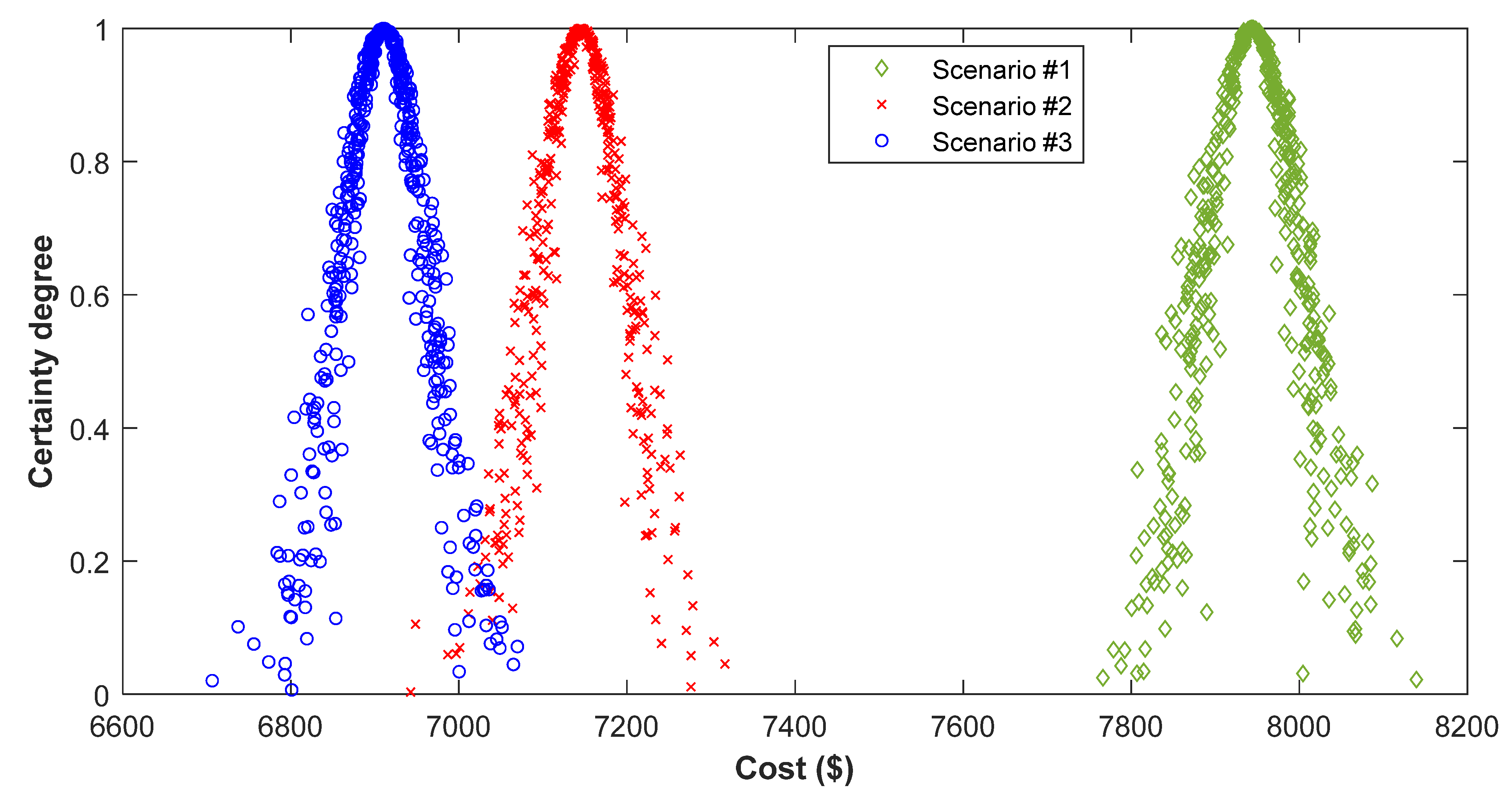
4.7. Stochastic Model Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farhat, O.; Khaled, M.; Faraj, J.; Hachem, F.; Taher, R.; Castelain, C. A Short Recent Review on Hybrid Energy Systems: Critical Analysis and Recommendations. Energy Rep. 2022, 8, 792–802. [Google Scholar] [CrossRef]
- Dong, H.; Fu, Y.; Jia, Q.; Wen, X. Optimal Dispatch of Integrated Energy Microgrid Considering Hybrid Structured Electric-Thermal Energy Storage. Renew. Energy 2022, 199, 628–639. [Google Scholar] [CrossRef]
- Benyaghoob-Sani, A.; Sedighizadeh, M.; Sedighizadeh, D.; Abbasi, R. A RA-IGDT Model for Stochastic Optimal Operation of a Microgrid Based on Energy Hub Including Cooling and Thermal Energy Storages. Int. J. Electr. Power Energy Syst. 2021, 131, 107092. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C.; Naidoo, R.; Onaolapo, K.A.; Bettayeb, M.; Olulope, P.K.; Sobowale, A.A. Design and Techno-Economic Assessment of a Standalone Photovoltaic-Diesel-Battery Hybrid Energy System for Electrification of Rural Areas: A Step towards Sustainable Development. Renew. Energy 2024, 227, 120556. [Google Scholar] [CrossRef]
- Liu, R.; Liu, M.; Xu, C.; Liu, M.; Yuan, W. Thermodynamic Study of a Novel Combined Heat and Power System Integrated with Solar Energy. Appl. Therm. Eng. 2023, 234, 121192. [Google Scholar] [CrossRef]
- Chen, M.; Lu, H.; Chang, X.; Liao, H. An Optimization on an Integrated Energy System of Combined Heat and Power, Carbon Capture System and Power to Gas by Considering Flexible Load. Energy 2023, 273, 127203. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, K.; González-Pino, I.; Song, J.; Yu, G.; Luo, E.; Markides, C.N. Techno-Economic Analysis of a Combined Heat and Power System Integrating Hybrid Photovoltaic-Thermal Collectors, a Stirling Engine and Energy Storage. Energy Convers. Manag. 2023, 284, 116968. [Google Scholar] [CrossRef]
- Pastore, L.M. Combining Power-to-Heat and Power-to-Vehicle Strategies to Provide System Flexibility in Smart Urban Energy Districts. Sustain. Cities Soc. 2023, 94, 104548. [Google Scholar] [CrossRef]
- Ren, F.; Lin, X.; Wei, Z.; Zhai, X.; Yang, J. A Novel Planning Method for Design and Dispatch of Hybrid Energy Systems. Appl. Energy 2022, 321, 119335. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, H.; Li, C.; Negnevitsky, M.; Wang, X. Stochastic Optimization of System Configurations and Operation of Hybrid Cascade Hydro-Wind-Photovoltaic with Battery for Uncertain Medium- and Long-Term Load Growth. Appl. Energy 2024, 364, 123127. [Google Scholar] [CrossRef]
- Yan, Y.; Huang, C.; Guan, J.; Zhang, Q.; Cai, Y.; Wang, W. Stochastic Optimization of Solar-Based Distributed Energy System: An Error-Based Scenario with a Day-Ahead and Real-Time Dynamic Scheduling Approach. Appl. Energy 2024, 363, 123099. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Park, J.; Adams, D.; Heo, S.; Lee, J.H. Multi-Period, Multi-Timescale Stochastic Optimization Model for Simultaneous Capacity Investment and Energy Management Decisions for Hybrid Micro-Grids with Green Hydrogen Production under Uncertainty. Renew. Sustain. Energy Rev. 2024, 190, 114049. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Guerrero, J.M. An Optimal Energy Management System for Islanded Microgrids Based on Multiperiod Artificial Bee Colony Combined With Markov Chain. IEEE Syst. J. 2017, 11, 1712–1722. [Google Scholar] [CrossRef]
- Saffari, M.; Kia, M.; Vahidinasab, V.; Mehran, K. Integrated Active/Reactive Power Scheduling of Interdependent Microgrid and EV Fleets Based on Stochastic Multi-objective Normalised Normal Constraint. IET Gener. Transm. Distrib. 2020, 14, 2055–2064. [Google Scholar] [CrossRef]
- Maleki, A.; Askarzadeh, A. Optimal Sizing of a PV/Wind/Diesel System with Battery Storage for Electrification to an off-Grid Remote Region: A Case Study of Rafsanjan, Iran. Sustain. Energy Technol. Assess. 2014, 7, 147–153. [Google Scholar] [CrossRef]
- Khavari, F.; Badri, A.; Zangeneh, A. Energy Management in Multi-Microgrids Considering Point of Common Coupling Constraint. Int. J. Electr. Power Energy Syst. 2020, 115, 105465. [Google Scholar] [CrossRef]
- Rawa, M.; Al-Turki, Y.; Sedraoui, K.; Dadfar, S.; Khaki, M. Optimal Operation and Stochastic Scheduling of Renewable Energy of a Microgrid with Optimal Sizing of Battery Energy Storage Considering Cost Reduction. J. Energy Storage 2023, 59, 106475. [Google Scholar] [CrossRef]
- Ashraf, M.A.; Liu, Z.; Alizadeh, A.; Nojavan, S.; Jermsittiparsert, K.; Zhang, D. Designing an Optimized Configuration for a Hybrid PV/Diesel/Battery Energy System Based on Metaheuristics: A Case Study on Gobi Desert. J. Clean. Prod. 2020, 270, 122467. [Google Scholar] [CrossRef]
- Bolurian, A.; Akbari, H.; Mousavi, S. Day-Ahead Optimal Scheduling of Microgrid with Considering Demand Side Management under Uncertainty. Electr. Power Syst. Res. 2022, 209, 107965. [Google Scholar] [CrossRef]
- Konneh, K.V.; Masrur, H.; Othman, M.L.; Wahab, N.I.A.; Hizam, H.; Islam, S.Z.; Crossley, P.; Senjyu, T. Optimal Design and Performance Analysis of a Hybrid Off-Grid Renewable Power System Considering Different Component Scheduling, PV Modules, and Solar Tracking Systems. IEEE Access 2021, 9, 64393–64413. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, X.; Huang, H.; Zhang, D.; Ghadimi, N. Optimal Economic Scheduling of Microgrids Considering Renewable Energy Sources Based on Energy Hub Model Using Demand Response and Improved Water Wave Optimization Algorithm. J. Energy Storage 2022, 55, 105311. [Google Scholar] [CrossRef]
- Jurasz, J.; Guezgouz, M.; Campana, P.E.; Kies, A. On the Impact of Load Profile Data on the Optimization Results of Off-Grid Energy Systems. Renew. Sustain. Energy Rev. 2022, 159, 112199. [Google Scholar] [CrossRef]
- Radosavljević, J.; Jevtić, M.; Klimenta, D. Energy and Operation Management of a Microgrid Using Particle Swarm Optimization. Eng. Optim. 2015, 48, 811–830. [Google Scholar] [CrossRef]
- Amara, S.; Toumi, S.; Salah, C.B.; Saidi, A.S. Improvement of Techno-Economic Optimal Sizing of a Hybrid off-Grid Micro-Grid System. Energy 2021, 233, 121166. [Google Scholar] [CrossRef]
- Goh, H.H.; Shi, S.; Liang, X.; Zhang, D.; Dai, W.; Liu, H.; Wong, S.Y.; Kurniawan, T.A.; Goh, K.C.; Cham, C.L. Optimal Energy Scheduling of Grid-Connected Microgrids with Demand Side Response Considering Uncertainty. Appl. Energy 2022, 327, 120094. [Google Scholar] [CrossRef]
- Yang, Z.; Ghadamyari, M.; Khorramdel, H.; Alizadeh, S.M.S.; Pirouzi, S.; Milani, M.; Banihashemi, F.; Ghadimi, N. Robust Multi-Objective Optimal Design of Islanded Hybrid System with Renewable and Diesel Sources/Stationary and Mobile Energy Storage Systems. Renew. Sustain. Energy Rev. 2021, 148, 111295. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, M.; Wei, Z.; Lu, M. The Energy Management and Economic Optimization Scheduling of Microgrid Based on Colored Petri Net and Quantum-PSO Algorithm. Sustain. Energy Technol. Assess. 2022, 53, 102670. [Google Scholar] [CrossRef]
- Chennaif, M.; Maaouane, M.; Zahboune, H.; Elhafyani, M.; Zouggar, S. Tri-Objective Techno-Economic Sizing Optimization of Off-Grid and On-Grid Renewable Energy Systems Using Electric System Cascade Extended Analysis and System Advisor Model. Appl. Energy 2022, 305, 117844. [Google Scholar] [CrossRef]
- Davoudkhani, I.F.; Dejamkhooy, A.; Nowdeh, S.A. A Novel Cloud-Based Framework for Optimal Design of Stand-Alone Hybrid Renewable Energy System Considering Uncertainty and Battery Aging. Appl. Energy 2023, 344, 121257. [Google Scholar] [CrossRef]
- Nowdeh, S.A.; Naderipour, A.; Davoudkhani, I.F.; Guerrero, J.M. Stochastic Optimization—Based Economic Design for a Hybrid Sustainable System of Wind Turbine, Combined Heat, and Power Generation, and Electric and Thermal Storages Considering Uncertainty: A Case Study of Espoo, Finland. Renew. Sustain. Energy Rev. 2023, 183, 113440. [Google Scholar] [CrossRef]
- Alanazi, A.; Alanazi, M.; Nowdeh, S.A.; Abdelaziz, A.Y.; El-Shahat, A. An Optimal Sizing Framework for Autonomous Photovoltaic/Hydrokinetic/Hydrogen Energy System Considering Cost, Reliability and Forced Outage Rate Using Horse Herd Optimization. Energy Rep. 2022, 8, 7154–7175. [Google Scholar] [CrossRef]
- Yue, X.; Pye, S.; DeCarolis, J.; Li, F.G.N.; Rogan, F.; Gallachóir, B.Ó. A Review of Approaches to Uncertainty Assessment in Energy System Optimization Models. Energy Strategy Rev. 2018, 21, 204–217. [Google Scholar] [CrossRef]
- Singh, V.; Moger, T.; Jena, D. Uncertainty Handling Techniques in Power Systems: A Critical Review. Electr. Power Syst. Res. 2022, 203, 107633. [Google Scholar] [CrossRef]
- Saini, V.K.; Al-Sumaiti, A.S.; Kumar, R. Data Driven Net Load Uncertainty Quantification for Cloud Energy Storage Management in Residential Microgrid. Electr. Power Syst. Res. 2024, 226, 109920. [Google Scholar] [CrossRef]
- Li, Z.; Simancas, N.S.N.; Vianna, S.S.V.; Zhang, B. A Mathematical Model for Hydrogen Dispersion Cloud Based on Dimensional Analysis and Computational Fluid Dynamics (CFD). Int. J. Hydrog. Energy 2024, 60, 229–240. [Google Scholar] [CrossRef]
- MiarNaeimi, F.; Azizyan, G.; Rashki, M. Horse Herd Optimization Algorithm: A Nature-Inspired Algorithm for High-Dimensional Optimization Problems. Knowl.-Based Syst. 2021, 213, 106711. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Zitar, R.A. Orthogonal Learning Rosenbrock’s Direct Rotation with the Gazelle Optimization Algorithm for Global Optimization. Mathematics 2022, 10, 4509. [Google Scholar] [CrossRef]
- Hemmati, M.; Mirzaei, M.A.; Abapour, M.; Zare, K.; Mohammadi-Ivatloo, B.; Mehrjerdi, H.; Marzband, M. Economic-Environmental Analysis of Combined Heat and Power-Based Reconfigurable Microgrid Integrated with Multiple Energy Storage and Demand Response Program. Sustain. Cities Soc. 2021, 69, 102790. [Google Scholar] [CrossRef]
- Liu, B. Optimal Scheduling of Combined Cooling, Heating, and Power System-Based Microgrid Coupled with Carbon Capture Storage System. J. Energy Storage 2023, 61, 106746. [Google Scholar] [CrossRef]
- Zhou, Y.; Min, C.; Wang, K.; Xie, L.; Fan, Y. Optimization of Integrated Energy Systems Considering Seasonal Thermal Energy Storage. J. Energy Storage 2023, 71, 108094. [Google Scholar] [CrossRef]
- Homayoun, R.; Bahmani-Firouzi, B.; Niknam, T. Multi-objective Operation of Distributed Generations and Thermal Blocks in Microgrids Based on Energy Management System. IET Gener. Transm. Distrib. 2021, 15, 1451–1462. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, Z.; Wang, L. Manta Ray Foraging Optimization: An Effective Bio-Inspired Optimizer for Engineering Applications. Eng. Appl. Artif. Intell. 2020, 87, 103300. [Google Scholar] [CrossRef]






| Resource | Parameter | Value |
|---|---|---|
| WT | pr (kW) | 1 |
| vci (m/s) | 3 | |
| vr (m/s) | 9 | |
| vco (m/s) | 20 | |
| Peak wind speed (m/s) | 15 | |
| 35 | ||
| αWT (USD) | 3200 | |
| (USD/year) | 5 | |
| Life span (year) | 20 | |
| CHP | ηT (%) | 38 |
| ηL (%) | 5 | |
| ηH (%) | 38 | |
| epc (USD/kg) | 0.0037 | |
| fpc (USD/l) | 1.24 | |
| χc (l/kWh) | 0.246 | |
| γc (l/kWh) | 0.0845 | |
| βc (kg/kW) | 3.25 | |
| (kW) | 11 | |
| αC (USD/kW) | 901.65 | |
| (USD/kW/year) | 4 | |
| Life span (year) | 20 | |
| κ (%) | 10 | |
| CF (%) | 70 | |
| Battery | (kWh) | 1.35 |
| (kWh) | 0.15 | |
| (%) | 90 | |
| 0.0002 | ||
| 90 | ||
| αB (USD) | 130 | |
| (USD/year) | 0 | |
| Life span (year) | 5 | |
| Inverter | (kW) | 3 |
| ηI (%) | 95 | |
| αI (USD) | 2000 | |
| (USD/year) | 0 | |
| Life span (year) | 10 | |
| TES | (kWh) | 1.5 |
| (kWh) | 0.15 | |
| (%) | 78 | |
| 0.0002 | ||
| 10 | ||
| αT (USD) | 210 | |
| (USD/year) | 1.6 | |
| Life span (year) | 10 |
| Device | Wind Turbine | Battery | Inverter | Cost (USD/Year) |
|---|---|---|---|---|
| Number/Value | 22 | 108 | 6 | 7638 |
| AIC (USD/year) | AMC (USD/year) | ||||||||||
| Wind turbine | Battery | Inverter | TES | CHP | AIC | WT | Battery | Inverter | TES | CHP | AMC |
| 3520 | 2808 | 1200 | - | - | 7528 | 110 | 0 | 0 | - | - | 110 |
| AOC (USD/year) | AEC (USD/year) | ||||||||||
| Wind turbine | Battery | Inverter | TES | CHP | AOC | WT | Battery | Inverter | TES | CHP | AEC |
| Without cost | - | 0 | Without cost | - | 0 | ||||||
| Device | Wind Turbine | Battery | Inverter | CHP Capacity (kW) | Cost (USD/Year) |
|---|---|---|---|---|---|
| Number/Value | 9 | 65 | 3 | 8.77 | 6856.59 |
| AIC (USD/year) | AMC (USD/year) | ||||||||||
| Wind turbine | Battery | Inverter | TES | CHP | AIC | WT | Battery | Inverter | TES | CHP | AMC |
| 1440 | 1690 | 600 | - | 395.39 | 4125.39 | 45 | 0 | 0 | - | 35.08 | 80.08 |
| AOC (USD/year) | AEC (USD/year) | ||||||||||
| Wind turbine | Battery | Inverter | TES | CHP | AOC | WT | Battery | Inverter | TES | CHP | AEC |
| Without cost | 2111.28 | 2111.28 | Without cost | 539.84 | 539.84 | ||||||
| Device | Wind Turbine | Battery | Inverter | CHP Capacity (kW) | TES | Cost (USD/Year) |
|---|---|---|---|---|---|---|
| Number/Value | 8 | 62 | 4 | 8.42 | 5 | 6777.61 |
| AIC (USD/year) | AMC (USD/year) | ||||||||||
| Wind Turbine | Battery | Inverter | TES | CHP | AIC | WT | Battery | Inverter | TES | CHP | AMC |
| 1280 | 1612 | 800 | 105 | 379.61 | 4176.61 | 40 | 0 | 0 | 8 | 33.68 | 81.68 |
| AOC (USD/year) | AEC (USD/year) | ||||||||||
| Wind Turbine | Battery | Inverter | TES | CHP | AOC | WT | Battery | Inverter | TES | CHP | AEC |
| Without cost | 2008.87 | 2008.87 | Without cost | 510.45 | 510.45 | ||||||
| Scenario/Item | Cost (USD/Year) |
|---|---|
| Scenario 1 | 7638.00 |
| Scenario 2 | 6856.59 |
| Scenario 3 | 6646.61 |
| Scenario | Best Cost (USD) | Mean Cost (USD) | Worst Cost (USD) | Std (USD) | CT (s) |
|---|---|---|---|---|---|
| IHHO | 6646.61 | 6664.03 | 6675.11 | 146.32 | 115 |
| HHO | 6655.04 | 6676.04 | 6690.04 | 309.33 | 144 |
| PSO | 6652.32 | 6672.61 | 6684.36 | 247.59 | 138 |
| MRFO | 6673.27 | 6688.54 | 6705.02 | 366.15 | 149 |
| CM Parameter | Demand |
|---|---|
| Ex | Base State |
| En | 10% Ex |
| He | 10% En |
| β | 5 |
| γ | 20 |
| Scenario 1 | Scenario 2 | Scenario 3 | |
|---|---|---|---|
| Ex | 7944 | 7145.15 | 6910.48 |
| En | 64.11 | 57.67 | 55.77 |
| He | 12.6 | 11.33 | 10.96 |
| Scenario/Item | Cost (USD/Year) | The Cost Increase Percentage Due to Uncertainties (%) | |
|---|---|---|---|
| Deterministic | Stochastic | ||
| Scenario 1 | 7638.00 | 7944.00 | 4.00 |
| Scenario 2 | 6856.59 | 7145.15 | 4.20 |
| Scenario 3 | 6646.61 | 6910.48 | 3.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghamdi, A.S. Cost-Effective Planning of Hybrid Energy Systems Using Improved Horse Herd Optimizer and Cloud Theory under Uncertainty. Electronics 2024, 13, 2471. https://doi.org/10.3390/electronics13132471
Alghamdi AS. Cost-Effective Planning of Hybrid Energy Systems Using Improved Horse Herd Optimizer and Cloud Theory under Uncertainty. Electronics. 2024; 13(13):2471. https://doi.org/10.3390/electronics13132471
Chicago/Turabian StyleAlghamdi, Ali S. 2024. "Cost-Effective Planning of Hybrid Energy Systems Using Improved Horse Herd Optimizer and Cloud Theory under Uncertainty" Electronics 13, no. 13: 2471. https://doi.org/10.3390/electronics13132471
APA StyleAlghamdi, A. S. (2024). Cost-Effective Planning of Hybrid Energy Systems Using Improved Horse Herd Optimizer and Cloud Theory under Uncertainty. Electronics, 13(13), 2471. https://doi.org/10.3390/electronics13132471






