Development of an On-Shaft Vibration Sensing Module for Machine Wearable Rotor Imbalance Monitoring
Abstract
:1. Introduction
2. Related Studies of Vibration-Based Imbalance Detection
2.1. Vibration-Based Condition Monitoring
2.2. MEMS Sensor-Based On-Shaft Acceleration Sensing
2.3. Integration of Novel Sensing and Computing Techniques
2.4. The Scope of This Investigation
3. Theoretical Analysis of Rotor Imbalance
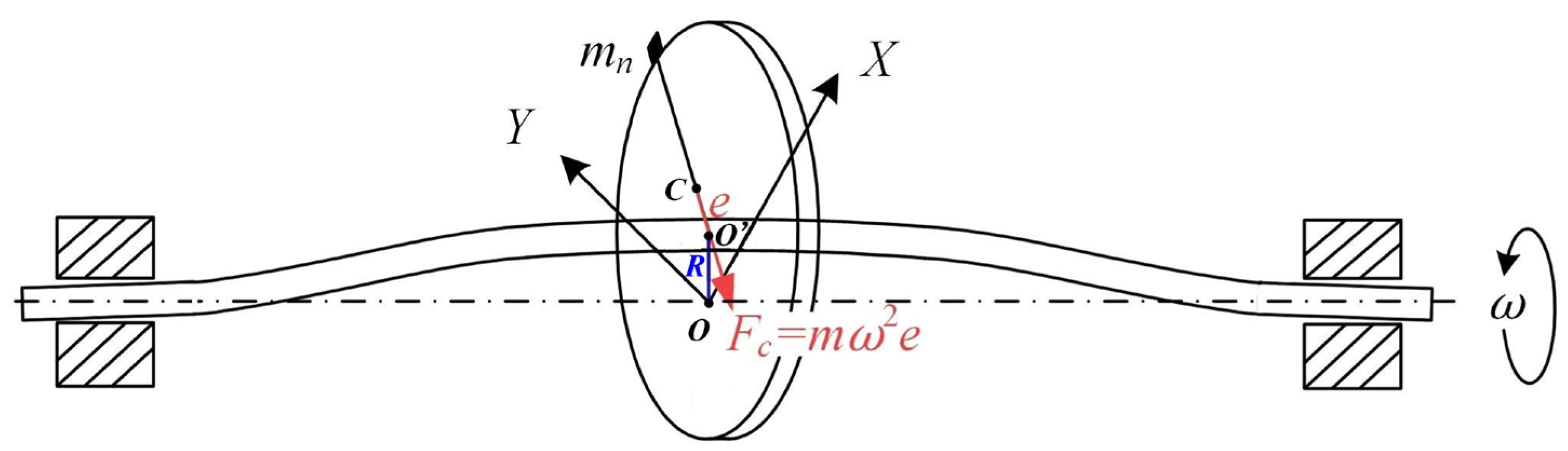
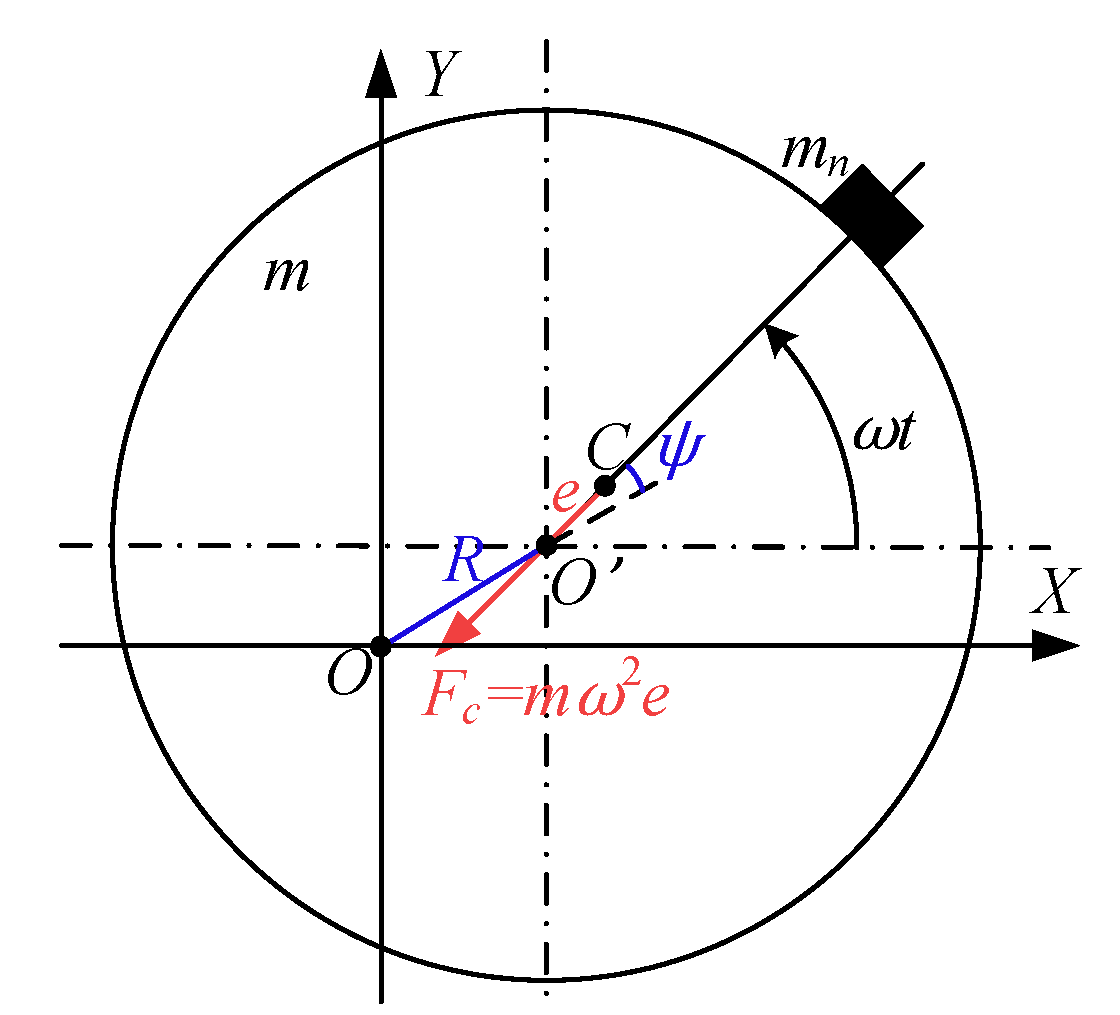
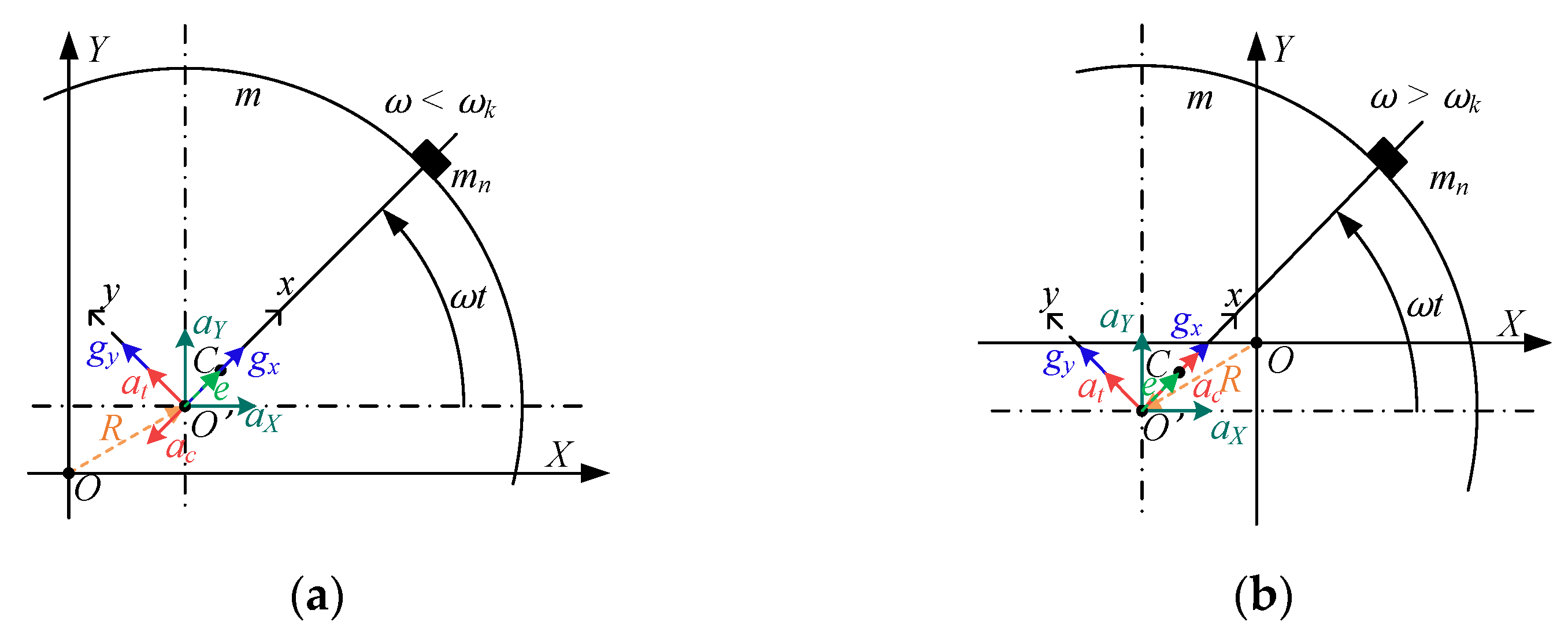
3.1. The Mechanism of Rotor Imbalance
3.2. Vibration Sensing with Shaft-End Mounted Accelerometer
4. Design and Implementation of a Machine Wearable Sensor Module
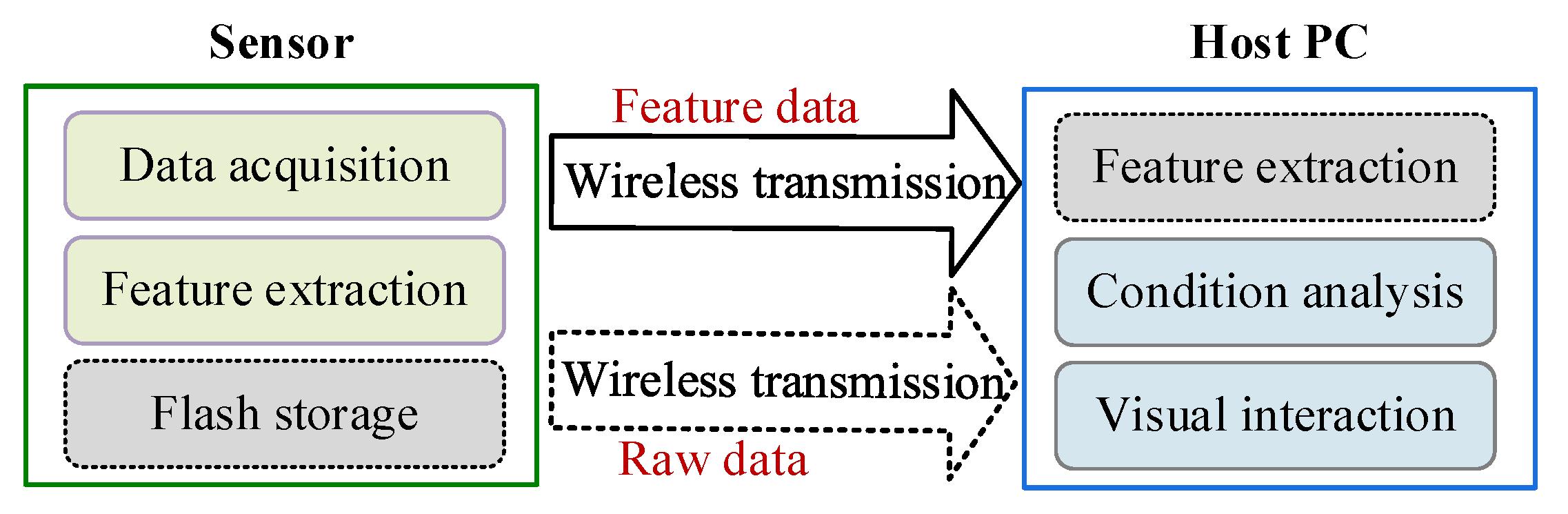
4.1. System Design of the OSVM Sensor System
4.2. WPT Design for a Battery-Less Power Supply
4.2.1. Circuits Design for Wireless Power Transfer
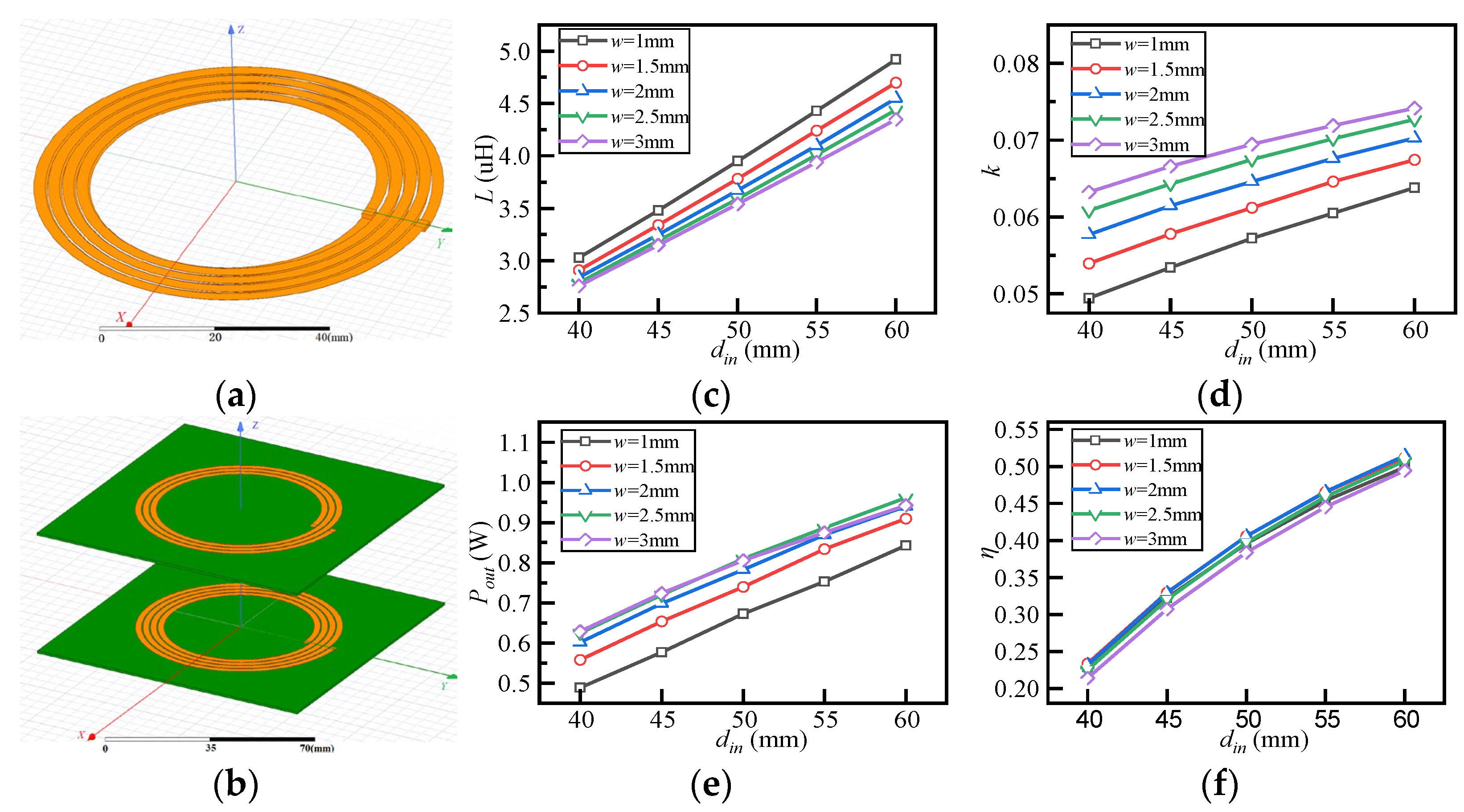
4.2.2. Design of Transmitting and Receiving Coils
4.3. The Data Computing for On-Shaft Vibration Sensing
4.3.1. The Computing Paradigm of the On-Shaft Vibration Sensor
4.3.2. Time and Frequency Domain Data Processing
4.3.3. In-Sensor Computing for Feature Extraction
5. Tests and Evaluations
5.1. Experimental Setup
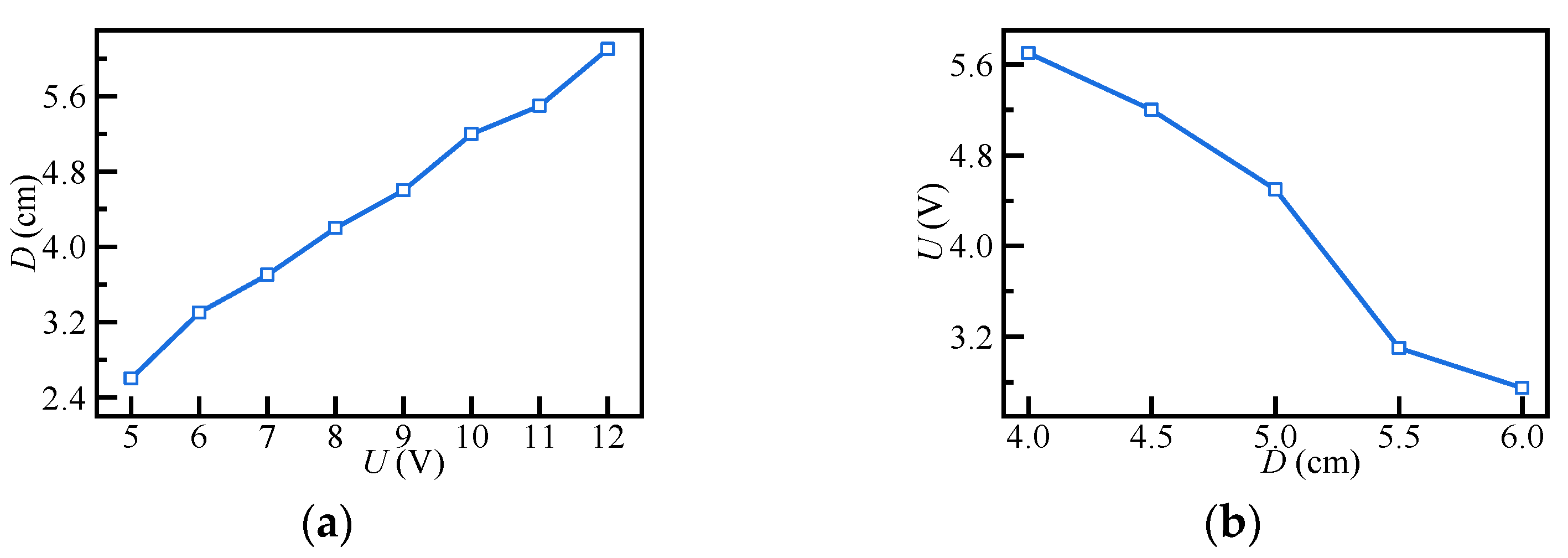
5.2. WPT Performance Evaluation
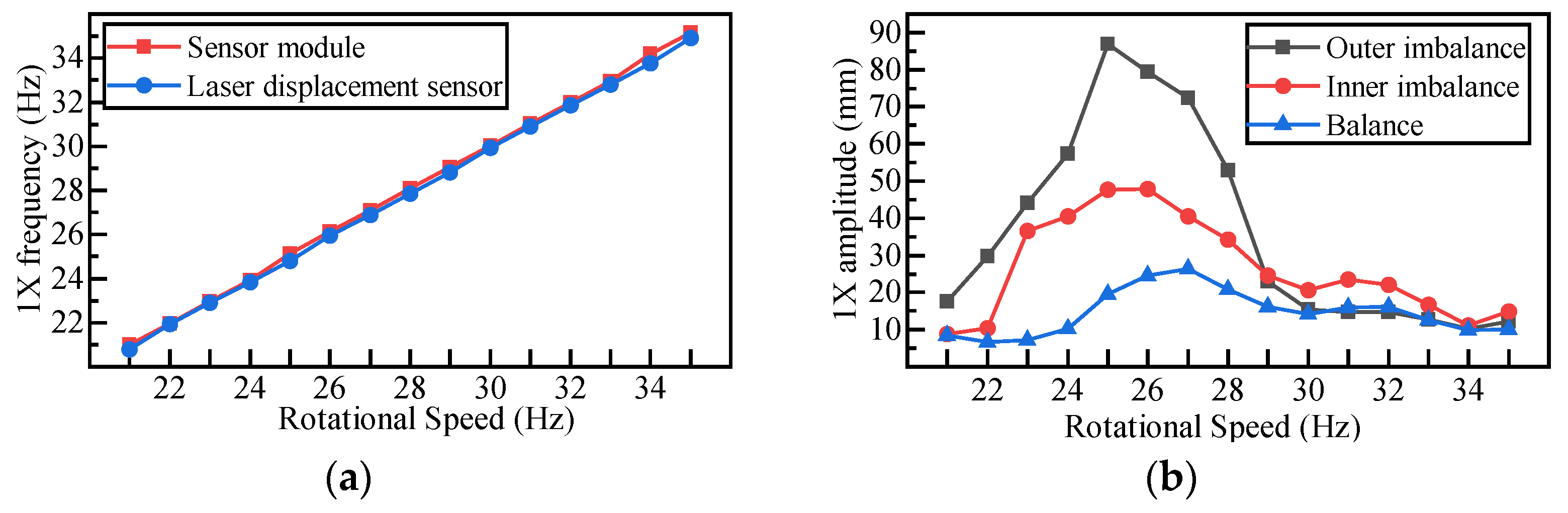
5.3. Effectiveness of the Acceleration Sensing
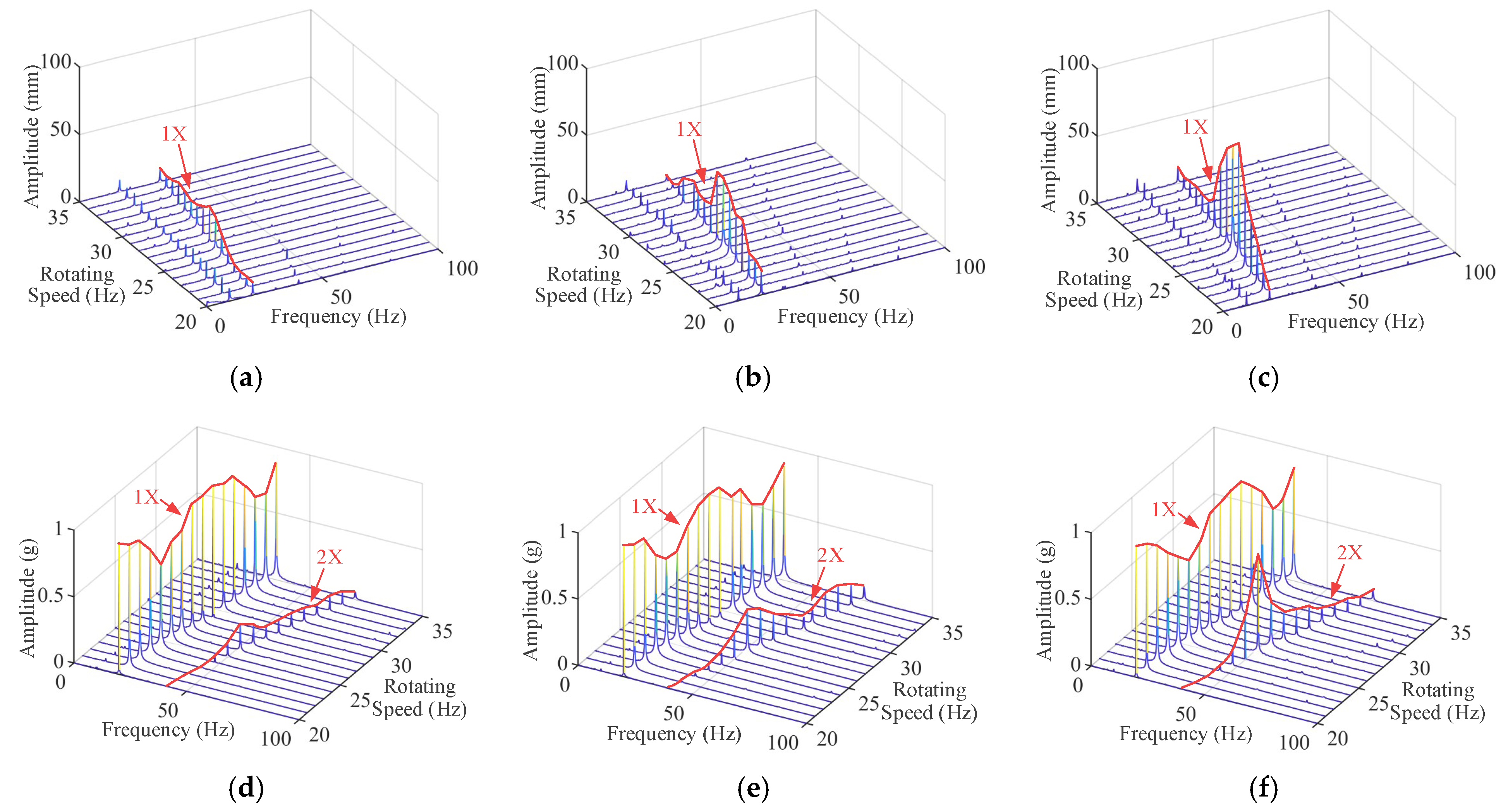
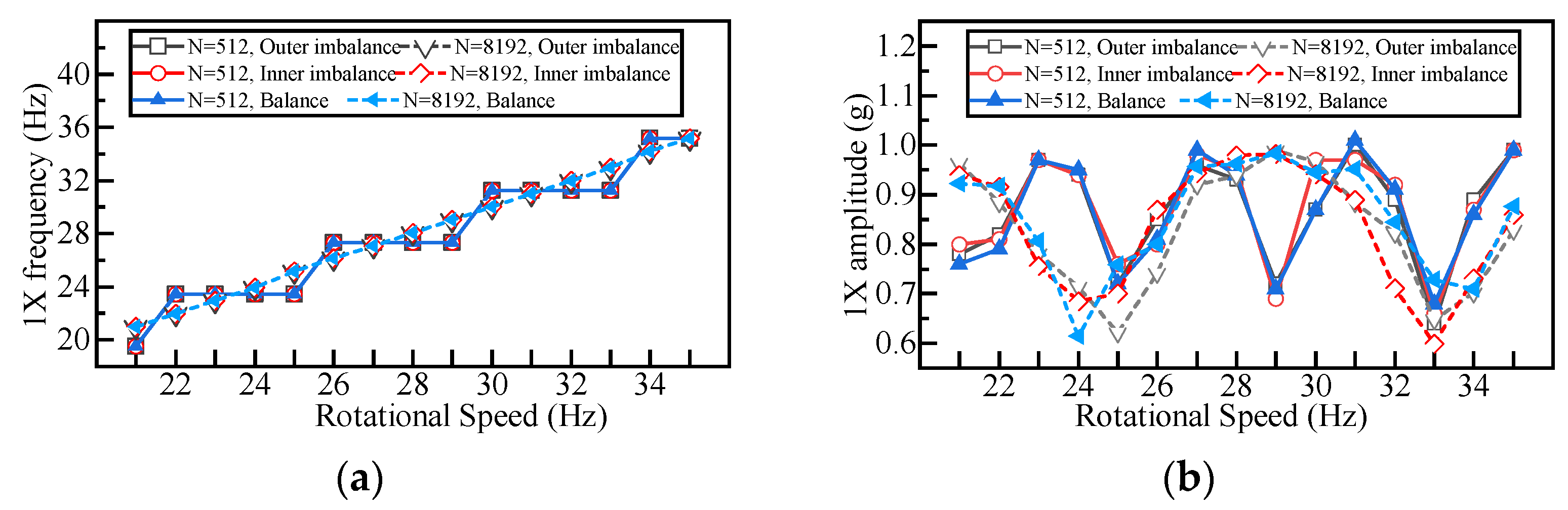
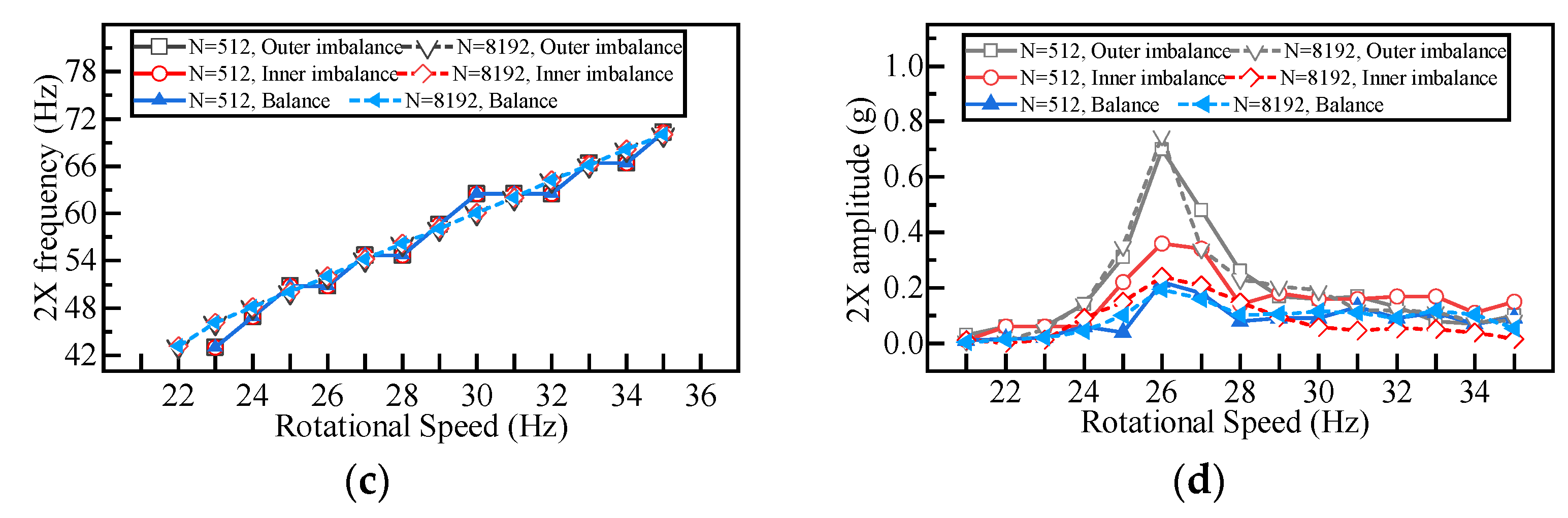
5.4. Verification of Imbalance Analysis
5.5. Verification of In-Sensor Processing
5.5.1. Frequency Domain Feature Extraction
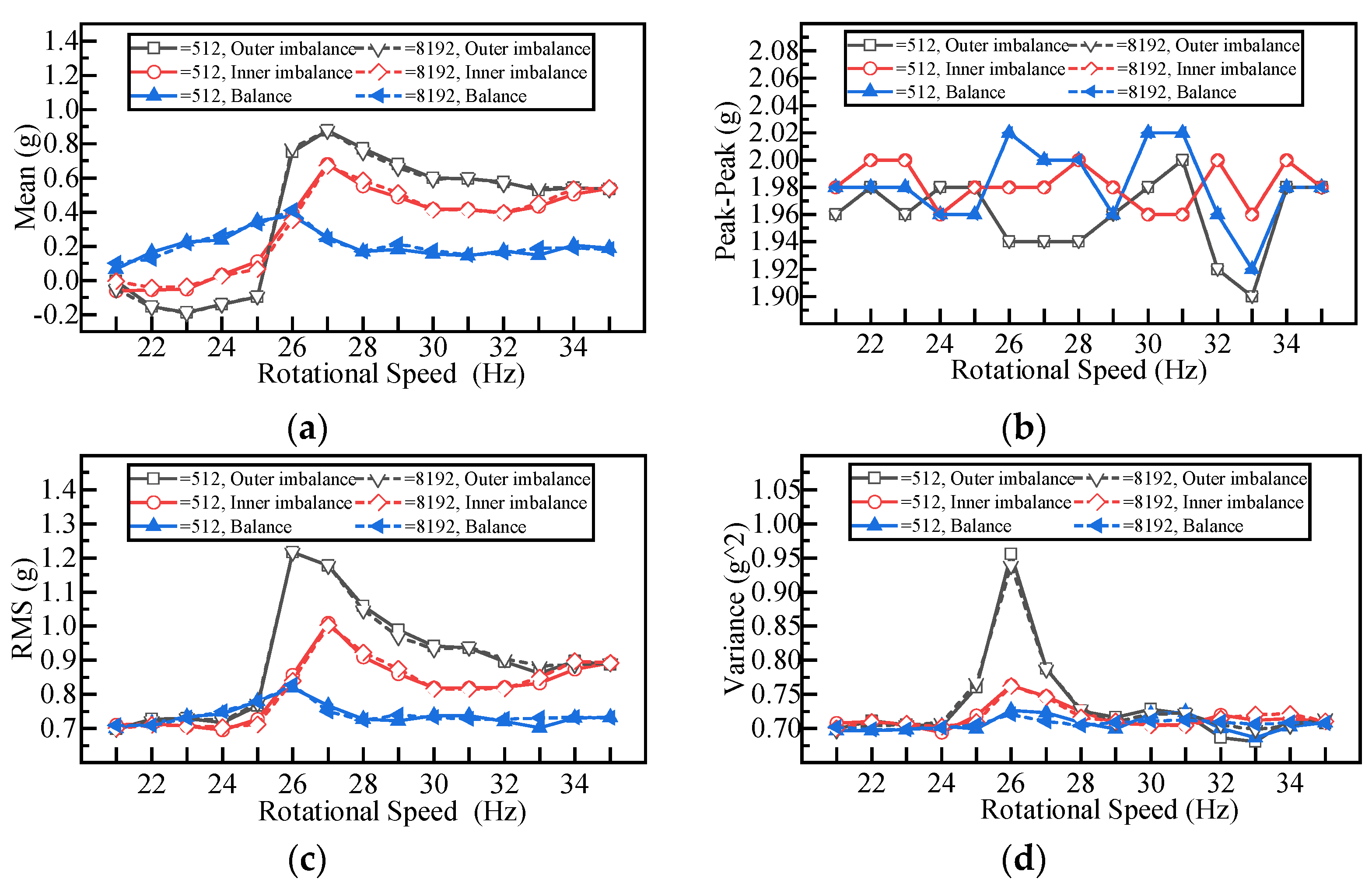
5.5.2. Time Domain Feature Extraction
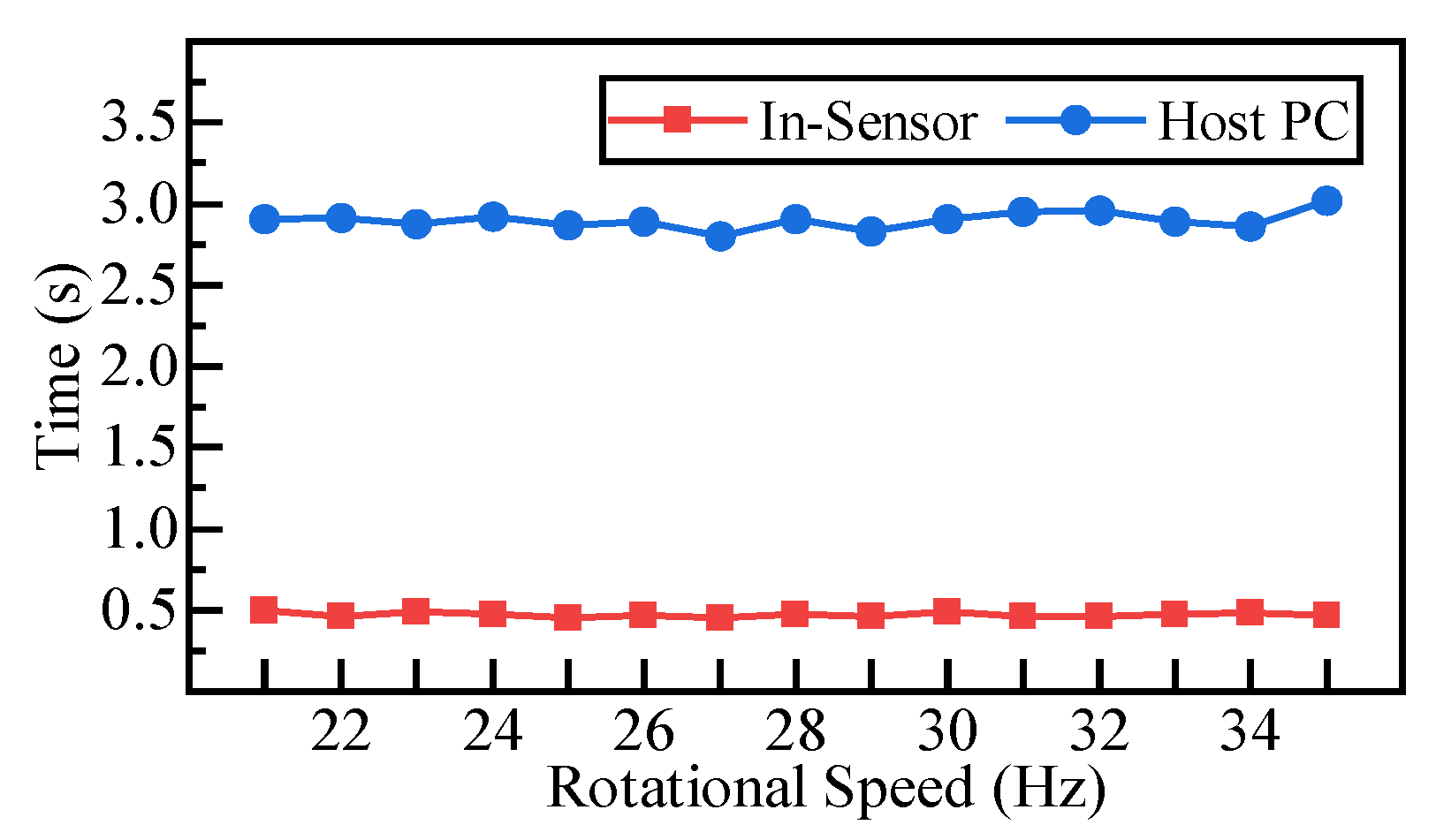
5.5.3. Feasibility and Performance of In-Sensor Processing
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reda, K.; Yan, Y. Vibration measurement of an unbalanced metallic shaft using electrostatic sensors. IEEE Trans. Instrum. Meas. 2019, 68, 1467–1476. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, Z.; Zuo, M.; Zhou, Z.; Zhang, J. A three-dimensional vibration data compression method for rolling bearing condition monitoring. IEEE Trans. Instrum. Meas. 2023, 72, 3506010. [Google Scholar] [CrossRef]
- Cui, M.; Wang, Y.; Lin, X.; Zhong, M. Fault diagnosis of rolling bearings based on an improved stack autoencoder and support vector machine. IEEE Sens. J. 2021, 21, 4927–4937. [Google Scholar] [CrossRef]
- Pozzato, G.; Strada, S.C.; Tanelli, M.; Savaresi, S.M.; Dambach, G. MEMS-enabled retrofitting of automobile wheel balancer for automatic unbalance detection. IEEE/ASME Trans. Mechatron. 2021, 26, 830–840. [Google Scholar] [CrossRef]
- Tiboni, M.; Remino, C.; Bussola, R.; Amici, C. A review on vibration-based condition monitoring of rotating machinery. Appl. Sci. 2022, 12, 972. [Google Scholar] [CrossRef]
- Maruthi, G.S.; Hegde, V. Application of MEMS accelerometer for detection and diagnosis of multiple faults in the roller element bearings of three phase induction motor. IEEE Sens. J. 2016, 16, 145–152. [Google Scholar] [CrossRef]
- Li, T.; Shi, C.; Tan, Y.; Zhou, Z. Fiber Bragg Grating sensing-based online torque detection on coupled bending and torsional vibration of rotating shaft. IEEE Sens. J. 2017, 17, 1999–2007. [Google Scholar] [CrossRef]
- Manikandan, K.G.; Pannirselvam, K.; Kenned, J.J.; Kumar, C.S. Investigations on suitability of MEMS based accelerometer for vibration measurements. Mater. Today Proc. 2021, 5, 6183–6192. [Google Scholar] [CrossRef]
- Zhou, F.; Chai, Y. Near-sensor and in-sensor computing. Nat. Electron. 2020, 3, 664–671. [Google Scholar] [CrossRef]
- Tarabini, M.; Scaccabarozzi, D. Uncertainty-based combination of signal processing techniques for the identification of rotor imbalance. Measurement 2018, 114, 409–416. [Google Scholar] [CrossRef]
- Yamamoto, G.K.; Costa, C.; Silva Sousa, J.S. A smart experimental setup for vibration measurement and imbalance fault detection in rotating machinery. Case Stud. Mech. Syst. Signal Process. 2016, 4, 8–18. [Google Scholar] [CrossRef]
- Ambur, R.; Rinderknecht, S. Self-sensing techniques of piezoelectric actuators in detecting unbalance faults in a rotating machine. Procedia Eng. 2016, 144, 833–840. [Google Scholar] [CrossRef]
- Koene, I.; Viitala, R.; Kuosmanen, P. Internet of Things Based Monitoring of Large Rotor Vibration with a Microelectromechanical Systems Accelerometer. IEEE Access 2019, 7, 92210. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, H.; Li, X.; Xiao, S.; Gu, F.; Shi, Z. Effects of wear on lubrication performance and vibration signatures of rotor system supported by hydrodynamic bearings. Lubricants 2023, 11, 107. [Google Scholar] [CrossRef]
- Li, T.L.; Tan, Y.G.; Wei, L.; Zhou, Z.D.; Zheng, K. A non-contact Fiber Bragg Grating vibration sensor. Rev. Sci. Instrum. 2014, 85, 015002. [Google Scholar] [PubMed]
- Li, T.; Tan, Y.; Zhou, Z.; Zheng, K. A non-contact FBG vibration sensor with double differential temperature compensation. Opt. Rev. 2015, 23, 26–32. [Google Scholar] [CrossRef]
- Roy, D.; Sinharay, A.; Bhowmick, B.; Rakshit, R.; Chakravarty, T.; Pal, A. A Novel RF-assisted-strobe system for unobtrusive vibration detection of machine parts. IEEE Sens. J. 2020, 20, 10924–10935. [Google Scholar] [CrossRef]
- Chai, S.; Wang, S.; Liu, C.; Liu, T.; Liu, X.; Xing, K. Using semantic segmentation network to measure vibration displacement of rotating body. IEEE Sens. J. 2023, 23, 7977–7991. [Google Scholar] [CrossRef]
- He, Q.; Wang, S.; Liu, T.; Liu, C.; Liu, X. Enhanced measurement precision for rotor vibration displacement via a progressive video super resolution network. IEEE Trans. Instrum. Meas. 2024, 73, 6005113. [Google Scholar] [CrossRef]
- Lee, J.K.; Seung, H.M.; Park, C.I.; Lee, J.K.; Lim, D.H.; Kim, Y.Y. Magnetostrictive patch sensor system for battery-less real-time measurement of torsional vibrations of rotating shafts. J. Sound Vib. 2018, 414, 248–258. [Google Scholar] [CrossRef]
- Okabe, S.; Tanaka, S. Measurement of shaft vibration using ultrasonic sensor. In Proceedings of the SICE Annual Conference, Fukui, Japan, 4–6 August 2003; pp. 1155–1158. [Google Scholar]
- Kakaley, D.E.; Altieri, R.E.; Buckner, G.D. Non-contacting measurement of torque and axial translation in high-speed rotating shafts. Mech. Syst. Signal Process. 2020, 138, 106520. [Google Scholar] [CrossRef]
- Dos Santos Pedotti, L.A.; Zago, R.M.; Giesbrecht, M.; Fruett, F. Low-cost MEMS accelerometer network for rotating machine vibration diagnostics. IEEE Instrum. Meas. Mag. 2020, 23, 25–33. [Google Scholar] [CrossRef]
- Arebi, L.; Gu, F.; Ball, A. A comparative study of misalignment detection using a novel wireless sensor with conventional wired sensors. J. Phys. Conf. Ser. 2012, 364, 012049. [Google Scholar] [CrossRef]
- Feng, G.; Hu, N.; Mones, Z.; Gu, F.; Ball, A.D. An investigation of the orthogonal outputs from an on-rotor MEMS accelerometer for reciprocating compressor condition monitoring. Mech. Syst. Signal Process. 2016, 76–77, 228–241. [Google Scholar] [CrossRef]
- Jiménez, S.; Cole, M.O.T.; Keogh, P.S. Vibration sensing in smart machine rotors using internal MEMS accelerometers. J. Sound Vib. 2016, 377, 58–75. [Google Scholar] [CrossRef]
- Koene, I.; Haikonen, S.; Tiainen, T.; Keski-Rahkonen, J.; Manngard, M.; Viitala, R. On-shaft wireless vibration measurement unit and signal processing method for torsional and lateral vibration. IEEE/ASME Trans. Mechatron. 2022, 27, 5857–5868. [Google Scholar]
- Li, C.; Li, B.; Gu, L.; Feng, G.; Gu, F.; Ball, A.D. Online monitoring of a shaft tuning process based on vibration signals from on-rotor sensor. In Proceedings of the 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing (WCMEIM), Shanghai, China, 4–6 December 2020. [Google Scholar]
- Okhionkpamwonyi, S.; Otuyemi, F.; Shi, D.; Gu, F.; Ball, A.D. Experimental investigation of vibration signals from an on-rotor sensing for diesel engine crankshaft lubrication monitoring. In Proceedings of the International Conference on the Efficiency and Performance Engineering Network, Baotou, China, 18–21 August 2022. [Google Scholar]
- Vitolo, P.; De Vita, A.; Benedetto, L.D.; Pau, D.; Licciardo, G.D. Low-power detection and classification for in-sensor predictive maintenance based on vibration monitoring. IEEE Sens. J. 2022, 22, 6942–6951. [Google Scholar] [CrossRef]
- Moin, A.; Zhou, A.; Rahimi, A.; Menon, A.; Benatti, S.; Alexandrov, G.; Tamakloe, S.; Ting, J.; Yamamoto, N.; Khan, Y.; et al. A wearable biosensing system with in-sensor adaptive machine learning for hand gesture recognition. Nat. Electron. 2021, 4, 54–63. [Google Scholar] [CrossRef]
- Xia, M.; Li, T.; Xu, L.; Liu, L.; Silva, C.W. Fault diagnosis for rotating machinery using multiple sensors and conventional neural networks. IEEE/ASME Trans. Mechatron. 2018, 23, 101–110. [Google Scholar] [CrossRef]
- Chen, W.J.; Gunter, E.J. Introduction to Dynamics of Rotor-Bearing Systems; Trafford Publishing: Trafford, UK, 2007. [Google Scholar]
- Friswell, M.I.; Penny, J.E.; Garvey, S.D.; Lees, A.W. Dynamics of Rotating Machines; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Genta, G. Dynamics of Rotating Systems; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Vance, J.M.; Zeidan, F.Y.; Murphy, B.G. Machinery Vibration and Rotordynamics; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Wang, J.; Peng, Y.; Qiao, W. Current-aided order tracking of vibration signals for bearing fault diagnosis of direct-drive wind turbines. IEEE Trans. Ind. Electron. 2016, 63, 6336–6346. [Google Scholar] [CrossRef]







| Methods | Sensor Components | Pros | Cons |
|---|---|---|---|
| On-bearing housing contact sensing [10,11,12] | Piezoelectric, accelerometer | Simple structure, long service life | Impacted by bearing structure dynamics, loss of accuracy during lifetime |
| Non-contact shaft displacement sensing [13,14,15,16,17,18,19,20] | Optical, conductive, ultrasonic, laser, eddy current, electrostatic, RF Doppler, capacitive | High sensitivity, good signal quality | Needs space for sensing devices and cabling, impact by ambient environment, costly |
| On-shaft acceleration sensing [4,21,22,23] | MEMS accelerometer and gyroscope | High sensitivity, good signal quality, less impact on system operation, low cost | Needs lightweight system design and balanced installation |
| Components | Model | Power | Key parameters | Footprint |
|---|---|---|---|---|
| BLE SoC with MCU | nRF52832 | 1.7–3.6 V | 64 MHz Cortex-M4 | 6 × 6 mm QFN |
| MEMS accelerometer | ADXL357 | 2.25–3.6 V | 4 KHz sampling rate | 6 × 6 mm LCC |
| Flash memory | W25N01 | 2.7–3.6 V | 1 G Bytes | 8 × 6 mm WSON |
| Sampling Rate /Hz | FFT | Curve Fitting | ||
|---|---|---|---|---|
| Measured Frequency /Hz | Error | Measured Frequency /Hz | Error | |
| 20 | 20.019 | 0.09% | 20.019 | 0.09% |
| 25 | 25.146 | 0.58% | 25.053 | 0.21% |
| 30 | 30.029 | 0.10% | 30.083 | 0.28% |
| 35 | 35.054 | 0.15% | 35.054 | 0.15% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Z.; Liu, Y.; Chen, Y.; Cheng, Z.; Feng, G.; Zhang, H.; Gao, N.; Zhang, Z. Development of an On-Shaft Vibration Sensing Module for Machine Wearable Rotor Imbalance Monitoring. Electronics 2024, 13, 2466. https://doi.org/10.3390/electronics13132466
Meng Z, Liu Y, Chen Y, Cheng Z, Feng G, Zhang H, Gao N, Zhang Z. Development of an On-Shaft Vibration Sensing Module for Machine Wearable Rotor Imbalance Monitoring. Electronics. 2024; 13(13):2466. https://doi.org/10.3390/electronics13132466
Chicago/Turabian StyleMeng, Zhaozong, Yirou Liu, Yang Chen, Zhen Cheng, Guojin Feng, Hao Zhang, Nan Gao, and Zonghua Zhang. 2024. "Development of an On-Shaft Vibration Sensing Module for Machine Wearable Rotor Imbalance Monitoring" Electronics 13, no. 13: 2466. https://doi.org/10.3390/electronics13132466
APA StyleMeng, Z., Liu, Y., Chen, Y., Cheng, Z., Feng, G., Zhang, H., Gao, N., & Zhang, Z. (2024). Development of an On-Shaft Vibration Sensing Module for Machine Wearable Rotor Imbalance Monitoring. Electronics, 13(13), 2466. https://doi.org/10.3390/electronics13132466







