High-Capacity Multiple-Input Multiple-Output Communication for Internet-of-Things Applications Using 3D Steering Nolen Beamforming Array †
Abstract
:1. Introduction
- A 3D beamforming MIMO system is established based on the 2D Nolen matrix phased array, including modeling of the communication channel and Nolen matrix network. Then, its capability of enhancing channel capacity has been demonstrated.
- The advancements of the proposed 3 × 3 tunable Nolen matrix are more deeply discussed and compared to other works on tunable beamforming networks.
2. Design Theory and Analysis
2.1. Model of the Proposed 3D MIMO System
2.2. Design of 2D Tunable Nolen Matrix Beamforming
2.3. 2D Phased Array for Full-Coverage Beamforming
3. Experimental Results and Discussion
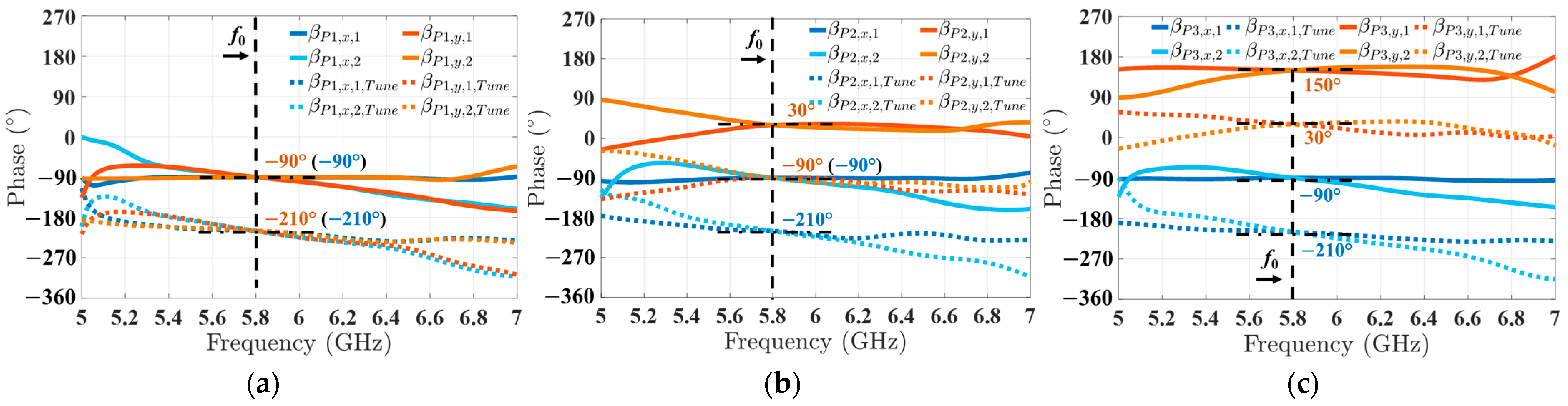
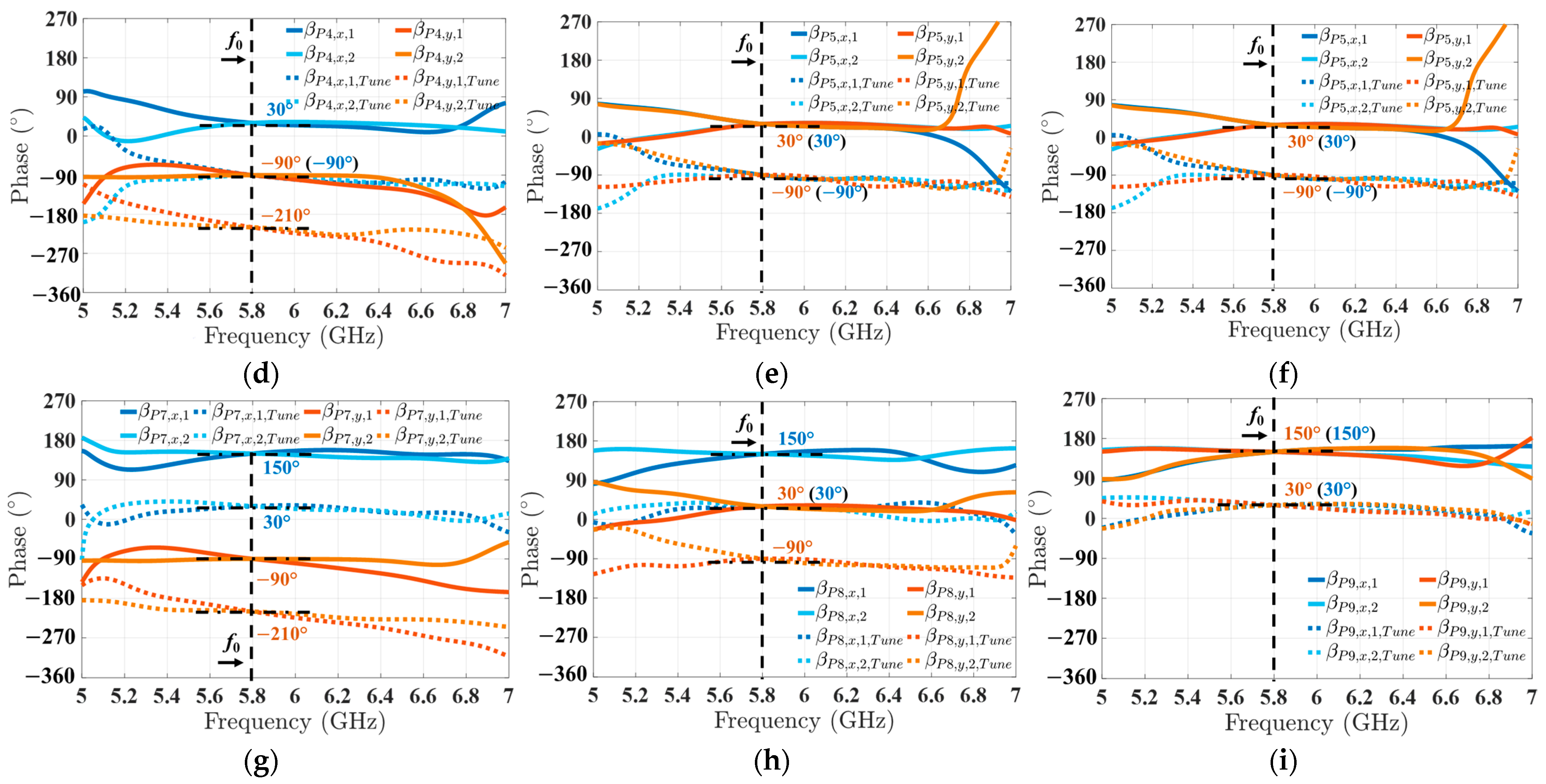
3.1. S Parameter of 3 × 3 Tunable Nolen Matrix
3.2. 3D Beamforming
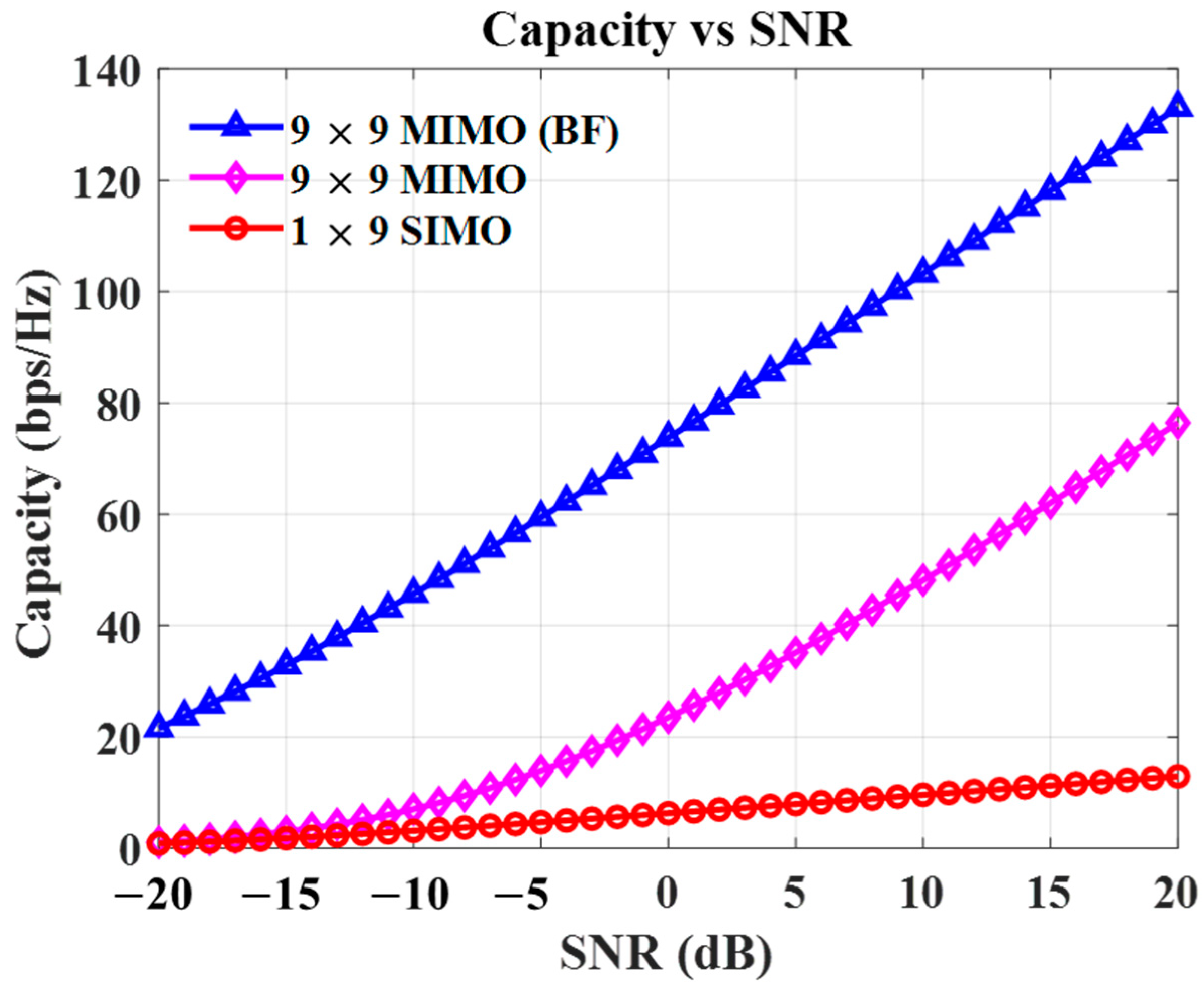
3.3. Evaluation of the Proposed Beamfomring MIMO Channel Capacity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grau, A.; Jafarkhani, H.; Flaviis, F.D.A. Reconfigurable Multiple-Input Multiple-Output Communication System. IEEE Trans. Wirel. Comms. 2008, 7, 1719–1733. [Google Scholar] [CrossRef]
- Agiwal, M.; Roy, A.; Saxena, N. Next Generation 5G Wireless Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2016, 18, 1617–1655. [Google Scholar] [CrossRef]
- Xu, L.; Chen, J.; Liu, M.; Wang, X. Active Eavesdropping Detection Based on Large-Dimensional Random Matrix Theory for Massive MIMO-Enabled IoT. Electronics 2019, 8, 146. [Google Scholar] [CrossRef]
- Cui, S.; Farha, F.; Ning, H.; Zhou, Z.; Shi, F.; Daneshmand, M. A Survey on the Bottleneck Between Applications Exploding and User Requirements in IoT. IEEE Internet Things J. 2022, 9, 261–273. [Google Scholar] [CrossRef]
- Rana, A.; Taneja, A.; Saluja, N.; Rani, S.; Singh, A.; Alharithi, F.S.; Aldossary, S.M. Intelligent Network Solution for Improved Efficiency in 6G-Enabled Expanded IoT Network. Electronics 2022, 11, 2569. [Google Scholar] [CrossRef]
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; De Silva, P.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Lee, A.; Kim, S.H.; Lee, D.M.; Kim, J.H.; Jang, T.H. The Generalization of Stage-Reduced STPS for Low-Loss Unequal 1 × 4 Phased Array Architecture for 5G IoT Applications. IEEE Internet Things J. 2024, 11, 19978–19987. [Google Scholar] [CrossRef]
- Jenn, D.C.; Flokas, V. In-band Scattering from Arrays with Parallel Feed Networks. IEEE Trans. Antennas Propag. 1996, 44, 172–178. [Google Scholar] [CrossRef]
- Kang, L.; Li, H.; Wang, X.; Zhou, J.; Huang, J. Circular Polarization-Agile and Continuous Beam-Steerable Array Antenna using A Hybrid Design Approach. IEEE Trans. Antennas Propag. 2022, 70, 1541–1546. [Google Scholar] [CrossRef]
- Ren, D.; Choi, J.H.; Itoh, T. Series Feed Networks for Dualpolarized Frequency Scanning Phased Array Antenna Based on Composite Right/Left-Handed Transmission Line. IEEE Trans. Microw. Theory Tech. 2017, 65, 5133–5143. [Google Scholar] [CrossRef]
- Abdalla, M.; Phang, L.; Eleftheriades, G. A Planar Electronically Steerable Patch Array Using Tunable PRI/NRI Phase Shifters. IEEE Trans. Microw. Theory Tech. 2009, 57, 531–541. [Google Scholar] [CrossRef]
- Fonseca, N.J.G. Printed S-band 4 × 4 Nolen Matrix for Multiple Beam Antenna Applications. IEEE Trans. Antennas Propag. 2009, 57, 1673–1678. [Google Scholar] [CrossRef]
- Chen, P.; Hong, W.; Kuai, Z.; Xu, J. A Double Layer Substrate Integrated Waveguide Blass Matrix for Beamforming Applications. IEEE Microw. Wireless Compon. Lett. 2009, 19, 374–376. [Google Scholar] [CrossRef]
- Grau, A.; Romeu, J.; Blanch, S.; Jofre, L.; De Flaviis, F. Optimization of Linear Multielement Antennas for Selection Combining by Means of a Butler Matrix in Different MIMO Environments. IEEE Trans. Antennas Propag. 2006, 54, 3251–3264. [Google Scholar] [CrossRef]
- Cetinoneri, B.; Atesal, Y.A.; Rebeiz, G.M. An 8 × 8 Butler matrix in 0.13-μm CMOS for 5–6 GHz Multibeam Applications. IEEE Trans. Microw. Theory Tech. 2011, 59, 295–301. [Google Scholar] [CrossRef]
- Shao, Q.; Chen, F.C.; Chu, Q.X.; Lancaster, M.J. Novel Filtering 180° Hybrid Coupler and its Application to 2 × 4 Filtering Butler Matrix. IEEE Trans. Microw. Theory Tech. 2018, 66, 3288–3296. [Google Scholar] [CrossRef]
- Chang, C.; Lee, R.; Shih, T. Design of a Beam Switching/Steering Butler Matrix for Phased Array System. IEEE Trans. Antennas Propag. 2010, 58, 367–374. [Google Scholar] [CrossRef]
- Chu, H.; Hoang, T.; Ji, K.; Ma, T. A Phase Distribution Network Using 2 × 4 Butler Matrix for Linear/Planar Beam-Scanning Arrays. IEEE Access 2021, 9, 133438–133448. [Google Scholar] [CrossRef]
- Ren, H.; Zhang, H.; Jin, Y.; Gu, Y.; Arigong, B. A Novel 2-D 3 × 3 Nolen Matrix for 2-D Beamforming Applications. IEEE Trans. Microw. Theory Tech. 2019, 67, 4622–4631. [Google Scholar] [CrossRef]
- Zhang, H.; Arigong, B. Full 3D Coverage Beamforming Phased Array with Reduced Phase Shifters and Control 2D Tunable 3 × 3 Nolen Matrix. In Proceedings of the IEEE International Symposium on Phased Array Systems & Technology, Waltham, MA, USA, 11–14 October 2022; pp. 1–6. [Google Scholar]
- Zhou, M.; Shao, J.; Arigong, B.; Ren, H.; Zhou, R.; Zhang, H. A Varactor Based 90° Directional Coupler with Tunable Coupling Ratios and Reconfigurable Responses. IEEE Trans. Microw. Theory Tech. 2014, 62, 416–421. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, M.; Gu, Y.; Arigong, B. A Tunable Transmission Line with Controllable Phase Shifting and Characteristic Impedance. IEEE Trans. Circuits Syst. II Exp. Briefs 2019, 67, 1720–1724. [Google Scholar] [CrossRef]

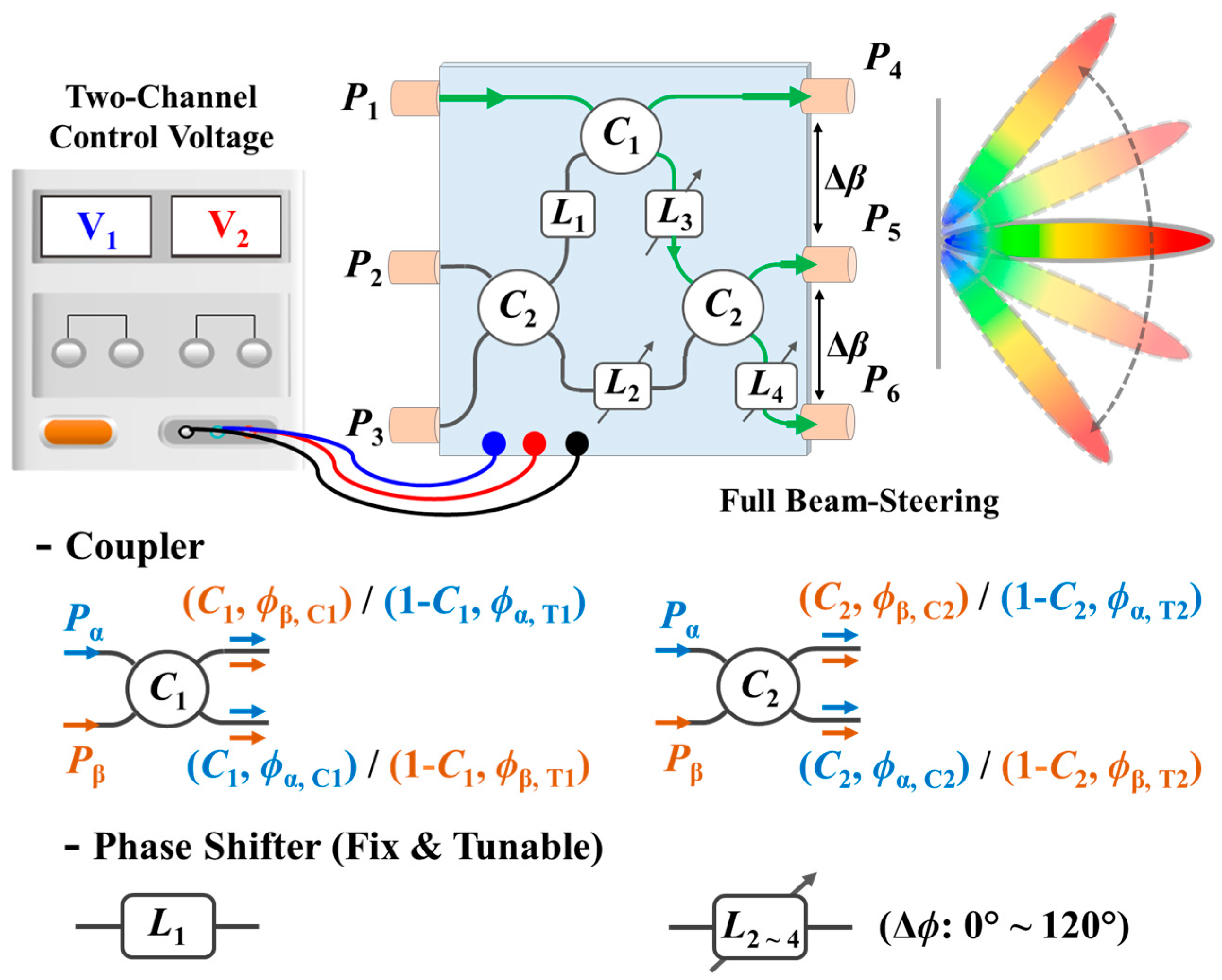


| Phase Differences in 3 × 3 Nolen Matrix | Example 1 (r = 0) | Example 2 (r = 0.5) |
|---|---|---|
| Δϕ1 = φ1,n − φ1,n−1 | 0° | +90° |
| Δϕ2 = φ2,n − φ2,n−1 | +120° | +30 |
| Δϕ3 = φ3,n − φ3,n−1 | −120° | −150° |
| Port Excitation | Progressive Phase (βx, βy) | Radiation Sector |
|---|---|---|
| 1 | (−90°, −90°) | Sec. 1 |
| 2 | (−90°, 30°) | Sec. 2 |
| 3 | (−90°, 150°) | Sec. 3 |
| 4 | (30°, −90°) | Sec. 4 |
| 5 | (30°, 30°) | Sec. 5 |
| 6 | (30°, 150°) | Sec. 6 |
| 7 | (150°, −90°) | Sec. 7 |
| 8 | (150°, 30°) | Sec. 8 |
| 9 | (150°, 150°) | Sec. 9 |
| [7] | [9] | [17] | [18] | This work | |
|---|---|---|---|---|---|
| Antenna Feed Type | Parallel | Parallel | Butler matrix | Butler matrix | Nolen matrix |
| Components Integration | Phase shifter, power divider, and amplifier | Divider, lumped element, and phase shifter | Coupler, power divider, and phase shifter | Coupler, crossover, and phase shifter | Coupler and phase shifter |
| MIMO Scale | 4 × 4 | N.A. | 4 × 4 | 4 × 4 | 9 × 9 |
| Scanning Dimension | 2D | 2D | 2D | 2D | 3D |
| Frequency (GHz) | 28 | 2.5 | 2.45 | 2.4 | 5.8 |
| Phase Shifters Number | 4 | 4 | 8 | 6 | 3 |
| Shifting Type | Switching | Continuous | Switching | Continuous | Continuous |
| Phase Shifting (°) | 180 | 90 | 142 | 360 | 120 |
| Progressive Phase (°) | 360 | 360 | 324 | 360 | 360 |
| DC Control Units | 4 | 7 | 8 | 6 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yan, H.; Liu, P.; Pour, S.Z.; Arigong, B. High-Capacity Multiple-Input Multiple-Output Communication for Internet-of-Things Applications Using 3D Steering Nolen Beamforming Array. Electronics 2024, 13, 2452. https://doi.org/10.3390/electronics13132452
Zhang H, Yan H, Liu P, Pour SZ, Arigong B. High-Capacity Multiple-Input Multiple-Output Communication for Internet-of-Things Applications Using 3D Steering Nolen Beamforming Array. Electronics. 2024; 13(13):2452. https://doi.org/10.3390/electronics13132452
Chicago/Turabian StyleZhang, Hanxiang, Hao Yan, Powei Liu, Saeed Zolfaghary Pour, and Bayaner Arigong. 2024. "High-Capacity Multiple-Input Multiple-Output Communication for Internet-of-Things Applications Using 3D Steering Nolen Beamforming Array" Electronics 13, no. 13: 2452. https://doi.org/10.3390/electronics13132452
APA StyleZhang, H., Yan, H., Liu, P., Pour, S. Z., & Arigong, B. (2024). High-Capacity Multiple-Input Multiple-Output Communication for Internet-of-Things Applications Using 3D Steering Nolen Beamforming Array. Electronics, 13(13), 2452. https://doi.org/10.3390/electronics13132452







