1. Introduction
A wireless sensor network (WSN) is a sophisticated high-tech technology that employs wireless sensor devices to detect environmental data within a given environment. The data collected by these devices are then integrated in real time to form a network connection. This represents one of the most significant technical forms of the Internet of Things. This technology offers substantial support for applications such as target tracking.
Target tracking represents a significant application field and a highly active research area within the domain of wireless sensor networks. In scenarios such as traffic monitoring and war detection, target tracking technology plays a pivotal role. The placement of the target in an environment equipped with wireless sensors enables the real-time collection of data on the target’s movement. These data can then be combined with the control of the tracking system to estimate the position of the tracked target in real time, thereby achieving accurate tracking.
In order to ascertain the location of mobile nodes within a wireless sensor network, the most straightforward approach would be to equip each node with a Global Positioning System (GPS) or a China’s Beidou Navigation Satellite System (BDS) module. However, this appears to be an impractical project due to considerations of cost, limitations on node energy, and the specific deployment environment required for GPS. Consequently, only a select number of nodes typically obtain their coordinates through the use of GPS or by being pre-deployed at specific locations. The remaining nodes calculate their distance from the anchor nodes based on their ranging or connectivity information. They then employ techniques such as maximum likelihood estimation or triangulation to determine their positions.
Generally speaking, wireless sensor network (WSN) tracking algorithms can be divided into algorithmic localization and filtering prediction. Localization algorithms are divided into two categories: distance-based and distance-free. In distance-measurement-based methods, the coordinates of two nodes are estimated by measuring the distance and angle between them. The RSSI (received signal strength indication), TOA (time of arrival) [
1], TDOA (time difference of arrival) [
2], and AOA (angle of arrival) [
3] are the most commonly used ranging techniques. These algorithms have high positioning accuracy but are limited by high measurement costs and power consumption and cannot be applied to some areas with harsh geographical environments. Algorithms that do not require distance measurement include APIT (approximate perfect point in tri-angulation test), DV, and Hop [
4], which rely on connectivity information between nodes to estimate the distance between them. Although these algorithms reduce costs and power consumption, positioning accuracy is often poor. However, these algorithms often have a large time delay when facing target tracking and cannot track a target for a long time. As such, filtering algorithms often become an important method for determining target tracking. Filtering algorithms are often divided into Kalman filtering and particle filtering algorithms, with particle filtering having significant advantages over Kalman filtering. It is not limited by linear and Gaussian noise distributions and can flexibly handle nonlinear and non-Gaussian problems, making it more widely applicable. The particle filter adopts a recursive structure algorithm, which has high real-time processing efficiency. The recursive process of Bayesian filtering is achieved through nonparametric Monte Carlo simulation, thereby more accurately estimating the target state and performing well in the field of target tracking [
5,
6].
Nevertheless, in wireless sensor networks (WSNs), there is a prevalent issue of particle poverty in particle filtering tracking, which can result in a considerable increase in tracking errors. Particle poverty is most commonly observed during the filtering process when the particle set is unable to fully represent the posterior distribution of the target state. Over time, some particles may gradually lose their representativeness toward the target state, resulting in a decrease in the diversity of the particle set. This can result in inaccuracy in the estimation of the target position by the particle filtering algorithm, with the potential for the target to be completely lost. Particle impoverishment not only affects the accuracy of target tracking but may also result in a reduction in tracking stability, thereby rendering it challenging for wireless sensor networks to maintain continuous and effective target tracking.
Although the particle filter has the potential to be an effective method for target tracking, it also has some notable limitations. For instance, the tracking accuracy of the particle filter may be diminished due to particle degradation. Concurrently, when confronted with intricate dynamic models, the sampling and updating process of particles may become inefficacious and time-consuming, which impinges upon the real-time performance of the algorithm. Furthermore, the particle filter is also relatively constrained in its ability to address the uncertainty of the observed data, which is susceptible to noise interference. The motivation for developing the golden-section gray wolf particle filter maneuvering target tracking algorithm was to address the aforementioned issues. The objective of the proposed algorithm is to optimize the particle sampling and updating process, reduce particle degradation, and improve tracking accuracy and stability. This has been achieved by combining the advantages of the golden-section search and gray wolf optimization algorithms. Concurrently, the algorithm is capable of more effectively addressing the uncertainty of observed data, enhancing resilience to noise interference, and improving the efficiency of the algorithm’s operation while maintaining the tracking performance necessary for real-time applications.
The particle filter algorithm is based on the Monte Carlo method, which necessitates a significant number of particles to achieve the desired estimation accuracy; the greater the number of particles, the greater the time complexity of the algorithm. In order to maintain local diversity during the process of particle swarm optimization, this paper proposes an improvement to the particle filtering algorithm. The proposed improvement is designed to address the issue of particle impoverishment and to resolve the defect of particle degradation.
There are various development directions in the field of modern particle filtering, among which the swarm intelligent optimization particle filtering algorithm is a relatively new development direction. The main idea of the swarm intelligent particle filter method is to carry out repeated iterative optimization of the particle distribution, and low-weight particles in the particle swarm do not have the problem of abandonment, thus increasing the diversity of the particle iterative process and fundamentally solving the problem of particle impoverishment. Evolutionary problems and particle filters essentially obtain optimal solutions through an iterative process of evaluation, selection, and updating [
6,
7,
8,
9]. Therefore, many researchers have used evolutionary methods to solve particle filter problems. Jie Cao [
10] and others proposed to combine the weighted dithering firefly algorithm and incomplete resampling to improve particle filtering and alleviate the problems of particle degradation and diversity exhaustion. However, the firefly algorithm is extremely easy to fall into the local optimum during the iteration process, which will verify the efficiency of particle filtering, which is often non-negligible in maneuvering target tracking. Liu Haitao [
11] proposed an improved low-weight particle intelligent filtering (IPF) processing strategy based on a genetic algorithm to improve the filtering accuracy. While improving the filtering performance, low-weight particle intelligent filtering also faces the problem of underoptimization or overoptimization. Weigang Li et al. [
12] proposed a new particle filtering method based on the improved gray wolf algorithm to improve the estimation accuracy of particle filtering, which has poorer search accuracy than the gray wolf algorithm in this paper, and it is extremely easy for the ordinary gray wolf algorithm to fall into the local optimum of the optimization algorithm. Chen Zhimin [
13] proposed a new particle filtering algorithm based on the bat algorithm, which uses particles to represent individual bats and simulates the process of searching for prey by bat populations, thus improving the overall quality and distribution rationality of particles. Li Ji [
14] combined the Harris hawk optimization algorithm with the hunting strategy and proposed a population intelligent optimization particle filtering method (EHHOPF) that effectively improves the system state estimation accuracy and filtering stability. The scalability of these algorithms may be limited as the size and complexity of the system increases. This is mainly due to the fact that intelligent algorithms require more computational resources and time when dealing with large-scale problems. All of the above methods improve the performance of the particle filtering algorithm, but most of them control the number of iterations of the intelligent algorithm through empirical values, which can easily lead to underoptimization or overoptimization, resulting in a decrease in estimation accuracy.
This illustrates the comprehensive research conducted on the utilization of intelligent optimization algorithms to enhance particle filtering. Consequently, it is also possible to utilize intelligent optimization particle filtering for the purpose of maneuvering target tracking. Nevertheless, the necessity for a system that can run quickly is often a prerequisite for the successful implementation of a maneuvering target tracking system. Consequently, the algorithms in question should be both simple and accurate.
Particle filtering has been demonstrated to possess unique advantages in applications within the field of target tracking. As a state estimation method based on Monte Carlo sampling, particle filtering approximates the probability distribution of the target state by a set of particles with weights, thereby enabling it to deal with nonlinear and non-Gaussian state estimation problems in complex environments. In a target tracking task, the state of the target may change dynamically with time and environment. This may include the updating of parameters such as position, velocity, and acceleration. Particle filtering is capable of tracking and predicting the motion trajectory of the target in real time by continuously and iteratively updating the position and weight of the particles, thereby achieving the fast and accurate tracking of maneuvering targets. In the tracking of maneuvering targets, the motion state of the target may change rapidly, necessitating the tracking system to possess the capacity for rapid response and accurate prediction. Particle filtering, in conjunction with intelligent optimization algorithms, enables rapid convergence to the vicinity of the true value of the target state, thereby facilitating the real-time tracking and prediction of maneuvering targets through information interaction between particles and the optimization of the update strategy. The particle filtering method, when combined with an intelligent optimization algorithm, can enhance the accuracy and efficiency of target tracking. Furthermore, it can address the uncertainty factors present in complex environments, such as noise interference and target occlusion. This results in a more reliable and stable target tracking system.
The gray wolf optimization algorithm represents a simplified and more robust approach to optimization. In addition to its intuitive nature, this algorithm is also straightforward to implement in program code. In contrast to other algorithms, the program code is relatively concise and can be readily employed to address a range of optimization issues [
15]. Moreover, in contrast to some recently developed optimization algorithms, the gray wolf optimization algorithm has been employed in a diverse range of applications.
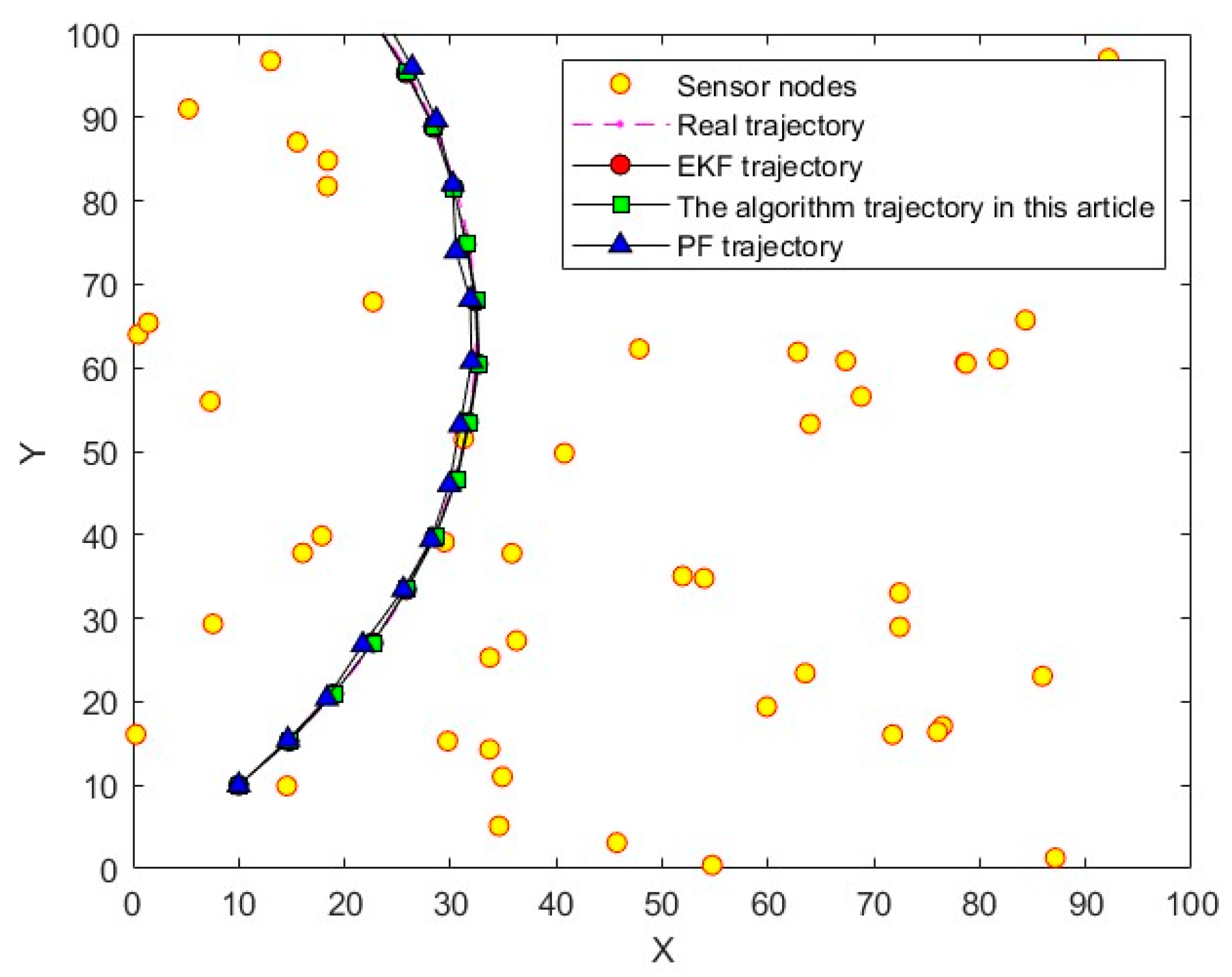
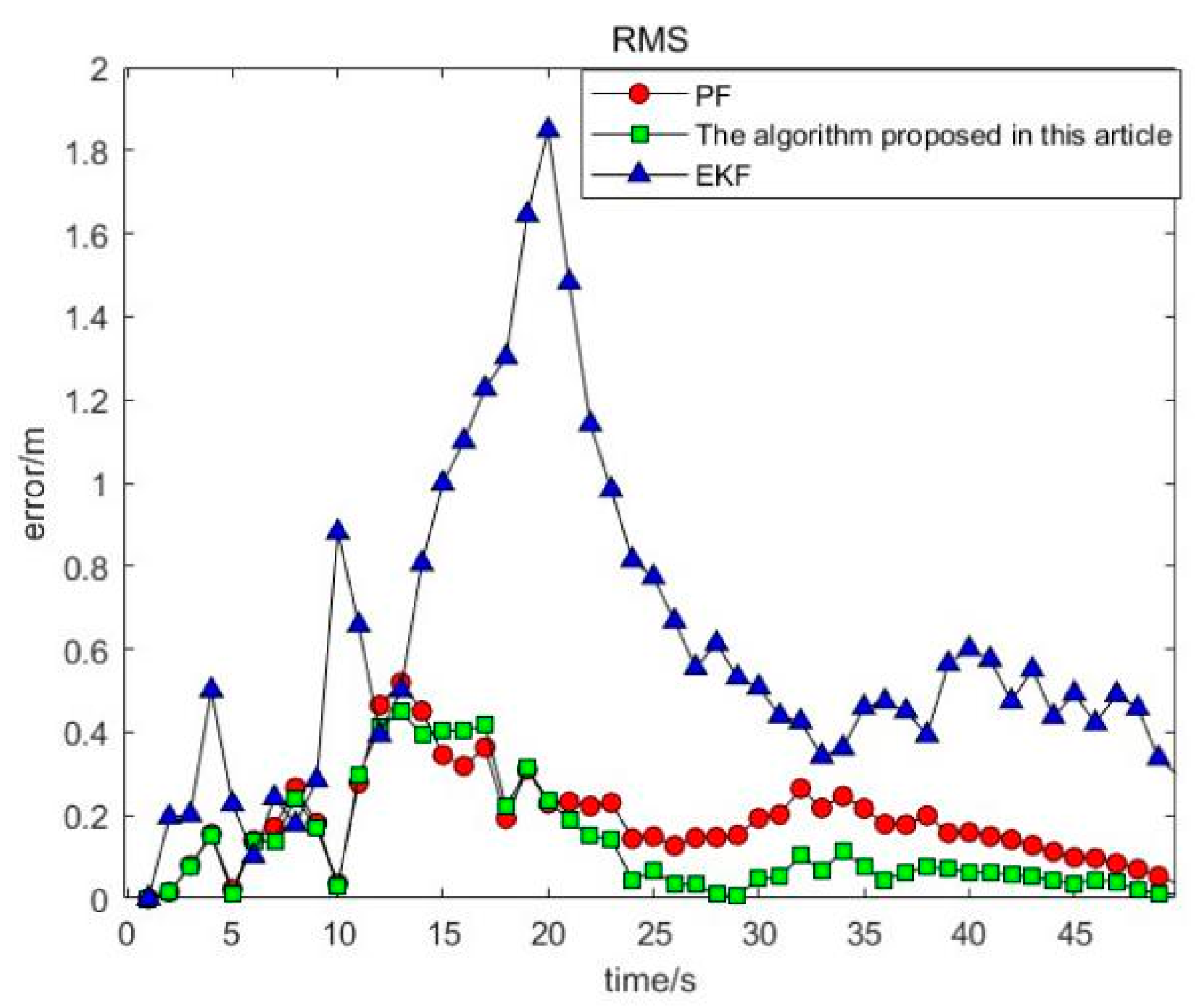
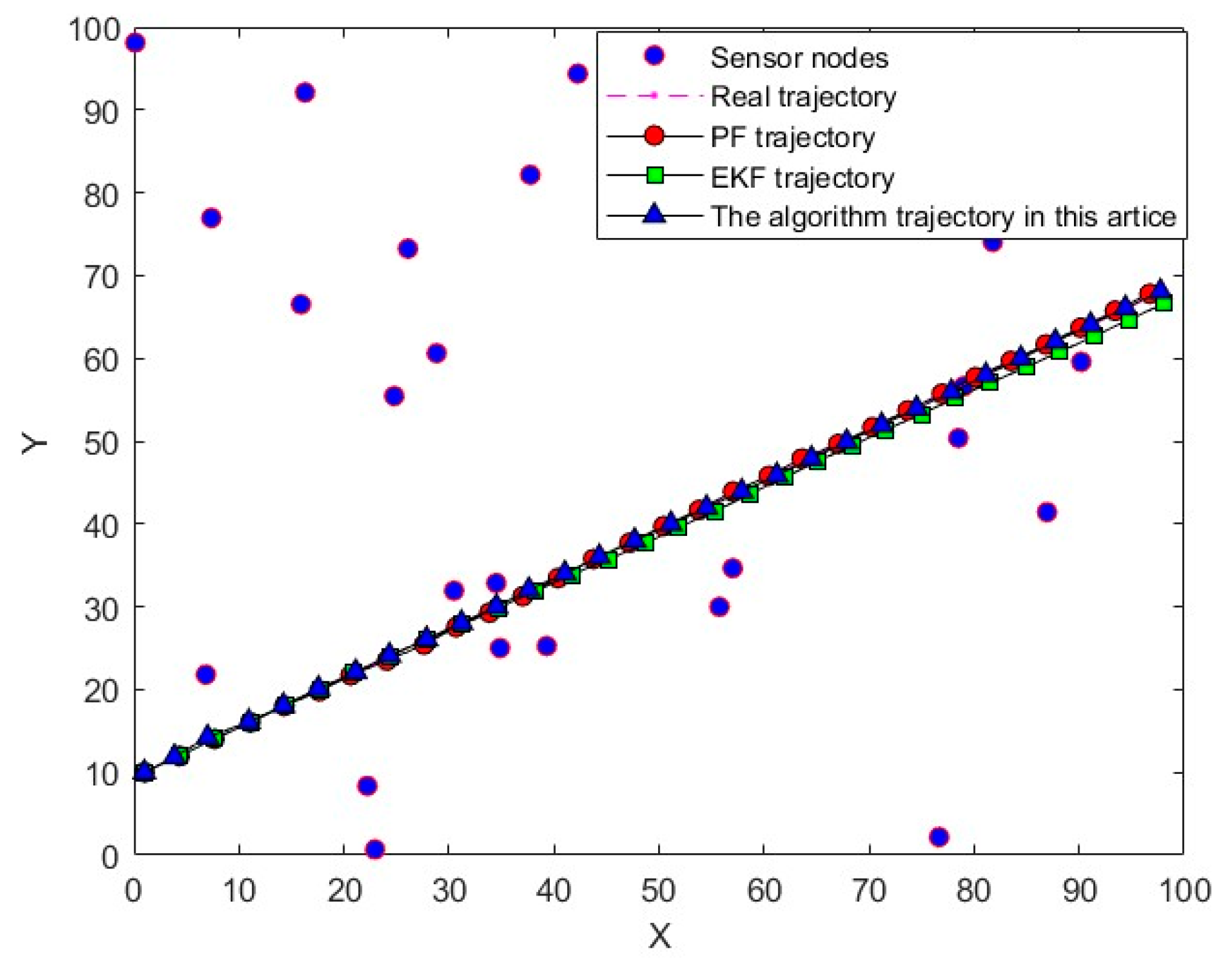
In this study, the gray wolf optimization algorithm, renowned for its simplicity, robustness, and ease of implementation, was further enhanced by integrating the golden ratio algorithm and introducing an adaptive adjustment strategy. This hybrid approach combines the global search capabilities of the gray wolf optimization algorithm with the local search precision of the golden ratio algorithm, thereby simulating the social behavior of gray wolves to strike a balance between global and local searches. To validate its performance, we designed experiments on benchmark optimization problems and applied the algorithm to real-world challenges, such as WSN maneuvering target tracking. The results demonstrate the effectiveness of this innovative fusion in efficiently solving complex optimization problems.
3. Translation of the Golden-Section Gray Wolf Filter Algorithm
In particle filtering, resampling represents a pivotal step employed to address the issue of particle degradation [
24]. The optimization of the resampling process through the utilization of the gray wolf optimization algorithm enables the selection of representative particles to be conducted in a more effective manner, thus avoiding oversampling or undersampling. Consequently, this results in an enhancement of the filtering performance and the accuracy of the filtering prediction.
3.1. Nonlinear Convergence Factor
The gray wolf algorithm exhibits robust optimization capabilities; however, the convergence factor of the gray wolf optimization algorithm declines linearly with the increase in iteration times. This may result in the algorithm becoming trapped in local optima. In the initial stages of the algorithm, the decay of the convergence factor is relatively low, which allows the wolf pack to move with a larger step size. This enables the algorithm to conduct a global search more effectively. As the number of iterations increases, the convergence factor declines, and the wolf pack’s movement step size diminishes. This enables a more precise local search, which ultimately leads to the identification of the optimal solution.
The convergence factor of the gray wolf algorithm can be enhanced in order to achieve a more balanced approach between global and local search, thereby enabling it to adapt more effectively to complex search processes [
25]. Consequently, the algorithm’s capacity to optimize is enhanced. In comparison to alternative methodologies, the nonlinear convergence factor is capable of more effectively balancing global and local search while maintaining the algorithm’s overall simplicity. Particle filtering is more computationally intensive than other filtering algorithms. Consequently, this paper employs a relatively simple nonlinear convergence factor, which not only markedly balances the search process but also significantly reduces the algorithmic complexity [
26,
27].
In the gray wolf particle filtering algorithm, the nonlinear convergence factor plays a decisive role. This factor balances the global and local search capabilities of the algorithm by nonlinearly adjusting the search behavior during iterations. At the beginning of the algorithm, the nonlinear convergence factor allows the algorithm to descend at a slower rate, which enhances the global search of the solution space and helps the algorithm discover potential optimal solution regions. As the iterations progress, the convergence factor decreases, speeding up the convergence of the algorithm and improving the search accuracy. In the gray wolf particle filtering algorithm, the nonlinear convergence factor is also used to adjust the state update process of the particle swarm and control the diffusion and convergence speed of the particles, thus maintaining the diversity of the particles while improving the convergence speed and accuracy of the algorithm. This flexible and effective adjustment strategy makes the gray wolf particle filtering algorithm show excellent performance.
The expression of the nonlinear convergence factor is as follows:
The term “max t” in the equation refers to the maximum number of iterations.
3.2. Fusion of Golden Sine
In the context of the gray wolf optimization algorithm, during the iteration process, the alpha wolf assumes the position with the highest fitness value, thereby leading the entire gray wolf population in hunting. However, there is a notable absence of communication between individual gray wolves. The incorporation of the golden sine can effectively compensate for this deficiency in the optimization algorithm. The steps of the golden sine are as follows:
Step 1: The fitness value of each discovered wolf individual is calculated, and they are sorted in descending order based on their fitness values.
Step 2: Subsequently, the updated positions of each discovered wolf individual are calculated in accordance with the mathematical formula of the golden sine function. The golden sine function enables the magnitude of the position update to be determined based on the current iteration count and the ranking of the discovered wolf individual.
Step 3: The positions of each discovered wolf individual are updated based on the calculated updated positions.
Step 4: Following the updating of the positions of all discovered wolf individuals, the fitness value of each individual must be recalculated, and they must be sorted in descending order based on their fitness values.
Step 5: The aforementioned steps are repeated until the predefined iteration count is reached or the stipulated stopping condition is met.
The introduction of the golden sine function facilitates enhanced communication between discovered wolf individuals, enabling the entire population to more effectively search for positions with higher fitness values. This, in turn, enhances the performance and effectiveness of the algorithm.
The expression of the golden sine function is as follows:
In the equation above, is the maximum number of iterations, is a random number between 0 and 1, and is the golden ratio.
3.3. Fusion of Golden-Section Gray Wolf Optimization Algorithm and Particle Filtering Algorithm
The golden-section gray wolf algorithm is a hybrid of the golden-section principle and the optimization strategies of the gray wolf algorithm. The algorithm is designed to identify optimal or satisfactory solutions to optimization problems through iterative search. This algorithm not only exhibits the characteristics of heuristic algorithms, which are constructed based on intuition or experience but also demonstrates enhanced global search capabilities and optimization performance through the integration of random strategies with local search.
The golden-section gray wolf algorithm represents an advanced optimization technique that combines the accuracy of the golden-section method with the group intelligence of the gray wolf optimization algorithm to form an efficient and powerful solution tool. The initial phase of the algorithm’s operation involves the gray wolf optimization algorithm rapidly identifying the region within the solution space of the problem that may contain the optimal solution, due to its exceptional global search capability. This is achieved by simulating the hunting behavior of gray wolf packs in nature, where information exchange and collaboration among individual gray wolves allows the algorithm to rapidly adapt to complex search environments.
Once the gray wolf algorithm has identified an approximate location for the optimal solution, the golden-section method employs its distinctive capabilities to refine the search process to a smaller area. The golden-section method determines the step size and range of the search by applying the golden-section ratio, thereby significantly enhancing the search accuracy of the algorithm while maintaining search efficiency. This degree of precision is of particular importance during the local search phase, as it enables the algorithm to identify the optimal or satisfactory solution to the problem with great accuracy.
In conclusion, the introduction of adaptive weight values has the potential to enhance the adaptability of global and local exploration, improve particle degeneration and local extremum problems, and increase the diversity of the particle swarm, thereby improving tracking performance. The algorithm displays enhanced adaptability and randomness. The repeated interaction of these two algorithms in iterative updates allows for improvement in particle diversity and the effective compression of particle scale while simultaneously enhancing computational efficiency and accuracy.
The particle filter resampling method of the golden-section gray wolf algorithm has the capacity to prevent particle degeneration and increase particle diversity while simultaneously stabilizing the scale of the particle set within a smaller range. Furthermore, it can enhance the computational accuracy of the particle filter algorithm and reduce the running time, thereby significantly enhancing real-time performance. To address the issue of particle degeneration in the particle filter algorithm, this paper employs the golden-section gray wolf optimization algorithm to replace the original resampling process within the particle filter algorithm. The implementation steps of the golden-section gray wolf particle filter are as follows:
Step 1: Set
j = 0 as the starting point for the algorithm and perform the initial sampling according to the distribution p(x0). The generated N particles may be utilized as the initial samples for the particle filtering algorithm, where x
k(
j) follows the importance density function as follows:
Step 2: Some particles are initialized in the particle filter algorithm and assigned initial weights in accordance with Equations (2) and (3).
Step 3: The golden-section gray wolf algorithm is used to identify particles. Firstly, the position of each particle in the search space must be determined in accordance with its weight. Subsequently, the positions of each particle are updated in accordance with the search strategy of the gray wolf algorithm.
(1) The initial particles for optimization are shown in Equation (8).
(2) In the gray wolf algorithm based on the golden section, particle samples are added. In accordance with the aforementioned steps, a novel set of particles is generated with each iteration update. Consequently, the outcome of each iteration is contingent upon the results of the previous iteration. The fitness function is employed to compute the fitness value of the filtering parameters generated in the current iteration. The fitness function employed in this algorithm is based on the golden-section gray wolf algorithm.
where
is the corresponding observation values, and R is noise variance.
(3) The golden-section gray wolf algorithm is employed in the resampling process of particle filtering.
(4) The importance weights of the particles are calculated once more, and the data are normalized.
(5) The mean of the particles is calculated following the application of the golden-section gray wolf particle filter.
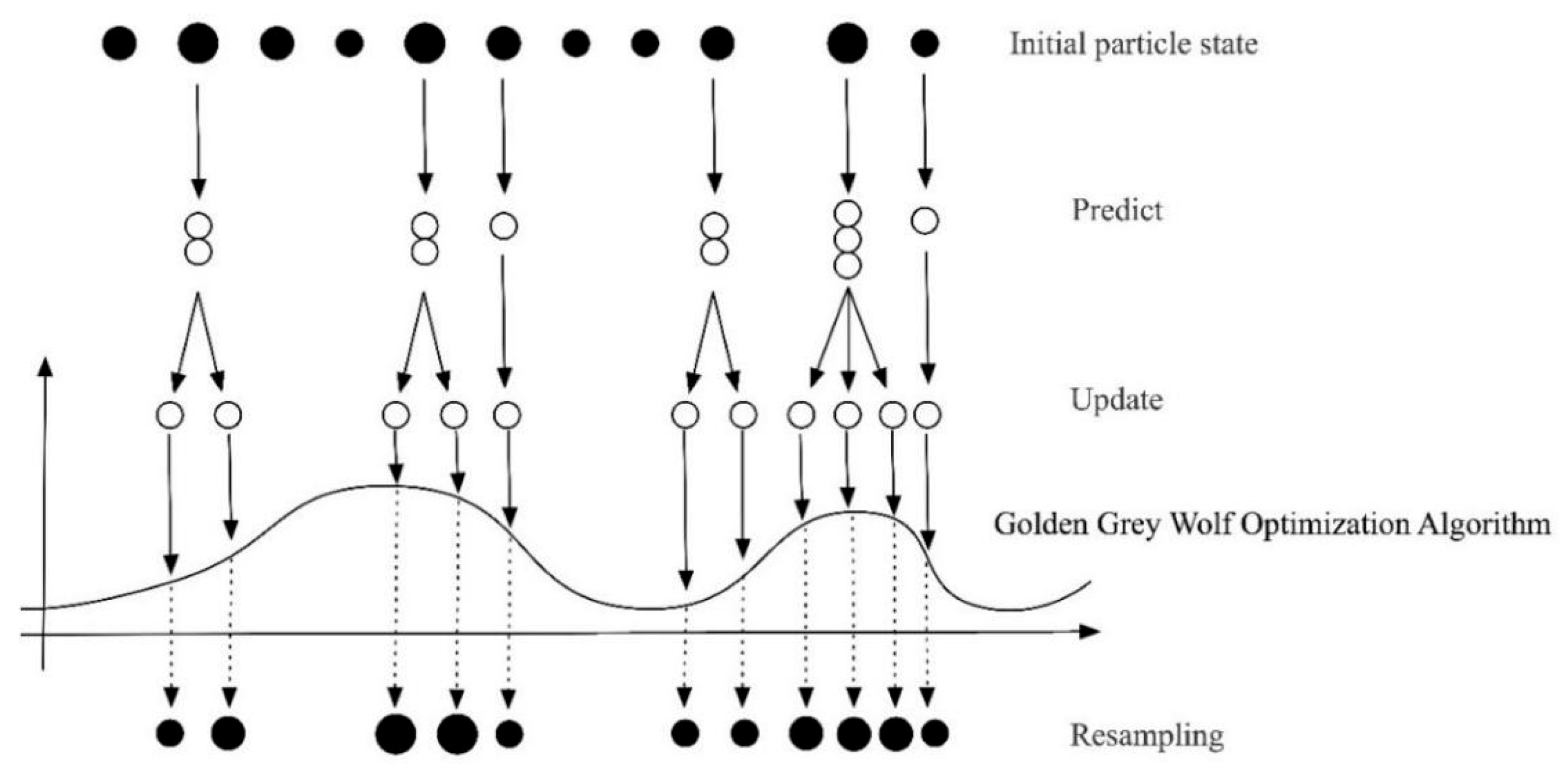
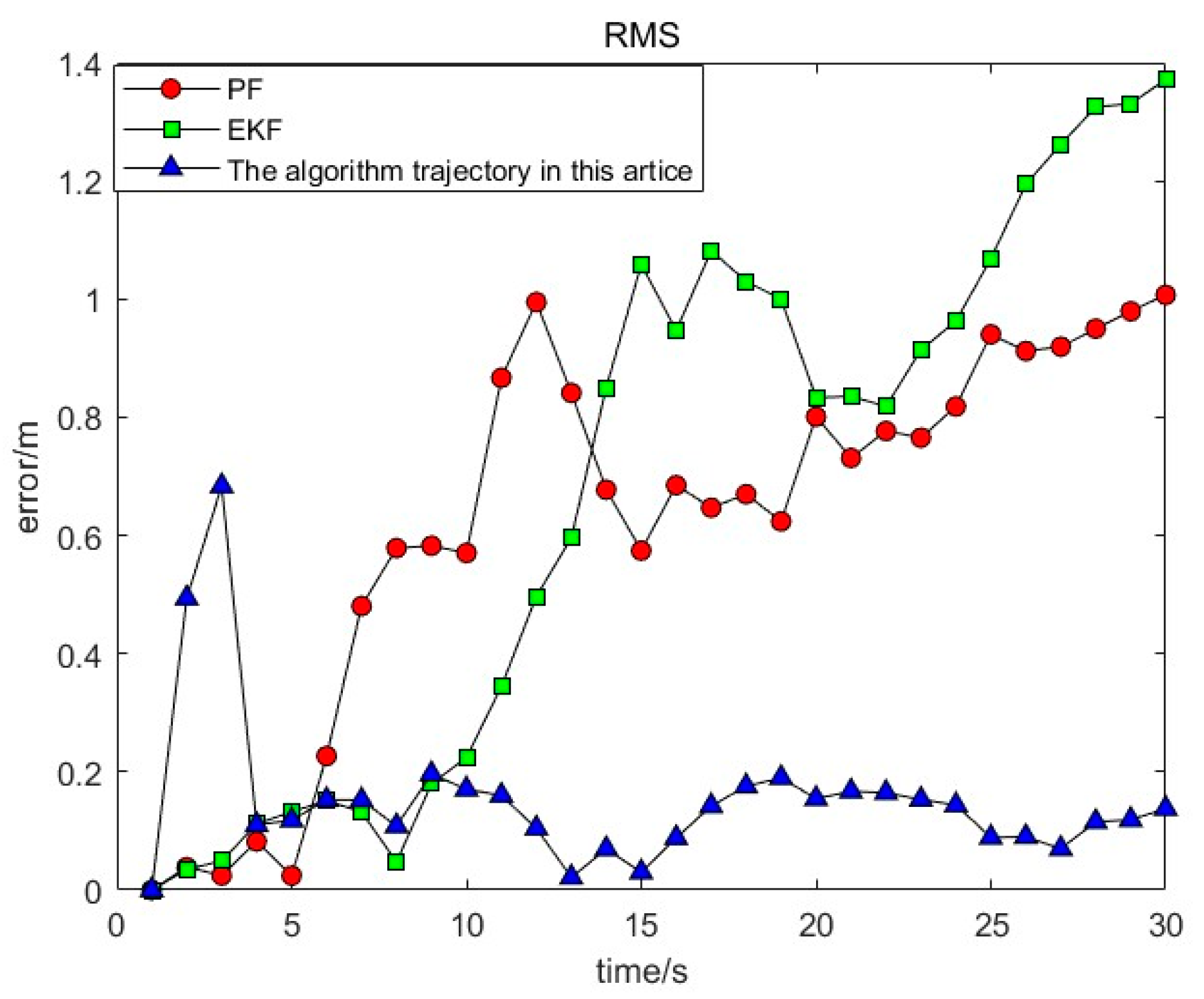
In terms of the convergence of the algorithm proposed in this article, each repetition of the algorithm generates the optimal position for the population, thereby enabling the random algorithm to achieve convergence. Following a number of iterations, the proposed algorithm improves the state of the population sequence of gray wolf positions, reaching the optimal state position. Consequently, the potential for an infinite search for the global optimum is eliminated. Consequently, the algorithm proposed in this article will converge to the global optimum. The schematic diagram of the golden-section gray wolf particle filter is presented below
Figure 1.