An FPGA-Accelerated CNN with Parallelized Sum Pooling for Onboard Realtime Routing in Dynamic Low-Orbit Satellite Networks

Abstract

This paper addresses the problem of real-time onboard routing for dynamic low earth orbit (LEO) satellite networks. It is difficult to apply general routing algorithms to dynamic LEO networks due to the frequent changes in satellite topology caused by the disconnection between moving satellites. Deep reinforcement learning (DRL) models trained by various dynamic networks can be considered. However, since the inference process with the DRL model requires too long a computation time due to multiple convolutional layer operations, it is not practical to apply to a real-time on-board computer (OBC) with limited computing resources. To solve the problem, this paper proposes a practical co-design method with heterogeneous processors to parallelize and accelerate a part of the multiple convolutional layer operations on a field-programmable gate array (FPGA). The proposed method was tested with a real heterogeneous processor-based OBC and showed that the proposed method was about 3.10 times faster than the conventional method while achieving the same routing results.

1. Introduction

Low earth orbit satellite networks (LEO-SN), which consist of tens to thousands of satellites located at relatively low altitudes (300 km to 1500 km), are used for a variety of applications, including communications, internet, and observation [1]. Compared to geostationary orbit satellites, LEO-SNs have the advantage of lower transmission losses and lower latency due to their low orbital rotation [2,3,4]. The most powerful aspect of LEO satellite networks, and a major topic of discussion among researchers, is whether they can achieve global coverage. In order to achieve global coverage in a low earth orbit satellite network, many satellites must be deployed, and accurate and fast routing techniques between LEO satellites are required. Therefore, in recent years, research on routing techniques for LEO satellite networks has been actively conducted.

Routing in a LEO satellite network is different from routing on the ground due to a number of considerations. First of all, low-orbit satellites travel at high speeds, so routing must be able to reflect the satellite topology [5,6,7,8,9].

Table 1. Routing algorithm research related to reinforcement learning.

Related Works	RL	Dynamic Environment	Link Disconnection	Parallelization
[10,11]	O	X	X	X
[12,13,14]	O	O	X	X
[15]	O	O	O	X
Proposed Method	O	O	O	O

summarizes the previous research on LEO satellite routing algorithms. LEO satellite routing algorithms have been actively studied; firstly, some research [10,11] applied reinforcement learning techniques to routing algorithms. In addition, some research [12,13,14] applied reinforcement learning techniques and included a dynamic environment. Next, one paper [15] included the previous topics but also included satellite link disconnection. The previous works described focus on LEO satellite routing algorithms, but they did not consider parallelization. Our proposed method is different in that it incorporates the previous topics and uses parallelization to accelerate the algorithm.

As discussed previously, LEO satellite networks require fast and accurate routing techniques that account for frequent changes in satellite topology, making it difficult to replicate conventional ground-based methods. In a real LEO satellite network, satellite positions change in real time, and there are link disconnects. In addition, in the space environment, each satellite needs to actively and adaptively schedule and map routes without relying on ground stations. Routing algorithms based on deep reinforcement learning can be a solution to these problems because they are highly adaptive to the real-time changing environment. However, most deep reinforcement learning-based algorithms are computationally intensive; so, it is necessary to reduce the computation time before it can be used for real-time LEO satellite network routing.

An additional problem is the constraints of the LEO satellite network environment. In the space environment, the computing resources used on the ground cannot be used, as such, due to the temporary alteration of bits by cosmic radiation (SEU), permanent damage to semiconductors (SEL), extreme environmental changes, and thermal differences due to the presence or absence of sunlight. Considering these problems, this paper assumes that the computing resources on a satellite are an on-board environment consisting of a central processing unit (CPU) and a field-programmable gate array (FPGA) instead of conventional ground resources. FPGAs are being studied in a variety of fields, because their reconfigurable architecture allows for development customized to user needs, offers the hardware advantage of parallel processing, and is resistant to heat and power consumption [16,17,18,19]. However, FPGAs also have a disadvantage in that the performance may be inferior to a CPU if the naive routing technique used in conventional computing resources is applied; so, careful adjustment is required [20].

In this paper, we propose a parallelized reinforcement learning-based routing algorithm for accurate and fast routing in a real-time LEO satellite network environment. The parallelism is achieved through a co-design of a CPU and an FPGA. The contributions of this paper are as follows.

-

A practical co-design method with heterogeneous processors to parallelize and accelerate the Dueling-DQN-based routing algorithm was proposed to solve the problem of real-time onboard routing for dynamic LEO satellite networks.

-

The sum pooling process in the Dueling-DQN was significantly accelerated on an FPGA by the proposed method, which can be applied to its other applications.

-

The proposed method was tested with a real heterogeneous processor-based OBC and showed significantly reduced computation time while achieving the same routing results as the conventional method.

The rest of the paper is organized as follows. Section 2 provides the problem description. In Section 3, the proposed method is described in detail. Section 4 shows the experimental results of the proposed method. Finally, Section 5 gives the conclusions.

2. Problem Description

2.1. Routing Problem in the LEO Network

The routing problem in LEO satellite networks refers to the series of problem of determining the path for each satellite to transmit data to the other satellites in a network consisting of multiple satellites. In this paper, Markov decision processes (MDP) are used to represent this problem mathematically, in particular, grid Markov decision processes [21]. The advantage of using a Grid MDP is that the underlying theory of reinforcement learning can be easily expressed mathematically. In addition, since the state space is organized in the form of a grid, the computation of state transitions and rewards is simpler than in a general MDP. In this paper, a deep reinforcement learning-based routing algorithm that can operate in the Grid MDP environment is used.

The Grid MDP is based on an assumption called the first-order Markov assumption, which states that the probability of a state at time n is only affected by the state at the previous time, n − 1. In a Grid MDP, the problem can be modeled in four terms: state, action, reward, and state transition probability. Here, state represents the location of each satellite and the data in the packet stored on that satellite, and action refers to the direction in which the satellite sends data. The reward is the score obtained for sending data in a certain direction, and the state transition probability represents the change in position due to packet transmission.

Using a reinforcement learning algorithm and applying it to a grid MDP eliminates the need to define a global state. In a conventional grid MDP environment, the state, actions, rewards, and state transition probabilities must be modeled in advance to be applied successfully; however, with reinforcement learning, they can be calculated and derived directly without any prior modeling [22,23]. In addition, information about states and rewards is collected in real time through learning, and based on this, the reinforcement learning algorithm helps determine the optimal routing path. Due to the characteristics of reinforcement learning, the initial performance is inferior, because the training data do not exist; however, the performance improves as the training is repeated. In summary, an MDP allows the learning processor to use dynamic programming algorithms such as value iteration or policy iteration to find the optimal value function or policy, and reinforcement learning allows the agent to gain direct experience through state observation and reward to learn the value function or policy. In conclusion, applying a reinforcement learning-based algorithm to low-orbit satellite network routing will require additional time due to the learning time required, but it will eliminate the modeling process of predefining the entire state. A Grid MDP can be used to find a robust policy, and reinforcement learning can be used to improve the results through learning, although the initial results may be unstable; so, it is suitable as a routing algorithm in this environment due to its high adaptability to the dynamically changing satellite network environment.

2.2. Dueling DQN-Based Reinforcement Learning Model

The existing DQN model is an algorithm that combines deep learning and reinforcement learning by constructing a Q-network through a CNN. The conventional DQN has a structure that takes the state as input and outputs a Q-function [24,25]. In this paper, we use Dueling DQN as a reinforcement learning technique, and Dueling DQN is a model that applies a dueling architecture that is more suitable for reinforcement learning instead of the existing neural network structure in the existing DQN model. Dueling DQN has the advantage of effective learning through state-value and noise-resistant learning [26]. The main feature of the Dueling DQN is that it explicitly separates the state-value and advantage functions and uses them to estimate the target. This allows the neural network to estimate the difference between state-value and advantage, which is the direct cause of its performance improvement over the DQN. The structure of a Dueling DQN is characterized by using the same inputs as a conventional DQN, but it adds a separate fully connected layer at the output that considers state-value and advantage. Dueling DQN is a structure that separates state-value and advantage and then combines them to output Q-values.

In dynamic LEO satellite networks and heterogeneous device environments, the computational complexity should be fully considered when using Dueling DQN-based routing algorithms. Since Dueling-DQN involves a complex computation process by a neural network, it is necessary to adjust the amount of computation or accelerate the computation by adjusting it appropriately.

2.3. Problem of On-Board Real-Time Inference

Reinforcement learning-based routing algorithms are effective for dynamic LEO. However, computing resource issues in the on-board environment and the heavy computation time of dueling DQNs are critical to the real-time performance of the algorithm. Reinforcement learning-based routing algorithms must provide optimal routing paths in response to the dynamic situation of the satellite network, which is updated periodically. The goal of this paper is to provide optimal routing paths while responding quickly to various factors such as bandwidth, latency, error rate, and satellite orbits.

However, the CNN-based training and inference process of reinforcement learning-based routing algorithms consumes an excessive amount of time, reducing real-time performance, and ultimately fails to find the optimal routing path. To solve this real-time problem, this paper proposes a heterogeneous device co-design-based inference parallelization method. In this paper, we perform heterogeneous device co-design using PYNQ-Z2, which has both a processing system (PS) that acts as a CPU and a programmable logic (PL) that has the advantages of a hardware FPGA. The dueling DQN-based LEO routing algorithm is basically performed on the PS, and the time-consuming inference process is accelerated in parallel on the PL. The proposed method can reduce the execution time of reinforcement learning and achieve real-time performance.

3. Proposed Method

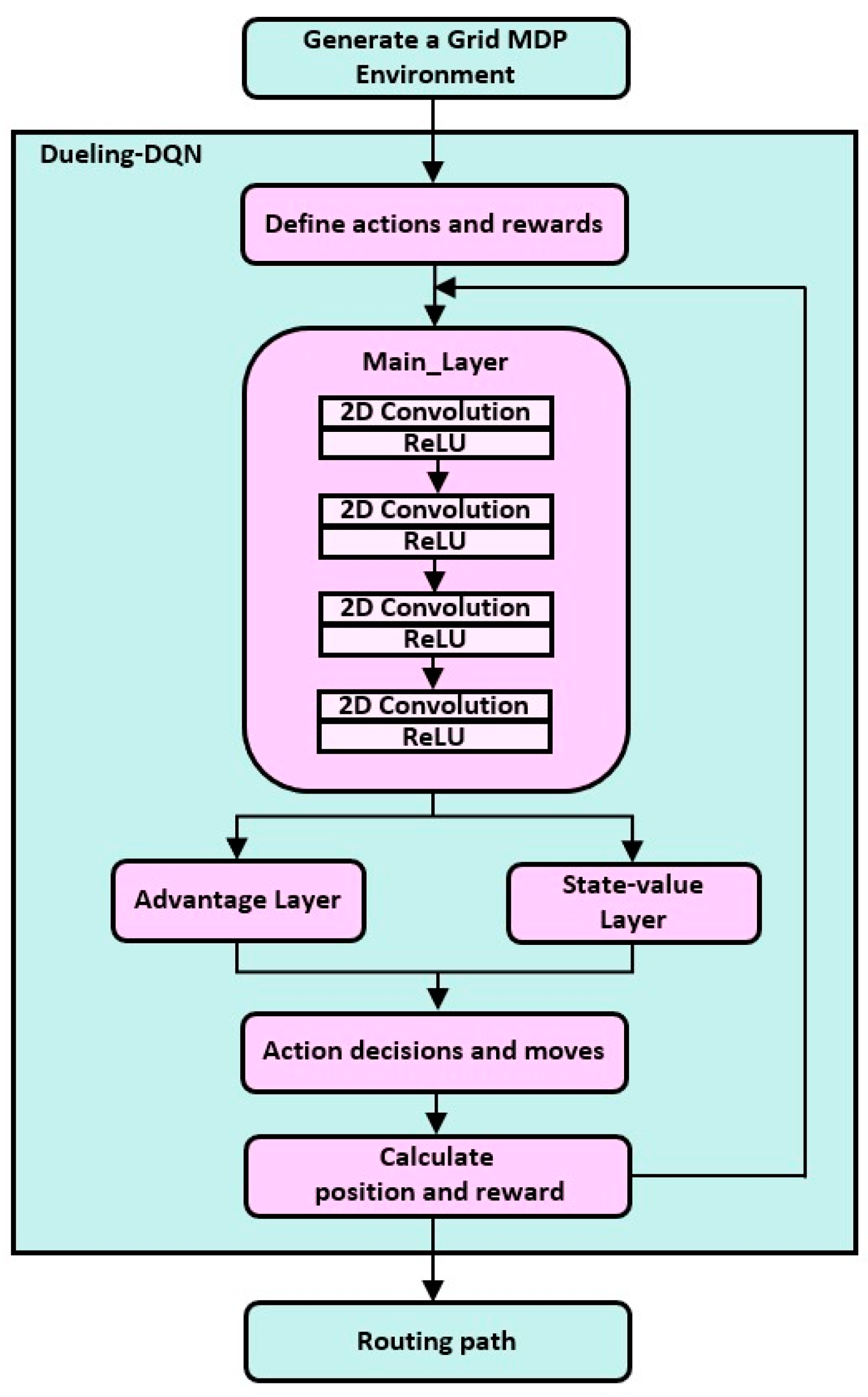
3.1. Overall Structure of the Dueling-DQN-Based Routing Algorithm

In this paper, the overall flow of the Dueling-DQN-based routing algorithm for LEO satellite networks is as follows. First, the grid environment generation, behavior, and reward are defined. Actions are defined as up, down, left, right, and stop from the current position of the agent. For rewards, −1 point is given for each time step, regardless of behavior, and 1 point is given for reaching the destination. If the agent collides with an obstacle (satellite link disconnection) while moving along the path, it will not be able to perform the action in the next time step, making the penalty larger.

With this predefinition, we proceed to the Dueling-DQN part. The method of Dueling-DQN used in this paper is as follows. First, 2D convolution and ReLU are performed four times through the main layer. This process takes up the most time in the algorithm and is the target of the parallelization described later. After this, the advantage layer and state-value layer perform linear operations. It determines the action that corresponds to the highest result, then performs the action and calculates the position and reward value after the action. The obtained position and reward values are then delivered to the Dueling-DQN as input states and iterated to find the optimal routing path. Figure 1 shows this process schematically.

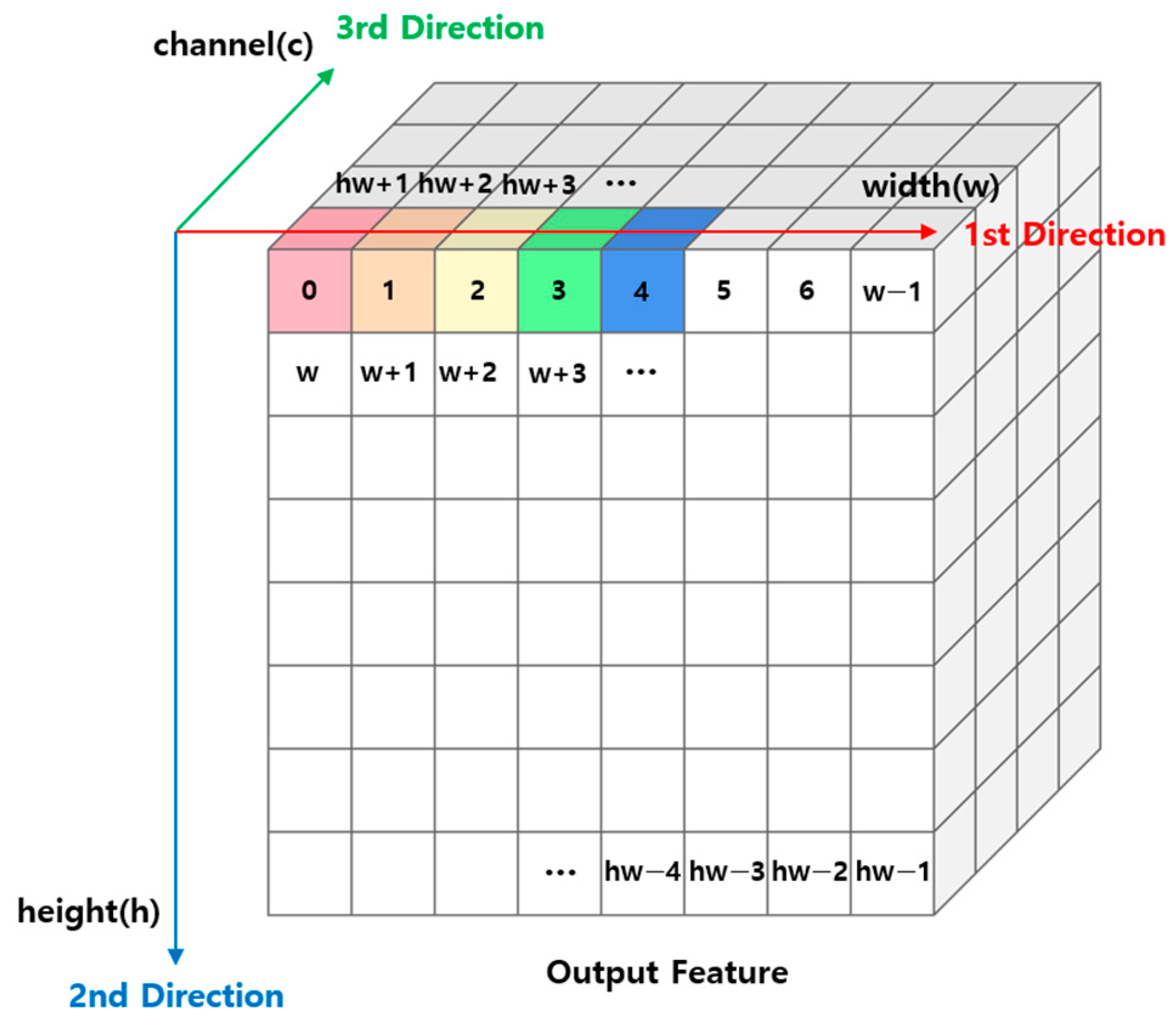
3.2. Dependency Analysis

As explained earlier, the part targeted for acceleration in this algorithm is the convolution operation in the main layer. The parts that proceed before the convolution operation are executed in PS, and the inputs required for the convolution operation are moved to PL for parallel operation and then moved back to PS. Algorithm 1 shows the flow of the operation with pseudo-code for the convolution operation. The Calculate in_idx and Calculate weight_idx of lines 8 and 9 are responsible for calculating the index for the current position in the convolutional input data matrix and the convolutional weight matrix. The key point to note here is line 10 in Algorithm 1. As shown, line 10 is where the accumulation sum operation is located. Since the operation of a CNN uses the pooling method of Sum pooling, there is no way to avoid the accumulation sum operation. However, the problem with this is that it introduces dependencies between loops. This structure, where the result of the previous loop affects the operation of the next loop, is not parallelizable because it is not possible to move to the next loop before the value of the previous loop is calculated. Parallelization in the parent loop is also limited because the operation that introduces the dependency is located in the innermost loop of the six-loop. The following sections describe how to overcome these loop dependencies.

Algorithm 1	The Conventional Sum Pooling Method
Input	conv_in[] conv_weight[], conv_bias[] input’s height, width, channel kernel size output’s height, width, channel
Output	conv_out[]
1.	for i = 0~output_channel
2.	for j = 0~output_width
3.	for k = 0~output_height
4.	float result = 0;
5.	for x = 0~input_channel
6.	for y = 0~kernel_size
7.	for z = 0~kernel_size
8.	Calculate in_idx
9.	Calculate weight_idx
10.	result += conv_in[in_idx] × conv_weight[weight_idx]
11.	end
12.	end
13.	end
14.	Calculate out_idx
15.	conv_out[out_idx] = result + conv_bias[i]
16.	If(conv_out[out_idx] <= 0)
17.	Conv_out[out_idx] = 0; //ReLU
18.	end
19.	end
20.	end
21.	end

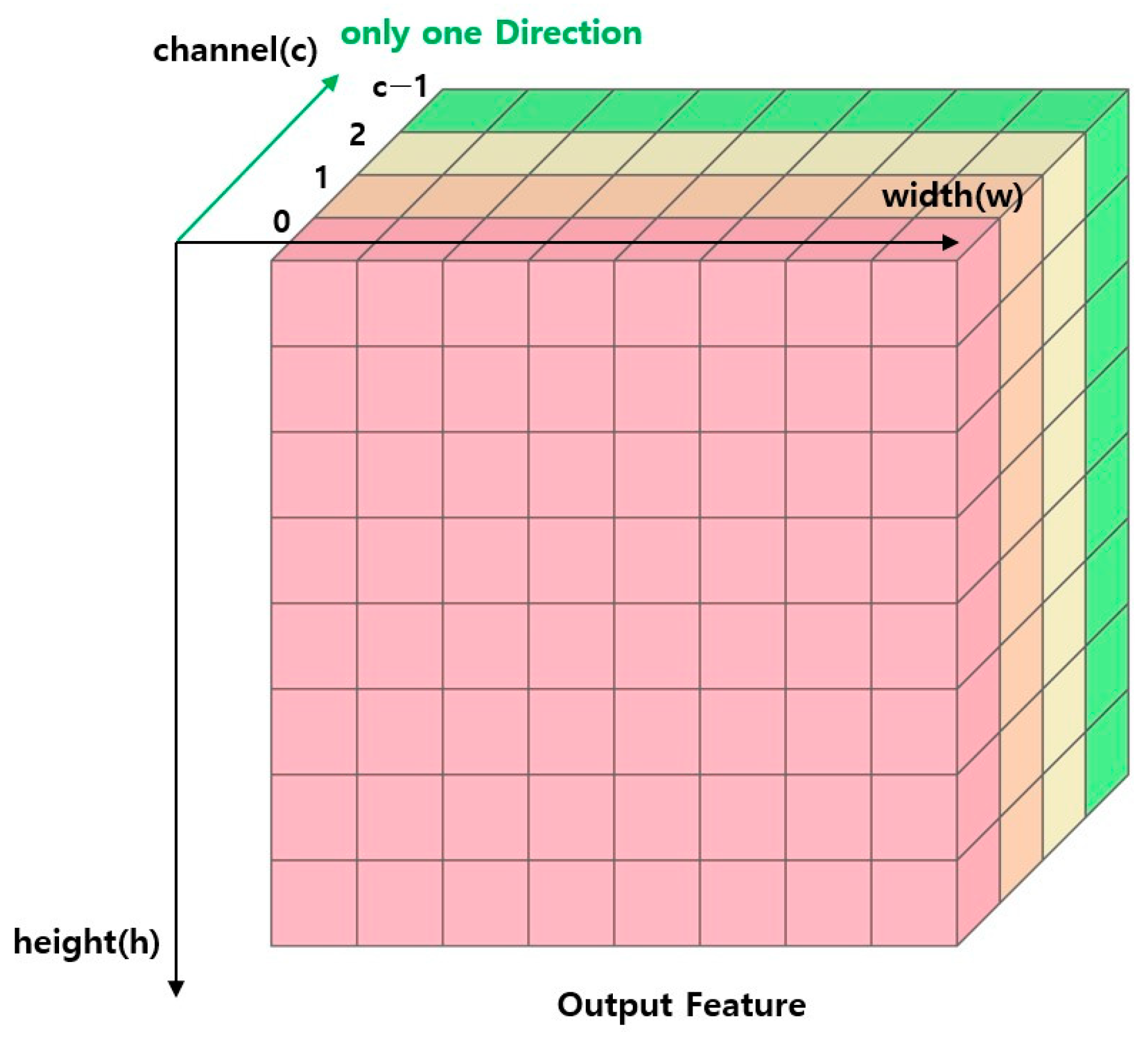
3.3. Parallelized Sum Pooling

In the previous subsection, we discussed the limitations of parallelizing CNNs due to the loop dependency of Sum-pooling. In this section, the process of parallelizing the operation by releasing this loop dependency is introduced. In this paper, a method is proposed to reconstruct the computational structure of the sum-pooling method of CNN to parallelize it. First, the sum-pooling operation of a typical CNN consists of moving a kernel of a predefined size over the input data by the height and width of the input, iterating over the number of channels, accumulating the obtained values, and determining a single feature of the output. As a result, the number of iterations of a single 2D Convolution operation $iter$ is calculated as follows:

$$iter=ou{t}_{channel}\times ou{t}_{width}\times ou{t}_{height}\times i{n}_{channel}\times kerne{l}_{size}^2$$

(1)

Figure 2 shows a schematic representation of the process and direction of the operation described above. The color change of the block means the direction of the operation. The iterative structure described above calculates one feature of the output and moves on to the next feature when the previous calculation is finished. In this paper, we propose a method to avoid loop dependency by calculating the value of all features belonging to a channel simultaneously based on one channel, rather than calculating one feature with a dependency on the output. Figure 3 shows a schematic representation of the sum-pooling method proposed in this paper.

In Figure 3, the direction of the operation is changed from the conventional Sum-pooling in Figure 2. Hear also the color change of the block means the direction of the operation. In the proposed method in Figure 3, the computation proceeds in the Channel direction so that the dependency can be ignored. This does not eliminate the data dependency, but it moves the loops with the data dependency away from each other, making it possible to ignore the dependency under specific conditions. The specific conditions are described in Section 3.4. As a result, this computational structure is a hardware-friendly computational processing structure that cannot be beneficial to CPUs with sequential processing but can be greatly beneficial to hardware FPGAs with parallel processing characteristics.

3.4. Buffer-Based Dependency Avoidance for Adaptive Pipelining

The implementation of the proposed method described in Section 3.3 is described in this part. In the previous section, it was mentioned that dependencies between loops in the Parallelized Sum pooling method are not eliminated but can be ignored under certain conditions. First, Algorithm 2 shows a pseudo-code that implements the structure described in Section 3.3 for the HLS tool. HLS is an abbreviation for High Level Synthesis. Verilog or VHDL languages are less productive in the hardware design process. Using higher abstraction-level languages, such as C/C++, has several advantages in terms of productivity. HLS is a tool that automatically generates RTL-level code just as a compiler compiles when C/C++ codes used for algorithmic technology, rather than Verilog/VHDL, which was traditionally used in hardware design. Parallelization techniques using HLS tools are already well researched due to their high productivity and portability [27]. The iterations for the output’s width and output’s height are moved to the lowest level, and a buffer equal to the size of the height multiplied by the width is placed under the top loop. The buffer in line 2 will serve as a buffer to store as many results as there are features in the output of one channel. Next, in Algorithm 2, the pipelining directive is placed on line 10, so it will attempt to pipeline lines 12 through 18. However, in this synthesis, the dependency on the accumulating sum in line 13 is determined to be valid, so pipelining does not proceed. Therefore, the directive in line 11 explicitly removes the dependency on the result. In this process, lines 12 through 18 are pipelined and can be parallelized.

Algorithm 2	The Proposed Parallelized Sum Pooling Method
Input	conv_in[] conv_weight[], conv_bias[] input’s height, width, channel kernel size output’s height, width, channel
Output	conv_out[]
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24.	for i = 0~output_channel  float result [output_width × output_height] = 0;  for x = 0~input_channel  for y = 0~kernel_size  for z = 0~kernel_size  Calculate weight_idx  float temp = conv_weight  for j = 0~output_width  for k = 0~output_height  #Pipeline II = 1  #ignore dependence variable = result  Calculate in_idx  result += conv_in[in_idx] × conv_weight[weight_idx]  Calculate out_idx  Calculate conv_out[out_idx]  If(conv_out[out_idx] <= 0)  Conv_out[out_idx] = 0; //ReLU  end  end end end end end end

For deep and complete pipelining, it is necessary to analyze the execution time of lines 12 to 18. If the latency of 12 to 18 exceeds the size of the buffer, deep and complete pipelining is not possible because the dependencies between the data become valid again. In this context, deep and complete pipelining means that the Initiation Interval is equal to 1. This condition is defined as follows:

$$C_{com}\le buffe{r}_{size}$$

(2)

In this application, the execution cycle Ccom for lines 12–18 is 14 clocks, which means that implementing a buffer of 14 clocks or more will allow for deep and complete pipelining.

4. Experimental Results

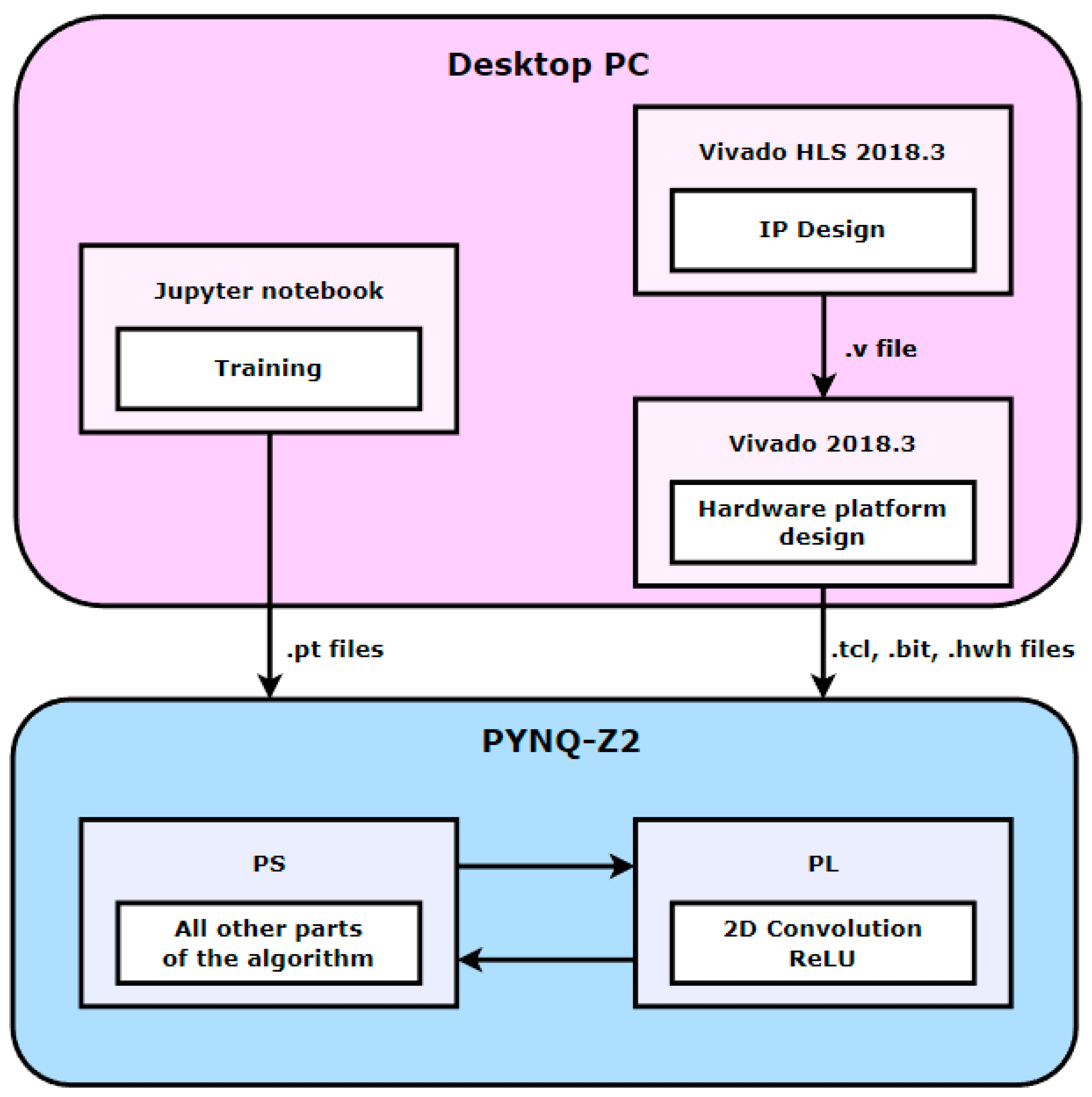
4.1. Experimental Setups

In this paper, the Dueling-DQN-based routing algorithm was evaluated in the following on-board environment. First, the training to obtain the .pt file containing the weight information was performed on a Jupyter notebook v7.0.8 in the Anaconda v24.3.0 virtual environment, and the training was performed on a desktop PC with i7-10700 and Nvidia Geforce RTX 3070. The model for training was a 15 × 15 grid map consisting of four channels: agent position, goal position, obstacles, and boundaries. The total number of training runs was 100, with a maximum number of steps per run of 300 and a batch size of 1024. In the convolution process, each kernel was set to 6 × 6, 4 × 4, 3 × 3, and 2 × 2, resulting in 15 × 15 × 4 inputs and 4 × 4 × 32 data outputs.

In addition, for the heterogeneous device co-design of CPU and FPGA, the Board of PYNQ-Z2, which has both PS and PL, was selected. The PYNQ-Z2 is based on the ZYNQ XC7z020-1CLG400C chipset, which includes a 650 MHz ARM Cortex-A9 dual-core processor and an Artix-7 level FPGA. Figure 4 shows the real experimental environment as configured. The FPGA development platform was Xilinx Vivado HLS 2018.3, Vivado 2018.3. First, the code for parallelization was configured in Vivado HLS 2018.3, and the .v file containing the IP information was extracted by synthesizing the configured code. The previously developed IP was then imported into Vivado 2018.3 to design the entire hardware platform. Finally, the .hwh, .tcl, and .bit files containing information about the hardware platform were extracted. PYNQ also provides various tools and libraries, of which we used the overlay library to develop through python. Figure 5 shows the development flow described above schematically.

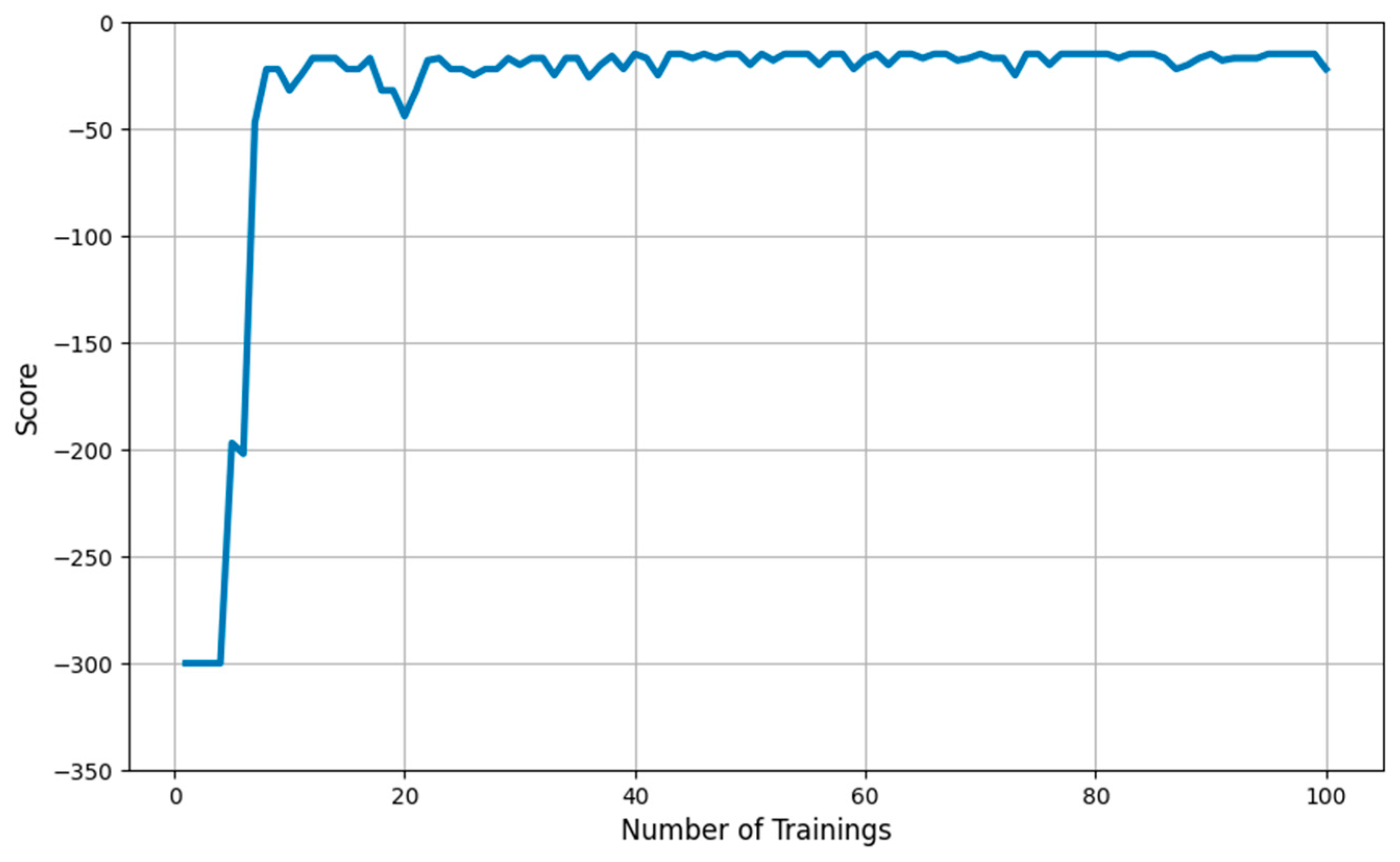
4.2. Training Results

The training results of Dueling-DQN in the environment described above are as follows. First, the starting position of the agent was fixed to (2,2), and the target position was fixed to (10,10). The training was executed a total of 100 times, and the training results are shown in Figure 6. From Figure 6, it is seen that at the beginning of the training, the agent repeatedly obtained the lowest score of −300, but after the initial score, it gradually found the path over time. In the experiment, at the 40th training, the best point (shortest path) was obtained for the first time and eventually converged to the best point.

Figure 7 shows these results in a grid environment, where blue represents the agent, red represents the goal location, black represents the obstacles (link disconnections), and the gray line represents the path obtained. In Figure 7b,d, there is a collision between the obstacle and the path; however, this can be ignored, as the path that was free of obstacles at the time of movement is marked with dynamically moving obstacle positions. As a result, the routing algorithm based on the Dueling-DQN obtained the shortest path.

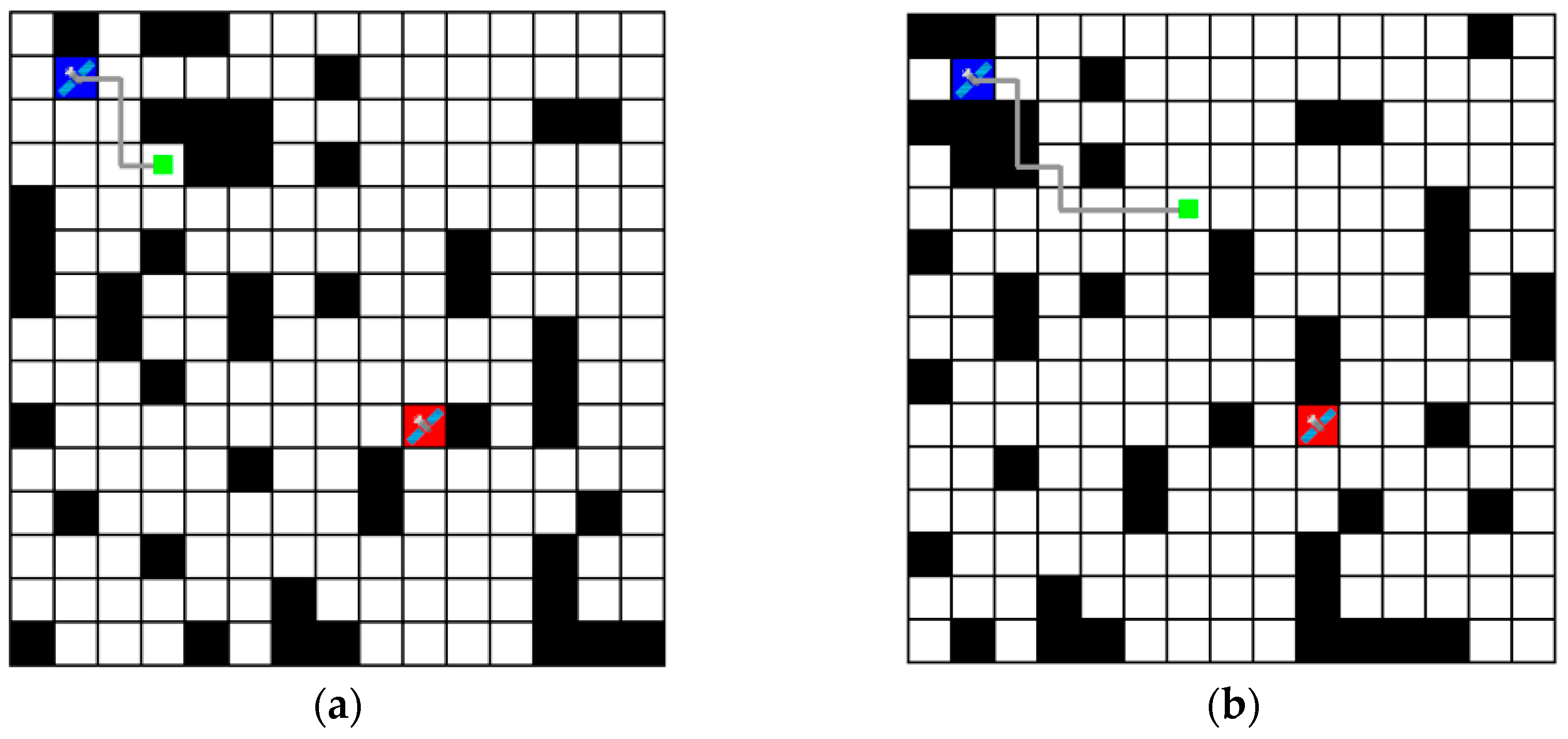
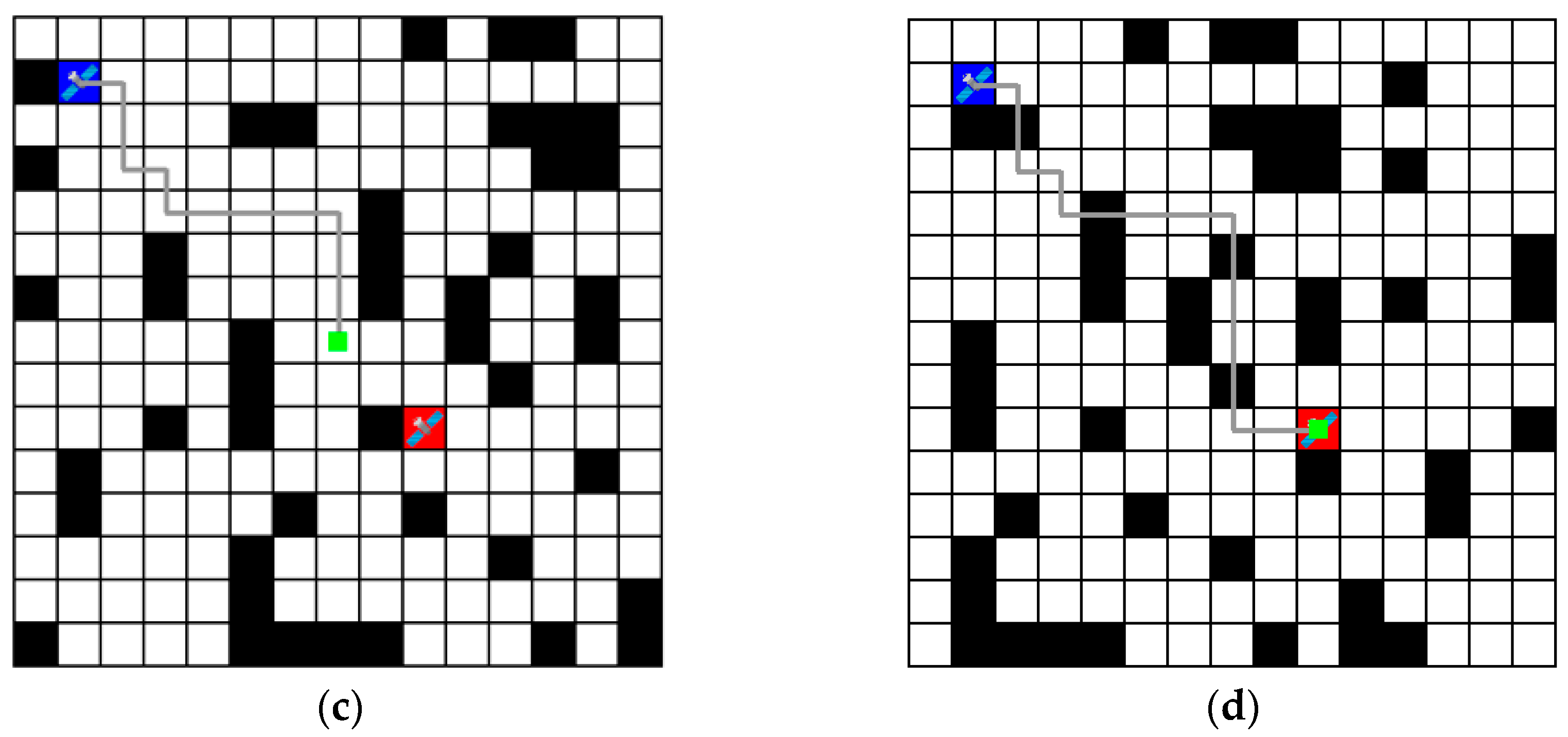
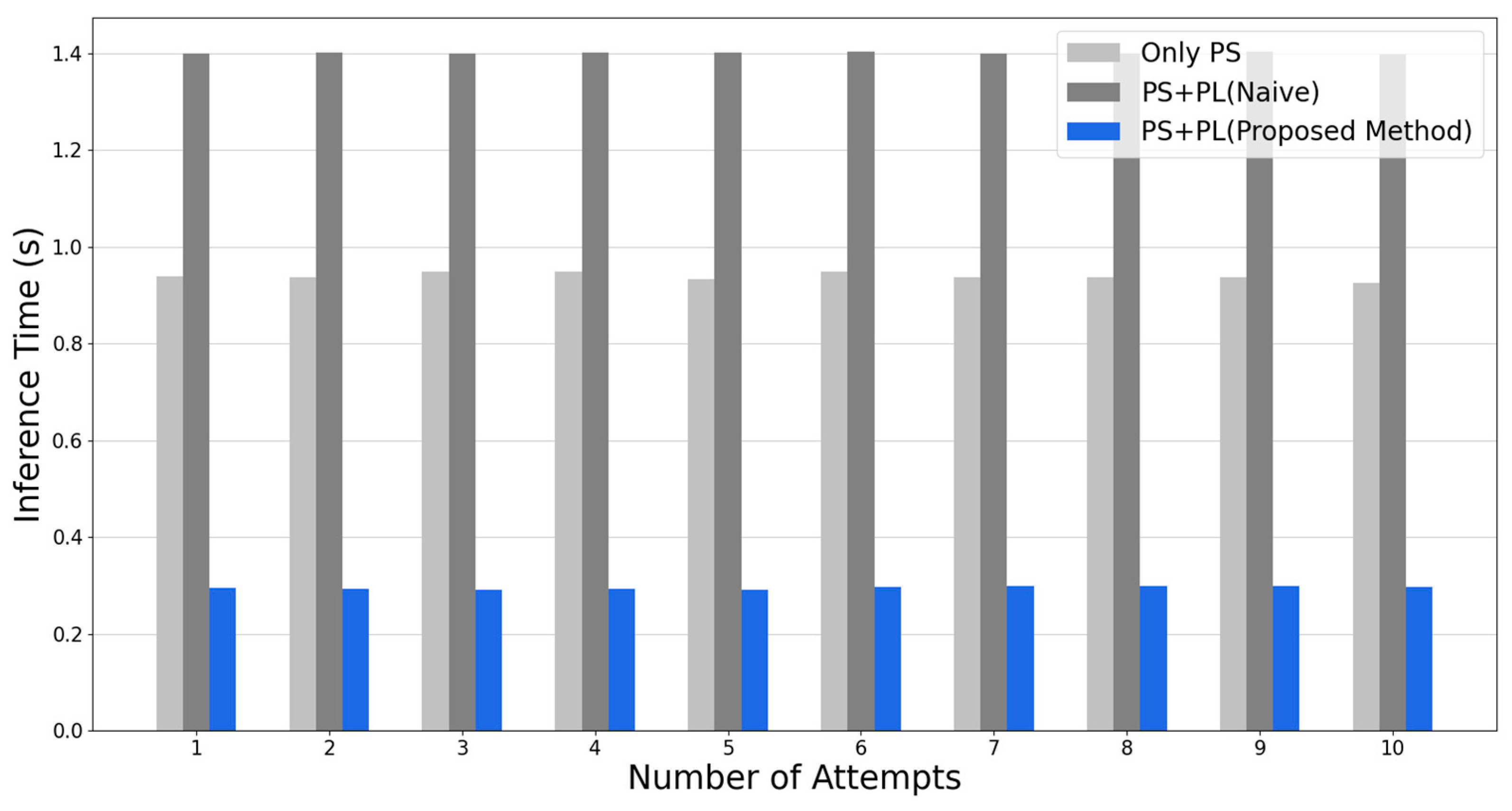
4.3. Inference Results

As described earlier, the results of inference in the actual on-board environment using the .pt file obtained from the training results and the .hwh, .bit, and .tcl files obtained from the hardware design are as follows. Figure 8 shows the results of inference using PYNQ-Z2, organized by execution time. The experiment was run 10 times for each method, and all results showed that the optimal routing path was found accurately. First, PYNQ-Z2 used only PS for inference, and the average execution time was 0.9396 s. Next, when PS and PL were co-designed, but the naive code was executed on PL without any parallelization process, the execution time was 1.4012 s on average. Finally, when the PS and PL were co-designed, and the 2D convolution operation was parallelized by applying the proposed method, the average execution time was 0.2991 s. When checking the experimental results, it can be seen that the naive method of using the same computation structure in the PL as in the PS without parallelization actually increased the execution time by about 1.51 times compared to the PS only. However, when the parallel 2D convolution operation was used following the proposed method, it was accelerated by about 3.10 times compared to the PS only and by about 4.68 times compared to the naive method. This shows that the proposed method improves real-time performance while maintaining accurate results.

Finally,

Table 2. Algorithm’s hardware resource usage.

	Available	Utilization (%)
		Naïve Method	Proposed Method
LUT	53,200	24.17	25.32
LUTRAM	17,400	4.22	4.76
FF	106,400	15.65	15.51
BRAM	140	22.50	25.36
DSP	220	9.09	9.09

summarizes the resources of the boards used to design the naive and proposed methods. Both the proposed method and naïve code required PS and PL to perform the work. The ZYNQ XC7z020-1CLG400C has a maximum hardware resource of LUT 53200, LUTRAM 17400, FF 106400, DSP 220, and BRAM 140. Table 2 shows that the proposed method utilized 25.32% of the total resources for LUTs, 4.76% for LUTRAM, 15.51% for FF, 25.36% for BRAM, and 9.09% for DSP, with a slight increase in the usage of the LUTs and BRAM compared to the naive code. However, since the proposed method significantly reduced the inference time, the results of almost the same or slight increase in resource usage compared to the naive code indicate that the proposed method is an efficient method.

5. Conclusions

This paper proposed a practical co-design method with heterogeneous processors to parallelize and accelerate a part of the multiple convolutional layer operations on an FPGA for onboard real-time routing in dynamic low-orbit satellite networks. Previous work has considered reinforcement learning, dynamic environments, and satellite link outages, but none has considered parallelization. This paper is different in that it includes the previous topics and proposes an FPGA-accelerated CNN with parallelized sum pooling for an onboard real-time routing method. In the sum-pooling structure of conventional CNNs, convolution and ReLU operations require excessive execution time, which is not suitable for the real-time requirements of dynamically changing low-orbit satellite network environments. The proposed method solved this problem by accelerating the algorithm through the co-design of CPU and FPGA, specifically by changing the computation structure of CNN. Experimental results with an OBC with heterogeneous processors including an FPGA showed that the proposed method was about 3.10 times faster than the conventional method while achieving the same routing results.